1
Изобретение относится к области вычислительной техники и может быть использовано для создания детерминированно-вероятностиых цифровых интегрирующих машин и однородных цифровых интегрирующих структур, для цифрового моделирования различных объектов, а также в системах автоматического регулирования и управления.
Известны детерминированные цифровые интеграторы, выполняющие интегрирование по Риману, которые содержат блок квантованной функции, вход которого соединен со входом интегратора, а выход подключен к блоку детерминированного приращения интеграла, соединенного с другим входом интегратора. Их недостатком является невысокая точность и низкое быстродействие.
Известны вероятностные интеграторы, выполняющие интегрирование по Риману, в основе которых лежит метод статистических испытаний (Монте-Карло). Для получения высокой точности работы такие интеграторы требуют реализации очень больщого числа статистических испытаний, что резко снижает их быстродействие.
Целью настоящего изобретения является повышение точности и скорости интегрирования.
В предлагаемом изобретении эта цель достигается путем перехода к комбинированному, детерминированно-вероятностному преобразованию информации в интеграторе и ее детерминироваино - вероятностному представлеиию на его входе и выходе.
Помимо известных - блока формирования квантованного значения подынтегральной функции и блока формирования приращения интеграла на основании квантованного значения подынтегральной функции, в предлагаемый детерминированно-вероятностный цифровой интегратор входят блок вероятностно-статистического формирования полного значения подынтегральной функции, блок формирования вероятностного потока одиночных приращений интеграла по остатку квантования подынтегральной функцин и, наконец, блок формирования полного значения приращения интеграла.
Итак, предлагаемый детерминированно-вероятностный цифровой интегратор, выполняющий операцию интегрирования по Риману, отличается от известных тем, что информация в нем представлена и обрабатывается не в детерминированной и не в вероятностной, а в комбинированной, детерминированно-вероятностной форме. Основные части подынтегральной функции и интеграла представлены в таком интеграторе в детерминированной, цифровой форме и вычисляются детерминированным методом на основе простейщей формулы прямоугольников, а корректирующие, небольшие части указанных величин, служащие для уточнения вычислений, представлены вероятностными имнульсными нотоками и вычисляются с помощью простых вероятностных и статистических операций. Предлагаемый детерминированно-вероятностный интегратор вычисляет приращение интеграла Римана: Д2(л:л1) J y(x)dx. Подынтегральная переменная и интеграл в детерминированно-вероятностном интеграторе представлены в виде суммы квантованных частей z{x) и у(х) и соответствующих остатков квантования „ , . ,, т / 47 (А-)и ( z{x)z(x) + (x)l; У(х)(х) + (х). Квантованные части Z (л:) и у(х) используются в детерминированной, цифровой форме, а остатки (x) и (х) отображаются ве/Г/1У
sig n U (Xi) + Д r/ 2 L ( () У () + jz ()
(/)
0, если у. (i) 25 i у (Xi) + y Пу1 (l I.
0 p. (/X max y, Az max i
signAt/ 2%, (У). если u, (yX
i(y)D, если p.i(y)
о (У) max 0 у (х); , max 0 у (х) Лл:
Здесь i(/), fii(/)-случайные величины с равномерными законами распределения.
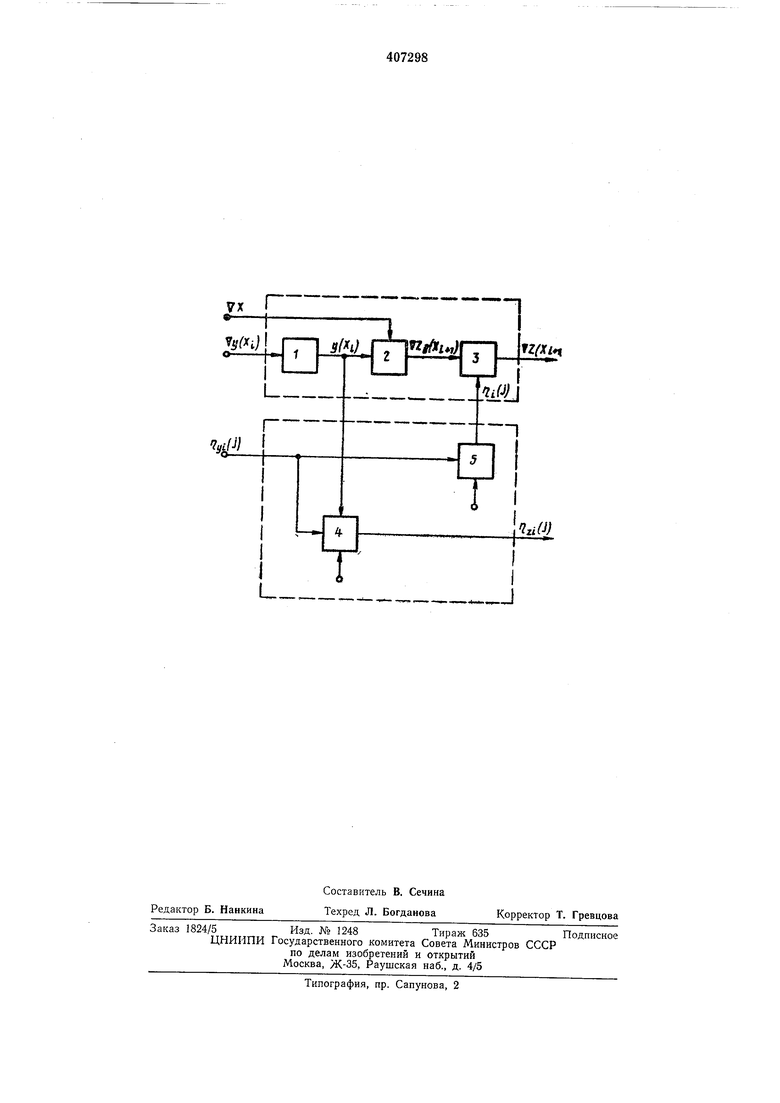
Па чертеже изображена структурная схема детерминированно-вероятностного цифрового интегратора, выполняющего операцию интегрирования по Риману в соответствии с приведенным алгоритмом.
Она состоит из блока 1 формирования квантованного значения подынтегральной функции (блок квантованной функции), блока 2 формирования приращения интеграла по квантованному значению подынтегральной функции (блок детерминированного приращения интеграла), блока 3 формирования полного значения приращения интеграла (блок фромирования полного приращения интеграла), блока 4 формирования полного значения подынтегральной функции (блок полной функции) и блока 5 формирования вероятностного потока единичных приращений интеграла по остатку квантования подынтегральной функции (блок вероятностных приращений интеграла).
Вход блока 1 является входом детерминированного канала интегратора. По нему в ин(4)
A I
Ау2%ЛА)
I
(5)
)
тегратор поступают приращения подынтегральной функции, представленные в детерминированной, цифровой форме. Выход блока 1 связан со входами блоков 2 и 4. Вторым входом блока 2 является входной канал интегратора, по которому поступают приращения переменной интегрирования. Выход блока 2 связан с одним из входов блока 3. Второй вход блока 3 связан с выходом блока 5. Выход
блока 3 является выходом детерминированного канала детерминированно-вероятностного интегратора. Вход вероятностного канала интегратора, по которому поступают вероятностные единичные приращения, связан со входами блоков 4 и 5. На другие входы этих блоков подаются случайные величины с равномерным законом распределения. Выход блока 4 является выходом вероятностного канала детерминированно-вероятностного интегратора.
На вход цифрового интегратора информация поступает по трем каналам в виде величин Vx и Vy(Xi), представленных в детерминированной цифровой форме, и вероятностного потока единичных приращений цУга). роятностными импульсными потоками приращений:О 2 (х) -. 7), (у); О у (X} 71, (у), таким образом, что (x),(j). 0,1У(Х)1: .-ПуЛЛС учетом представления переменных в виде основных квантованных величин и остатков, изобра каемых вероятностными импульсными потоками приращений, в основу построения алгоритма детерминированно-вероятностного интегратора, выполняющего операцию интегрирования но Риману, кладется следующий алгоритм: У () У () + V У (xi); 7 Zg() - y(x ул:; V 2 (XL, i) V Z, (Xi+i) А Zi 2i -/if (У); (3) Приращение подынтегральной функции Vy(Xi) поступает на вход блока 1, в котором суммируется с предыдущим значением подынтегральной функции y(Xi-i), хранящимся в этом блоке, в результате чего образуется величина подынтегральной функции y(Xi) в /-той точке интегрирования. Образовавшаяся величина у(Хг) поступает на вход блока 2. На второй вход блока 2 подается приращение переменной интегрирования Vx. В блоке 2 величины у(Хг) и Vx перемножаются, в результате чего получается «детерминированная часть приращения интеграла VZg(x.i+i). Приращение Vzg(Xi+i) направляется на один из входов блока 3. На второй вход блока 3 подается вероятностный поток приращений (/), который суммируется в блоке 3 и формирует «вероятностное приращение интеграла V2c(Xt+i). Полученная «вероятностная величина приращения интеграла VZc(Xi+i), суммируясь затем в блоке 3 с «детерминированным приращением интеграла Vzg(Xi+i), образует полное приращение интеграла Vz(Xi+i), поступающее на выход детерминированного канала, детерминированно-вероятностного интегратора. На вход блока 4 поступают вероятностный поток приращений rjj/,, (/) и величина у(Хг) с выхода блока 1. Кроме того, на вход блока 4 подается случайная величина ,и(/). Величина у(Хг) помещается в блок 4 и суммируется с потоком приращений TI (/). В каждом /-том такте результат суммирования сравнивается со случайной величиной .ц/). Если сумма, образовавшаяся в блоке 4, по модулю больще случайной величины i(i), то после сравнения блок 4 выдает на выходе положительную или отрицательную единицу в зависимости от зналгка суммы у(Хг) S Цу1). в остальных случаях на выходе выдается нуль. Образованный таким образом вероятностный импульсный поток г (/) изображает остаток интеграла z(Xi) и выдается на выходе «вероятностного канала детермииированно-вероятностного интегратора. На вход блока 5 подаются вероятностный поток (i), а также случайная величина ui(/). Поток Tiyf(i) суммируется в блоке 5 и образовавшаяся величина сравнивается в каждом /-том такте со случайной величиной j.i(/). Если образовавшаяся сумма больше по модулю, чем i-ii(/), то после сравнения блок 5 выдает на выходе единицу, знак которой совпадает со знаком сравниваемой суммы. В остальных случаях на выходе выдается нуль. Образующийся таким образом вероятностный импульсный ноток поступает на вход блока 3. Предмет изобретения Цифровой интегратор, содержащий блок формирования квантованной функции, вход которого соединен с первым входом интегратора, а выход подключен к первому входу блока формирования детерминированного приращения интеграла, второй вход которого соединен со вторым входом интегратора, отличающийся тем, что, с целью повышения точности работы интегратора, он содержит блоки формирования полной функции, вероятностного приращения интеграла и блок формирования полного приращения интеграла, выход которого соединен с первым выходом интегратора, первый вход блока формирования полного приращения интеграла соединен с выходом блока формирования детерминированного приращения интеграла, а второй вход соединен с выходом блока формирования вероятностных приращений интеграла, вход которого подключен к третьему входу интегратора и к первому входу блока формирования полной функции, второй вход которого соединен с выходом блока формирования квантованной функции, а выход подключен ко второму выходу интегратора.


| название | год | авторы | номер документа |
|---|---|---|---|
| ДЕТЕРМИНИРОВАННО-ВЕРОЯТНОСТНЫЙ ЦИФРОВОЙ ИНТЕГРАТОР | 1972 |
|
SU428412A1 |
| Детерминированно-вероятностный цифровой интегратор | 1975 |
|
SU595749A1 |
| Детерминированно-вероятностныйиНТЕгРАТОР | 1979 |
|
SU840859A1 |
| Детерминированно-вероятностный цифровой интегратор | 1975 |
|
SU600574A1 |
| Детерминированно-вероятностный интегратор | 1979 |
|
SU857990A1 |
| Детерминированно-вероятностный интегратор | 1976 |
|
SU667974A1 |
| Цифровой интегратор | 1985 |
|
SU1365081A1 |
| Цифровой интегратор для решения краевых задач | 1984 |
|
SU1211712A1 |
| Аналого-цифровой интегратор | 1979 |
|
SU842868A1 |
| Цифровой интегратор | 1984 |
|
SU1171789A1 |


Авторы
Даты
1973-01-01—Публикация