I
Изобретение относится к области вычислительной техники и может быть использовано для создания детерминированно-вероятностных цифровых интегрир|уюш.их машин и однородных цифровых интегрирующих струк тур, для цифрового моделирования различных объектов, а также в системах автоматического регулирования и управления.
Известны детерминированные цифровые интеграторы, выполняющие интегрирование по Стилтьесу, которые строятся на основе простейшей формулы прямоугольников при использовании одноразрядных пр,ирашений. Их недостатком является невысокая точность и низкое быстродействие.
Известны детерминированные цифровые интеграторы, выполняющие интегрирование по Стилтьесу, которые строятся на основе более точных формул численного интегрирования и многоразрядных приращений. В частности, строятся интеграторы с (применением формул трапеций, квадратичных и кубичных парабол. Такие интеграторы отличаются высокими точностью и быстродействием. Однако структура их сложна и треб|ует больших затрат оборудования.
Известны вероятностные интеграторы, выполняющие интегрирование по Стилтьесу, в основе которых лежит статистический метод Монте-Карло. Для получеиия высокой точности
работы такие интегратору требуют реализации очень большого числа статистических испытаний, что резко снижает их быстродействие.
Целью изобретения является создание детерминированно-вероятностного цифрового интегратора, выполняющего интегрирование по Стилтьесу и обеспечивающего высокую точность интегрирования, а также значительное быстродействие при отиоситель 1о небольщих затратах оборудования.
Помимо известных блока образования подьинтегральной функции и блока вычисления по формуле прямоу1гольников приращений интеграла в описываемый интегратор входят блок формирования вероятностного потока приращений остатка интеграла, блок образования корректирующего вероятностного потока приращежий и блО|К образования вероятностного потока приращений второй разности интеграла.
Предлагаемый детерминированио-вероятностный цифровой интегратор, выполняющий
операцию интегрирования по Стилтьесу, отличается от известных тем, что информация в нем представлена и обрабатывается не в детерминированной и не в вероятностной, а в смешенной детерм.инированно-вероятностной форме.
Основные части подынтегральной функции, неремепной интегрирования и интеграла представлены в таком интеграторе в цифровой форме и вычисляются детерминированным методом на основе простейшей форм|улы прямоугольинков, а корректирующие небольшие части указанных велигчдан, служашие для уточнения вычислений представлены в виде вероятностных потоков единичных приращений и вычисляются статистическим методом Монте-Карло.
Вычисление основной детерминироващюй части интеграла выполняется очень просто с пОхМощью формулы прямоугольников на основе многоразрядных приращений с высокой точностью. Небольшая уточняющая часть интеграла вычисляется статистическим методом с относительно невысокой точностью при помощи небольщого числа .статистических испытаний. Однако, как показывает теоретический анализ, общая результирующая точность вычисления интеграла подобным методом оказывается очень высокой и сравнима с точностью, которая получается при вычислении интеграла на основе формулы квадратичных парабол.
Принцип вычисления в интеграторе основной части интеграла в детерминированной форме с помощью простейшей формз-лы прямоугольников, а |уточняющей части вероятностным методом, дает возможность получить простую структуру интегратора, требующую небольших затрат оборудования, и позволяет одновременно обеспечить высокую точность интегрирования, а Т9;кже значительное быстродействие при относительно небольшом количестве статистических испытаний.
Предлагаемый детерминированно-вероятностный интегратор вычисляет приращение интеграла Стилтьеса
Уг (Xi+i - УР (х) dyi, (х), х/
где УР (х) - подынтегральная функция, Уf/ (х) - переменная интегрирования,
X - (Независимая перемен-иая, z{x) - интеграл.
Каждая из переменных /в предлагаемом интеграторе представлена в виде суммы квантованной частн н остатка Ov:
z(x) ,г((л:), У, (х) УР(Х) + О,- 1Ур(х), Ун (х) Уа(х + Ол.;(л:).
Квантованные части z(x), ур(х) и уQ(X) используются в детерминированной цифровой форме/ а остатки изображаются вероятностными потоками единичных цриращений
(x (/). ,.(O., (х) - (i),
О-с,{г/ (х)} - (i, с таким расчетом, чтобы
O.,,,) « Аг iizi(/), у /
т
O,v,, () Аг/р2 (рП/), т
Qxi{yq(x,n) Ауд 2 (l}
где rizi(/) - вероятностный поток приращений остатка интеграла, ЛрИ/) - вероятностный поток приращений остатка подынтегральной
функции,
4f/i(/) - вероятностный поток приращений остатка переменной интегрирования. С учетом предстаВления каждой переменпой в виде главной квантованной величины и остатка, изображаемого вароятностньгм потоком приращений, в ocnoBiy построения алгоритма детерминированно - вероятностного И1 тегратора, выполняющего операцию интегрирования по Стилтьесу, кладется ряд выражен.ий.
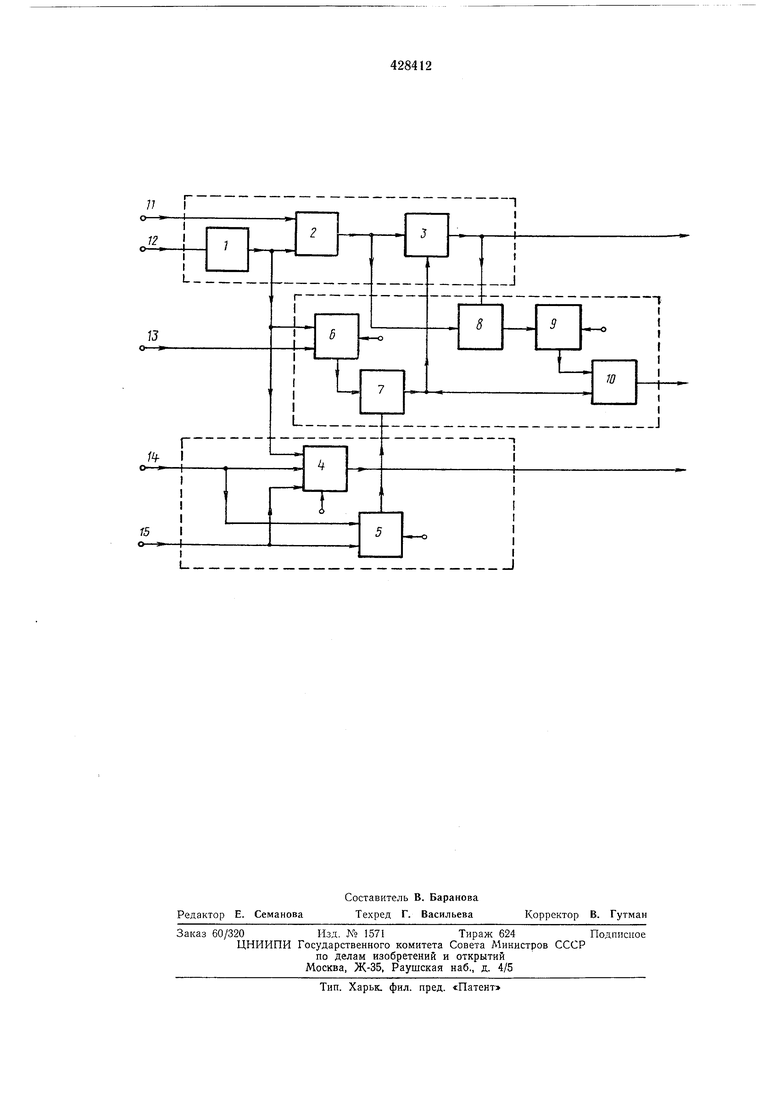
На чертеже изображена блок-схема детерминированно-вероятностного цифрового интегратора, выполняющего операцию интегрирования по Стилтьесу в соответствии с выведенным алгоритмом.
Предлагаемое устройство содержит блок / формирования -подынтегральной функции; блок 2 вычисления детерминированной части
приращения интеграла; блок 3 вычисления полного приращения интеграла; блок 4 формирования вероятностного потока приращений остатка интеграла; блок 5 формирования корректирующего вероятностного потока приращений по остатку подынтегральной функции; блок 6 формирования корректирующего вероятностного потока приращений по второй разности переменной интегрирования; блок 7 образования суммарного корректирующего
вероятностного потока приращений; блок 8 вычисления вспомогательной разности; блок 9 формирования вероятностного потока приращений вспомогательной разности; блок 10 образования вероятностного потока приращеПИЙ второй разности интеграла; шину // приращ-ения переменной иетегрирования; шину 12 приращения подынтегральной функций; ЩИ1НЫ 13 Вероятностного потока приращений второй разности переменной интегрирования;
шину 14 |Вероятностного потока приращений остатка переменной интегрирования и шину 15 верояТ|НО|СТ1наго потока етриращений остатка подынтегральной функции.
Предлагаемая схема интегратора состоит
из трех групп функциональных блоков.
Первая группа включает в себя блоки /-3 и выполняет операцию вычисления приращения интеграла Vz;(Xj+i). При этом в блоке / вычисляется значение подынтегральной
функции УР (xi) в точке Xi в блоке 2 определяется детерминированная часть приращения интеграла (Хг + 1), в блоке 3 вычисляется полное значение приращения интеграла. Вторая irpynna включает в себя блоки 4 и 5 и выполняет операцию выч-исления вероятностного потока единичных приращений (i), который изображает остаток интеграла O.,{z(x). Операция вычисления стохастического потока т)гг(/) осуществляется в блоке ;. Блок 5 служит для вычисления корректирующего вероятностного потока приращений т|1г(/), который определяется и используется в дальнейщем в третьей группе блоков. Третья npyiona блоков включаете себя блоки 6-10 и служит для вычисления вероятностного потока единичных приращений (/), изображающего втор|ую разность интеграла, п суммарного корректирующего вероятностного потока единичных приращений Т1г(/). который используется в первой группе блоков для вычисления корректирующей вероятностной составляющей приращения интеграла. В блоке 6 вычисляется корректирующий вероятностный поток приращений ii2i(/). В блоке 7поток 11и(/), поступающий из третьей группы блоков, и поток (/) суммируются, В результате чего образуется поток i,-(/). Блок 8 служит для вычисления величины V 2з(л:г+) 8блоке 9 определяется вспомогательный вероятностный поток единичных приращений TisiO)- Блок 10 служИТ для суммирования потоков Г1г(/) и TisiC/) и определения вероятностного потока приращений (i), изображающего вторую разность интеграла. На вход детерминированно-вероятностного цифрового интегратора информация поступает по пяти щинам в виде величин У(,(Х,-)И (Х(), представлепных в цифровой форме, и стохастических потоков единичных нриращений ттугС/), r.id) и (i). Приращение подынтегральной функции Vy (л:,-) поступает па вход блока /, в котором суммируется с предыдущим значение. подынтегральной функции yj,(), хранящимся в регистре блока, в результате чего образ|уется величина подынтегральной функции yp(xi) в 1-ой точке интегрирования. Образовавщаяся величина у (х,) поступает на вход блока 2. На второй вход блока 2 подается приращение переменной интегрирования Vi/gC ;,). В блоке 2 величины ) и 7yg{xj) перемножаются, в результате чего получается детерминированная часть приращения интеграла VZa (. Приращение 72j(;+i) направляется на один из ВХОДОВ блока 3. На второй вход блока 3 подается вероятностный ноток приращений Т1г(/), который суммируется в реверсивном счетчике блока 3. Полученная величина, суммируясь затем в блоке 5 с детерминированной частью приращения интеграла V 2(Xi+i), образует полное приращение интеграла Vz(:,-+i), выдаваемое на одном из трех выходов интегратора. На вход блока 4 поступают вероятностные отоки приращений Tjyif/) с щины 14 и (j} щины 15 и величина Ур(Х{) с выхода блока 1. Кроме этого, на вход блока 4 подается случайная величина )-i(/). Величина Ур(Хг) помещается в реверсивный счетчик блока 4 и суммируется с потоком приращений Щр/Ц). В каждо.м /-ОМ такте результат суммирования сравнивается со случайным числом |.i-(/), которое находится в дополнительном регистре блока 4. Если сумма, образовавщаяся в реверсивном счетчике блока 4, по модулю больше случайной величины j.i(/), то схема сравнения (на чертеже не указана) блока 4 выдает на выходе положительную или отрицательную единицу iB зависимости от знака r,/i(j). В нротивном случае, а также при ijid) О на выходе выдается нуль. Образованный таким образом вероятностный поток единичных приращений iiziQ) изображает остаток интеграла z(Xj) и выдается на одном из трех выходов детерминированно-вероятностного интегратора. На вход блока 5 подаются вероятностные потоки 11р/(/) и Tigj(/), а также случайная велич1И1на ,ui(/). Поток л/;/(/) суммируется в реверсивном счетчике (на чертеже не указан) блока 5, и образовавщаяся величина сравнивается в каждом /-ОМ такте со случайной величиной -ii(/). Если образовавщаяся в счетчике блока 5 сумма больще по модулю, чем |Л1(/), и если 1Тд,-(/) отлична от нуля, то схема сравнения блока 5 выдает па выходе единицу, знак которой совпадает со знаком )В нротивном случае на выходе выдается Н|уль. Образовавшийся таким образом вспомогательный вероятностный поток приращений 1Т1г(/) направляется на вход блока 7. На вход бло;ка 6 постгупает величина Ур(Хг). вероятностный поток приращений fqiU) и случайная величина 2(/). Величины yp(Xi) и Ц2(/) сравниваются в каждом /-ОМ такте. Если |Ур(.Г;)) J.i2(/), то в результате сравнения на выходе блока 6 образуется единица, знак которой совпадает со знако.м (/)- В противном случае на выходе блока 6 выдается нуль. Полученный ia выходе блока 6 вероятностный поток приращений zid поступает на вход блока 7, на второй вход которого подается вероятпостный поток приращений г|и(/). Оба нотока Tiii(/) и ii2,-(/) суммир|уются в блоке 7, в результате чего образуется вероятностный поток единичных приращений (i), подаваемый с выхода блока 7 на входы блоков 3 и W. На входы блока 8 поступает -с выхода блока 2 детерминированная составляющая приращения интеграла 72л(л:,ч1) а с выхода блока 3 - полное приращение интеграла (xi+). В регистре блока 8 приращение (xi+i) задерживается на время полного щага интегрировапия, а в сумматоре блока 8 образуется разность величин У2д( i) к z(Xi). Полученная на выходе блока 8 разность поступает на вход блока 9, на второй вход которого подается случайная величина |мз(/)Если указанная разность ло модулю больше (is(У), то на выходе блока 9 образуется единица со знаком разности, а в противном случае - Н)уль. Полученый таким образом в блоке 9 вероятностный лоток приращений (/) направляется на вход блока 10, на второй вход котораго поступает вероятностный поток т)г(/). Суммируясь в блоке 10, потоки (j) и Чзг(/) образуют вероятностный поток приращений tfzid}, который изображает вторую разность интеграла и выдается на одном из трех выходов интегратора. Предмет изобретения Детерминированно-вероятностный цифровой интегратор, содержащий блок формирования подынтегральной функции, выход которого соединен с блоком вычисления детерминироваяЗой части приращения интеграла отличающийся тем, что, с целью повышения точности интегрирования, в него введены блок формирования вероятностного потока приращений остатка интеграла, к входам которого подключены щины вероятностного потока приращений остатка переменной интегрирования и вероятностного потока приращений остатка подынтегральной функции,-и выход блока образования подынтегральной функции; блок формирования корректирующего вероятностного потока приращений по остатку подынтегральной функции, к входам которого подключены щины вероятностного потока приращений остатка переменной интегрирования и вероятпостного потока приращений остатка подынтегральной функции; блок формирования корректирующего вероятностного потока приращений по второй разности переменной интегрирования, к вход|у которого подключена щина вероятностного потока приращений второй разности переменной интегрирования, и выход блока образования подынтегральной функции; блок образования суммарного корректирующего вероятностного потока приращений, входы которого подключены к блокам формИрования корректирующего вероятностного потока приращений по остатку лодынтегральной функции иформирования корректирующего вероятпостного потока приращеиий по второй разности переменной интегрирования; блок вычисления вспомогательной разности, на входы которого подключены выходы блока вычисления детерминированной части приращения интеграла и блока вычисления полного приращения интеграла; блок формирования вероятностного потока приращений вспомогательной разности, на вход которого подключен выход блока вычисления вспомогатель}юй разности; блок образования вероятност}1ого потока приращений второй разности интеграла, на входы которого подключены выходы блока образования суммарного корректирующего вероятностного потока приращений и блока формирования вероятностного потока приращений вспомогательной разности; блок вычисления полного приращения интеграла, входы которого подключены к блоку вычисления детерминированной части приращения интеграла и к блоку образования суммарного корректирующего вероятностного потока приращений, а выход подключен к блоку вычисления вспомогательной разности.



| название | год | авторы | номер документа |
|---|---|---|---|
| ЦИФРОВОЙ ИНТЕГРАТОР | 1973 |
|
SU407298A1 |
| Детерминированно-вероятностныйиНТЕгРАТОР | 1979 |
|
SU840859A1 |
| Детерминированно-вероятностный интегратор | 1976 |
|
SU667974A1 |
| Детерминированно-вероятностный цифровой интегратор | 1975 |
|
SU600574A1 |
| Детерминированно-вероятностный интегратор | 1979 |
|
SU857990A1 |
| Детерминированно-вероятностный цифровой интегратор | 1975 |
|
SU595749A1 |
| Интегратор с воспроизведением вариаций интеграла | 1985 |
|
SU1335994A1 |
| Интегрирующее устройство интегрирующей машины последовательного типа | 1974 |
|
SU526927A1 |
| ЦИФРОВОЙ ИНТЕГРАТОР | 1973 |
|
SU409248A1 |
| Цифровой интегратор | 1975 |
|
SU650084A1 |


Даты
1974-05-15—Публикация
1972-05-22—Подача