00 О5
ел
о
СХ)
Изобретение относится к автоматике и информационно-измерительной тех нике и предназначается для цифровой обработки информации.
Цель изобретения - повышение точности.
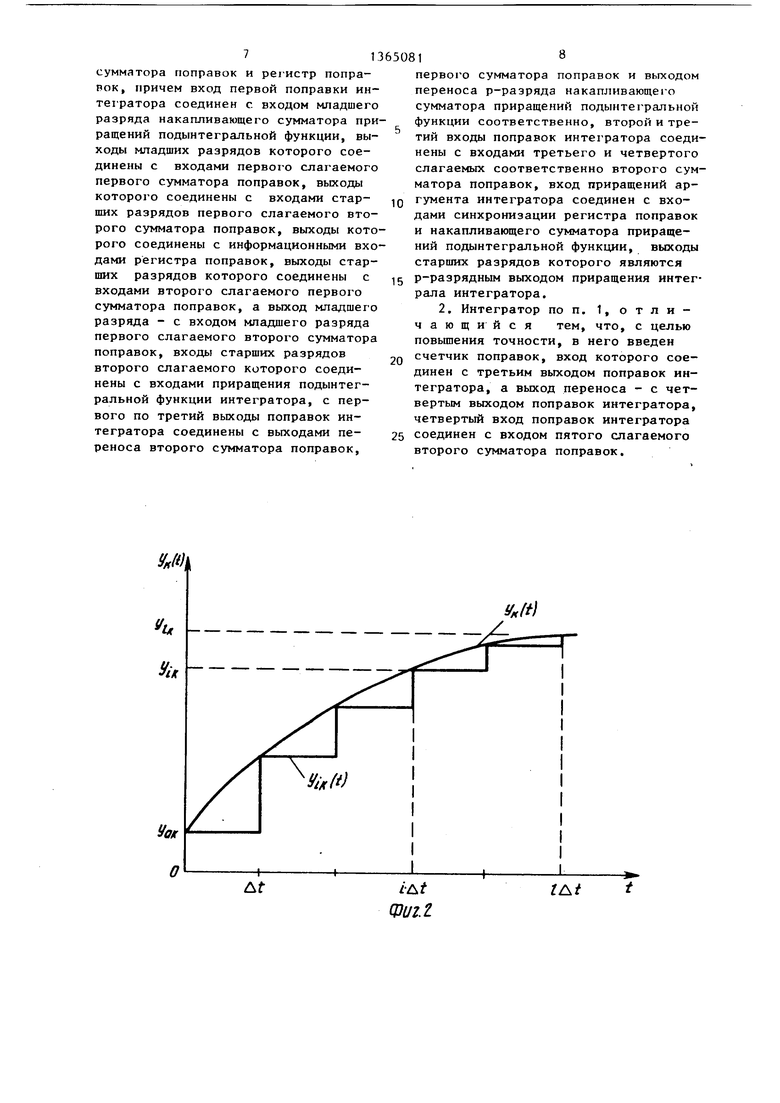
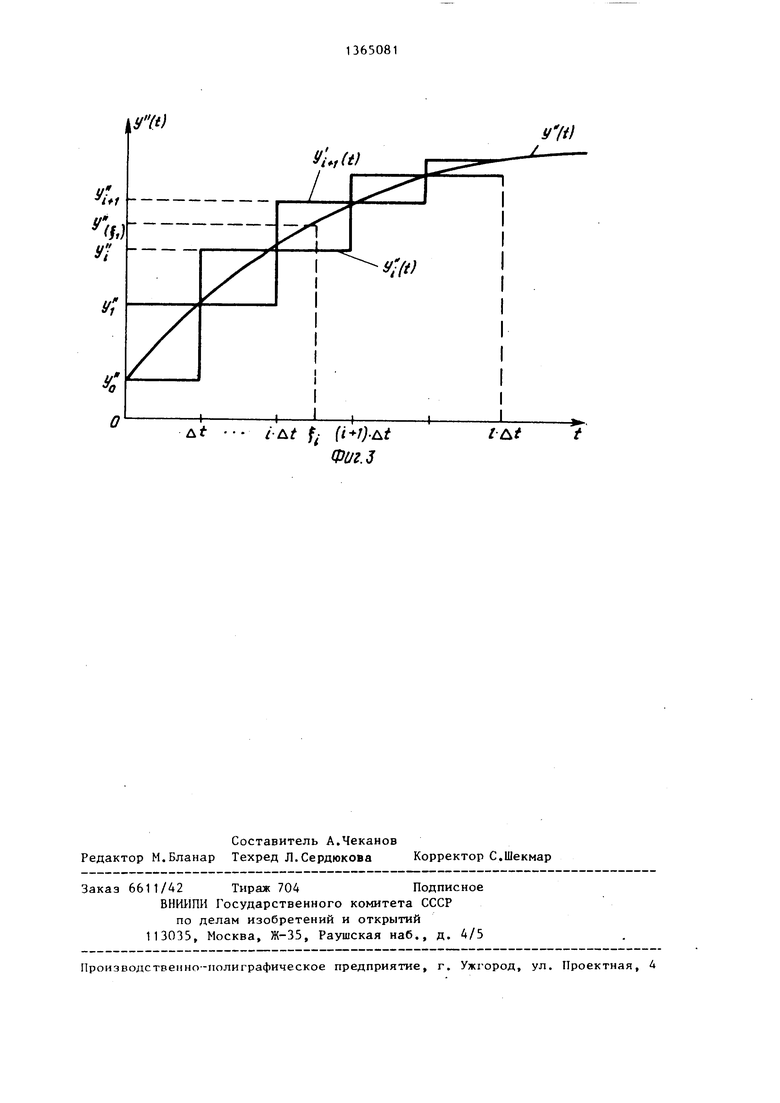
Ла фиг. 1 представлена структура интeгpaтopai на фиг. 2 и 3 - графики поясняющие процесс вычислений попра вок.
Цифровой интегратор (фиг. 1) содержит блок 1 вычисления интеграла, первый 2 и второй 3 сумматоры поправок, сумматор 4 приращений подынтег- ральной функции, регистр 5 поправок, регистр 6 подынтегральной функции, триггер 7, элемент И 8, счетчик 9 приращений интеграла, счетчик 10 поправок, входы 11 приращений подынтег ральной функции, первый вход 12 поправки, вход 13 приращений аргумента второй 14, третий 15 и четвертый 16 входы поправок, выходы 17 интеграла, выходы 18-21 поправок с первого по четвертый.
Устройство работает следующим образом.
В отличии от известного оно реализует по формуле трапеций не интеграл Стилтьеса, а интеграл Римана, т.е. действует в соответствии с уравнениями
-iZ;,( 0,5 ay.,, ).4t, (1)
е у, - значение подынтегральной функции в рассматриваемой i-й точке; п - разрядность ее двоичного
представления,40
Р у . 2L у . 2 У« значения
1-го двоичного разряда, равные О или 1),
2 - масштабный коэффициент, 45 ,, ij у . - соответственно приращения
интеграла и подынтегральной функции на рассматриваемом участке интегрирования, причем Jy ;,, у ;,-у, . в (1) входит в общем случае неизстное перед началом вычисления
50
35
л V i
значение приращения подынтегральной функции (йу.). Поэтому для
вычисления л - нужно либо организовать некоторьп интерационный процесс, либо использовать экстраполяцию значения J y-t-1 на основе информации о
приращениях функции в предыдущих точках, т.е. лу (, г - О, 1, 2, .... В известном устройстве используется именно второй способ, для чего требуется специальное устройство (экстрапо- лятор приращений) и на начальном участке работы нужно каким-то образом получать как минимум два значения ДУ ( и л у j, , так как они неизвестны. Это усложняет работу с цифровым интегратором. В предлагаемом устройстве экстраполятор приращений не используется, а получающаяся вследствие этого погрещность интегрирования компен- - сируется путем введения соответствующих связей. Причем предполагается,что на каждый цифровой интегратор в структуре, реализующей требуемую функциональную зависимость, подается не более одного приращения подынтегральной функции-(т.е. интегрирующая структура не содержит сумматоров выходных приращений интеграторов). Практически этого достаточно для Вычисления большинства элементарных функций.
Чтобы оценить образующуюся при этом погрешность экстраполяции, рассмотрим достаточно очевидный, итерационный процесс вычисления Л Z , происходящий в соответствии с системой уравнений:
,,4Z;, +2 лу. it-, L ,
у( z :
k
о,
(2)
iZ
где индексом j обозначим номер итерации (J 1, 2, 3,...), индекс k обозначает цифровой интегратор, выход которого является входом приращения подынтегральной функции рассматриваемого интегратора, JZ - квантованное приращение 4Z.
В зтом случае итерационный процесс идет следующим образом.
Первый шаг: для всех цифровых интеграторов принимается лу , О и в соответствии с формулой (1) вырабатываются квантованные приращения выходного интеграла 4 Z - .
Второй шаг: ду|., лZ j . На выходе всех цифровых интеграторов в структуре появляется уточненное приращение интеграла л2ц .
Третий шаг: л у; Z ,,к-± ,4i .
j-й шаг: лу JZ V/tk- - .,
Чтобы определить необходимое число итераций, оценим величину
V Z J л Z - л Z - в зависимости от номера итерации j (в дальнейшем с целью упрощения записи индекс i в обозначениях опускают) .
Из (1) следует, что
, --Л-1
vZ 2 -а t Оу - ay - ) Учитывая (2), получают VZ . Jt(/IZ ( -JZ V )i
(3)
.,
Подставляя (3), получают
. 5
y,.t
vz
Используя (4), имеют
vz a . у,.(5)
Таким образом, погрешность, обра- зующаяся из-за неточности вычисления dZ - , при использовании только двух итераций с высокой точностью оценивается выражением (5) и имеет одинаковый порядок с погрешностью интег- рирования по формуле трапеций, которая выражается известной формулой (3)
-1г
.r -u - P
где - некоторая точка на рассматриваемом i-M интервале интег- рирования, 2 - нормирующий коэффициент.
Оценим образующуюся в этом случае погрешность итерационного процесса н большом интервале интегрирования
A. ivz., ,ti
IrO 0
Величина суммы в последнем выражении равна приращению интеграла от у (t) (что соответствует приращению функции y(t) за вычетом площади криволинейных треугольников, заключенУ,-иных между ступенчатой функцией у , и функцией y(t) (фиг. 2). f
/It
y,-y,x2-ry,..t.2-(y -yjf
i-O
Отсюда
(УГУо)-о.5(у,,-у,),
Тог да
2
1)Т
t4(yryo).t()J. jt4y,-y).(7)
Ha основе (6) оценивают погрешность интегрирования по формуле тра- 1Q пеций на большом интервале интегрирования. Для этого воспользуют соотношение
,;-,;.2- I ,(.) At ± f,
15 где 8 определяется разностью площадей, заключенных между ступенчатыми функциями y(t) и у 1 (t) (фиг. 3). f-1 f-
. у Mt-2- Z. |у;,) ti
20
2 1У|-у;| 4t.
пП
-пП
Для ut 2
огда
Р
,J I IAp,l -j2- t -I|y %)
- л Г-Л
Р
kp
1-0
J
ut . , ,,.,2- ..t o
IУ ГУ:, I25ЗО
35
40
Формулы (7) и (8) дают возможность построить цифровой интегратор с компенсацией погрешности итерационного процесса и формулы трапеций. Тогда порядок погрешности интегратора соответствует порядку погрешности интегрирования по формуле квадратичных парабол.
Каждый следующий квант приращения компенсирующего с/ должен добавляться в интеграл при изменении подынтегральной функции на некоторую величину ЛУ, значение которой можно определить из соотношения
,5 c/ ,, .t.jy, получаемого из (7).
А лучше всего компенсировать возникающую погрешность в тот момент, когда ее величина достигнет одного кванта самого младшего разряда накапливающего сумматора интеграла (ней), образуемого сумматором 3 и регистром 4. При п+1 разрядом НСН вес
„ - п р - f
2 дис- Поэто50
этого кванта соответствует крета подынтегральной функции. Поэ му, положив , Ч 2, имеют лу .
Таким образом, при каждом изменении y(t) на эту величину в НСИ
должен добавляться (суммироваться или вычитаться в зависимости от изменения модуля y(t) квант приращения, . компенсирующего ,,). Этот поток при- ращений можно снимать с выхода переноса р-го разряда счетчика 9,
Аналогично из (8) получают соотношение
-п-
4.
jy
3-2
-2- - ,t
2
имеют
Последовательность приращений, компенсирующих , можно снимать с того же выхода переноса счетчика 9, но она должна делиться на 3, что лучше всего сделать с помощью двухразрядного двоичного счетчика 10 с коэффициентом пересчета, равным 3. Знак получаемых приращений определяется кривизной (выпуклостью или вогнутостью) подынтегральной функции интегратора.
Структура интегратора (фиг. 1) характеризуется тем, что все разряды подынтегральной функции (реализуемой в накапливающем сумматоре 1) делятся на р старших и п-р младших. За интервал времени приращение интеграла от старщих разрядов подынтегральной функции (равное 2
-2всег-
Р
1у
г1 да содержит целое число квантов, а
значение старших разрядов накапливающего сумматора 1 представляют собой основную часть приращений интеграла. Уточнение приращения интеграла производится за счет суммирования и последующего квантования всех поправок в сумматоре 3, сигнал переноса с которого и являются результирующей квантованной поправкой к приращению интеграла от старших разрядов подынтегральной функции. Считывание старших разрядов со счетчика 9 фактически представляет собой основную часть первой итерации описанного итерационного процесса, оставшаяся часть которой (формирование приращения интеграла от младших разрядов подынтегральной функции) реализуется во время второй Итерации с помощью сумматора 2, выход переноса с которого наряду с поправками от погрешности итерационного процесса и формулы интегрирова
0
5
0
5
ния является квантованной попрапкой к основному приращению интеграла.
Таким образом, цифровой интегратор (фиг. 1) функционирует следуюгдим образом.
При нулевом потенциале на синхро- входе И t осуществляется суммирование всех значений в сумматорах 2-4 и запись сигнала переноса с последнего в триггере 7. По переднему фронту t происходит запись содержимого сумматоров 3 и 4 в регистры 5 и 6, через элемент И 8 содержимое триггера 7 добавляется в р-разрядный счетчик 9. Выход переноса с младшего разряда счетчика 9 формирует поправки итерационного процесса и погрешности формулы трапеций. Таким образом, в единичном полутакте сигнала at в регистр 6 устанавливается значение подынтегральной функции у,-, , а в нулевом полутакте с помощью сумматоров 2 и 3 формируется поправка к приращению 5 интеграла, основное значение которого снимается с разрядов счетчика 9.
Выходы 17 и 19 являются выходами приращения интеграла. Приращения подынтегральной функции поступают по двум входам 11 и 12, причем по первому - основное р-разрядное значение, а по второму - одноразрядная без учета знака поправка. Р-разрядный вход 13 и одноразрядный 14 с помощью сумматоров 2 и 3 и регистра 5 осуществляет работу устройства по формуле трапеций (1) без учета погрешности итерационного процесса. Входу 14 соответствует выход 18 с сумматора 2, осуществляющего выработку квантованной поправки приращения интеграла от младших разрядов подынтегральной функции.
Квантованная поправка итерационного процесса с выхода 20 в случае необходимости подается на вход 15, а поправка погрешности формулы трапеций с выхода 21 - на вход 16.
0
0
5
Формула изобретения
1. Цифровой интегратор, содержащий накапливающий сумматор приращений подынтегральной функции, входы младших разрядов которого являются р-раз- рядным входом приращения подынтегральной функции интегратора, отличающийся тем, что, с Целью повьш1ения точности, он содержит два
сумматора поправок и регистр поправок, причем вход первой поправки интегратора соединен с входом младшего разряда накапливающего сумматора приращений подынтегральной функции, выходы младших разрядов которого соединены с входами первого слагаемого первого сумматора поправок, выходы которого соединены с входами старших разрядов первого слагаемого второго сумматора поправок, выходы которого соединены с информационными входами регистра поправок, выходы старших разрядов которого соединены с входами второго слагаемого первого сумматора поправок, а выход младшего разряда - с входом младшего разряда первого слагаемого второго сумматора поправок, входы старших разрядов второго слагаемого которого соединены с входами приращения подынтегральной функции интегратора, с первого по третий выходы поправок интегратора соединены с выходами переноса второго сумматора поправок.
первого сумматора поправок и выходом переноса р-разряда накапливающего сумматора приращений подынтегральной функции соответственно, второй и третий входы поправок интегратора соединены с входами третьего и четвертого слагаемых соответственно второго сумматора поправок, вход приращений аргумента интегратора соединен с входами синхронизации регистра поправок и накапливающего сумматора приращений подынтегральной функции, выходы старших разрядов которого являются р-разрядным выходом приращения интеграла интегратора.
2. Интегратор по п. 1, отличающийся тем, что, с целью повышения точности, в него введен счетчик поправок, вход которого соединен с третьим выходом поправок интегратора, а выход переноса - с четвертым выходом поправок интегратора, четвертый вход поправок интегратора соединен с входом пятого слагаемого второго сумматора поправок.


| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой интегратор | 1982 |
|
SU1042015A1 |
| Цифровой интегратор | 1984 |
|
SU1171789A1 |
| Модуль интегрирующей вычислительной структуры | 1984 |
|
SU1257641A1 |
| Модуль интегрирующей вычислительной структуры | 1982 |
|
SU1101821A1 |
| Цифровой интегратор | 1979 |
|
SU840969A1 |
| Интегроарифметическое устройство | 1990 |
|
SU1784975A1 |
| Решающий блок цифровой интегрирующей структуры | 1983 |
|
SU1104514A1 |
| Устройство для обработки чисел в избыточном последовательном коде | 1985 |
|
SU1330629A1 |
| КОМБИНИРОВАННАЯ ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА | 1966 |
|
SU224910A1 |
| Детерминированно-вероятностныйиНТЕгРАТОР | 1979 |
|
SU840859A1 |
Изобретение относится к области вычислительной техники и может быть использовано для вычисления элементарных функций. Целью изобретения является повышение точности. Указанная цель достигается тем, что в интегратор, содержащий блок 1 вычисления интеграла, сумматор 4 приращений подынтегральной функции, регистр 6 подынтегральной функции, триггер 7, элемент И 8 и счетчик 9 приращений интеграла, введены два сумматора поправок 2, 3, регистр 5 поправок и счетчик 10 поправок. 1 з.п. ф-лы, 3 Ш1.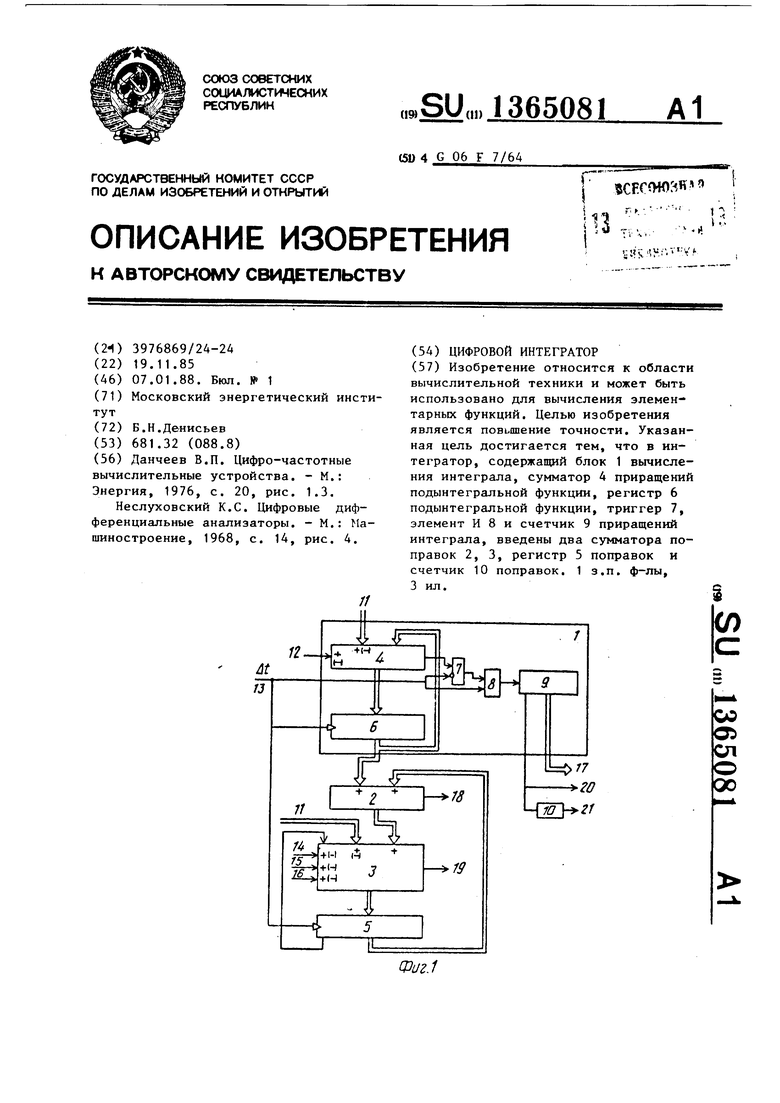
y W
At
f ().t
Фии


| Данчеев В.П | |||
| Цифро-частотные вычислительные устройства | |||
| - М.: Энергия, 1976, с | |||
| Прибор для промывания газов | 1922 |
|
SU20A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Неслуховский К.С | |||
| Цифровые дифференциальные анализаторы | |||
| - М.: Машиностроение, 1968, с | |||
| Паровоз для отопления неспекающейся каменноугольной мелочью | 1916 |
|
SU14A1 |
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
Авторы
Даты
1988-01-07—Публикация
1985-11-19—Подача