(54) ДЕТЕРМИНИРОВАННО-ВЕРОЯТНОСТНЫЙ ИНТЕГРАТОР



| название | год | авторы | номер документа |
|---|---|---|---|
| ДЕТЕРМИНИРОВАННО-ВЕРОЯТНОСТНЫЙ ЦИФРОВОЙ ИНТЕГРАТОР | 1972 |
|
SU428412A1 |
| ЦИФРОВОЙ ИНТЕГРАТОР | 1973 |
|
SU407298A1 |
| Детерминированно-вероятностный цифровой интегратор | 1975 |
|
SU595749A1 |
| Детерминированно-вероятностныйиНТЕгРАТОР | 1979 |
|
SU840859A1 |
| Детерминированно-вероятностный цифровой интегратор | 1975 |
|
SU600574A1 |
| Детерминированно-вероятностный интегратор | 1979 |
|
SU857990A1 |
| Цифровой интегратор | 1980 |
|
SU920721A1 |
| Цифровой интегратор | 1980 |
|
SU879586A1 |
| Цифровой интегратор для решения краевых задач | 1988 |
|
SU1501054A1 |
| Интегроарифметическое устройство | 1990 |
|
SU1784975A1 |
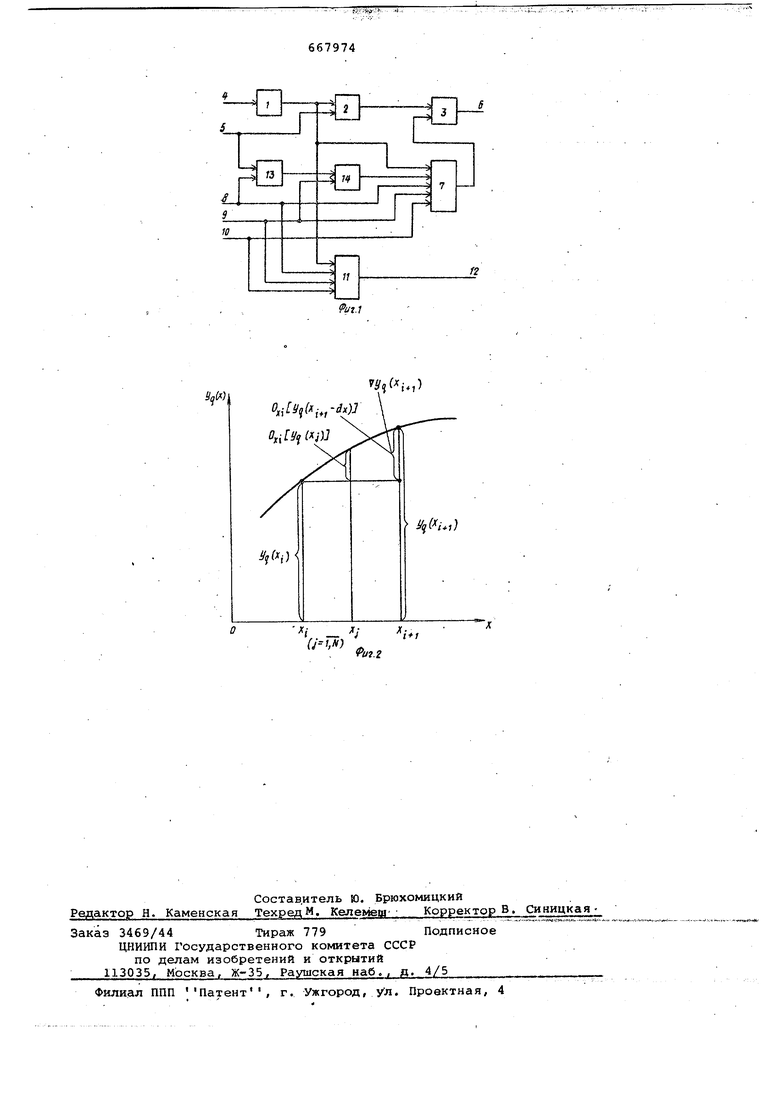

Изобретение относится к области вычислительной техники и может най применение при построении детерминированнб-вероятностных цифровых интегрирующих машин и структур. Известен детерминированный цифр вой интегратор, выполняющий операцию численного интегрирования по Стилтьесу 1. Недостатком этого интегратора является невысокая точность интегрирования на больших интервалах. Наиболее близким техническим ранением к данному изобретению явл ется детерминированно-вероятностный интегратор, содержащий блок подинтегральной функции, вход которого подк.шочен ко входу детерминированного приращения подинтегральной функции интегратора, выход блока подинтегральной функции соединен с первыми входами блока детерминированных приращений интеграла, блока вероятностной коррекции интеграла, блока вероятностных приращений интеграла , второй вход которого объединен со вторым входом блока вероят ностной коррекции интеграла, первым входом блока вероятностного преобра зования приращения переменной интегрирования и подключен ко входу случайных чисел инт,егратора, третий вход блока вероятностных приращений интеграла объединен с третьим входом блока вероятностной коррекции интеграла и соединен со входом вероятностных приращений переменной интегрирования, вход вероятностных приращений подинтегральной функции интегратора подключен к четвертым входам блока вероятностных приращений интеграла и блока вероятностной коррекции интеграла, выход которого соединен с первым входом блока полных приращенийинтеграла, второй вход которого соединен с выходом блока детерминированных приращений интеграла, второй вход которого подключен ко входу детерминированных приращений переменной интегрирования интегратора, выход блока вероятностных приращений интеграла является вероятнс,стным выходом интегратора, а выход блока полных приращений интеграла является детерминированным выходом интегратора 2. Интегратор реализует соотношения 2(X.(X.)vY(X;) + Yp(C,).H)+ I Ox 2{xU J{Vpfx,)O EVpfx)}d0.()J (2f - . „-,---- -- . )Yp(X.Y (X,)-VZ/X,)p(X;), 1 Ox.p(X)jdO,,tVfy) , (Ъ) ()- приращение интеграла 2 Y (X.)- подинтегральная функци V (X) переменная интегрирова °ния; Х)(;) .(ЧИ приращение и оаяногтть п« пйрая разность пере менной интегриро- . вания; X - независимая переменна о„ YP (X) , о,; )J и 0, Z fx) остатки квантования по X подинт.егральной функции, переменной интегрирования и интеграла соответственно;(x - вторая разность интегр .Недостатком этого интегратора яв резкое снижение точности интегрирования при увеличении интервала, вызванное возрастанием веса импульсов в вероятностной последовательности приращений второй разно ти интеграла .при одновременном.умен шении числа этих импульсов. Целью изобретения является увеличение точности интегратора и его упрощение. Поставленная цель достигается тем, что второй вход блока вероятностного преобразования приращения переменной интегрирования соединен входом детерминированных приращений перемен-ной интегрирования интеграт.о ра, выход блока вероятностного пре образования приращения переменной интегрирования подключен к первому входу блока.второй разности перемен ной интегрирования, второй вход кот рого соединен со входом вероятност ных приращений переменной интегрирования, а выход блока второй разности переменной интегрирования под 44 ключен к пятому входу блока вероятНОСТ.НОЙ коррекции интеграла. Структурная схема интегратора приведена на фиг. 1. Интегратор содержит последовательно соеяиненрше блок 1 подинтегральной функции, блок 2 детерминированных приращений интеграла и блок 3 полных приращений интеграла. Вход блока 1 соединен со входом 4 детерминированных приращений подинтегральной функции интегратора, а второй вход блока 2 - со входом 5 детерминированных приращений переменной интегрирования интегратора. Выход бло.ка 3 является детерминированным выходом 6 интегратора. Блок 7 вероятностной коррекции интеграла первым входом подключен к выходу блока 1, вторым входом -. ко входу 8 случайных чисел интегратора, третьим входом ко входу 9 вероятностных приращений переменной интегрирования, четвертым входом - ко входу 10 вероятностных приращений подинтегральной функции интегратора, а выходом - ко второму входу блока 3. Блок 11 вероятностных приращений интеграла первым входом соединен с выходом блока 1, вторым входом - со входом 8 интегратора, .третьим и четвертым входами - со входами 9 и 10 интегратора соответственно, а выходом - с вероятностным выходом 12 интегратора. Блок 13 вероятностного преобразования приращений переменной интегрирования соединен последовательно с блоком 14 второй разности переменной интегрирования. Первый вход блока l3 подключен ко входу 8 интегратора, второй вход - ко входу 5 интегратора, второй вход блока 14 соединен со входом 9 интегратора, а выход - с пятым входом блока 7. В основу алгоритма предлагаемого интегратора положены выражения (1), (2) и выражение ((in 4l) ( где величина УЛХ. ) в точке Х Х. -dx равна остатку0.Yt(X)J. (фиг. 2) Алгоритм интегратора имеет вид . Vp(X.)-Yp(X..jK7YpfX.);
,))Y(X.);
P;i| h,,(),;,.,,C)
г; 4Р{к41 г/ -22Л1-) ,
В алгоритме (5) вероятностная последовательность ( вычисляется только через последовательность ij j() вероятностных приращений переменнойинтегрирования, вес ее после суммирования удваивается, но последовательность с удвоенньлм весом не вьвдается на выход интеграто-i pa. Поэтому при соединении интеграторов между собой отсутствует увеличение веса импульсов последовательности q,-
6
. 667974
S-S n pOC O+AYpE.K),
ecAH(|)/Yp(X;HAYp| p.(K)/,
0, eWHjU(),|Yp(X.)AYp|,.|K)l,
)22if)4;a;
06ju(|.)ma.|Yp(x)t , aZ maxlYp(x)luY ;
jsign AYp j -1 p. (Ю.если ) p, (K) I 0,ecAVjUfi.)|YpE i-.CK) ,
, O /jfj-) i max |vYpfx)|, , mox vYpfX)|uY )
(Sign vY(x.), если /;ff)|vY,(x,-)|,
(5)
о,если Я())1, 04ju)4mQx )i ;
fbg Vp(Xj), если /Jf lYpOt,}, -0, ес/1И /и(|) |Yp(x.)|,
04jU(|,)4rnax lYp(X)|,
2,,fi-) 7,.|(}), . max Vp(K)
4Z.2mox ) i
04 0,1,2, .. .. n, K,i- f/2,.. ., N Интегратор работает следующим образом. В начале ( -1)-го шага интегрирования в блоках 1, 7 и 11 интегратора находится значение подинтегральной функции YpfX) , а в блоках 2 и 13 - значение приращения vYq(Xi) переменной интегрирования. В точках Х Х; {j.l,2,...,l ) изменения аргумента на вероятностные входы 8, 9 и 10 интегратора поступают соответственно случайные числа yj(-) и вероятностные последовательности 4,ifj ИТ}.) В блоке 13 прнрлщенке fVIXj), сравниваясь со случайными числами- ijfi-) , в соответствии с методом Монте-Карло, преобразуется в вероятностную последовательность 7 )(И что соответствует п. 5 алгоритма (5). Блок 14 выполняет алгебраическое сложение последовательности7о(И поступающей на второй вход со входа 9 интегратора, и последовательности .Л-) ( I ) поступающей на первый вход этого блока :С выхода блока 13. Результатом суммирования является последовательность второй разности tj li-l /п- 6 алгоритма (5)/. В блоке 7 подинтегральная функция Yp(Xj преобразуется в вероятностную последователь.ность ) и умножается на последовательность 7 () , поступающую с выхода блока 14 на пятый вход блока 7 п.7 , В блоке 7, кроме того, накапливается значение остатка подинтегральной функции, текущее значение которого, интегрируется методом Монте-Карло с последующим умножением на последоБательносты(;(|-) (п. 4° ) . Полученные слагаемые вероятностной коррекции интеграла суммируются в последовательносты; (i-) (п. 8) и поступают с выхода блока 7 на второй вход блок 3. В блоке 11 находится текущее значение подинтегральной функции % (Х-) равное сумме величин Vp (Х) и ,(х)}. Эта величина также интегрируется методом Монте-Карло с умножением на последовательность ) В результате образуется последовательность вероятностных приращений интеграла t2j,(i-) (п. .3°) . На этом работа вероят ностного канала в данном шаге инте грирования заканчивается. в точках X. Xj (i 0,l,2,,..,n ) изменения аргумента вычисляется зна ,. чение полного приращения интеграла. Блок 2 вычисляет детерминированное приращение интегралаvz lX,) (п. 2) которое поступает на первый вход блока 3. Блок 3 суммирует приращени Z,(Jf) с вероятностной коррекцией А .); накопленной в счетчике этого блока, в результате образуется полное приращение интеграла72 (Х- } (п. 9 ). В блоке 1 формируется значение подинтегральной функции в .соответствии с п. 1 алгоритма (5 Посту-пившее на вход интегратора приращениепеременной интегрирования vY(X,) запоминается в блоках 2 и 13, а вычисленное значение подин-, тегральной функции Yp(x ) запоминает в блоках 1, 7 и 11. Далее, на каждом шаге интегрирования рабочий цикл ин тегратора повторяется. Устранение цепи вычисления второй разности переменной интегрирования позволяет повысить точность интегра тора и упростить его. Формула изооретения Детерминированис-вероятностный нтегратор, содержащий блок подинегральной функции, вход которого одключен ко входу детерминированных риращений подинтегральной функции нтегратора, выход блока подинтегральой функции соединен с первьами вхоами блока детерминированных приращений интеграла, блока вероятностной коррекции интеграла, блока вероятностных риращений интеграла, второй вход оторого объединен со вторым входом лока вероятностной коррекции интеграла , первым входом блока вероятностного преобразования приращения переменной интегрирования и подключен ко входу случайных чисел интегра- тора, третий вход блока вероятностных приращений интеграла объединен с третьим входом блока вероятностной коррекции интеграла и соединен со входом вероятностных приращений переменной интегрирования, вход вероятност-. ных приращений подинтегральной функции интегратора подключен к четвертым входам блока вероятностных приращений интеграла и блока вероятностной коррекции интеграла, выход которого соединен с первым входом блока полных приращений интеграла, второй входкоторого соединен с выходом блока детерминированных приращений интеграла , второй вход которого подключен ко входу детерминированных приращений переменной интегрирования интегратора, выход блока вероятностных приращений интеграла является вероятностным выходом интегратора, а выход блока полных приращений интеграла является детерминированным выходом интегратора, о т л и ч и и с я тем, что, с целью повышения точности интегратора и упрощения, второй вход блока вероятностного преобразования приращения переменной интегрирования соединен со входом детерминированных приращений переменной интегрирования интегратора, выход блока вероятностного преобразования приращений переменной интегрирования подключен к первому входу блока второй разности переменной интегрирования, второй вход которого соединен со входом вероятностных приращений переменной интегрирования, а выход блока второй разности переменной интегрирования подключен к пятому входу блока вероятностной коррекции интеграла. Источники информации, принятые во .внимание при экспертизе 1.Авторское свидетельство СССР 418864, кЛ. а 06 а 1/02, 1972. 2.Авторское свидетельство СССР 428412, кл. а 06 D 1/02, 1973.
h
0,., ,liXj)
/.. .,
Г/-,лг;
i.,)
.;
.г
Авторы
Даты
1979-06-15—Публикация
1976-01-04—Подача