1
Изобретение относится к области вычислительной техники, в частности к разделу арифметических устройств цифровых вычислительных машин, и может быть использовано при проектировании арифметических устройств, работающих в двоично-десятичном коде 8-4-2-1.
Известны суммирующие устройства для кода 8 4-2-1, содержащие двоичные сумматоры и логические схемы «И, «ИЛИ, «НЕ.
Недостатком этих типов арифметических устройств являются большие затраты. С целью сокращения затрат .на обо,,ние за счет исключения устройства обращения кодов и благодаря применению особых цепей коррекции и специальной схемы знаковой логики устройство может работать со смешанными кодами.
Ниже приводится математическое обоснование построения логической схемы для суммирующего устройства:
X, Y - первое и соответственно второе слагаемое, десятичные числа из п десятичных разрядов;
Xi, yi - десятичные цифры в i-ом разряде чисел -X и Y соответственно;
si - i-ый разряд некорректнрованной суммы;
Si - 1-Ы11 разряд суммы с учетом коррекции;
Xi, yi. Si - инверсные коды двоично-десятичных тетрад;
i lS-Xi -формулы получения инверсных i 15-yi кодов десятичных чисел (эти i 15-Si коды совпадают с обратными кодами их двоичных изображений) ;
А - сигнал со схемы знаковой логики, означает наличие одинаковых знаков слагаемых: sign Y;
А - сигнал условия sign Y; Р - сигнал переноса в старшую тетраду;
Р - сигнал отсутствия переноса в
старшую тетраду; Н - сигнал нарушения кода 8-4-
2-1;
Н - сигнал отсутствия нарушения
кода 8-4-2-1; ЦП - сигнал циклического переноса;
ЦП - сигнал отсутствия цик.чического переноса; Зн 2 - сигнал отрицательного знака
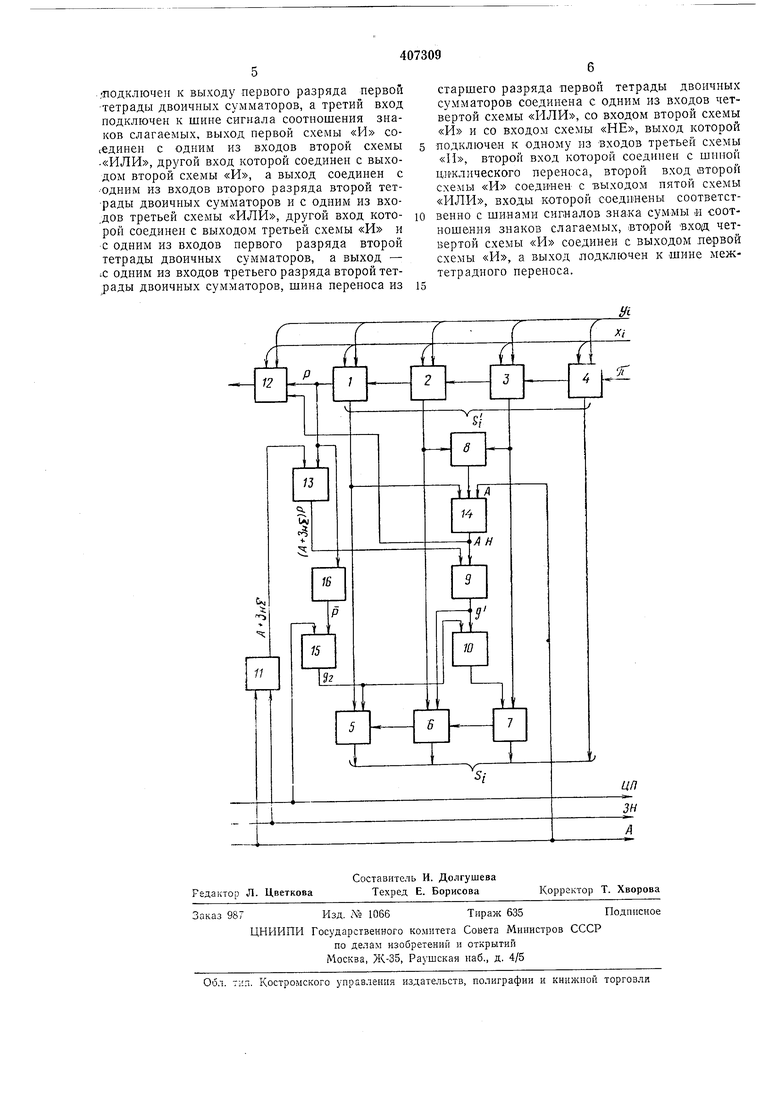
суммы; Зн 2 -сигнал положительного знака суммы; ; 22-i - двоичный сумматор; Gz-i - двоичный полусумматор. При условии л предлагается проводить еложение в прямых кодах и сумме присваивать знак одного из слагаемых. I.При услави.и А возможны случаи: а) , при этом из тетрады переноса нет (Р), нет нарушения кода (Н), следовательно, и коррекции не требуется: +yi si;: б) xi+yi: 15, в этом случае переноса (Р) из тетрады нет и имеет место нарушение кода (Н). Необходимо организовать перенос и исключить нарушение кода: si si+gi, где gi - искусственное дополнение, равное шести (); в) si xi+yi 15, в этом случае возникает перенос (Р) и нарушение кода (Н). Поскольку перенос при десятичном счете должен быть не от 16, а от 10, то код тетрады sl имеет недостаток, равный шести единицам: Si si+g. Работа десятичного сумматора при зсловии Л известна и имеет схемную реализацию. II.При условии А (sign X sign Y) отрицательные числа изображаются инверсным кодом двоично-десятичных тетрад в отличие от общепринятых дополнительных и обратных кодов. 1.Результат сложения отрицателен. Как известно, в этом случае отсутствует циклический перенос (ЦП). При этом: а)si xi+y; 15, нарушения инверсного кода нет (Н), следовательно si Si Xi-f-yi; б)si xi+yi 15, здесь возникает перенос (Р). Это значит, что тетрада отрицательного числа по абсолютной величине меньше положительной и возникновение переноса эквивалентно занятию единицы из старшей тетрады весом в «16. Следовательно, инверсный код данной тетрады уменьшится на 16, а не на 10, как должио быть. Итак, Si si+gi, где . 2.Результат сложения положителен: А (sign Y). Как известно, в этом случае возникает циклический перенос (ЦП). При этом возможны следующие варианты: а) si xi-i-yi l5, т. е. , что означает необходимость занятия «1 из старшей тетрады, в которой должна появиться «-1. Следовательно, доллсно иметь вид si (10+yi)-xi, если из данного десятичного разряда не было занятия единицы в младший. С другой стороны: si( и Si si+g2(15-xi)+yi+g2 10+yi-Xi, т. е. g2 5, Si S i-о. Прн условии всегда . Поэтому si si-5 :si+5 si-f-10 16. Следовательно, после сложения sl и «10 всегда будет перенос, который следует погасить, т. е. si si-j-10-j-l -16. Итак, независимо от того, был ли циклический перенос в даиную тетраду ИЛИ его не было (что означдет занятие в ближайшую младшую тетраду из данной), при отсутствии переноса в старшую тетраду необходимо корректировать результат суммы в данной тетраде на дополнение , si si-f . б) Si-xi+yi 15. Это означает, что в старшую тетраду возник перенос, ибо , Si -si(l5-xi)- -yi-16 yi4-xi-I. «-1 гасится или не гасится переносом из младшей тетрады или единицей циклического переноса, как и в предыдущем случае. Итак, корректированная сумма иолучаетея из некорректированной посредством сложения последней -с искусственным дополнением или нулем. Как видно из математического обоснования, условие выработки искусственного дополнения g следующее: gi A-H+A-P-4-А-ЦР-Р. При условии А и отсутствии циклического переноса ЦПзнак суммы отрицателен:(Зн2), А-ЦП :ЗнЕ; т. е. (A+A-nn.P) А-Н-|-() Р. Условие выработки дополнения . Схема предлагаемого устройства приведена на чертеже. Устройство содержит: двоичные сумматоры 1-7, схемы «ИЛИ 8--12, схемы «И 13-45, схема «НЕ 16. Двоичйые сумматоры 1-4 производят сложение по правилам сложения двоичных чисел. На входы этих сумматоров числа поступают в прямых кодах при выполнении условия А, а при условии А отрицательное число поступает инверсным кодом. Результат сложения корректируется слециальныМИ цепями в зависимости от следуюшИх условий: Н, Зн2, А-ЦП. Корректиров ка осуществляется (путем введения дополнений gi, gs или «О. Схема коррекции построена согласно формулам (A+3HS) Р; g2 PЦП. Сигнал АН вырабатывается схемами «ИЛИ 8 и «И 14; схема «ИЛИ 11 формирует сигнал (A-J-ЗнЕ); схема «И 13 формирует сигнал (А+Зн) Р; схема «ИЛИ 9 формирует сигнал gb сигнал дополнения g2 формирз ется схемами «НЕ 16 и «И 15. Перенос из двоичного ариматора 5 не используется. Результат алгебраического сложения получаем на выходе двоичных сумматоров 5, 6, 7, 4 ъ прямом коде при условии А, а также при условии А и . При условии А и результат получаем в инверсном коде. Предмет изобретения Одноразрядное суммирующее устройство комбинационного тина для кода 8-4-2-1, содержащее две тетрады двоичных сумматоров и логические схемы «И, «ИЛИ, «НЕ, отличающееся тем, что, с целью сокращения затрат оборудования, выходы второго и третьего разрядов первой тетрады двоичных сумматоров подключены ко входам первой схемы «ИЛИ, выход которой соединен с одним входом первой схемы «И, второй вход которой
подключен к выходу первого разряда первой -тетрады двоичных сумматоров, а третий вход подключен к шине сигнала соотношения знаков слагаемых, выход нервой схемы «И соссдинен с одним из входов второй схемы «ИЛИ, другой вход которой соединен с выходом второй схемы «И, а выход соединен с ОДНИМ из входов второго разряда второй тетрады двоичных сумматоров и с одним из вхо.дов третьей схемы «ИЛИ, другой вход которой соединен с выходом третьей схемы «И и с одним из входов первого разряда второй тетрады двоичных сумматоров, а выход - i.c одним из входов третьего разряда второй тетрады двоичных сумматоров, шина переноса из
старшего разряда первой тетрады двоичных сумматоров соединена с одним из входов четвертой схемы «ИЛИ, со входом второй схемы «И и со входом схемы «НЕ, выход которой подключен к одному нз входов третьей схемы «И, второй вход которой соединен с шнной циклического переноса, второй вход второй схемы «И соединен с выходом пятой схемы «ИЛИ, входы которой соедпиены соответственно с шинами сигналов зна.ка суммы .и соотношения знаков слагаемых, старой вход четвертой схемы «И соединен с выходом первой схемы «И, а выход подключен к шине межтетрадного переноса.
15

| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО для СУММИРОВАНИЯ | 1973 |
|
SU393740A1 |
| Устройство для суммирования и вы-чиТАНия дВОичНО-дЕСяТичНыХ КОдОВ | 1978 |
|
SU813415A1 |
| ДЕСЯТИЧНЫЙ СУММАТОР | 1969 |
|
SU238231A1 |
| Устройство для суммирования двоично-десятичных кодов | 1977 |
|
SU684542A1 |
| СПОСОБ И УСТРОЙСТВО СУММИРОВАНИЯ И ВЫЧИТАНИЯ ДВОИЧНО-ДЕСЯТИЧНЫХ КОДОВ | 2008 |
|
RU2389064C1 |
| СПОСОБ И УСТРОЙСТВО СУММИРОВАНИЯ ДВОИЧНО-ДЕСЯТИЧНЫХ ЧИСЕЛ | 2007 |
|
RU2402803C2 |
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ | 1966 |
|
SU183484A1 |
| Устройство для суммирования фибоначчиево-десятичных кодов | 1981 |
|
SU945862A1 |
| Устройство для вычисления модуля комплексного числа | 1990 |
|
SU1753472A1 |
| Последовательный двоично-десятичный сумматор-вычитатель | 1977 |
|
SU693369A1 |

I
Авторы
Даты
1973-01-01—Публикация