Изобретение относится к области аналоговой вычислительной техники.
Известны устройства для решения задач нелинейного программироваиия, содержащие блок интеграторов, вход которого подключен к выходу блока сумматоров, а выход соединен со входами блока градиента онтимизируемой функции и блок;а ограничений, подключенных соответственно ко входам блока усилителей и блока коэффициентов, выход которого соединен с первым входом блока сумматоров.
Известные устройства имеют недостаточно высокие точность и быстродействие.
Предложенное устройство отличается от известных тем, что оно содержит блок ортогонализации, входы которого подключены к выходам блока усилителей и блока коэффициентов, а выход соединен со вторым входом блока сумматоров.
Это повышает точность и быстродействие устройства.
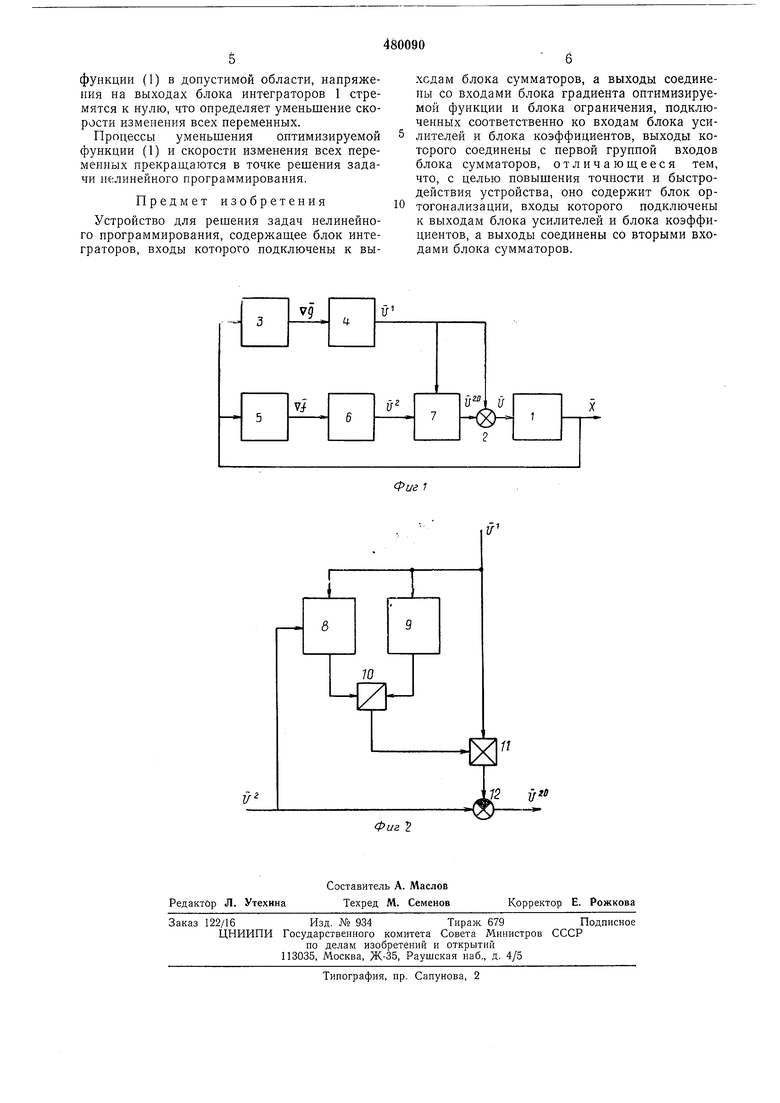
На фиг. I приведена блок-схема устройства; на фиг. 2 - блок-схема блока ортогонализации.
Устройство содержит блок интеграторов для изменения переменных; блок сумматоров 2, блок ограничений 3 для формирования сигнала, зависяш;его от функций ограничений и их градиентов; блок коэффициентов 4 для задания скорости движения и допустимой области; блок градиента 5 оптимизируемой функции; блок усилителей 6 для задания направления и скорости движения к экстремуму и
блок ортогонализации 7.
Блок ортогонализации 7 может, например, содержать блок 8 скалярного произведения вектора управления на выходе канала ограничений на вектор управления на выходе канала оптимизации, блок 9 для получения квадрата модуля вектора управления на выходе канала ограничений, блок IQ для деления выходных напряжений блоков 8 и 9, блок 11 множительных устройств для умножения
вектора управления на выходе канала ограничений на выходное нанряжение блока 10, блок 12 для вычитания нанряжений на выходах блока усилителей 6 и на выходах блока 11.
В качестве элементов устройства можно использовать, например, операционные усилители, множительные и делительные блоки и функциональные преобразователи, выполненные, например, на диодах и резисторах. Блок скалярных нроизведений и блок квадрата модуля вектора можно, в частности, реализовать на указанных мнол ительных блоках. В качестве элементов блока интеграторов можно использовать аналоговые интеграторы, выпол ненные, например, на онерационных усилителях. Устройство предназначено для нахождения значений переменных, нри которых функция (x), где X-я-мерный вектор, достигает экстремума в допустимой области изменения переменных, определяемой системой ограничений в форме равенств и(или) неравенств ,.(2) Требуемое изменение во времени переменных производится с помощью интеграторов блока 1, описываемых дифференциальными уравнениями Ic - и,(2,а) где и - вектор управляющих воздействий интеграторов. Закон управления интеграторами таков W « + й,(3) где и - вектор управления, определяющий движение к допустимой области (2); J20 - ортогонализованный вектор оптимизации, определяющий движение к экстремуму функции (1). Основное требование к векторам I/ и заключается в том, чтобы они всегда были ортогональны, т. е. их скалярное произведение должно быть равно нулю (ы, О 0.(4) Вектор управления U формируется так же, как и Б схеме прототипа, т. е. по методу «штрафных функций: U - ayg.(5) где - коэффициент, определяющий скорость движения к допустимой области и реализуемый в блоке 4, а Vg - градиент некоторой положительно определенной функции ограничений g; gfeiv..,gj.(5,3) Градиент Vg получают в блоке 3. Вид функции (5, а) выбирают таким, что при выполнении условий (2), т. е. в допустимой области, выполняются также соотношения ,vg 0.(5,6) Вектор оптимизации U равен и - Tov7,(6) где V/ - градиент функции (1), получаемый в блоке 5; YO - коэффициент, определяющий направление и скорость движения к экстремуму функции (1) и реализуемый в блоке 6. Ортогонализоваппый вектор оптимизации (6) можно вычислить, например, по формуле (а,а) -, которая определяет структуру блока 7 (фиг. 2). В этой формуле U U - скалярное произведение векторов (5) и (6), реализуемое в блоке 8; |/7, И - квадрат модуля вектора (5), реализуемый в блоке 9. Требуемая для реализации выражения (7) операция деления производится в блоке 10, операция умножения - в блоке 11, операция вычитания векторов - с помощью блока 12. При законе управления (3) скорость изменения функции ограничений (5,а) с учетом выражений (2, а, 5) равна ё (Vg. X) - (УёГ. и) а (MS Agf) + + - (и ). Так как и в силу свойства ортогональности (4), это выражение примет вид g а (vg, Ag) О, что определяет устойчивое монотонное движение к допустимой области (2), независимое от изменения оптимизируемой функции (1). Скорость изменения оптимизируемой функции при законе управления (3) равна / (ДТ, ) (у/; «)-(vf, «) + (vfi «). (9) в силу свойства (5, б) вектор V при приближении к допустимой области (2) стремится к нулю. При этом знак скорости изменения оптимизируемой функции стремится к требуемому коэффициенту оси -уо- В самой допустимой области, учитывая выражения (6,7), получаем:/ Tfl(V/, Af), т. е. при достижении допустимой области, которое в силу условия (8) обязательно наступает, движение происходит по градиенту оптимизируемой функции. Устройство работает следующим образом. Пусть, например, необходимо найти минимум функции (1). Пачальные значения напряжения на выходах блока интеграторов таковы, что заданные ограничения (2) не соблюдаются. В этот же момент времени на выходах блока коэффициентов 4 появляются такие напряжения, что функция ограничения (5, а) начинает стремиться к нулю, т. е. происходит движение системы к допустимой области. Процесс изменения во времени функции (5, а) при этом не зависит от изменения напряжения на выходах блока усилителей 6. При приближении к допустимой области напряжения на выходах блока 4 приближаются к нулю. При этом напряжения на выходах блока сумматоров 2 становятся такими, что оптимизируемая функция (1) начинает уменьшаться. После этого напряжения на выходах блока градиентов 5 и соответственно на выходах блока усилителей 6 и блока ортогонализации 7 также уменьшается. Таким образом, при достижении минимума оптимизируемой




Авторы
Даты
1975-08-05—Публикация
1974-02-08—Подача