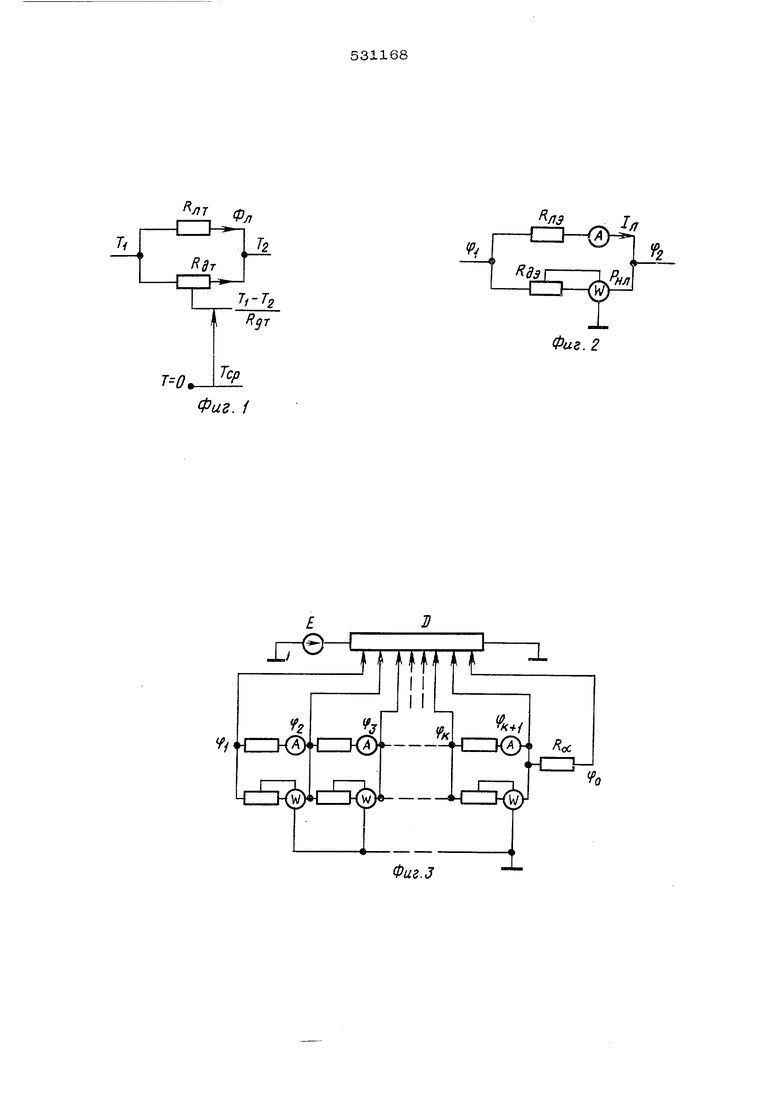
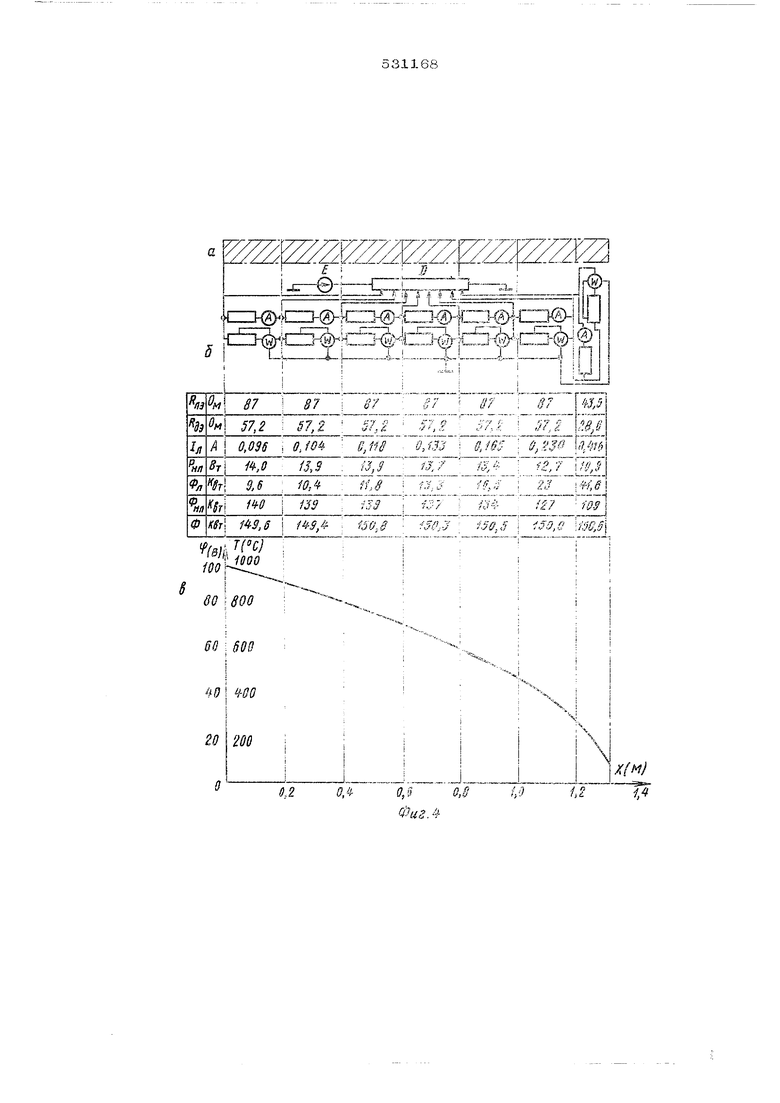
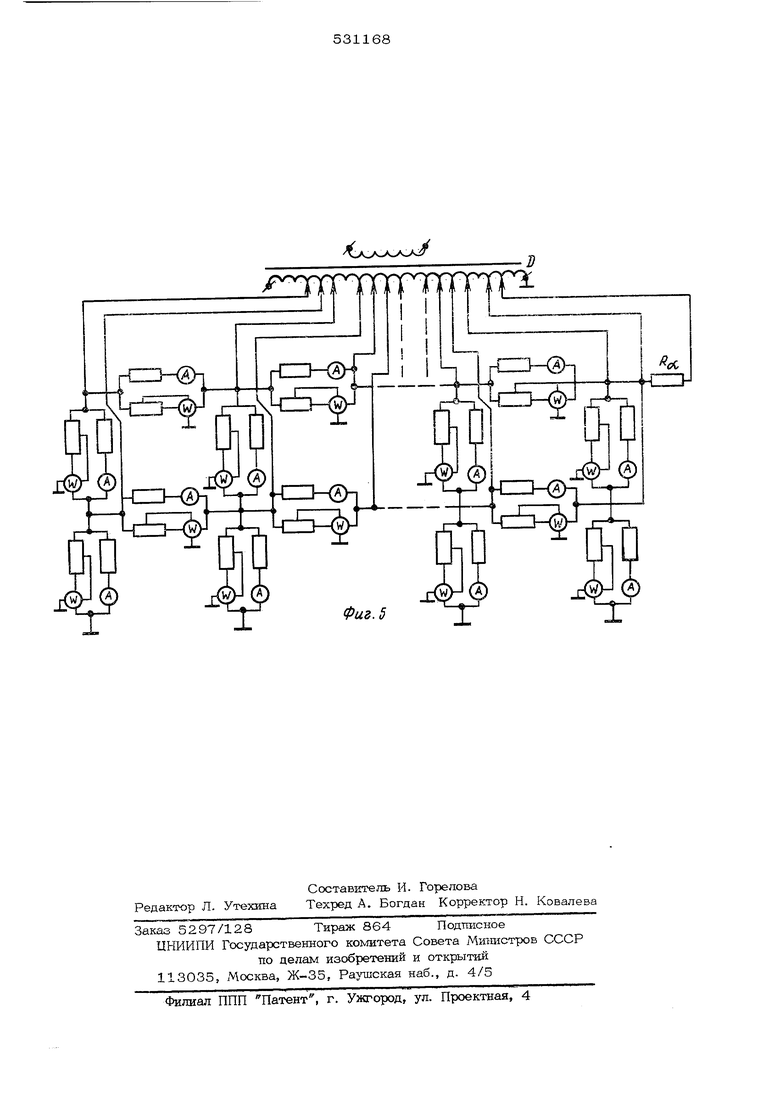
уравнений тепловых процессов и математическими выражениями уравнений эпектрических цепей. I-ia фиг. 1 показана термическая схема одного слоя теплотехнического устройства; на фиг.2 - схема устройства для электричес кого моделирования нелинейной теплопроводности установившихся тепловых процессов в одном слое теплотехнического устройства; на фиг. 3 - электрическая схема устройства для моделирования плоской стенки, разбитой на К слоев, с граничными условиями 1-го рода на левой поверхности и граничными условиями 3-го рода на правой поверх ности; на фиг. 4 - схема плоской стенки (а), ее схема электрического моделирования и график распределения температуры вдоль стенки (в), полученный электрическим моделированием; на фиг. 5 - cxeVia для электрического моделирования термического устройства с двухмерным тепловым полем.
Математическое обоснование предлагаемого способа электрического моделирования, реализуемого предложенным устройством, про- ведем на примере плоской стенки. Каждый участок представляет собой элек трическую модель одного слоя термического устройства, тепловой поток в котором определяется по формуле; Ф();(1) где Ф - тепловой поток через слой (Вт Л - коэффициент теплопроводности (Вт/м к); о - толщина слоя (м); S - площадь сечения слоя, перпендикулярного направлению теплового потока (м ); Т. - Т- - температура на границах слоя В расчетах обычно берется линейная зависимость коэффициента теплопроводности от температуры; л A(-.t.) Aj, - значение коэффициента теплопроводности при О С (Вт/мК Ь - температурный коэффициент теплопроводности (1 /К); ТА среднее значение температуры внутри слоя (к). Учитывая выражение (2), тепловой пото определяется так: ф(Т,-Т,)..6.т,р(Т,-Т,) .(3)
S
ет
-0
(8)
С учетом формул (7), (8) уравнения (5) и (6; примут вид: Разделим тепловой поток на две составщие: линейную «Ьд и нелинейную ФНАФ Ф - Ф л НА Линейной не зависящей от температуры тавляющей, является первое слагаемое мулы 13 (Т,-Т,) , § -1 -2 нелинейной составляющей теплового поа - второе слагаемое формулы (з) Р ч Л Тдр (Т.,-Т2) Введем обозначения: линейное термичессокротивпе гее слоя }i , К/Вт) R,, ,. дифференциальное термическое сопротивле(К /3т) слоя Фл --- / - ,- -s ,- 1Ч .-т.). (6-) Значения d, Л , S и t полагакп ся постонным для слоя, поэтому для каждого слоя iOv.si, т ccnsi. Таки.м образом, тепловой поток данного слоя тep жчecкoгo устройства согласно фо-рулам (4), is}, (б ) определяется как ()4 Тср(Т,-Г,.).9) Второе слагаемое данной формулы можно представить себе как дифференциальный тепловой поток (т.е. тепловой поток, приходящийся на 1 град, температуры), протекающий через линейное теркжческое сопротивление Т д.,- при разнсотн температур на границах слоя ( Т. - TT ), укгаоженный на среднюю температуру данного слоя. Первое слагаемое есть поток, протекающий через линей-tioe терчтеческое сопротивление Я д. при тех температурах Т , Т, на границах слоя. Таким образом, выражение (9) формально можно реализовать в виде параллельного соединения двух термических резисторов (фиг 1). в неразветвленной чести этого сое динения протекает фиктивный поток как будет показано в дальнейшем, не влияющий на результаты моделирования. Реальный тепловой поток следует подсчитывать путем алгебраического сложения л нл Последний определяется путем -гаожения велина среднюю температуру участка , что можно производить на моделирующем устройстве с помощью измерительных приборов. Термическая схема фиг. 1 моделируется электрической схемой с соответствующими измерительными прибора ;И (фиг. 2). Аналогом Ф л служит ток Тд (А) через линейное сопротивление Т- д ; измеряемый измерителем тока (амперметоом) А. Л Ф. где тиф масштабный коэффициент линейной составляющей теплового потока (Вт/А). Аналогом - нлслужит мощность TJ нл (Вт, ВА), измеряемая ваттметром, вкл ченным в нижнюю ветвь следующим образом токовая катушха (измеритель тока) последовательно с моделирующим резистором катушка напряжения (измеритель напряжения) меж ду точкой схемы, соответствующей нулевой температуре, и отпайкой от середины резистора m FМ -1) нл Фц, нлгде Т ф- масштабный коэффициент не линейной составляющей тепло вого потока (р личина безраз мерная) . За аналог температуры принят электри ческий потенциал точки цепи ср (В). -т - масштабный коэффициент температуры (к/В). Аналогом линейного термического сопрогивления R ду принято электрическое сопротивление резистора верхней ветви д, (ОМ л Где -дд - масштабный коэффициент линейного сопротивления (К-Вт Ом). За аналог дифференциального термического сопротивле аия R дт принято электрическое сопротивление резистора ниж-ней ветви R д (Ом). . где -R д - масштабный коэффициент диф ференциального сопротивления (KV3T Ом).. Выражение для ток; в первой ветви: Сч-.-Ф ) () Выражение для мощности Р... ) Структура формул (15) и (16) аналогична структуре формул (5) и (б ).Подставив в формулы (5 ) и (б ) значения параметров через масштабные коэфф5гциенты и имея ввиду уравнения (15) и (1б), получим соотношения между масштабными коэффициентамиМоделирование производится следующим образом. Исследуемое термическое зстройство условно разбивается на слои, для которых А, S и Ь можно принять постоянными (берутся средние значения). Для каждого L-го слоя по формулах (7) и (8) определяются Тг. . и АЗ - Если участок не является ЛУ - 1 ПЛОСКОЙ стенкой, то при моделировании учитываются эквивалентные дифферекщиальньге и линейные термические сопротивления. Резисторы с этизч-ш сопротивлениями включаются в схему в соответствии с термической схемой моделируемого участка. На фиг. 3 представлена электрическая модель плоской стенки, разбитой на К слоев, с граничными условиями 1-го рода на левой поверхности и граничными условиями 3-го рода на правой поверхности f R с - аналог термического сопротивления теплоотдачи от стенки). Катушка напряжения каж;аого ваттметра включена, на среднее напряжение каждого «р Ч- ч (-2-J относительно потенциала. соответствующего нулевой тек1Пературе шкалы Значения температур поверхностей стенки задаются при помощи делителя напряжения D (выбирают таким, чтобы оно не оказывало влияния на распределение потенциалов в устройстве), в виде потенциалов f. , f., , JГ -I При граничных условиях III -го рода на правой поверхности стенки устанавливаются потенциалы Ч , и Чд, где - потенциал, соответствующий температуре окружающей среды правой стенки. Изменяя значетгя потенциалов узловых точек Ч .Ч;7--- , добиваются одинаковой суммы тепловых потоков, показываемых амперметром и ваттметром (с учетом масштабных коэффициентов) на канадом участке для реей цепи, что соответствует постоянству теплового потока в стационарном режиме. Причем показания ваттметра складываются с показаниями амперметра при t) О и вычитываются при Ь : О. Измеряя значения потенциалов в узловых точках, получаем значения температуры на границах слоев. При отсутствии достаточного числа измерительных приборов моделирование можно вес ти с помощью одного ваттметра и одного ам перметра, включая их поочередно в цепь каждого участка. В качестве примера на фиг. 4 приведена схема плоской стенки (а), ее электрическая модель ( 6) и график распределения температуры вдоль стенки, полученный моде.ш.рованием (в). Толщина угольной стенки и 1,3 м , ало- , КОЭфф11S 1 М ща,дь поперечного сечения циент теплопроводности Я (23-Ю,35)Штрих-пунктирными линиями обе; границы разбиения плоской стеккн. Стенжэ разделена на 7 слоев. Между границами раз биения расположены участки электрической схемы, моделирующие данный слой, а также таблица, в которую включены показаний из мерительных приборов и значения тепловых потоков {линейной и нелинейной составлн1-ощей, а также суммарного). Значения температуры, полученные в ре зультате моделирования, показывают хорошее совпадение с данными теоретического расчета по известным формулам. Точность полученных значений определяется только то ностью применяемых измерительных приборо Предложенное устройство для эле.к:тричесого моделирования позволяет моделировать емпературную нелинейность стационарной теплопроводности на линейных злектрическюс сопротивлениях, процессы теплопроводности в сложных теплотехнических устройствах и граничные условия рода при условии линейна-кусочной аппроксимации температурной зависимости коэффициента теплоотдачи, а также при соответствующей аппроксимации моделирования процесса теплоизлучения. Кроме того, точность электрического моделирова1щя по сравнению с точностью моде тировакия на нелинейных электрических сопротивлен.иих повыщена, изготовление модел:я Т рощено г;о с завнению с изготовлением модели па нелинейных элементах, а методика экспер хмента упрощена по сравнению- с электрическим моделированием при использовакии метода итерации. Формула изобретения Устройство для эпехстрического моделирований нелинейной теплопроводности установивтиихся тепловых процессов, содержащее источник пктанкя с де.гштелем напряжения к ячейки С9ТОТНОЙ модеш--: из линейно зависимых от те.чтпературы сопротивлений с из. арителя -, тохов и напряжений, о т л и ч а ю д е е с п тем, что. с целью упрощения т;:роцесса моде-гп-гооБания, каждый узел сеточной модели соединен окога зящим контактом с дэлителем ;ппря)1€9нпя. а каждая ячейка -leTo-itx :. .одеш;: ct EepJiCKT, по крайней сопротивлениг, в горых, включен измеритель TCiVti, ь. :vjt.;x.uy средней точкой одного ;ула 01:-: шиной источника нэпряжеш-1Я. Г1:знп :тые во вниЦ. Электрические про- Энергия, 1958г. Исаченко В. П., Осинова В. А., СукоТеплэпере.цача. Москва, ЭнерТ 0
(Pi
Фиг. 2
. - -г---гггР: Т ТГ : - : :
I}, :1
I -Ч шччииичц Хf upcr-j. J.,/««- i- i-e-tH I J i
.--J -iL™3 Jl-ll 3
. .. ......- ;.,j1(Ii- j,
c:5Mi5%/r-t5--M r5
i If II I



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для моделирования граничных условий | 1988 |
|
SU1547004A1 |
| Устройство для решения обратной задачи теплопроводности | 1988 |
|
SU1522248A1 |
| Устройство для моделирования процесса теплопередачи в теплообменном аппарате | 1983 |
|
SU1103258A1 |
| Устройство для решения нелинейных задач теплопроводности | 1983 |
|
SU1152002A1 |
| Устройство для моделирования процесса теплопередачи в теплообменном аппарате | 1982 |
|
SU1016801A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ МНОГОЛЕТНЕ-МЕРЗЛЫХ ПОРОД ВОКРУГ СКВАЖИНЫ И ТЕМПЕРАТУРЫ ФЛЮИДА В СКВАЖИНЕ | 2014 |
|
RU2588076C2 |
| Устройство для решения нелинейных сопряженных задач | 1979 |
|
SU858015A1 |
| Устройство для решения нелинейных задач теплопроводности | 1973 |
|
SU475629A2 |
| Устройство для моделирования нелинейных граничных условий | 1980 |
|
SU902032A1 |
| СПОСОБ ОЦЕНКИ ВНЕШНИХ И ВНУТРЕННИХ ПАРАМЕТРОВ УЗЛОВ ТРЕНИЯ ПРИ ИСПЫТАНИИ В СТЕНДОВЫХ УСЛОВИЯХ | 2015 |
|
RU2647338C2 |

0,20,i
X(M)
hO1-,2
0,S
1,
.
Авторы
Даты
1976-10-05—Публикация
1973-08-08—Подача