Предметом настоящего изобретения является интегратор для вычисления горизонтальных градиентов ускорения силы тяжести, создаваемых подземным телом конечных размеров, по плану этого тела в горизонталях, с целью интерпретации наблюдений с гравитационным вариометром при разведке полезных ископаемых.
В прикладной гравиметрии определение величины, формы и глубины залегания подземной массы, создающей наблюдаемую аномалию, производится двояко: либо приписывают этой массе правильную и притом простую геометрическую форму, либо подбирают конфигурацию этой массы путем ряда пробных вычислений по методу последовательных приближений. Вычисления эти, особенно во втором случае, Столь сложны и трудоемки, что очень часто приходится от них отказываться и ограничиваться лишь качественной интерпретацией.
Из величин, измеряемых гравитационным вариометром, для интерпретации большее значение имеют так называемые градиенты, т. е. величины
аю ,, .
, , и -, где и- потенциал сиdxdz dydU
лы тяжести, Z - вертикальная, х, у - горизонтальные координаты точки наблюдения. Весьма часто в практике количественной интерпретации ограничиваются использованием этих двух величин, как наиболее надежных и точно измеряемых. При этих вычислениях подземному телу приписывается обычно или геометрически правильная форма или вид цилиндра бесконечного простирания с произвольным контуром сечения.
Для трехмерного тела неправильной формы необход имые вычисления столь громоздки и трудоемки , что в действительности никогда не производятся. Между тем, этот случай представляется в практике наиболее естественным. Предлагаемый интегратор дает возможность производить вычисления градиентов для случая трехмерного тела произвольной формы весьма быстро и просто - путем обвода штифтом прибора горизонталей предполагаемого тела на плане. Тем самым открывается возможность применения количественной интерпретации в гораздо больщем числе случаев при значительной экономии; времени и средств.
Представим себе тело конечхЧых размеров, пересеченное через известные промежутки рядом горизонтальных плоскостей. Если это тело имеет плотность У , постоянную во всех точ- I ках или изменяющуюся лишь в вер- i тикальном направлении, и промежутки между секущими плоскостями достаточно малы, то можно приближенно принять массу тела, сосредоточен- i пую в бесконечно тонких пластинах равномерной плотности, считая пла- I стины совпадающими с секущими ;
плоскостями и ограниченными конту- рами пересечения их с поверхностью
заданного тела. Для простоты расчетов в большинстве случаев можно i предполагать все расстояния между i плоскостями равными одной и той : же величине АЛ и поверхностную плотность с каждой пластины равной ;
о у. А Л(I)
Однако, для дальнейших рассуждений эти условия необязательны, важно лишь полагать с постоянной в | пределах каждого плоского слоя, j Очевидно, что интегрирование какой- 1 либо функции по всему объему дан- ного тела можно приближенно заме- : нить суммированием значений этой функции, вычисленных для каждой |
из упомянутых пластин. Таким обра- i зом задача сводится к определению i вдоль осей координат градиентов си- j лы тяжести, создаваемых бесконечно тонкой горизонтальной пластиной, | ограниченной произвольным контуром, i Предлагаемый интегратор сводит эту задачу, в свою очередь, к механиче- : скому интегрирЬванию по контуру. Из вышеизложенного ясно, что контуры тех пластин, па которые мы разбиваем тело, будучи спроектированы на одну из секущих плоскостей, дадут план тела в горизонталях. Поэтому для производства вычислений достаточно массу, производящую аномалию, задать графически на плане, нанеся там же точку наблюдения (ауфпункт) и оси X н У.
Пусть гравит1ирующая масса имеет вид плоской бесконечно тонкой го- I ризонтальной пластины Т, ограниченной произвольным замкнутым конту- j ром S и имеющей постоянную по-
верхностную платность о. Возьмем систему цилиндрических координат с началом в центре тяжести коромысла вариометра. Паправим ось Z вертикально вниз. Пусть г - горизонтальное расстояние элемента пластины Т от оси Z и ф - его азимут, а Z Л - глубина залегания, по условию, постоянная для всех точек пластины Т. Обозначая потенциал силы тяжести в начале координат через U и гравитационную константу через k, будем иметь (если ось X совпадает с плоскостью ):
d-U /zr-coso , , ., ЗАО (2)
dxdz
(fi +
d4J / г-sines
ЗЬ 1- drdj (3) dydz
(
(CM. A. A. Михайлов. Курс гравиметрии и теории фигуры земли, 1933 г.). Если в формулах, приведенных на стр. 359 этого учебника, положить:
Ddz - z - Zo - h
ТО придем к вышеуказапным выражениям.
Перейдем теперь к сферической системе координат с тем же началом, отсчитывая угол О от оси Z и обозначая радиус-вектор через р. Имеем:
1
()(4)
r higfJ(5)
dr --, dr) fdfi(6)
COS-fjfl
1 - 1 r r ,r т -sm 6 cos 0 (7)
1 h (/z -f/--2)2
Обозначая интеграл для -j-j- по
всей поверхности Т через Uxz и таd U..
кои же интеграл для - , через Uyz,
а/У d
получим из формул (2), (3) и (7):
и. Зй - J sin 6 cos е cos 9 йЫ (8) т
Uy : Зй - J J sin б COS о sin- (9) т
Интегрируя по в от О до 0, переходим к интегралам по контуру S;
о J sin О cos О fife у sin4 (Ю)
L. ( sin ecos-f (11)
7у, |)sin 6sinc uf9 (12)
(тут Оно обозначают уже координаты контура S), Подставляя:
sinHj 1-sin 8 - sin 36 (13)
получаем:
1 о г Uxz -r-k --г (3 Ф sin 6 cos J d-f -
-(j)sin36cosc i 9)(14) iJyz -r- (3 d) sin б sin 9 -
-cj)sin30sin-pfi 9)(15) Если принять формулу (1), то:
fJxK 1Г JT (3 Ф sin е cos -
-(i)sin30cosf rff)(16)
i
,, 1 , ДА Г . л j - Цуг -д- ди- -т-(3 Ф sm 6 sm sfiff -
-( sin Зе sin ср ф)(17)
Предлагаемый интегратор дает возможность получать величины:
Ф sin б cos f Ф Ф sin 6 sin и d- Ф cos cpuff sin 36 sin rf-з
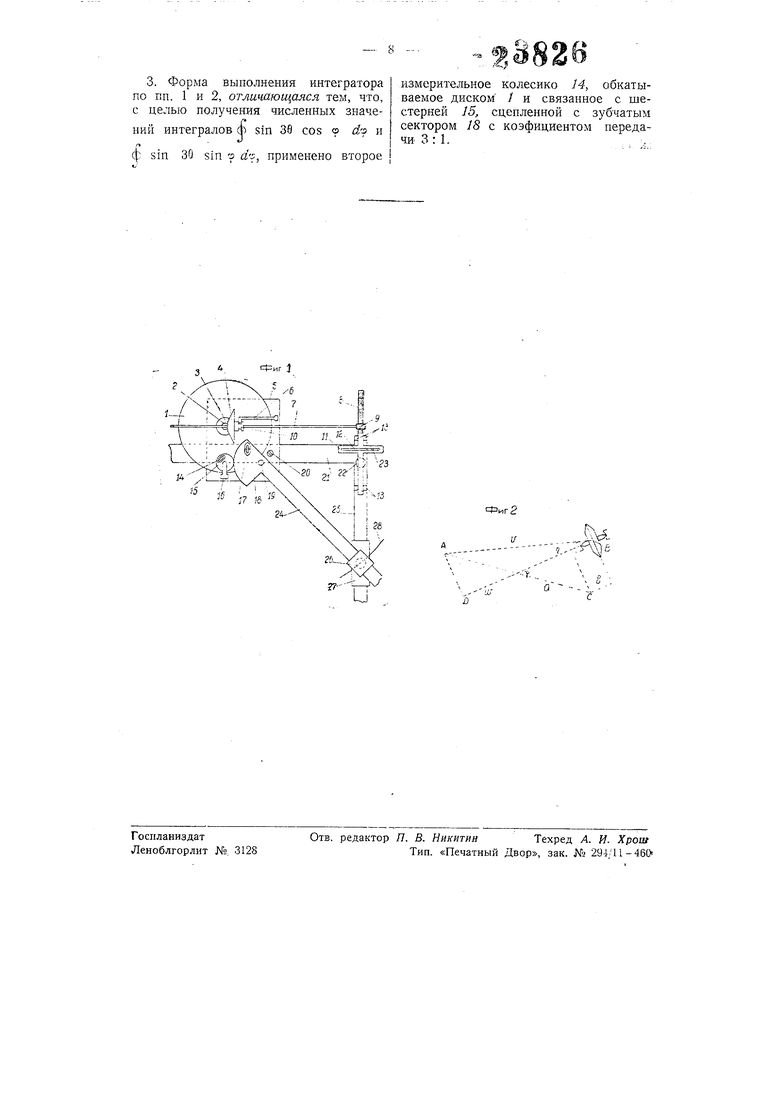
и таким образом вычислять Цгг и Uy по вышеприведенным формулам. . Сущность изобретения поясняется чертежом, на котором фиг. 1 изображает вид интегратора сверху, фиг. 2 поясняет теорию прибора.
Интегратор, в основном, состоит из системы рычагов, интегрирующего механизма, синусного механизма, передаточного механизма и подвижношарнирного соединения. Система рычагов и подвижно-шарнирное соединение не отличаются от таковых интегратора телесных углов (см. Бюллетень нефтяной геофизики, вып. IV, 1937 г. статья Е. Н. Л ю с т и х.- Простой механический интегратор для вычисления G-, а также авторское свидетельство № 49291 по кл. 42с, 12, выданное 31 августа 1936 г.).
Система рычагов образована, тремя горизонтальными стержнями 2J, 24 и 25. Рычаги 21 и 25 жестко соединены под прямым углом друг к другу и вращаются на неподвижной вертикальной оси 22, укрепленной в щтативе (на черт:ел е не показанном) прибора. С этими рычагами неподвижно скреплены направляющие /5 синусного механизма. По рычагу 21 может передвигаться каретка 5. Вдоль рычага 25 свободно движется ползун 27. Рычаг 24 вращается вокруг вертикальной оси 19, укрепленной в каретке 5. Вдоль рычага 24 свободно двигается ползун 26. С рычагом 24 наглухо соединен зубчатый сектор 18.
Интегрирующий механизм монтируется на каретке 5, которая может быть закреплена на рычаге 21 на любом расстоянии от центральной оси 22 с помощью стопорного винта 20. Каретка 5 несет на себе ось 2, водитель 6, стойку 16 и ось 9. На оси 2 вращается плоский горизонтальный диск }, жестко скрепленный с конической шестерней 3, которая получает вращение от конической шестерни 4. Водитель 6 представляет собой стойку с вилкой, входящей в кольцевой паз муфты 10, подвижной вдоль вала 7 при передвижении каретки 5 вдоль рычага 21. Стойка 16 поддерживает над диском- / вертикальную ось зубчатого колеса 15. Зубчатое колесо 15 находится в сцеплении с зубчатым
сектором 18, причем радиус колеса 15 втрое меньше радиуса сектора 18. В зубчатом колесе 15 имеется прорезь, в которой укреплено на горизонтальной оси мерительное колесико 14, катящееся по диску I. Мерительное колесико 14 соединено со счетным механизмом (иа чертеже не показанным), отсчитываюш;им число оборотов и доли оборота мерительного колесика 14. Мерительное колесико 14 установлено так, что при повороте рычага 24 в положение, перпендикулярное к рычагу 21, ось колесика 14 становится параллельно радиусу диска 1, проходящему через ось зубчатого колеса 15. В зубчатом секторе 18 имеется прорезь, в которой укреплено на горизонтальной оси мерительное колесико 17, катящееся по диску / и соединенное со счетным механизмом (на чертеже не показанным), отсчитывающим число оборотов и доли оборота мерительного колесика /7. Мерительное колесико 17 установлено так, что при повороте рычага 24 в положение, перпендикулярное к рычагу 21, ось колесика 17 становится перпендикулярно к радиусу диска 1, проходящемучерез ось 19.
Синусный механизм (см. М. Я. К р у г е р и Б. М. К у л и ж н о в. - Конструирование оптико-механических приборов. Л-,М. 1937 г., стр. 232-233) состоит из кулисы 11, в щель 12 которой входит неподвижный палец 23, укрепленный на штативе (па чертеже не показанном) прибора. Кулиса // перемещается вместе с зубчатой рейкой 8 в направляющих 13, которые жестко связаны с рычагами 2/ и 25 и вращаются вместе с этими рычагами вокруг оси 22. Возможен синусный механизм какойлибо иной конструкции.
Передаточный механизм состоит из зубчатой рейки 8, шестеренки 9, вала 7 и муфты 10 с конической шестерней 4. Зубчатая рейка 5, составляющая одно целое с кулисой //, при своем передвижении в направляющих 13 вращает вал 7 через посредство шестеренки 9. На валу 7 надета муфта 10, оканчивающаяся конической щестерней 4. Муфта 10 вращается вместе с валом 7, но может свободно
передвигаться вдоль него. Коническая шестерня 4 передает вращение вала 7 диску / через посредство конической шестерни 3. Муфта 10 снабжена кольцевым пазом, в который входит вилка водителя 6, благодаря чему шестерня 4 не может отойти от шестерни 3 и потерять с ней сцепление. Возможна и другая схема передаточпого механизма, например, движение кулисы 11 вдоль рычага 21 с заменой вала 7 длинной зубчатой рейкой, непосредственно связанной с кулисой, и конической шестерни 5- цилиндрической шестерней, непосредственно получающей вращение от этой зубчатой рейки.
Подвижно-шарнирное соединение может быть выполнено самыми различными способами, соблюдая при этом, чтобы рычаги 24 и 25 всегда перекрещивались над обводным штифтом. На чертеже показано соединение посредством двух ползунов 26 и 27, связанных вертикальной осью; обозначенной на чертеже пунктиром. Нижний ползун несет на себе снизу обводный штифт. Для действия прибора . безразлично, расположен ли стержень 24 выше или ниже стержня 25. Обводный штифт может быть заменен крестом, начерченным на прозрачной пластинке, скользящей по чертежу, или иным указателем. Весь интегратор с помощью штатива укрепляется над горизонтальной чертежной доской так, чтобы обводным штифтом ползуна 27 можно было обвести любой контур 28 на приколотом к доске чертеже. На фиг. 1 показана только часть контура, а штатив, обводный штифт и доска не показаны.
Для вычисления величины градиента
d-U
силы тяжести вдоль оси иксов -.-,-
dxaz
создаваемого в точке Q каким-либо телом, план этого тела в горизонталях закрепляется на доске интегратора так, чтобы геометрическая ось вращения интегратора 22 нроходила через изображение точки Q на плане и чтобы прямая, соединяющая ось 22 и центр нальца 23, была перпендикулярна к нанесенной на плане координатной оси X. Каретка 5 закрепляется винтом 20 на рычаге 21 так, чтобы расстояние геометрической оси вращения 19 от оси 22 было равно в масштабе плана глубине залегания одной из горизонталей, подразумевая под глубиной залегания вертикальное расстояние данной горизонтали от точки наблюдения. Обводный штифт устанавливается в какой-либо точке MO избранной горизонтали, и записываются показания счетных механизмов при колесиках 14 и 17. Затем обводный штифт двигают по горизонтали до возраш;ения в исходную точку MO. Записывают опять показания обоих счетных механизмов. Эти oneрации повторяют для каждой горизонтали плана, устанавливая, конечно, каждый раз каретку 5 в новое положение на рычаге 21. Затем вычисляют для каждой горизонтали величину:
(/Ci«i-f Аз/г.г),
где
Л - глубина залегания данной горизонтали,
П - разность показаний (до и после обвода) счетного механизма при колесике 17,
П2 - то же для колесика 14.
KI и KZ - постоянные коэфициенты, зависящие от устройства прибора.
Сумма всех Uxz, умноженная на ., где f - предполагаемая плотность тела, АЛ - сечение горизонталей, даст нам искомую величину U.. для заданного тела.
Вычисление t/,,, ведется совершенно так же, с тем лишь отличием, что при обводе линия, соединяющая ось 22 с пальцем 23 должна быть перпендикулярна к координатной оси У.
Во время работы интегратора каретка 5 остается неподвижно закрепленной на рычаге 21 стопорным винтом 20. При обводе обводным штифтом контура 28 ползун 27 скользит вдоль рычага 25 и одновременно поворачивает этот рычаг, а с ним и все части интегратора, кроме штатива и пальца 23, вокруг оси 22. Ползун 27 увлекает с собой ползун 26, будучи связан с ним вертикальной осью. Ползун 26 при движении вдоль рычага 25 скользит по рычагу 24 и одновременно поворачивает этот рычаг, а с ним и зубчатый сектор 18, вокруг оси 19. При этом мерительное колесико 17, укрепленное на секторе 18, изменяет свое положение относительно оси вращения диска 1, не теряя фрикционного сцепления с этим диском. Зубчатый сектор 18, вращаясь, поворачивает зубчатое колесо 15, благодаря чему мерительное колесико 14 тоже перемещается относительно диска /. В ,то же самое время при вращении всего интегратора вокруг оси 22 кулида //, придерживаемая неподвижным пальцем 23, передвигается в направляющих /5 вместе с зубчатой рейкой 5. Рейка 8 вращает шестеренку 9; это вращение передаточным механизмом передается диску /. Диск /, пробегая под мерительными колесиками 14 к 17, вращает их. Счетные механизмы этих колесиков отсчитывают обороты и доли оборотов.
Рассмотрим прежде всего, как зависит число оборотов мерительного колесика от его положения относительно диска. Пусть мерительное колесико (фиг. 2) прижимается к диску в точке В на расстоянии v от оси вращения диска Л. Пусть прямая BD представляет собой геометрическую ось вращения мерительного колесика. Опустим на эту прямую из точки А перпендикуляр, который пересечет ее в точке D на расстоянии W от точки В. Пусть деталь, поддерживающая мерительное колесико, поворачивается вокруг оси С. Положение колесика относительно этой детали фиксируется расстоянием b от точки С до плоскости ободка колесика и расстоянием от точки Ci до его оси вращения. Обозначим через угол между осью колесика и прямой, соединяющей точки Л и С, и через п - угол между осью колесика и радиусом диска, проходящим через точку касания В.
Если диск повернется на бесконечно малый угол da, то точка В пройдет по поверхности диска путь
(18)
ds v da и ободок мерительного колесика повернется на дугу dl cosTi ds г cos-Г) (/я оя (19) Следовательно, элементарная дуга поворота колесика всегда равна произведению элементарного угла поворота диска на расстояние от оси диска до плоскости ободка колесика. Применяя это правило к вращению детали, поддерживающей колесико, вокруг оси С при неподвижном диске (что равносильно вращению диска вокруг оси С), получим в этом случае:dL b-dl(20) где ds, - элементарный угол поворота упомянутой детали. Если происходят оба вращения одновременно, то dl i }-du- b-db(21) ffi/ acosi-r 5
Подставляя формулу (22) в (21) и интегрируя, получаем:
я J cos 6 do. L 5 J «я -;- b J (23)
Однако счетный механизм показывает не длину дуги I, а число оборотов п. Обозначая радиус колесика через с, имеем:
.сп(24)
Следовательно, а f п - I COS6(a-|+41В интегрирующем механизме предлагаемого прибора вращение диска производится синусным механизмом, а угол 9 для каждого колесика определяется положением системы рычагов. В теории интегратора телесных углов, система рычагов которого тождественна рассматриваемой, доказывается, что угол между рычагами 24 и 21 всегда равен в (см. Бюллетень нефтяной геофизики, вып. IV, 1937 г..
Действие синусного механизма видно из фиг. 1 чертежа. Когда система рычагов приведена в такое положение, что направление движения рейки S в направляющих 13 перпендикулярно к прямой, соединяющей центр пальца 23 с геометрической осью вращения интегратора 22, то средина щели 12 совпадает с осью 22. При повороте системы рычагов из этого положения на угол ср, щель 12 отойдет от оси 22 на расстояние: Е. Н. Л ю с т и X. - Простой механический интегратор для вычисления С,, I а также авторское свидетельство j Afb 49291 от 31 августа 1936 г.). ПриI нимая это во внимание, нетрудно видеть из описания интегрирующего механизма и фиг. 1чертежа, что угол между осью колесика 17 и прямой, соединяющей оси 2 и 19, всегда равен . Поэтому для колесика 17 в формуле (25) надо положить: - ; Так как зубчатое колесо /5 поворачивается на втрое больщий угол, I чем зубчатый сектор 18, то для мерительного колесика 14 будем иметь: + 30 /6 15 sin где q - расстояние пальца 23 от оси 22. Настолько же, очевидно, передвинется и зубчатая рейка 8. При изменении угла 9 на бесконечно малую величину df рейка 5 передвинется на cossd (31) Если К - коэфициент, зависящий от устройства передаточного механизма и указывающий отнощение угла поворота диска 1 к линейному передвижению рейки 8, то предыдущая формула дает: с/ос Kdt Kq cos d 9 (32) Пусть Ci - радиус мерительного колесика П, п - отсчет его счетного механизма, Са и П2 - то же для колесика 14. Из формул (25), (26), (27) и (32) получаем: ааК с . f., . «1 9 sin О COS 9 Й9 --f | lcos cf -H cfrf6 (33) .6 b Последние два члена тождественно равны нулю, так что остается: «1 --- Ф sin б cos V d- (34) eJ Таким же образом из формул (25), (28), (29) и (32) получаем: - - -§ { sin 03 cos 9 (35) J Чтобы угол Y в этих формулах соответствовал углу ср в формуле (16), необходимо расположить план гравитирующего тела на доске интегратора таким образом, чтобы координатная ось X на- плане была перпендикулярна к прямой, соединяющей ось 22 и палец 23. Если повернуть чертеж из этого положения на 90° (или переставить соответственно палец 23), то вместо формул (34) и (35) будем иметь: aqf{ С . ,, . . «1 ф sin б sin 9 б eJ 2 Ф sin 36 sin 9 d-f (37) С.) tj Сопоставляя формулы (34) и (35) с (16), получаем: T. f Щ. я, 2.aqK , / (8) Суммируя значение f/.v Для всех горизонталей, получаем величину градиента вдоль оси X для всего тела (при равномерном сечении горизонталей) -(3.,, Для подсчетов, быть может, удобнее это выражение представить в виде: К.1 (40) K-.V h Ц,., fiA/z {/Ci / -Г--Г где Al и /(2 - коэфициенты, определенные раз навсегда по формулам: Формзлы (36) и (37) в сопоставлении с формулой (17) дают точно такое же выражение для градиента вдоль оси У для всего тела: . ,АМ/С,) (43) ля 11ляя II / Разница лишь та, что отсчеты п и Пч производятся при другом расположении плана на доске интегратора. Во всех случаях следует обращать внимание, чтобы знаки у П| и соответствовали теоретическим. Выше был указан несколько иной порядок суммирования при тех же значениях /Ci и /Са. Предмет изобретения. 1.Интегратор для вычисления горизонтальных градиентов ускорения силы тяжести по плану с горизонталями гравитирующего тела, выполненный в виде интегратора по авторскому свидетельству № 49291, отличающийся тем, что для обкатывания измерительного колесика /7 применен лобовой диск 7, монтированный на подвижной вдоль полярного рычага 2/ каретке 5 и вращаемый синусным механизмом, с целью получения численных значений интегралов типа ф sin 6 cos 9 rf и Ф sin б sin vd 2.Форма выполнения интегратора цо ц. 1, отличающаяся применением- в качестве синусного механизма - кулисы //, расположенной в скользящих направляющих /5 радиального рычага 25, взаимодействующей с неподвижно установленным в штативе интегратора пальцем 23 и снабженной кремальерой 8, приводящей во вращение лобовой диск при помощи передачи 9, 7, 4 w. 3.
3. Форма выполнения интегратора по пп. 1 и 2, отличающаяся тем, что,
с целью получения численных значеНИИ интегралов ф sin 36 cos 9 и
ф sin 30 sin f af, применено второе
измерительное колесико 14, обкатываемое диском / и связанное с шестерней J5, сцепленной с зубчатым сектором 18 с коэфициентом нередачиЗ:1.






| название | год | авторы | номер документа |
|---|---|---|---|
| Интегратор для измерения телесных углов | 1936 |
|
SU49291A1 |
| Аппарат для автоматического выполнения совместной горизонтальной и вертикальной топографической съемки | 1932 |
|
SU37857A1 |
| Механический интегратор | 1982 |
|
SU1034047A1 |
| Механизм для перемещения плоской торцевой поверхности инструмента касательно к поверхности шестеренного зуба эвольвентного профиля | 1946 |
|
SU69852A1 |
| Тахеометр | 1983 |
|
SU1165131A1 |
| ПРИБОР ДЛЯ ПОСТРОЕНИЯ НАГЛЯДНЫХ ИЗОБРАЖЕНИЙОБЪЕКТА | 1968 |
|
SU211795A1 |
| Интеграф | 1949 |
|
SU97011A1 |
| Механическое вычислительное устройство | 1980 |
|
SU935975A1 |
| Гармонический анализатор | 1937 |
|
SU62684A1 |
| Полярный интеграф | 1958 |
|
SU120653A1 |

сриг J
if

Авторы
Даты
1940-01-01—Публикация
1938-11-19—Подача