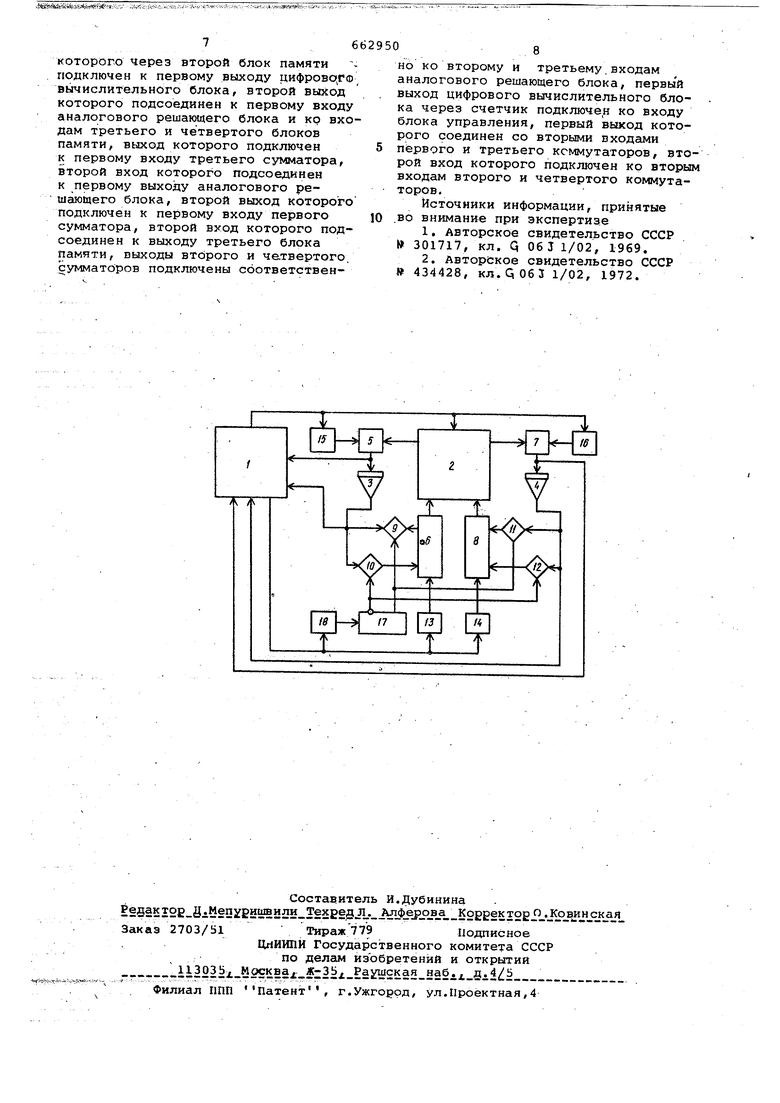
. , 1 . Изобретение относится к области гибридной вычислительной техники и может быть использовано в с6став«г цифровых машин, а также автономно для быстрого решения систем дифференциальных уравнений с высокой . (цифровой) точностью. Известно цифровое вычислительное устройство для решения обыкновенных дифференциальных уравнений, содержа щее цифровой автомат, блок синхрони зации, коммутатор, согласующий регистр l . Наиболее близким техническим реш нием к изобретению является гибрид,ное устройство для решения систем дифференциальных уравнений, содержа щее цифровой вычислительный блок, интеграторы, блоки памяти, аналоговый решаюйщй блок и блок управления 2 . недостатком известных устройств является их сложность. Целью изобретения является упрощение устройства. Указанная цель достигается тем, что в устройство рведёны коммутаторы, счетчик и сумматоры, выход первого, сумматора непосредственно подкл чен к первому ЛХОДУ цифрового вычислительного бло ка и через первый интегратор ко второму входу цифрового вычислительного блока и к первым.входам первого и второго коммутаторов, выходы которых подключены соответственно к первому и второму входам второго сумматора, третий вход которого через первый блок памяти подключен к первому- выходу цифрового вычислительного блока, третий вход которого подключен к выходу третьего сумматора, соединенного через второй интегратор с четвертым входом цифрового вычислительного блока и с первыми входами третьего и четвертого коммутаторов, выходы которых подключены соответственно к первому и второму входам четвертого сумматора, третий вход которого через второй блокпамяти подключен к первому выходу цифрового вычислительного блока, второй выход которого подсое- динен к первому входу аналогового решакнцего блока и ко входам третьего и четвертого блоков памяти, выход которого подключен к первому входу третьего сумматора, второй вход которого подсоединен к первому выходу аналогового решающего блока,второй выход которого-подключен к первому входу рервого сумматора,второй вход которо662950го подсоединен к выходу третьего бло ка памяти, выходы второго и четвертого сумматоров подключены соответст венно ко второму и третьему, входам (аналогового решающбгб блока, первый (выход цифрового вычислительного блок через счетчик подключен ко входу бло управления, первый выход которого соединен со вторыми входами первого и третьего коммутаторов, второй вход которого подключен ко вторым входам jsTOporo и,четвертого коммутаторов. I ria чертеже представлена структурная схема гибридного устройства для решения систем дифференциальных ура внений. Устройство содержит .вьгчислительный блок I, аналоговый решающий блок,2, интеграторы 3, 4, сумматоры 5-8, коммутаторы 9-12, бло ки, памяти 13-16, блок управления 17 и; счетчик 18, . Исходная система нелинейных дифференциальных уравнений % i{z,7.(o) o (1) в известном устройстве решается ите рационным методом Пикара. ria первой итерации счетчик записывает в тригг единицуf на прямом выходе триггера Имеется высокий потенциал, одна группа коммутаторовj подключающих . входы интеграторов.к выходам аналог вого блока, замыкается. Аналоговый решающий блок и интеграторы образую на первой итерации структуру, кото рая решает систему уравнения, анало гичную (1) А .. . y i{yiV,yi(o) yio,. (2) гдеи1 гf ( аналоговая (прибл1 женная) реализация нелинейных зависимостей . i(i),y,();; Уд- начальные условия, устанав ливаемые в интеграторах; Д2д- .погрешность установки н,ачальных условий. Решение системы (2) и его производная вводятся в вычислительный цифровой блок, где они демасштабируются: 4.1 аУ1- (4) Здесь и далее для простоты мы прёд полаГаём, что масштабы по переменны и их производным одинаковы. . Вычислительный цифровой блок с использованием величин (3), (4) вычисляет невязки i(Vz;, (5) й2,о о-МоУоъ (6) Далее вычислительный цифровой бл вычисляет величины V-MiE,, (7) . 8) где масштаб второй итерации. ri-i второй и последующих итерациях риггер находится в нулевом состояии, входы интеграторов отключены т аналогового решающего блока и подлючены через вторую группу коммутаторов к блокам памяти, на второй итеации, в б,локи- памяти записываются ункции (7), в интеграторах устанавливаются начальные условия (8) и реается таким образом система уравнеНИИ I . uy;-b Mi l{Zibziil-, uyj(o)-uy,o.(9) Величины Ду и Ayj вводятся в вычислиельный цифровой блок и демасштабируютсяI - . , (10) u2,j M;4yJ/ (11) после чего вычислительный цифровой блок вычисляет новые решения .j,4AZ,i, (12) 21 7.,-t-Az,. (13) ЬаШ-й итерации решается система . (.l (4) ynito A Izo-2;(o). Система (14) может быть решена аналитически, ее решение после демасштабирования имеет вид: :.t (15) где да гпо - погрешность установки на.чальных условий на итерации. полняя суммирование типа (12) , получаем новое приближение решения: . (16) t ,r.i(o)ji(Zrr,c5t,Огде 2.j,(0)2o+A2 o. Формула (16) описывает метод Пикара итерационного решения системдифференциальный уравнений. Вычислительный цифровой блок 1 осуществляет ввод и вывод информации. ria первой итерации блок управления, выполненный в виде триггера 17, находится в единичном состоянии,.на его прямом выходе имеется высокий потенциал, коммутаторы 9 и 11 замкнуты, крммутаторы 10 и 12 разомкнуты. Блоки памяти 13-16 на первой итерации на всем интервале решения выдают на выходах нули.{ria первой итерации устройство решает систему (2). Решение системы (2) и его производная вводятся в вычислительныйцифровой . блок, где они демасштабируются в соответствии с выражениями (3), (4). Далее вычислительный цифровой блок вычисляет невязки | и SID по формулам . (5) и (6) и величины Ь и д у |g по формулам (7) и (8) . ria высших итерациях блок управления 17 находится в нулевом состоянии , i коммутаторы 9 и 11 разомкнуты, коммутаторы 10 и 12 замкнуты, началь- ные условия в интеграторах 3 и 4 ус танавливаются равными / Уш Л Я о-МоУ Ю). Величины bi в соответствии с формуло (7) являются функциями времени, они записываются в блоки памяти 15 и 16. Кроме того, вычислительный цифровой блок засылает в блоки памяти величины у j. MO 2-1 . Таким образом, в устройстве решается система уравнений yi-(yi FiAai)Mi iUj-a; -Moz;,. y,.(o)l. ..г (1&) Уравнения (18) при нулевых значениях невязок (см.(5)) и начальных условий АУ,, (см. (17)) имеют нулевые решения. Действительно, линеаризуя функцию i( ду) , для этого случа получим уравнения AUlMytl-Mo lTtW-fb iyj uyi(o) 0, ) I - матрица Якоби L9y; J ii bi функции i (у). Учитывая (2), получаем тождество . - ,. .после чего система (19) приобретает , uyi(. (21) Система (21) является линейной, однородной, с нулевыми начальньмн условиями. Такая система имеет нулевые решения. Таким образом, появление поправок на выходах интеграторов 3 и 4 при решении уравнений (18) выз вано наличием в блоках памяти невязок (5), увеличенных масштабом. Поправки ду иду , вводятся ввычис тельный цифровой блок,который их демасштабирует в соответствии с формул ми (10) и (11) и вычисляет новое при ближение ршйения г и его производну zj по формулам (12) и (13) .Яа этом. вторая итерация заканчивается.Прслед ющие итерации проводятся по схеме вт рой итерации. Ham-и итерации вычисления ведутс вычислительным цифровым блоком, в блоки памяти 15 и 16 заносятся вели чины . -f .1, V (22).: в блоки памяти 13 и 14 - величины . , (23) в интеграторах 3 и 4 устанавливаются начальные, условия yaioA mt o-M- U lo). (24) Ов i В устройстве решается система уравн ений lAym-ilym f mAam bm ). Ду р.С25) Поправки луп,и 4у , получаемые на выходах Интеграторов 3 и 4 и сумматоров 5 и 7,вводятся в вычислительный цифровой блок, который их демасштабирует по Формулам 1-1 m 7 3т (27) и вычисляет (т+1)-ве приближение решения , . увеличением числа итераций томасштабы Mm возрастают и поправки (26}f (27) уменьшаются по абсолютной величине. Вычисления прекращаются естественны} образом, когда невязки (%)-2;;,.2.-м;у(о) превращаютсяв машинные нули цифрового блока. В этом случае поправки тоже будут равны нулю. Вычисления могут быть прекращены несколько ранее, а именно, при выполнении условия , где об - допустимая погрешность решения. . . . Использование новых элементов выгодно отличает устройство от известных технических решений. Формула изобретения Гибридное устройство для решения систем дифференциальных уравнений, содержащее цифровой вычислительный .блок, инте.граторы76лЬкипамяти, аналоговый решакяций блок и бЯок управления, от л и ч а ю щ в е с я тем, что, с целью уйрощенйя устройства, в него введены коммутаторы/ и сумматоры/ вькЬд первого сумматора непосредственно подключен к первому входу цифрового вычислительного блока и через первый интегратор ко ;второму входу цифрового вычислитель ного блока и к первым входам первого и второго коммутаторов, выходы которых подключены соответственно к первому и вторсму входам второго сумматора, третий вход которого через первый блок памяти подключен к первому выходу цифрового вычислительного блока, третий вход которого подключен к выходу третьего сумматора, соединенного через второй интегратор с четвертым вхоДом цифрового вычислительного блока и с первыми входами третьего и четвертого коммутаторов выходы которых подключены соответственно к первому и второму входам етвертого сумматора, третий вход
которого через второй блок памяти подключен к первому выходу цифрово ГФ, вычислительного блока, второй выход которого подсоединен к первому входу аналогового решающего блока и ко входам третьего и четвертого блоков памяти, выход которого подключен к первому входу третьего сумматора, второй вход которого подсоединен к первому выходу аналогового решающего блока, второй выход которого подключен к первому входу первого сумматора, второй вход которого подсоединен к выходу третьего блока памяти, выходы второго и четвертого, сумматоров подключены соответствен8
но ко второму и третьему.входам аналогового решающего блока, первый выход цифрового вычислительного блока через счетчик подключен ко входу блока управления, первый выход которого соединен со вторыми входами первого и третьего коммутаторов, второй вход которого подключен ко вторы входам второго и четвертого коммутаторов.
Источники информации, принятые .во внимание при экспертизе
1,Авторское свидетельство СССР I 301717, кл. Q 06 3 1/02, 1969.
2.Авторское свидетельство СССР 434428, кл. Q063 1/02, 1972.


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для решения дифференциальных уравнений в частных производных | 1979 |
|
SU781840A1 |
| Устройство для моделирования трубопроводных систем | 1978 |
|
SU750520A1 |
| Устройство для решения систем дифференциальных уравнений | 1977 |
|
SU674030A1 |
| Устройство для решения систем линйныхАлгЕбРАичЕСКиХ уРАВНЕНий | 1978 |
|
SU824217A1 |
| Устройство для решения систем алгебраических уравнений | 1977 |
|
SU674051A1 |
| Устройство для расчета режимов трубопроводных сетей | 1981 |
|
SU1007111A1 |
| Устройство для решения системлиНЕйНыХ уРАВНЕНий | 1979 |
|
SU830396A1 |
| Устройство для решения краевых задач | 1989 |
|
SU1624489A1 |
| Устройство для вычисления обратной функции | 1980 |
|
SU942035A1 |
| Вычислительная система для решения дифференциальных уравнений | 1978 |
|
SU771674A1 |


Авторы
Даты
1979-05-15—Публикация
1977-02-01—Подача