1 Изобретение относится к дискретным беспоисковым самонастраивающимся системам автоматического управления для нейтральных объектов и может быть . .с спользовано, например, в самонастраивакйцихся системах управления движением летательных аппаратов при незвестйых заранее значениях коэффииента эффективности управления- объ- JQ екта и внешнего возмущения.
.Известна дискретная самонастраивающаяся система, содержащая ключ, соединенный через корректирующее устройство с фиксирующим звеном нулевого порядка, 6 блоков памяти, 7 бло- 5 ков суммирования, 6 блоков усиления, 2 блока умножения и 2 блока деления р.. Недостатком известной системы является наличие, большого количества блоков памяти, суммирования, умноже- 2U ния и деления, аппаратурная реализуемость которых особенно затруднительна, и дополнительного корректирующего устройства. Кроме того, эта система е обладает недостаточно высоким быстродействием, так как необходимые для . идентификации неизвестных параметров объекта управления условия создаются только через время, равное трем периодам дискретности системы. 30
Наиболее близкой к предлагаемой по технической сущности и достигае- мому результату является дискретная самонастраивающаяся система, содержащая последовательно соединенные первый- сумматор и коммутатор, первый выход которого соединен с первыми входами второго и третьего сумматоров, а через первый блок памяти со вторым входом второго сумматора, а также третий блок памяти, вход и выход которого подключены к соответствующим входам четвертого сумматора выход которого через последовательно соединенные блок деления и блок умножения подключен к первому входу пятого сумматора, второй вход которого подключен к выходу четвертого блока памяти и первому входу шестого сумматора, а выход через последовательно соединённые четвертый и пятый блоки памяти и шестой сумматор подключен ко второму входу блока деления, а через фиксирукндие., устройства нулевого порядка - ко входу объекта, выход которого соединен с одним из входов первого сумматора ,
Недостатками ее являются низкая динамическая надежность и ыедос аточное быстродействие.
Цель изобретения - повышение динамической надёжности и быстродействия система.
Поставленная цель достигается тем, что в системе выход первого блоха памяти соединен со вторым входом третьего сумматора, выход второго бло)(а памяти соединен с третьими входами второго и третьего сумматоров, выход третьего сумматора соединен со входом третьего влока памяти и четвертым входом второго сумматора, выход которого соединен со вторым входом блока умножения.
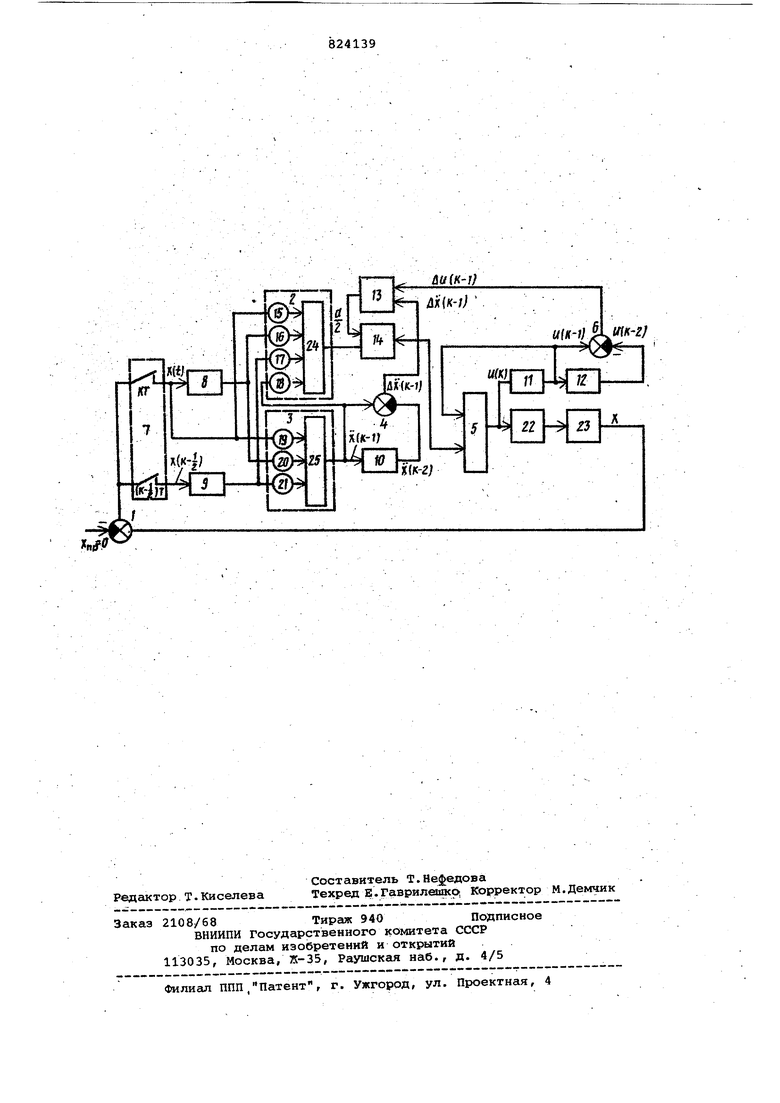
На чертеже представлена блок-схема системы.
Схема содержит первый 1, второй 2 третий 3, четвертый 4, пятый 5 и шестой б суммато1 л, коммутатор 7, первый 8, второй 9, третий 10, четвертый 11 и пятый 12 блоки, памяти, блок 13 деления, блок 14 умножения, первый 15, второй 16, третий 17, четвертый 18, пятый 19, шестой 20 и седьмой 21 масштабирующие элементы, фиксирующее устройство .22 нулевого порядка, объект 23, первый 24 и второй 25 суммирующие элементы, регулируемую координату X, управляющее воздействие О, первую X и вторую х производные регулируемой координаты, дискретный момент k времени .
Движение объекта 23 описывается линейным дифференциальным уравнением второго порядка
aU(t) + f(t)
x(t)
(1) де x(t)
- .значение выходной регулируемой кординаты объекта 23 в момент времени t;
X(t) - 3 начение ускорения . этой координаты в тот же момент времени,
и(t) и f(t) - значения соответственно, входного управляющего и входного возмущающего воздействий в мрмент времени t, а коэффициент эффективности управляющего воздействия.
В векторно-матричной форме уравение (l) имеет вид
xltl
00 10
ot
UW+
iW xW
vH)«Axlt)+BUW4CPW,,
где
т
00
a
,B
,c
.A
iltl
10
Поскольку згодача самонастройки рицается в дискретной системе, то представим указанное уравнение в вийе векторно-матричного раз ностного уравнения параметров состояния. При этом получаем
IxlkM)
xUV
и1к)4т2
аТ. T
0 Ti
MX) |x()
xlKj «2
t г
)-Фх(к)+Н.ии)),
де X(R), x{k+l) - .значения регулируемой координаты . в дискретные МО-. менты времени и t(k+1)Т (,1,2,...), соответственно,
x(k) , x(k-H) значения скорости изменения этой координаты в те же моменты времени, период Дискретности (период опроса) системы,
U(k)
управляющее воздействие , кусочнопостоянное на каждом периоде дискретности (k+1 )Т-kT;
f(k)
- входное возмущаю- . щее воздействие, кусочно-постоянное на каждом периоде дискретности (k+1)T-kT(k 0,l ,2)
Алгоритм управления дискретной самонастраивакяцейся системы примем в виде линейной структуры
U(k)kx.x(k)+kx.x(k)+kjf(k) (k)
Из сравнения соотношений (1) и (3) получаем, что для выполнения условия .инвариантности движения системы по отношению к внешнему возмущению:, f(k) необходимо обеспечение равенства
+ 0,т.е.
Примем, что во время работы системы реаается задача идентификации f(k) и при полученном значении коэффициента закона управления k (j) обеспечивается компенсация f(k).
Тогда для анализа динамики замкнутой системы примем алгориткы управления (3) в более простом виде
ilR)
и(к)кхх1к).х(к
K-x.kx
Пк
Устойчивость к качество переходных процессов в замкнутой дискретной системе определяются собственными значениями , матрицы этой системы.
ИЗ соотношений (2) и (5) получим выражение для матрицы замкнутой системы
Ф + Н /kx, kx/ Известно, что для устойчивости замкнутой дискретной системы необхо димо и достаточно, чтобы указанные собственные значения Д Jig находи лись внутри окружности единичного радиуса, т.е. по модулю были бы меньше 1, а форма г|ереходных процес сов исвязанные с ней перерегулиро вание и время переходного процесса) определялась распределением этих значений внутри окружности единичного радиуса. В соответствии с этим собственны значения матрицы замкнутой системы определяются из соотношения ае1|лЕ-Фэ| (иД+Моф-а 1(71-Л2), где , Я-г собственные значения матрицы замкнутой системы (U, Д. - -Л 2 ,( коэффициенты характеристического многочле на этой матрицы; Е - единичная матрица размерами (2 . 2), символ det обозначает операци вычисления определителя матрицы После несложных преобразований п лучаем (u,-2-aTKi-b-jKx,fUo i+o{TKx-a к Из этих соотношений при заданных предварительно значениях JUo , (U и вычисленном коэффициенте а определи требуемые значения коэффициентов ал горитма управления (,5) в виде i i(o-(U.-3),Kx(-(u,-pJ,);. Таким образом, выражение для пол ного алгоритма управления 3) принимает вид ииь1р ы :М-1)хЦ ))) ь;...,-я,.л,а-5) Ьх.(Я,.) заданные постоянные коэффициенты, значения которых задаются предварительно в зависимости от требований ,к движению дискретной замкнутой сие- темы и в процессе движения системы, не изменяются. Следовательно, предварительно задавая необходимые, (желаемые) собственные значения Л , 7 g (и соответ ствующие им коэффициенты (li, 2 Hpj(j . 2) и определяя в процессе нормального функционирования замкнутой систекы фактически .(возмущенные) значения параметра объекта управлёния (1)(а - коэффициент эффективности управлякмцего воздействия) и внешнего возмущающего воздействия f(k), необходимо на основе соотношений (4) и (7) изменять коэффициенты kx, kx, k. алгоритма управления (3) и (7) таким образом, чтобы обеспечить требуемый характер движения замкнутой системой и независимость (инвариантность) его от значений а и f(k). Для решения этой задачи необходи- , МО идентифицировать параметр объекта управления 1/а, внешнее возмущение f(k) и неизмеряемую координату x(k) в процессе нормального функционирования cHCTefvftj, т.е. при отсутствии пробных (тестовых) воздействий, Для решения этой заДачи рассмотрим движение объекта управления (1) на интервале времени (k-l)T ( kT при условии, что.управлякщеевоздействие U(k) (3) и (7) формируется сразу же после момента времени . В реальных системах выходной измеряемой переменной обычно является выходная координата x(t). На рассматриваемом интервале времени, она изменяется при воздействии постоянного. .на данном интервале времени ускорения (k-1)+f(k-1) и начального значения скорости (k-1) в соответст.вии с уравнением x(t)Xg+Xgt + где XQ x(k-1) , kTer t (k-1)T , Более просто это соотношение можно представить в виде ,x(k-l)T+t -xpu-l)fl Xo-t ollO- ) Для определения двух неизвестных XQ, необходимого в дальнейшем для пределения Xo(k), и XQ, необходит рго для определения а и f(k), еобходимо использовать уравнеи.е (8) при двух значениях t. Поэтоу наряду с основным (первым) ключей, амыкающимся в -дискретные моменты ремени (k 0 ,1, 2, .. .) введен ополнительный (второй) ключ, замыагацийся с тем же периодом дискретости Т, но в моменты времени t (k-j-T) сдвинутые относительно осовного на половику периода дискретости . Таким образом, для двух искретных моментов времени замыкаия вспомогательного (второго) и осовного (первого) ключей t ( k - - Т получим на основе соотнсниения 8) совместную систему двух алгебраиеских уравнений . . . . .,. , j2 X K-lj-xtK-D X Xg . „т )-x(,K-l)XoT- -x - Из,этой системы .уравнений получае )+4x((u.-t) 4iR-l); (K-|j+xlKM)xlR-t aUU. ).- / , ,/ Поскольку X(k)x(k-1)-x(k-1)т, т получаем 4Ub xUb4x|K-i) + U-l). Для определения значений а и f и пользуем соотношения для определени , при t(k-1)T и t ( k.-2)T. В итоге получик систему уравнени x(k-1)aU(k-l) + f,{k-l) (I) x(k-2)aU{k-2)+f(k-2) Предположим, что на интервале вр мени идентификации kt-g t {k-2)T, равном двум периодам дискретности, объекта управления а и вне нее возмущение f являются постоянны т.е. f(k-2)f(k-1)f. Это допущение вполне приемлемо, так как в известных дискретных сист мах управления период дискретности .(период опроса) имеет достаточно ма лое значение. Тогда система уравнений принимает вид . x(k-1)aU(k-1)+fV x{k-2)aU(k-2)+f Из этой системы уравнений получа UiK- VUU-2V 4 axiK-ibxl -ar « UU-1bU{i4-2) . )- - Таким образом, используя соотнош ния (3), (4), (7), (9), (10) и (11) получаем выражение для закона управ ления дискретной самонастраивающейс системы в виде iUU-a) и1к1 и1к-1)4 Лхи-М) c,,j,x|k-i)(K4l, xivt- li C54Ul Cg,x(K-l)4CyX(4H), С Ьх+5.Ъ,С2 -4Ъх,Сз-,С4 И, CS-CT-, ,uOU-«) UUH)-UU AxU - U-2V -- Работа системы состоит в запоминании значений дискретных сигналов x(k-1)v. x(k-) с помощью блоков 8 и 9 памяти, суммировании сигналов x{k), x() и x(k-1) с соответству щим их масштабированием в элементах 15-17 и 19-21 с помощью сумматоров 2 и 3, формировании сигналов x(k-l) и i(k-2) с помощью сумматора 3 и блока 10 памяти, подаче промасштабиров нного элементом 18 сигнала x(k-l) на вход элемента 24 суммирования для учета при формировании управлякидего воздействия внешнего возмущения, формировании с помощью сумматора 4 сигнала x(k-l) для определения значения коэффициента эффективности управления объекта 23, запоминании с помощью блоков 11 и 12 памяти значений дискретных сигналов управляющих воздействий U(k-1)и U(k-2), формировании с помощью сумматора б сигнала bU(k-l), который совместно с .выходным сигналом Ax(k-l) сумматора 4 с помощью блока 13 деления позволяет определить значение - , где а - фактическое значение коэффициента эффективности управления объекта, умножении выходного сигнала сумматора 2 на полученный коэффициент усиления, задаваемый выходным сигналом блока 13 деления, с помощью блока 14 умножения и формировании требуемого управляющего воздействия U(k) с помощью сумматора 5, на входы которого поступают выходные сигналы с блока 11 памяти и блока 14 умножения. Управлягацее воздействие U(k) с выхода сумматора 5 поступает на фиксируквдее звено нулевого порядка 22 и через него на объект 23 управления. Через время создаются условия для идентификации значений коэффициента эффективности управления объекта а и внешнего возмущения f. На основе этих значений изменяются выходной сигнал сумматора 2 и козф.фициент усиления регулятора, реализуемый с помощью блока 14 умножения, так, чтобы определить оптимальное управление U(k) , которое обеспечит требуемую точнос.ть и надежность рабОты замкнутой системы при отсутстВИИ начальной информации о действительных значениях аи f. При этом характер переходного процесса замкнутой сИсте1 и независим от значения а и f, определяется только предварительно з-аданныМи собственными значениями матрицы замкнутой системы. Это приводит к повышению не только точности, но и надежности, как свойства системы сохранять свои характе ристики в заданных пределах при изменении условий функционирования системы непредвиденным образом. . Кроме того, в известной схеме, условия для идентификации коэффициента объекта управления а и возмущения f создаются только через время t-ЗТд. В предлагаемой схеме эти условия создаются раньше, чем время t 2Tcjf.e. эта схема является более быстродействующей. Указанный выход следует из конечного выражения для закона
управления регулятора. Для определения U(k) необходимо предварительно определить K(k-1)х(k-2)-х(k-2), а для вычисления $(k-2) необходимо измерение сигнала x(k-2).
Таким образом, в предлагаемой схеме условия для идентификации коэффициента объекта управления а и внеш- . него возмущения f создаются через. время , . После этого переходный процесс в замкнутой дискретной системе проходит в соответствии с заданными собственными значениями матрицы замкнутой системы и не зависит от значений а и f.
Следует отметить,-что в предлагаемом устройстве, в отличие от известного, отсутствует отдельное корректирующее устройство; что приводит к еще большему его упрощению.
Дискретный самонастраивающийся регулятор удовлетворяет условию физической реализуемости, так как для формирования управляющего воздействия U{k) требуется только текущая и прошедшая измеряемая информация о
U(k-1)/ x(k-i),x(k-l), x(k-1) и x(k-2).
Предлагаемый дискретный самонастраивающийся регулятор имеет простую структурную схему и выгодно отличается от известных аналоговых схем, так как для его реализации требуется минимальное количество типовых вычислительных устройств автоматики. Это позволяет не проводить большие и дорогостоящие исследования при проектировании дискретной системы управления, так как регулятор способен быстро-(в течение двух периодов прерывания) определять реальные значения коэффициента эффективности управления объекта и внешнего возмущения, а затем настроить коэффициенты закона управления заранее из вестной структуры с целью-обеспече:ния заданной цели управления.
Формула изобретения5 Дискретная самонастраивающаяся система, содержащая последовательно соединенные первый сумматор и комму. татор, первый выход которого соединен с первыми входами второго и тре10 тьего сумматоров, а через первый
блок памяти - со вторым входом второго сумматора, а также третий блок памяти, вход и выход которого подключены к соответствующим входам четвер5 того сумматора, выход которого через последовательно соединенные блок деления и блок умножения подключен к первому входу пятого сумматора, второй вход которого подключен к выходу Q четвертого блокапамяти и первому входу шестого сумматора, а выход через последовательно соединенные четвертый и пятый блоки памяти, и шестой сумматор подключен ко второму входу блока деления, а через фиксирующее
5 устройство нулевого порядка - ко входу объекта, выход которого соединен .с одним из входов первого сумматора, о т Ли ч а юща я с я тем что, с целью повышения динамической надежности и -точности с1:стемы,. в ней выход первого блока памяти соединен со вторым входом, третьего сумматора, выход второго блока памяти соединен с третьими, входами второго и третьего сумматоров, выход третьего сумма- . тора соединен со входом третьего блока памяти и четвертым входом второго сумматора, выход которого соединен со вторым входом блока . 0 умножения. - .
Источники информации, принятые во внимание при экспертизе 1,-Авторское свидетельство СССР №544942, кл. G 05 В 13/02, 02.04.73.
2. Авторское свидетельство СССР 5 по заявке № 2706577/18-24,
кл. G 05 В 13/02, 04.01.79 (прототип)
&U(K-1J




| название | год | авторы | номер документа |
|---|---|---|---|
| Самонастраивающаяся система комбинированного регулирования | 1986 |
|
SU1388826A2 |
| Дискретный самонастраивающийся регулятор | 1973 |
|
SU544942A1 |
| Самонастраивающаяся система комбинированного регулирования | 1986 |
|
SU1511734A1 |
| Самонастраивающаяся система комбинированного регулирования | 1985 |
|
SU1254433A1 |
| Самонастраивающаяся система комбинированного регулирования | 1986 |
|
SU1339494A1 |
| Самонастраивающаяся система | 1980 |
|
SU983649A1 |
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ | 2016 |
|
RU2616219C1 |
| Самонастраивающаяся система комбинированного регулирования | 1986 |
|
SU1386957A1 |
| Самонастраивающаяся система комбинированного регулирования | 1987 |
|
SU1509828A1 |
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА КОМБИНИРОВАННОГО РЕГУЛИРОВАНИЯ | 1989 |
|
RU2022313C1 |


Авторы
Даты
1981-04-23—Публикация
1979-06-04—Подача