Изобретение относится к вычислительной технике и может быть использовано при реализации двоичных линейных рекуpрент на элементной базе, ориентированной на многозначную логику.
Известен способ реализации n-разрядной двоичной линейной рекурренты с характеристическим многочленом
1⊕ x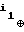 ... ⊕ x
... ⊕ x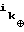 xn, 0< i1 < . . . . < ik < n,
xn, 0< i1 < . . . . < ik < n,
путем побитового сдвига n-разрядного двоичного регистра в сторону младших разрядов (с потерей выдвинутых за пределы регистра разрядов) и записи на освободившееся место суммы по модулю два первого, (i1 + 1)-го, . . . , (ik+1)-го битов исходного состояния регистра.
Данный способ осуществляет поразрядный сдвиг рекуpренты и требует выполнения операций над отдельными битами, что в ряде случаев бывает неудобно, так как усложняет и замедляет процесс обновления состояния рекурренты.
Целью изобретения является ускорение процесса работы рекурренты и исключение при этом операций над отдельными битами.
Цель достигается тем, что при реализации n-разрядной рекурренты осуществляют одновременный сдвиг ее на t ≅ n-ik разрядов, для чего сначала по модулю два суммируют k+1 исходных состояний реализующего рекурренту регистра, предварительно сдвинутых на 0, i1, . . . , ik разрядов в сторону младших разрядов, затем полученную сумму сдвигают на n-t разрядов в сторону старших разрядов и к результату прибавляют по модулю два исходное состояние регистра, предварительно сдвинутое на t разрядов в сторону младших разрядов.
Цель также может быть достигнута тем, что при ik ≅ n/2 осуществляют одновременный сдвиг рекурренты на n-ik ≅ t ≅ 2(n-ik) разрядов, для чего сначала по модулю два суммируют k+1 исходных состояний реализующего рекурренту регистра, предварительно сдвинутых на 0, i1, . . . , ik разрядов в сторону младших разрядов, затем из полученного n-разрядного двоичного числа сдвигом на t-n, 2n-t-i1, . . . , 2n-t-ik разрядов в сторону младших разрядов, если число отрицательное, и в сторону старших разрядов, если число положительное, получают k+1 n-разрядных чисел, которые складывают по модулю два, и к полученной сумме прибавляют по модулю два исходное состояние регистра, сдвинутое на t разрядов в сторону младших разрядов.
Одновременный сдвиг двоичной линейной рекурренты сразу на несколько разрядов осуществляется при помощи операций n-битной логики, причем количество требуемых для этого операций соразмерно с количеством двоичных операций, используемых в известном способе, для сдвига рекуррентны лишь на один разряд. Кроме того, если точки съема на регистре сдвига расположены так, что ik ≅ n/2, то предлагаемым способом можно сразу сдвинуть рекурренту на n разрядов и полностью обновить ее состояние.
Двоичная линейная рекуррента, задаваемая характеристическим многочленом
1⊕ x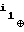 ... ⊕ x
... ⊕ x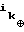 xn, (1) где 0 = i0 < i1 < . . . < ik < n; ⊕ - сложение по модулю два, переводит текущее состояние
xn, (1) где 0 = i0 < i1 < . . . < ik < n; ⊕ - сложение по модулю два, переводит текущее состояние
А = (a1, a2, . . . , an), ai = 0,1, i = 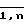 ,
,
в следующее состояние:
(a2, . . . , an, a1⊕ a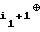 . . . ⊕ a
. . . ⊕ a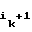 ).
).
Обозначим через At n-разрядное двоичное число, полученное путем сдвига А на t разрядов в сторону младших разрядов с потерей выдвинутых разрядов. Старшие t разрядов числа At нулевые.
Обозначим через A-t n-разрядное двоичное число, полученное путем сдвига А на t разрядов в сторону старших разрядов с потерей выдвинутых разрядов. Младшие t разрядов числа A-t нулевые. Очевидно, что An и A-n - n-разрядные нули.
В течение t ≅ n-ik тактов работы регистра вновь образованные биты зависят лишь от разрядов исходного состояния А, так как только в (n-ik+1)-й такт новый бит через (ik+1)-ю точку съема задействован в функции обратной связи. Поэтому состояние регистра через t ≅n-ik тактов работы имеет вид
At⊕ 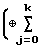 A
A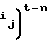 . (2)
. (2)
Формула (2) задает следующий порядок действий для получения состояния регистра через t тактов. Сначала по модулю два суммируются (k+1) исходных состояний А, предварительно сдвинутых на 0, i1, . . . , ikразрядов в сторону младших разрядов, затем полученная сумма сдвигается на n-t разрядов в сторону старших разрядов и к результату по модулю два прибавляется исходное состояние А, предварительно сдвинутое на t разрядов в сторону младших разрядов. Как видно, в описанной последовательности действий операций с отдельными разрядами нет. Кроме того, сдвигая рекурренту сразу на несколько разрядов, ускоряют в ней процесс обновления информации.
Если выполняется ограничение ik ≅n/2, то подобным образом рекурренту можно сдвинуть и на n разрядов, т. е. полностью обновить в ней информацию.
Пусть В - состояние рекурренты через n-ik сдвигов, а С - ее состояние через n сдвигов. Тогда в силу (2) справедливы равенства
B= A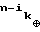
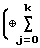 A
A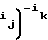 ;
;
C= B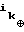
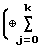 B
B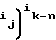 ,
,
так как ik ≅ n-ik.
Справедливы равенства
A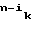 = (
= (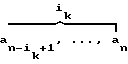 ,
, 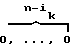 );
);
A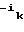 = (
= (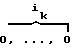 ,
, 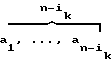 );
);
(A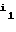 )
)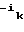 = (
= (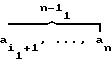 , 0, . . . , 0
, 0, . . . , 0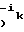 = (O, . . . , 0,
= (O, . . . , 0, 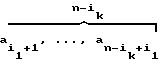 );
);
(A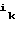 )
)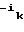 = (
= (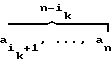 , 0, . . . , 0)
, 0, . . . , 0)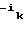 = (0, . . . , 0,
= (0, . . . , 0, 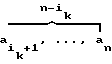 );
);
B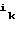 = (
= (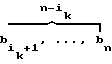 ,
, 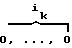 );
);
B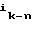 = (
= (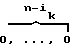 ,
, 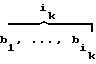 );
);
(B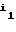 )
)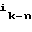 = (
= (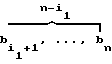 , 0, . . . , 0)
, 0, . . . , 0)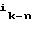 = (0, . . . , 0,
= (0, . . . , 0, 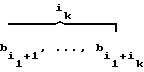 );
);
(B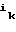 )
)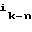 = (
= (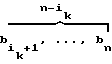 , 0, . . . , 0)
, 0, . . . , 0)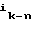 = (0, . . . , 0,
= (0, . . . , 0, 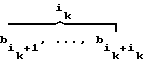 ).
).
Поэтому b1 = a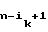 ;
;
. . . . . . . . . . . . . . . . . . . . . . . . . .
bik= an;
b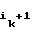 = a1⊕ a
= a1⊕ a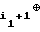 . . . ⊕ a
. . . ⊕ a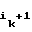 ;
;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
bn= a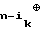 a
a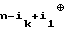 an;
an;
C1= b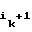 = a1⊕ a
= a1⊕ a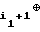 . . . . ⊕ a
. . . . ⊕ a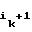 ;
;
. . . . .
C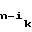 = bn= a
= bn= a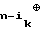 a
a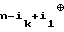 ... an;
... an;
C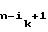 = b1⊕ b
= b1⊕ b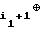 ... ⊕ b
... ⊕ b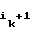 ; (3)
; (3)
. . . . .
Cn= b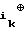 b
b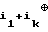 ... ⊕ b
... ⊕ b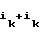 .
.
Отсюда
b1= a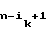 , . . . , b
, . . . , b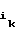 = an; b
= an; b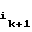 = c1 , . . . , b
= c1 , . . . , b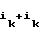 = c
= c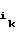 ,
,
так как ik ≅ n-ik.
Следовательно, равенства (3) можно переписать в виде суммы столбцов 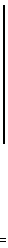
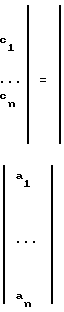
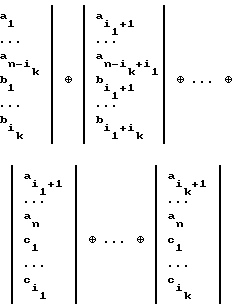
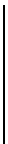
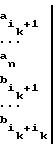 =
=
т. е. через n сдвигов состояние рекуррентны будет
D 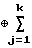 D
D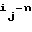 где D=
где D= 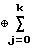 A
A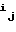 (4)
(4)
Формула (4) задает следующий порядок действий для получения состояния регистра через n тактов. Сначала по модулю два суммируются k+1 исходных состояний А, предварительно сдвинутых на 0, i1, . . . , ik разрядов в сторону младших разрядов. Затем из полученного n-разрядного двоичного числа сдвигом на 0, n-i1, . . . , n-ik разрядов в сторону старших разрядов получают k+1 n-разрядных чисел, складывая которые по модулю два, получают искомое результирующее состояние регистра.
Например, если 127-разрядная рекуррента задается характеристическим многочленом 1 ⊕ x63⊕ x127 , то через 127 тактов ее состояние станет D ⊕ D-64 , где D = A ⊕ A63, где А = (а1, . . . , а127) - исходное состояние, т. е. для получения состояния рассматриваемой рекурренты через 127 тактов надо сложить по модулю два исходное состояние с самим собой, сдвинутым на 63 разряда в сторону младших разрядов, а вновь полученное двоичное число снова сложить с самим собой, сдвинутым на 64 разряда в сторону старших разрядов.
(56) Гили А. Линейные последовательностные машины. М. : Наука, 1974, с. 41-45.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ "АЛБЕР" | 1991 |
|
RU2024209C1 |
| СПОСОБ ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ И УСТРОЙСТВО ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА - "АЛБЕР" | 1994 |
|
RU2099890C1 |
| УСТРОЙСТВО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ "АЛБЕР" | 1991 |
|
RU2050697C1 |
| УСТРОЙСТВО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ "АЛБЕР" | 1991 |
|
RU2007884C1 |
| СПОСОБ ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1995 |
|
RU2097931C1 |
| УСТРОЙСТВО ДЛЯ ПАРАЛЛЕЛЬНОГО ДЕЛЕНИЯ ЧИСЕЛ | 1991 |
|
RU2010311C1 |
| ГЕНЕРАТОР ФУНКЦИЙ ХААРА | 1991 |
|
RU2010308C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ НАТУРАЛЬНОГО ЛОГАРИФМА КОМПЛЕКСНОГО ЧИСЛА | 1991 |
|
RU2010312C1 |
| ЛИНЕЙНО-КРУГОВОЙ ИНТЕРПОЛЯТОР | 1991 |
|
RU2010293C1 |
| СИСТЕМА ЗАСЕКРЕЧЕННОЙ ПЕРЕДАЧИ И ПРИЕМА РЕЧЕВОЙ ИНФОРМАЦИИ, СИСТЕМА СИНХРОНИЗАЦИИ ДЛЯ СИСТЕМЫ ЗАСЕКРЕЧЕННОЙ ПЕРЕДАЧИ И ПРИЕМА РЕЧЕВОЙ ИНФОРМАЦИИ И УСТРОЙСТВО ШИФРАЦИИ ИЛИ ДЕШИФРАЦИИ ИНФОРМАЦИИ ДЛЯ СИСТЕМЫ ЗАСЕКРЕЧЕННОЙ ПЕРЕДАЧИ И ПРИЕМА РЕЧЕВОЙ ИНФОРМАЦИИ | 1996 |
|
RU2099885C1 |
Изобретение относится к вычислительной технике и может быть использовано при реализации двоичных линейных рекуррент на элементной базе, ориентированной на многозначную логику. Данным способом n-разрядная двоичная линейная рекуррента одновременно сдвигается сразу на несколько разрядов с использованием операций n-битной логики. При этом количество требуемых n-битных операций для сдвига рекурренты сразу на несколько разрядов соразмерно с количеством двоичных операций, необходимых для сдвига рекурренты лишь на один разряд. В ряде случаев данным способом можно сразу сдвинуть рекурренту на n разрядов и полностью обновить ее состояние. 1 з. п. ф-лы.
Авторы
Даты
1994-03-30—Публикация
1992-07-20—Подача