гих сечениях зуба что вызывает диагональ- ность контакта.
Предлагаемый способ позволяет профилировать зуб в требуемой зоне контакта и по длине зуба при переменном движении обкатки, начиная с профилирования зуба со стороны внутреннего торца и заканчивал наружным торцем колеса. Эти положения составляют существенные отличия способа.
На фиг.1 и 2 показана обработка вогнутой и выпуклой сторон кругового зуба соответственно, представлены схемы способа, где 1 - нарезаемое колесо с вершиной конуса О, Св. CD - положения оси резцовой головки, I - ширина венца колеса на котором располагается требуемое пятно контакта, m - расстояние от внутреннего торца колеса до начала пятна контакта. Коррекция переменным движением обкатки профиля зуба по всей длине производится следующим образом. Используя зависимости коррекции прототипа,
у ср cos Ф/ sin д (cos Доз ±
±sin Actitgcti) ,
Дед ±(«i -a),
a an ± arctg tq ft sin (pn - fk ) .
0)
i 1,2 для вогнутой и выпуклой сторон зуба соответственно, знаки (+) в выражении (1) представляются (+) для вогнутой и (-) для выпуклой сторон кругового зуба, Дсц - переменное угловое отклонение оси резцовой головки от нормали к начальной конической поверхности. а - угол между стороной зуба резцовой головки и нормалью к начальной поверхности конусно-вершинного производящего колеса, д - угол делительного коне- са /Jn - угол наклона средней линии впадины зуба, ал -угол профиля резцовой головки, у,у -углы поворота нарезаемого и производящего колеса, ft- угол ножки зуба колеса. Для определения зависимостей коррекции А«| по длине зуба установим изменение параметров 2Иу8п, как функции угла поворота производящего колеса с учетом процесса начала и конца обработки сторон кругового зуба. По формуле (1) прототипа коррекция профиля зуба производится в среднем сечении. Учитывая, что профилирование по длине кругового зуба с углом наклона / производится начиная с внутреннего торца и кончая наружным, угол по которому корректировался профиль зуба с среднем сечении по прототипу надо сделать переменным в соответствии с переменным законом профилирования кругового
зуба. Угол р2 будет переменным и будет изменяться от (рв до ра резцовой головки. Граничные условия обработки формы кругового зуба показывает, что углы образованные сторонами треугольниках ОСВ и ОСД0 является переменными, т.к. меняется конусное расстояние от 0В до ОД с поворотом производящего колеса. Зависимость изменения углов (pi , определяется по следующей схеме. По теореме косинусов выразим в общем случае углы , из треугольника ОСвВ, где OB Rxcos 0f
15
р их arccos A2 + (Ry cos Of f-r2 /2ARxcos Of,
Јxn arcsin r2 + (Rxcosft)2
/ 2 r Rx cos ft,
где А - радиус движения оси резцовой головки, г- номинальный радиус резцовой головки,
RX - переменное конусное расстояние. Конусное расстояние Rx меняется с поворотом производящего колеса на угол р и
является радиусом-вектором спирали Архимеда меняющимся от 0В до ОД. Выражение RX представляется в полярных координатах в виде Rx Ri + m + а (р где Ri внутренне
w конусное расстояние, а -г где V- посто°
янная скорость изменения радиуса вектора
Rx, ft - постоянная угловая скорость вращения радиуса вектора Rx. Представим скорости в виде
VH/t
о) (р )/t
I - ширина участка пятна контакта колеса;
рн ,РК углы начала и конца коррекции кругового зуба. Подставляя полученные выражения и делая преобразования, получим зависимости угловых поворотов нарезаемого и производящего колес, позволяющие нарезать круговые зубья конических колес с теоретически правильным профилем по длине контакта
jJ q COS6| 5mJ(co5UO i±SiTi&(; igA :0 Aoi-,-±C«;-(),0(; oip-|±arct {t 0Ј5in(cp1- A24(Rxco50f)V
-arccosЈARxcos0Ј
, A(Rxco50{)2-A2
.... f arcsm л оn
552гкхсо50.{
R,-B;4m + eip/(
Знаки (+) в выражении (2) аналогичны знакам зависимости (1). Учитывая особенности профилирования сторон кругового зуба при односторонней обработке, отметим, что стороны профилируются при разных углах поворота производящего колеса. Вогнутая сторона зуба профилируется от угла Зн1 (фиг.1) выпуклая от (фиг,2). С учетом определенных углов поворота производящего колеса необходимо составить программы корректирования профилирования сторон кругового зуба по формулам (2).
Доказательства выполнения коррекции профиля по длине кругового зуба конического колеса.
Исходные данные - коническое колесо с круговыми зубьями осевой формы 1. ГОСТ 19326-73.
Число зубьев Z 20. Модуль внешний окружной пгщ 4,5 Средний угол наклона зуба /Зт 35° на начальном конусе
Внешнее конусное расстояние RI 63,639607
Ширина зубчатого венца b 20 Среднее конусное расстояние Rm 53,639607
Внутреннее конусное расстояние Ri 43,639607
Угол делительного конуса д 45° Нормальный модуль mn 3,106565 Угол ножки зуба ,141189° Угол головки зуба Qa 4,141189 Внешняя высота зуба hi 8,4387221 Угол конуса впадин & 40,858811° Угол конуса вершин да 49,141189° Диаметр зуборезной головки 2г 3,5 , г « 44,45
Угол профиля исходного контура a 20.
Средняя нормальная толщина зуба резцовой головки Snm 2,6564476
Средняя нормальная ширина впадины зубьев колеса, bnm 4,88
Ширина развода резцов w 1.
По расчетным формулам прототипа определяются требуемые параметры. Известны граничные условия нарезания зубьев, где углы рн начала и ср конца обработки представляются зависимостями
Cjyarccos c-6 -ca)(-&2),
circcos c-D -c2)H-D2); (f,(piW/2)
3)()2 /2АГ; 90 } F Re/cos9Q -i
A4(Rmcos6 2r(Rmcos0|)sin/3n
Подставляя соответствующие параметры в формуле после расчетов имеем А - 45,88747, 90,25945°, 13,41283°.
Для параметров коррекции примем I 14 мм, m 3 мм. Определим значения углов
рв arccos
arccos
:R,+m)2-r2 А( RI + m )
A2 + RI - m ) - г2
2 A ( RI - m )
Подставляя параметры в формуле после расчетов, имеем рв рнг 53,39954°, ро рк, 46,83745°.
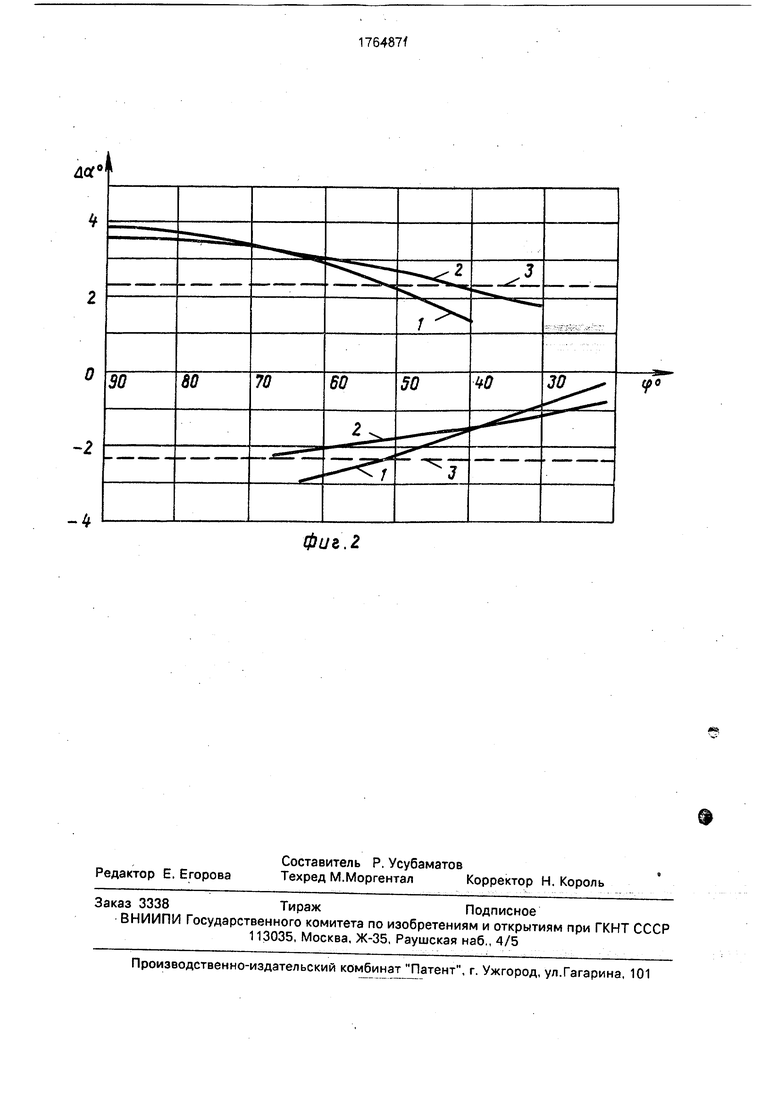
Поскольку в формуле (2) изменения касаются параметра До) все расчеты выполнены для определения его величины изменения по прототипу и предлагаемому решению. Результаты расчетов представлены на фиг.З, где видно расхождение между кривыми 1 и 2 по вогнутой и выпуклой сторонам, которые компенсируются при обработке предлагаемым способом, чем достигается более качественная обработка.
% Предлагаемая формула изобретения по заявке позволяет компенсировать отклонение углов профиля (Доз) зуба по расчетной длине зуба.
Имеющиеся отклонения Дач, показанные в расчетах показывают на наличие диа- гональности контакта, аналогично тому, что
при нарезании круговых зубьев конусовер- шинным производящим колесом также имеют место диагональность контакта, но меньшая, чем при нарезании плосковершинным производящим колесом.
Полученные зависимости коррекции движений при обработке круговых зубьев конических колес позволяют обрабатывать теоретически правильные формы зуба. По сравнению с прототипом предлагаемый
способ позволяет нарезать правильные профили зубьев по длине, качественные конические колеса с круговыми зубьями, повысить качество зацепления пары, долговечность ее работы что экономически
выгодно.
Формула изобретения Способ коррекции формы круговых зубьев конических колес методом обката, включающем вращение оси резцовой головки по заданному радиусу и относительное переменное вращение нарезаемого конического колеса, отличающийся тем, что, с целью повышения точности формообразования круговых зубьев по длине колеса, относительное переменное вращение задают с учетом влияния переменности отклонения профиля зуба от внешнего до внутреннего торца по выпуклой и вогнутой сторонам в соответствии с зависимостями:
Jz(|C056Ј/ s nS(co5UOi li (Х;) , (,
tf .-tfp-.iarctgltgQjsiTiJq),
.A(R /cosef)..Ae
+g-arcco5
-arccosI
AMRyCosfyW 2AMcos9{
2pRx/cos9i Rx--R;+n,tE4(tp(-tb),
где ,2 для вогнутой и выпуклой сторон кругового зуба соответственно. (+) - знаки (+), (-) для выпуклой и вогнутой сторон кругового зуба, Aai - переменное угловое отклонение оси резцовой головки от нормали к начальной конической поверхности, Доз -
0
5
0 5
угол между стороной зуба резцовой головки и нормалью к начальной поверхности конус- новершинного производящего колеса,
д - угол делительного конуса колеса;
Of - угол ножки зуба;
ал -угол профиля резцовой головки;
А - радиус движения оси резцовой головки производящего колеса;
г- номинальный радиус резцовой головки;
RI - внутреннее конусное расстояние колеса;
I - длина пятна контакта;
m - расстояние от внутреннего торца до края пятна контакта;
р, з -угол поворота радиуса оси вращения резцовой головки соответственно начала и конца коррекции профиля по длине кругового зуба;
р- угол поворота радиуса оси вращения резцовой головки;
у- угол поворота нарезаемого колеса;
а- номинальный угол профиля зуба.


| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС ГИПОИДНОЙ ПЕРЕДАЧИ | 1996 |
|
RU2111094C1 |
| СПОСОБ НАРЕЗАНИЯ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1992 |
|
RU2041034C1 |
| СПОСОБ НАРЕЗАНИЯ КОНИЧЕСКИХ КОЛЕС | 1991 |
|
RU2043186C1 |
| СПОСОБ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС, ОБРАЗУЮЩИХ ГИПОИДНУЮ ПЕРЕДАЧУ | 1991 |
|
RU2043187C1 |
| СПОСОБ НАРЕЗАНИЯ КРУГОВЫХ ЗУБЬЕВ КОНИЧЕСКИХ КОЛЕС | 1995 |
|
RU2106939C1 |
| СПОСОБ НАРЕЗАНИЯ КРУГОВЫХ ЗУБЬЕВ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1991 |
|
RU2043185C1 |
| Способ изготовления зубчатой пары с круговыми зубьями | 1986 |
|
SU1468692A1 |
| СПОСОБ ОБРАБОТКИ ЗУБЧАТЫХ КОЛЕС С КРИВОЛИНЕЙНЫМИ ЗУБЬЯМИ | 1998 |
|
RU2123410C1 |
| Способ нарезания обкаткой дуговых зубьев конических колес | 1971 |
|
SU550247A1 |
| Способ нарезания круговых зубьев | 1990 |
|
SU1776221A3 |


Фиг.1
Фиг. 2

Авторы
Даты
1992-09-30—Публикация
1990-06-28—Подача