Изобретение относится к машиностроению и может быть использовано при обработке конических колес с круговыми зубьями.
За аналог принят способ обработки конических колес зуборезной головки с номерными резцами, углы заточки которых определены по формуле
αu=α±Δα, (1) где α номинальный угол профиля резца,
(-) относится к внешней кромке резца, (+) к внутренней кромке резца. Ближайший аналог представлен в книге: Кедринский В.И. Писманник К.Н. Станки для обработки конических колес М. Машиностроение, 1967, с. 421. Формула (8.13).
Недостатком ближайшего аналога является неточная геометрия резцов, которая не обеспечивает нарезание качественной формы круговых зубьев.
Целью изобретения является повышение точности обработки круговых зубьев колес на обычных зуборезных станках путем изменения геометрии режущей части резцов зуборезной головки.
Представленная цель достигается расчетом углов заточки режущих кромок резцов для обработки вогнутой и выпуклой сторон кругового зуба.
Сущность изобретения состоит в правильном определении угла наклона режущей кромки резцов формирующей стороны круговых зубьев, обеспечивающих номинальный профиль зуба.
Существующие углы режущих кромок резцовой зуборезной головки определены из геометрических выкладок по нормальному сечению профиля зуба колеса, когда линия окружности, очерченная номинальным радиусом зуборезной головки проходит через середину впадины зуба и находится в плоскости, касательной к образующей конуса впадины колеса. Отклонение угла профиля зуба определено по формуле (1)
Δα=±tgθfsinβn, где θf угол ножки зуба,
βn угол наклона кругового зуба в среднем сечении зуба,
(+) (-) знаки, относящиеся к выпуклой и вогнутой сторонам кругового зуба.
Рассчитываемые углы резцов по формуле (1) не обеспечивают номинальный профиль зуба нарезаемого колеса, так как не учитывается положение переменности отклонения профиля зуба резца в процессе обработки зубьев гипоидной передачи.
Фактическое отклонение профиля кругового зуба в процессе нарезания конического колеса является переменным и в общем виде этого положения представлено в статье Р. Н. Усубаматова "Коррекция угла давления при нарезании круговых зубьев конических колес на станке с ЧПУ". Известия ВУЗов. Машиностроение, 1986, N 11, c. 115-119. В статье представлены зависимости переменного движения плоско-вершинного и нарезаемого колеса, позволяющее корректировать профиль кругового зуба по среднему сечению зуба. Действительное отклонение профиля зуба определяется по формуле Δα=±arctg[tgθfsin(ϕ-ϕ1+βn)] (2) где ϕ угол обката нарезания зуба колеса
ϕ1arccos 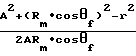 где А радиус движения зуборезной головки (1)
где А радиус движения зуборезной головки (1)
A=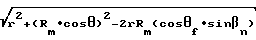
θf угол ножки зуба
Rm среднее конусное расстояние
r номинальный радиус зуборезной головки
ϕ1 угол при вершине конуса колеса, образованный радиусом А движения оси зуборезной головки, номинальным радиусом зуборезной головки и средним конусным расстоянием колеса,
βn угол наклона кругового зуба.
Отклонение профиля зуба Δα в начальный и конечный моменты обработки по вогнутой и выпуклой сторонам зубьев рассчитываются по формуле (2) при известных углах начала и конца нарезания сторон зубьев ϕн и ϕк соответственно.
Для вогнутой и выпуклой сторон зуба начала ϕн и конца ϕкнарезания зуба по среднему сечению определяются по известным формулам (Р.Н. Усубаматов. Обработка конических колес с круговыми зубьями на станках с ЧПУ. Известия ВУЗов. Машиностроение, 1983, N 8, с. 95-98).
Углы ϕн и ϕк рассчитываются по формулам для вогнутой стороны ϕ=ϕ1+ +arccos (cos δa/cosδf ) ϕк= ϕ1 (3)
для выпуклой стороны ϕн= ϕ1
ϕк= ϕ1-arccos (cos δa /cos δf) (4)
δa,δf угол конуса выступов и впадин зубьев
Подставляя полученные расчетные выражения углов ϕн и ϕк по зависимости (3, 4) в уравнение (2) определим отклонение угла профиля зуба Δαн в начальный момент и Δαк в конечный момент нарезания кругового зуба. Формула (2) показывает, что действительное отклонение угла профиля зуба Δα значительно отличается от рекомендуемых для профилирования сторон резцов по формуле (1). Это расхождение необходимо учесть для обработки более точных круговых зубьев гипоидных передач.
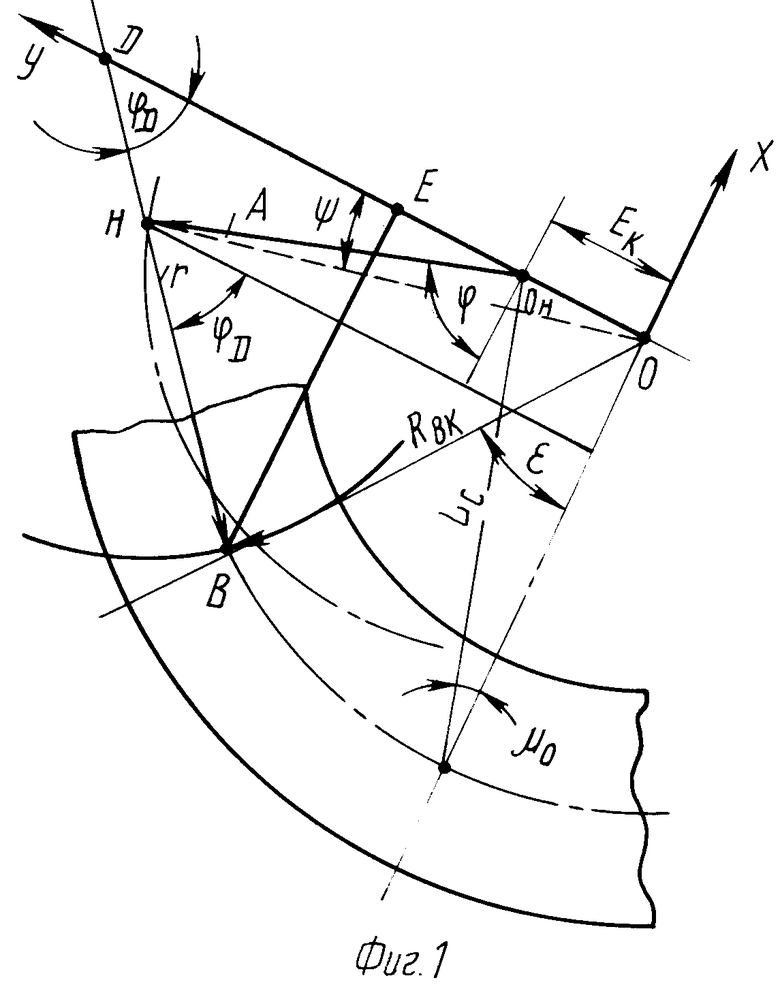
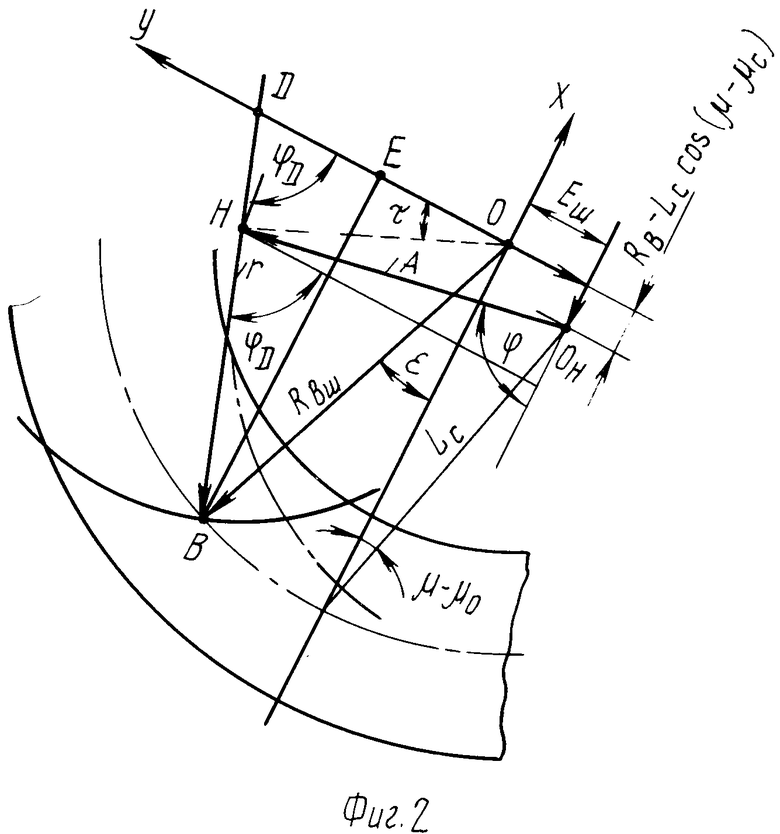
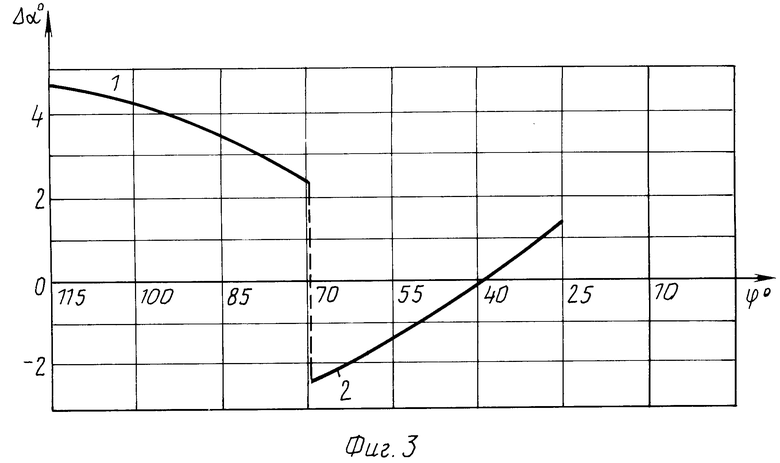
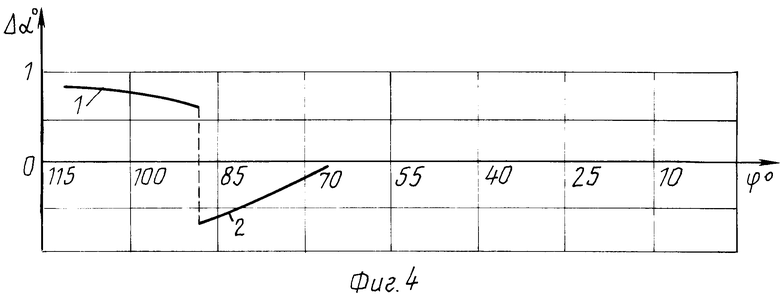
На фиг. 1, 2 представлены расчетные схемы для определения отклонения угла профиля зуба гипоидного колеса и шестерни соответственно; на фиг. 3, 4 графики отклонения угла профиля зубьев колеса и шестерни в процессе обработки.
Для определения аналитических зависимостей отклонения сторон профилей зубьев гипоидной передачи воспользуемся формулой прототипа (2) изменения профиля кругового зуба конического колеса в процессе нарезания, которая показывает, что отклонение профиля зуба зависит от постоянных составляющих θf, βn и от переменного параметра ϕD, являющегося углом, лежащим в плоскости вершин зубьев производящего колеса, образованного нормально к линии кругового зуба в среднем сечении в произвольном положении оси зуборезной головки и перпендикулярном к образующей конуса впадин.
Для гипоидных передач углы ножки зуба колеса и шестерни являются величинами постоянными. Переменными будут углы ϕD и углы наклона спирали зуба, находящиеся в зависимости от угла ϕD. Для определения отклонения профилей круговых зубьев колеса и шестерни гипоидной передачи воспользуемся аналитическими методами кинематического анализа. Представим элементы производящего колеса и гипоидной передачи в виде векторного контура, геометрическая сумма которого равна фазовому вектору структурной группы.
На фиг. 1 и 2 представлены расчетные схемы изменения угла ϕDколеса и шестерни гипоидной передачи векторные уравнения которых соответственно записываются в следующем виде: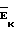 +
+ +
+ =
=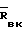
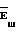 +
+ +
+ +
+ =
= 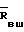 где Ек, Еш гипоидные смещения колеса и шестерни соответственно; А радиус движения оси зуборезной головки; r номинальный радиус зуборезной головки.
где Ек, Еш гипоидные смещения колеса и шестерни соответственно; А радиус движения оси зуборезной головки; r номинальный радиус зуборезной головки.
Rвк=Rmк cos θfк, Rвш=Rmшcos θfш
Rmк; Rmш среднее конусное расстояние колеса и шестерни соответственно; θfк, θfш углы ножек зубьев колеса и шестерни соответственно.
Проектируя обе части этих векторных равенств на оси х и у приходим к выводу уравнений для колеса:
Ек+ Аsin ϕ-rcos ϕD= Rвкsin ε, (5) где ϕ угол поворота производящего колеса. Введем обозначения где Asin ϕ+Ек=а, (Аcos ϕ=B), тогда уравнения (5)
принимают вид: a-r cos ϕD=Rвкsin ε
b-r sin ϕD=Rвкcos ε
Возводя обе части каждого из этих равенств в квадрат, складывая почленно, и преобразовывая, получим: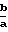 sin ϕD-cos ϕD= (R
sin ϕD-cos ϕD= (R
Представляя угол базового вектора в виде 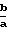 tgΨ, производя тригонометрические преобразования, имеем
tgΨ, производя тригонометрические преобразования, имеем
cos( ϕD+ Ψ)=(R2вк-а2-b2-r2)cosΨ /2ra
После подстановок выражений а и b, и преобразований выражения угла ϕD представится так  cos arctg
cos arctg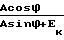 (6)
(6)
Производя аналогичные выкладки по определению выражения угла ϕDдля шестерни, имеем
-Еш+ Аsin ϕ -rcos ϕD=Rвшsin ε
D+Acos ϕ + rsin ϕD=Rвшcos ε (7)
Вводя обозначения уравнения (3) принимают вид:
c-r ˙cos ϕDRвш ˙ cos ε
d+r ˙sin ϕDRвш ˙sin ε
После представления угла базового вектора в виде 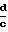 =tg τ алгебраических, тригонометрических преобразований и подстановок выражения угла ϕD будет иметь вид
=tg τ алгебраических, тригонометрических преобразований и подстановок выражения угла ϕD будет иметь вид c
c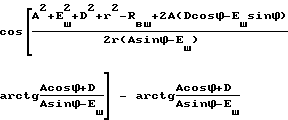 ×
×
(8)
D=Rmш cos θfш-Lccos( μ-μo); где Lc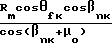
Lc расстояние от оси производящего инструментальные колеса до середины венца нарезаемого зубчатого колеса в плоскости касательной образующего конуса впадин.
μ- разность углов шестерни и колеса
μo- угол гипоидного смещения.
Переходя к формулам отклонения угла наклона режущих кромок зубонарезных головок в процессе нарезания зубьев колеса и шестерни гипоидной передачи по аналогии с формулой (2) получим
Δαi= arctg[tgθfi sin ϕDi] (9) где i=к, ш индексы колеса и шестерни; θfi угол ножки зуба; выражение углов ϕDi представлено формулами (6), (8) для колеса и шестерни соответственно.
На фиг. 3 и 4 приведены графики отклонения угла профиля кругового зуба колеса и шестерни в процессе обработки на углах обката. Графики построены при исходных данных по формулам (6) и (8)
для колеса r 114,3 βnк=29,58о
А= 110,6 θf=4,916 Ек=0 μo 0
Rк= 92,98 δf=70,55o δa=76,31о
ϕн= 114,45 ϕк24,98о μ= 18,71о
для шестерни βnш=48,016о
δf= 13,001о δa=18,466 θf=0,8o
ϕн= 110,65о ϕк=68,55 Еш=29,4 Rш=119,46
Для получения более точного профиля зубьев необходимо компенсировать отклонение профиля зубьев заточкой лезвий не определенные углы.
Для получения номинального угла профиля зуба колеса или шестерни на требуемом конусе компенсируемое отклонение профиля зуба Δα рассчитывается по формулам (9), (6), (8). В формулах (6), (8) параметр углового положения ϕD оси зуборезной головки определяется по координате угла, когда лезвия резцов начинает профилировать зуб в середине венца на начальном или требуемом конусе. Аналитическая зависимость угла ϕ в этом случае определяется по формулам граничных параметров нарезания зубьев гипоидной передачи, представленных в (2), где параметры Ri, Reзаменяются на Rm, δa на δ θa на 0 где Ri, Rm, Re, внутреннее, среднее и внешнее конусное расстояние.
δa угол конуса выступов зубьев;
δ угол делительного конуса;
θa угол головки зуба.
Обобщая полученные результаты, формула расчета углов наклона режущих лезвий резцов зуборезной головки для обработки колеса и шестерни гипоидной передачи представится в виде
αu=α±arctg(tgθfisinϕDi) где  r
r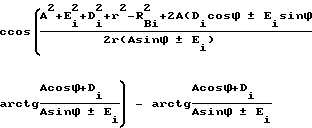 ×
×
ϕ=arccos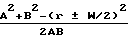 ± arctg
± arctg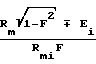
B=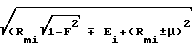
F=cos δi /cos δf
D= Rmшcos θfш-Lc cos( μ-μo) для шестерни D= 0 для колеса, W развод резцов, δi угол делительного конуса, α номинальный угол профиля резцов, iк, ш, индексы колеса и шестерни соответственно, знаки (±) после α, перед W/2 относятся так: верхний знак для внутренней, нижний для внешней стороны резцов знаки перед вторым слагаемым в формуле (+) для вогнутой (-) для выпуклой стороны зуба остальные знаки (±) верхний для колеса, нижний для шестерни. Остальные параметры в соответствии с формулами (9), (6), (8).
Представленные зависимости коррекции формулы кругового зуба колеса и шестерни гипоидной передачи изменением геометрии углов наклона режущих лезвий зуборезной головки (9) при их использовании для процессов зубонарезания позволяют повысить точность обработки гипоидных передач.
П р и м е р реализации. Расчет углов профилей резцов зуборезной головки для нарезания зубьев гипоидной передачи колеса и шестерни имеющих следующие параметры А=110,6 βnк=29,58о Rmк=92,98 Ек=0 r=114,3 μ=0 θfк=4,916о δк=75,5о δfк=70,55о α=20о
для шестерни А=110,6 δfш=13о Rmш=119,46 Еш=29,4 μo=0 α=20о r=114,3 βnш= 48,016о θfш=0,8о δш=13.8о
Расчет углов профилей резцов зубонарезной головки производится по формуле
αn=α±Δαi где (+) для внутренней,
(-) для внешней стороны резца,
Δαi=arctg(tgθfi˙sinϕDi)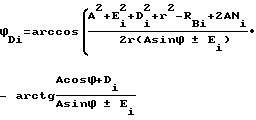 cos arctg
cos arctg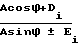 -
-
ϕ=arccos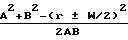 ± arctg
± arctg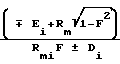
B=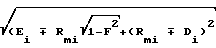
F=cos δi/cosδfi
i к, ш индексы колеса и шестерни
Dк=0
Dш Rmш cos θfш-Lc cos ( μ-μo)
Lc=Rк cos θfк сos βнк/сos(βnк+μo)
μ=βnш-βnк
Nк=Екsin ϕ
Nк= Dшcos ϕ-Eшsin ϕ
Rвi=Rmi cos θfi
Знаки (±) перед Rmi, W, arctg, относятся верхний знак для вогнутой, нижний для выпуклой стороны круговых зубьев, остальные знаки (±) верхний для колеса, нижний для шестерни.
На основании проведенных расчетов по заданным параметрам передачи углы профилей резцов зуборезных головок для обработки колеса и шестерни гипоидной передачи составит:
для колеса
αвнутрен 20+ 0,619=20,619о
αвнешн=20-4,33=15,67о
для шестерни
αвнутрен 20+ 0,1002= 20,1002о
αвнешн=20-0,645=19,355о
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС, ОБРАЗУЮЩИХ ГИПОИДНУЮ ПЕРЕДАЧУ | 1991 |
|
RU2043187C1 |
| СПОСОБ НАРЕЗАНИЯ КРУГОВЫХ ЗУБЬЕВ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1991 |
|
RU2043185C1 |
| СПОСОБ НАРЕЗАНИЯ КОНИЧЕСКИХ КОЛЕС | 1991 |
|
RU2043186C1 |
| СПОСОБ НАРЕЗАНИЯ КРУГОВЫХ ЗУБЬЕВ КОНИЧЕСКИХ КОЛЕС | 1995 |
|
RU2106939C1 |
| СПОСОБ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС ГИПОИДНОЙ ПЕРЕДАЧИ | 1996 |
|
RU2111094C1 |
| Способ коррекции формы круговых зубьев конических колес | 1990 |
|
SU1764871A1 |
| Способ обработки зубчатых изделий | 1990 |
|
SU1776502A1 |
| Станок для обработки конических зубчатых колес с круговыми зубьями | 1990 |
|
SU1776222A3 |
| Зубодолбежная головка | 1990 |
|
SU1745446A1 |
| Способ настройки зубообрабатывающего станка для чистовой обработки зубьев | 1988 |
|
SU1627347A1 |
Изобретение относится к машиностроению, в частности к производству зубчатых колес. Сущность изобретения заключается в уточнении "номерной поправки", обеспечивающей угол наклона режущей кромки резцов, формирующей правую и левую стороны круговых зубьев колес, образующих шпоночную пару. 4 ил.
СПОСОБ НАРЕЗАНИЯ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС в условиях обката зуборезной головки, углы заточки режущих элементов которой определяются с учетом "номерной поправки", отличающийся тем, что при изготовлении зубчатых колес, образующих гипоидную передачу, "номерную поправку" определяют по формуле
± Δαi= arctg(tgQfi·sinϕDi),
где Qfi угол ножки зуба;
i индексы колеса и шестерни;
знаки (±) относятся так: (+) для внутренней, (-) для внешней стороны резца;
ϕDi угол, образованный нормалью к линии кругового зуба в середине зубчатого венца в точке пересечения режущих лезвий резцов зуборезной головки образующей начального конуса в точке полюса зацепления и нормалью к образующей конуса впадин.
| Кедринский В.И., Писманик К.Н | |||
| Станки для обработки конических колес | |||
| М.: Машиностроение, 1967, с.21. |
Авторы
Даты
1995-08-09—Публикация
1992-05-08—Подача