Изобретение относится к машиностроению и может быть использовано при обработке гипоидных передач.
За аналог принят способ обработки гипоидных передач на зуборезных станках.
Недостатком аналога является неточное нарезание зубьев гипоидных передач плосковершинным производящим колесом. Способ требует применения разнообразных поправок для улучшения геометрии форм зубьев.
За прототип принят способ обработки гипоидной передачи на зуборезных станках, содержащий движение обката, вращение нарезаемого колеса или шестерни, согласованное с вращением зуборезной головки. Недостатком прототипа является неточное нарезание зубьев передачи, требующее дополнительных коррекций в обработке.
Целью изобретения является повышение точности нарезания зубьев гипоидных передач.
Это достигается путем сообщения нарезаемому колесу или шестерне переменного движения по определенному закону, позволяющего нарезать точные профили кругового зуба в среднем сечении.
Сущность изобретения состоит в определении закономерности переменного вращательного движения нарезаемого колеса или шестерни, позволяющая компенсировать отклонения в профилях вогнутой и выпуклой сторон круговых зубьев гипоидной передачи.
Зависимость движений обката с коррекцией профиля вогнутой и выпуклой сторон кругового зуба колеса и шестерни гипоидной передачи определяется по следующей схеме.
Воспользуемся положениями, представленными в статье Р.Н. Усубаматов Коррекция угла давления при нарезании круговых конических колес на станке с ЧПУ. Известия вузов. Машиностроение. 1986, N 11, с. 115-119. В статье представлены зависимости переменного движения плосковершинного и нарезаемого конического колеса, позволяющие корректировать отклонения профиля кругового зуба по среднем сечению зуба. Зависимость движения обката с коррекцией действительного отклонения профиля зуба представлена по формуле
γ ϕ cos θ f cos (α ± Δ α)/cos α sin δ;
Δα arctg tgθfsin
tgθfsin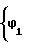 arcsin
arcsin 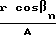 +
+ 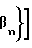 где ϕ1 угол начала нарезания зуба;
где ϕ1 угол начала нарезания зуба;
γ, ϕ углы поворота нарезаемого и производящего колеса;
A 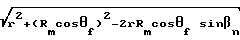
радиус движения зуборезной головки;
θf угол ножки зуба;
Rm среднее конусное расстояние;
r номинальный радиус зуборезной головки;
βn угол наклона кругового зуба;
знаки (+) и (-) относятся к вогнутой и выпуклой стороне кругового зуба соответственно.
Используя положения статьи, определяем выражения отклонения профилей сторон круговых зубьев колеса и шестерни гипоидной передачи по следующей схеме.
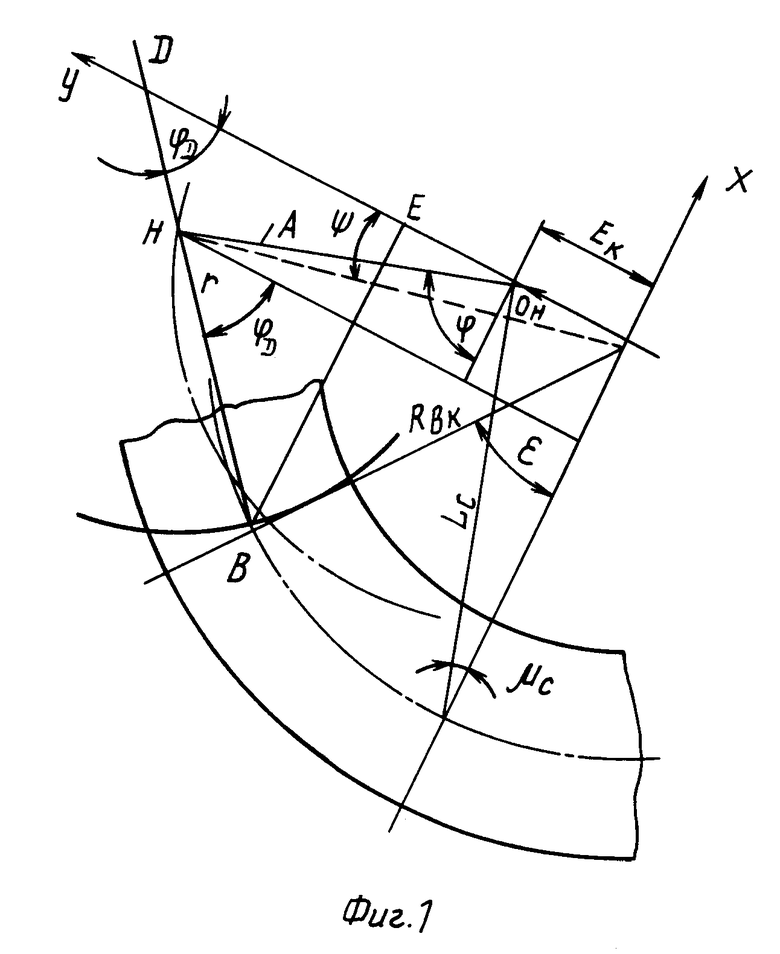
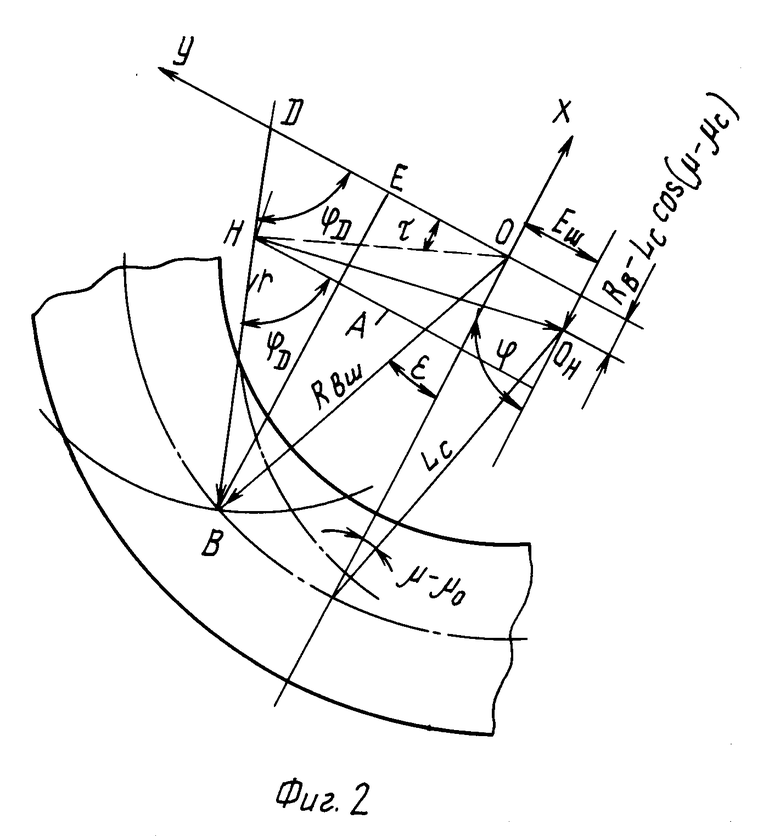
На фиг. 1 и 2 представлены схемы расчета отклонения угла наклона режущих кромок резцов зуборезной головки в процессе обработки колеса и шестерни соответственно.
По аналогии с положениями статьи необходимо найти изменение угла ϕD, образованного нормалью BD, к линии кругового зуба в произвольной точке по среднему сечению зуба и осью координат ОУ.
Изменение угла ϕD зависит от угла поворота производящего колеса и геометрических параметров гипоидного колеса или шестерни. Для определения выражения угла ϕD используемся аналитическим методом кинематического анализа.
Представляя элементы производящего колеса и гипоидной передачи в виде векторов, направленных как показано на фиг. 1, имеем
Для колеса (фиг. 1)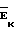 +
+ +
+
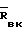
Для шестерни (фиг. 2)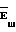 +
+ +
+ +
+
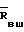
Проектируя обе части этих векторных равенств на оси Х и Y, приходим к уравнениям для колеса:
Ек+Asin ϕ -rcos ϕD= RBksin ε (1)
Acos ϕ +rsin ϕD=Rвкcos ε
Введем обозначения Asin ϕ +Ek=a; Аcosϕb
Уравнения (1) принимают вид
a-rcos ϕD=RВкsin ε
b+rsin ϕD=RВкcos ε (2)
Возводя обе части каждого из этих равенств в квадрат и складывая их почленно, получаем
a2+b2+2r(bsin ϕD-acos ϕD)+r2-RВк2=0
или sinϕD-cosϕD=
sinϕD-cosϕD= 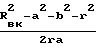
представляя  tgΨ делая тригонометрические преобразования, получаем
tgΨ делая тригонометрические преобразования, получаем
cos(ϕD+Ψ) 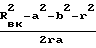 · cosΨ или, делая подстановки и преобразования
· cosΨ или, делая подстановки и преобразования
ϕD= arccos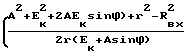 ×
×
× cos arctg 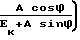 -arctg
-arctg 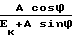
(3)
Для шестерни
-Еш+Аsin ϕ -rcos ϕD=Rвшsin ε (4)
D+Acos ϕ +rsin ϕD=Rвшсosε
Введем обозначения
Asin ϕш=с; Асos ϕ+D=d
Уравнения (3) принимают вид
c-rcos ϕD=Rвшsinε
d+rsin ϕD=Rвшcosε (5)
Производя преобразования, аналогичные уравнениям (2), получим
c2+d2+2r(d sin ϕD-c cos ϕD)+r2-Rвш2=0 или sinϕD-cosϕD=
sinϕD-cosϕD= 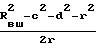 представляя
представляя  tgτ делая тригонометрические преобразования и подстановки, получим
tgτ делая тригонометрические преобразования и подстановки, получим
ϕD= arccos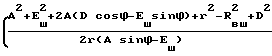 ×
×
× cos arctg 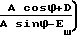 -arctg
-arctg 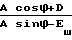
(6)
В уравнениях (3) и (6) приняты следующие обозначения:
А радиус движения зуборезной головки;
r номинальный радиус зуборезной головки
Rв.к.= Rm.к.cos θfk; Rв.ш.=Rmш cos θfm; Rm.к. и Rm.ш. среднее конусное расстояние колеса и шестерни соответственно θfk, θfш угол ножки зуба колеса и шестерни соответственно; ϕ угол поворота производящего колеса; Ек, Еш гипоидное смешение колеса и шестерни соответственно
D=Rmш ˙ cos θfш Lc cos (μ μо)
Lc= Rm.к. ˙ cos θf.k. ˙ cos βn.k./cos( βn.k.+ + μо), μ βш βк. разность углов наклона круговых зубьев гипоидных колес и шестерни, μо- угол гипоидного смещения.
Отклонение угла профиля кругового зуба колеса или шестерни гипоидной передачи определяется по формуле (1)
Δ αi= arctg (tg θfi ˙ sin ϕDi), где ϕDi определяется по формулам (3) и (6) i=к, ш, индексы колеса и шестерни соответственно.
Используя зависимости движений обката при нарезании колеса и шестерни гипоидной передачи (см. Кабатов Н.Ф. Лопато Г.А. Конические колеса с круговыми зубьям М. Машиностроение, 1966-299 с.), движение обката при нарезании зубьев гипоидной передачи с коррекцией отклонения профилей зубьев представляется в следующем виде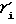 =
= 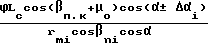 (7)
(7)
Lc= Rm.k. ˙ cos θf.k. ˙ cos βn.k./cos (βn.k+ μo), где γi ϕ углы поворота нарезаемой заготовки гипоидной передачи и производящего колеса соответственно; rmi средний радиус начальной окружности колеса или шестерни; α номинальный угол профиля зуба; (+) знак, (+), (-) для вогнутой и выпуклой сторон кругового зуба соответственно; остальные параметры по формуле (2) и (3).
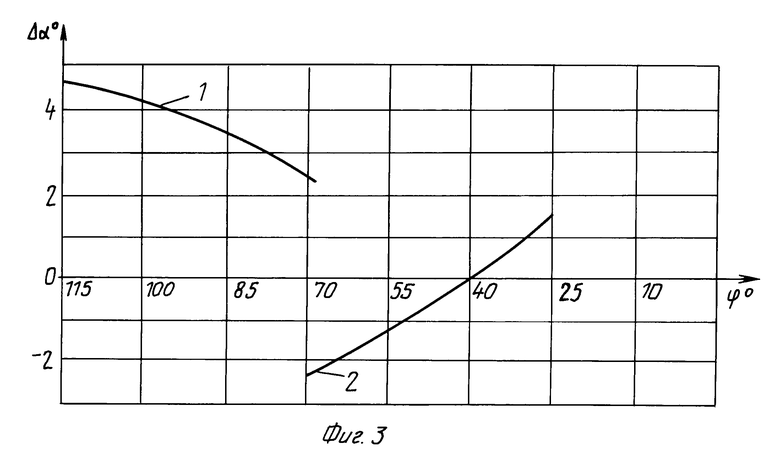
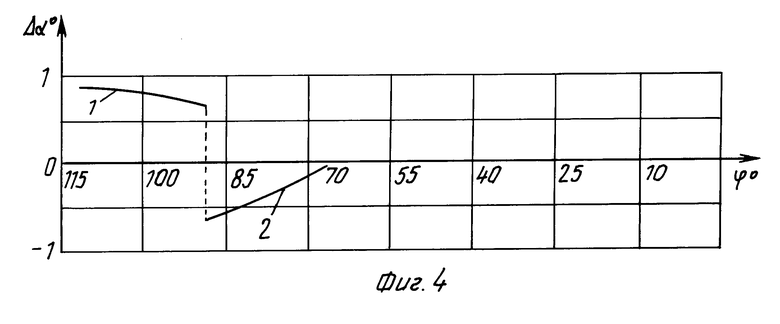
На фиг. 3 и 4 приведены графики отклонения профилей кругового зуба в нормальном сечении по среднему конусу по вогнутой и выпуклой сторонам в процессе нарезания колеса и шестерни, рассчитанные по формулам (7) и (6), (3) при следующих параметрах обработки:
А=110,6 мм Rк=92,98 мм r=114,3 мм
μо=0 βк=29,583оθf.к.4.916о
θак 0,85о δf.к.=70,55оδа.к.76,316о
Rш=119,46 мин Еш=29,4 мм δш=13,816о
μ=18,433о δf.ш=13,016оδаш=18,483о
θаш= 4,666о θf.ш.0,8оβш=48,016о
В зависимости обкатки при нарезании зубьев гипоидной шестерни и колеса, представленные в формуле (7), позволяют компенсировать отклонения угла профиля их зубьев.
Зависимости движения обката с коррекцией профилей зубьев колеса и шестерни гипоидной передачи по формуле (7) могут быть реализованы на зуборезных станках с модификаторами обката при соответствующем подборе параметров механизмов или на станках с программным управлением. Обкатки гипоидных передач по предлагаемому способу позволяют повысить их точность.
Результаты расчетов коррекции формы зуба колеса шестерни гипоидной передачи приведены в таблице.
Расчетные даные по γ и ϕ показывают переменность движения обката, следовательно теоретические зависимости обката с коррекцией формы верны.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НАРЕЗАНИЯ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1992 |
|
RU2041034C1 |
| СПОСОБ НАРЕЗАНИЯ КОНИЧЕСКИХ КОЛЕС | 1991 |
|
RU2043186C1 |
| СПОСОБ НАРЕЗАНИЯ КРУГОВЫХ ЗУБЬЕВ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1991 |
|
RU2043185C1 |
| СПОСОБ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС ГИПОИДНОЙ ПЕРЕДАЧИ | 1996 |
|
RU2111094C1 |
| СПОСОБ НАРЕЗАНИЯ КРУГОВЫХ ЗУБЬЕВ КОНИЧЕСКИХ КОЛЕС | 1995 |
|
RU2106939C1 |
| Способ коррекции формы круговых зубьев конических колес | 1990 |
|
SU1764871A1 |
| Способ обработки зубчатых изделий | 1990 |
|
SU1776502A1 |
| Станок для обработки конических зубчатых колес с круговыми зубьями | 1990 |
|
SU1776222A3 |
| Зубодолбежная головка | 1990 |
|
SU1710227A1 |
| Зубодолбежная головка | 1990 |
|
SU1745446A1 |

Изобретение относится к машиностроению, в частности к производству зубчатых колес. При нарезании зубчатых колес, образующих гипоидную передачу, движения обката выполняют переменными в соответствии с приведенной аналитической зависимостью, что позволяет нарезать точные профили круговых зубьев в среднем сечении. Переменное движение обката может быть реализовано на зубообрабатывающих станках с модификаторами обката или на станках с программным управлением. 4 ил. 1 табл.
СПОСОБ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС, ОБРАЗУЮЩИХ ГИПОИДНУЮ ПЕРЕДАЧУ, резцовой головкой, режущие элементы которой в процессе обката имитируют производящее инструментальное колесо при согласовании углов поворота нарезаемого и производящего колес, отличающийся тем, что угол поворота нарезаемого колеса выбирают по формуле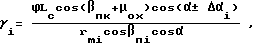
при этом
Δαi= arctg(tgθfi·sinϕDi),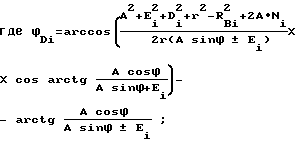
i к, ш индексы колеса и шестерни;
θfi угол ножки зуба;
A радиус движения резцовой головки;
Lс расстояние от оси производящего инструментального колеса до середины венца нарезаемого зубчатого колеса в плоскости касательной образующей конуса впадин;
μOX угол гипоидного смещения;
Ei гипоидное смещение;
D 0 для колеса;
Dm= Rmшcosθfш-Lccos(μ-μo) для шестерни,
μ = βпш-βпк разность углов наклона круговых зубьев гипоидных колеса и шестерни;
Nк= Eкsinϕ для колеса,
Nш= D cosϕ-Eшsinϕ,
RBi= Rmicosθfi для шестерни;
Rmi среднее конусное расстояние;
rmi средний радиус начальной окружности,
r номинальный радиус резцовой головки;
знаки (± Δαi)-(+) для вогнутой, (-) для выпуклой сторон зуба, остальные знаки (±) верхний для колеса, нижний для шестерни;
γi, ϕ углы поворота элементов гипоидной передачи и производящего колеса соответственно.
| Писманик К.М., Гипоидные передачи, М.; Машиностроение, 1964, с | |||
| Способ получения смеси хлоргидратов опийных алкалоидов (пантопона) из опийных вытяжек с любым содержанием морфия | 1921 |
|
SU68A1 |
Авторы
Даты
1995-09-10—Публикация
1991-12-02—Подача