Изобретение относится к области расчета переходных процессов.
Известен способ построения переходных процессов методом преобразования Лапласа, в котором действительные функции времени (оригиналы) заменяют изображениями (см. М.Р. Нейман, К.С. Демирчян. Теоретические основы электротехники. М. : Энергия. Т1, 1967. - 524 с.). Эти преобразования выбираются так, чтобы операции дифференцирования и интегрирования оригинала заменялись алгебраическими операциями над их изображениями. В таком случае дифференциальные уравнения для оригиналов переходят в алгебраические уравнения для их изображений.
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относится то, что в известном способе для сложной электрической цепи с распределенными параметрами обратное преобразование Лапласа практически невыполнимо. Данный способ применим только для ограниченного числа элементов цепи.
Наиболее близким способом того же назначения к заявленному изобретению по совокупности признаков является расчет длинных линий, в котором преобразуются по Лапласу соответствующие уравнения в частных производных длинной электрической цепи с распределенными параметрами, сведением этих уравнений к обыкновенным дифференциальным уравнениям и их интегрированию, с последующим нахождением обратного преобразования по Лапласу (см. М.А. Лаврентьев, Б.В. Шабат. Методы теории функции комплексного переменного. М.: Наука. 1965. - 716 с.), принятый за прототип.
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, принятого за прототип, относится то, что в известном способе расчет переходных процессов возможен только для простейших электрических цепей.
Сущность изобретения заключается в следующем. Для отдельных участков линии с постоянными характеристиками, дифференциальные уравнения которой преобразуются по Лапласу, решается краевая задача по нахождению изображения краевых токов через изображения краевых напряжений. Затем составляются уравнения Кирхгофа, выражающие условия равенства нулю суммы токов, сходящихся в узле. Затем, полагая p = iω, осуществляется построение амплитудно-фазочастотной характеристики (АФЧХ). Далее по построенным АФЧХ строится переходный процесс в интересующей нас точке линии или осуществляется обратное преобразование путем численного интегрирования, так как особые точки соответствующих выражений лежат в левой полуплоскости.
Технический результат - получена методика построения переходных процессов в сложных электрических цепях.
Указанный технический результат при осуществлении изобретения достигается тем, что известен способ расчета переходных процессов в сложных электрических цепях с распределенными параметрами, заключающийся в преобразовании по Лапласу соответствующих уравнений в частных производных длинной электрической цепи с распределенными параметрами, сведением этих уравнений к обыкновенным дифференциальным уравнениям и их интегрированию, с последующим нахождением обратного преобразования Лапласа.
Особенность заключается в том, что сложную электрическую цепь с распределенными параметрами разбивают на участки, так же с распределенными параметрами, но с постоянными погонными параметрами, для которых уравнения длинной линии преобразуют по Лапласу, и решают краевую задачу, заключающуюся в нахождении краевых токов через краевые напряжения, затем по второму закону Кирхгофа составляют уравнения суммы токов, сходящихся в узле, затем, полагая p = iω, осуществляют построение АФЧХ, после чего по построенным АФЧХ, используя численное интегрирование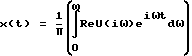 ,
,
строят переходный процесс для интересующей нас узловой точки электрической цепи, что эквивалентно обратному преобразованию Лапласу, где ReU(iω) - вещественная часть АФЧХ.
Сущность заключается в том, что получена новая методика для расчета переходных процессов в сложных электрических цепях с распределенными параметрами путем точного построения АФЧХ с последующим численным обратным преобразованием для построения переходного процесса.
Рассмотрим дифференциальные уравнения длинной линии: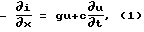
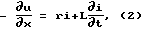
где величины u и i представляют напряжение и ток линии; величины L и r представляют индуктивность и сопротивление пары проводов на единицу длины линии; c и g представляют емкость и проводимость утечки между проводами на единицу длины линии. Координата x отсчитывается от некоторой точки линии, в частности от начала координат.
Исключим из уравнений (1) и (2) токи. В результате получим следующее уравнение: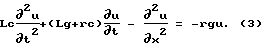
Преобразуем уравнение (3) по Лапласу: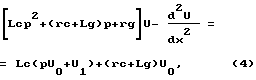
где U - вектор напряжения, преобразованный по Лапласу; U0 - начальный вектор напряжения; U1 - начальная скорость изменения напряжения. Введя обозначение
a = -l2[Lcp2 + (rc+Lg)p + rg], (5)
вместо (4) получим: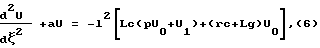
где 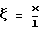 - безразличная координата; l - длина линии. Рассмотрим однородное уравнение (6):
- безразличная координата; l - длина линии. Рассмотрим однородное уравнение (6):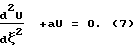
Решим задачу Коши для однородного уравнения (7), полагая известными следующие начальные условия: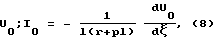
где I0 - начальный вектор тока.
Обозначим
mk = -[Lc(pU0 + U1) + (rc + Lg)U0].
Решение уравнения (7) запишется в виде:
U = C1cosαξ+C2sinαξ, (10)
где 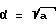 . Постоянные интегрирования C1 и C2 находим из начальных условий. Тогда в нашем случае получим:
. Постоянные интегрирования C1 и C2 находим из начальных условий. Тогда в нашем случае получим:
C1 = U0;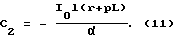
Рассмотренному решению соответствует матрица переноса: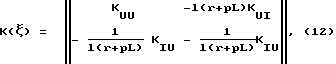
где KUU = cosαξ; 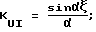 KIU = αsinαξ; KII = KUU.
KIU = αsinαξ; KII = KUU.
Пользуясь матрицей переноса (12), напишем соотношения метода начальных параметров: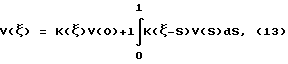
VT(O) = (I0, U0),
VT(S) = (O, cL(pU0 + U1)-(rc+Lg)U0),
где S - переменная интегрирования.
Рассмотрим первую строчку матричного соотношения (13), полагая U0 = Un, где Un - напряжение в начале участка. Тогда получим соотношение для тока начала и конца линии:
In = QUn - RUk + R[Uk], (14)
Ik = QUk - RUn + R[Un], (15)
где 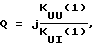
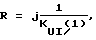
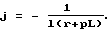
Величины в квадратных скобках для начала и конца линии можно записать следующим образом: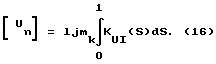
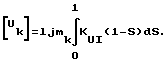
По формулам (14) и (15) находим напряжение или ток в начале или конце линии и при p = iω строим АФЧХ.
Зная передаточную функцию, можем построить переходный процесс тока или напряжения в интересующей нас точке по формуле:
Кроме того, поскольку R и Q получены точным интегрированием, то длина участка цепи может быть любой, что повышает эффективность разработанного метода. Учет узловой нагрузки с любым комплексным сопротивлением не вносит принципиальные трудности в разработанный метод.
Проведенный заявителем анализ уровня техники, включающий поиск по патентным и научно-техническим источникам информации, и выявление источников, содержащих сведения об аналогах заявленного изобретения, позволил установить, что заявитель не обнаружил источник, характеризующийся признаками, тождественными всем существенным признакам заявленного изобретения. Определение из перечня выявленных аналогов прототипа как наиболее близкого по совокупности существенных признаков аналога позволил установить совокупность существенных по отношению к усматриваемому заявителей техническому результату отличительных признаков в заявленном способе, изложенных в формуле изобретения.
Следовательно, заявленное изобретение соответствует условию "новизна".
Для проверки соответствия заявленного изобретения условию "изобретательский уровень" заявитель провел дополнительный поиск известных решений, чтобы выявить признаки, совпадающие с отличительными от прототипа признаками заявленного способа. Результаты поиска показали, что заявленное изобретение не вытекает для специалиста явным образом из известного уровня техники, поскольку из уровня техники, определенного заявителем, не выявлено влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение технического результата, в частности, заявленным изобретением не предусматриваются следующие преобразования:
- дополнение известного средства какой-либо известной частью, присоединяемой к нему по известным правилам, для достижения технического результата, в отношении которого установлено влияние именно такого дополнения:
- замена какой-либо части известного средства другой известной частью для достижения технического результата, в отношении которого установлено влияние именно такой замены;
- исключение какого-либо действия с одновременным исключением обусловленной его наличием функции и достижением при этом обычного для такого исключения результата;
- увеличение количества однотипных действий для усиления технического результата, обусловленного наличием в средстве именно таких действий;
- выполнение известного средства или его части из известного материала для достижения технического результата, обусловленного известными свойствами этого материала;
- создание средства, состоящего из известных частей, выбор которых и связь между которыми осуществлены на основании известных правил, рекомендаций, и достигаемый при этом технический результат обусловлен только известными свойствами частей этого средства и связей между ними.
Описываемое изобретение не основано на изменении количественного признака, представлении таких признаков во взаимосвязи либо изменении ее вида. Имеется в виду случай, когда известен факт влияния каждого из указанных признаков на технический результат, и новые значения этих признаков или их взаимосвязь могли быть получены исходя из известных зависимостей.
Следовательно, заявленное изобретение соответствует условию "изобретательский уровень".
На фиг. 1 представлена длинная линия конечной длины с разомкнутым правым концом. Параметры линии имеют следующие значения: l = 100 км, c0 = 10-6 Ф/км, L0 = 0,36 • 10-3 Гн/км, r0 = 0,1 • 10-4 Ом/км, g0 = 0 См/км, Un = 1.
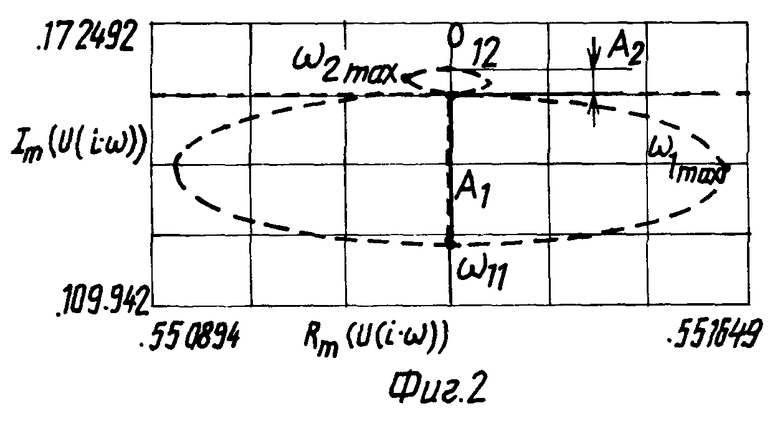
На фиг. 2 представлена АФЧХ длинной линии, показанной на фиг. 1,
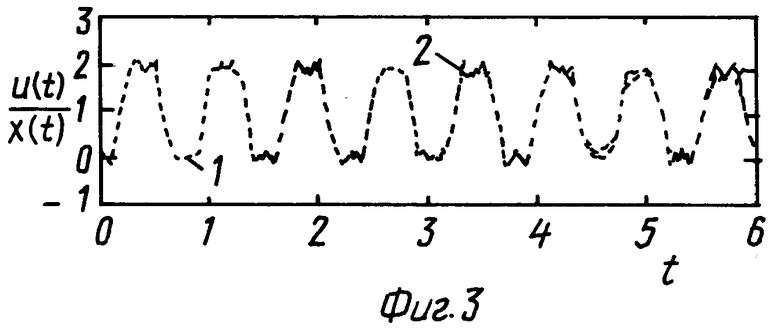
На фиг. 3 показан переходный процесс для длинной линии фиг. 1, построенный по формуле (20) и точным решением.
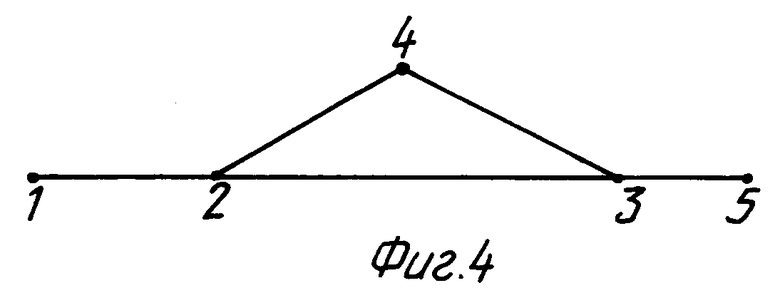
На фиг. 4 представлена сложная электрическая цепь, состоящая из пяти узлов. Параметры этой цепи имеют следующие значения: l = 100 км, c0 = 10-6 Ф/км, L0 = 0,36 • 10-3 Гн/км, r0 = 0,1 • 10-4 Ом/км, g0 = 0 См/км, Un = 1, l12 = 15 км, l23 = 60 км, l35 = 25 км, l24 = 20 км, l43 = 40 км.
Сведения, подтверждающие возможность осуществления изобретения с получением вышеуказанного технического результата: Рассмотрим длинную линию, показанную на фиг. 1. Напряжение в конце линии, решая систему (14) и (15), запишется в следующем виде: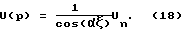
Положив p = iω, строим АФЧХ, показанную на фиг. 2. Используя формулу (17), строим переходный процесс в конце этой линии, показанный на фиг. 3 (кривая 1). На фиг. 3 (кривая 2) показан переходный процесс, построенный точным решением (см. М.А. Лаврентьев, Б.В. Шабат. Методы теории функций комплексного переменного. М.: Наука, 1965. - 716 с.):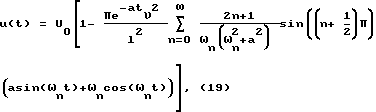
где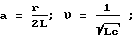
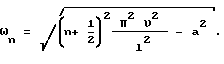
Переходный процесс, построенный по формуле (19) и (17), практически совпадает, но формула (17) более простая и пригодна для сколь угодно сложной электрической цепи в то время, как формула (19) имеет сложную структуру и пригодна лишь для электрической цепи, показанной на фиг. 1. Для подтверждения эффективности данного способа рассмотрим сложную электрическую цепь, состоящую из пяти узлов (см. фиг. 4). Система уравнений для каждого узла имеет следующий вид:
Q12U1 - R12U2 = 0;
-R12U1 + (Q12 + Q23 + Q24)U2 - R23U3 - R24U4 = 0;
-R23U2 + (Q23 + Q43 + Q35)U3 - R43U4 - R35U5 = 0; (20)
-R24U2 - R43U3 + (Q24 + Q43)U4 = 0;
-R35U3 + Q35U5 = 0.
Решая систему уравнений (20), найдем напряжение в конце линии (узел 5). АФЧХ и переходный процесс, построенные по формуле, полученной из системы (21), и по формуле (19), практически совпадают при Q23= 0 и R23 = 0.
Таким образом, изложенные сведения свидетельствуют о выполнении при использовании заявленного способа следующей совокупности условий:
- средство, воплощающее заявленный способ при его осуществлении, предназначено для использования в промышленности, а именно в автомобилестроении и задачах электропривода;
- для заявленного способа в том виде, как он охарактеризован в независимом пункте изложенной формулы изобретения, подтверждена возможность его осуществления с помощью описанных в заявке или известных до даты приоритета средств и методов.
Следовательно, заявленное изобретение соответствует условию "Промышленная применимость".
Изобретение относится к расчету переходных процессов, в сложных электрических цепях с распределенными параметрами. Технический результат - возможность использования полученного способа для сложных электрических цепей. Полученные формулы позволяют построить переходный процесс в любой узловой точке сложной электрической цепи, в частности в длинной линии, при этом длина участка цепи может быть любой, т.к. соответствующие соотношения получены точным интегрированием. Кроме того, возможен учет узловой нагрузки с любым комплексным сопротивлением, что повышает эффективность, разработанность метода. В данном способе предлагается частный метод решения задачи построения переходных процессов в сложных электрических цепях. Для отдельных участков цепи с постоянными характеристиками, дифференциальные уравнения которой преобразуются по Лапласу, решается краевая задача по нахождению изображения краевых токов через изображения краевых напряжений. Затем составляются уравнения Кирхгофа, выражающие условия равенства нулю суммы токов, сходящихся в узле, и, полагая p = iω, осуществляется построение амплитудно-фазочастотной характеристики (АФЧХ). Далее по построенным АФЧХ по формуле численного интегрирования 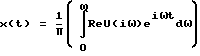 строим переходный процесс для интересующей нас узловой точки электрической цепи, что эквивалентно обратному преобразованию по Лапласу, где ReU(iω) - вещественная часть АФЧХ. 4 ил.
строим переходный процесс для интересующей нас узловой точки электрической цепи, что эквивалентно обратному преобразованию по Лапласу, где ReU(iω) - вещественная часть АФЧХ. 4 ил.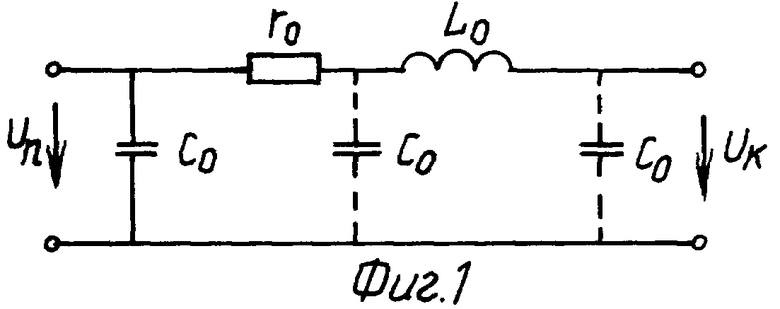
Способ расчета переходных процессов в сложных электрических цепях с распределенными параметрами, заключающийся в измерении погонной индуктивности, сопротивления, емкости и проводимости утечки участка линии с постоянными параметрами, преобразовании по Лапласу соответствующих уравнений в частных производных длинной электрической цепи с распределенными параметрами, сведением этих уравнений к обыкновенным дифференциальным уравнениям и их интегрированию, с последующим нахождением обратного преобразования Лапласа, отличающийся тем, что сложную электрическую цепь с распределенными параметрами разбивают на участки, также с распределенными параметрами, но с постоянными погонными параметрами, для которых уравнения длинной линии преобразуют по Лапласу и решают краевую задачу, заключающуюся в нахождении краевых токов через краевые напряжения, преобразованные по Лапласу, получают формулы для преобразованных токов в начале и конце участка линии
In = QUn - RUk + R[Uk],
Ik = QUk - RUn + R[Un],
затем по законам Кирхгофа составляют уравнения суммы токов, сходящихся в узле, затем, полагая p = iω и решая полученную систему уравнений для дискретных значений ω, осуществляют построение амплитуднофазочастотной характеристики (АФЧХ), после чего по построенным АФЧХ, используя численное интегрирование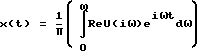
строят переходный процесс для интересующей нас узловой точки электрической цепи, что эквивалентно обратному преобразованию Лапласа, где ReU(iω) - вещественная часть АФЧХ;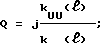
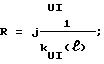
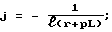
Un - напряжение в начале участка;
Uk - напряжение в конце участка;
kUU = cosαξ;
kUI = sinαξ;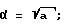
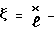 безразмерная координата;
безразмерная координата;
l - длина линии;
a = -l2[Lср 2 + (rc + Lg)p + rg];
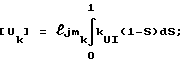
S - переменная интегрирования;
mk = -[Lс(pU0 + U1) + (rc + Lg)U0];
U0 - начальный вектор напряжения;
U1 - начальная скорость изменения напряжения;
L, r - индуктивность и сопротивление пары проводов на единицу длины линии;
c, g - емкость и проводимость утечки между проводами на единицу длины линии;
х - координата, отсчитываемая от некоторой точки линии.
| НЕЙМАН М.Р., ДЕМИРЯЧАН К.С | |||
| Теоретические основы электротехники | |||
| - М.: Энергия, т.1, 1967 | |||
| ЛАВРЕНТЬЕВ М.А., ШАБАТ Б.В | |||
| Методы теории функции комплексного переменного | |||
| - М.: Наука, 1965 | |||
| Способ размножения копий рисунков, текста и т.п. | 1921 |
|
SU89A1 |
| Набор олигодезоксирибонуклеотидных праймеров для диагностики сердечно-сосудистых заболеваний и выявления риска их развития на основе биомолекулярного маркера микроРНК hsa-miR-143-3p методом количественной ПЦР и его применение | 2025 |
|
RU2838257C1 |
| RU 94013008 A1, 20.12.1999. | |||
Авторы
Даты
2000-11-27—Публикация
1999-09-17—Подача