Предлагаемая система относится к области радиоэлектроники, в частности ближней радиолокации, и может быть использована в системах предотвращения столкновений транспортных средств и контроля дорожного движения.
В последнее десятилетие наблюдается бурное развитие радиолокационных средств определения обстановки на автомобильных транспортных магистралях, основным достоинством которых является возможность предоставления водителям транспортных средств и сотрудникам органов, контролирующих дорожное движение, объективных данных о скоростях и координатах объектов на магистралях в любое время суток и в любых погодных условиях. В настоящее время в развитых странах подобными системами, работающими в миллиметровом диапазоне длин волн, оснащаются автобусы и грузовой транспорт, ожидается, что к 2005 году более 1 млн. систем будут установлены на легковые автомобили. Сдерживающим фактором широкого применения автомобильных радиолокаторов (радаров) является их относительно высокая стоимость (см. журнал “Microwave Journal”, 2001, vol.44, №5, р.271).
Анализ патентной и научно-технической информации позволяет сделать вывод, что основной причиной высокой стоимости систем этого класса является сложность аналогового приемопередатчика радиолокатора, содержащего, как правило, большое количество дорогостоящих микроволновых узлов.
В большинстве известных технических решений для зондирования используют сигнал с линейной частотной модуляцией (или сочетание его с непрерывным немодулированным сигналом), а информацию о скорости и дальности объектов получают измерением мгновенной разности частот излучаемого и принятого сигнала.
Примером такого решения является радиолокатор и реализуемый им способ измерения параметров объектов, в котором относительно высокие технические параметры обеспечиваются применением сложной схемы формирования зондирующего сигнала в передатчике и двойного преобразования частоты в приемнике (см. Millimeter-Wave Radar Sensor for Automotive Intelligent Cruise Control (ICC), IEEE Transactions on Microwave Theory and Techniques, vol. 45, № 12, December 1997).
Другим примером является способ определения дальности в доплеровских измерителях вектора скорости для летательных аппаратов (см. патент РФ №2018864 от 10.07.92), в котором используется частотная модуляция зондирующего сигнала по ступенчато-пилообразному закону с заданной величиной скачка частоты на ступеньку и длительностью ступеньки с возможностью измерения фазы в ней. Дальность определяют по разности фаз частотно-модулированного излучаемого и отраженного сигнала на частоте модуляции. Недостатком известного способа измерения является низкая чувствительность, обусловленная тем фактом, что преобразованный принятый сигнал (сигнал промежуточных частот) лежит в области низких частот, где имеет место большой уровень фликкер-шума.
Общим недостатком метода радиолокации с линейной частотной модуляцией (метода ЛЧМ) является, как известно, ограничение разрешающей способности и точности измерения дальности длительностью периода частотной модуляции, что обусловлено тем, что принятый сигнал анализируется во временной области.
Предпосылки к альтернативному способу радиолокации, использующему обработку сигнала в частотной области (спектральный подход) отражены в монографии (см. Мухаммед Абд Аль-Вахиб Исмаил, Радиолокационный высотомер с двойной частотной модуляцией. Изд. Иностранной литературы, М., 1957 (пер. с англ.) или Mohamed Abd-El Wahab Ismael, A Study of the Double Modulated F.M.Radar, Verlag Leeman, Zurich, 1955). Некоторые результаты, изложенные в разделе 2 первой главы монографии, в частности, полученное автором выражение (29) для спектра выходного сигнала смесителя, перемножающего излучаемый и принятый частотно-модулированные по гармоническому закону сигналы, являются отдаленным аналогом предлагаемого способа радиолокации. Автором монографии, однако, при выводе формулы (29) сделаны упрощения, скрывшие некоторые особенности спектра, в частности, зависимость фаз гармоник модулирующего сигнала от расстояния до отражающего объекта.
Близким к изобретению является способ измерения параметров объектов, реализуемый гомодинным радиолокатором непрерывного излучения с частотной модуляцией, в котором модулируемый по частоте генератор СВЧ колебаний служит одновременно генератором передатчика и гетеродином приемника, с последующей обработкой сигнала смесителя.
Способом - прототипом предлагаемого изобретения является способ радиолокационного измерения скоростей и координат объектов, включающий излучение периодически модулированного по частоте зондирующего сигнала, прием отраженных от объектов сигналов, перемножение излучаемого и принятых сигналов, усиление в заданной полосе частот и анализ полученного в результате перемножения гомодинного сигнала. Расстояние до объекта вычисляют по измеренной амплитуде гармоники спектра выходного (гомодинного) сигнала смесителя, а скорость - по доплеровской частоте изменения этой амплитуды (см. “Справочник по радиолокации”, в четырех томах под редакцией М. Сколника (далее “Справочник”), том 3, Москва, “Советское радио”, 1976-1979 (пер. с английского “RADAR HANDBOOK”, Editor-In-Chief M.I.Skolnik, McGRAU-HILL BOOK COMPANY, 1970)”, том 3, 1979, стр.258-262). Недостатками известного способа является низкая предельная дальность, обусловленная не оптимальностью приема отраженных сигналов, большая погрешность измерения дальности объектов, обусловленная сильной зависимостью амплитуды гармоник от дестабилизирующих факторов, а также отсутствие возможности определения знака радиальной скорости.
По наибольшему количеству существенных признаков системой - прототипом предлагаемого изобретения является автомобильная радарная система (см. патент США №5,325,097 от 28 июня 1994, “Multimode Radar for Road Vehicle Blind-zone Target Discrimination”). Известная система для радиолокационного измерения скоростей и координат объектов содержит соединенные микроволновыми входами и выходами антенно-фидерное устройство, обеспечивающее излучение зондирующего и прием отраженных от измеряемых объектов сигналов, и приемопередающее устройство, обеспечивающее формирование зондирующего сигнала, перемножение с ним принятых сигналов и усиление полученного гомодинного сигнала, а также аналого-цифровой преобразователь и процессор, вход управления частотой зондирующего сигнала и выходы приемопередающего устройства соединены соответственно с аналоговым выходом процессора и входами аналого-цифрового преобразователя, а процессор наделен программами управления частотой приемопередающего устройства и вычисления скоростей и координат объектов. Приемопередающее устройство включает формирователь зондирующего сигнала, вход управления частотой которого соединен через модулятор с цифровым процессором, смеситель, первый вход которого соединен с выходом формирователя зондирующего сигнала, второй вход подключен к входу приемопередающего устройства, а выход через полосовой усилитель соединен с выходом приемопередающего устройства. Антенно-фидерное устройство выполнено в виде передающей и приемной антенн.
Способ, реализуемый системой-прототипом определения параметров транспортного средства использует линейно частотно-модулированный сигнал с линейно растущей и линейно уменьшающейся частотой, а также режим с постоянной частотой излучаемого сигнала. Излучаемый и принятый сигналы перемножают, выделяют и усиливают гомодинный сигнал, который преобразуют в цифровую форму и анализируют во временной области с помощью цифрового процессора с учетом собственной скорости транспортного средства.
Недостатком системы - прототипа является недостаточная предельная дальность и точность измерений, обусловленная описанными выше особенностями метода ЛЧМ, а также сильным влиянием фликкер-шума.
Для устранения вышеуказанных недостатков была поставлена задача создания способа и системы для радиолокационного измерения скорости и координат объектов, обеспечивающих при минимальной стоимости достаточную для целей безопасности дорожного движения предельную дальность, разрешающую способность и точность измерения скоростей и координат объектов.
Поставленная задача решается тем, что в способе радиолокационного измерения скоростей и координат объектов, включающем излучение периодически модулированного по частоте зондирующего сигнала, прием отраженных от объектов сигналов, перемножение излучаемого и принятых сигналов, усиление в заданной полосе частот полученного в результате перемножения гомодинного сигнала, согласно изобретению, из гомодинного сигнала формируют сигнал промежуточных частот в виде последовательности цифровых фрагментов заданной длительности, формируют двумерную матрицу базисных сигналов, номера столбцов которой соответствуют множеству средних ожидаемых значений дальности, а номера строк - множеству средних ожидаемых значений скорости, вычисляют последовательность матриц значений функций взаимной корреляции матрицы базисных сигналов и каждого из фрагментов сигнала промежуточных частот, обнаруживают объекты путем выявления элементов матрицы функций взаимной корреляции любого фрагмента, значения которых превышают заданный пороговый уровень, и определяют дальность и скорость обнаруженных объектов по номерам, соответственно, столбца и строки выявленных элементов.
Цифровые фрагменты сигнала промежуточных частот могут быть сформированы, например, путем, по крайней мере, однократного возведения в квадрат гомодинного сигнала и исключения из полученного сигнала постоянной составляющей.
Дополнительно, согласно изобретению, формируют квадратурную, по отношению к основной, двумерную матрицу базисных сигналов, вычисляют последовательность квадратурных матриц значений функций взаимной корреляции квадратурной матрицы базисных сигналов и каждого из фрагментов сигнала промежуточных частот, обнаруживают объекты путем выявления элементов квадратурной матрицы функций взаимной корреляции любого фрагмента, значения которых превышают заданный пороговый уровень, и определяют дальность и скорость обнаруженных объектов по номерам, соответственно, столбца и строки выявленных элементов.
Также дополнительно, согласно изобретению, из элементов последовательности матриц функций взаимной корреляции формируют матрицу корреляционных сигналов, каждый элемент которой представляет собой последовательность соответствующих номеру столбца и строки значений функций взаимной корреляции каждой из последовательности матриц, определяют спектр корреляционных сигналов путем преобразования Фурье, обнаруживают объекты путем выявления элементов матрицы корреляционных сигналов, значения выделенных составляющих спектра которых превышают заданный пороговый уровень, и определяют дальность и скорость обнаруженных объектов по номерам, соответственно, столбца и строки выявленных элементов.
Также дополнительно, согласно изобретению, по частоте выделенной составляющей спектра корреляционного сигнала выявленных элементов вычисляют уточняющую поправку к значению скорости обнаруженного объекта, причем знак уточняющей поправки определяют по знаку разности фаз выделенной составляющей в элементе основной матрицы и идентичном по номеру столбца и строки элементе квадратурной матрицы корреляционных сигналов.
Целесообразно, если базисные сигналы в матрицах и сигналы промежуточных частот каждого фрагмента формируют в виде функций времени, а матрицы значений функций взаимной корреляции вычисляют перемножением сигнала промежуточных частот каждого фрагмента с каждым из базисных сигналов матриц с последующим интегрированием результата перемножения по времени фрагмента.
Также целесообразно, если базисные сигналы в матрицах формируют в виде коэффициентов спектра, формируют последовательность спектров фрагментов сигнала промежуточных частот путем преобразования Фурье с сигналом каждого из фрагментов, а матрицы значений функций взаимной корреляции вычисляют перемножением коэффициентов спектра сигнала промежуточных частот каждого фрагмента с коэффициентами спектра каждого из базисных сигналов матриц с последующим суммированием результата перемножения.
Дополнительно, согласно изобретению, вычисляют уточненное значение дальности обнаруженного объекта, при этом для каждого выявленного элемента матриц спектров базисных сигналов выбирают номера нескольких гармоник с наибольшими амплитудами, из последовательности спектров фрагментов сигнала промежуточных частот для каждой выбранной гармоники формируют последовательности пар коэффициентов гармоник - действительного и мнимого, которые представляют как пары сигналов гармоник, с полученными сигналами выполняют дискретное преобразование Фурье, по отношениям мнимого и действительного коэффициентов выделенных составляющих спектра определяют фазу каждой гармоники и фазочастотную характеристику обнаруженного объекта, по крутизне которой вычисляют уточненное значение дальности.
Поставленная задача решается также тем, что во втором варианте способа радиолокационного измерения скоростей и координат объектов, включающем излучение периодически модулированного по частоте зондирующего сигнала, прием отраженных от объектов сигналов, перемножение излучаемого и принятых сигналов, усиление в заданной полосе частот и анализ полученного в результате перемножения гомодинного сигнала, согласно изобретению, прием отраженного сигнала, его перемножение с излучаемым сигналом и усиление в заданной полосе частот осуществляют, по крайней мере, еще в одной позиции, пространственно отнесенной от первой, при этом в каждой позиции из гомодинного сигнала формируют сигнал промежуточных частот в виде последовательности цифровых фрагментов заданной длительности, формируют трех- или четырехмерную матрицу базисных сигналов, номера столбцов первого измерения которой соответствуют множеству средних ожидаемых значений дальности, номера столбцов второго и третьего измерений - множеству средних ожидаемых значений первой и второй угловых координат соответственно, а номера строк - множеству средних ожидаемых значений скорости, вычисляют в каждой позиции последовательность матриц значений функций взаимной корреляции матрицы базисных сигналов и каждого из фрагментов сигнала промежуточных частот, соответственно количеству фрагментов вычисляют последовательность суммарных матриц путем суммирования соответствующих столбцу и строке значений функций взаимной корреляции, полученных во всех позициях, обнаруживают объекты путем выявления элементов любой суммарной матрицы функций взаимной корреляции, значения которых превышают заданный пороговый уровень, и определяют в случае использования трехмерной матрицы дальность, первую угловую координату и скорость, а в случае использования четырехмерной матрицы - дальность, первую и вторую угловые координаты и скорость обнаруженных объектов по номерам, соответственно, столбцов и строки выявленных элементов.
Цифровые фрагменты сигнала промежуточных частот могут быть сформированы, например, путем, по крайней мере, однократного возведения в квадрат гомодинного сигнала и исключения из полученного сигнала постоянной составляющей.
Согласно изобретению, в каждой позиции дополнительно формируют квадратурную, по отношению к основной, трехмерную или четырехмерную матрицу базисных сигналов, вычисляют в каждой позиции последовательность квадратурных матриц значений функций взаимной корреляции квадратурной матрицы базисных сигналов и каждого из фрагментов сигнала промежуточных частот, соответственно количеству фрагментов вычисляют последовательность квадратурных суммарных матриц путем суммирования соответствующих столбцу и строке значений функций взаимной корреляции, полученных во всех позициях, обнаруживают объекты путем выявления элементов суммарной квадратурной матрицы функций взаимной корреляции любого фрагмента, значения которых превышают заданный пороговый уровень, и определяют в случае использования трехмерной квадратурной матрицы дальность, первую угловую координату и скорость, а в случае использования четырехмерной квадратурной матрицы - дальность, первую и вторую угловые координаты и скорость обнаруженных объектов по номерам, соответственно, столбцов и строки выявленных элементов.
Также, согласно изобретению, дополнительно вычисляют уточняющую поправку к любой из угловых координат, при этом из позиций приема выделяют две группы позиций, вычисляют соответственно столбцам и строке выявленных элементов суммарные основную и квадратурную матрицы значений функций взаимной корреляции для каждой группы, определяют фазу принятого в каждой из групп позиций сигнала из отношения соответствующих номеру столбца и строки значений функций корреляции основной и квадратурной суммарных матриц, вычисляют разность фаз сигналов, принятых группами позиций и определяют по ним с учетом расстояния между центрами групп позиций величину и знак поправки к значению угловой координаты.
Также, согласно изобретению, дополнительно из суммарных матриц функций взаимной корреляции формируют матрицу суммарных корреляционных сигналов, каждый элемент которой представляет собой последовательность соответствующих номерам столбцов и строк элементов суммарных матриц функций взаимной корреляции, определяют спектр корреляционных сигналов путем преобразования Фурье, обнаруживают объекты путем выявления элементов матрицы суммарных корреляционных сигналов, значения выделенных составляющих спектра которых превышают заданный пороговый уровень, и определяют дальность, угловые координаты и скорость обнаруженных объектов по номерам, соответственно, столбцов и строк выявленных элементов.
Кроме того, дополнительно по частоте выделенной составляющей спектра суммарного корреляционного сигнала выявленных элементов вычисляют уточняющую поправку к значению скорости обнаруженного объекта, причем знак уточняющей поправки определяют по знаку разности фаз выделенной составляющей в элементе основной матрицы и идентичном по номерам столбцов и строки элементе квадратурной матрицы корреляционных сигналов.
Также, согласно изобретению, дополнительно вычисляют уточняющую поправку к любой из угловых координат, при этом из позиций приема выделяют две группы позиций, вычисляют соответственно столбцам и строке выявленных элементов суммарные корреляционные сигналы для каждой группы, по отношению амплитуд выделенных составляющих спектра корреляционных сигналов основной и квадратурной матриц определяют фазу принятого в каждой из групп позиций сигнала, вычисляют разность фаз сигналов, принятых группами позиций и определяют по ним с учетом расстояния между центрами групп позиций величину и знак поправки к значению угловой координаты.
Целесообразно, если базисные сигналы в матрицах и сигналы промежуточных частот каждого фрагмента формируют в виде функций времени, а матрицы значений функций взаимной корреляции вычисляют перемножением сигнала промежуточных частот каждого фрагмента с каждым из базисных сигналов матриц с последующим интегрированием результата перемножения по времени фрагмента.
Целесообразно также, если базисные сигналы в матрицах формируют в виде коэффициентов спектра, формируют последовательность спектров фрагментов сигнала промежуточных частот путем преобразования Фурье сигнала каждого из фрагментов, а матрицы значений функций взаимной корреляции вычисляют перемножением коэффициентов спектра сигнала промежуточных частот каждого фрагмента с коэффициентами спектра каждого из базисных сигналов матриц с последующим суммированием результата перемножения.
Поставленная задача решается также тем, что в систему для радиолокационного измерения скоростей и координат объектов, содержащую соединенные микроволновыми входами и выходами антенно-фидерное устройство, обеспечивающее излучение зондирующего и прием отраженных от измеряемых объектов сигналов, и приемопередающее устройство, обеспечивающее формирование зондирующего сигнала, перемножение с ним принятых сигналов и усиление полученного гомодинного сигнала, а также аналого-цифровой преобразователь и процессор, вход управления частотой зондирующего сигнала и выходы гомодинных сигналов приемопередающего устройства соединены соответственно с аналоговым выходом процессора и входами аналого-цифрового преобразователя, а процессор наделен программами управления частотой приемопередающего устройства и вычисления скоростей и координат объектов, согласно изобретению, введен коррелометр, соединенный шиной данных с аналого-цифровым преобразователем и процессором, причем процессор наделен базой данных или программой формирования базы данных матриц базисных сигналов, номера столбцов первого измерения которых соответствуют множеству средних ожидаемых значений дальности, номера столбцов второго и третьего измерения - множествам средних ожидаемых значений первой и второй угловых координат, а номера строк - множеству средних ожидаемых значений скорости, а коррелометр наделен программой формирования из гомодинного сигнала - сигнала промежуточных частот в виде цифровых фрагментов заданной длительности, а также вычисления из последовательности фрагментов и матриц базисных сигналов последовательности матриц значений функций взаимной корреляции и матрицы корреляционных сигналов, каждый элемент которой представляет собой последовательность соответствующих номеру столбца и строки значений функций взаимной корреляции каждой из последовательности матриц, параметры которых служат для определения скоростей и координат отражающих объектов.
Приемопередающее устройство, согласно изобретению, может содержать формирователь зондирующего сигнала, смеситель и полосовой усилитель, а антенно-фидерное устройство может содержать циркулятор и приемопередающую антенну, причем выход формирователя подключен к микроволновому выходу приемопередающего устройства, вход управления частотой формирователя является входом управления частотой приемопередающего устройства, первый вход смесителя соединен с микроволновым входом приемопередающего устройства, второй вход подключен к выходу формирователя, а выход гомодинного сигнала смесителя подключен через полосовой усилитель к выходу гомодинного сигнала приемопередающего устройства, первое и второе плечи циркулятора являются входом и выходом антенно-фидерного устройства, а третье плечо подключено к приемопередающей антенне.
Вход управления частотой приемопередающего устройства может быть выполнен двухканальным, а формирователь зондирующего сигнала в этом случае может содержать задающий генератор, два балансных модулятора и сумматор, причем выход задающего генератора соединен с первым входом первого модулятора непосредственно, с входом второго модулятора - через фазовращатель, вторые входы модуляторов подключены соответственно к первому и второму каналам входа управления частотой формирователя, а выходы модуляторов через сумматор связаны с выходом формирователя.
Целесообразно, если антенно-фидерное устройство дополнительно содержит включенный между третьим плечом циркулятора и приемопередающей антенной компенсатор с управляемым по фазе коэффициентом отражения, а приемопередающее устройство - схему управления компенсатором, вход которой соединен с выходом смесителя, а выход схемы управления подключен к входу управления компенсатора.
Целесообразно также, если приемопередающее устройство дополнительно содержит детектор, подключенный к микроволновому входу, выход детектора соединен со вторым входом схемы управления, а компенсатор имеет второй вход управления модулем коэффициента отражения, подключенный ко второму выходу схемы управления.
Также, согласно изобретению, приемопередающее устройство может быть выполнено в виде автодинного узла, выход-вход и вход управления частотой которого являются соответственно микроволновым выходом-входом и входом управления частотой приемопередающего устройства, выход гомодинного сигнала автодинного узла через полосовой усилитель подключен к выходу гомодинного сигнала приемопередающего устройства, а антенно-фидерное устройство выполнено в виде приемопередающей антенны.
Во втором варианте системы, согласно изобретению, приемопередающее устройство содержит формирователь зондирующего сигнала и, по крайней мере, два смесителя и два полосовых усилителя, а антенно-фидерное устройство содержит передающую антенну и несколько - по числу смесителей - приемных антенн, подключенных соответственно к микроволновому входу и микроволновым выходам антенно-фидерного устройства, причем выход формирователя зондирующего сигнала подключен к микроволновому выходу приемопередающего устройства, а вход управления частотой является соответственно входом управления частотой приемопередающего устройства, первые входы смесителей соединены с микроволновыми входами приемопередающего устройства, вторые входы соединены с выходом формирователя зондирующего сигнала, а выходы - подключены через полосовые усилители к выходам гомодинного сигнала приемопередающего устройства.
Вход управления частотой приемопередающего устройства может быть выполнен двухканальным, а формирователь зондирующего сигнала в этом случае содержит задающий генератор, два балансных модулятора и сумматор, причем выход задающего генератора соединен с первым входом первого модулятора непосредственно, с входом второго модулятора - через фазовращатель, вторые входы модуляторов подключены соответственно к первому и второму каналам входа управления частотой формирователя, а выходы модуляторов через сумматор соединены с выходом формирователя.
Сущность предложенного изобретения заключается в том, что гомодинные сигналы, полученные перемножением непрерывного частотно-модулированного зондирующего излучаемого сигнала с принятыми сигналами, отраженными от измеряемых объектов, обрабатываются с применением корреляционно-фильтровых методов.
Передающей антенной в сторону измеряемого объекта или объектов излучается формируемый генератором зондирующий сигнал (далее - излучаемый сигнал), который в общем случае имеет вид:
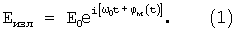
Принятый отраженный от объекта сигнал на выходе приемной антенны имеет вид:

где E0 - ЭДС зондирующего сигнала на клеммах передающей антенны, ω =2π f - частота излучаемого сигнала, ω 0=2π f0=2π с/λ 0 - круговая частота центрального колебания излучаемого сигнала, λ 0 - его длина волны, ϕ м(t) - составляющая фазы излучаемого сигнала, обусловленная частотной модуляцией генератора, τ =2L/с - время задержки принятого отраженного сигнала относительно излучаемого, γ - коэффициент ослабления сигнала на трассе "передающая антенна - объект - приемная антенна", L - дальность (расстояние между объектом и радиолокатором), с - скорость распространения электромагнитного сигнала в среде.
Излучаемый и принятый отраженный сигналы поступают на входы смесителя, выполняющего их перемножение. Если поступающая на смеситель мощность излучаемого сигнала много больше мощности принятого отраженного сигнала, то амплитуда низкочастотной (разностной) составляющей выходного сигнала смесителя пропорциональна амплитуде принятого отраженного сигнала, а фаза равна разности фаз излучаемого и принятого отраженного сигналов:
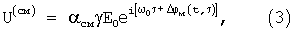
где α см - коэффициент передачи смесителя, Δ ϕ м(t, τ ) - составляющая разности фаз, обусловленная модуляцией частоты излучаемого сигнала. В тригонометрической форме действительная часть выражения (3) - низкочастотная составляющая результата перемножения принятого и излучаемого сигналов, далее - гомодинный сигнал, приобретает вид:
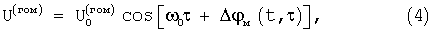
где 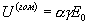 - амплитуда напряжения гомодинного сигнала на выходе смесителя.
- амплитуда напряжения гомодинного сигнала на выходе смесителя.
Первое слагаемое в квадратных скобках - произведение постоянной величины (центральной частоты излучаемого сигнала) на постоянное или медленно меняющееся время задержки принятого сигнала говорит о наличии в гомодинном сигнале составляющей с доплеровской частотой или постоянной составляющей, зависящей от времени задержки (τ ). Второе слагаемое ответственно за появление в гомодинном сигнале периодической составляющей, являющейся следствием частотной модуляции. Если зависимость частоты генератора от напряжения управления линейна, то мгновенное значение частоты излучаемого сигнала определяется при законе модуляции η f(t) выражением f=f0+Δ fм=f0+Δ f0η f/(t) (здесь η f(t) - периодическая функция частотной модуляции с единичной амплитудой). При этом второе слагаемое выражения (4) определится, как

Функция η f(t) может быть представлена в виде ряда Фурье: 
где ξ =1, 2, 3, ... - числа натурального ряда. Тогда после несложных преобразований получаем:

где 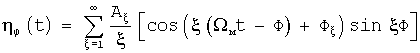 - функция фазовой модуляции гомодинного сигнала, φ 0=Δ f0/Fм - индекс частотной модуляции зондирующего сигнала, Ф=Ω мτ /2, Δ f0 - девиация частоты, Ω м=2π Fм - круговая частота модуляции. В частном случае гармонической модуляции, когда гармоники отсутствуют (A1=1, A2-∞ =0, Ф1=0), при обозначении Ψ =2φ 0sinФ закон изменения разности фаз (6) принимает вид:
- функция фазовой модуляции гомодинного сигнала, φ 0=Δ f0/Fм - индекс частотной модуляции зондирующего сигнала, Ф=Ω мτ /2, Δ f0 - девиация частоты, Ω м=2π Fм - круговая частота модуляции. В частном случае гармонической модуляции, когда гармоники отсутствуют (A1=1, A2-∞ =0, Ф1=0), при обозначении Ψ =2φ 0sinФ закон изменения разности фаз (6) принимает вид:
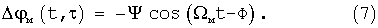
Обозначив разность фаз центральных спектральных составляющих излучаемого и принятого сигналов как Δ ϕ =ω 0τ =2ω 0L/c, получим:
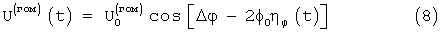
или 
В общем случае гомодинный сигнал порождается множеством сигналов, отраженных от множества kmax, движущихся и неподвижных объектов. Если k-тый объект движется, например, с постоянной радиальной скоростью Vk=dLk/dt, то время задержки отраженного сигнала τ k изменяется во времени:

а разность фаз излучаемого и принятого сигналов этого объекта Δ ϕ k определится как:
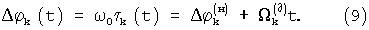
Здесь k - номер объекта, Lk - текущая дальность k-того объекта,  - дальность k-того объекта в начальный момент времени (t=t(н)),
- дальность k-того объекта в начальный момент времени (t=t(н)),  - соответствующая начальная разность фаз, с - скорость света, Vk - радиальная скорость объекта, которая может быть положительной величиной (объект удаляется) или отрицательной (объект приближается), а
- соответствующая начальная разность фаз, с - скорость света, Vk - радиальная скорость объекта, которая может быть положительной величиной (объект удаляется) или отрицательной (объект приближается), а 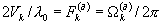 - доплеровский сдвиг частоты принятого сигнала. Результирующий усиленный в К(ус) раз гомодинный сигнал (
- доплеровский сдвиг частоты принятого сигнала. Результирующий усиленный в К(ус) раз гомодинный сигнал ( в зависимости от знака радиальной скорости может быть положительной или отрицательной) описывается выражением:
в зависимости от знака радиальной скорости может быть положительной или отрицательной) описывается выражением:
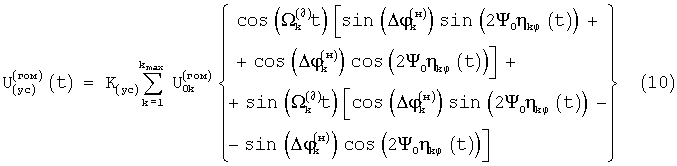
Важно, что, как следует из (6) и (10), гомодинный сигнал k-того объекта имеет две ортогональные составляющие: основную и квадратурную, содержащие соответственно 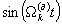 и
и 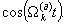 Эта особенность гомодинного сигнала дает возможность определения знака радиальной скорости объектов по знаку разности фаз доплеровских сигналов. Зависимость гомодинного сигнала от
Эта особенность гомодинного сигнала дает возможность определения знака радиальной скорости объектов по знаку разности фаз доплеровских сигналов. Зависимость гомодинного сигнала от  позволяет определить угловые координаты объекта, измеряя разность фаз сигналов, принятых в двух и более пространственных позициях.
позволяет определить угловые координаты объекта, измеряя разность фаз сигналов, принятых в двух и более пространственных позициях.
В целях обработки быстродействующими вычислительными средствами усиленный гомодинный сигнал удобно представить в виде последовательности из М фрагментов (m - номер фрагмента, 1≤ m≤ М) сигнала промежуточных частот (СПЧ). Каждый из фрагментов СПЧ формируют определенной (линейной или нелинейной) операцией преобразования гомодинного сигнала продолжительностью T1 (например, один или несколько периодов). Фрагмент СПЧ имеет продолжительность, меньшую или равную T1. В простейшем случае фрагмент СПЧ представляет собой усиленную копию гомодинного сигнала – U(СПЧ)(t)=K(ус)U(гом)(t).
Для повышения отношения сигнал/шум сигнала промежуточных частот относительно гомодинного может быть применен известный в импульсной радиолокации принцип накопления (интегрирования) (см “Справочник”, том 1, стр.41). В данном изобретении положительный эффект усиливается применением следующего алгоритма череспериодного суммирования, то есть получения накопленного в серии периодов гомодинного сигнала:
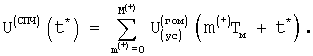
Здесь t=m(+)Tм+t*, 0≤ t*≤ Tм - время, отсчитываемое от начала периода, Tм=1/Fм - период модулирующего сигнала, m(+) - номер периода в серии, состоящей из М(+) периодов. Увеличение отношения сигнал/шум составляет 10logM(+) дБ, продолжительность гомодинного сигнала (время накопления) T1=Tм× M(+), а продолжительность фрагмента СПЧ равна периоду модуляции. Череспериодное суммирование может сочетаться с череспериодным вычитанием, когда накопленный в одной серии сигнал вычитается из сигнала, накопленного в предыдущей серии. В этом случае подавляются сигналы, отраженные от неподвижных объектов и подчеркиваются сигналы движущихся объектов с определенными доплеровскими частотами.
Для повышения точности измерения скоростей и координат объектов может быть реализовано умножение частоты усиленного гомодинного сигнала. Для этого усиленный гомодинный сигнал вида (8), один или более (ν -1) раз возводят в квадрат, исключая каждый раз из полученного сигнала постоянную составляющую, и получая в результате фрагменты сигнала ПЧ соответствующей кратности (ν ). После первого возведения в квадрат (ν =2) получаем СПЧ второй кратности:
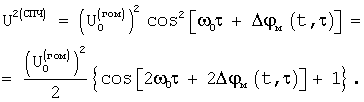
Если из этого сигнала исключить постоянную составляющую, то форма его будет полностью соответствовать форме гомодинного сигнала для увеличенных вдвое значений частоты зондирующего сигнала, девиации частотной модуляции и частоты модуляции. Операция возведения в квадрат и исключения постоянной составляющей может последовательно проводиться несколько раз, тогда в общем случае для v=1, 2, 3... сигнал ПЧ будет иметь вид:

Изложенные далее алгоритмы и соотношения корреляционно-фильтровой обработки применимы для умноженного гомодинного сигнала при условии, что учитывается увеличение в 2v-1 раз значений девиации частоты, частоты модуляции и доплеровской частоты.
Во временной области каждый фрагмент сигнала промежуточных частот имеет вид цифровой последовательности дискретных значений 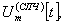 определенных для дискретных значений времени t. Во всех последующих выкладках дискретность представления всех величин подразумевается по умолчанию. Для каждого из фрагментов преобразованием Фурье могут быть вычислены коэффициенты спектра (например, коэффициенты комплексного спектра) для момента времени tm, привязанного к началу, средине или концу интервала анализа T1. Таким образом, сигнал ПЧ определится в частотной области:
определенных для дискретных значений времени t. Во всех последующих выкладках дискретность представления всех величин подразумевается по умолчанию. Для каждого из фрагментов преобразованием Фурье могут быть вычислены коэффициенты спектра (например, коэффициенты комплексного спектра) для момента времени tm, привязанного к началу, средине или концу интервала анализа T1. Таким образом, сигнал ПЧ определится в частотной области:

где N - номер гармоники модулирующего сигнала, АmN и ВmN - коэффициенты, характеризующие спектр m-то фрагмента гомодинного сигнала, которые могут вычисляться операциями преобразования Фурье (например, быстрое преобразование Фурье (БПФ) или оконное БПФ). Последовательность М спектров фрагментов характеризует изменение спектра СПЧ во времени.
Для частного случая (7) гармонической частотной модуляции из (8) может быть легко получено (см. “Справочник по радиолокации”, в четырех томах под редакцией М. Сколника, том 3, Москва, “Советское радио”, 1976-1979 (пер. с английского “RADAR HANDBOOK”, Editor-In-Chief M.I.Skolnik, McGRAU-HILL BOOK COMPANY, 1970)”, том 3, 1979, стр.258-262) спектрально-временное аналитическое выражение для спектра усиленного в заданной полосе частот ((2nmin-1)Ω м-2nmaxΩ м) гомодинного сигнала:
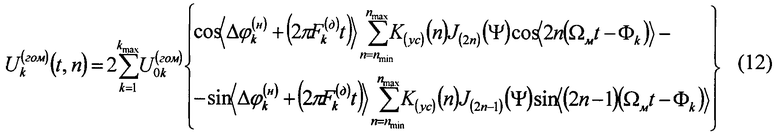
Здесь K(ус)(n) - амплитудно-частотная характеристика усиления гомодинного сигнала, причем К(ус)(0)=0, nmin и nmax - числа, определяющее номера низшей (Nmin=2nmin-1) и высшей (Nmax=2nmax) заданных гармоник в полосе усиления, то есть в спектре гомодинного сигнала, Фk=Ω мτ k/2=2π Lk/Λ , Λ =c/Fм - длина волны модулирующего колебания. При наличии сигнала от одного отражающего объекта зависимость фазы гармоники от частоты (фазовый спектр сигнала ПЧ) линейна: (ФNk=NФk). Очевидно, что спектр гомодинного сигнала содержит множество дискретных спектральных составляющих - гармоник модулирующего сигнала (далее - гармоники). При 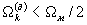 амплитуда гармоник (11) изменяется с доплеровской частотой по закону амплитудно-модулированного сигнала с подавленной несущей. Множество фаз ФN гармоник спектра несет информацию о фазовом спектре принятого отраженного сигнала (фазочастотной характеристике измеряемого пространства), то есть о временах задержки отраженных сигналов и дальности объектов. В общем случае имеет место нелинейная (периодическая) зависимость ФN(N). От дальности объекта зависят также амплитуды гармоник, определяемые функциями Бесселя.
амплитуда гармоник (11) изменяется с доплеровской частотой по закону амплитудно-модулированного сигнала с подавленной несущей. Множество фаз ФN гармоник спектра несет информацию о фазовом спектре принятого отраженного сигнала (фазочастотной характеристике измеряемого пространства), то есть о временах задержки отраженных сигналов и дальности объектов. В общем случае имеет место нелинейная (периодическая) зависимость ФN(N). От дальности объекта зависят также амплитуды гармоник, определяемые функциями Бесселя.
Для определения скоростей и координат объектов гомодинный сигнал представляют в цифровой форме в виде последовательности фрагментов сигнала промежуточных частот заданной длительности и вычисляют значения функции корреляции каждого фрагмента СПЧ и искусственно созданных базисных (или опорных) сигналов. Поскольку гомодинный и базисные сигналы могут быть представлены как во временной, так и в спектральной областях (формах), то существуют два основных варианта вычисления функций корреляции. Во временной области ее получают путем перемножения и интегрирования СПЧ и базисного сигнала. В частотной области значение функции корреляции вычисляют перемножением спектров СПЧ и комплексно сопряженного базисного сигнала (или наоборот). В последнем случае процесс определения функции корреляции можно представить как пропускание СПЧ через набор параллельно включенных гребенчатых фильтров, коэффициенты передачи которого на частотах гармоник равны комплексно сопряженным коэффициентам Фурье-разложения базисных сигналов, с последующим детектированием и сложением полученных выходных сигналов. В общем случае значение функции корреляции зависит от величины времени задержки принятого сигнала относительно излучаемого (то есть от дальности объекта) и от текущего времени (в частности, если отражающий объект движется). В дальнейшем для обозначения закона изменения значений функции корреляции во времени соответственно последовательности фрагментов (при определенной дальности) будем использовать термин “корреляционный сигнал”. Корреляционный сигнал есть последовательность значений функций корреляции, вычисленных из фрагментов СПЧ для соответствующих моментов времени tm.
Первый вариант способа. Формируют основную двумерную (дальность, скорость) матрицу базисных сигналов, каждый из которых имитирует временного функцию или спектр ожидаемого гомодинного сигнала. Из последовательности фрагментов гомодинного сигнала (сигнала ПЧ) и матрицы базисных сигналов во временной или в частотной области вычисляют последовательность двумерных (дальность, скорость) матриц значений функций корреляции и матрицу корреляционных сигналов. По превышению значением функции корреляции любого фрагмента или составляющей спектра корреляционного сигнала в одной из ячеек матрицы заданного уровня обнаруживают отражающий объект. Дальность и скорость определяют по координатам ячейки, то есть номерам столбца и строки матрицы. Дополнительно существует возможность более точного измерения дальности по параметрам фазового спектра гомодинного сигнала и скорости по частоте составляющей спектра корреляционного сигнала. При необходимости дополнительно к основной создается квадратурная матрица базисных сигналов и вычисляется, соответственно, квадратурная матрица функций корреляции.
Второй вариант способа применяется в случаях, когда чувствительности одной позиции приема недостаточно для достижения заданной предельной дальности или необходимо определение угловых координат объектов. Он состоит в применении алгоритмов первого варианта способа к сигналам ПЧ, полученным из отраженных сигналов, принятых в нескольких пространственно разнесенных позициях. В каждой позиции формируют трех- или четырехмерные матрицы (дальность, одна или две угловые координаты, скорость) базисных сигналов и вычисляют соответствующие последовательности матриц функций корреляции базисных сигналов с последовательностью фрагментов сигнала ПЧ. Суммированием полученных в позициях приема матриц функций корреляции получают суммарные матрицы функций корреляции, а из последовательности суммарных матриц функций корреляции формируют суммарную матрицу корреляционных сигналов. По превышению значением суммарной функции корреляции любого фрагмента или составляющей спектра корреляционного сигнала в одной из ячеек матрицы заданного уровня обнаруживают отражающий объект. Координаты и скорость обнаруженного объекта определяют по номерам столбцов и строки суммарной матрицы. При необходимости создаются квадратурные матрицы базисных сигналов и вычисляются соответствующие им квадратурные матрицы функций корреляции и корреляционных сигналов.
В рамках настоящего изобретения допустимы и иные принципы формирования базисных сигналов. Спектры и, следовательно, временные функции базисных сигналов могут выбираться, например, по желаемой форме (зависимости от времени задержки) функции корреляции. В процессе измерения по любому варианту способа могут изменяться по заданной программе частота модулирующего сигнала Fм и девиация частотной модуляции Δ f0. На форму функций корреляции можно влиять, также изменением амплитудно-частотной характеристики усиления гомодинного сигнала.
Разобьем полный интервал измеряемых дальностей Lmin-Lmax на Р интервалов, обозначим множество средних значений интервалов, то есть ожидаемых дальностей Lp, а множество средних значений ожидаемого времени задержки отраженного сигнала -τ p=2Lp/c. Разобьем полный интервал измеряемых радиальных скоростей Vmin-Vmax на R интервалов, обозначим множество средних значений интервалов, то есть ожидаемых скоростей Vr, а множество ожидаемых средних значений доплеровских частот -  Отметим, что и скорости Vr, и частоты
Отметим, что и скорости Vr, и частоты 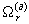 могут принимать и положительные и отрицательные значения. Базисный сигнал для значения дальности Lp при значении скорости Vr определяется, например из (10), выражением:
могут принимать и положительные и отрицательные значения. Базисный сигнал для значения дальности Lp при значении скорости Vr определяется, например из (10), выражением:

Массив базисных сигналов для интервала дальностей Lmin-Lmax и интервала скоростей Vmin-Vmax удобно представить в виде двумерной (столбец-строка) прямоугольной таблицы, номер столбца которой (р) соответствует номеру интервала дальности, а номер строки (r) - номеру интервала скорости, а базисный сигнал 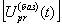 записывается в ячейку таблицы на пересечении столбца (р) и строки (r). Подобные таблицы, обозначаемые термином “матрица”, широко применяется в математике (см., например, Ф.Р.Гантмахер, Теория матриц, М., “Наука”, 1967). В настоящем изобретении методы матричного исчисления (за исключением простейших свойств матриц) не используются, а применение понятия “матрица” обусловлено, во-первых, наглядностью матричного представления массивов величин и функций, а во-вторых - удобством обработки информации, представленной в матричной форме, современными вычислительными средствами. Выражение для двумерной матрицы базисных сигналов (здесь и далее матрицы обозначаются квадратными скобками) при условии, что
записывается в ячейку таблицы на пересечении столбца (р) и строки (r). Подобные таблицы, обозначаемые термином “матрица”, широко применяется в математике (см., например, Ф.Р.Гантмахер, Теория матриц, М., “Наука”, 1967). В настоящем изобретении методы матричного исчисления (за исключением простейших свойств матриц) не используются, а применение понятия “матрица” обусловлено, во-первых, наглядностью матричного представления массивов величин и функций, а во-вторых - удобством обработки информации, представленной в матричной форме, современными вычислительными средствами. Выражение для двумерной матрицы базисных сигналов (здесь и далее матрицы обозначаются квадратными скобками) при условии, что  имеет вид:
имеет вид:
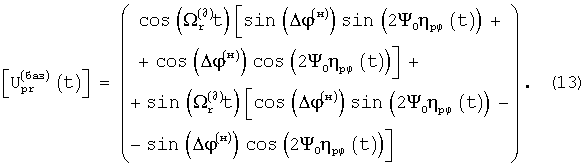
Поскольку в отраженном принятом сигнале все значения начальной разности фаз  равновероятны, то для извлечения полной информации об отражающем объекте необходимы в идеале два варианта базисных сигналов для разных Δ ϕ (н), например “основное” (Δ ϕ (н)=0) и “квадратурное” (Δ ϕ (н)=π /2). При наличии одного варианта часть энергии отраженного сигнала может быть утрачена, однако операции обнаружения объектов, а также определения их координат и скорости будут выполнены. Из (13) получаем “основную” двумерную матрицу базисных сигналов во временной области (форме):
равновероятны, то для извлечения полной информации об отражающем объекте необходимы в идеале два варианта базисных сигналов для разных Δ ϕ (н), например “основное” (Δ ϕ (н)=0) и “квадратурное” (Δ ϕ (н)=π /2). При наличии одного варианта часть энергии отраженного сигнала может быть утрачена, однако операции обнаружения объектов, а также определения их координат и скорости будут выполнены. Из (13) получаем “основную” двумерную матрицу базисных сигналов во временной области (форме):
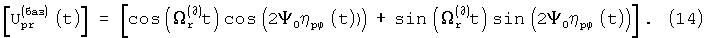
При необходимости дополнительно создается “квадратурная” матрица базисных сигналов:
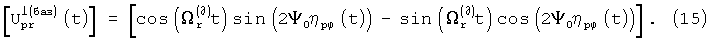
Если выполнить преобразование Фурье с каждым элементом матриц (14) и (15), то будут получены соответствующие основная  и, дополнительно, квадратурная
и, дополнительно, квадратурная  матрицы базисных сигналов в частотной области (спектральная форма).
матрицы базисных сигналов в частотной области (спектральная форма).
В комплексной форме эти матрицы имеют вид:
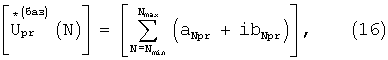
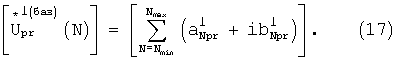
Коэффициенты aNpr, bNpr, 
 могут быть либо определены в аналитической форме, либо вычислены применением, например, стандартных приемов разложения функций (14) и (15) в ряд Фурье.
могут быть либо определены в аналитической форме, либо вычислены применением, например, стандартных приемов разложения функций (14) и (15) в ряд Фурье.
По общему правилу оптимальной обработки (согласованной фильтрации) принятого сигнала (см., например, “Справочник”, том 3, стр.400-402) для определения дальности необходимо найти номер интервала дальности р, в котором имеет место максимум функции корреляции комплексной огибающей задержанного излучаемого и принятого сигналов. Из него определяются значения времени задержки  и дальности Lp. В нашем случае дальность определяется по максимуму, по крайней мере, одной из функций взаимной корреляции сигнала ПЧ и базисных сигналов. Особенностью настоящего способа является непрерывность излучаемого и принятого сигналов, а также то, что определяются функции взаимной корреляции (далее - функции корреляции) между гомодинным сигналом (фрагментом сигнала ПЧ) и базисными, искусственно созданными сигналами. Дальности объектов определяется по номерам столбцов, а скорости - по номерам строк элементов матриц, в которых находятся главные максимумы функций корреляции гомодинного (то есть СПЧ) и базисных сигналов.
и дальности Lp. В нашем случае дальность определяется по максимуму, по крайней мере, одной из функций взаимной корреляции сигнала ПЧ и базисных сигналов. Особенностью настоящего способа является непрерывность излучаемого и принятого сигналов, а также то, что определяются функции взаимной корреляции (далее - функции корреляции) между гомодинным сигналом (фрагментом сигнала ПЧ) и базисными, искусственно созданными сигналами. Дальности объектов определяется по номерам столбцов, а скорости - по номерам строк элементов матриц, в которых находятся главные максимумы функций корреляции гомодинного (то есть СПЧ) и базисных сигналов.
Во временной области матрицы значений (на момент времени tk) функции корреляции сигнала ПЧ (10) и базисных сигналов (13, 14) определяются, например, вычислением интеграла:


где Тф - продолжительность одного фрагмента, при отсутствии череспериодного сложения или вычитания равная времени первичного накопления сигнала T1, которое может быть равно или кратно периоду модулирующего сигнала, tm - время (момент) отсчета функции корреляции - начало фрагмента, m=0, 1, 2,..., М - номер фрагмента.
В частотной области основная и квадратурная матрицы функций корреляции вычисляются перемножением коэффициентов Фурье сигнала ПЧ (11) и базисных сигналов (16, 17) с последующим суммированием результата:


Функции корреляции вида (18-21) имеют главный максимум при Lk=Lp,  и побочные максимумы с меньшим уровнем (боковые лепестки) при некоторых иных значениях Lk и
и побочные максимумы с меньшим уровнем (боковые лепестки) при некоторых иных значениях Lk и  Операция первичного обнаружения отражающего объекта проводится путем сравнения вычисленных (для любого m) значений элементов матриц (18, 19) или (20, 21) с заданными пороговыми уровнями, при этом выявляются элементы (рk, rk) любой из матриц значений функций корреляции, превышающие заданный пороговый уровень. Наличие объектов определяется по превышению вычисленной функцией корреляции заданного порогового значения, а дальность и скорость объекта - по номерам, соответственно, столбца pk и строки rk матрицы. Время накопления сигнала при этом равно T1, то есть времени интегрирования (18, 19) или времени анализа при выполнении преобразования Фурье (11).
Операция первичного обнаружения отражающего объекта проводится путем сравнения вычисленных (для любого m) значений элементов матриц (18, 19) или (20, 21) с заданными пороговыми уровнями, при этом выявляются элементы (рk, rk) любой из матриц значений функций корреляции, превышающие заданный пороговый уровень. Наличие объектов определяется по превышению вычисленной функцией корреляции заданного порогового значения, а дальность и скорость объекта - по номерам, соответственно, столбца pk и строки rk матрицы. Время накопления сигнала при этом равно T1, то есть времени интегрирования (18, 19) или времени анализа при выполнении преобразования Фурье (11).
При недостаточности времени T1, для обнаружения сигналов слабых отражающих объектов проводят вторичное накопление за время T2, существенно большее T1. Для этого из последовательности матриц функций корреляции (18-21) создают матрицу корреляционных сигналов, каждый элемент которой является последовательностью идентичных по номерам столбцов и строк элементов матриц значений функций корреляции. Как очевидно из (10) и (13) перемножение сигнала ПЧ и любого из базисных сигналов порождает (из-за нелинейности преобразования) при определении функции корреляции сложное колебание, содержащее составляющие с частотами 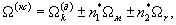 где
где 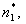
 - произвольные целые числа). Если принять Ω r=rΩ м, и учесть усреднение сигнала по времени накопления T1, то получим, что частота обусловленных эффектом Доплера осцилляций корреляционного сигнала (частота составляющей спектра корреляционного сигнала) равна
- произвольные целые числа). Если принять Ω r=rΩ м, и учесть усреднение сигнала по времени накопления T1, то получим, что частота обусловленных эффектом Доплера осцилляций корреляционного сигнала (частота составляющей спектра корреляционного сигнала) равна 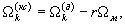 причем она не может быть больше половины частоты модуляции
причем она не может быть больше половины частоты модуляции 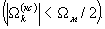 Вторичное накопление сигнала проводят дискретным преобразованием Фурье каждого из корреляционных сигналов матрицы, в результате которого для последовательности М значений (при tm=t1-tм) функций корреляции (18-19) или (20-21), получают значения пар (например, действительные и мнимые
Вторичное накопление сигнала проводят дискретным преобразованием Фурье каждого из корреляционных сигналов матрицы, в результате которого для последовательности М значений (при tm=t1-tм) функций корреляции (18-19) или (20-21), получают значения пар (например, действительные и мнимые 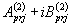 для комплексной формы спектра) коэффициентов Фурье составляющих спектра корреляционного сигнала в полосе анализа Δ Ω (д)=2π /T2 на частоте, например,
для комплексной формы спектра) коэффициентов Фурье составляющих спектра корреляционного сигнала в полосе анализа Δ Ω (д)=2π /T2 на частоте, например,  Сравнивая значения модуля (амплитуды) выделенных составляющих спектра с заданными пороговыми уровнями, по превышению модулем порогового уровня выявляют элемент (pk, rk) матрицы и выделяют составляющую спектра jk с обнаруженным сигналом. По номерам столбца рk и строки rk матрицы определяют дальность и скорость обнаруженного объекта. Время вторичного накопления сигнала Т2=МТ1 больше времени первичного накопления, что позволяет обнаружить объекты со слабым отраженным сигналом, пропущенным при первичном накоплении, то есть повысить предельную дальность радиолокатора.
Сравнивая значения модуля (амплитуды) выделенных составляющих спектра с заданными пороговыми уровнями, по превышению модулем порогового уровня выявляют элемент (pk, rk) матрицы и выделяют составляющую спектра jk с обнаруженным сигналом. По номерам столбца рk и строки rk матрицы определяют дальность и скорость обнаруженного объекта. Время вторичного накопления сигнала Т2=МТ1 больше времени первичного накопления, что позволяет обнаружить объекты со слабым отраженным сигналом, пропущенным при первичном накоплении, то есть повысить предельную дальность радиолокатора.
Дополнительно появляется возможность в М раз уменьшить погрешность измерения радиальной скорости объекта по определяемой из очевидного соотношения доплеровской частоте  Значение уточняющей поправки
Значение уточняющей поправки 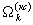 к доплеровской частоте rΩ м, определяемой по основному алгоритму, равно
к доплеровской частоте rΩ м, определяемой по основному алгоритму, равно  а ее знак в этой формуле определяется по знаку разности фаз выделенной составляющей спектра частоты
а ее знак в этой формуле определяется по знаку разности фаз выделенной составляющей спектра частоты  в элементе (pk, rk) основной матрицы и идентичном по номеру столбца и строки элементе (рk, rk) квадратурной матрицы корреляционных сигналов.
в элементе (pk, rk) основной матрицы и идентичном по номеру столбца и строки элементе (рk, rk) квадратурной матрицы корреляционных сигналов.
Очевидным вариантом изложенного алгоритма является совместная обработка основного и квадратурного корреляционных сигналов, для чего создают полные корреляционные сигналы суммируя, например, основной сигнал с производной и(или) интегралом квадратурного. С полученными полными корреляционными сигналами проводят преобразование Фурье и по уровню выделенных составляющих спектра обнаруживают объект. Отношение сигнал/шум увеличивается при этом на 3 дБ, но вдвое увеличивается и объем вычислений.
Если вычисление функций корреляции производят в частотной области через коэффициенты Фурье гомодинного сигнала, то операция вторичного накопления может быть дополнена определением уточненного значения дальности обнаруженного объекта. Для этого вычисляется задержка сигнала через отношение полной фазы гармоники сигнала ПЧ к ее частоте. Как следует из выражения (12), для этого достаточно определить ряд главных значений фаз ФNk=2π NLk/Λ для нескольких выбранных значений N. Поскольку точность определения фазы гармоники ФNk пропорциональна ее уровню, то выбор величин N проводят по критерию максимальных значений амплитуды (модуля) гармоники в базисном сигнале выявленного элемента (pk, rk) матрицы, причем для устранения неоднозначности вычисление ФNk следует проводить, по крайней мере, для двух значений N (N1 и N2). Для выбранных номеров гармоник из СПЧ (11) формируются пары (например, действительные и мнимые AmN[tm] и BmN[tm]) сигналов гармоник, представляющие собой последовательности М пар коэффициентов преобразования Фурье (11). С каждым из пары сигналов каждой выбранной гармоники проводят преобразование Фурье и через арктангенс отношения мнимой и действительной оставляющих спектра сигнала гармоники на частоте, выделенной при обнаружении объекта составляющей 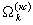 корреляционного сигнала, определяют главное значение фазы этой, гармоники, обусловленной обнаруженным объектом. Полученные для нескольких выбранных значений N фазы гармоник позволяют вычислить известными методами (см., например, метод трех частот или патент РФ №2158937 от 10 ноября 2000 г.) полную фазу
корреляционного сигнала, определяют главное значение фазы этой, гармоники, обусловленной обнаруженным объектом. Полученные для нескольких выбранных значений N фазы гармоник позволяют вычислить известными методами (см., например, метод трех частот или патент РФ №2158937 от 10 ноября 2000 г.) полную фазу  гармоники, а из нее (по формуле
гармоники, а из нее (по формуле  ) дальность k-го объекта.
) дальность k-го объекта.
В ряде случаев реализация заданных значений предельной дальности затруднительна либо по причине технической сложности получения достаточно большого уровня мощности излучаемого сигнала, либо из-за административных ограничений на уровень этой мощности. Для решения этой проблемы применяют многопозиционный прием, то есть когерентное сложение сигналов, принятых в нескольких пространственно разнесенных позициях (см. “Справочник”, том 4, стр.193). Поскольку при этом суммируются амплитуды принятых отраженных от объектов сигналов и мощности некоррелированных шумов, то каждая дополнительная позиция приема увеличивает отношение сигнал/шум на 3 дБ. Учитывая, что предельная дальность пропорциональна корню четвертой степени излучаемой мощности, приемом отраженного сигнала в восьми позициях может быть достигнуто удвоение предельной дальности. Поскольку расстояния, пройденные отраженным сигналом от объекта до разных позиций, как и разности фаз центральных колебаний принятых в них сигналов, зависят от угла направления на отражающий объект, то появляется возможность определения угловых координат объектов.
Возможность когерентного суммирования сигналов, принятых в нескольких, например двух, позициях (s=0) и (s=1), базируется на известном соотношении, полученном для разности фаз центральных колебаний сигналов, принятых в этих позициях (см. Сайбель А.Г. “Основы радиолокации”, “Советское радио”, М., 1961, стр.165):
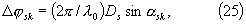
где α sk - угол между нормалью отрезка, соединяющего позиции, и направлением на k-тый объект, Ds - расстояние между нулевой позицией (s=0) и позицией номер s (s>0), общее число позиций (S+1). Это соотношение справедливо для любой пары из любого множества позиций приема. Зондирующий сигнал при этом излучают из произвольной позиции, которая в частном случае может совпадать с одной из позиций приема.
Сигналы, принятые в каждой позиции, по общему алгоритму способа перемножают (смешивают) с излучаемым сигналом, усиленные гомодинные сигналы, являющиеся суперпозицией сигналов, полученных от kmax объектов, имеют вид (см. выражения (10 и 11)), соответственно во временной и частотной областях:
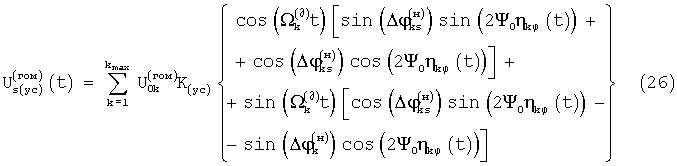

Если, как принято для (26-27), расстояния между позициями приема много меньше длины волны модулирующего колебания, а амплитуды гомодинных сигналов в позициях равны, то сигналы (26-27) в позициях отличаются либо по амплитудам четных и нечетных составляющих (для неподвижных объектов), либо по фазам доплеровских составляющих. Из гомодинных сигналов в позициях формируют цифровые фрагменты сигнала ПЧ.
Сущность второго варианта способа состоит в применении алгоритмов первого варианта способа к обработке сигналов ПЧ, полученных при многопозиционном приеме. Разобьем полный интервал измеряемых дальностей Lmin-Lmax на Р интервалов, обозначим множество средних значений интервалов, то есть ожидаемых дальностей Lp, а множество средних значений ожидаемого времени задержки отраженного сигнала - τ р=2Lp/с. Разобьем полный интервал измеряемых радиальных скоростей Vmin-Vmax на R интервалов, обозначим множество средних значений интервалов, то есть ожидаемых скоростей Vr, а множество ожидаемых средних значений доплеровских частот -  Отметим, что и скорости Vr и частоты
Отметим, что и скорости Vr и частоты  могут принимать и положительные и отрицательные значения. Предположим, что позиции приема расположены на прямой, перпендикулярной лучу с нулевым значением угловой координаты α (например, азимута) в полярных координатах α , L (см. Математическая энциклопедия, том 4, М., 1984, стр.479). Разобьем полный интервал наблюдения по угловой координате α на Q интервалов, присвоим им номера q и обозначим каждый интервал α q. При необходимости, если позиции приема размещены не на одной прямой, возможен переход к сферической системе координат α , α 2, L (см. Математическая энциклопедия, том 5, М., 1985, стр.293), где будут определяться две угловые координаты α , α 2 (например, азимут и угол места). В этом случае полный интервал наблюдения по второй угловой координате разбивают на Q2 интервалов, которым присваиваются номера q2. Вычислим по вытекающей из (25) формуле
могут принимать и положительные и отрицательные значения. Предположим, что позиции приема расположены на прямой, перпендикулярной лучу с нулевым значением угловой координаты α (например, азимута) в полярных координатах α , L (см. Математическая энциклопедия, том 4, М., 1984, стр.479). Разобьем полный интервал наблюдения по угловой координате α на Q интервалов, присвоим им номера q и обозначим каждый интервал α q. При необходимости, если позиции приема размещены не на одной прямой, возможен переход к сферической системе координат α , α 2, L (см. Математическая энциклопедия, том 5, М., 1985, стр.293), где будут определяться две угловые координаты α , α 2 (например, азимут и угол места). В этом случае полный интервал наблюдения по второй угловой координате разбивают на Q2 интервалов, которым присваиваются номера q2. Вычислим по вытекающей из (25) формуле  основные значения начальной разности фаз
основные значения начальной разности фаз  для каждой позиции и каждого направления α q. Значения
для каждой позиции и каждого направления α q. Значения  для определения второй угловой координаты определяются аналогичным образом. Далее операции показаны для случая одной угловой координаты, однако они легко распространяются на случай двух угловых координат. Определим из (26) в соответствии с этими разбиениями в каждой позиции приема для каждого заданного значения начальной разности фаз
для определения второй угловой координаты определяются аналогичным образом. Далее операции показаны для случая одной угловой координаты, однако они легко распространяются на случай двух угловых координат. Определим из (26) в соответствии с этими разбиениями в каждой позиции приема для каждого заданного значения начальной разности фаз 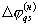 основную трехмерную размера P× Q× R матрицу базисных сигналов, номер столбца p которой есть номер интервала дальности, номера других столбцов q - номер интервала угловой координаты, а номер строки r - номер интервала скорости:
основную трехмерную размера P× Q× R матрицу базисных сигналов, номер столбца p которой есть номер интервала дальности, номера других столбцов q - номер интервала угловой координаты, а номер строки r - номер интервала скорости:

Трехмерная (дальность - угловая координата - скорость) матрица базисных сигналов может быть представлена как комбинация Q двумерных матриц (дальность - скорость). При необходимости формируется аналогичная квадратурная матрица:

В “нулевой” позиции (s=0), выбираемой произвольно, принимается  тогда вид базисных сигналов во временной области совпадает с (14, 15):
тогда вид базисных сигналов во временной области совпадает с (14, 15):
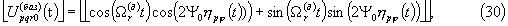

Основные и квадратурные матрицы базисных сигналов для каждой позиции в частотной области (спектральная форма) в комплексной форме имеют вид:
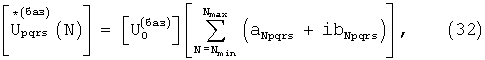
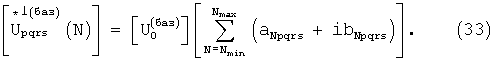
Матрицы коэффициентов аNpqrs, bNpqrs, aNpqrs, bNpqrs, могут быть вычислены, например, применением стандартных приемов разложения функций (28) и (29) в ряд Фурье. Отметим, что при расположении позиций приема на поверхности (например, двумерной), матрицы базисных сигналов каждой позиции должны быть четырехмерными, что позволит определить дальность, скорости и обе угловые координаты объектов.
Полученные в каждой позиции гомодинные сигналы усиливают, как и в первом варианте способа, и формируют из них сигналы промежуточных частот (ПЧ) в виде последовательности цифровых фрагментов заданной продолжительности. Далее в каждой позиции вычисляют (соответственно последовательности фрагментов) последовательность основных и, при необходимости, квадратурных матриц значений функций корреляции сигналов ПЧ, полученных в каждой позиции, и базисных сигналов, сформированных для этой позиции. Эта операция может проводиться как во временной, так и в частотной областях.
Полученные в каждой позиции гомодинные сигналы усиливают, как и в первом варианте способа, и формируют из них сигналы промежуточных частот (ПЧ) в виде последовательности цифровых фрагментов заданной продолжительности. Далее в каждой позиции вычисляют (соответственно последовательности фрагментов) последовательность основных и, при необходимости, квадратурных матриц значений функций корреляции сигналов ПЧ, полученных в каждой позиции, и базисных сигналов, сформированных для этой позиции. Эта операция может проводиться как во временной, так и в частотной областях.
Во временной области матрицы мгновенных (на момент времени tк) значений функции корреляции сигналов ПЧ в позициях (26) и базисных сигналов (28, 29) определяются, например, вычислением интеграла:


где Тф - продолжительность одного фрагмента, при отсутствии череспериодного сложения или вычитания, равная времени первичного накопления сигнала T1, которое может быть равно или кратно периоду модулирующего сигнала, tк - время (момент) отсчета функции корреляции, к=0, 1, 2, ... - номер отсчета. В частотной области основные и квадратурные матрицы функций корреляции в позициях вычисляются перемножением коэффициентов Фурье сигнала ПЧ (27) и базисных сигналов (30, 31) и суммированием результата:
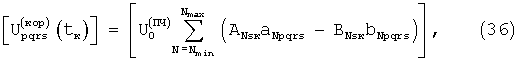
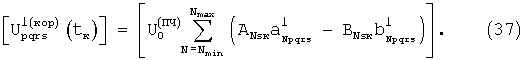
Далее из (34-35) или из (36-37) вычисляются суммарные по позициям трехмерные основные и квадратурные матрицы функций корреляции для момента времени tк:
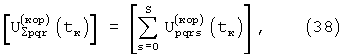
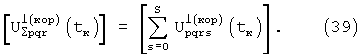
Суммарные функции корреляции вида (38-39) имеют главный максимум при Lk=Lp,  α k=α q, причем поскольку суммируются когерентные сигналы амплитуда его в S раз больше амплитуды главного максимума функции корреляции одной позиции. Поскольку шумы в сигналах позиций не коррелированы и при суммировании сигналов позиций складываются их мощности, то очевидно, что выигрыш в величине отношения сигнал/шум составляет 3 дБ на каждую дополнительную позицию. Функции корреляции вида (38-39) имеют также и побочные максимумы с меньшим уровнем (боковые лепестки) при некоторых иных значениях координат и скорости.
α k=α q, причем поскольку суммируются когерентные сигналы амплитуда его в S раз больше амплитуды главного максимума функции корреляции одной позиции. Поскольку шумы в сигналах позиций не коррелированы и при суммировании сигналов позиций складываются их мощности, то очевидно, что выигрыш в величине отношения сигнал/шум составляет 3 дБ на каждую дополнительную позицию. Функции корреляции вида (38-39) имеют также и побочные максимумы с меньшим уровнем (боковые лепестки) при некоторых иных значениях координат и скорости.
Операция первичного обнаружения отражающего объекта проводится, как и в первом варианте способа путем сравнения вычисленных (для любого m) значений элементов суммарных матриц (38) или (39) с заданными пороговыми уровнями, при этом выявляются элементы (pk, qk, rk, а для четырехмерной матрицы pk, qk, q2k, rk) любой (основной или квадратурной, а также по номеру m) суммарной матрицы значений функций корреляции, превышающие заданный пороговый уровень. Наличие объектов определяется по превышению вычисленной функцией корреляции заданного значения, а дальность, угловая координата и скорость объекта - по номерам, соответственно, столбцов рk, qk и строки rk, этого элемента матрицы. Время накопления сигнала при этом равно T1, то есть времени интегрирования (34, 35) или времени анализа при выполнении преобразования Фурье (27).
Как и в алгоритме первого варианта способа, из последовательности суммарных матриц функций корреляции (38-39) могут быть созданы матрицы (основная и квадратурная) суммарных корреляционных сигналов, каждый элемент которой являются последовательностью идентичных по номерам столбцов и строк элементов суммарных матриц функций корреляции. Вторичное накопление сигнала проводят дискретным преобразованием Фурье каждого из заданных корреляционных сигналов суммарной матрицы, в результате которого для последовательности М значений (при tm=t1-tM) функций корреляции (36-37) или (38-39), получают значения пар (например, действительные и мнимые для комплексной формы спектра  ) коэффициентов Фурье составляющих спектра суммарного корреляционного сигнала, выделенных в полосе анализа
) коэффициентов Фурье составляющих спектра суммарного корреляционного сигнала, выделенных в полосе анализа 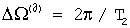 на частоте, например,
на частоте, например,  Сравнивая значения модуля (амплитуды) выделенных составляющих спектра корреляционного сигнала с заданными пороговыми уровнями, по превышению модулем порогового уровня выявляют элемент pk, qk, rk матрицы и выделяют составляющую спектра jk с обнаруженным сигналом. По номерам столбцов и строки pk, qk, rk матрицы определяют дальность, угловые координаты и скорость обнаруженного объекта. Время вторичного накопления сигнала T2=МТ1 больше времени первичного накопления, что позволяет обнаружить объекты со слабым отраженным сигналом, пропущенным при первичном накоплении, то есть повысить предельную дальность радиолокатора.
Сравнивая значения модуля (амплитуды) выделенных составляющих спектра корреляционного сигнала с заданными пороговыми уровнями, по превышению модулем порогового уровня выявляют элемент pk, qk, rk матрицы и выделяют составляющую спектра jk с обнаруженным сигналом. По номерам столбцов и строки pk, qk, rk матрицы определяют дальность, угловые координаты и скорость обнаруженного объекта. Время вторичного накопления сигнала T2=МТ1 больше времени первичного накопления, что позволяет обнаружить объекты со слабым отраженным сигналом, пропущенным при первичном накоплении, то есть повысить предельную дальность радиолокатора.
Как и в первом варианте способа, дополнительно появляется возможность в М раз уменьшить погрешность измерения радиальной скорости объекта по определяемой из очевидного соотношения доплеровской частоте  где
где  - частота составляющей спектра, выделенной из суммарного корреляционного сигнала.
- частота составляющей спектра, выделенной из суммарного корреляционного сигнала.
Значение уточняющей поправки к доплеровской частоте, определяемой по основному алгоритму, равно 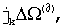 а ее знак в этой формуле определяется по знаку разности фаз выделенной составляющей спектра частоты
а ее знак в этой формуле определяется по знаку разности фаз выделенной составляющей спектра частоты  в элементе pk, qk, rk основной матрицы суммарных корреляционных сигналов и идентичном по номеру столбца и строки элементе pk, qk, rk квадратурной матрицы суммарных корреляционных сигналов.
в элементе pk, qk, rk основной матрицы суммарных корреляционных сигналов и идентичном по номеру столбца и строки элементе pk, qk, rk квадратурной матрицы суммарных корреляционных сигналов.
Угловая координата (или обе координаты) выявленного по координате и(или) скорости k-го объекта могут более точно определяться по значению разности фаз отраженных сигналов, принятых в разных позициях (или по значению разности фаз отраженных сигналов суммированных в группах позиций). Для этого выбирают две группы позиций (группу G с числом позиций SG и номерами позиций sG и группу Н с числом позиций SH и номерами позиций sH). Каждая из групп может содержать произвольное число произвольно выбранных позиций, при этом точность определения угловой координаты тем выше, чем больше расстояние между центрами групп, а предельная дальность радиолокатора тем больше, чем больше позиций в каждой группе. Для каждой группы вычисляют элементы рk, qk, rk суммарных основных и квадратурных матриц, номера столбцов и строк которых соответствуют номерам столбцов и строк pk, qk, rk, выявленных при операции обнаружения элементов полной матрицы (38, 39):
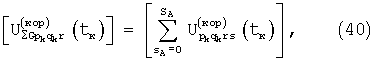

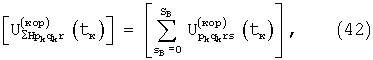

Из полученных значений вычисляют фазы отраженного от k-то обнаруженного объекта и принятого в группах позиций сигнала:
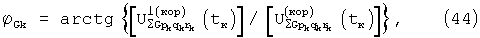

а из них, с учетом (25) вычисляется уточняющая поправка к значению угловой координаты:
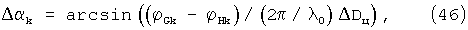
где Δ Dц - среднее расстояние между центрами групп позиций приема, которое может быть определено, например, как разность среднеарифметических координат Ds (см. (25)) позиций группы G и группы 
При использовании в операции обнаружения объектов составляющих спектра корреляционного сигнала 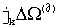 для выделенных групп позиций формируют из выявленных элементов рk, qk, rk основных и квадратурных матриц функций корреляции основные и, при необходимости, квадратурные корреляционные сигналы
для выделенных групп позиций формируют из выявленных элементов рk, qk, rk основных и квадратурных матриц функций корреляции основные и, при необходимости, квадратурные корреляционные сигналы 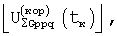

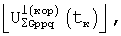
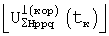 вида (38, 39) и с каждым из них проводят преобразование Фурье, в результате которого определяют коэффициенты Фурье, например,
вида (38, 39) и с каждым из них проводят преобразование Фурье, в результате которого определяют коэффициенты Фурье, например, 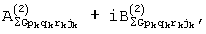
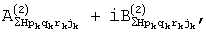
 и
и  а из них - амплитуды и фазы составляющих спектра корреляционных сигналов:
а из них - амплитуды и фазы составляющих спектра корреляционных сигналов:



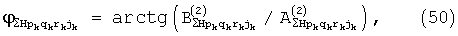


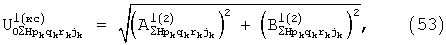

Фазы центральных колебаний отраженного от k-го обнаруженного объекта и принятого в группах позиций сигнала вычисляют по формулам:

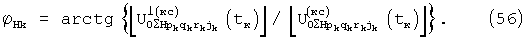
Разность фаз центральных колебаний (ϕ Gk-ϕ Hk) вычисляется либо из (55, 56), либо по любой из формул:
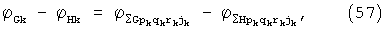

Уточняющую поправку к значению угловой координаты вычисляют по формуле (42).
Система для реализации изложенного выше способа измерения дальности и скорости объектов содержит, как и прототип, антенно-фидерное устройство (АФУ), излучающее зондирующий и принимающее отраженные сигналы, приемопередающее устройство (ППУ), выполняющее функции формирования частотно-модулированного микроволнового зондирующего сигнала, перемножения (смешения) с ним принятых отраженных сигналов и усиления полученных гомодинных сигналов, а также процессор, формирующий сигнал управления частотой ППУ и определяющий координаты и скорости отражающих объектов. Усиленные полосовыми усилителями гомодинные сигналы с выхода усилителя преобразуются аналого-цифровым преобразователем (АЦП) в цифровой код. Существенным отличием предлагаемого устройства является то, что к выходу АЦП подключен коррелометр, выполненный, например, на базе цифрового сигнального процессора, наделенный программами формирования из гомодинного сигнала - сигнала промежуточных частот в виде последовательности цифровых фрагментов заданной длительности, вычисления значений функций взаимной корреляции фрагментов сигнала ПЧ и базисных сигналов, матрицы которых формируются процессором или хранятся в его базе данных. При необходимости коррелометр наделяется также программами формирования матриц корреляционных сигналов и анализа их спектра.
Первый вариант предлагаемого способа может реализовываться двумя основными конструктивными вариантами структуры системы, отличающимися составом приемопередающего устройства (ППУ). Первый вариант структуры ППУ содержит формирователь зондирующего сигнала, то есть передающий канал, и канал приема отраженного сигнала, содержащий, как минимум, смеситель и полосовой усилитель.
В реальной системе, построенной по первому варианту структуры, часть мощности зондирующего сигнала за счет недостаточной развязки циркулятора, а также отражений от антенны сигнала попадает в виде помехи на вход канала приема (вход смесителя), ухудшая его чувствительность. Влияние помехи может быть устранено, если управляемая неоднородность тракта - компенсатор, включенный между циркулятором и антенной, создает на входе смесителя сигнал, равный помехе по амплитуде и противоположный по фазе. Эта задача решается системой автоматического регулирования фазы и амплитуды (АРФА) отраженного сигнала, состоящей из компенсатора и схемы управления компенсатором, входы которой подключены к выходам балансного смесителя и детектора, подключенного параллельно смесителю. Выходное напряжение смесителя зависит от разности фаз излучаемого сигнала и сигнала помехи, а напряжение на выходе детектора - от мощности помехи. Установка фазы и модуля коэффициента отражения компенсатора двухканальной системой автоматического регулирования по критериям, соответственно, нулевых напряжений на выходах смесителя и детектора устраняет влияние помехи. При относительно небольшом уровне помехи достаточно применить одноканальную систему (АРФ), устанавливающую фазу отраженного сигнала по критерию нулевого напряжения на выходе смесителя, восстанавливающую балансные свойства смесителя.
Во втором варианте структуры, применимом в простейшем варианте системы, ППУ выполнен в виде автодинного узла.
Второй вариант способа измерения реализуется третьим вариантом структуры ППУ, отличающимся от первого варианта наличием дополнительных, по числу позиций приема приемных каналов. Простейший формирователь зондирующего сигнала представляет собой генератор, частота которого управляется напряжением. Более сложные схемы формирователя первого и третьего вариантов структуры ППУ могут содержать высокостабильные генераторы, умножители и делители частоты, фильтры, усилители мощности и т.п. Каналы приема могут быть выполнены по супергетеродинной схеме, содержащей дополнительные смесители и УПЧ, когда одна операция получения гомодинного сигнала перемножением принятого сигнала с излучаемым заменяется двумя или более последовательными преобразованиями частоты. Формирователь частоты создает, в этом случае, гетеродинные сигналы. В частных случаях существенно необходимая для реализации способа частотная модуляция может быть дополнена импульсной модуляцией зондирующего сигнала и стробированием (на время зондирующего импульса) приемных каналов, что, не являясь существенным признаком изобретения, позволит увеличить мощность зондирующего сигнала и увеличить предельную дальность системы.
Далее изобретение поясняется с помощью чертежей, где
на фигуре 1 представлена общая структурная схема системы для измерения скоростей и координат объектов,
на фигурах 2 и 3 представлены схемы соединенных приемопередающего и антенно-фидерного устройств первого варианта структуры системы для измерения скоростей и координат объектов без использования и с использованием схемы компенсации помехи соответственно,
на фигуре 4 представлена схема соединенных автодинного варианта приемопередающего устройства и антенно-фидерного устройств второго варианта структуры системы для измерения скоростей и координат объектов,
на фигуре 5 представлена схема соединенных приемопередающего и антенно-фидерного устройств третьего варианта структуры системы для измерения скоростей и координат объектов,
на фигуре 6 представлена схема одного из возможных вариантов формирователя зондирующего сигнала,
на фигуре 7 показана блок-схема алгоритма обнаружения и измерения скорости объектов с использованием матрицы базисных сигналов - функций времени,
на фигуре 8 показана блок-схема алгоритма обнаружения и измерения скорости объектов с использованием матрицы базисных сигналов - коэффициентов спектра,
на фигуре 9 показан типичный вид зависимости значения функции корреляции гомодинного и базисного сигналов от дальности объекта.
Система для измерения скоростей и координат объектов (см. фигуру 1) содержит антенно-фидерное устройство (АФУ) 1, приемопередающее устройство (ППУ) 2, аналого-цифровой преобразователь (АЦП) 3, коррелометр 4, процессор 5 и дисплей 6. Микроволновый выход (в вариантах структуры выход-вход) ППУ 2 подключен к входу (в вариантах системы входу-выходу) АФУ 1, в выходы АФУ 1 подключены к входам ППУ 2. К выходам гомодинного сигнала (ГС) ППУ 2 подключены входы аналого-цифрового преобразователя 3. При этом могут использоваться как несколько АЦП, подключенные к соответствующим выходам ППУ 2, так и единственный АЦП, подключенный либо непосредственно к единственному выходу ГС ППУ 2, либо через коммутатор (не показано), входящий в состав АЦП 3 и управляемый коррелометром 4 - к нескольким выходам ПЧ. АЦП 3, коррелометр 4, процессор 5 и дисплей 6 соединены шиной передачи цифровых данных 7 (далее - шина данных), которая может быть связана с внешней информационной сетью. ППУ 2 имеет вход управления частотой зондирующего сигнала, соединенный с аналоговым выходом процессора 5.
ППУ 2 в зависимости от особенностей применения может выполняться в нескольких отличающихся по структуре вариантах, определяющих варианты структуры системы.
В первом варианте структуры системы (фиг.2) ППУ 2 имеет микроволновые выход и вход, а АФУ 1 - соединенные с ними вход и выход. ППУ 2 содержит формирователь 8 зондирующего сигнала (далее формирователь), имеющий вход управления частотой, который является входом управления частотой ППУ 2, смеситель 9 и полосовой усилитель 10. АФУ 1 содержит ферритовый циркулятор 11 и приемопередающую антенну 12. Выход генератора 8 подключен к микроволновому выходу ППУ 2 и первому входу смесителя 9, второй вход которого соединен с микроволновым входом ППУ 2, а выход гомодинного сигнала соединен с входом полосового усилителя 10. Выход полосового усилителя 10 подключен к выходу ГС приемопередающего устройства 2. Первое и второе плечи циркулятора 11 являются входом и выходом антенно-фидерного устройства, а третье плечо подключено к приемопередающей антенне 12.
В варианте системы со схемой компенсации помехи, обусловленной просачиванием излучаемого сигнала в канал приема отраженного сигнала (см. фиг.3), АФУ 1 дополнительно содержит включенный между третьим плечом циркулятора 11 и приемопередающей антенной 12 компенсатор 13 с управляемым по фазе коэффициентом отражения, а ППУ 2 дополнительно содержит схему управления компенсатором 14 (далее схема управления), вход которой соединен с выходом смесителя 9. Выход схемы управления 14 подключен к входу управления компенсатора 13. ППУ 2 может дополнительно содержать детектор 19, подключенный к его микроволновому входу, выход детектора 19 соединен со вторым входом схемы управления 14, а компенсатор 13 в этом случае имеет второй вход управления модулем коэффициента отражения, подключенный ко второму выходу схемы управления 14. Компенсатор 13 может быть, например, выполнен в виде направленного ответвителя 15, первое и второе плечи которого соединены соответственно с третьим плечом циркулятора 11 и приемопередающей антенной 12, а третье плечо подключено к последовательно соединенным аттенюатору 16, фазовращателю 17 и короткозамыкателю 18. Управляющие входы фазовращателя 17 и аттенюатора 16 подключены соответственно к первому и второму входам управления компенсатора 13.
Во втором варианте структуры (см. фиг.4) системы приемопередающее устройство 2 выполнено в виде автодинного узла 20, выход-вход и вход управления частотой которого являются соответственно микроволновым выходом-входом и входом управления частотой ППУ 2. Кроме того, ППУ 2 содержит полосовой усилитель 10, а АФУ 1 выполнено в виде приемопередающей антенны 12. Вход-выход АФУ 1, то есть антенны 12, подключен к выходу-входу ППУ 2, а выход гомодинного сигнала автодинного узла 20 через полосовой усилитель 10 подключен к выходу ГС ППУ 2. Автодинный узел 20 представляет собой автогенератор, выполняющий одновременно функции смесителя (см., например Воторопин С.Д., Юрченко В.И. Автодины на диодах Ганна и устройства на их основе. “Электронная промышленность”, 1998. - Вып.1-2. - стр.110-115; Воторопин С.Д., Носков В.Я. Приемопередающие модули на слаботочных диодах Ганна для автодинных систем. “Электронная техника”. Сер. СВЧ-техника, 1993. - Вып.4 (458). - стр.70-72).
Третий вариант структуры системы предназначен для реализации алгоритма многопозиционного приема и образован из структуры первого варианта дополнением АФУ одной или несколькими приемными антеннами, а ППУ - соответствующим числом смесителей и полосовых усилителей.
В третьем варианте системы (см. фиг.5) АФУ 1 содержит передающую антенну 21 и несколько приемных 22а, 22б, 22в антенн, вход и выходы которых являются соответственно входом и выходами АФУ 1. В варианте АФУ передающая и одна приемная антенна заменяются циркулятором (не показаны), первое и второе плечи которого являются входом и одним из выходов АФУ 1, а третье подключено к приемопередающей антенне. ППУ 2 содержит формирователь 8 зондирующего сигнала, имеющий вход управления частотой, который является входом управления частотой ППУ 2, несколько смесителей 9а, 9б, 9в и полосовых усилителей 10а, 10б, 10в. Выход формирователя 8 подключен ко второму входу каждого из смесителей 9 и к микроволновому выходу ППУ 2, первые входы смесителей 9а, 9б, 9в подключены к микроволновым входам ППУ 2, а выходы соединены, соответственно, с входами полосовых усилителей 10а, 10б, 10в. Выходы полосовых усилителей подключены к выходам ГС ППУ 2. Число приемных антенн 22, смесителей 9, полосовых усилителей 10 и выходов ГС равно числу позиций приема.
Вход управления частотой ППУ 2 может быть выполнен двухканальным, а формирователь 8 зондирующего сигнала (см. фиг.6) в этом случае содержит задающий генератор 23, два балансных модулятора 24 и 25, сумматор 26 и фазовращатель 27, причем выход задающего генератора 23 соединен с первым входом первого модулятора 24 непосредственно, с входом второго модулятора 25 - через фазовращатель 27, вторые входы модуляторов 24 и 25 подключены соответственно к первому и второму каналам входа управления частотой формирователя 8, а выходы модуляторов 24 и 25 через сумматор 26 связаны с выходом формирователя 8.
Предлагаемый способ измерения скоростей и координат объектов с использованием предлагаемой системы осуществляют следующим образом.
Приемопередающим устройством 2 формируют периодически модулированный по частоте зондирующий микроволновый сигнал, передают его в антенно-фидерное устройство 1, посредством которого излучают его в пространство и принимают в одной или нескольких пространственных позициях отраженный от объектов сигнал. С помощью процессора 5 формируют периодический сигнал управления частотой зондирующего сигнала (модулирующий сигнал) и передают его в аналоговой форме на первый вход ППУ 2, а в цифровой форме через шину данных - в коррелометр 4. Принятые АФУ 1 сигналы передают в приемопередающее устройство 2, где отдельно перемножают (смешивают) их с излучаемым сигналом и, выделяя низкочастотные (разностные) компоненты результатов перемножения, получают гомодинные сигналы, усиливают заданную часть их спектра и направляют на соответствующие выходы гомодинного сигнала ППУ 2. Аналого-цифровым преобразователем 3 усиленные гомодинные сигналы переводят в цифровой код и передают через шину данных 7 в коррелометр 4, где формируют из них последовательности цифровых фрагментов сигнала промежуточных частот заданной длительности. На базе модулирующего сигнала, используя специальную программу коррелометра 4, в каждой позиции приема формируют двумерные, трехмерные или четырехмерные матрицы базисных сигналов, номера столбцов первого измерения которых соответствуют множеству средних ожидаемых значений дальности, номера столбцов второго и третьего измерений - множеству средних ожидаемых значений первой и второй угловых координат соответственно, а номера строк - множеству средних ожидаемых значений скорости. В варианте системы коррелометр может быть наделен базой данных базисных сигналов. При многопозиционном приеме указанные матрицы формируются для каждой позиции отдельно. Затем в каждой позиции вычисляют последовательности матриц значений функций взаимной корреляции матриц базисных сигналов и каждого из фрагментов принятого в позиции сигнала ПЧ, а также суммарные по позициям или группам позиций последовательности матриц функций корреляции. При необходимости, в каждой позиции формируют из них матрицы корреляционных сигналов, каждый элемент которой представляет собой последовательность соответствующих номеру столбца и строки значений функций взаимной корреляции каждой из последовательности матриц. При многопозиционном приеме вычисляют суммарные по позициям приема матрицы корреляционных сигналов. Полученную информацию передают в процессор 5, который, сравнивая уровни вычисленных функций корреляции или составляющих спектра корреляционных сигналов с пороговыми уровнями обнаруживает объекты и определяет их скорости и координаты. При необходимости, информацию, полученную процессором, отображают на дисплее 6 или передают через шину данных 7 во внешнюю информационную сеть для дальнейшей обработки.
На фиг.7 приведена блок-схема базового алгоритма обнаружения, а также измерения скоростей и координат отражающих объектов системой, показанной на фиг.1, во временной области. Обозначения выполнены для многопозиционного приема и трехмерной матрицы, обработка сигнала при использовании четырехмерной матрицы, а также принятого в единственной позиции (двумерная матрица) проводится на основе того же, очевидным образом измененного алгоритма. Все операции, показанные на схеме, выполняются в цифровой области. Посредством программы коррелометра 4 (для каждой позиции) поочередно перемножают (блок 3) сигнал каждого m-го фрагмента сигнала ПЧ (блок 2) и базисные сигналы (блок 4) основной или квадратурной матрицы вида (14, 15, 28 или 29) для заданных значений р, q, r, а результат интегрируют (блок 5), получая соответствующую функцию корреляции вида (18, 19, 34 или 35). При многопозиционном приеме матрицы функций корреляции позиций суммируются, образуя матрицу суммарных функций корреляции (38 или 39). В блоке 9 посредством программы процессора 5 проводят сравнение уровня функций корреляции с заданным пороговым уровнем U* и делают вывод о наличии или отсутствии отражающего объекта. По номерам столбцов и строки матрицы определяют координаты и скорость обнаруженного объекта. Вне зависимости от результата операции обнаружения цикл вычисления (блоки 2-8) повторяют при измененных (блок 7) значениях р, q, r. Если начальные значения р, q, r равны единице, то количество циклов вычислений, обеспечивающее обзор заданного пространства равно P× R× Q. При достижении p=P, r=R, q=Q блок 10 выдает команду на окончание вычислений. Изложенный алгоритм предусматривает последовательное вычисление матрицы функций корреляции, но при необходимости сокращения, например, времени вычислений возможно и параллельное вычисление элементов матрицы.
При необходимости полученная блоком 6 и накопленная в памяти коррелометра последовательность матриц функций корреляции преобразуется в матрицу корреляционных сигналов, из каждого из которых преобразованием Фурье выделяются составляющие спектра (на блок-схеме не показано). Данные о спектре передаются в процессор, который проводит по их уровню обнаружение объекта, а по параметрам - вычисляет уточненные значения координат и скорости.
Блок-схема алгоритма обнаружения и измерения координат и скорости объектов в частотной (спектральной) области показана на фиг.8. Отличие от алгоритма (фиг.7) состоит в том, что с каждым фрагментом сигнала промежуточных частот проводится блоком 3 преобразование Фурье (ПФ), в результате которого вычисляются пары коэффициентов (на блок-схеме - действительные и мнимые). База данных содержит (или программа коррелометра формирует) базисные сигналы матрицы (основной и(или) квадратурной) в виде их спектров (блок 4). Вычисление значений функций корреляции в этом варианте проводится блоком 6 перемножением соответствующих коэффициентов Фурье m-го фрагмента сигнала ПЧ и базисных сигналов (16, 17, 32 или 33) с последующим суммированием результата. В остальном алгоритмы (и блок-схемы - фиг.7 и 8) идентичны.
Возможность обнаружения объекта и определения его дальности поясняется фиг.9, где приведены расчетные зависимости значения функции корреляции гомодинного и базисного сигналов для двух значений ожидаемой дальности: 300 и 900 метров. Расчеты выполнены для радара контроля дорожного движения. Очевидно, что главные максимумы функций корреляции имеют место при равенстве ожидаемой Lp и фактической дальности, а ширина главного лепестка имеет для данного случая величину Δ Lp=12 м. Поэтому если диапазон измеряемых дальностей 1200 метров разбить, например, на 100 равноотстоящих интервалов, средняя дальность Lр которых кратна 12 метрам, сформировать для них опорные сигналы временных нечетного и четного множеств и вычислить множество функций корреляции сигнала ПЧ и опорных сигналов, то сигнал, отраженный от объекта, находящегося на расстоянии Lр± 6 м, обусловит максимальный уровень соответствующей функции корреляции, по которому он будет обнаружен, а его дальность определена. Зависимость (не показана) значения функции корреляции от доплеровской частоты (скорости) имеет вид sin x/x при ширине около удвоенной частоты модуляции. Вид зависимости значения функции корреляции от угловой координаты зависит от количества и взаимного положения позиций приема и может быть определен с использованием известных методов расчета фазированных антенных решеток.
В первом варианте структуры системы (см. фиг. 2) частотно-модулированный зондирующий сигнал формирователем 8 подают через микроволновый выход на вход АФУ 1 и через ферритовый циркулятор 11 излучают его приемопередающей антенной 12 (или в варианте передающей антенной). Отраженный, принятый приемопередающей антенной 12 (или приемной антенной) сигнал через циркулятор 11, выход АФУ 1, микроволновый вход ППУ 2 подают на смеситель 9, где смешивают (перемножают) с сигналом формирователя 8, то есть с излучаемым сигналом. Полученный на выходе смесителя 9 гомодинный сигнал вида (8) усиливают в заданной полосе частот полосовым усилителем 10 и подают на выход полосового усилителя ППУ 2. Система, структура которой построена по первому варианту, является наиболее универсальной и может применяться, например, в полицейских радарах с уровнем излучаемой мощности 50-100 милливатт.
При двухканальной компенсации помехи (см. фиг.3) часть мощности зондирующего сигнала отводится направленным ответвителем 15 на последовательно включенные управляемые аттенюатор 16 и фазовращатель 17, нагруженные на короткозамыкатель 18. Отраженный от него сигнал, имеющий амплитуду и фазу, зависящие от затухания и установленной фазы аттенюатора 16 и фазовращателя 17, проходит снова через аттенюатор 16 и фазовращатель 17 и направляется через циркулятор 11 на вход смесителя 9. Если выход смесителя 9 связан схемой управления 14 с входом управления фазой компенсатора 13 (вход 1), то реализуется система автоматического регулирования фазы (АРФ) компенсирующего сигнала. Если дополнительно выход детектора 19 связан схемой управления 14 с входом управления модулем коэффициента отражения компенсатора 13 (вход 2), то реализуется двухканальная система автоматического регулирования фазы и амплитуды (АРФА) компенсирующего сигнала. В одноканальной системе АРФ с использованием варакторного диода, схема управления может представлять собой операционный усилитель (не показано). В двухканальной системе АРФА с рассмотренным выше компенсатором 13 схема управления 14 может содержать два операционных усилителя (не показано), входы которых подключены к выходам смесителя 9 и детектора 19, а выходы - к входам управления фазовращателя 17 и аттенюатора 16, являющиеся входами управления компенсатора 13. Детектор (19) может быть исключен из структуры ППУ, если для индикации уровня (мощности) помехи используется постоянная составляющая напряжения на одном из диодов смесителя (вариант - сумма напряжений на диодах).
Принцип работы автодинного варианта системы (см. фиг. 4) не отличается от основного варианта. Автодинный вариант системы наиболее прост и дешев, однако из-за низкой чувствительности и, соответственно, малой предельной дальности он может быть рекомендован для датчиков препятствий при движении транспортного средства задним ходом.
В третьем варианте системы (см. фиг.5) частотно-модулированный зондирующий сигнал формирователя 8 подают через микроволновый выход на вход АФУ 1 и излучают его передающей антенной 21 (или в варианте приемопередающей антенной). Отраженные, принятые антеннами 22а, 22б, 22в сигналы с выходов АФУ 1 через микроволновые входы ППУ 2 подают на смесители 9а, 9б, 9в, где смешивают (перемножают) с сигналом формирователя 8, то есть с излучаемым сигналом. Полученные на выходе смесителей 9а, 9б, 9в гомодинные сигналы усиливают в заданной полосе частот полосовыми усилителями 10а, 10б, 10в и подают на соответствующие выходы ГС ППУ 2.
Простейшим вариантом формирователя зондирующего сигнала является автогенератор с частотой, управляемой напряжением, зачастую не обеспечивающий, однако, требуемого высокого качества сигнала. В первом и третьем вариантах структуры системы может быть применен формирователь зондирующего сигнала 8 (см. фиг.6), содержащий задающий генератор 23 (ЗГ), обеспечивающий высокую стабильность частоты и низкий уровень собственных шумов монохроматического выходного сигнала вида 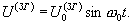 Балансные модуляторы 24 и 25 перемножают сигналы задающего генератора 23 и сигналы управления частотой с двухканального выхода сигнала управления частотой процессора 5. На вход одного из модуляторов (25) сигнал ЗГ подается через фазовращатель 27 со сдвигом фазы на π /2. Выходные сигналы модуляторов 24, 25, каждый из которых представляет собой AM сигнал с подавленной несущей (SSD), складываются сумматором 26, выход которого связан с выходом формирователя зондирующего сигнала 8. Данный вариант формирователя функционирует следующим образом. Если на управляющих входах модуляторов 24, 25 действуют сформированные процессором 5 сигналы управления частотой первого и второго каналов.
Балансные модуляторы 24 и 25 перемножают сигналы задающего генератора 23 и сигналы управления частотой с двухканального выхода сигнала управления частотой процессора 5. На вход одного из модуляторов (25) сигнал ЗГ подается через фазовращатель 27 со сдвигом фазы на π /2. Выходные сигналы модуляторов 24, 25, каждый из которых представляет собой AM сигнал с подавленной несущей (SSD), складываются сумматором 26, выход которого связан с выходом формирователя зондирующего сигнала 8. Данный вариант формирователя функционирует следующим образом. Если на управляющих входах модуляторов 24, 25 действуют сформированные процессором 5 сигналы управления частотой первого и второго каналов.
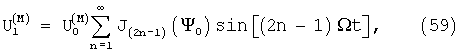
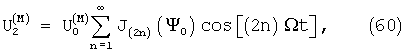
то на выходе сумматора 26 будет получен сигнал со спектром, отличающийся от спектра частотно модулированного (ЧМ) колебания только отсутствием центральной составляющей:
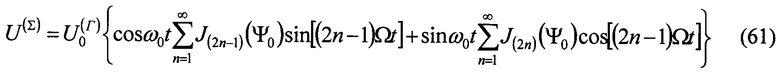
Формулы (59, 60 и 61) справедливы для гармонической частотной модуляции с любым индексом. Для формирования ЧМ сигнала с более сложным законом модуляции необходимо использовать аналогичные выражения, полученные преобразованием Фурье требуемого ЧМ сигнала. В состав формирователя 8 могут входить также умножители частоты, усилители, фильтры и другие вспомогательные каскады, наличие которых не является существенным признаком.
Зондирующий сигнал в автодинном варианте системы (фиг.4) генерируют, например, диодом Ганна и излучают приемопередающей антенной АФУ 1. Принятый АФУ 1 отраженный сигнал поступает на диод Ганна где, благодаря его нелинейности, перемножается с излучаемым сигналом. Гомодинный сигнал извлекают, например, из цепи питания диода Ганна с помощью трансформатора (не показано).
Таким образом, варианты предлагаемых способа и системы для радиолокационного измерения скоростей и координат объектов позволяют решить проблемы создания нескольких видов оборудования для обеспечения безопасности дорожного движения: от простейших датчиков препятствий до радаров, определяющих скорости, дальности и угловые координаты объектов дорожного движения. Сочетание гомодинного приемопередатчика с простой частотной модуляцией зондирующего сигнала и корреляционного анализа принятого сигнала позволит в ближайшей перспективе создать ряд недорогих и малогабаритных радаров. Быстрое развитие техники цифровой обработки сигналов позволит в будущем в рамках предложенной технической идеологии решать все более сложные задачи, в том числе и в других областях применения ближней радиолокации, при снижении стоимости систем.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДЛЯ РАДИОЛОКАЦИОННОГО ИЗМЕРЕНИЯ СКОРОСТЕЙ И КООРДИНАТ ОБЪЕКТОВ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2416807C2 |
| СПОСОБ И СИСТЕМА ДЛЯ РАДИОЛОКАЦИОННОГО ИЗМЕРЕНИЯ СКОРОСТЕЙ И КООРДИНАТ ОБЪЕКТОВ (ВАРИАНТЫ) | 2002 |
|
RU2239845C2 |
| Приёмо-передающее устройство гомодинного радиолокатора | 2021 |
|
RU2787976C1 |
| ПРИЕМНО-ПЕРЕДАЮЩЕЕ УСТРОЙСТВО ГОМОДИННОГО РАДИОЛОКАТОРА | 2000 |
|
RU2189055C2 |
| СПОСОБ УПРАВЛЕНИЯ ВЕЛИЧИНОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ РАДИОЛОКАЦИОННОЙ СТАНЦИИ | 2013 |
|
RU2533198C1 |
| Способ обработки цифрового радиолокационного сигнала и радиолокатор обнаружения препятствий высокого разрешения | 2022 |
|
RU2792971C1 |
| РАДИОЛОКАЦИОННАЯ СИСТЕМА ДЛЯ ОБНАРУЖЕНИЯ ПРОВОДОВ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧ | 2006 |
|
RU2310885C1 |
| РАДИОЛОКАТОР С НЕПРЕРЫВНЫМ ШУМОВЫМ СИГНАЛОМ И СПОСОБ РАСШИРЕНИЯ ДИАПАЗОНА ИЗМЕРЯЕМЫХ ДАЛЬНОСТЕЙ В РАДИОЛОКАТОРЕ С НЕПРЕРЫВНЫМ СИГНАЛОМ | 2015 |
|
RU2589036C1 |
| СПОСОБ ИЗМЕРЕНИЯ РАССТОЯНИЯ И РАДИАЛЬНОЙ СКОРОСТИ | 2024 |
|
RU2840790C1 |
| Способ построения системы диаграммообразования приемной цифровой антенной решетки | 2021 |
|
RU2774214C1 |
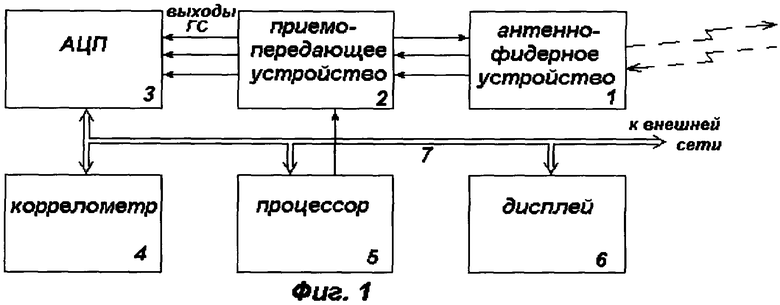
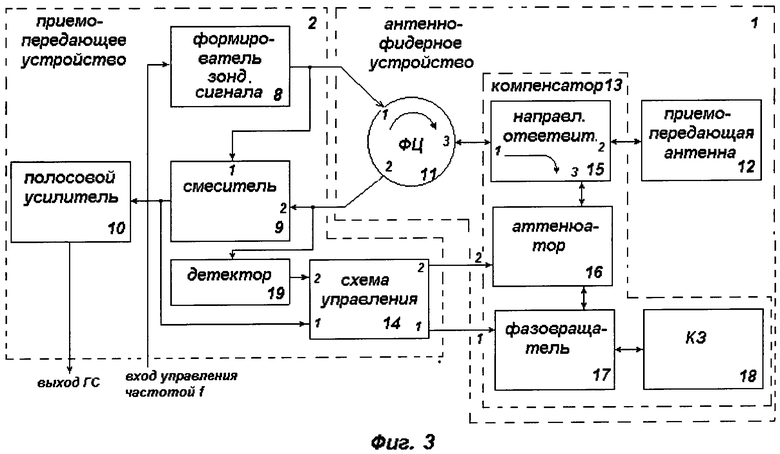


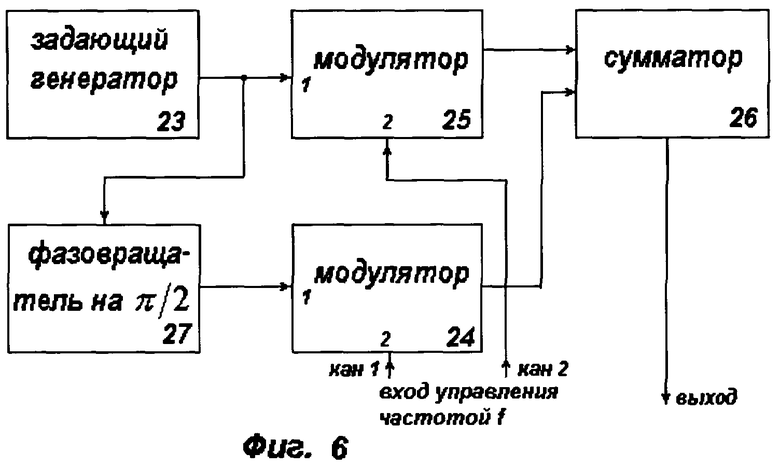



Изобретение относится к радиолокации и может быть использовано в системах дорожного контроля и предотвращения столкновений транспортных средств. Способ измерения скоростей и координат объектов осуществляют путем излучения непрерывного частотно-модулированного зондирующего сигнала, приема отраженного сигнала в одной или нескольких пространственных позициях, перемножения его с излучаемым сигналом и вычисления матрицы значений функций корреляции (ФК) полученного гомодинного сигнала и двумерной (дальность, скорость) матрицы базисных сигналов, сформированных из модулирующего сигнала. Дальности и скорости обнаруженных объектов вычисляют по номерам элементов матрицы ФК, в которых значения ФК превышают пороговый уровень. Значение скорости уточняют вычислением частот составляющих спектра корреляционных сигналов, полученных как последовательность значений ФК за время накопления сигнала. При приеме отраженного сигнала в нескольких пространственно разнесенных позициях формируют для каждой позиции трех- (дальность, скорость, угловая координата) или четырехмерную матрицу базисных сигналов и по номерам соответствующей матрицы суммарных по позициям ФК определяют дальности, угловые координаты и скорости обнаруженных объектов. Система для измерения скоростей и координат объектов содержит антенно-фидерное устройство, гомодинное приемопередающее устройство, коррелометр, формирующий матрицы базисных сигналов и вычисляющий функции корреляции и корреляционные сигналы, и процессор, формирующий модулирующий сигнал и вычисляющий скорости и координаты объектов. Достигаемым техническим результатом является повышение точности измерения скоростей и координат объектов, предельной дальности, разрешающей способность при обеспечении безопасности дорожного движения. 3 н. и 23 з.п. ф-лы, 9 ил.
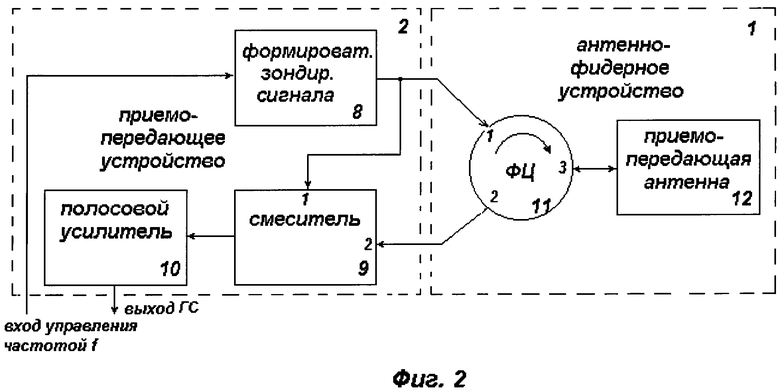
| US 5325097 А, 28.06.1994 | |||
| RU 2001123692 А, 27.06.2003 | |||
| ПРИЕМОПЕРЕДАЮЩИЙ МОДУЛЬ РАДИОВОЛНОВОГО ДОПЛЕРОВСКОГО КАНАЛА ОХРАННОГО ИЗВЕЩАТЕЛЯ | 1999 |
|
RU2163743C2 |
| РАДИОЛУЧЕВОЙ ДАТЧИК ОХРАНЫ | 1992 |
|
RU2079889C1 |
| US 4660040 A, 21.04.1987 | |||
| US 4697184 A, 29.09.1987. | |||
Авторы
Даты
2005-06-27—Публикация
2003-07-07—Подача