Изобретение относится к технике косвенных измерений координат летательного аппарата (ЛА), которые могут быть использованы в комплексных системах управления полетом ЛА.
Известен способ определения координат ЛА [Бабич О.А. Обработка информации в навигационных комплексах. - М.: Машиностроение, 1991, с.171, 185-188], по методу измерения дальностей, согласно которому на борту ЛА измеряют дальности ЛА до трех ориентирных точек, находящихся в зоне его прямой видимости. Измерение дальности осуществляют с помощью позиционного навигационного датчика, например, бортового радиолокационного дальномера [Радиолокационные измерители дальности и скорости. Том 1. Под ред. В.Н.Саблина. - М.: Радио и связь, 1999, с.146, 150], по сигналам которого вычисляют координаты ЛА путем решения геометрических соотношений, носящих вид системы нелинейных алгебраических уравнений для приращений координат относительно опорной точки, которая решается итерационным способом.
Недостатком известного способа является то, что он не обеспечивает достаточно высокой точности измерения координат ЛА, необходимой, в частности, для выполнения захода на посадку и посадки, а также непрерывности измерения координат при срыве измерений дальности позиционным навигационным датчиком, например, при маневрировании ЛА.
Цель изобретения - повышение точности определения координат ЛА и обеспечение непрерывности оценок координат для их использования в комплексной системе управления полетом.
Поставленная цель достигается за счет того, что согласно предлагаемому способу определения координат ЛА, включающему операции измерения дальностей ЛА до группы наземных радиомаяков, находящихся в зоне его прямой видимости, с помощью позиционного навигационного датчика, полученные результаты измерений дальностей комплексируют в бортовом вычислителе с результатами измерений бортовых трехкоординатных датчиков линейных перегрузок ДЛУ, трехкоординатных датчиков угловых скоростей ДУС и курсовертикали, измеряющей углы крена, тангажа и рысканья, и производят оценку координат и скоростей ЛА для текущего момента времени на скользящем интервале времени [t0, t],
где t0 - начальное время измерения;
t=t0 + Т - текущий момент реального времени;
Т - длина скользящего интервала времени наблюдения измерений,
для момента времени t0 по измерениям позиционного навигационного датчика, ДЛУ, ДУС и курсовертикали производят оценку трех проекций скорости на оси связанной системы координат и трех координат ЛА путем итерационного решения системы алгебраических уравнений для приращений оценок относительно их априорных значений, а затем по измерениям перегрузок, угловых скоростей и углов крена, тангажа и рысканья производят оценку координат ЛА для момента времени t путем решения дифференциальных уравнений, описывающих изменения трех проекций скорости и трех координат ЛА на скользящем интервале времени [t0, t], с начальными условиями, равными оценкам координат и скоростей ЛА для момента времени to, оценку координат ЛА повторяют в каждый дискретный момент времени наблюдения, отличающийся от предыдущего на величину, определяемую быстродействием бортового вычислителя.
Таким образом, предлагаемый способ измерения координат ЛА основан на согласовании измерений дальностей позиционным навигационным датчиком с оценками дальностей, получаемыми с помощью воспроизведения траектории ЛА путем решения дифференциальных уравнений его движения, в которые подставляются измерения бортовых датчиков ДУС, ДЛУ и курсовертикали.
На борту ЛА с помощью позиционного навигационного датчика измеряются дальности в общем случае до М радиомаяков: {D1, D2,..., DM}. Кроме того, на борту измеряются перегрузки, угловые скорости и углы ориентации ЛА: {nх, nу, nz, ωх, ωу, ωz, υ, γ, ψ},
где υ, γ, ψ - углы тангажа, крена и рысканья.
Способ реализуется с помощью специального алгоритма оценивания координат и скоростей ЛА в реальном времени, который решается бортовым цифровым вычислителем с малым шагом дискретизации по времени Δt, величина которого определяется быстродействием вычислителя. При реализации алгоритма используются следующие основные соотношения.
Координаты ЛА определяются в местной плановой (нормальной) прямоугольной земной системе координат.
Для учета сигналов ДУС, ДЛУ и курсовертикали используются известные дифференциальные уравнения для скоростей и координат ЛА [Кожевников Ю.В., Сигаев А.Ю. Идентификация фазовых характеристик и ветровых возмущений самолета по результатам летных испытаний //Жур. «Авиационная техника», Известия вузов, 1993, №1, с.27]:
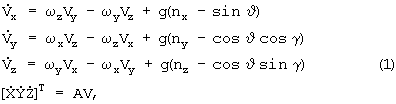
где Vx, Vy, Vz - проекции скорости полета ЛА на оси связанной системы координат;
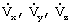 - первые производные скорости полета по времени;
- первые производные скорости полета по времени;
g - ускорение свободного падения;
VT=[VxVyVz] - вектор проекций скорости на связанные оси;
X, Y, Z - координаты ЛА в земной системе координат;
А=[е]ij - известная матрица направляющих косинусов, размерности (3,3), описывающая переход от связанной к местной плановой земной системе координат, элементы которой вычисляются с помощью измерений углов тангажа, крена и рысканья:
e11=cos ψ cos ϑ, e12=sin γ sin ψ - cos γ cos ψ sin ϑ,
e13=cos γ sin ψ + sin γ cos ψ sin ϑ, e21=sin ϑ,
e22=cos γ cos ϑ, e23=-sin γ cos ϑ, e31=-sin ψ cos ϑ,
e32=sin γ cos ψ + cos γ sin ψ sin ϑ, e33=cos γ cos ψ - sin γ sin ψ sin ϑ.
Вектор фазовых координат системы уравнений (1) имеет вид:
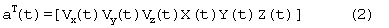
Уравнения измерений дальностей до радиомаяков имеют вид:
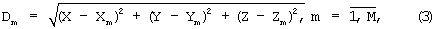
где Xm, Ym, Zm - координаты радиомаяков.
Для учета измерений дальностей до каждого из радиомаяков на скользящем интервале времени [t0, t] составляется вектор совокупности измерений дальностей ZT={Dm(ti)}, где ti - дискретные моменты времени измерения дальностей.
Для связи измерений дальностей с начальными условиями дифференциальных уравнений (1) формируется матрица функций чувствительности вектора ZT к начальным условиям a(t0), которая является матрицей частных производных, приближенно заменяемых отношением приращений:
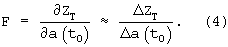
Здесь Δa(t0) - вектор фиксированных малых приращений начальных условий;
ΔZT - вектор приращений оценок измерений дальностей при приращении начальных условий.
Матрица F вычисляется путем интегрирования системы уравнений (1) на скользящем интервале [t0, t] один раз при заданных априорных начальных условиях a(t0) и шесть раз при начальных условиях с приращениями отдельных компонент вектора a(t0). Матрица F состоит из шести столбцов, размерность которых равна размерности вектора ZT.
По методу определения параметров с помощью функций чувствительности [Справочник по теории автоматического управления. Под ред. А.А.Красовского - М.: Наука. Гл. ред. физ.-мат. лит., 1987, с.631-632], выполняется определение оценки â(t0) вектора начальных условий системы уравнений (1). Для этого итерационным способом решается система алгебраических уравнений относительно â(t0), которая описана ниже.
Для определения координат ЛА для момента времени t выполняется интегрирование уравнений (1) на интервале [t0, t] с начальными условиями â(t0). При интегрировании дифференциальных уравнений (1) в их правые части подставляются дискретные измерения ДУС, ДЛУ и курсовертикали: nх, nу, nz, ωх, ωу, ωz, υ, γ, ψ на отрезке времени [t0, t]. В результате производится оценка вектора фазовых координат â(t), которая содержит искомые оценки координат X(t), Y(t), Z(t) для момента реального времени t.
Алгоритм оценивания координат и скоростей ЛА является итерационным и имеет вид:
Шаг 1. Задается начальный номер итераций k=1 и априорное начальное приближение вектора ak-1(t0)=a0(t0), в котором используется одно условие, заключающееся в том, что скорость ЛА по продольной оси связанной системы координат не равна нулю: a0(t0)=[Vx0, 0, 0, 0, 0, 0]. Здесь Vx0 - априорное значение оценки составляющей скорости Vх в связанной системе координат, которое определяется типом ЛА.
Шаг 2. Начало цикла из N итераций, в котором решаются шаги 2-7 алгоритма. Выполняется интегрирование системы дифференциальных уравнений (1) 6-го порядка на отрезке времени [t0, t]. Интегрирование уравнений (1) выполняется с начальными условиями:
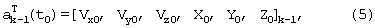
Шаг 3. Вычисляется вектор-столбец оценок измерений дальностей:
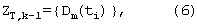
Шаг 4. Вычисляется матрица функций чувствительности для текущей итерации:
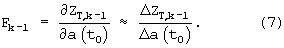
Шаг 5. По методу определения параметров с помощью функций чувствительности решается переопределенная система линейных алгебраических уравнений вида:
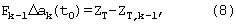
здесь Δak(t0) - вектор приращений начальных условий относительно приближения ak-1(t0). Разность ZT-ZT,k-1 является вектором невязок между измерениями и оценками дальностей.
Система линейных алгебраических уравнений (8) решается, например, методом наименьших квадратов:
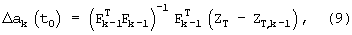
либо любым другим известным методом решения алгебраических уравнений, что не является принципиальным.
Решение существует, если матрица 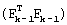 не вырождена. Число уравнений в системе уравнений (8) должно быть не менее шести. При решении определяются приращения Δak(t0), которые минимизируют среднеквадратическое значение невязки между измерениями дальностей до радиомаяков и значениями дальностей, которые рассчитываются путем решения системы дифференциальных уравнений (1) и соотношений (3).
не вырождена. Число уравнений в системе уравнений (8) должно быть не менее шести. При решении определяются приращения Δak(t0), которые минимизируют среднеквадратическое значение невязки между измерениями дальностей до радиомаяков и значениями дальностей, которые рассчитываются путем решения системы дифференциальных уравнений (1) и соотношений (3).
Шаг 6. Выполняется замена значений вектора начальных условий на его очередное приближение:
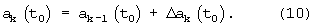
Шаг 7. Выполняется проверка числа выполненных итераций. Если оно меньше N, то выполняется увеличение номера итераций: k:=k+1 и переход к шагу 2. Если число итераций равно N, то принимается, что найдена оценка вектора 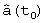 .
.
Шаг 8. Выполняется интегрирование системы дифференциальных уравнений (1) на отрезке времени [t0,t] с начальными условиями â(t0) и производится оценка â(t).
В результате проделанных операций определяют координаты ЛА для текущего момента времени t.
Условием применения предлагаемого способа является обеспечение не вырожденности системы уравнений (8).
Данное условие обеспечивается достаточным числом радиомаяков и их расстановкой так, чтобы ЛА и радиомаяки составляли геометрическую фигуру в виде многогранника с числом граней не менее трех.
При ограничении на зону, в которой определяются координаты ЛА, достаточно трех радиомаяков.
Для произвольного положения летательного аппарата требуется четыре радиомаяка, которые находятся в зоне прямой видимости.
При увеличении числа радиомаяков имеет место повышение точности определения координат.
Другим условием применения способа является достаточная величина длины скользящего интервала времени Т, позволяющая произвести не менее двух измерений дальности для каждого радиомаяка. При этом число линейно независимых наблюдений дальностей составляет не менее шести, что обеспечивает не вырожденность системы линейных алгебраических уравнений (8).
Повышение точности оценивания координат достигается за счет:
- комплексного использования измерений дальностей и измерений ДЛУ, ДУС и курсовертикали;
- использования множества измерений дальностей и измерений ДЛУ, ДУС и курсовертикали на скользящем интервале времени наблюдений [t0, t].
Непрерывность измерения координат при срыве измерения дальностей обеспечивается за счет того, что при срыве измерений позиционного навигационного датчика, например, при маневрировании летательного аппарата, выполняется продолжение интегрирования дифференциальных уравнений (1) на шаге 8 алгоритма оценивания при подстановке начальных условий, равных конечным условиям от предыдущего шага интегрирования. При этом используются измерения датчиков ДУС, ДЛУ и курсовертикали, а измерения позиционного навигационного датчика не используются.
Таким образом, заявляемый способ обеспечивает определение координат ЛА на расстоянии прямой видимости радиомаяков и позволяет определять координаты летательного аппарата при произвольной траектории полета с высокой точностью, необходимой, например, при заходе на посадку и при посадке, а также обеспечивает непрерывность определения координат при срыве измерений позиционного навигационного датчика, например, при маневрировании летательного аппарата.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2002 |
|
RU2244262C2 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ КУРСОВЕРТИКАЛЬ | 2014 |
|
RU2564379C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2256154C1 |
| Адаптивная бесплатформенная инерциальная курсовертикаль | 2016 |
|
RU2647205C2 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2646954C2 |
| СПОСОБ КОРРЕКЦИИ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2014 |
|
RU2564380C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВОГО ПОЛОЖЕНИЯ УПРАВЛЯЕМОГО АППАРАТА, ПОДВЕШЕННОГО К САМОЛЕТУ-НОСИТЕЛЮ | 2014 |
|
RU2553776C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВ ПРОСТРАНСТВЕННОЙ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2594631C1 |
| СПОСОБ ОЦЕНКИ ОШИБОК И КОНТРОЛЯ ДАТЧИКОВ ПЕРВИЧНОЙ ИНФОРМАЦИИ В СОСТАВЕ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ В НАЗЕМНЫХ УСЛОВИЯХ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2537513C2 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ О ПЕРЕМЕЩЕНИИ ЛЕТАТЕЛЬНОГО АППАРАТА | 2010 |
|
RU2436047C1 |
Изобретение относится к технике косвенных измерений координат летательного аппарата (ЛА), которые могут быть использованы, в частности, в комплексных системах управления полетом ЛА. Способ измерения координат ЛА основан на согласовании измерений дальностей ЛА до группы наземных радиомаяков, находящихся в зоне его прямой видимости, с помощью позиционного навигационного датчика с оценками дальностей, получаемыми с помощью воспроизведения траектории ЛА путем решения дифференциальных уравнений его движения, в которые подставляются измерения бортовых датчиков ДУС, ДЛУ и курсовертикали. Способ позволяет определять координаты летательного аппарата при произвольной траектории полета с высокой точностью, необходимой, например, при заходе на посадку и при посадке, а также обеспечивает непрерывность определения координат при срыве измерений позиционного навигационного датчика, например, при маневрировании летательного аппарата.
Способ определения координат летательного аппарата (ЛА), включающий операции измерения дальностей ЛА до группы наземных радиомаяков, находящихся в зоне его прямой видимости, с помощью позиционного навигационного датчика, отличающийся тем, что полученные результаты измерений дальностей комплексируют в бортовом вычислителе с результатами измерений бортовых трехкоординатных датчиков линейных перегрузок ДЛУ, трехкоординатных датчиков угловых скоростей ДУС и курсовертикали, измеряющей углы крена, тангажа и рысканья, и производят оценку координат и скоростей ЛА для текущего момента времени на скользящем интервале времени [t0, t], где t0 - начальное время измерения; t = t0 + Т - текущий момент реального времени; Т - длина скользящего интервала времени наблюдения измерений, для момента времени t0 по измерениям позиционного навигационного датчика, ДЛУ, ДУС и курсовертикали производят оценку трех проекций скорости на оси связанной системы координат и трех координат ЛА путем итерационного решения системы алгебраических уравнений для приращений оценок относительно их априорных значений, а затем по измерениям перегрузок, угловых скоростей и углов крена, тангажа и рысканья производят оценку координат ЛА для момента времени t путем решения дифференциальных уравнений, описывающих изменения трех проекций скорости и трех координат ЛА на скользящем интервале времени [t0, t], с начальными условиями, равными оценкам координат и скоростей ЛА для момента времени t0, оценку координат ЛА повторяют в каждый дискретный момент времени наблюдения, отличающийся от предыдущего на величину, определяемую быстродействием бортового вычислителя.
| БАБИЧ О.А., Обработка информации в навигационных комплексах, М., Машиностроение, 1991, с | |||
| Аппарат для передачи изображений на расстояние | 1920 |
|
SU171A1 |
| СПОСОБ ИЗМЕРЕНИЯ КУРСА ЛЕТАТЕЛЬНОГО АППАРАТА | 2000 |
|
RU2178145C1 |
| КОМПЛЕКСНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2000 |
|
RU2178147C1 |
| КОМПЛЕКС БОРТОВЫХ ТРАЕКТОРНЫХ ИЗМЕРЕНИЙ | 1995 |
|
RU2116666C1 |
| WO 00/36376 А1, 22.06.2000. | |||
Авторы
Даты
2005-11-20—Публикация
2004-12-17—Подача