Заявляемое изобретение относится к технике косвенных измерений угловых положений летательного аппарата (ЛА).
Известна система измерения угловых положений ЛА [1], содержащая датчики угловых скоростей (ДУС), датчики линейных ускорений (ДЛУ) и спутниковую навигационную систему (СНС), связанные с соответствующими входами цифрового вычислителя, функционирующего по алгоритму интегрированной первичной обработки поступающих от этих систем сигналов и комплексной вторичной обработки, которая в первую очередь предполагает уточнение углов ориентации, оценку и уточнение калибровки параметров датчиков, таких как дрейфы гироскопов, масштабные коэффициенты, смещения акселерометров.
Недостатком известной системы является то, что несмотря на применение высокоточного источника информации, каким является СНС, не снимается задача определения ошибок датчиков первичной информации, зависящих от их технического исполнения, причем точность измерения угловых положений ЛА недостаточно высока для управления им в условиях маневрирования, в частности, при кратковременном пропадании приема сигнала от СНС.
Цель изобретения - устранение указанных недостатков путем создания алгоритмической курсовертикали, определяющей угловое положение ЛА с необходимой для его управления точностью, не зависящей от времени полета при использовании спутниковой информации и обеспечивающей завершение полета летательного аппарата при полном прекращении приема спутникового сигнала.
Поставленная цель достигается за счет того, что в системе измерения угловых положений ЛА, содержащей датчики угловых скоростей, датчики линейных ускорений, спутниковую навигационную систему и цифровой вычислитель, цифровой вычислитель функционально выполнен в виде последовательного соединенных модуля оценки вектора начальных условий на текущем скользящем интервале времени, связанного с цифровым выходом спутниковой навигационной системы, модуля пересчета в ускоренном времени оценки вектора начальных условий на текущий дискретный момент реального времени, модуля формирования оценок углов в реальном времени, причем каждый из модулей связан с цифровыми выходами датчиков угловых скоростей и датчиков линейных ускорений, и модуля вычисления углов, выход которого является выходом цифрового вычислителя.
Сущность изобретения поясняется чертежом, где представлена функциональная схема системы измерения угловых положений ЛА.
Система содержит датчики 1 линейных ускорений, датчики 2 угловых скоростей, спутниковую навигационную систему 3 и цифровой вычислитель 4.
ДЛУ 1 и ДУС 2 являются стандартными системами трехкоординатных датчиков соответственно линейных ускорений и угловых скоростей, имеющих цифровые выходы для связи с цифровым вычислителем 4. СНС 3 является стандартной спутниковой системой, также имеющей цифровой выход для связи с цифровым вычислителем 4.
Цифровой вычислитель 4 функционально выполнен в виде четырех последовательно соединенных модулей: модуля 5 оценки вектора начальных условий на текущем скользящем интервале времени, модуля 6 пересчета в ускоренном времени оценки вектора начальных условий на текущий дискретный момент реального времени, модуля 7 формирования оценок углов тангажа, крена и рысканья. Модули 5, 6, 7 связаны с цифровыми выходами ДЛУ 1 и ДУС 2. Модуль 5, кроме того, связан с цифровым выходом СНС 3. Выход модуля 8 является выходом цифрового вычислителя 4.
Цифровой вычислитель 4 осуществляет синхронный прием данных от информационных систем и обеспечивает в реальном времени согласование траектории, формируемой по сигналам ДЛУ 1 и ДУС 2, с траекторией, измеряемой СНС 3, а также функционирование рекуррентного алгоритма оценивания углов крена, тангажа и рысканья ЛА на скользящем интервале времени.
Согласование траекторий выполняется на уровне производных по времени, то есть осуществляется согласование скорости полета, измеряемой СНС 3 и скорости полета, определяемой с помощью измерений перегрузок и угловых скоростей.
Для каждого текущего положения скользящего интервала определяются начальные условия системы дифференциальных уравнений [2], описывающих движение ЛА на основе совместного использования информации от ДЛУ 1, ДУС 2 и СНС 3

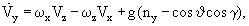

где υ, γ, ψ - углы тангажа, крена и рысканья; ωx,y,z - проекции вектора угловой скорости ЛА на связанные оси, nx,y,z - проекции вектора перегрузки ЛА на связанные оси, Vx,у,z - проекции скорости на связанные оси.
Значения углов, найденные на левом конце скользящего интервала времени, пересчитываются на текущий момент реального времени с использованием информации от ДУС и ДЛУ без использования информации от СНС согласно уравнениям [2]:
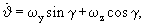
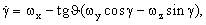
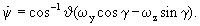
Таким образом, значения углов прогнозируются относительно последнего имеющегося на данный момент времени измерения СНС 3, что обеспечивает определение углов ЛА при сбоях и пропадании сигналов СНС 3 с точностью автономного вычисления углов.
Например, определим углы ЛА для некоторого фиксированного положения скользящего интервала времени [t0, t], на котором сигналы ДУС 2 и ДЛУ 1 наблюдаются на всем отрезке, где [t0, t0+T] - отрезок времени между наблюдениями сигналов СНС, t=(t0+Т+τ) - текущий момент реального времени. Тогда отрезок времени [t0+T, t0+T+τ] является отрезком, на котором прогнозируются оценки углов ЛА по отношению к последнему измерению СНС 3.
Определение углов ЛА выполняется путем интегрирования указанных дифференциальных уравнений при подстановке в них измерений перегрузок и угловых скоростей, если известны шесть начальных условий в момент времени to для вектора a(t) фазовых координат совместной системы уравнений
aT(t)=[Vx(t)Vy(t)Vz(t)υ(t)γ(t)ψ(t)].
Траектория полета в пределах текущего скользящего интервала времени определяется в местной прямоугольной (плановой) системе координат OXYZ. Начало координат местной прямоугольной системы задается точкой с геодезическими координатами широтой В, долготой L и высотой Н местоположения ЛА, соответствующими моменту времени t0. Ось ОХ направлена на север, ось OZ на восток, а ось OY по геодезической вертикали. Данная система координат назначается отдельно для каждого положения во времени скользящего интервала наблюдений.
Траектория полета ЛА кусочно аппроксимируется набором частных траекторий, представляемых в местных прямоугольных системах координат, каждая из которых соответствует конкретному фиксированному положению отрезка [t0+T, t0+Т+τ]. При этом в рамках одного положения скользящего интервала имеют место уравнения для вектора W скоростей ЛА в местной прямоугольной земной системе координат:
W=AV,  VT=[VxVyVz],
VT=[VxVyVz],
где X, Y, Z - координаты ЛА в земной системе; А - матрица [3] направляющих косинусов, описывающая переход от связанной к земной прямоугольной системе координат.
Приемник СНС 3 выдает координаты В, L, Н местоположения ЛА в геодезической системе координат, а также скорости VN, VE, Vн летательного аппарата по направлению на север, на восток и по высоте. Полагается, что в пределах дальности полета, соответствующей отрезку времени [t0, t0+T] скорости по осям местной прямоугольной системы координат равны скоростям, измеряемым спутниковой навигационной системой



Определение вектора начальных условий a(t0) выполняется методом функций чувствительности [3], как наиболее приемлемым в условиях статистической неопределенности относительно статистик ошибок измерений и ошибок приближения, обусловленных сделанными упрощениями. Оцениваемыми параметрами являются компоненты вектора начальных условий. При решении выполняется линеаризация зависимости вектора наблюдений

где VNT, VET, Vнт - векторы-строки частных совокупностей измерений СНС 3 отдельных составляющих скорости VN, VE, VН на отрезке [t0, t0+T] от искомых начальных условий в точке оценки вектора a(t0).
Процесс определения вектора a(t0) является итерационным и для его начала задается начальное приближение a0(t0). На каждом шаге итерационного процесса решается система линейных алгебраических уравнений для очередного приращения Δak(t0) относительно предыдущего приближения

где Zт, k-1 - оценка вектора Zт, определяемая при приближении вектора начальных условий ak-1(t0); F - матрица функций чувствительности вектора ZT; N - максимальное допустимое число итераций.
Вектор Zт, k-1 и матрица F функций чувствительности определяются интегрированием уравнений для скоростей полета и угловых положений, с использованием уравнений связи между проекциями вектора скорости в связанной и в земной системе координат. Сходимость итерационного процесса контролируется по степени малости приращения оценок. Скорость сходимости итерационного процесса зависит от априорных значений компонент вектора a(t0), от вида процессов изменения линейных и угловых скоростей ЛА на отрезке времени [t0, t0+Т], а также от числа достоверных измерений СНС. При недостаточном числе отсчетов измерений СНС 3 решение повторяется для нового положения скользящего интервала, а текущая оценка углов поддерживается за счет их прогнозирования по сигналам ДУС 2 и ДЛУ 1.
После определения оценки вектора начальных условий a(t0) уравнения для скоростей полета и угловых положений решаются на отрезке времени [t0, t0+T+τ] и, таким образом, определяется оценка вектора a(t), содержащая оценки углов на указанном отрезке времени, включающем текущий момент реального времени t.
В модуле 5 цифрового вычислителя 4 производится оценка вектора a(t0) начальных условий. На выходе модуля 5 формируется сигнал, соответствующий оценке вектора a(t0j), где j - номер текущего скользящего интервала времени, которая определяется по информации от СНС 3, ДУС 2 и ДЛУ 1, накопленной на отрезке времени [t0j, t0j+T]. Оценки векторов запаздывают по отношению к текущему моменту реального времени на величину (Т+τ). Оценку повторяют с периодом nΔt, n - параметр сдвига отрезка времени наблюдения сигналов СНС 3; при каждой повторной оценке левая граница скользящего интервала t0j увеличивается на величину nΔt.
В модуле 6 производится пересчет в ускоренном времени оценки a(t0j) на текущий дискретный момент реального времени tj с использованием сигналов ДУС 2 и ДЛУ 1 на этом отрезке; пересчет выполняется интегрированием уравнений для скоростей полета и угловых положений с начальными условиями a(t0j) и повторяется с периодичностью оценки в модуле 5.
В модуле 7 формируются оценки углов в реальном времени с шагом Δt регистрации сигналов ДУС 2 и ДЛУ 1. На каждом шаге Δt выполняется решение уравнений для скоростей полета и угловых положений с начальными условиями, полученными от предыдущего шага, или с начальными условиями, равными a(tj), поступающими из модуля 6, если к данному моменту времени выполнено решение модулей 5, 6; взаимодействие модуля 6 с модулем 7 сводится к периодической коррекции вектора a(tj), которая выполняется в дискретные моменты времени tj; начальный запуск алгоритма выполняется при задании априорного значения вектора a0(t0 0), который используется в модуле 5 для его уточнения и в модуле 7 для начала вычисления текущих оценок углов; по истечении времени Т в модуле 5 вычисляется оценка a(t0 0), которая является уточнением вектора a0(t0 0).
В модуле 8 осуществляется вычисление угла курса по углу рысканья и сглаживание оценок углов для устранения резких бросков оценок углов в модуле 7 при их коррекции от модуля 6; расчет курса выполняется с учетом выбранного направления оси ОХ текущей местной прямоугольной системы координат на север.
Алгоритм обеспечивает работу при кратковременном пропадании сигналов СНС, так как на текущем отрезке накопления информации СНС [t0j, t0j+T] не требуется наличия всех отсчетов измерений СНС. При пропадании небольшой части измерений решение модуля 5 поддерживается за счет достаточно большой величины отрезка [t0j, t0j+T], обеспечивающей избыточность измерений СНС для получения достаточно точных оценок углов ЛА.
При пропадании значительной части измерений СНС, такой, что решение модуля 5 не может быть выполнено, поддержка текущих оценок углов выполняется путем продолжения интегрирования уравнений для скоростей полета и угловых положений в модуле 7 при использовании в качестве начальных условий оценок углов, полученных на предыдущем шаге интегрирования. В этом случае имеет место некоторое снижение точности оценивания углов, но работоспособность алгоритма сохраняется в течение нескольких периодов nΔt, число которых определяется точностью измерений ДУС 2 и ДЛУ 1. Восстановление коррекции оценок углов выполняется по мере накопления достаточного числа отсчетов измерений СНС 3, необходимых для решения модуля 5.
Источники информации.
1. Джанджгава Г.И., Чернодаров А.В. Интегрированная первичная обработка информации в бесплатформенных инерциально-спутниковых системах ориентации и навигации. С.-Петербург, Материалы 4-й международной конференции по интегрированным навигационным системам, 1997 г, стр. 52-58.
2. Лебедев А.А., Чернобровкин Л.С. Динамика полета беспилотных летательных аппаратов. М., Машиностроение, 1973 г., стр. 102-103.
3. Справочник по теории автоматического управления. Под. ред. Красовского А.А., Гл. ред. Физ.-мат. Литературы, 1987 г., стр. 631-635.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2256154C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2264598C1 |
| Способ коррекции углов ориентации БИНС на скользящем интервале | 2022 |
|
RU2790076C1 |
| Способ коррекции углов ориентации ЛА по сигналам от одноантенной СНС | 2022 |
|
RU2790081C1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ О ПЕРЕМЕЩЕНИИ ЛЕТАТЕЛЬНОГО АППАРАТА | 2010 |
|
RU2436047C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ КУРСОВЕРТИКАЛЬ | 2014 |
|
RU2564379C1 |
| СПОСОБ КОРРЕКЦИИ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2014 |
|
RU2564380C1 |
| Способ коррекции углов ориентации БИНС | 2022 |
|
RU2796328C1 |
| Адаптивный способ коррекции углов ориентации БИНС | 2020 |
|
RU2754396C1 |
| Адаптивный корректор углов ориентации для БИНС | 2020 |
|
RU2749152C1 |
Изобретение относится к технике косвенных измерений угловых положений летательного аппарата. Устройство содержит датчики угловых скоростей и линейных ускорений, спутниковую навигационную систему и цифровой вычислитель. Цифровой вычислитель осуществляет синхронный прием данных от информационных систем и обеспечивает в реальном времени согласование траектории, формируемой по сигналам датчиков угловых скоростей и линейных ускорений, с траекторией, измеряемой спутниковой навигационной системой. Кроме того, вычислитель обеспечивает функционирование рекуррентного алгоритма оценивания углов крена, тангажа и рысканья на скользящем интервале времени. Изобретение позволяет определить угловое положение летательного аппарата с необходимой для его управления точностью, не зависящей от времени полета. 1 ил.

Система измерения угловых положений летательного аппарата, содержащая датчики угловых скоростей, датчики линейных ускорений, спутниковую навигационную систему и цифровой вычислитель, отличающаяся тем, что цифровой вычислитель функционально выполнен в виде последовательно соединенных модуля оценки вектора начальных условий на текущем скользящем интервале времени, связанного с цифровым выходом спутниковой навигационной системы, модуля пересчета в ускоренном времени оценки вектора начальных условий на текущий дискретный момент реального времени, модуля формирования оценок углов в реальном времени, причем каждый из модулей связан с цифровыми выходами датчиков угловых скоростей и датчиков линейных ускорений, и модуля вычисления углов, выход которого является выходом цифрового вычислителя.
| ДЖАНДЖГАВА Г.И | |||
| и др | |||
| Интегрированная первичная обработка информации в бесплатформенных инерциально-спутниковых системах ориентации и навигации | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| - СПб., 1997, с.52-58 | |||
| RU 2071034 C1, 27.12.1996 | |||
| БАБИЧ О.А | |||
| Обработка информации в навигационных комплексах | |||
| - М.: Машиностроение, 1991, с.6-8. | |||
Авторы
Даты
2005-01-10—Публикация
2002-12-27—Подача