Изобретение относится к области приборостроения инерциальных навигационных систем, в частности к области построения датчиков угловых координат для систем автоматического управления движением, главным образом в качестве курсовертикали, и может использоваться для определения угловой ориентации летательных аппаратов любого типа. Техническим результатом является упрощение способа, снижение стоимости его приборной реализации и повышение точности определения угловой ориентации объекта.
Известны способ и устройство построения невозмущаемой безгироскопной вертикали, представленные в патенте RU № 2258907, МПК G01C 19/44, опубликованном 20.08.2005 г., принятые нами за соответствующие прототипы.
Согласно указанному выше способу построения невозмущаемой безгироскопной вертикали подвижного объекта, включающему измерения текущих углов отклонения осей связанной системы координат от плоскости местного горизонта (вертикали) - тангажа и крена с помощью двух линейных горизонтальных акселерометров с продольной и поперечной ориентацией осей их чувствительности, возмущенных линейными ускорениями объекта, формирование оценок вышеупомянутых возмущающих линейных ускорений (северной и восточной составляющих αN и αЕ соответственно) осуществляют по данным спутникового навигационного приемника путем численного дифференцирования соответствующих скоростей или способом наименьших квадратов, пересчитывают эти составляющие в проекции αx и αy связанной системы координат с использованием курса от системы курсоуказания объекта и вводят непрерывно или дискретно коррекцию в возмущенные этими ускорениями измерения акселерометров, чем достигают построения невозмущаемой вертикали (углы тангажа ϑ и крена γ) по формулам для линейных акселерометров:
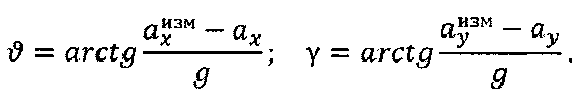
Устройство построения невозмущаемой безгироскопной вертикали, реализующее данный способ? содержит систему курсоуказания, два линейных акселерометра с продольной и поперечной ориентацией осей их чувствительности, систему автоматического управления движением, приемник спутниковой навигации, осуществляющий формирование оценок линейных ускорений объекта, и вычислительный блок, например микрокомпьютер, в котором возмущаемые ускорениями объекта измерения текущих углов отклонения осей связанной системы координат и местной вертикали, полученные с помощью линейных акселерометров, непрерывно корректируются значениями этих ускорений от приемника спутниковой навигации и курсоуказателя.
Однако описанный выше способ обладает сравнительно низкой точностью из-за необходимости восстановления ускорений путем дифференцирования составляющих земной скорости, измеренных спутниковой навигационной системой (СНС), что приводит к дополнительной погрешности измерения углов. Кроме того, исследования показывают слабую наблюдаемость в канале измерений крена и тангажа при отсутствии учета вертикальной скорости от СНС и отсутствии вертикального акселерометра.
Целью предложенного изобретения является повышение точности, упрощение способа и снижение стоимости его реализации для определения угловой ориентации летательного аппарата при отсутствии бортовых измерителей угловых скоростей.
Для достижения поставленной цели предлагается способ определения углов пространственной ориентации летательного аппарата (ЛА), включающий измерение линейных перегрузок вдоль продольной оси nx и поперечной оси nz ЛА, измерение проекций земной скорости на горизонтальную плоскость, согласно которому дополнительно измеряют проекцию земной скорости на вертикальную ось, нормальную перегрузку ny вдоль оси y ЛА, определяют линейные ускорения a x, a y, a z и далее, путем интегрирования ускорений, определяют линейные скорости Vx, Vy, Vz по осям связанной системы координат (СК), которые пересчитывают в нормальную земную СК, составляют функционал J из разности трех проекций земной скорости спутниковой навигационной системы (СНС) и трех составляющих земной скорости, полученных путем интегрирования линейных ускорений, с учетом дисперсий погрешностей R измерителя скорости определяют угловые скорости ЛА ωx, ωy, ωz методом параметрической идентификации, определяют начальные углы γ0, ϑ0, ψ0 ориентации ЛА по измеренным сигналам трех датчиков линейных перегрузок, определяют углы пространственной ориентации: крен γ, тангаж ϑ и угол рыскания ψ, интегрируя найденные угловые скорости, при этом в случае пропадания сигналов от СНС летательный аппарат переводят в горизонтальный полет с постоянной скоростью (установившийся режим полета) и углы крена и тангажа определяют по сигналам трех датчиков линейных перегрузок в режиме начальной выставки.
Устройство определения углов пространственной ориентации летательного аппарата, реализующее данный способ, включающее в себя блок датчиков перегрузок, содержащий два измерителя линейных перегрузок вдоль продольной оси nx и поперечной оси nz ЛА, и спутниковую навигационную систему (СНС), дополнительно содержит третий измеритель линейных перегрузок ny в составе блока датчиков перегрузок, расположенный вдоль вертикальной оси ЛА, последовательно соединенные блок определения линейных ускорений, первый интегратор, блок формирования матрицы направляющих косинусов, блок определения функционала, блок минимизации функционала и блок определения угловых скоростей, последовательно соединенные блок определения начальных углов ориентации и второй интегратор, выход блока датчиков перегрузок подключен к входу блока определения начальных углов ориентации и к первому входу блока определения линейных ускорений, второй вход которого соединен с первым выходом второго интегратора, а третий вход блока определения линейных ускорений является входом для сигнала, соответствующего значению ускорения свободного падения g, вторые входы первого интегратора и блока определения функционала соединены с выходом СНС, причем третий вход блока определения функционала является входом для сигналов, соответствующих значениям дисперсионной матрицы погрешностей измерения земных скоростей R, выход блока определения угловых скоростей подключен к третьему входу первого интегратора и к второму входу второго интегратора, второй выход которого подключен к второму входу блока формирования матрицы направляющих косинусов, а третий выход второго интегратора является выходом устройства.
Сущность заявленного изобретения заключается в следующем. Предлагаемый способ оценивания углов тангажа, крена и рыскания в полете основан на совместной обработке измерений датчиков перегрузок и измерений скорости ЛА спутниковой навигационной системой.
Рассмотрим математические модели, устанавливающие связи между различными параметрами полета. Проекции ускорений на оси связанной системы координат определяются следующими выражениями:
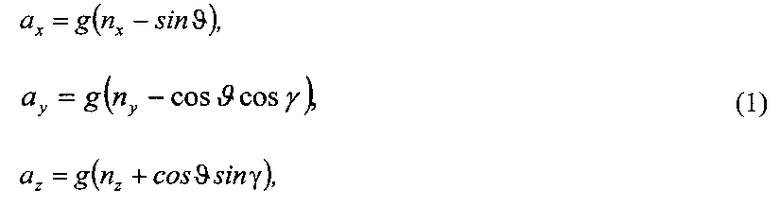
где nx, ny, nz - проекции перегрузок на оси связанной системы координат, измеряемые датчиками перегрузок, установленными на борту ЛА;
ϑ, γ - углы тангажа и крена, подлежащие оцениванию;
g - ускорение свободного падения.
Проекции ускорений на оси связанной системы координат используют для нахождения линейных скоростей ЛА. Для этого необходимо решить систему дифференциальных уравнений
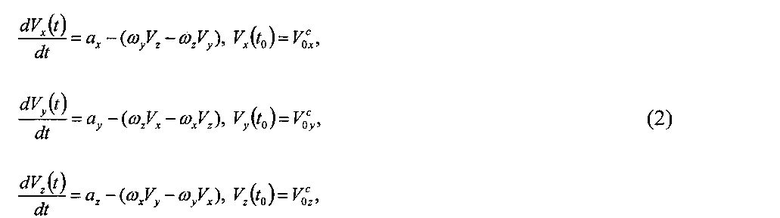
где последние слагаемые в правых частях учитывают вращение осей связанной системы координат с угловыми скоростями ωx, ωy, ωz, измерения которых на борту ЛА отсутствуют. Начальные условия для дифференциальных уравнений (2) вычисляются по данным спутниковой навигационной системы.
Для нахождения оценок углов пространственной ориентации применим систему дифференциальных уравнений, на вход которых поступают угловые скорости ωx, ωy, ωz:
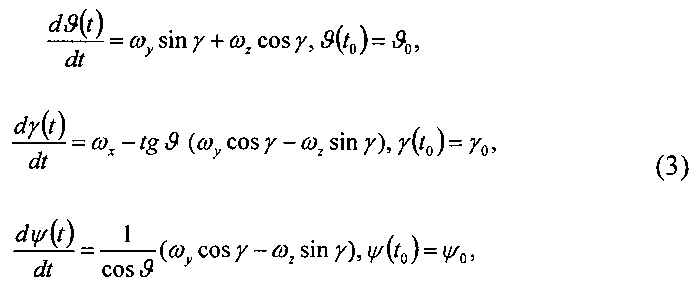
где ϑ, γ, ψ - углы тангажа, крена, рыскания.
Для использования выражений (2) и (5) необходимо ввести математическую модель, позволяющую восстановить отсутствующие измерения угловых скоростей. Рассмотрим скользящий интервал длительностью 0,1…1 с, пробегающий весь участок обработки полетных данных. Поскольку длительность интервала мала, аппроксимируем каждую угловую скорость прямолинейным отрезком:

где t - время от начала скользящего интервала,
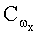
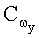
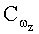
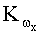
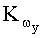
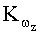
Определение начального углового положения разделяется на два процесса: горизонтальная выставка (крен и тангаж) и азимутальная выставка (курс).
Начальные значения углов пространственной ориентации γ0, ϑ0, ψ0, представляющие собой начальные условия для дифференциальных уравнений (3), определяют по сигналам трех датчиков линейных перегрузок.
Горизонтальную выставку осуществляют по сигналам трех акселерометров, измеряющих на неподвижном основании проекции ускорения силы тяжести на свои оси чувствительности в соответствии с выражением (1). В этом случае численные значения измерений акселерометров будут равны:
a x=g sin ϑ,
a y=-g cos ϑ cos γ,
a z=g cos ϑ sin γ.
Из выражения следует, что углы крена и тангажа могут быть найдены на основании сигналов трех датчиков линейных перегрузок по формулам:
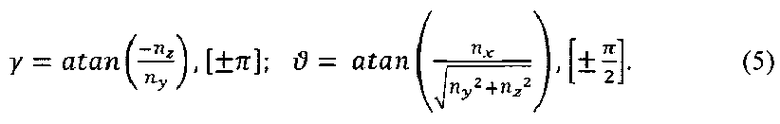
С целью устранения влияния шумов измерений, присутствующих в выходных сигналах акселерометров, их предварительно усредняют на некотором промежутке времени.
Выставку и дальнейшую коррекцию азимутального канала осуществляют по информации от датчика магнитного курса. При наличии информации о начальных координатах в соответствии с мировой моделью магнитного поля Земли находят значение магнитного склонения, которое учитывают при определении истинного курса из магнитного.
Оценку неизвестных параметров 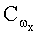
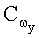
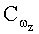
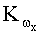
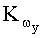
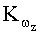
При численном интегрировании уравнений (2) и (3) в них подставляют аппроксимации угловых скоростей на скользящем интервале (4).
Бортовая СНС обеспечивает измерение трех проекций скорости ЛА на оси земной нормальной системы координат. Как известно, матрица направляющих косинусов (МНК), т.е. перехода от земной нормальной СК к связанной СК, имеет вид:
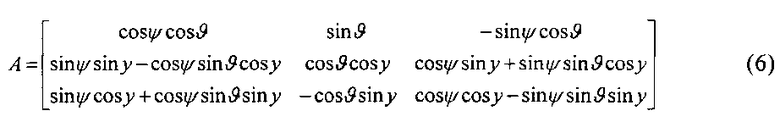
Соответственно, для обратного перехода необходимо использовать транспонированную матрицу AT. Тогда начальные условия для уравнений (2), представляющие собой проекции скорости в связанной системе в начальный момент времени, определяют по следующему выражению:

где Vx_g0, Vy_g0, Vz_g0 - проекции скорости ЛА в земной нормальной системы координат в начальный момент времени.
Аналогично, проекции скоростей в связанной системе, рассчитанные согласно уравнениям (2), переводятся в земную нормальную систему по формуле

где Vx_g, Vy_g, Vz_g - проекции скоростей ЛА, определенные путем интегрирования сигналов от датчиков перегрузок, на оси земной нормальной системы координат.
Выражения (1)-(7) составляют модель объекта.
Для получения модели наблюдений используем измеренные СНС проекции скорости ЛА в земной нормальной системе координат:
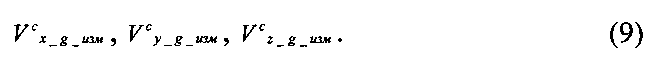
Эти величины используем для формирования модели наблюдений, которая принимает вид:

где величины (9) принимаются в качестве элементов вектора наблюдений 
ξT(ti)=[ξx(ti)ξy(ti)ξz(ti)] - шум наблюдений, представляющий собой векторную нормальную случайную последовательность типа белого шума с нулевым математическим ожиданием и известной дисперсионной матрицей R(ti).
Скорости в правых частях (10) определяют по модели объекта (1)-(7), в которые входят неизвестные величины угловых скоростей в начале скользящего интервала и коэффициенты, характеризующие углы наклона приращений угловых скоростей

Представленные выше модели объекта и наблюдений можно представить в следующей общей векторной форме:


где y(t), u(t) - векторы выходных и входных сигналов размерности n и m соответственно,
z(ti) - вектор наблюдений размерности r,
a - вектор неизвестных параметров, подлежащий идентификации,
ξ(ti) - шум наблюдений, представляющий собой векторную нормальную случайную последовательность типа белого шума с нулевым математическим ожиданием и известной дисперсионной матрицей R(ti). Шумы наблюдений представляют собой нормальные и независимые случайные величины. Поэтому их совместная плотность распределения вероятностей равна произведению плотностей для каждого момента ti, 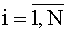
Известно, что максимум функции правдоподобия при указанных допущениях о свойствах шумов приводит к несмещенным и эффективным оценкам. Функционал максимума правдоподобия имеет следующий вид:
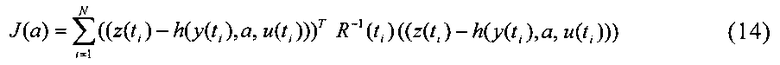
Несложно заметить, что (14) представляет собой функционал метода наименьших квадратов с матрицей весовых коэффициентов R(ti)-1. Таким образом, при указанных выше допущениях о свойствах шумов функционал максимума правдоподобия совпадает с взвешенным функционалом метода наименьших квадратов.
Для минимизации (14) используют одну из модификаций классического метода Ньютона:

где:
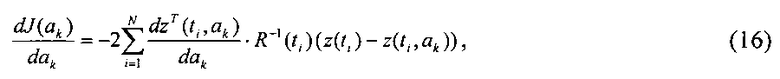
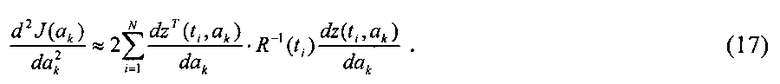
Производные оценок прогноза определяют численно для моментов времени ti, 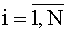
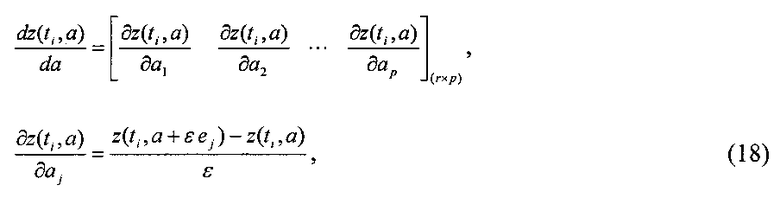
где ej - вектор размерности p, все элементы которого равны нулю, за исключением j-го элемента, который равен 1; ε - малое число, обычно задаваемое на уровне 0,001…0,1% от номинального значения параметров.
Оценки z(ti, a), 
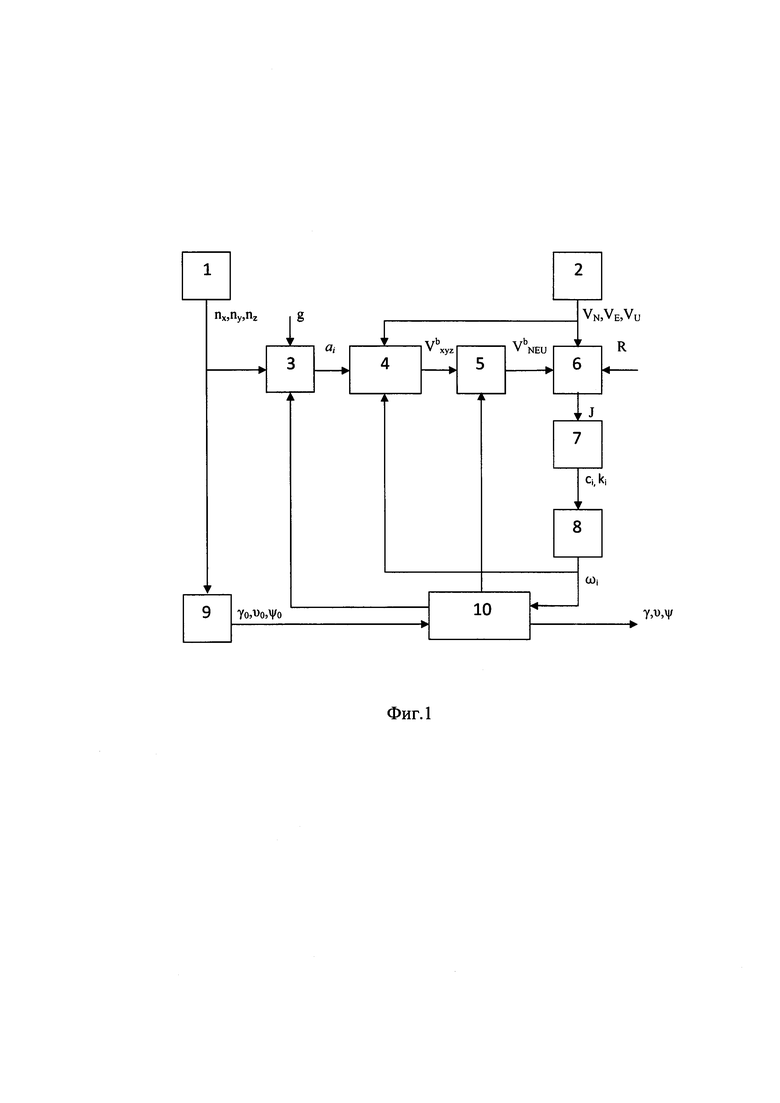
На фиг. 1 представлена структурная схема устройства, реализующего данный способ определения углов пространственной ориентации.
Устройство содержит блок 1 датчиков перегрузок, спутниковую навигационную систему 2, блок 3 определения линейных ускорений, первый интегратор 4, блок 5 формирования матрицы направляющих косинусов, блок 6 определения функционала, блок 7 минимизации функционала, блок 8 определения угловых скоростей, блок 9 определения начальных углов ориентации, второй интегратор 10.
Предлагаемое устройство работает следующим образом. По сигналам от блока 1 датчиков перегрузок и по значениям углов ориентации от второго интегратора 10 с учетом константы g в блоке 3 определения ускорений определяют линейные ускорения a
x, a
y,
a
z согласно выражениям (1). С учетом начальных значений проекций скоростей в связанной системе координат от СНС по сигналам линейных ускорений от блока 3 и угловых скоростей от блока 8 определения угловых скоростей, с учетом начальных значений проекций скоростей от СНС 2, в первом интеграторе 4 определяют линейные скорости Vx, Vy, Vz. При этом интегрируют выражения системы (2). В блоке 5 формирования МНК скорости проецируют на земную нормальную систему координат, используя матрицу А (6). Сравнивая сигналы от СНС 2 и от блока 5 формирования МНК, в блоке 6 определения функционала, с учетом матрицы дисперсии R погрешности скоростей, находят функционал J согласно выражению (14). В блоке 7 минимизации функционала, минимизируя функционал J, идентифицируют неизвестные параметры 
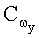
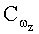
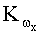
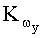
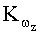
При пропадании сигналов от СНС летательный аппарат переводят в установившийся режим полета и углы крена и тангажа определяют по сигналам трех датчиков линейных перегрузок в режиме начальной выставки.
Техническим результатом предложенного изобретения является повышение точности определения угловой ориентации объекта при отсутствии бортовых измерителей угловых скоростей.
Изобретение может быть использовано во всех типах летательных аппаратов. Для реализации могут быть использованы широко применяемые в ЛА акселерометры и спутниковые приемники. Блоки интегрирования и определения параметров могут быть реализованы на стандартных элементах ЭВМ.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВ ПРОСТРАНСТВЕННОЙ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2589495C1 |
| Адаптивный корректор углов ориентации для БИНС | 2020 |
|
RU2749152C1 |
| Способ коррекции углов ориентации БИНС | 2022 |
|
RU2796328C1 |
| Малогабаритный навигационный комплекс | 2016 |
|
RU2644632C1 |
| Адаптивный способ коррекции углов ориентации БИНС | 2020 |
|
RU2754396C1 |
| Способ коррекции углов ориентации ЛА по сигналам от одноантенной СНС | 2022 |
|
RU2790081C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2256154C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ КУРСОВЕРТИКАЛЬ | 2014 |
|
RU2564379C1 |
| Комплексный способ навигации летательных аппаратов | 2016 |
|
RU2646957C1 |
| СИСТЕМА ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2002 |
|
RU2244262C2 |
Изобретение относится к области приборостроения инерциальных навигационных систем и может использоваться для определения угловой ориентации летательных аппаратов любого типа. Сущность изобретения состоит в совместной обработке измерений датчиков перегрузок и измерений скорости летательного аппарата (ЛА) спутниковой навигационной системой (СНС) при отсутствии датчиков угловых скоростей. Угловые скорости ЛА определяют методом параметрической идентификации. Устройство, реализующее данный способ, включает в себя блок датчиков перегрузок, содержащий три измерителя линейных перегрузок, установленных вдоль продольной, поперечной и вертикальной осей ЛА, спутниковую навигационную систему, блок определения линейных ускорений, два интегратора, блок определения функционала, блок формирования матрицы направляющих косинусов, блок минимизации функционала, блок определения угловых скоростей и блок определения начальных углов ориентации, соединенные между собой определенным образом. Технический результат - упрощение способа, снижение стоимости его приборной реализации и повышение точности определения угловой ориентации объекта при отсутствии бортовых измерителей угловых скоростей. 2 н.п. ф-лы, 1 ил.
1. Способ определения углов пространственной ориентации летательного аппарата (ЛА), включающий измерение линейных перегрузок вдоль продольной оси nx и поперечной оси nz ЛА, измерение проекций земной скорости на горизонтальную плоскость, отличающийся тем, что дополнительно измеряют проекцию земной скорости на вертикальную ось, нормальную перегрузку ny вдоль оси y ЛА, определяют линейные ускорения ax, ay, az и далее, путем интегрирования ускорений, определяют линейные скорости Vx, Vy, Vz по осям связанной системы координат (СК), которые пересчитывают в нормальную земную СК, составляют функционал J из разности трех проекций земной скорости спутниковой навигационной системы (СНС) и трех составляющих земной скорости, полученных путем интегрирования линейных ускорений, с учетом дисперсий погрешностей R измерителя скорости определяют угловые скорости ЛА ωx, ωy, ωz методом параметрической идентификации, определяют начальные углы γ0, ϑ0, ψ0 ориентации ЛА по измеренным сигналам трех датчиков линейных перегрузок, определяют углы пространственной ориентации: крен γ, тангаж ϑ и угол рыскания ψ, интегрируя найденные угловые скорости, при этом в случае пропадания сигналов от СНС летательный аппарат переводят в горизонтальный полет с постоянной скоростью (установившийся режим полета) и углы крена и тангажа определяют по сигналам трех датчиков линейных перегрузок в режиме начальной выставки.
2. Устройство определения углов пространственной ориентации летательного аппарата (ЛА), включающее в себя блок датчиков перегрузок, содержащий два измерителя линейных перегрузок вдоль продольной оси nx и поперечной оси nz ЛА, и спутниковую навигационную систему (СНС), отличающееся тем, что оно дополнительно содержит третий измеритель линейных перегрузок ny в составе блока датчиков перегрузок, расположенный вдоль вертикальной оси ЛА, последовательно соединенные блок определения линейных ускорений, первый интегратор, блок формирования матрицы направляющих косинусов, блок определения функционала, блок минимизации функционала и блок определения угловых скоростей, последовательно соединенные блок определения начальных углов ориентации и второй интегратор, выход блока датчиков перегрузок подключен к входу блока определения начальных углов ориентации и к первому входу блока определения линейных ускорений, второй вход которого соединен с первым выходом второго интегратора, а третий вход блока определения линейных ускорений является входом для сигнала, соответствующего значению ускорения свободного падения g, вторые входы первого интегратора и блока определения функционала соединены с выходом СНС, причем третий вход блока определения функционала является входом для сигналов, соответствующих значениям дисперсионной матрицы погрешностей измерения земных скоростей R, выход блока определения угловых скоростей подключен к третьему входу первого интегратора и к второму входу второго интегратора, второй выход которого подключен к второму входу блока формирования матрицы направляющих косинусов, а третий выход второго интегратора является выходом устройства.
| УСТРОЙСТВО ДЛЯ ПОЛЕТНОГО КОНТРОЛЯ ДАТЧИКОВ ПИЛОТАЖНОЙ ИНФОРМАЦИИ (ВАРИАНТЫ) | 1993 |
|
RU2078367C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ КУРСОВЕРТИКАЛЬ | 2014 |
|
RU2564379C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2256154C1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ О ПЕРЕМЕЩЕНИИ ЛЕТАТЕЛЬНОГО АППАРАТА | 2010 |
|
RU2436047C1 |
Авторы
Даты
2016-08-20—Публикация
2015-05-08—Подача