Заявляемое изобретение относится к технике косвенных измерений угловых положений летательных аппаратов (ЛА).
Известен способ измерения угловых положений самолета [Джанджгава Г.И., Чернодаров А.В. Интегрированная первичная обработка информации в бесплатформенных инерциально-спутниковых системах ориентации и навигации. Материалы 4-й Международной конференции по интегрированным навигационным системам. С-Петербург, 1997, с.52-58], согласно которому измерение углов крена, тангажа и курса осуществляют в соответствии с трехуровневым алгоритмом, выполняющим комплексирование информации от бесплатформенной инерциальной навигационной системы (БИНС) и от спутниковой навигационной системы (СНС).
На первом уровне выполняют прогнозирование проекций угловой скорости на связанные оси самолета на один шаг дискретизации по времени с помощью прогнозирующих фильтров Левинсона.
На втором уровне выполняют сглаживание оценок угловых скоростей, получаемых на первом уровне, с помощью фильтра Калмана, используя в качестве измерений разности между прогнозируемыми значениями угловой скорости и значениями угловой скорости, измеряемыми с помощью датчиков угловых скоростей.
На третьем уровне с помощью фильтра Калмана выполняется уточнение оценок угловых положений, получаемых на втором уровне по информации от бортовых приемников спутниковой навигации, используя в качестве измерений разности первого и второго порядков матриц направляющих косинусов, определяемых с помощью алгоритма БИНС и с помощью информации от бортовых приемников СНС.
Недостатком данного способа является его невысокая точность при маневрировании ЛА, что обусловлено:
- возрастанием ошибок прогноза угловых скоростей на первом уровне алгоритма при маневрировании ЛА;
- возрастанием статистической неопределенности фильтра Калмана на втором уровне алгоритма за счет неточности задания постоянной времени корреляции и среднеквадратического значения гироскопического дрейфа в условиях маневрирования ЛА;
- неточностью оценки матрицы направляющих косинусов, рассчитываемой в бесплатформенной инерциальной системе, которая используется на третьем уровне алгоритма и ошибки оценивания которой возрастают при маневрировании ЛА;
- накоплением ошибок фильтрации, которое имеет место на втором и третьем уровнях за счет рекуррентной обработки сигналов измерений при неточном учете статистических характеристик используемых измерений в условиях маневрирования ЛА.
Цель изобретения - повышение точности измерения углов крена, тангажа и курса ЛА в условиях маневрирования.
Поставленная цель достигается за счет того, что согласно предлагаемому способу измерения угловых положений ЛА, основанному на использовании информации от спутниковой навигационной системы и от датчиков угловых скоростей, измерение угловых положений ЛА производят в соответствии с алгоритмом оценивания, реализуемым в вычислительном устройстве, по информации от приемника СНС, измеряющего составляющие скорости ЛА на север, восток и по высоте, и от трехкоординатных датчиков угловых скоростей (ДУС) и датчиков линейных ускорений (ДЛУ), установленных на борту ЛА, на скользящем интервале времени наблюдения [t0, t0+T+τ], где:
t0 - начальное время измерений;
Т - длина отрезка времени однократного наблюдения имерений приемника СНС;
τ - длина отрезка времени прогноза угловых положений ЛА по отношению к последнему измерению СНС на скользящем интервале времени;
t0+T+τ=t - текущий момент реального времени,
причем сначала для момента времени t0 по измерениям ДУС, ДЛУ и СНС на отрезке времени [t0, t0+T] производят оценку трех проекций скорости ЛА на оси связанной системы координат и оценку углов тангажа, крена и рысканья путем итерационного решения системы алгебраических уравнений, составляемых по методу функций чувствительности, при решении которой минимизируется среднеквадратическое значение невязки между измерениями скоростей с помощью СНС и оценками скоростей с помощью ДУС И ДЛУ, которые рассчитываются путем решения системы дифференциальных уравнений для производных проекций скорости ЛА на оси связанной системы координат с пересчетом связанных скоростей на оси местной плановой прямоугольной земной системы координат и дифференциальных уравнений для производных углов тангажа, крена и рысканья, а затем для момента времени t по измерениям ДУС и ДЛУ на скользящем интервале времени производят оценку углов тангажа, крена и рысканья путем решения дифференциальных уравнений для производных углов тангажа, крена и рысканья, после чего угол рысканья пересчитывают в угол курса, при сдвиге скользящего интервала в сторону увеличения времени на величину τ измерения угловых положений ЛА в соответствии с алгоритмом оценивания повторяют, оценку углов тангажа, крена и курса производят в каждый дискретный момент реального времени, отличающийся от предыдущего на величину τ.
При реализации предлагаемого способа косвенного измерения угловых положений ЛА измерения ДУС и ДЛУ выполняются в связанной системе координат ЛА OX1Y1Z1. Приемник СНС принимает сигналы спутников и вычисляет составляющие вектора скорости VN, VE, VH по направлениям на север, на восток и по высоте [Соловьев Ю.А. Системы спутниковой навигации. - М.: ЭКО-ТРЕНДЗ, 2000, с.56, с.59].
Для всех измерений СНС для одного положения скользящего интервала принимается, что скорости VN, VE, VH приближенно равны скоростям 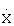 ,
, 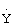 ,
, 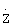 в местной плановой прямоугольной системе координат OXYZ, в которой ось ОХ направлена на север, ось OZ направлена на восток, а ось OY направлена по местной вертикали вверх. Ошибками приближения можно пренебречь при относительно небольших величинах Т и τ, при которых траекторию полета ЛА можно достаточно точно рассматривать в местной плановой прямоугольной системе координат.
в местной плановой прямоугольной системе координат OXYZ, в которой ось ОХ направлена на север, ось OZ направлена на восток, а ось OY направлена по местной вертикали вверх. Ошибками приближения можно пренебречь при относительно небольших величинах Т и τ, при которых траекторию полета ЛА можно достаточно точно рассматривать в местной плановой прямоугольной системе координат.
Обозначим а - вектор, содержащий три составляющих скорости ЛА в связанной системе координат и три угла ориентации ЛА:
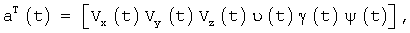
здесь индексом Т обозначена операция транспонирования;
Vx,Vy,Vz - проекции скорости ЛА на оси связанной системы координат;
ϑ, γ, ψ - углы тангажа, крена и рысканья соответственно.
Алгоритм оценивания является итерационным и имеет вид:
Шаг 1. Задается начальный номер итераций k=1 и начальное приближение вектора ak-1(t0)=a0(t0), в котором используется одно условие, заключающееся в том, что скорость ЛА по продольной оси связанной системы координат не равна нулю:
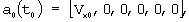
здесь Vx0 - априорное значение оценки составляющей скорости Vx в связанной системе координат, которое определяется типом ЛА.
Шаг 2. Начало цикла из N итераций, в котором решаются шаги 2-7 алгоритма. Выполняется интегрирование системы дифференциальных уравнений 6-го порядка на отрезке времени [t0, t0+T], которая состоит из двух систем уравнений 3-го порядка:
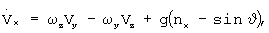
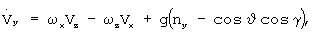
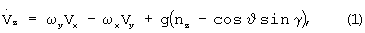
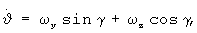
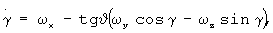
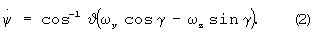
В правые части систем уравнений (1), (2) подставляются измерения перегрузок nх, nу, nz, которые являются сигналами ДЛУ в единицах g, и измерения угловых скоростей, которые являются сигналами ДУС. Система уравнений (1) следует из известного факта о том, что сигнал ДЛУ равен проекции на его измерительную ось разности абсолютного ускорения точки установки датчика и ускорения земного притяжения [Белоцерковский С.М. и др. Введение в аэроавтоупругость. - М.: Наука. Гл. ред. физ.-мат. лит., 1980, с.109].
В системе уравнений (1) имеем:
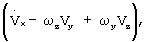
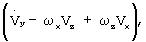
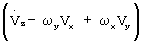 - проекции вектора абсолютной скорости на связанные оси OX1, OY1, OZ1;
- проекции вектора абсолютной скорости на связанные оси OX1, OY1, OZ1;
(-g sinϑ), (-g cosϑ cosγ), (g cosϑ sinγ) - проекции ускорения земного притяжения на связанные оси OX1, OY1, OZ1.
Система уравнений (2) содержит известные уравнения для производных углов тангажа, крена и рысканья [Красовский А.А. Системы автоматического управления полетом и их аналитическое конструирование. - М.: Наука. Гл. ред. физ.-мат. лит., 1973, с.27].
Решение дифференциальных уравнений (1), (2) выполняется с начальными условиями:
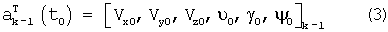
Шаг 3. Вычисляется вектор-столбец оценок измерений СНС по измерениям ДУС, ДЛУ
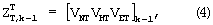
где VNT, VET, VHT - векторы-строки оценок составляющих земной скорости на север, восток и по высоте.


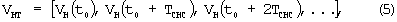
где: 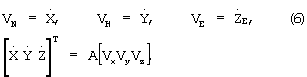
Размерность векторов-строк VNT, VET, VHT равна числу NCHC измерений СНС на отрезке времени [t0, t0+T].
Здесь ТCHC - дискретность измерений СНС;
NCHC - число отсчетов измерений СНС на отрезке времени [t0, t0+T];
A=[e]ij - матрица направляющих косинусов, размерности (3,3), описывающая переход от связанной к местной плановой земной системе координат, элементы которой вычисляются с помощью оценок углов тангажа, крена и рысканья, полученных при решении системы уравнений (1), (2) с помощью известных соотношений [Красовский А.А. Системы автоматического управления полетом и их аналитическое конструирование. - М.: Наука. Гл. ред. физ.-мат. лит., 1973, с.26]:

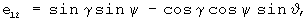
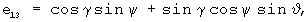
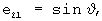
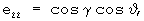

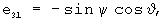
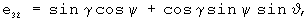
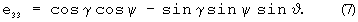
Шаг 4. Вычисляется матрица F размерности (3·NCHC, 6) функций чувствительности измерений СНС к приращениям компонент вектора ak-1(t0).
Для этого система уравнений (1) решается 6 раз, с разными начальными условиями, равными:
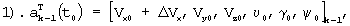
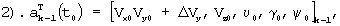
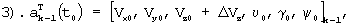
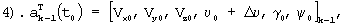

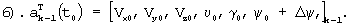
Здесь ΔVx, ΔVу, ΔVz, Δυ, Δγ, Δψ - задаваемые фиксированные малые приращения.
Из полученных 6 решений системы (1) формируется 6 векторов-столбцов вида:
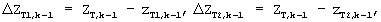
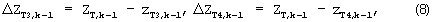
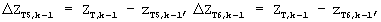
где векторы-столбцы: zT1,k-1, zT2,k-1, zT3,k-1, zT4,k-1, zT5,k-1, zT6,k-1 формируются аналогично тому, как это описано соотношениями (4), (5), (6).
Формируется матрица функций чувствительности F, которая является матрицей частных производных, которые приближенно заменяются отношением приращений:
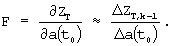
Здесь Δa(t0) - вектор фиксированных малых приращений, задаваемых для приближенного вычисления частных производных. Подробнее:
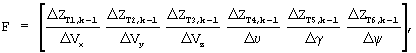
Матрица F содержит 6 столбцов, каждый из которых имеет (3·NCHC) строк.
Шаг 5. Составляется и решается переопределенная система линейных алгебраических уравнений вида:
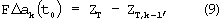
которая следует из метода параметрической идентификации на основе функций чувствительности [Справочник по теории автоматического управления. Под ред. А.А.Красовского. - М.: Наука. Гл. ред. физ.-мат. лит., 1987].
Здесь Δak(t0) - вектор искомых приращений относительно приближения ak-1(t0);
zT - вектор измерений земной скорости ЛА с помощью СНС;
ZT,k-1 - вектор оценок измерений земной скорости, вычисленный на шаге 3;
F - матрица функций чувствительности.
Разность ZT - ZT,k-1 является вектором невязок между измерениями скоростей с помощью СНС и оценками этих измерений, получаемыми с помощью ДУС и ДЛУ.
Система уравнений (9) состоит из 3·NCHC уравнений и имеет 6 неизвестных, которыми являются приращения компонент вектора Δak(t0).
Система линейных алгебраических уравнений (9) решается методом наименьших квадратов
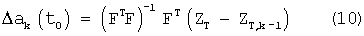
либо решается любым другим известным методом решения алгебраических уравнений, что не является принципиальным. Решение существует, если матрица (FТF) не вырождена. Число уравнений в системе уравнений (9) должно быть не менее шести. При решении определяются приращения Δak(t0), которые минимизируют среднеквадратическое значение невязки.
Шаг 6. Выполняется замена значений вектора начальных условий на его очередное приближение в указанном соответствии с методом функций чувствительности:
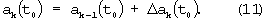
Шаг 7. Выполняется проверка числа выполненных итераций. Если оно меньше N, то выполняется увеличение счетчика числа итераций k:=k+1 и переход к шагу 2. Если число итераций равно N, то принимается, что найдена оценка вектора а для момента t0, запаздывающего относительно реального времени t на величину Т+τ.

Шаг 8. Выполняется интегрирование системы дифференциальных уравнений (2) 3-го порядка на отрезке времени [t0, t0+T+τ] с начальными условиями
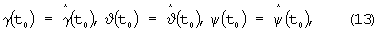
при подстановке в нее измерений nх, nу, nz, ωх, ωу, ωz от датчиков ДУС и ДЛУ.
В результате производится оценка углов крена, тангажа и рысканья для момента реального времени t=t0+T+τ.
Шаг 9. Вычисляется угол курса, который однозначно связан с рысканьем и с учетом принятого направления оси ОХ земной системы координат на север равен 2π-ψ.
Условием решения алгоритма является обеспечение не вырожденности системы уравнений (9), для чего требуется не менее двух отсчетов измерений СНС за время Т.
Так как каждое измерение СНС содержит 3 составляющих скорости VN, VE, VH, то при двух отсчетах измерений СНС имеется 6 скалярных измерений составляющих скорости, равное числу неизвестных в системе уравнений (9).
Конкретные значения параметров Т, τ, N определяются путем моделирования ошибок и проверяются по экспериментальным данным.
Таким образом, предлагаемый способ позволяет осуществить косвенное измерение угловых положений ЛА с повышенной точностью в условиях маневрирования.
Повышение точности оценивания угловых положений ЛА достигается за счет:
- согласования совокупности измерений проекций скорости ЛА с помощью СНС на скользящем интервале времени с совокупностью проекций скорости ЛА, которые рассчитываются по измерениям ДУС и ДЛУ;
- исключения накапливания ошибок оценивания за счет использования конечной совокупности измерений для однократного определения углов ориентации и отказа от процедур рекуррентной обработки типа фильтра Калмана, обладающих этим недостатком;
- применения вычислительных процедур, не использующих статистические характеристики измерений, и, таким образом, исключения влияния ошибок задания априорных статистик ошибок измерений.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2002 |
|
RU2244262C2 |
| Способ коррекции углов ориентации ЛА по сигналам от одноантенной СНС | 2022 |
|
RU2790081C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2264598C1 |
| Способ коррекции углов ориентации БИНС | 2022 |
|
RU2796328C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ КУРСОВЕРТИКАЛЬ | 2014 |
|
RU2564379C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2635820C1 |
| Способ коррекции углов ориентации БИНС на скользящем интервале | 2022 |
|
RU2790076C1 |
| СПОСОБ КОРРЕКЦИИ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2014 |
|
RU2564380C1 |
| Бесплатформенная инерциальная курсовертикаль | 2016 |
|
RU2643201C2 |
| Способ выставки БИНС ЛА корабельного базирования и устройство для его осуществления | 2016 |
|
RU2635398C2 |
Изобретение относится к технике косвенных измерений угловых положений летательных аппаратов (ЛА). Способ основан на использовании информации от приемника спутниковой навигационной системы (СНС), измеряющего составляющие скорости ЛА на север, восток и по высоте, и от трехкоординатных датчиков угловых скоростей (ДУС) и линейных ускорений (ДЛУ), установленных на борту ЛА. Измерение угловых положений ЛА производят в соответствии с алгоритмом оценивания, реализуемым в вычислительном устройстве, на скользящем интервале времени. Техническим результатом является повышение точности измерения углов крена, тангажа и курса ЛА в условиях маневрирования.
Способ измерения угловых положений летательного аппарата (ЛА), основанный на использовании информации от спутниковой навигационной системы (СНС) и от датчиков угловых скоростей, отличающийся тем, что измерение угловых положений ЛА производят в соответствии с алгоритмом оценивания, реализуемым в вычислительном устройстве, по информации от приемника СНС, измеряющего составляющие скорости ЛА на север, восток и по высоте, и от трехкоординатных датчиков угловых скоростей (ДУС) и датчиков линейных ускорений (ДЛУ), установленных на борту ЛА, на скользящем интервале времени наблюдения [t0, t0+Т+τ],
где t0 - начальное время измерений;
Т - длина отрезка времени однократного наблюдения измерений приемника СНС;
τ - длина отрезка времени прогноза угловых положений ЛА по отношению к последнему измерению СНС на скользящем интервале времени;
t0+T+τ=t - текущий момент реального времени,
причем для момента времени to по измерениям ДУС, ДЛУ и СНС на отрезке времени [t0, t0+Т] производят оценку трех проекций скорости ЛА на оси связанной системы координат и оценку углов тангажа, крена и рысканья путем итерационного решения системы алгебраических уравнений, составляемых по методу функций чувствительности, при решении которой минимизируется среднеквадратическое значение невязки между измерениями скоростей с помощью СНС и оценками скоростей с помощью ДУС и ДЛУ, которые рассчитываются путем решения системы дифференциальных уравнений для производных проекций скорости ЛА на оси связанной системы координат с пересчетом связанных скоростей на оси местной плановой прямоугольной земной системы координат и дифференциальных уравнений для производных углов тангажа, крена и рысканья, а затем для момента времени t по измерениям ДУС и ДЛУ на скользящем интервале времени производят оценку углов тангажа, крена и рысканья путем решения дифференциальных уравнений для производных углов тангажа, крена и рысканья, после чего угол рысканья пересчитывают в угол курса, при сдвиге скользящего интервала в сторону увеличения времени на величину τ измерения угловых положений ЛА в соответствии с алгоритмом оценивания повторяют, оценку углов тангажа, крена и курса производят в каждый дискретный момент реального времени, отличающийся от предыдущего на величину τ.
| ДЖАНДЖГАВА Г.И | |||
| и др | |||
| Интегрированная первичная обработка информации в бесплатформенных инерциально-спутниковых системах ориентации и навигации | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| СПб, 1997, с.52-58 | |||
| СПОСОБ ИЗМЕРЕНИЯ КУРСА ЛЕТАТЕЛЬНОГО АППАРАТА | 2000 |
|
RU2178145C1 |
| КОМПЛЕКСНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2000 |
|
RU2178147C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРБИТЫ КОСМИЧЕСКОГО АППАРАТА | 1999 |
|
RU2150414C1 |
| WO 00/36376 A1, 22.06.2000 | |||
| Способ контроля содержания кислорода в кремнии | 1980 |
|
SU999128A1 |
Авторы
Даты
2005-07-10—Публикация
2004-06-16—Подача