Изобретение относится к области гироскопической техники и может быть использовано для контроля подвеса сферического поплавка в сферической камере гидродинамического гироскопа, используемого в качестве измерителя угловых перемещений. На чертеже представлена конструктивная схема гироскопа со сферическим гидродинамическим подвесом сферического чувствительного элемента (ЧЭ) - поплавка (шарового ротора). Известный гидродинамический гироскоп (ГДГ) показан в [3] на стр. 7. При этом реально существующая конструктивная схема гидродинамического гироскопа показана на чертеже. ГДГ представляет собой вращающуюся в подшипниках качения сферическую камеру 1, частично заполненную жидкостью (которая не показана) и помещенный в нее сферический поплавок 2 (ЧЭ) [1]. Механическое устройство предварительного центрирования поплавка 2 относительно камеры 1, выполненное в виде шарика 3, закрепленного в центре поплавка 2, и упоров 4, установленных в торцах сферической камеры 1 [1]. Система съема сигнала (датчик угла) ГДГ представляет собой (см. [2] стр.11) постоянный магнит 5 (ротор), закрепленный в диаметральной плоскости поплавка 2, и кольцевую сигнальную катушку 6 (статор), закрепленную в корпусе прибора. Ось катушки при сборке ГДГ устанавливают соосно с осью вращения камеры 1 и поплавка 2. Для разделения сигналов между измерительными осями служат две обмотки опорных напряжений, закрепленных на каркасе сигнальной системы и смещенных друг относительно друга на угол 90 градусов. Важным узлом ГДГ является устройство стабилизации плавучести чувствительного элемента (поплавка) в широком диапазоне температурных воздействий (возмущений). Это устройство 7 представляет собой торцевые цилиндрические полости (камеры), соосные с осью собственного вращения подвеса ЧЭ ГДГ определенных размеров. Поплавковая камера вместе с устройством стабилизации плавучести представляет собой вращающийся в подшипниках качения 8 гироузел. Рабочую жидкость заливают в поплавковую камеру через торцевые отверстия 9. Устройство механического центрирования поплавка размещается в осевом его отверстии 10. Подвес ЧЭ ГДГ (т.е. поплавковую камеру) вращает электродвигатель 11.
Аналогом для заявляемого технического решения является способ гидродинамического подвеса сферического чувствительного элемента (поплавка) гидродинамического гироскопа, см. [2], включающий полное заполнение жидкостью радиального зазора между сферическим поплавком и камерой, обеспечивающее при этом нейтральную плавучесть поплавка, а также собственное вращение сферической камеры и поплавка.
Недостатком аналога является зависимость плавучести чувствительного элемента гидродинамического гироскопа (ЧЭ ГДГ) от температуры окружающей среды из-за изменения от температуры плотности поддерживающей поплавок жидкости. В связи с этим для получения необходимой точности измерения параметров углового движения основания гидродинамический гироскоп необходимо термостатировать, что усложняет конструкцию подвеса ЧЭ и прибора в целом.
Прототипом для заявляемого способа выбран способ подвеса ЧЭ ГДГ, представленный в книге Андрейченко К.П. [3] (глава 6), который включает частичное заполнение радиального зазора между поплавком и камерой рабочей жидкостью, обеспечивающей равенство массы поплавка и вытесненной им жидкости в аксиальном направлении, и собственное вращение подвеса поплавка гироскопа.
Недостатком прототипа является отсутствие возможности оценить качество изготовления ГДГ и оценки основных параметров, определяющих его точность и работоспособность в условиях применения. Такими параметрами являются "дрейф нуля" ("нулевой сигнал" - порог чувствительности) ГДГ и односторонние осевые зазоры Δ1, Δ2 в устройстве осевого центрирования поплавка, а также коэффициент перекрестных связей между измерительными каналами ГДГ, его постоянная времени То, коэффициенты передачи S ГДГ и его системы съема сигнала Ксс. Причем дрейф нуля ГДГ имеет по крайней мере три основные составляющие, обусловленные механикой подвеса ЧЭ ГДГ. К ним относятся возмущающие моменты М(еm) и M(d), обусловленные радиальным еm и аксиальным d смещением центра масс относительно его геометрического центра, возмущающий поплавок момент М(Δm), обусловленный ненулевой аксиальной плавучестью Δm (стр. 104, 99 [3], соответственно)
Задачей технического решения является контроль качества реализованной настройки ГДГ посредством определения его параметров и погрешностей в поле силы тяжести с учетом последующих условий эксплуатации прибора в составе динамичных движущихся объектов для последующего машинного динамического моделирования, а также выяснения причин возникновения брака в изготовленных приборах, не прошедших приемо-сдаточные испытания.
Решение поставленной задачи состоим в том, что способ контроля гидродинамического гироскопа, включающий частичное заполнение радиального зазора между поплавком и камерой рабочей жидкостью, обеспечивающее нейтральную аксиальную плавучесть поплавка, и собственное вращение подвеса поплавка и определение основных параметров ГДГ в отсутствие входных угловых воздействий, имеет особенность такую, что определяют скорость собственного вращения подвеса ω1, определяют "нулевой сигнал" ГДГ Uo и Uo1 при вертикальной оси собственного вращения подвеса при рабочем и "обратном" направлении его собственного вращения, устанавливают ось собственного вращения горизонтально и разворачивают ГДГ вокруг оси собственного вращения до получения наибольшей величины "нулевого сигнала" Uomax и измеряют его Uo1, в случае совпадения "нулевых сигналов" Uo и Uo1 при вертикальной и горизонтальной оси собственного вращения делают заключение, что в контролируемом ГДГ аксиальное смещение центра масс поплавка d и аксиальная плавучесть поплавка Δm близки к нулю и вычисляют инструментальную погрешность ГДГ в соответствии с соотношением: U(θ*)=(Uo+Uo1)/2; в противном случае, центрируют поплавок относительно камеры и снова измеряют "нулевой сигнал" гироскопа Uo2 при горизонтальной оси собственного вращения, в случае совпадения величин напряжений Uo1 и Uo2 делают заключение, что аксиальная плавучесть поплавка Δm близка к нулю, вычисляют составляющие инструментальных погрешностей по формулам: U(θ*)=(Uo+U1o)/2; U(d)=|Uo2-Uo|,
в противном случае, дополнительно устанавливают ось собственного вращения подвеса не горизонтально, следят за изменением выходного нулевого сигнала до момента возникновения контакта элементов центрирующего устройства, затем устанавливают ось собственного вращения горизонтально и измеряют выходное напряжение Uo1*, вычисляют составляющие инструментальных погрешностей по формулам:
U(θ*)=(Uo+Uo1)/2; U(Δm)=|Uo1*-Uo2|; U(d)=|Uo2-Uo|, где
U(θ*) - величина нулевого сигнала гироскопа, обусловленная радиальным смещением центра масс поплавка относительно его геометрического центра;
U(Δm) - величина "нулевого сигнала" гироскопа, обусловленная остаточной ненулевой плавучестью поплавка;
U(d) - величина "нулевого сигнала" гироскопа, обусловленная аксиальным смещением центра масс относительно его геометрического центра;
затем определяют знак плавучести чувствительного элемента (ЧЭ) ГДГ, направление аксиального смещения центра масс ЧЭ ГДГ по отношению к направлению вектора кинетического момента, вычисляют величину возмущающих моментов, обусловленных инструментальными погрешностями ГДГ, затем определяют параметры на подвижном основании.
При этом после определения ГДГ параметров в отсутствие входных угловых воздействий вращают ГДГ относительно одной из осей чувствительности с заданной угловой скоростью ωвх и определяют величину выходного напряжения Ucc и его сдвиг фаз Δϕ относительно одного из опорных напряжений, скачком останавливают платформу поворотной установки и определяют время переходного процесса tпп уменьшения выходного напряжения ГДГ до величины его "нулевого сигнала" Uo, вычисляют коэффициент S передачи ГДГ по формуле S=Ucc/ωвх, постоянную времени То вычисляют по формуле То=tпп/3, а коэффициент передачи системы съема сигнала ГДГ Ксс - по формуле: Ксс=S/То.
Для определения знака плавучести ЧЭ ГДГ устанавливают больший осевой зазор в верхнее положение относительно центра подвеса ЧЭ ГДГ и определяют время t1 перемещения ЧЭ из центра камеры до одного из упоров центрирующего поплавок устройства, устанавливают в верхнее положение меньший зазор подвеса ЧЭ ГДГ и снова определяют время t2 перемещения поплавка из центра камеры до одного из упоров и если t1>t2 делают заключение о наличии положительной плавучести ЧЭ, если t1<t2, то делают заключение о наличии отрицательной плавучести ЧЭ, затем определяют направление аксиального смещения центра масс ЧЭ ГДГ по отношению к направлению вектора кинетического момента для чего устанавливают ось собственного вращения подвеса ЧЭ ГДГ горизонтально и определяют выходное напряжение, центрируют поплавок относительно камеры и снова определяют выходное напряжение, если после аксиального центрирования поплавка относительно камеры величина выходного напряжения уменьшилась, то делают заключение, что центр масс смещен в направлении вектора угловой скорости собственного вращения подвеса, в противном случае, когда после центрирования поплавка относительно камеры величина выходного напряжения увеличилась, то делают заключение, что центр масс поплавка смещен относительно камеры в сторону, противоположную направлению вектора угловой скорости собственного вращения подвеса ЧЭ ГДГ, вычисляют величину возмущающего момента M(em), обусловленного радиальным смещение центра масс em, и величину смещения по формулам: M(em)=(U(θ*)/Kcc)*(2b), em=(U(θ*)/Kcc)/(m2 E ω1), вычисляют величину отклоняющего поплавок момента М(Δm), обусловленного остаточной ненулевой плавучестью поплавка Δm, и ее величину по формулам:
M(Δm)=(U(Δm)/Kcc)*(b1 ω1); Δm=U(Δm)*b1*ω1/Kcc g e cosα,
вычисляют величину момента M(d), обусловленного аксиальным смещение центра масс d и его величину по формулам:
M(d)=(U(d)/Kcc)(b1*ω1); d=(U(d)/Kcc)(b1*ω1)/(2*m2*g); где
b1 - коэффициент момента сил вязкого трения поплавка (камеры) о жидкость; ω1 - измеренная скорость вращения подвеса поплавка; g - ускорение силы тяжести;
Ксс - коэффициент передачи системы съема сигнала с подвеса ЧЭ ГДГ;
Е - амплитуда аксиальных колебаний камеры подвеса поплавка при вращении ее в подшипниках качения; е≈Δ - односторонний осевой зазор в устройстве аксиального центрирования поплавка ГДГ,
α - угол наклона оси собственного вращения к плоскости горизонта (α=0),
b1≈b2=2πμ(R2)4(cosθ1+(cosθ1)3/3)/(2v/ω1)l/2 - коэффициент сил вязкого трения поплавка b2 и камеры b1 о жидкость, причем b=b2/2,
R2 и m2 - радиус и масса поплавка, соответственно;
θ1=arccos((1/R2)(3m2/4πρ)1/3) - фактический угол свободной поверхности жидкости; μ, v и ρ - динамическая, кинематическая вязкость и плотность поддерживающей поплавок жидкости, соответственно.
Решение задачи технического решения состоит в том, что способ определения односторонних осевых зазоров, включающий частичное заполнение радиального зазора между поплавком и камерой рабочей жидкостью, обеспечивающей радиальное центрирование поплавка и практическую устойчивость подвеса в радиальном направлении, и собственное вращение подвеса поплавка гироскопа, имеет особенность такую, что предварительно калибруют измерительную систему, используя подвес ЧЭ ГДГ с известным осевым зазором Δэ, заливают его известным количеством жидкости ΔVп, осуществляют собственное вращение подвеса с известной скоростью ω1э, центрируют поплавок относительно камеры и находят параметры ΔVэ или Δtэ, которые будут использованы как эталонные, где ΔVэ - величина эталонного объема добавляемой в радиальный зазор подвеса жидкости для смещения поплавка из центра камеры, a Δtэ - время перемещения поплавка из центра камеры к одному из упоров под действием силы тяжести, затем центрируют поплавок относительно камеры контролируемого подвеса, фиксируют один из параметров: количество жидкости ΔV или время перемещения поплавка Δt в момент возникновения контакта элементов центрирующего устройства и вычисляют соответствующие одностороннему осевому зазору перемещения поплавка по заданному ΔV или определенному Δt параметру.
При калибровке измерительной системы горизонтально, находят величину добавляемого эталонного объема жидкости ΔVэ на основе предварительного расчета и добавляют его во внутреннюю полость подвеса ЧЭ ГДГ со стороны противоположной известного эталонного осевого зазора Δэ, при возникновении контакта элементов центрирующего поплавок устройства удаляют из внутренней полости подвеса добавленный объем жидкости ΔVэ, уменьшают объем жидкости ΔVэ на n%, при этом n≈10% ΔVэ, и повторно добавляют во внутреннюю полость подвеса объем жидкости ΔVl=(100-n)ΔVэ/100 и определяют наличие или отсутствие контакта поверхностей элементов центрирующего устройства и т. д. до момента, когда после добавления известного объема жидкости ΔVl-1 будет зафиксировано отсутствие механического контакта элементов центрирующего поплавок устройства, в случае отсутствия контакта элементов центрирующего поплавок устройства после добавления расчетного эталонного объема жидкости ΔVэ удаляют его из внутренней полости подвеса, увеличивают объем добавляемой жидкости ΔVэ на n% и повторно добавляют объем жидкости ΔVι-1=(100+n)ΔVэ/100 во внутреннюю полость подвеса и определяют при этом наличие или отсутствие контакта поверхностей элементов центрирующего устройства и т.д. до момента, когда после добавления известного объема жидкости ΔVι будет зафиксирован механический контакт элементов центрирующего поплавок устройства, делают заключение, что объем жидкости ΔVэ, соответствующий эталонному осевому зазору Δэ, находится в пределах ΔVι-1<ΔVэ<ΔVι, уточняют найденную величину эталонного объема ΔVэ таким образом, что вычисляют уточняющий объем жидкости по формуле: ΔVy=(ΔVι+ΔVι-1)/2, повторно добавляют его во внутреннюю полость подвеса и, в случае возникновения контакта элементов центрирующего поплавок устройства делают заключение, что величина эталонного объема находится в пределах ΔVι-1<ΔVэ<ΔVy, в случае отсутствия контакта элементов центрирующего поплавок устройства делают заключение, что величина эталонного объема жидкости находится в пределах ΔVу<ΔVэ<ΔVι, фиксируют величину эталонного объема ΔVэ из соотношений: ΔVι-1<ΔVэ<ΔVу или ΔVу<ΔVэ<ΔV(ι).
При калибровке измерительной системы устанавливают ось собственного вращения подвеса горизонтально, центрируют поплавок относительно камеры, устанавливают ось собственного вращения подвеса ЧЭ ГДГ вертикально таким образом, чтобы эталонный осевой зазор был ниже центра поплавковой камеры, определяют скорость собственного вращения подвеса ω1э и время Δtэ перемещения поплавка из центра камеры к одному из упоров устройства его механического центрирования, где установлен эталонный осевой зазор Δэ, при этом момент начала перемещения поплавка фиксируют в момент установки оси собственного вращения подвеса в вертикальное положение, конечную границу интервала времени перемещения поплавка фиксируют в момент возникновения механического контакта между элементами центрирующего поплавок устройства.
Определяют осевые односторонние зазоры таким образом, что заливают в подвес то же количество жидкости ΔVп, устанавливают ось собственного вращения подвеса горизонтально, добавляют объем жидкости ΔVэ во внутреннюю полость подвеса и определяют наличие или отсутствие контакта элементов устройства механического центрирования поплавка, в случае возникновения контакта элементов центрирующего поплавок устройства удаляют из внутренней полости подвеса добавленный объем жидкости ΔVэ, уменьшают объем добавляемой жидкости ΔVэ на n%, при этом n%≈10% ΔVэ, и повторно добавляют объем жидкости ΔVι=(100-n) ΔVэ/100 во внутреннюю полость подвеса и определяют при этом наличие или отсутствие контакта поверхностей элементов центрирующего устройства и т.д. до момента, когда после добавления фиксированного известного объема жидкости ΔVι-1 будет зафиксировано отсутствие механического контакта элементов центрирующего поплавок устройства, в случае отсутствия контакта элементов центрирующего поплавок устройства после добавления эталонного объема жидкости ΔVэ, удаляют из внутренней полости подвеса добавленный объем жидкости ΔVэ, увеличивают объем добавляемой жидкости ΔVэ на n% и повторно добавляют объем жидкости ΔVι-1=(100+n)ΔVэ/100 во внутреннюю полость подвеса и определяют при этом наличие или отсутствие контакта поверхностей элементов центрирующего устройства и т.д. до момента, когда после добавления известного объема жидкости ΔVι будет зафиксирован механический контакт элементов центрирующего поплавок устройства, вычисляют величины перемещений x(ι-1), x(ι) поплавка, в соответствии с соотношениями:
x(ι)=ΔэΔVι/ΔVэ, x(ι-1)=ΔэΔVι-1/ΔVэ,
делают заключение, что односторонний зазор Δ контролируемого гироскопа находится в пределах: x(ι-1)<Δ<x(ι), уточняют (в случае необходимости) найденную величину зазора таким образом, что вычисляют уточняющий объем жидкости из соотношения: ΔVy=(ΔVι+ΔVι-1)/2, повторно добавляют его во внутреннюю полость подвеса и в случае возникновения контакта элементов центрирующего поплавок устройства делают заключение, что величина зазора находится в пределах x(ι-1)<Δ<xy, в случае отсутствия контакта элементов центрирующего поплавок устройства делают заключение, что величина зазора находится в пределах xy<Δ<x(ι), вычисляют уточненную величину ху осевого перемещения Х поплавка по формуле: ху=ΔэΔVy/ΔVэ и окончательно фиксируют определенную величину зазора Δ из найденных соотношений: x(ι-1)<Δ<ху или xy<Δ<x(ι).
Определяют осевые односторонние зазоры таким образом, что заливают в подвес то же количество жидкости ΔVп, осуществляют собственное вращение подвеса с известной угловой скоростью ω1, устанавливают ось собственного вращения подвеса горизонтально, центрируют поплавок относительно камеры, устанавливают ось собственного вращения подвеса ЧЭ ГДГ вертикально, определяют время Δt перемещения поплавка из центра камеры к одному из упоров устройства его механического центрирования, при этом начало перемещения поплавка фиксируют в момент установки оси собственного вращения в вертикальное положение, конечную границу интервала времени перемещения поплавка фиксируют в момент возникновения механического контакта между элементами центрирующего его устройства, вычисляют величину одностороннего осевого зазора Δ из соотношения: Δ=Δэ(ω1э/ω1)2Δt/Δtэ, где Δэ, ω1э - эталонная величина одностороннего зазора в устройстве механического центрирования поплавка и эталонная угловая скорость собственного вращения подвеса ЧЭ ГДГ, соответствующие эталонному времени Δtэ его аксиального перемещения.
Новизна данного технического решения состоит в определении односторонних осевых зазоров устройства осевого центрирования поплавка, определение и разделение на составляющие "дрейфа нулевого сигнала" ГДГ, а также в вычислении величин моментов с использованием измеренных параметров, обусловленных инструментальными погрешностями изготовления и параметров ЧЭ ГДГ их порождающих. Найденные величины моментов и фактические параметры ГДГ предлагается использовать для оценки качества изготовления подвеса ЧЭ ГДГ и в виде входных данных для динамического моделирования на ЭВМ движений ЧЭ изготовленных ГДГ при действии угловых и поступательных входных возмущений.
Особенность решения поставленной задачи состоит в определении осевых зазоров в подвесе ЧЭ ГДГ, которая проводится после настройки коэффициента перекрестных связей между измерительными каналами в момент окончательной настройки центрирующей части подвеса ЧЭ ГДГ, когда еще не получена нулевая аксиальная плавучесть ЧЭ. Остальные же параметры определяются уже после проведения настройки центрирующей части подвеса ЧЭ ГДГ.
Впервые предложена методика определения знака плавучести ЧЭ ГДГ и направления аксиального смещения центра масс относительно его геометрического центра. Это стало возможным после определения величин осевых зазоров в устройстве аксиального центрирования ЧЭ ГДГ.
Особенно полезным предложенное решение окажется при определении причин возникновения брака ГДГ, не прошедших приемосдаточные испытания после изготовления. Обоснование способа контроля ГДГ.
Способ контроля гидродинамического гироскопа при определении осевых зазоров в устройстве аксиального центрировании его ЧЭ предложен в двух вариантах исполнения. Вариант первый основан на перемещении поплавка на фиксированную величину при формировании перепада давлений между торцевыми частями подвеса ЧЭ ГДГ. Перепад давления формируют при этом посредством импульсного (скачкообразного) изменения радиуса свободной поверхности в одной из торцевых частей подвеса ЧЭ ГДГ. Для формирования разности радиусов свободной поверхности предложено добавлять ("впрыскивать") известный фиксированный объем жидкости в один из торцевых зазоров подвеса ЧЭ ГДГ. Искусственно созданная скачком разность давлений в торцевых частях подвеса ЧЭ ГДГ формирует аксиальную уменьшающуюся силу, которая и перемещает поплавок в течение переходного процесса уравнивания давлений жидкости в торцевых его радиальных зазорах.
Данное решение задачи является техническим следствием теоретической работы по построению математической модели аксиальных движений ЧЭ ГДГ при ускоренном аксиальном перемещении сферического гидродинамического подвеса ЧЭ (см. в [4]). Идея перемещения поплавка относительно камеры посредством формирования разности давлений между торцевыми частями гидродинамического подвеса теоретически обоснована и экспериментально проверена (см. в [6]). Для формирования начального контрольного эталонного объема жидкости ΔVэ предлагается использовать соотношение, связывающее величину перемещений поплавка и величину объема жидкости добавляемую в радиальный зазор подвеса ЧЭ ГДГ:
х(l)=0,95 ΔVФ(θ1)/2π(R2)2cosθ1, (X*)
где Ф(θ1)=((2cosθ1/(-Lntg2(θ1/2)-sin2θ1)(-Lntg2(θ1/2)-2cosθ1)-(2(cosθ1-(cos3θ1)/3)-4cos2θ1/(-Lntg2(θ1/2)))/{0,4(cosθ1-(cos3θ1)/3)-2,4sin4θ1cosθ1-(4/3)sin2θ1cos3θ1-sin4θ1Lntg2(θ1/2)+(sin2θ1/cosδ1){(2/3)cos3θ1-sin2θ1(-Lntg2(θ1/2))+2cosθ1sin2θ1)}
Данное соотношение с точностью порядка 10% позволяют предсказать необходимое количество жидкости (ΔVэ), которое нужно добавить в радиальный зазор физической модели подвеса, чтобы переместить поплавок именно на величину известного эталонного зазора (Δэ). Величина его выдержана при сборке подвеса ЧЭ прибора. Важным инженерным следствием из данного соотношения является факт прямой пропорциональности аксиального перемещения поплавка относительно камеры его гидродинамического подвеса и величины добавляемого объема жидкости в его торцевую часть. При этом следует иметь в виду, что данное соотношение справедливо, когда жидкость впрыскивается непосредственно в торцевую часть радиального зазора δ. Как известно из [6], эксперимент проведен на физической модели подвеса ЧЭ ГДГ. В реальной конструкции в торцевых частях подвеса размещены цилиндрические камеры 7 (см. чертеж) стабилизации плавучести шириной Н, которые также заполнены жидкостью. Поэтому для создания эквивалентного перепада давления в торцевых частях радиального зазора физической модели и перепада давлений в торцевых радиальных зазорах в реальном ГДГ необходимо добавить в торцевую часть подвеса скачком объем жидкости в (δ cosθ1+H+L)/δcosθ1 раз больше. При этом необходимо учесть, что подвес имеет пару таких камер, т.е. он симметричен относительно центра поплавковой камеры. В процессе перетекания ровно половина впрыснутой жидкости перемещается из одной торцевой части подвеса в другую. В предложенном же решении для моделирования осевого перепада давления предложено применить прозрачную насадку шириной, соизмеримой с шириной камер температурной стабилизации. Насадка размещена только на одном торце подвеса ЧЭ ГДГ. Именно поэтому в нее необходимо добавить в (δcosθ1+H+L)/δcosθ1 раз жидкости больше, чем в радиальный зазор физической модели. Кроме этого, из геометрических соображений уточнено проверенное экспериментально соотношение (X*) в части подстановки в расчетную формулу вместо радиального зазора δ его уточненный эквивалент δcosθ1. Таким образом, окончательно соотношение, связывающее аксиальное перемещение ЧЭ ГДГ на величину эталонного осевого зазора Δэ и объем добавляемой жидкости в используемую насадку для формирования эквивалентного перепада давлений между торцевыми частями подвеса ЧЭ ГДГ и его физической модели, может быть рассчитано по формуле:
ΔVэ=Δэ(πR22cosθ1)(δcosθ1+H+L)/(δcosθ1)/(0,95Ф(θ1)). (X)
Здесь следует помнить, что ширина насадки L=(δcosθ1+H), поэтому перед π в (X) коэффициент 2 отсутствует.
Численная оценка ΔV для параметров физической модели ГДГ с параметрами R2=2,5 см, θ1=0,4114, показывает, что для перемещения поплавка на расстояние Δэ=0,02 см требуется
ΔVэ*=Δэ(2πR22cosθ1)/(0,95Ф(θ1))=(6,28·6,25·0.916515/1,7955)Δэ=(35,9732/1,7855)Δэ=20,03·0,02=0,4{см3}, (Ф(θ1)=1.89), для параметров ГДГ, например, с шириной камер стабилизации плавучести ЧЭ ГДГ Н=0,4 см, потребуется жидкости в (δcosθ1+H+L)/(δcosθ1) раз больше, чем для физической модели подвеса ЧЭ с радиальным зазором δ1=0.21 см:
ΔVэ=Δэ(πR22cosθ1)((δ1cosθ1+H+L)/(δ1cosθ1))/(0,95 Ф(θ1))=(ΔVэ/2)*(δ1cosθ1+H+L)/(δ1cosθ1)=(0,4/2)(0,19246+0,4+0,19246+0,4)/0.19246=(1.1849/0.19246)(0,4/2)=1,23 см3
При этом для перемещения поплавка на расстояние Δэ=0.02 см(200 мкм)
Непосредственно в ГДГ с радиальным зазором δ=0,0 8см потребуется жидкости ΔVэ**=ΔVэ*(δ/δ1)=0,4·(0.08/0.21)=0.15 см3, если добавить жидкость непосредственно в радиальный зазор. Если добавлять жидкость в насадку 12, то потребуется ΔVэ=(ΔVэ**/2)(δcosθ1+H+L)/(δcosθ1)=(0.15/2)(0,07332+0,4+0.07332+0,4)/0.07332)=0.075·12.911=0.9683 см3 ≈1 см3.
Из (X) следует пропорциональность добавляемого эталонного объема жидкости ΔVэ и перемещения поплавка Х на величину эталонного зазора Δэ. Поэтому соотношение для вычисления перемещения поплавка в контролируемом подвесе ЧЭ ГДГ выглядит следующим образом:
x(ι)=ΔэΔVι/ΔVэ.
При этом для создания идентичных условий при проведении контроля подвеса ЧЭ ГДГ и условий калибровки измерительной системы необходимо фиксировать (заносить в протокол) и объем жидкости ΔVп, который был залит во внутреннюю полость подвеса ЧЭ ГДГ. Тем самым обеспечивается соответствие угла свободной поверхности жидкости θ1 при проведении контроля осевого зазора и углу свободной поверхности жидкости θ1э при калибровке измерительной системы (θ1≈θ1э). При этом скорость собственного вращения не фиксируется, т.к. от ее величины перемещение поплавка здесь не зависит. Это обусловлено тем, что и перемещающая поплавок сила и сопротивление перемещению (т.е. гидродинамическое демпфирование аксиальных движений поплавка) одновременно пропорциональны квадрату угловой скорости собственного вращения подвеса ЧЭ ГДГ.
Замечание. Предложенное решение задачи использует прозрачную насадку, как вспомогательный инструмент для формирования перепада давления между торцевыми частями подвеса ЧЭ ГДГ. При этом задача также может быть решена и без нее. В этом случае возможно осуществить перемещение поплавка на величину эталонного зазора, впрыскивая во внутреннюю полость подвеса ЧЭ ГДГ (в камеру стабилизации плавучести 7 фиг.1) объем жидкости, равный:
ΔVэ*=Δэ(2πR22cosθ1)((δcosθ1+H)/(δcosθ1))/(0,95Ф(θ1))
Кроме этого, необходимо иметь в торцевой части подвеса ЧЭ ГДГ специальный канал (фигурное отверстие), связывающий внешнюю среду с внутренней полостью цилиндрических камер стабилизации плавучести 7 поплавковой камеры 1. Канал должен начинаться в торцевых частях полуосей подшипников подвеса гироузла и заканчиваться на торцевой стенке цилиндрической камеры. Предложенная же съемная прозрачная насадка позволит обойтись без доработок конструкции ГДГ.
Вариант второй реализации способа контроля осевого зазора также основан на разработанной математической модели аксиальных движений ЧЭ ГДГ. Данная математическая модель позволила выявить второй параметр подвеса ЧЭ ГДГ, который связан с аксиальным перемещением поплавка. Этим параметром является время Δt аксиального перемещения поплавка из центра камеры в сторону одного из упоров.
Эта математическая модель с точностью порядка 10% позволяют подсчитать время (Δtэ) аксиального перемещения поплавка вдоль эталонного осевого зазора Δэ из центра камеры к одному из упоров. Однако проще просто провести контрольные замеры времени аксиального перемещения поплавка из центра камеры к упору, где установлен при сборке подвеса ЧЭ ГДГ данный эталонный осевой зазор. Именно поэтому при калибровке измерительной системы по второму варианту исполнения предложено определение времени Δtэ перемещения поплавка на известную величину эталонного осевого зазора Δэ. Рассмотрим далее как связаны время Δtэ и осевой зазор Δэ.
В поле силы тяжести (стр. 91 книге [3]) скорость z* аксиального перемещения поплавка, когда ось собственного вращения подвеса ЧЭ ГДГ вертикальна, может быть определена по формуле:
z*=Δmg/(Кμ+Кρ), (2.1)
где Δm - аксиальная плавучесть ЧЭ ГДГ; g - ускорение силы тяжести; Kμ, Кρ(ω12) - коэффициенты вязкого и гидродинамического демпфирования аксиальных движений поплавка ГДГ.
Полагая в (2.1) z*=Δэ/Δtэ, находим связь плавучести ЧЭ ГДГ и времени Δtэ его перемещения в пределах одностороннего эталонного осевого зазора устройства центрирования ЧЭ ГДГ (3,4 фиг.1):
1/Δtэ=Δmg/(Kμ+Kρ)Δэ, (2.2)
где Δэ - односторонний эталонный осевой зазор между шариком 3, закрепленным в центре поплавка 2, и упором 4, установленным в торце поплавковой камеры 1.
Отсюда следует, что время перемещения поплавка tэ при известной скорости ω1 собственного вращения подвеса ЧЭ ГДГ пропорционально величине эталонного зазора Δэ. Именно поэтому, определив время перемещения поплавка в контролируемом подвесе ЧЭ ГДГ, величину зазора можно оценить по формуле:
Δ=ΔэΔt/Δtэ (2.3).
Из [3] (стр. 91) известно, что коэффициенты инерционного гидродинамического Кρ и вязкого Кμ демпфирования связаны соотношением: Kρ≫Kμ. Причем Кρ пропорционален ω12, поэтому при определении осевого зазора и вращении подвеса ЧЭ ГДГ с угловой скоростью ω1, отличной от эталонной ω1э, необходимо учесть поправку в соотношении (2.3):
Δ=Δэ(ω1э/ω1)2Δt/Δtэ, (2.4)
Именно поэтому в протокол испытаний необходимо занести и скорость собственного вращения подвеса ЧЭ ГДГ при калибровке ω1э и учесть ее (ω1) при определении осевого зазора в контролируемом подвесе ЧЭ ГДГ.
Кроме того, дополнительно предложено заносить в протокол и количество жидкости ΔVп, залитое во внутреннюю полость подвеса ЧЭ ГДГ. Это условие необходимо выполнить, чтобы плавучесть Δm ЧЭ ГДГ, также соответствовала той эталонной плавучести Δmэ поплавка, которая имела место при калибровке измерительной системы (см. соотношение (2.2)).
Замечание. Предложенные способы определение осевых зазоров имеют соответственно каждый свои преимущества. Первый не требует значительного времени на его реализацию. Необходимо только тщательная подготовка добавляемых объемов жидкости во внутреннюю полость подвеса ЧЭ ГДГ. Второй требует значительного времени из-за очень медленных перемещений поплавка вдоль эталонного осевого зазора. При этом не требуется особой квалификации исполнителя для измерения времени перемещений поплавка ГДГ.
Обоснование разделения на составляющие выходного напряжения ГДГ, т.е. его "дрейфа нулевого сигнала" при отсутствии входных угловых воздействий. В книге [3] (стр. 104, 99) рассмотрены основные причины возникновения инструментальных погрешностей ГДГ, обусловленных механикой подвеса его ЧЭ. Так, отклонение поплавка вызывает аксиальное и радиальное смещение центра масс поплавка из геометрического центра. Кроме этого, причиной дополнительного отклонения поплавка относительно камеры и системы съема сигнала может быть ненулевая остаточная его плавучесть. В связи с этим для разделения на составляющие выходного напряжения "дрейфа нуля" ГДГ необходимо выбирать положения ГДГ относительно поля силы тяжести и создавать условия такие, при которых будет проявляться по очереди каждая из составляющих.
Далее обоснуем выявление каждой из составляющих инструментальных погрешностей и поставим им в соответствие расчетные соотношения из [3]. Разделение на составляющие даст возможность оценить долю каждой из них в выходном напряжении "дрейфа нуля" ГДГ. А расчетные соотношения позволят оценить величины отклоняющих поплавок моментов, которые затем можно подставить, как исходные данные, в математическую модель ЧЭ ГДГ и осуществить динамическое моделирование движений ЧЭ реального гироскопа. Это позволит, в конечном счете, оценить точность управления движением динамичного объекта, где установлен ГДГ как измеритель угловых перемещений (ИУП).
Анализ технологии изготовления элементов подвеса ЧЭ ГДГ показывает, что с целью минимизации основных инструментальных погрешностей осуществляется только тщательная аксиальная балансировка (т.е. минимизируется аксиальное смещение центра масс d). Радиальная балансировка не производится, а обеспечивается конструктивно. Кроме этого, с целью разгрузки аксиального устройства предварительного центрирования поплавка, осуществляют тщательную настройку центрирующей части подвеса ЧЭ ГДГ. В результате добиваются обеспечения аксиальной плавучести поплавка, близкой к нулю. Поэтому наибольшей составляющей в выходном напряжении "дрейфа нуля" ГДГ является инструментальная погрешность, обусловленная радиальным смещением еm центра масс U(θ*). Соотношение для оценки величины угла отклонения поплавка (стр.104 [3]) при этом выглядит следующим образом:
θ*=еmm2Еω1/(2b);
где b1≈b2=2b - коэффициент момента сил вязкого трения поплавка (камеры) о жидкость (см. стр.100 [3]); ω1 - измеренная угловая скорость собственного вращения подвеса поплавка; m2 - масса поплавка; Е - амплитуда аксиальных колебаний камеры подвеса поплавка при вращении ее в подшипниках качения (наибольшая величина определяется величиной осевого зазора в подшипниковом узле поплавковой камеры).
Далее рассмотрим, каким образом выявляется инструментальная погрешность ГДГ - "дрейф нуля", обусловленный радиальным смещением центра масс поплавка относительно его геометрического центра.
Из [3] стр. 103 известно, что возмущающий и отклоняющий момент, приложенный к ЧЭ ГДГ, обусловленный аксиальной качкой поплавковой камеры в подшипниках качения, при совпадении частоты качки и частоты собственного вращения (что имеет место на практике) зависит от частоты этой качки (внутренней аксиальной вибрации в подшипниках качения) поплавковой камеры. Так, осевая качка поплавковой камеры ГДГ, обусловленная несовершенством элементов конструкции подшипников качения и неидеальностью их установки относительно оси собственного вращения подвеса при наличии радиального смещения центра масс Cm поплавка относительно оси собственного вращения, приводит к возникновению постоянного по величине возмущающего поплавок момента, следствием чего является отклонение поплавка относительно камеры на определенный угол θ* (который иногда называют "дрейфом нуля" ГДГ). При этом данный угол формируется, когда частота собственного вращения поплавка и поплавковой камеры совпадают (что имеет место при регулировании датчика угла ГДГ в поле силы тяжести).
С учетом этого электрическая ось сигнальной катушки совмещается с осью собственного вращения поплавка, что обеспечивает получение на выходе ГДГ минимального выходного напряжения Uo на рабочей частоте собственного вращения поплавка и камеры. Такая регулировка датчика угла обеспечивает схемную компенсацию внутреннего вибрационного отклоняющего поплавок момента, а, следовательно, и начального углового положения θ* поплавка относительно сигнальной катушки датчика угла, жестко закрепленной на корпусе ГДГ. Регулировка системы съема сигнала производится при вертикальной оси собственного вращения подвеса ЧЭ ГДГ. Величина напряжения Uo определяет неточность установки сигнальной катушки относительно вращающегося поплавка и напряжение помех, обусловленных качеством изготовления сигнальной катушки.
В ГДГ, где применена схемная компенсация возмущающего поплавок момента, при изменении направления вектора кинетического момента ("обратное вращение") с сохранением частоты собственного вращения подвеса ЧЭ, выходной сигнал U1o существенно превышает величину Uo, имеющую место при рабочем направлении вектора угловой скорости собственного вращения. Следовательно, в рассматриваемом случае угловое положение поплавка не совпадает с положением, соответствующем угловому положению сигнальной катушки относительно корпуса и поплавковой камеры ГДГ, зафиксированному при настройке сигнальной системы. Это явление можно объяснить тем, что независимо от направления вращения поплавковой камеры, величина угла между осями собственного вращения поплавка и камеры определяется соотношением θ*=(α2+β2)l/2 (см. [3] стр.101), которая пропорциональна радиальному смещению центра масс ещ ЧЭ ГДГ и интенсивности аксиальной качки поплавковой камеры в подшипниках качения, а фаза выходного напряжения зависит от направления вращения камеры. При этом сигнальная катушка датчика угла ГДГ установлена в нем таким образом, что ее угловое положение относительно корпуса ГДГ совпадает с угловым положением поплавка относительно поплавковой камеры (т.е. корпуса ГДГ) только при определенном (рабочем) направлении вращения поплавковой камеры. Отсюда следует, что при изменении направления вращения камеры, поплавок занимает угловое положение относительно сигнальной катушки, которое определяется соотношением 2θ*=2(α2+β2)1/2. Т.е. отклоняется относительно корпуса на тот же угол, но в противоположном направлении. Именно поэтому относительно сигнальной катушки он отклоняется на удвоенный угол.
Отсюда следует, что суммарное выходное напряжение при рабочем Uo и "обратном" U1o собственном вращении подвеса ЧЭ ГДГ соответствует удвоенному углу отклонения поплавка относительно камеры θ*. Поэтому инструментальную погрешность ГДГ, обусловленную радиальным смещением центра масс предложено оценивать (выявлять) по формуле:
U(θ*)=(Uo+U1o)/2. (2.5)
Рассмотрим далее, как проявляются инструментальные погрешности ГДГ, обусловленные аксиальным смещением центра масс и не нулевой плавучестью ЧЭ ГДГ. В [3] (стр. 99) получено соотношение для приращения угла между осями поплавка и камеры, обусловленного разбалансировкой системы жидкое тело - поплавок:
α2*=m2(g+Wx1)d/(b2ω1)-(1/b1ω1){Δm(g+Wx1)ez-m2(g+Wx1)d},
где b1 - коэффициент сил вязкого трения камеры (или поплавка, т.к. b1≈b2) о жидкость, ω1 - скорость вращения подвеса поплавка, g - ускорение силы тяжести.
Вводя в рассмотрение коэффициент передачи датчика угла Ксс системы съема сигнала, приращение выходного напряжения прибора, обусловленное аксиальным смещением центра масс и ненулевой аксиальной плавучестью только в поле силы тяжести (при Wx1=0), будет равно:
Uo1*=Ксс(m2gd/(b2ω1)-(1/b1ω1){Δmgez-m2gd})=U(d)+U(Δm). (2.6)
А приращение выходного напряжения, обусловленное радиальным смещением центра масс относительно геометрического центра, поплавка будет равно
U(θ*)=Кссθ*=еmm2Еω1/(b1).
При этом для разделения на составляющие необходимо, чтобы отклонения поплавка, обусловленные всеми причинами происходили в одной плоскости.
Так отклонения поплавка α2*, обусловленные разбалансировкой системы жидкое тело-поплавок (см. (2.6)) в поле силы тяжести проявляются при горизонтальной оси собственного вращения (1 условие). При этом поплавок отклоняется от оси вращения камеры на угол α2* в горизонтальной плоскости (см. стр. 99 [3]).
Рассмотрим далее отклонение поплавка, обусловленноо радиальным смещением центра масс. Как показано в [3] (стр. 104) ось собственного вращения поплавка с радиальным смещением центра масс отклоняется в пространстве на углы (α2, β2) и "дрейфует" на картинной плоскости (α2, β2), относительно оси собственного вращения камеры случайным образом. Именно поэтому необходимо таким образом сориентировать гироскоп, чтобы отклонение поплавка на результирующий угол θ* (определяемый углами α2 и β2, обусловленными радиальным смещением центра масс) тоже имело место в горизонтальной плоскости (2 условие). Для выполнения "условия 1" устанавливают ось собственного вращения подвеса ЧЭ ГДГ горизонтально. А для выполнения "условия 2" разворачивают прибор вокруг нее до момента формирования наибольшего выходного напряжения Uo1 ГДГ. Так находят положение ГДГ, когда отклонение поплавка, обусловленное всеми инструментальными погрешностями, имеет место в одной горизонтальной плоскости, при этом еще и алгебраически суммируются. Таким образом, выходное напряжение "дрейфа нуля" ГДГ при горизонтальной оси собственного вращения имеет вид:
Uo1=Uo1*+Uo=U(d)+U(Δm)+Uo. (2.7)
Из (2.6) следует, что если устремить к нулю ez, тогда выходное напряжение ГДГ при горизонтальной оси собственного вращения в поле силы тяжести будет определяться только аксиальным смещением центра масс поплавка и величиной "нулевого сигнала" Uo: (2.8)
Uo2=Kcc(m2gd/(b2ω1)+m2gd/b1ω1))+Uo≈2Kccm2gd/(b1ω1)+Uo.
или Uo2=U(d)+Uo, где U(d)=2Kccm2gd/(b1ω1).
Устремить к нулю смещение поплавка относительно камеры возможно посредством искусственного активного центрирования поплавка. Методика центрирования поплавка ранее была предложена, см. [5]. Для этого разгоняют подвес ЧЭ ГДГ до угловой скорости собственного вращения, превышающей номинальную, и осуществляют интенсивное его торможение до номинальной угловой скорости собственного вращения. При этом формируется сила, приложенная к поплавку, которая и центрирует его относительно камеры. В результате в выходном сигнале ГДГ остаются составляющие, обусловленные аксиальным смещением центра масс U(d) и остаточным напряжением Uo.
Рассуждая таким образом, приходим к соотношениям для оценки инструментальных погрешностей ГДГ: ( U)
U(θ*)=(Uo+U1o)/2; U(Δm)=|Uo1-Uo2|; U(d)=|Uo2-Uo|,
где U (θ*)-величина нулевого сигнала гироскопа, обусловленная радиальным смещением центра масс поплавка относительно его геометрического центра;
U(Δm) - величина "нулевого сигнала" гироскопа, обусловленная остаточной ненулевой плавучестью поплавка;
U(d)- величина "нулевого сигнала" гироскопа, обусловленная аксиальным смещением центра масс относительно его геометрического центра.
Обоснование методики контроля качества настройки подвеса ЧЭ ГДГ на вращающемся основании. Из книги [3] стр. 101, известно, что передаточная функция ГДГ с минимизированным коэффициентом перекрестной связи между измерительными каналами имеет вид: П(s)=-То/(Tos+1), где s-оператор дифференцирования, а То - постоянная времени ГДГ. Для такого гироскопа выходной величиной является угол отклонения поплавка относительно камеры α2 и системы съема сигнала, а входной величиной является угловая скорость собственного вращения основания ωвх: П10=α2/ωвх. Вводя в рассмотрение коэффициент передачи системы съема сигнала Ксс, получим: U/ωвх=-Kcc*To/(Tos+1). Левую часть этого равенства называют коэффициентом передачи S ГДГ. При этом в установившемся режиме вращения основания с заданной угловой скоростью ωвх (то есть при s→0), коэффициент передачи S может быть определен из соотношения: S=U/ωвх. Из теории автоматического регулирования известно, что для апериодического звена время переходного процесса tпп связано с постоянной времени То соотношением: tпп≅3To. Из этих рассуждений следует инженерная методика определения параметров подвеса ЧЭ ГДГ на вращающемся основании.
Вращая платформу поворотной установки с заданной угловой скоростью ωвх и определяя выходное напряжение U, коэффициент передачи ГДГ может быть найден по формуле: S=U/ωвх.
Осуществляя скачкообразный останов платформы поворотной установки и определяя время переходного процесса снижения выходного напряжения U, можно найти остальные параметры подвеса - постоянную времени То и коэффициент передачи системы съема сигнала Ксс по формулам:
To=tпп/3; Kcc=S/To.
Рассмотрим далее обоснование определения коэффициента перекрестной связи по сдвигу фаз выходного напряжения ГДГ относительно одного из опорных напряжений. Выпишем из [3] стр.101 передаточные функции измерительных каналов ГДГ с поплавком (ЧЭ), имеющим отклонения формы поверхности от идеальной сферы, т.е. С≠0:
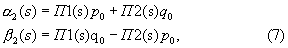
где П1(s)=(-Tob2ω2/(b2ω2+C2))(Tos+1)/(T12s2+2ξT1+1);
П2(s)=(-Н20С/(b2ω2+С2))(T2s+1)/(T12s2+2ξT1+1);
T1=(H20/(b2ω2+C2)1/2), T2=(b/C)(1-Iэ2/Iz2), ξ=bω/(b2ω2+C2)1/2.
При формировании момента, отклоняющего поплавок, относительно только одной из осей чувствительности (например, qo = 0, так же как в предлагаемом решении) отношение углов отклонения поплавка
β2(s)/α2(s)=(П1(s)q0-П2(s)p0/(П1(s)p0+П2(s)q0),
представляющее собой tgϕ (ϕ - сдвиг фаз выходного напряжения относительно одного из опорных напряжений системы съема сигнала ГДГ), преобразуется к виду: β2(s)/α2(s)=-П2(s)/П1(s), что в установившемся режиме с учетом выражений для П1(s) и П2(s) соответствует соотношению: tg ϕ=β2(s)/α2(s)=-С/bω, что и принято называть коэффициентом упругих перекрестных связей между измерительными каналами ГДГ. При С≪bω (что реализуется на практике при настройке подвеса ЧЭ ГДГ), окончательно получаем: ϕ=-С/bω, что и требовалось обосновать.
Замечание. Сдвиг фаз выходного напряжения относительно одного из опорных (входного) напряжений при решении задачи измеряется в момент начала переходного процесса уменьшения выходного сигнала ГДГ.
Рассмотрим определение знака плавучести ЧЭ ГДГ и направления осевого смещения центра масс по отношению к направлению вектора угловой скорости собственного вращения подвеса ЧЭ ГДГ.
Знак плавучести ЧЭ ГДГ можно оценить после определения каждого из осевых зазоров Δ1, Δ2 устройства аксиального центрирования поплавка. Определение этого знака основано на том, что поплавок с положительной аксиальной плавучестью всегда перемещается в поле силы тяжести в крайнее верхнее положение, т.е. "всплывает". А поплавок с отрицательной аксиальной плавучестью в поле силы тяжести перемещается в крайнее нижнее положение, т.е. "тонет". При определении знака плавучести ЧЭ ГДГ предложено поочередно устанавливать, например, в верхнее положение больший, а затем меньший зазоры. Затем оценивают время перемещения поплавка вдоль одного из зазоров. При этом, если большему зазору (Δ1>Δ2), установленному в верхнее положение соответствует большее время (t1>t2) перемещения поплавка, то делают заключение, что в контролируемом подвесе ЧЭ ГДГ имеет место положительная плавучесть поплавка: Δm>0. В противном случае, когда большему зазору (Δ1>Δ2) в верхнем положении соответствует меньшее время перемещения поплавка (t1<t2), делают заключение, что в исследуемом подвесе ЧЭ ГДГ имеет место его отрицательная плавучесть ЧЭ ГДГ: Δm<0.
Определяют направление аксиального смещения центра масс ЧЭ ГДГ на основе соотношения (2.6)-(2.7) и анализа изменений напряжения "дрейфа нуля" при горизонтальной оси собственного вращения подвеса ЧЭ ГДГ до Uo1 и после Uo2 центрирования поплавка.
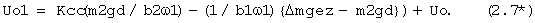
Если при положительной аксиальной плавучести ЧЭ ГДГ (Δm>0) после аксиального центрирования поплавка относительно камеры величина выходного напряжения Uo1 уменьшается, то делают заключение в контролируемом подвесе ЧЭ ГДГ центр масс смещен в направлении вектора угловой скорости собственного вращения подвеса, в противном случае, т.е. когда после центрирования поплавка относительно камеры величина выходного напряжения Uo1 увеличивается, то делают заключение, что аксиальное смещение центра поплавка относительно камеры масс имеет место в сторону, противоположную направлению вектора угловой скорости собственного вращения подвеса ЧЭ ГДГ. Действительно при положительной плавучести поплавка (Δm>0) до центрирования его относительно камеры выходное напряжение ГДГ равно
Uo1=Kcc(m2gd/(b2ω1)-(1/b1ω1({Δmgez-m2gd})+Uo,
а после центрирования оно станет равным
Uo2=Ксс(m2gd/(b2ω1)+(1/b1ω1){m2gd})+Uo и уменьшится, то смещение центра масс имеет место ( в соответствии с рис.6.7 стр.99 [3]) в направлении вектора угловой скорости собственного вращения подвеса ЧЭ ГДГ. Если же выходное напряжение после центрирования поплавка станет равным Uo2=Ксс(m2gd/(b2ω1)+(1/b1ω1){m2gd})+Uo и увеличится, то центр масс (см рис. 6.7 стр.99 [3]) в направлении, противоположном вектору угловой скорости собственного вращения подвеса ЧЭ ГДГ.
Замечание. При этом направление вектора кинетического момента во время проведения контроля ГДГ при вертикальной оси собственного вращения направляется в сторону противоположную направлению вектора ускорения силы тяжести (т.е. направляется вверх). Тем самым однозначно задается система координат связанная с поплавком, относительно которой и определяется смещением центра масс ЧЭ ГДГ.
Если при отрицательной аксиальной плавучести ЧЭ ГДГ (Δm<0) после аксиального центрирования величина выходного напряжения Uo1 увеличивается, то делают заключение в контролируемом подвесе ЧЭ ГДГ центр масс смещен в направлении, противоположном вектору угловой скорости собственного вращения подвеса, в противном случае, т.е. когда после аксиального центрирования поплавка относительно камеры, величина выходного напряжения уменьшается, то делают заключение, что аксиальное смещение центра масс имеет место в направлении вектора угловой скорости собственного вращения подвеса ЧЭ ГДГ. Действительно при отрицательной плавучести поплавка (Δm<0) до центрирования его относительно камеры выходное напряжение ГДГ равно
Uo1=Ксс(m2gd/(b2ω1)-(1/b1ω1){Δmgez-m2gd})+Uo,
а после центрирования оно станет равным
Uo2=Ксс(m2gd/(b2ω1)+(1/b1ω1){m2gd})+Uo
и увеличится по абсолютной величине, то смещение центра масс имеет место ( в соответствии с рис.6.7 стр.99 [3]) в направлении, противоположном вектору угловой скорости собственного вращения подвеса ЧЭ ГДГ. Если же выходное напряжение Uo1 после центрирования поплавка станет равным
Uo2=Kcc(m2gd/(b2ω1)+(1/b1ω1){m2gd})+Uo
и уменьшится, то смещение центра масс имеет место ( см. рис. 6.7 стр.99 [3]) в направлении вектора угловой скорости собственного вращения подвеса ЧЭ ГДГ.
Обоснование соотношений для вычисления отклоняющих поплавок моментов. В процессе контроля ГДГ определены выходные напряжения (U):
U(θ*)=(Uo+U1o)/2; U(Δm)=|Uo1-Uo2|; U(d)=|Uo2-Uo|.
При этом данные выходные напряжения пропорциональны соответствующим углам отклонения поплавка относительно системы съема сигнала ГДГ:
U(θ*)=Kccθ*(em); U(Δm)=Kcc*(α2(Δm)); U(d)=Kcc*(α2(d))
Ограничивает отклонение поплавка относительно камеры так называемая угловая "жесткость гидродинамической пружины": (b1ω1≈b2ω2). Это коэффициент пропорциональности между углом отклонения ЧЭ ГДГ (α2, β2) и внешним или внутренним отклоняющим поплавок моментом. В [3] стр. 98 обозначены b1, b2 - коэффициенты сил вязкого трения, соответственно, между жидким телом и камерой и жидким телом и поплавком ГДГ. Причем в силу малости радиального зазора δ в сравнении с радиусами камеры R1 и поплавка R2, т.е. при δ≪R1, R2, выполняется соотношение b1≈b2=2b (см. стр. 100 [3]). Отсюда следует, что произведения углов отклонения поплавка
θ*(em)=U(θ*)/Kcc; α2(Δm)=U(Δm)/Kcc; α2(d)=U(d)/Kcc
на угловую "жесткость гидродинамической пружины" (b1ω1) представляют собой те самые моменты, которые необходимо оценить по результатам измерений и разделений величин напряжений "нулевого сигнала" ГДГ на составляющие
М(еm)=(θ*)*(b1ω1), M(Δm)=(α2(Δm))*(b1ω1); M(d)=(α2(d))*(b1*ω1).
Величины углов отклонения поплавка ГДГ: θ*(еm); α2(Δm); α2(d) связаны с параметрами подвеса ЧЭ ГДГ упомянутыми выше соотношениями
θ*=emm2Е(ω1)2/(b1*ω1)=еmm2Еω1/(2b) и α2*=α2(d)+α2(Δm)=m2(g)d/(b2ω1)-(1/b1ω1){Δm(g)ez-m2(g)d}, (2.6) при Wx1=0, где α2(d)=2m2gd/(b1ω1); α2(Δm)=-(1/b1ω1)*Δmgez.
Отсюда следуют соотношения для вычисления величин возмущающих моментов: М(em), обусловленного радиальным смещением центра масс em, и его численного значения: M(em)=(U(θ*)/Kcc)*(2b); em=(U(θ*)/Kcc)(2b)/(m2Eω1), M(Δm), обусловленного остаточной ненулевой плавучестью поплавка Δm и ее численного значения:
M(Δm)=(U(Δm)/Kcc)*(b1ω1); Δm=(U(Δm)/Kcc)(b1ω1)/gecosα, (ΔM),
M(d), обусловленного аксиальным смещение центра масс d и его численного значения:
M(d)=(U(d)/Kcc)(b1*ω1); d=(U(d)/Ксс)(b1*ω1)/(2*m2*g);
где b1 -коэффициент момента сил вязкого трения камеры( ЧЭ ГДГ) о жидкость;
ω1 - измеренная скорость вращения подвеса поплавка; g - ускорение силы тяжести; Kcc - коэффициент передачи системы съема сигнала с подвеса ЧЭ ГДГ, определенный в процессе контроля ГДГ на подвижном основании;
e≈Δ - односторонний осевой зазор в устройстве аксиального центрирования поплавка ГДГ, определенный при контроле подвеса ЧЭ ГДГ,
α - угол наклона оси собственного вращения к плоскости горизонта (α=0),
Е - амплитуда аксиальных колебаний камеры подвеса поплавка при вращении
ее в подшипниках качения (наибольшая величина определяется величиной осевого зазора в подшипниковом узле поплавковой камеры).
b1≈b2=2πμ(R2)4(1-(R3/R2)2)1/2+(1-(R3/R2)2)3/2/3)/(2ν/ω1)l/2=2πμ(R2)4(cosθ1+(cosθ1)3/3)/(2ν/ω1)1/2; (см. стр.99 [3]), т.к. R1≈R2 (при δ=R1-R2≪R1, R2, причем b=b2/2 (см. стр.100 [3])
Находят с использованием вычисленных b1 и измеренных величин ω1 и То осевой момент инерции Iz2 и кинетический момент Н20 ГДГ в соответствии с соотношениями Iz2=2То* b1; Н20=2То* b1*ω1 (см. стр.101 [3]). Важным элементом здесь является какой именно зазор Δ1 или Δ2 следует подставлять вместо е в расчетном соотношении для определения плавучести ЧЭ ГДГ в формуле (ΔМ). Для однозначного решения этого вопроса при установке поплавковой камеры в корпус ГДГ отмечают положение большего и меньшего осевых зазоров относительно, например, расположения электродвигателя или устанавливаемой на противоположном торце ГДГ крышки. Пустьбольший зазор (Δ1>Δ2) установлен со стороны электродвигателя (что наиболее предпочтительнее для режима ускоренного перемещения подвеса ЧЭ ГДГ и его нестационарного вращения в условиях применения, т.к. поплавок перемещается именно в этом направлении во время переходного процесса преобразования формы свободной поверхности жидкости). Меньший же осевой зазор при этом будет иметь место со стороны крышки корпуса ГДГ. В этом случае при установке ГДГ в вертикальное положение (электродвигателем выше корпуса прибора) больший зазор окажется в верхнем положении. Известный знак плавучести ЧЭ ГДГ позволит однозначно указать какой именно осевой зазор следует использовать при расчете аксиальной плавучести ЧЭ ГДГ в соответствии с формулой (ΔM). Так, например, при положительной аксиальной плавучести ЧЭ ГДГ смещение поплавка будет иметь место именно вдоль большего осевого зазора. Поэтому в формулу (ΔM) необходимо подставлять осевой зазор Δ1. При отрицательной плавучести ЧЭ ГДГ при установке в вертикальное положение оси собственного вращения прибора с электродвигателем выше корпуса ГДГ поплавок будет перемещаться вдоль меньшего осевого зазора Δ2. Поэтому в формуле (ΔМ) необходимо использовать численное значение меньшего осевого зазора Δ2.
Замечание. Величину Е для вычисления em можно оценить при помощи селективного вольтметра и пьезодатчика. Для этого его чувствительный элемент устанавливают непосредственно на полуось подшипникового узла поплавковой камеры. Его выходной сигнал, пропорциональный интенсивности осевых колебаний, подают через селективный вольтметр (например, типа В6-4) на вход частотомера (например, типа Ч3-33) для контроля частоты регистрируемого сигнала. При помощи селективного вольтметра измеряют интенсивность колебаний гироузла (поплавковой камеры). А частотомер при этом позволяет проконтролировать, что интенсивность колебаний измерена именно на частоте собственного вращения подвеса ЧЭ ГДГ.
Частоту собственного вращения поплавка и поплавковой камеры (подвеса ЧЭ ГДГ) ω1 определяют при помощи другого частотомера (типа Ч3-33), подключенного к одной из обмоток опорного напряжения. Амплитуда осевого ускорения Wx1 аксиальных колебаний подвеса ЧЭ ГДГ, скорость осевой вибрации Vx1 и выходное напряжение Ux1 пъезодатчика связаны следующим образом: Wx1=ω1*Vx1; Vx1=Kп*Ux1, где Кп - постоянный коэффициент определяемый конструктивными особенностями пъезодатчика. При этом предварительно оценивают этот коэффициент при помощи, например, измерительного комплекса - шумомера фирмы "Брюль и Къер" типа 2203 (Франция). Данный комплекс предназначен для узкополосного анализа спектра осевых движений подшипникового узла и позволяет определить амплитуду аксиальных колебаний оси собственного вращения подвеса ЧЭ ГДГ при различных угловых скоростях собственного вращения. Проведя измерения амплитуды колебаний оси собственного вращения поплавковой камеры на определенной известной частоте собственного вращения поочередно при помощи пъезодатчика и на фирменном измерительном комплексе, можно определить Кп - коэффициент передачи пьезодатчика. Затем использовать его для определения амплитуды колебаний каждого из исследуемых ГДГ. Скорость аксиальных колебаний Vx1 и ускорение Wx1 связаны с амплитудой Е этих колебаний в соответствии с соотношениями Vx1=E*ω1, Wx1=E*(ω1) (см. стр.103[3]). Измеренная с помощью пъезодатчика скорость осевых колебаний Vx1=Kп*Ux1, позволяет определить их амплитуду Е.
Из уравнения Кп*Ux1=Vx1=E*ω1 следует, что амплитуду осевых колебаний можно оценить по формуле: Е=Кп*Ux1/ω1.
Предложенный способ контроля ГДГ реализуется следующим образом.
(имеет следующую последовательность действий).
Способ контроля гидродинамического гироскопа, включающий частичное заполнение радиального зазора между поплавком и камерой рабочей жидкостью, обеспечивающее нейтральную аксиальную плавучесть поплавка, и собственное вращение подвеса поплавка и определение основных параметров ГДГ в отсутствии входных угловых воздействий, имеет особенность такую, что
- определяют скорость собственного вращения подвеса ω1, определяют "нулевой сигнал" ГДГ Uo и U1o при вертикальной оси собственного вращения подвеса при рабочем и "обратном" направлении его собственного вращения,
- устанавливают ось собственного вращения горизонтально и разворачивают ГДГ вокруг оси собственного вращения до получения наибольшей величины "нулевого сигнала" Uomax и измеряют его Uo1,
- в случае совпадения "нулевых сигналов" Uo и Uo1 при вертикальной и горизонтальной оси собственного вращения делают заключение, что в контролируемом ГДГ аксиальное смещение центра масс поплавка d и аксиальная плавучесть поплавка Δm близки к нулю и вычисляют инструментальную погрешность ГДГ в соответствии с соотношением: U(θ*)=(Uo+U1o)/2;
- в противном случае, центрируют поплавок относительно камеры и снова измеряют "нулевой сигнал" гироскопа Uo2 при горизонтальной оси собственного вращения, в случае совпадения величин напряжений Uo1 и Uo2 делают заключение, что аксиальная плавучесть поплавка Δm близка к нулю, вычисляют составляющие инструментальных погрешностей по формулам:
U(θ*)=(Uo+U1o)/2; U(d)=|Uo2-Uo|,
- в противном случае, дополнительно устанавливают ось собственного вращения подвеса не горизонтально, следят за изменением выходного нулевого сигнала до момента возникновения контакта элементов центрирующего устройства, затем устанавливают ось собственного вращения горизонтально и измеряют выходное напряжение Uo1*, вычисляют составляющие инструментальных погрешностей по формулам:
U(θ*)=(Uo+U1o)/2; U(Δm)=|Uo1*-Uo2|; U(d)=|Uo2-Uo|, где
U(θ*) - величина нулевого сигнала гироскопа, обусловленная радиальным смещением центра масс поплавка относительно его геометрического центра;
U(Δm) - величина "нулевого сигнала" гироскопа, обусловленная остаточной ненулевой плавучестью поплавка;
U(d)- величина "нулевого сигнала" гироскопа, обусловленная аксиальным смещением центра масс относительно его геометрического центра;
- затем определяют знак плавучести чувствительного элемента (ЧЭ) ГДГ, направление аксиального смещения центра масс ЧЭ ГДГ по отношению к направлению вектора кинетического момента, вычисляют величину возмущающих моментов, обусловленных инструментальными погрешностями ГДГ,
- затем определяют параметры ГДГ на подвижном основании.
При этом после определения ГДГ параметров в отсутствии входных угловых воздействий вращают ГДГ относительно одной из осей чувствительности с заданной угловой скоростью ωвх и определяют величину выходного напряжения Ucc и его сдвиг фаз Δϕ относительно одного из опорных напряжений,
- скачком останавливают платформу поворотной установки и определяют время переходного процесса tпп уменьшения выходного напряжения ГДГ до величины его "нулевого сигнала" Uo, вычисляют коэффициент S передачи ГДГ по формуле s=Ucc/ωвх, постоянную времени То вычисляют по формуле То=tпп/3, а коэффициент передачи системы съема сигнала ГДГ Ксс - по формуле: Ксс=S/To.
Для определения знака плавучести ЧЭ ГДГ устанавливают больший осевой зазор в верхнее положение относительно центра подвеса ЧЭ ГДГ и определяют время t1 перемещения ЧЭ из центра камеры до одного из упоров центрирующего поплавок устройства,
- устанавливают в верхнее положение меньший зазор подвеса ЧЭ ГДГ и снова определяют время t2 перемещения поплавка из центра камеры до одного из упоров и если t1>t2, делают заключение о наличии положительной плавучести ЧЭ, если t1<t2, то делают заключение о наличии отрицательной плавучести ЧЭ, затем определяют направление аксиального смещения центра масс ЧЭ ГДГ по отношению к направлению вектора кинетического момента для чего устанавливают ось собственного вращения подвеса ЧЭ ГДГ горизонтально и определяют выходное напряжение Uo1,
-центрируют поплавок относительно камеры
-и снова определяют выходное напряжение Uo2, если после аксиального центрирования поплавка относительно камеры величина выходного напряжения уменьшилась, то делают заключение, что центр масс смещен в направлении вектора угловой скорости собственного вращения подвеса, в противном случае, когда после центрирования поплавка относительно камеры величина выходного напряжения увеличилась, то делают заключение, что центр масс поплавка смещен относительно камеры в сторону, противоположную направлению вектора угловой скорости собственного вращения подвеса ЧЭ ГДГ,
-вычисляют величину возмущающего момента М(еm), обусловленного радиальным смещение центра масс ещ и величину смещения по формулам:
M(em)=(U(θ*)/Kcc)*(2b), em=(U(θ*)/Kcc)/(m2Eω1),
-вычисляют величину отклоняющего поплавок момента М(Δm), обусловленного остаточной ненулевой плавучестью поплавка Δm и ее величину по формулам:
M(Δm)=(U(Δm)/Kcc)*(b1ω1); Δm=U(Δm)*b1*ω1/Kccgecosα,
- вычисляют величину момента M(d), обусловленного аксиальным смещение центра масс d и его величину по формулам:
M(d)=(U(d)/Kcc)(b1*ω1); d=(U(d)/Kcc)(b1*ω1)/(2*m2*g); где
b1 - коэффициент момента сил вязкого трения поплавка (камеры) о жидкость; ω1 - измеренная скорость вращения подвеса поплавка; g -ускорение силы тяжести; Ксс - коэффициент передачи системы съема сигнала с подвеса ЧЭ ГДГ;
Е - амплитуда аксиальных колебаний камеры подвеса поплавка при вращении ее в подшипниках качения;
е≈Δ - односторонний осевой зазор в устройстве аксиального центрирования поплавка ГДГ, α - угол наклона оси собственного вращения к плоскости горизонта (α=0),
b1≈b2=2πμ(R2)4(cosθ1+(cosθ1)3/3)/(2v/ω1)l/2 - коэффициент сил вязкого трения поплавка b2 и камеры b1 о жидкость, причем b=b2/2,
R2 и m2 - радиус и масса поплавка, соответственно;
θ1=arccos((1/R2)(3m2/4πρ)1/3) - фактический угол свободной поверхности жидкости; μ, v и ρ - динамическая, кинематическая вязкость и плотность поддерживающей поплавок жидкости, соответственно.
Способ определения односторонних осевых зазоров, включающий частичное заполнение радиального зазора между поплавком и камерой рабочей жидкостью, обеспечивающей радиальное центрирование поплавка и практическую устойчивость подвеса в радиальном направлении, и собственное вращение подвеса поплавка гироскопа, имеет особенность такую, что
- предварительно калибруют измерительную систему, используя подвес ЧЭ ГДГ с известным осевым зазором ΔVэ,
- заливают его известным количеством жидкости AVп,
- осуществляют собственное вращение подвеса с известной скоростью ω1э,
- центрируют поплавок относительно камеры и находят параметры ΔVэ или Δtэ, которые будут использованы как эталонные, где ΔVэ - величина эталонного объема добавляемой в радиальный зазор подвеса жидкости для смещения поплавка из центра камеры, а Δtэ - время перемещении поплавка из центра камеры к одному из упоров под действием силы тяжести,
- затем центрируют поплавок относительно камеры контролируемого подвеса,
- фиксируют один из параметров: количество жидкости ΔV или время перемещения поплавка Δt в момент возникновения контакта элементов центрирующего устройства и вычисляют соответствующие одностороннему осевому зазору перемещения поплавка по заданному ΔV или определенному Δt параметру.
При калибровке измерительной системы горизонтально находят величину добавляемого эталонного объема жидкости ΔVэ на основе предварительного расчета и
- добавляют его во внутреннюю полость подвеса ЧЭ ГДГ со стороны противоположной известного эталонного осевого зазора ΔVэ, при возникновении контакта элементов центрирующего поплавок устройства удаляют из внутренней полости подвеса добавленный объем жидкости ΔVэ, уменьшают объем жидкости ΔVэ на n%, при этом n≈10% ΔVэ, и
- повторно добавляют во внутреннюю полость подвеса объем жидкости ΔVι=(100-n)ΔVэ/100 и определяют наличие или отсутствие контакта поверхностей элементов центрирующего устройства и т.д. до момента, когда после добавления известного объема жидкости ΔVι-1 будет зафиксировано отсутствие механического контакта элементов центрирующего поплавок устройства,
- в случае отсутствия контакта элементов центрирующего поплавок устройства после добавления расчетного эталонного объема жидкости ΔVэ удаляют его из внутренней полости подвеса, увеличивают объем добавляемой жидкости ΔVэ на n% и повторно добавляют объем жидкости AVι-1=(100+n)ΔVэ/100 во внутреннюю полость подвеса и определяют при этом наличие или отсутствие контакта поверхностей элементов центрирующего устройства и т.д. до момента, когда после добавления известного объема жидкости ΔVι будет зафиксирован механический контакт элементов центрирующего поплавок устройства,
- делают заключение, что объем жидкости ΔVэ, соответствующий эталонному осевому зазору ΔVэ, находится в пределах ΔVι-1<ΔVэ<ΔVι, уточняют найденную величину эталонного объема ΔVэ таким образом, что вычисляют уточняющий объем жидкости по формуле: ΔVy=(ΔVι+ΔVι-1)/2,
- повторно добавляют его во внутреннюю полость подвеса и в случае возникновения контакта элементов центрирующего поплавок устройства делают заключение, что величина эталонного объема находится в пределах ΔVι-1<ΔVэ<ΔVy,
- в случае отсутствия контакта элементов центрирующего поплавок устройства делают заключение, что величина эталонного объема жидкости находится в пределах ΔVу<ΔVэ<ΔVι, фиксируют величину эталонного объема ΔVэ из соотношений: AVι-1<ΔVэ<ΔVy или ΔVy<ΔVэ<ΔV(ι).
При калибровке измерительной системы устанавливают ось собственного вращения подвеса горизонтально,
- центрируют поплавок относительно камеры,
- устанавливают ось собственного вращения подвеса ЧЭ ГДГ вертикально таким образом, чтобы эталонный осевой зазор был ниже центра поплавковой камеры,
- определяют скорость собственного вращения подвеса ω1э и время Δtэ перемещения поплавка из центра камеры к одному из упоров устройства его механического центрирования, где установлен эталонный осевой зазор Δэ, при этом момент начала перемещения поплавка фиксируют в момент установки оси собственного вращения подвеса в вертикальное положение, конечную границу интервала времени перемещения поплавка фиксируют в момент возникновения механического контакта между элементами центрирующего поплавок устройства.
Определяют осевые односторонние зазоры таким образом, что заливают в подвес тоже количество жидкости ΔVп,
- устанавливают ось собственного вращения подвеса горизонтально, добавляют объем жидкости ΔVэ во внутреннюю полость подвеса и
- определяют наличие или отсутствие контакта элементов устройства механического центрирования поплавка,
- в случае возникновения контакта элементов центрирующего поплавок устройства удаляют из внутренней полости подвеса добавленный объем жидкости ΔVэ, уменьшают объем добавляемой жидкости ΔVэ на n%, при этом n%≈10%ΔVэ, и
-повторно добавляют объем жидкости ΔVι=(100-n)ΔVэ/100 во внутреннюю полость подвеса и определяют при этом наличие или отсутствие контакта поверхностей элементов центрирующего устройства и т.д. до момента, когда после добавления фиксированного известного объема жидкости ΔVι-1 будет зафиксировано отсутствие механического контакта элементов центрирующего поплавок устройства,
- в случае отсутствия контакта элементов центрирующего поплавок устройства после добавления эталонного объема жидкости ΔVэ, удаляют из внутренней полости подвеса добавленный объем жидкости ΔVэ, увеличивают объем добавляемой жидкости ΔVэ на n% и
- повторно добавляют объем жидкости ΔVι-1=(100+n)ΔVэ/100 во внутреннюю полость подвеса и определяют при этом наличие или отсутствие контакта поверхностей элементов центрирующего устройства и т.д. до момента, когда после добавления известного объема жидкости ΔVι будет зафиксирован механический контакт элементов центрирующего поплавок устройства,
- вычисляют величины перемещений x(ι-1), x(ι) поплавка, в соответствии с соотношениями: x(ι)=Δэ/ΔVι/ΔVэ, x(ι-1)=Δэ ΔVι-1/ΔVэ,
- делают заключение, что односторонний зазор Δ контролируемого гироскопа находится в пределах: x(ι-1)<Δ<x(ι),
- уточняют (в случае необходимости) найденную величину зазора таким образом, что вычисляют уточняющий объем жидкости из соотношения:
ΔVy=(ΔVι+ΔVι-1)/2,
- повторно добавляют его во внутреннюю полость подвеса и в случае возникновения контакта элементов центрирующего поплавок устройства делают заключение, что величина зазора находится в пределах x(ι-1)<Δ<xy, в случае отсутствия контакта элементов центрирующего поплавок устройства делают заключение, что величина зазора находится в пределах xy<Δ<x(ι),
- вычисляют уточненную величину ху осевого перемещения Х поплавка по формуле: ху=ΔэΔVy/ΔVэ и окончательно фиксируют определенную величину зазора Δ из найденных соотношений: x(ι-1)<Δ<ху или ху<Δ<x(ι).
Определяют осевые односторонние зазоры таким образом, что заливают в подвес тоже количество жидкости ΔVn, осуществляют собственное вращение подвеса с известной угловой скоростью ω1, устанавливают ось собственного вращения подвеса горизонтально,
- центрируют поплавок относительно камеры,
- устанавливают ось собственного вращения подвеса ЧЭ ГДГ вертикально,
- определяют время Δt перемещения поплавка из центра камеры к одному из упоров устройства его механического центрирования, при этом начало перемещения поплавка фиксируют в момент установки оси собственного вращения в вертикальное положение, конечную границу интервала времени перемещения поплавка фиксируют в момент возникновения механического контакта между элементами центрирующего его устройства,
- вычисляют величину одностороннего осевого зазора Δ из соотношения: Δ=Δэ(ω1э/ω1)2 Δt/Δtэ, где Δэ, ω1э - эталонная величина одностороннего зазора в устройстве механического центрирования поплавка и эталонная угловая скорость собственного вращения подвеса ЧЭ ГДГ, соответствующие эталонному времени Δtэ его аксиального перемещения.
Использование данного способа контроля ГДГ позволит решить задачу №2 данного технического решения (т.е. получить технический результат): осуществить контроль качества реализованной настройки ГДГ посредством определения его параметров и погрешностей в поле силы тяжести с учетом последующих условий эксплуатации прибора в составе динамичных движущихся объектов и для последующего машинного динамического моделирования. При этом предложенное решение может быть использовано для выяснения причин возникновения брака в изготовленных приборах, не прошедших приемосдаточные испытания. Решение обеспечит точность управления динамичными движущимися объектами за счет установки (и регулировки, если потребуется) контролируемых осевых зазоров в устройстве центрирования ЧЭ после регулировки перекрестных связей между измерительными каналами ГДГ.
Технический эффект
- в определении односторонних осевых зазоров устройства осевого центрирования поплавка и разделении на составляющие "дрейфа нулевого сигнала" ГДГ,
- в вычислении величин моментов с использованием измеренных параметров, обусловленных инструментальными погрешностями изготовления и параметров ЧЭ ГДГ их порождающих.
Найденные величины моментов и фактические параметры ГДГ предлагается использовать для оценки качества изготовления подвеса ЧЭ ГДГ и в виде входных данных для динамического моделирования на ЭВМ движений ЧЭ изготовленных ГДГ при действии угловых и поступательных входных возмущений.
Особенность решения поставленной задачи состоит в определении осевых зазоров, которое проводится после регулировки коэффициента перекрестных связей между измерительными каналами в момент окончательной настройки центрирующей части подвеса ЧЭ ГДГ, когда еще не получена нулевая аксиальная плавучесть ЧЭ ГДГ. Остальные же параметры определяются уже после проведения настройки центрирующей части подвеса ЧЭ ГДГ.
Кроме этого, технический эффект дополнительно включает
- осуществление калибровок измерительной системы для последующего определения осевых зазоров подвеса ЧЭ ГДГ;
- определение знака плавучести ЧЭ в изготовленном ГДГ посредством оценки соответствия (пропорциональности) времени аксиального перемещения поплавка и величины осевого зазора, вдоль которого поплавок перемещался;
- определение направления аксиального смещения центра масс ЧЭ ГДГ по отношению к направлению вектора кинетического момента посредством оценки изменения выходного напряжения ГДГ в горизонтальном положении до и после центрирования поплавка.
Список использованных источников:
1. Патент ФРГ №2226737. Гироскопический прибор с установленным в жидкости шаровым ротором, G 01 с 19/00. Изобретения за рубежом №13, 1974 г. (частичная заливка, устройство центрирования поплавка).
2. Горенштейн И.А. Гидродинамические гироскопы. Москва. Машиностроение, 1972 г (аналог, съем сигнала с поплавка стр. 10, 11, 104, 105).
3. Андрейченко К.П. Динамика поплавковых гироскопов и акселерометров. Москва, Машиностроение, 1987, (прототип способа подвеса с.7, глава 6).
4. Андрейченко К.П., Иващенко В.А., Смарунь А.Б. Динамика поступательного движения чувствительного элемента гидродинамического гироскопа с частичным заполнением камеры рабочей жидкостью. Рукопись (Саратовский политехнический институт. - Саратов, 1987. - деп. 13.01.88 в ВИНИТИ №187-В88).
5. Андрейченко К.П., Смарунь А.Б. Об эффекте возникновения аксиальной инерционной движущей силы в сферической гидродинамической опоре. (Саратовский политехнический институт. - Саратов, 1983. - деп. в ВИНИТИ №3937 В83).
6. Андрейченко К.П., Иващенко В.А., Смарунь Экспериментальные исследования динамики движения поплавка в сферическом гидродинамическом подвесе при ускоренном аксиальном перемещении камеры. (Саратовский политехнический институт. - Саратов, 1987. - деп. 13.01.88 в ВИНИТИ №165-В88).
Изобретение относится к области гироскопической техники и может быть использовано для контроля подвеса сферического поплавка в сферической камере гидродинамического гироскопа (ГДГ). При контроле ГДГ разделяют на составляющие сигнал прибора при отсутствии внешних угловых и поступательных возмущений. Определение осевых зазоров в устройстве центрирования чувствительного элемента ГДГ осуществляется посредством аксиального перемещения его при искусственном формировании разности давлений жидкости в торцевых частях радиального зазора и по времени аксиального его перемещения из центра камеры вдоль определяемого зазора. Техническим результатом является возможность контроля качества изготовления ГДГ с учетом последующих условий эксплуатации. 2 с. и 6 з.п. ф-лы, 1 ил.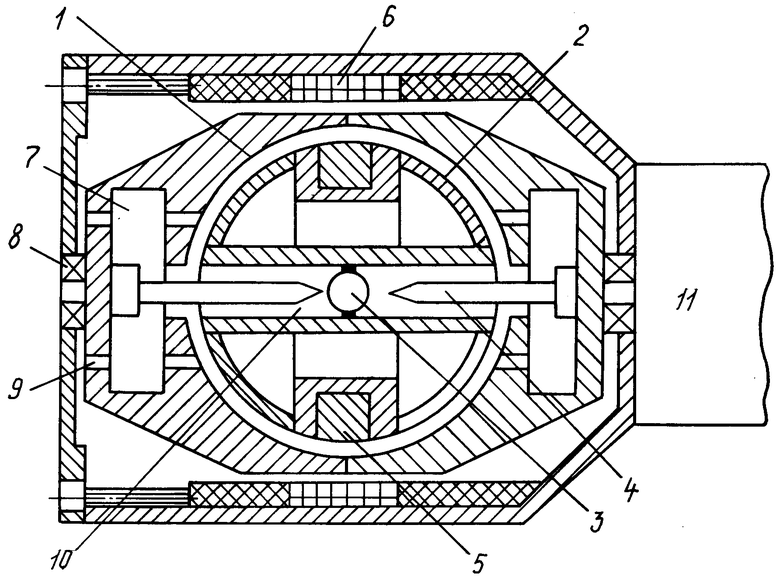
U(θ*)=(Uo+U1o)/2; U(d)=|Uo2-Uo|,
в противном случае дополнительно устанавливают ось собственного вращения подвеса негоризонтально, следят за изменением выходного нулевого сигнала до момента возникновения контакта элементов центрирующего устройства, затем устанавливают ось собственного вращения горизонтально и измеряют выходное напряжение Uo1*, вычисляют составляющие инструментальных погрешностей по формулам
U(θ*)=(Uo+U1o)/2; U(Δm)=|Uo1*-Uo2|; U(d)= |Uo2-Uo|,
где U(θ*) - величина нулевого сигнала гироскопа, обусловленная радиальным смещением центра масс поплавка относительно его геометрического центра;
U(Δm) - величина «нулевого сигнала» гироскопа, обусловленная остаточной ненулевой плавучестью поплавка;
U(d) - величина «нулевого сигнала» гироскопа, обусловленная аксиальным смещением центра масс относительно его геометрического центра,
затем определяют знак плавучести чувствительного элемента (ЧЭ) ГДГ, направление аксиального смещения центра масс ЧЭ ГДГ по отношению к направлению вектора кинетического момента, вычисляют величину возмущающих моментов, обусловленных инструментальными погрешностями ГДГ, затем определяют параметры ГДГ на подвижном основании.
вычисляют величину отклоняющего поплавок момента М(Δm), обусловленного остаточной ненулевой плавучестью поплавка Δm и ее величину по формулам M(Δm)=(U(Δm)/Kcc)*(b1 ω1); Δm=U(Δm)*b1*ω1/Kcc g e cosα, вычисляют величину момента M(d), обусловленного аксиальным смещением центра масс d и его величину по формулам M(d)=(U(d)/Kcc)(b1*ω1); d=(U(d)/Kcc)(b1*ω1)/(2*m2*g), где b1 - коэффициент момента сил вязкого трения поплавка (камеры) о жидкость; ω1 - измеренная скорость вращения подвеса поплавка; g - ускорение силы тяжести;
Ксс - коэффициент передачи системы съема сигнала с подвеса ЧЭ ГДГ;
Е - амплитуда аксиальных колебаний камеры подвеса поплавка при вращении ее в подшипниках качения;
е≈Δ - односторонний осевой зазор в устройстве аксиального центрирования поплавка ГДГ,
α - угол наклона оси собственного вращения к плоскости горизонта (α=0),
b1≈b2=2πμ(R2)4(cosθ1+(cosθ1)3/3)/(2v/ω1)l/2 - коэффициент сил вязкого трения поплавка b2 и камеры b1 о жидкость, причем b=b2/2,
R2 и m2 - радиус и масса поплавка соответственно;
θ1=arccos((1/R2)(3m2/4πρ)1/3) - фактический угол свободной поверхности жидкости; μ, v и ρ - динамическая, кинематическая вязкость и плотность поддерживающей поплавок жидкости соответственно.
| ГИДРОДИНАМИЧЕСКИЙ ГИРОСКОП | 2002 |
|
RU2217700C1 |
| АНДРЕЙЧЕНКО К.П | |||
| Динамика поплавковых гироскопов и акселерометров, М., Машиностроение, 1987, с.7, 87-104 | |||
| ГИДРОДИНАМИЧЕСКИЙ ГИРОСКОП | 1995 |
|
RU2116623C1 |
| Способ определения изменения параметров маятникового поплавкового компенсационного акселерометра | 1990 |
|
SU1755205A1 |
| US 4451990 A, 05.06.1984 | |||
| JP 61237011 А, 22.10.1986 | |||
| US 6557392 B1, 06.05.2003 | |||
| МАГНИТОГИДРОДИНАМИЧЕСКИЙ СПОСОБ ПРЕОБРАЗОВАНИЯ ТЕПЛОВОЙ ЭНЕРГИИ В ЭЛЕКТРИЧЕСКУЮ ЗАМКНУТОГО ЦИКЛА | 2002 |
|
RU2226737C2 |
| ПРЕОБРАЗОВАТЕЛЬ ВЛАЖНОСТИ ГАЗОВ | 1987 |
|
SU1492919A1 |
Авторы
Даты
2005-12-20—Публикация
2004-04-23—Подача