Изобретение относится к полигонным испытаниям образцов вооружения и военной технике, контролю за полетом ракетно-космической техники на космодромах и может быть использовано при определении параметров движения цели (объектов наблюдения, испытания, контроля) по данным оптико-электронных (оптических) средств траекторных измерений.
При определении пространственных координат цели используется информация, полученная с оптических траекторных средств, положение точек стояния которых считаются известными. При этом, как правило, положение точки стояния каждого траекторного средства задается в виде геодезических координат: широты (В), долготы (L) и высоты (Н). Указанные координаты определяют i-местную измерительную систему координат (СК) данного i-траекторного средства: ось Оi Xi лежит в плоскости местного меридиана и горизонта (обычно направлена на Север), ось Оi Yi направлена по нормали к земному эллипсоиду вверх, а ось Oi Zi дополняет систему до правой. Начало i-СК в случае использования оптического траекторного средства совмещается с главной точкой объектива.
Кроме совокупности подобных местных измерительных систем, связанных с точками стояния траекторных средств и участвующих в совместных измерениях (цель находится в зоне их видимости), используется еще некоторая общая СК (О Х У Z), начало которой совмещено, например, с точкой старта. В этой СК ось О Х лежит в плоскости местного горизонта и направлена относительно местного меридиана под углом Ao (например, азимута стрельбы). Ось О У направлена вверх и О Z дополняет СК до правой. Тогда все расчеты пространственных координат цели выполняются в стартовой СК известными способами (см., например, Жданюк Б.Ф. Основы статистической обработки траекторных измерений. - М.: Сов. радио. 1978. - 384 с., ил. с.57-66).
Аналогом заявляемого изобретения может служить так называемый пеленгационный способ определения пространственных координат цели по данным оптической траекторией информации с двух и более средств измерений, разнесенных на местности. Положение цели в пространстве в этом случае определяется как точка пересечения n-линий визирования, где n - число оптических траекторных средств, задействованных в измерениях. При этом каждая линия визирования в пространстве определяется азимутом (α) и углом места (β), где α, β - измеренные угловые координаты цели с соответствующего оптического средства.
Для измерения угловых координат цели каждое оптическое средство горизонтируют и внутреннюю систему отсчета ориентируют относительно местных меридиана и горизонта, используя, например, геодезические опорные точки (вехи).
Под опорными точками здесь понимаются точки с известными направлениями в пространстве (например, задаваемые значениями азимута и угла места) относительно местной измерительной СК, совмещенной с точкой стояния оптического средства (главной точкой объектива). Иными словами, используя опорные точки, формируют высокоточные системы ориентации для каждого оптического средства относительно осей "своей" местной измерительной системы координат.
Точность измеряемых угловых координат цели в значительной степени зависит от точности оценок положения опорной СК относительно осей измерительной системы координат. Кроме этого, также необходимо знать с достаточной точностью и ряд других элементов ориентирования: численного значения фокусного расстояния оптического средства, положение оптического центра на кадре и т.д. В итоге при реализации подобных измерений требуется проведение всякого рода юстировочных, оценочных и геодезических работ. Эти особенности затрудняют широкое использование пеленгационного способа измерений особенно с временных пунктов и в необорудованных районах.
Ближайшим аналогом к изобретению является способ измерения цели на фоне опорных точек (см. Лобанов А.Н. Фотограмметрия. Издание второе. М.: Недра, 1984, с.61-64). В полигонной практике этот способ часто применяется при измерениях с помощью широко-польных баллистических камер типа фоторегистрирующей станции "Дятел" с полем зрения 25°×25°.
Сущность способа заключается в следующем.
Перед регистрацией цели каждое оптическое средство горизонтируется и с помощью геодезических (наземных) опорных точек ориентируется относительно осей местной измерительной СК. По данным целеуказаний каждое оптическое средство наводится на предполагаемый район появления цели. Регистрация цели выполняется, например, на фоне звезд.
После регистрации цели и звезд проводится обработка полученных кадров с данной информацией. Сначала выполняются измерения изображений цели и звезд в картинной СК, две оси которой лежат в плоскости кадра, а третья перпендикулярна этой плоскости и проходит через центр кадра. Измеренные картинные координаты звезд и данные ориентации оптического средства относительно осей местной измерительной СК используются затем для опознания звезд, изображение которых получено в кадре, с каталогом. Далее, используя картинные и каталожные координаты опознанных звезд, выполняется уточнение элементов ориентирования данного оптического средства. И, наконец, с учетом вычисленных элементов ориентирования и измеренных картинных координат цели выполняется вычисление их угловых координат, по которым затем определяются пространственные координаты цели. Определение пространственных координат цели может быть реализовано, например, точно так же, как и в пеленгационном способе.
Основным недостатком данного способа является зависимость применения способа от времени суток и величины установочных углов. Возможная регистрация звезд выполняется только в сумеречное или ночное время. Кроме этого, установочные углы (в основном - по углу места) также определяют эффективность регистрации цели на фоне звезд. Так, при установочном угле по месту, равном и менее 10°, число зарегистрированных звезд не превысит 3-5 с расположением в верхней половине кадра. Такое количество звезд является недостаточным для эффективного использования способа в целях повышения точности определения угловых координат цели, а значит и их пространственных координат.
Целью изобретения является упрощение процесса измерения за счет исключения из регистрации и обработки опорных точек и разработка способа обработки измерений, полученных в этих условиях.
Указанная цель достигается тем, что каждое оптическое средство, привлекаемое к измерениям по данному объекту наблюдения, ориентируют произвольно относительно плоскости местного меридиана (по азимуту). Что касается ориентирования относительно плоскости местного горизонта, то выполняется грубое ориентирование с погрешностью до пяти угловых минут от фактического значения установочного угла по углу места. В этом случае используются упрощенные способы ориентирования по углу места. К ним можно отнести ориентирование по Полярной звезде при работах в сумеречное и ночное время, по уровню - с определением предварительно место нуля (место зенита) в любое время суток и т.д. Ниже рассматривается аргументация по оценке ориентации по углу места с погрешностью до 5 угл. мин.
Главное в этой ситуации сохранить начальную ориентацию каждого оптического средства неизменной на время сеанса измерений.
Проблема наведения разрешается достаточно просто. Так, для района старта момент запуска (стрельбы) фиксируется на удалении десятков километров от старта и всегда имеется возможность ручного наведения на объект наблюдения (цель). Кроме этого, существующие современные узкоугольные оптические средства имеют обзорный канал с полем зрения 6°...10°, что позволяет осуществлять поиск и наведение узкоугольного измерительного канала на цель предварительно с использованием целеуказаний и, например, компаса. Что касается широкопольных средств (поле зрения 20°×20° и более) наведение на объект наблюдения может быть осуществлен с погрешностью 2°...5° по целеуказаниям с помощью компаса.
Что касается районов падения, то проблема наведения для современных существующих узкоугольных средств также может быть решена при наличии обзорного канала с использованием целеуказаний и компаса.
Для широкопольных средств наведение на предполагаемый район появления объекта наблюдения с погрешностью в несколько градусов с помощью целеуказаний и компаса, является достаточным, чтобы обеспечить регистрацию цели.
После того, как будет реализовано произвольное ориентирование каждого оптического средства указанным выше образом, выполняется наведение на цель (на район появления объекта наблюдения) с использованием, например, целеуказаний и компаса. Регистрация цели выполняется при выбранной таким образом ориентации каждого оптического средства, которая должна быть неизменной на все время сеанса измерения.
После дешифрирования результатов регистрации цели выполняется измерение ее картинных координат в системе координат, две оси которой лежат в плоскости кадра, а третья перпендикулярна этой плоскости и проходит через центр кадра. Обычно центр кадра считается совмещенным с оптическим центром. Тогда, имея измеренные картинные координаты цели и угловые координаты оптической оси (центра кадра), вычисляются угловые координаты цели. Вычисленные таким образом угловые координаты цели с каждого оптического средства будут смещены относительно каждой своей измерительной СК на неизвестные поправки по азимуту и углу места. Однако именно указанные данные являются той исходной информацией, которую используют для вычисления пространственных координат цели.
Отметим здесь, что обработка полученной таким образом информации выполняется по относительным измерениям, полученным для каждой выбранной пары точек по времени на измеренной траектории в виде разностей измерений соответствующих параметров. Например, при траекторных оптических измерениях в качестве исходной информации для вычисления координат цели на моменты измерения t1, t2 используются значения Δα1-2=α1-α2, Δβ1-2=β1-β2, где α1, β1 - измеренные угловые координаты с данного оптического средства на момент измерения по времени t1, а α2, β2 - на момент t2.
Заметим здесь, что благодаря использованию относительных измерений и удается исключить в основном погрешности ориентирования каждого оптического средства относительно "своей" местной измерительной СК.
При обработке с использованием относительных измерений координаты цели и оценки точности их определения вычисляют сразу на два выбранных момента (t1, t2) при условии, что число измеренных параметров цели равно или больше числа определяемых координат цели на два выбранных момента времени. В данном случае число измеренных параметров должно быть равно или больше 6 (t1, X1, Y1, Z1 и t2, X2, Y2, Z2). При измерениях только угловых координат (направляющих косинусов) достаточное число разнесенных на местности измерительных средств равно трем (3×2=6), а при дальномерно-угломерных измерениях достаточное число средств равно двум (2×3=6). Что касается оценки точности, то их значения вычисляются с учетом диагональных элементов ковариационной матрицы определяемых координат, которая вычисляется также на два выбранных момента времени.
Обработка полученной измерительной информации для вычисления координат цели выполняется в два этапа.
На первом из них вычисляются предварительные координаты цели, которые выбираются из результатов решения оптимальной комбинации. Каждая комбинация есть результат решения по относительным измерениям на две временные точки, первая из которых есть измерения на данную искомую временную точку, а измерения на вторую временную точку при решении очередной комбинации подставляются каждый раз поочередно из всей совокупности измеренных временных точек на траектории по каждому оптическому средству, начиная с первой и исключая данную искомую точку. При решении каждой комбинации вычисляются как координаты цели на две временные точки, так и элементы ковариационной матрицы определяемых координат, но выбор выполняется только на искомую точку (условно на t1). Оптимальной считается такая комбинация, для которой значение следа ковариационной матрицы определяемых координат искомой точки (сумма диагональных элементов ковариационной матрицы применительно к искомой точке, т.е. условно на t1) будет наименьшим из всех значений следов остальных комбинаций.
Значение следа оптимальной комбинации и координаты цели на второй выбранной момент в данной паре (условно на t2) сохраняются и затем используются для окончательного вычисления координат цели и их оценок точности.
Вычисленные таким образом предварительные координаты всех временных точек на измеренной траектории затем используются для вычисления невязок по каждому измеренному параметру каждого оптического средства. Величина каждой расчетной невязки есть разность между измерением на данный временной момент и значением целеуказаний на этот же момент времени. Значения целеуказаний на этот выбранный момент времени рассчитываются с учетом уже вычисленных предварительных координат цели (на этот момент времени) и координат точки стояния соответствующего оптического средства. Затем выполняется суммирование полученных невязок на интервале измерений и вычисление средних арифметических значений по каждому параметру каждого оптического средства. Здесь значения средних арифметических невязок рассматриваются как апостериорные погрешности измерений каждого параметра каждого оптического средства.
На заключительном этапе выполняется окончательный расчет координат цели и их оценок точности каждой измеренной точки по времени. При этом расчеты также выполняются по относительным измерениям на каждый искомый временной момент путем поиска такого положения в пространстве координат второй точки в комбинации с данной искомой точкой, которое обеспечило бы глобальный минимум следа ковариационной матрицы определяемых координат искомой точки. Поиск такой точки начинается с координат второй точки из оптимальной комбинации искомой точки, которая принимается за начальную точку, относительно которой выполняется построение сетки в виде плоских квадратов. Размеры квадрата определяются величиной задаваемого шага построения сетки (например, величиной Δ). При этом принимают координаты начальной точки за центр первого квадрата, а координаты каждой вершины вычисляют следующим образом. Во-первых, принимают ординату (Y) центра первого квадрата постоянной во всех дальнейших расчетах, связанных с данной искомой точкой (Y=const).
Зная значение шага построения сетки Δ (значение Δ в процессе обработки по данной искомой точки изменяется по определенному правилу) координаты каждой вершины вычисляются следующим образом:
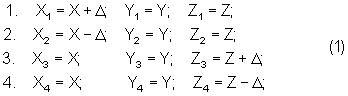
где 1, 2, 3, 4 - условные номера вершин квадрата;
X, Y, Z - координаты центра квадрата;
Δ - заданное (текущее) значение шага построения сетки.
Вычисленные таким образом координаты каждой вершины квадрата затем используются для вычисления параметров целеуказаний для каждого оптического средства с использованием координат точки стояния их в некоторой СК (например, стартовой СК). Полученные параметры целеуказаний затем преобразуют в фиктивные измерения путем суммирования параметров вычисленных целеуказаний с соответствующими средними арифметическими невязками, вычисленными с использованием предварительных координат цели, выбранных по результатам решения оптимальных комбинаций.
Полученные фиктивные измерения каждой вершины квадрата затем подставляются как измерения вторых точек в комбинации с измерениями искомой точки. В результате этих решений вычисляются координаты и значения следа ковариационной матрицы определяемых координат искомой точки, из которых выбирают значения координат искомой точки с наименьшим значением следа. В свою очередь, выбранное наименьшее значение следа сравнивается со значением следа центра квадрата. Так для первого квадрата значения координат центра и следа выбираются из оптимальной комбинации данной искомой точки при расчете предварительных координат.
Если полученное значение следа будет меньше следа для точки центра квадрата, то координаты соответствующей вершины принимаются за новый центр квадрата, вычисляются координаты 4-х вершин нового квадрата, вычисляются параметры целеуказаний для каждой из вершин, выполняется преобразование их в фиктивные измерения и вычисления в паре с измерениями искомой точки - координат искомой точки и значений следа. Затем путем сравнения определяют одну из вершин квадрата с наименьшим значением следа и сопоставляют со значением следа центра данного квадрата. Если это значение следа одной из вершин квадрата окажется меньше следа центра данного квадрата, то продолжаются вычисления координат вершин нового квадрата, преобразования и сравнения.
В противном случае выполняется уменьшение шага построения сетки, например, в два раза и продолжают аналогичные вычисления с новым шагом (текущим значением) и координатами последнего центра квадрата перед уменьшением шага. Продолжают вычислять координаты вершин нового квадрата с новым шагом, формировать фиктивные измерения, проводить все необходимые вычисления и сравнения. Указанный процесс продолжают до тех пор, пока шаг не станет меньше заданной величины. Тогда за окончательные значения координат искомой точки принимаются такие значения, которые получены последними с наименьшим значением следа ковариационной матрицы определяемых координат искомой точки.
Указанным образом выполняется расчет окончательных значений координат цели и оценок точности их определения последовательно всех измеренных точек на траектории.
Рассмотрим реализацию способа на примере регистрации цели оптическими траекторными средствами, размещенными на измерительных пунктах (ИП), которые разнесены на местности.
Каждое оптическое средство горизонтируют, а затем ориентируют произвольно относительно плоскости местного меридиана (по азимуту), а в плоскости местного горизонта - с погрешностью по абсолютной величине не более пяти угловых минут от фактического значения установочного угла по углу места (установка нуля угломестного датчика). В этом случае для ориентации в плоскости местного горизонта могут быть использованы упрощенные приемы. Например, в ночное время может быть использована Полярная звезда, что обеспечивает установку относительно плоскости горизонта с погрешностью порядка 1,0...1,5 угл.мин. Днем для этих целей можно использовать Солнце или при визировании на любой удаленный предмет определяют место нуля (место зенита) оптического средства, а затем угол места на данный предмет, установка значения которого на угломестный датчик позволяет обеспечить ориентирование в плоскости местного горизонта с погрешностью порядка 1...3 угл.мин.
После указанных подготовительных операций каждое оптическое средство визируют в район предполагаемого появления цели. Для этого могут быть использованы, например, параметры целеуказаний и компас.
После регистрации объекта наблюдения всеми оптическими средствами выполняются измерения картинных координат цели (х, у).
Располагая измеренными картинными координатами цели (х, у) на момент времени t и установочными углами (αо, βо), достаточно просто вычисляются угловые координаты цели на момент t по известным соотношениям:
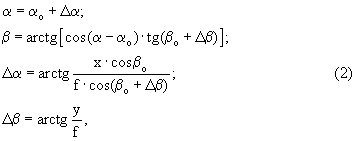
где f - фокусное расстояние оптического средства.
Соотношения (2) и их анализ позволяют сделать вывод о возможности произвольного ориентирования оптического средства в плоскости местного меридиана (по азимуту) при переходе на обработку относительных измерений. Так, например, разность измеренных азимутов на моменты t2 и t1 будет равна:
Δα2-1=(αо+Δα2)-(αо+Δα1)=Δα2-Δα1.
Что касается ориентирования относительно местного горизонта (по углу места) основной вклад за счет отклонения установочного угла по месту от фактического приходится на долю параметра Δα (имеется ввиду итоговая погрешность в Δα). В величине Δβ=β2-β1 такая погрешность в 3...6 раз меньше, чем в Δα.
Принятая величина погрешности отклонения установочного угла места от фактического на уровне 5 угл. мин в итоге обеспечивает погрешность, равную примерно 1/3 от паспортной погрешности данного оптического средства с фокусным расстоянием от f=100 мм до f=500...600 мм. Что касается длиннофокусных средств с f=1000 мм и более допустимая величина отклонения установочного угла по месту от фактического может составить уже 10 угл.мин. В этом случае погрешность в Δα не превысит 6...8 угл.с при измерениях по углу места до 50° - (паспортная погрешность до 25...30 угл.с). Величина погрешности в Δβ не будет превышать 2...3 угл.с.
После вычисления угловых координат цели с использованием соотношений (2) будем располагать следующей информацией:

где m - число измеренных точек на траектории.
Располагая указанной исходной информацией, выполняются вычисления предварительных координат цели, сущность которого сводится к следующему.
Итак, пусть измерения представлены в виде (3). Известны также средние квадратические погрешности измерений с каждого ИП (например, паспортные σαi, αβi) и координаты точек их стояния в выбранной общей системе координат (Xoi, Yoi, Zoi, где 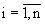 , n - число средств в обработке). Вычисление координат точек стояния каждого оптического средства в общей СК с использованием их геодезических координат выполняется по известным соотношениям (см., например, Жданюк Б.Ф. Основы статистической обработки траекторных измерений. - M.: Сов. Радио, 1978, - 384 с., ил., с.193-201).
, n - число средств в обработке). Вычисление координат точек стояния каждого оптического средства в общей СК с использованием их геодезических координат выполняется по известным соотношениям (см., например, Жданюк Б.Ф. Основы статистической обработки траекторных измерений. - M.: Сов. Радио, 1978, - 384 с., ил., с.193-201).
С ИП-1 на моменты t1 и t2 массива (3) выбраны угловые координаты цели в виде:

Переходя к новому типу измерений, которые здесь определены как относительные, будем иметь на Δt=t2-t1:
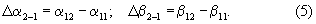
Известна функциональная связь между измеренными угловыми координатами и координатами цели в общей СК - X, У, Z, которую представим в следующем виде (нижние индексы частично опущены), например, для ИП-1:
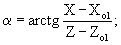
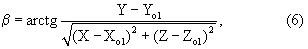
где X01, У01, Z01 - координаты точки стояния измерительного средства на ИП-1;
X, У, Z - координаты цели на фиксированный момент измерения.
Тогда выражение (5) представим следующим образом:
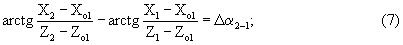
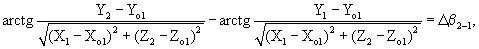
где X1, Y1, Z1, X2, Y2, Z2 - координаты цели на моменты измерения t1 и t2.
Зная приближенные значения координат цели, разложим в ряд Тейлора выражение (7) и, ограничиваясь производными первого порядка, получим следующие уравнения поправок:
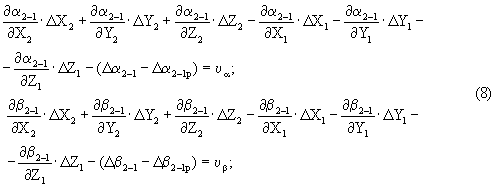
где ΔX1, ΔY1, ΔZ1, ΔX2, ΔY2, ΔZ2 - поправки к приближенным значениям координат цели на t1 и t2;
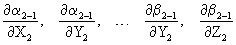 - частные производные от относительных измерений по оцениваемым параметрам;
- частные производные от относительных измерений по оцениваемым параметрам;
υα, υβ - соответствующие поправки.
Частные производные вычисляются с использованием следующих соотношений:
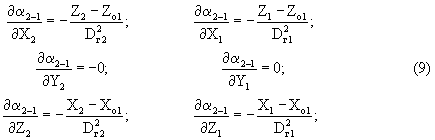
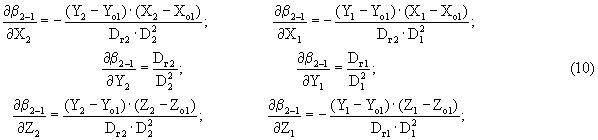

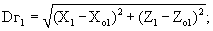
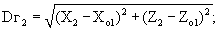
Расчетные значения Δα2-1p, Δβ2-1p вычисляются с учетом оцениваемых координат, полученных в предыдущем сближении.
Аналогичные уравнения получаем по измерениям на моменты t1 и t2 с других измерительных средств.
Поскольку известны приближенные значения координат в точках t1 и t2, то решение выполняется по способу наименьших квадратов под условием:
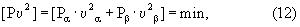
где Pα, Pβ - соответствующие веса относительных измерений, равные

с - некоторая выбранная постоянная;
[•] - символ Гаусса, означающее суммирование по всем измерениям на t1, t2.
С учетом того, что уравнения поправок (8) содержат 6 неизвестных и каждое измерение дает одно уравнение, то для решения достаточно 6 измерений на t1, t2. Иными словами, достаточными при оптических измерений следует считать измерения с 3-х точек (ИП, средств измерения, разнесенных на местности).
Если, к примеру, выполняются дальномерно-угломерные измерения (например, каждое измерительное средство выполняет измерения дальности и угловых координат), то достаточным будет измерения с 2-х ИП (тоже 6 измеренных параметров). Помимо уравнений поправок по углам (см. (8)) в этом случае добавляется уравнение поправок по дальности, имеющее следующий вид:
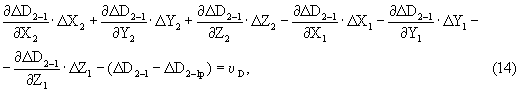
где 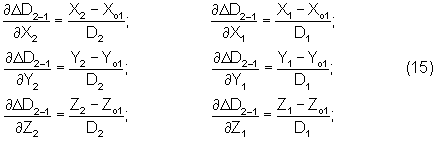
D2 и D1 - измеренные дальности на t2, t1.
Значение ΔD2-1p вычисляется с учетом оцениваемых координат, полученных в предыдущем сближении.
Оценка точности выполняется стандартно с использованием вычисленных элементов ковариационной матрицы определяемых координат (на t2, t1):

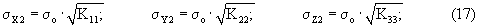

К11, К22, ..., К66 - диагональные элементы ковариационной матрицы;
[Pυ2]=[Pα·υ2 α+Pβ·υ2 β] - сумма средневзвешенных невязок.
Если выполняются достаточные измерения (на моменты t1 и t2 измеряется 6 параметров), то принимается σo=1.
При практической реализации предлагаемого способа обработки относительных траекторных измерений следует обратить внимание на то обстоятельство, что величина выбранного временного интервала обработки (Δt=tk-tн, где tk, tн - время конца и начала интервала измерений) играет в определенном смысле ключевую роль при оценках точности результатов решения - чем больше интервал Δt, тем "выше" точность определяемых координат цели. Ниже затем уточним данное утверждение.
Отсюда вполне логичным является вариант решения с перебором некоторых комбинаций по времени и выбора из них оптимальной комбинации с использованием некоторого численного критерия. При этом, чем дальше точки друг от друга, тем точнее может быть результат решения.
В упрощенном виде (алгоритмически реализуется проще) перебор в нашем случае представляет собой совокупность комбинаций, каждая из которых есть свой интервал по времени (Δt). При этом первая точка (по времени) является очередной в интервале измерений, а вторая - текущая - поочередно подставляемая из данного интервала измерений. Если, например, интервал измерений включает в себя точки t1, t2, t3, то выполняется обработка измерений по следующим комбинациям: t1, t2; t1, t3. Из комбинаций выбирается оптимальная по заданному критерию, в результате чего будем в итоге располагать следующими оценками: t1, X1, Y1, Z1, σХ1, σY1, σz1. В этом случае из результатов решения выбираются данные условно на t1, хотя сразу вычисляются координаты и второй точки. После выполнения операций с первой точкой (условно t1) выбираются измерения очередной точки, выполняется формирование комбинаций (t2, t1; t2, t3) и решение каждой, выбор оптимальной и на этой основе выбор очередных оценок и т.д.
Что касается численной величины критерия, то здесь целесообразно выбрать след ковариационной матрицы на точку условно t1, который представляет собой объем эллипса ошибок определяемых координат (сумма диагональных элементов ковариационной матрицы - дисперсий определяемых координат на момент условно t1). Тогда оптимальной будет та комбинация, для которой сумма дисперсий (след ковариационной матрицы) определяемых координат будет наименьшей (наибольшая точность определяемых координат цели условно на t1).
Как следует из предлагаемой схемы обработки, для решения необходимо знать приближенные значения координат в точках условно t1, t2 (как начальные условия).
Как показывают результаты исследований на моделированной информации, решение устойчиво обеспечивается при задании начальных условий в диапазоне ±10...12 км от фактических значений координат. В принципе после решения первой комбинации (условно на t1, t2) полученные значения координат могут быть использованы для решения следующей комбинации условно на t1, t3. В этом случае расчетные значения координат условно на t2 подставляются для решения в комбинации условно на t3 (в комбинации t1, t3). При этом разница Δt=t3-t1 не должна превышать 2...3 с. В качестве начальных условий могут быть выбраны также координаты ЛА из расчетных моделей движения.
Еще раз вернемся к "связке" значения выбранного интервала измерений Δt и точности получаемых результатов решения.
Надо отметить, что значение временного интервала (Δt) не совсем точно отражает функциональную связь с точностью определяемых параметров. Например, при пролетных траекториях и близких расстояний измерителя от траектории контролируемого объекта (несколько сот метров и километров) его регистрация может составить всего несколько секунд. В то же время обработка таких результатов измерений позволяет, в основном, получить оцениваемые параметры с высокой точностью.
В общем случае целесообразно говорить относительно точности определяемых параметров в "связке" с величинами углового расстояния между линиями визирования на крайние точки (первая и последняя) регистрируемой траектории для каждого измерительного средства. Например, при измерениях угловых координат цели величина углового расстояния (ω) может быть определена следующим образом (на моменты 1 и k):
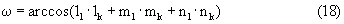
где l, m, n - направляющие косинусы соответственно первой и последней точек измерений на траектории цели для данного оптического средства (нижние индексы опущены):
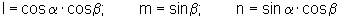
α, β - соответственно азимут и угол места.
Как показали проведенные исследования с использованием моделированной информации, вполне приемлемые результаты по точности определяемых координат (соответствующие измерениям) могут быть получены при ω>25°.
При увеличении углового расстояния (примерно ω˜40...100°) заметно уменьшается значение величины следа ковариационной матрицы, а значит повышается точность определяемых координат цели.
В результате обработки траекторных измерений указанным способом будут получены координаты цели (X, Y, Z) и оценки точности их определения:
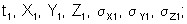
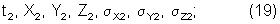
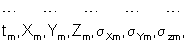
На фиг.1, 2 приводятся оценки отклонений расчетных координат, вычисленных при обработке относительных измерений, от эталонных. Расчетные значения координат получены по результатам обработки моделированной информации.
Моделирование измерений выполнялось для трех оптических средств (ИП-1, 2, 3) на интервалах по времени Δt=21 с и по высоте: 53 км ...8 км. Фокусное расстояние принималось равным ˜400 мм. ИП-1, 2 размещались примерно в створе и перпендикулярно плоскости стрельбы с перелетом от точки падения. ИП-3 размещался примерно параллельно плоскости стрельбы влево и с недолетом до точки падения. На интервале измерений наклонные дальности составляют соответственно с высотой: ИП-1: 127...24 км; ИП-2: 145...44 км; ИП-3: 107...74 км.
Измерения моделировались с шагом h=1 с в двух вариантах.
В первом варианте ориентирование каждого оптического средства относительно местных меридиана и горизонта выполнялось с помощью установочных углов (αo, βo).
Вначале были вычислены картинные координаты цели при заданных фактических углах установки (αоф, βоф). Затем ориентирование относительно местных меридиана и горизонта принималось равными:
для ИП-1: αо1=αоф1+100°;
βо1=βоф1+4 мин 36 с;
для ИП-2: αo2=αоф2+200°;
βо2=βоф2+4 мин 42 с;
для ИП-3: αо3=αоф3+300°;
βо3=βоф3+4 мин 12 с,
где αo1, βo1,...; αо3, βо3 - установочные углы при измерениях по цели;
αоф1, βоф1,..., αоф3, βоф3 - фактические значения установочных углов;
1000, 200°, 300° - принятые погрешности ориентирования по азимуту в данном варианте.
С использованием значений αo1, βo1,..., αо3, βо3 и картинных координат (х, у) по соотношениям (2) рассчитывались значения угловых координат (α, β) цели для каждого оптического средства, на которые затем "накладывались" погрешности измерений, рассчитываемых по правилу
Δα(Δβ)∈N(0; 30 угл.с).
Для второго варианта моделирование информации выполнялось тем же путем с заменой знака принятых погрешностей ориентирования с плюса на минус. После вычисления угловых координат цели погрешности измерений учитывались по правилу
Δα(Δβ)∈N(0; 10 угл.с).
Кроме этого, для решения классическим (существующим) способом (обработка с использованием измеренных угловых координат цели) моделирование угловых координат цели в этом случае выполнялось с учетом фактических значений установочных углов (αоф1, βоф1,..., αоф3, βоф3), картинных координат (х, у) и наложением погрешностей измерений по правилу: Δα(Δβ)∈N(0; 10 угл.с).
На фиг.1 приведены результаты решения, полученные при обработке относительных измерений (предлагаемый способ обработки) с σαβ=30 угл.с. При этом приводятся оценки отклонений предварительных значений координат от эталонных (выборка из результатов решения оптимальных комбинации) (фиг.1а) и окончательных значений координат от эталонных (фиг.1б). Представленные данные фиг.1 позволяют сделать вывод об эффективности использования двух этапов при расчете координат цели в случае обработки относительных измерений.
На фиг.2 приведены сравнительные оценки отклонений расчетных координат от эталонных в зависимости от способа обработки (обработка относительных измерений и классический способ - обработка измерений угловых координат) с σαβ=10 угл.с.
При анализе представленных данных фиг.2 следует заметить, что при обработке угловых координат (классический способ - см. фиг.2б) в измерениях отсутствуют погрешности ориентирования при наличии только погрешностей измерений. При обработке предлагаемым способом (обработка относительных измерений - см. фиг.2а) в измерениях присутствуют как погрешности измерений, так и остаточные погрешности ориентирования. Последние погрешности вызваны за счет отклонения установочного угла по месту относительно фактического значения угла места. Указанное отклонение, как отмечалось выше, приводит к появлению остаточной погрешности, величина которой не превышает 1/3 от паспортной погрешности измерений данного оптического средства.
Средние квадратические погрешности определения координат цели при обработке относительных измерений приводятся на первую и последнюю точки измеренной траектории при σо=1:
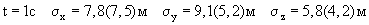
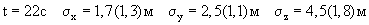
В скобках приводятся оценки точности определения координат при обработке угловых координат (классический способ обработки).
Таким образом, анализ данных, представленных на фиг.1, 2, показывает, что предлагаемый способ определения координат цели, получаемых в процессе обработки относительных измерений, является работоспособным и позволяет получать удовлетворительные результаты при полном отсутствии регистрации опорных точек. В этом случае ориентирование оптического средства относительно местных меридиана и горизонта выполняется произвольно - по азимуту и в пределах 5 утл.мин - по углу места.
Кроме этого, обработка относительных измерений позволяет также уменьшить влияние постоянных погрешностей, сопровождающих измерения угловых координат цели. В частности, для оптических траекторных измерений к таким погрешностям относятся:
- погрешности определения и учета поправок за коллимацию (отклонение от перпендикулярности визирной оси и горизонтальной оси вращения оптического средства);
- погрешности, обусловленные наклоном вертикальной оси вращения оптического средства от нормали к плоскости местного горизонта;
- погрешности, обусловленные наклоном горизонтальной оси вращения оптического средства к плоскости местного горизонта;
- погрешности учета поправок за рефракцию и т.д.
Предлагаемый способ определения координат цели позволяет упростить как собственно измерения, так и их организацию особенно в необорудованных районах. При этом исключается трудоемкая операция по установке опорных точек и поддержанию их в рабочем состоянии (контроль стабильности направлений с точки стояния оптического средства на опорные точки). Что касается определения координат точек стояния оптических средств, то в настоящее время эта задача может быть оперативно решена с использованием космической навигационной сети.

Изобретение относится к измерительной технике, а именно к технике коррекции позиционной погрешности в навигационных системах. Технический результат - повышение точности определения координат движущегося объекта. Для достижения данного результата осуществляют оценку состояния каждого оптического средства на основе суммирования соответствующих невязок и вычислении их средних арифметических значений по каждому измеряемому параметру каждого оптического средства. При этом данные состояния рассматриваются как апостериорные погрешности измерений каждого параметра состояния соответствующего оптического средства. Каждое оптическое средство ориентируют произвольно относительно плоскости местного меридиана, а относительно плоскости местного горизонта - с погрешностью по абсолютной величине не более пяти угловых минут и с этой ориентацией визируют на цель, регистрируют ее, измеряют картинные координаты цели и вычисляют ее угловые координаты. Затем вычисляют предварительные значения координат цели каждой измеренной временной точки. 2 ил.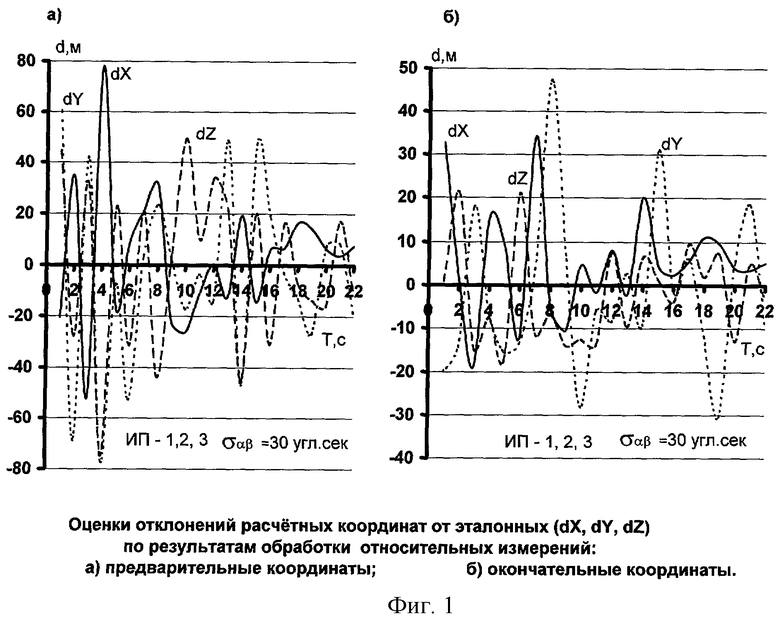
Способ определения пространственных координат цели по результатам измерений оптических траекторных средств, заключающийся в выборе n опорных точек, визировании и регистрации цели и опорных точек из N точек с известными координатами, дешифрировании изображений цели и опорных точек, измерений картинных координат опорных точек и цели в системе координат, две оси которой лежат в плоскости кадра, а третья перпендикулярна этой плоскости и проходит через центр кадра, вычислении координат цели с учетом априорно известных и измеренных координат опорных точек, оценки точности определения координат цели на каждый момент измерения с учетом диагональных элементов ковариационной матрицы определяемых координат цели, использовании вычисленных координат цели для расчета невязок как разностей между измерениями на соответствующий момент времени и целеуказаниями, вычисленными по координатам цели и точки состояния каждого оптического средства, суммировании соответствующих невязок и вычислении их средних арифметических значений по каждому измеряемому параметру каждого оптического средства, которые рассматриваются как апостериорные погрешности измерений каждого параметра каждого оптического средства, отличающийся тем, что каждое оптическое средство ориентируют произвольно относительно плоскости местного меридиана, а относительно плоскости местного горизонта - с погрешностью по абсолютной величине не более пяти угловых минут и с этой ориентацией визируют на цель, регистрируют ее, измеряют картинные координаты цели и вычисляют ее угловые координаты, по которым затем вычисляют вначале предварительные значения координат цели каждой измеренной временной точки, которые выбирают из результатов решения оптимальной комбинации, а каждая комбинация есть результат решения по относительным измерениям на две временные точки, первая из которых есть измерения последовательно на данную искомую временную точку, измерения на вторую точку при решении очередной комбинации подставляются каждый раз поочередно из всей совокупности измеренных временных точек на траектории по каждому оптическому средству, начиная с первой и исключая данную искомую точку, а относительные измерения есть разности измерений соответствующих параметров на выбранную пару точек по времени на измеренной траектории, при этом координаты цели и оценки точности их определения вычисляют сразу на два выбранных момента времени при условии, что число измеренных параметров цели равно или больше числа определяемых координат цели на два выбранных момента времени, считают оптимальной ту комбинацию, у которой значение следа ковариационной матрицы определяемых координат искомой точки будет наименьшее из всех значений следов остальных комбинаций, сохраняют значение следа и вычисленные координаты второй точки каждой оптимальной комбинации, рассчитывают невязки и их средние арифметические значения по каждому измеренному параметру каждого оптического средства с учетом значений предварительных координат цели, а окончательный расчет координат выполняют на каждый искомый измеренный временной момент путем поиска такого положения в пространстве координат второй точки в комбинации с данной искомой точкой, которое обеспечивает глобальный минимум следа ковариационной матрицы определяемых координат искомой точки, за начальные координаты такой точки принимаются координаты второй точки из оптимальной комбинации искомой точки, которые принимают за начальные координаты центра первого квадрата и с него начинают построение сетки в виде плоских квадратов, принимая ординату центра первого квадрата постоянной величиной во всех следующих расчетах по данной искомой точке, вычисляют координаты каждой из четырех вершин квадрата путем использования значений абсциссы и аппликаты центра квадрата, при этом координаты первых двух вершин вычисляют при неизменной аппликате с использованием абсциссы путем первый раз суммирования абсциссы и заданного шага построения сетки, а второй раз - вычитанием шага, а координаты двух оставшихся вершин вычисляют при неизменной абсциссе с использованием аппликаты также первый раз суммированием аппликаты и шага, а затем вычитания, вычисляют по полученным таким образом координатам каждой вершины квадрата параметры целеуказаний для каждого оптического средства, преобразуют их в фиктивные измерения путем суммирования параметров вычисленных целеуказаний с соответствующими средними арифметическими невязками, вычисленными с учетом предварительных координат цели, подставляют поочередно полученные фиктивные измерения каждой вершины квадрата как измерения вторых точек в комбинации с измерениями искомой точки, вычисляют для каждой пары точек координаты и значение следа ковариационной матрицы определяемых координат искомой точки, выбирают наименьшее из четырех значений следа и сравнивают со значениями следа, где вторая точка с искомой точкой есть центр данного квадрата и если оно меньше, то принимают вычисленные координаты соответствующей вершины с наименьшим значением следа за центр очередного квадрата и продолжают аналогичные вычисления и сравнения, в противном случае выполняют уменьшения шага построения сетки, например, в два раза и начинают аналогичные вычисления с новым шагом и координатами последнего центра квадрата перед уменьшением шага, продолжают вычислять координаты вершин нового квадрата с новым шагом, формировать фиктивные измерения, выполнять расчеты координат искомой точки, значений следов и их сравнений, выбирать координаты нового центра и продолжают аналогичный процесс вычислений, сравнений и выбора до тех пор, пока новый шаг не станет меньше наперед заданной величины и тогда принимают за окончательные значения координат цели искомой точки последнее из вычисленных координат с наименьшим значением следа ковариационной матрицы определяемых координат искомой точки с оценкой их точности и таким образом определяют окончательные значения координат цели и оценки точности их определения поочередно всех измеренных точек траектории.
| Лобанов А.Н | |||
| Фотограмметрия | |||
| Издание второе | |||
| - М.: Недра, 1984, с.61-64 | |||
| Попов А.П | |||
| Теория навигации | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| - М.: МО СССР, 1982, с.30, 124 | |||
| Васмут А.С | |||
| Моделирование в картографии с применением ЭВМ | |||
| - М.: Недра, 1983, с.144 | |||
| DE 10146333 A1, 02.05.2002 | |||
| US 6041280 А, 21.03.2000 | |||
| ПРИЕМНИК СИГНАЛОВ СИСТЕМЫ GPS И СПОСОБ ОБРАБОТКИ СИГНАЛОВ СИСТЕМЫ GPS | 1996 |
|
RU2236692C2 |
| Позиционные системы программного управления подвижными объектами | |||
| - М.: ИПРЖ "Радиотехника", 1998, с.28 | |||
| ЭРЛИФТ ЗЕМСНАРЯДА | 1965 |
|
SU216535A1 |
Авторы
Даты
2006-03-20—Публикация
2004-08-06—Подача