Изобретение относится к полигонным испытаниям образцов вооружения и военной техники, контролю за полетом ракетно-космической техники на космодромах и может быть использовано при определении параметров движения цели (объектов наблюдения, испытаний, контроля) по данным оптико-электронных и радиотехнических средств траекторных измерений, а также при оценках координат планового положения точки стояния траекторного средства (широты, долготы), который участвует в совместных измерениях по цели, но у которого на момент измерения отсутствует информация о координатах положения точки его стояния.
При определении пространственных координат цели используется информация, полученная с траекторных средств, положение точек стояния которых считаются известными. При этом, как правило, положение точки стояния каждого траекторного средства задается в виде геодезических координат: широты (В), долготы (L) и высоты (Н). Указанные координаты определяют начало (Оi) i-местной измерительной системы координат (СК) данного i-траекторного средства, ось OiXi лежит в плоскости местного меридиана и горизонта (обычно направлена на север), ось ОiYi направлена по нормали к эллипсоиду вверх, а ось OiZi дополняет систему до правой.
Кроме совокупности подобных местных измерительных систем, связанных с точками стояния траекторных средств и участвующих в совместных измерениях (цель находится в зоне их видимости) используется еще некоторая общая СК (OXYZ), начало которой, например, совмещено с точкой старта. В этой СК ось ОХ лежит в плоскости местного горизонта и направлена относительно местного меридиана под углом Aо (например, азимут стрельбы). Ось ОУ направлена по нормали вверх и OZ дополняет СК до правой. Тогда обычно все расчеты пространственных координат цели выполняются в стартовой СК известными способами (см. , например, Жданюк Б. Ф. Основы статистической обработки траекторных измерений. - М.: Сов. радио, 1978. - 384 с., ил., с. 57-66).
После вычисления пространственных координат цели по измерительной информации с тех траекторных средств, положение точек стояния которых известно, может быть решена задача по определению координат точки стояния траекторного средства, которые считаются неизвестными. В этом случае вычисленные пространственные координаты цели рассматриваются как опорные точки, по которым выполняется определение координат точки стояния этого траекторного средства с учетом его измерений по цели. В полигонной практике обычно определяются широта и долгота точки стояния траекторного средства, а высота считается известной.
При дальномерном методе измерений с траекторного средства, положение точки стояния которой неизвестно, функциональная связь между измеренной наклонной дальностью (Di) и определяемыми параметрами на момент ti может быть представлена следующим образом:
Di=Di(В, L, H, Xi, Yi, Zi, Ао, Во, Lо, Но), (1)
где Xi, Yi, Zi - координаты цели, вычисленные по результатам измерений с траекторных средств, положение точек стояния которых известно;
Ао, Во, Lо, Но - параметры ориентации и положения общей СК.
Если имеются результаты n измерений 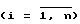 , то можно сформировать систему уравнений, включающих n уравнений, подобных (1).
, то можно сформировать систему уравнений, включающих n уравнений, подобных (1).
Далее выполняется линеаризация системы (1) в окрестностях расчетных значений оцениваемых параметров и формирование уравнений поправок вида, например, применительно к неизвестным - широте, долготе: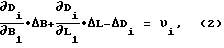
где ΔDi - свободный член и равен разности ΔDi=Di-Dpi;
Di, Dpi - измеренное и расчетное значение наклонной дальности;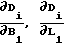 - частные производные функции Di по оцениваемым параметрам;
- частные производные функции Di по оцениваемым параметрам;
υi - соответствующая невязка.
Сформированные подобным образом уравнения поправок вида (2) решаются методом наименьших квадратов последовательными приближениями.
Аналогом заявляемого изобретения может служить навигационные определения с применением искусственных спутников земли (ИСЗ) (см., например, Инженерный справочник по космической технике. 2-е изд., перераб. и доп./ Под ред. А.В. Солодова. - М.: Воениздат МО СССР, 1977. - 430 с., ил., с. 128-129). В этом случае используются данные прогнозирования орбиты ИСЗ и собственные измерения с данного траекторного средства. Указанный набор данных является достаточным для выполнения геодезической привязки точки стояния траекторного средства. Указанный способ имеет следующие недостатки:
требуется специальная аппаратура для выполнения работ с ИСЗ;
низкая точность определяемых координат точки стояния траекторного средства (несколько десятков метров);
измерительная информация с определяемого пункта не используется в целях уточнения орбитальных параметров.
Ближайшим аналогом заявляемому способу является способ использования спутниковой радионавигационной системы (СРНС) в интересах навигации (см. Шебшаевич B.C., Дмитриев П.П. и др. Сетевые спутниковые радионавигационные системы. - М.: Радио и связь, 1982. - 272 с., ил., с. 35-44,141-144).
Имеется ввиду способ, когда во время навигационного сеанса выполняются траекторные измерения с наземных пунктов, положение которых известно и результаты этих измерений используются для уточнения орбитальных параметров. С пункта, положение которого определяется, также выполняются измерения, которые затем и используются для решения задачи.
Сущность способа при дальномерных измерениях сводится к формированию "расширенного" уравнения типа (2) (расширенного в том смысле, что определению подлежат три параметра, а не 2 как в (2), характеризующих положение точки на земле). Сформированные таким образом по числу измерений уравнения поправок решаются методом наименьших квадратов последовательными приближениями.
К недостаткам указанного способа следует отнести:
требуется специальная навигационная аппаратура;
должно быть необходимое количество навигационных искусственных спутников земли (не менее 4-х по критерию наивыгоднейшей конфигурации);
низкая точность (метры) определения координат положения точки на земле (точки стояния измерительного средства) применительно к требованиям по геодезическому обеспечению высокоточных существующих и перспективных траекторных средств;
измерительная информация с определяемого пункта не используется в целях уточнения орбитальных параметров.
Целью изобретения является повышение точности определяемых пространственных координат цели по результатам обработки совместных измерений траекторных средств, разнесенных на местности, у одного из которых на момент измерений неизвестны данные о координатах точки его стояния. При этом траекторное средство участвует в совместных измерениях.
Указанная цель достигается тем, что дополнительно измеряют не менее одного расстояния между точкой стояния траекторного средства, положение которого на момент измерений неизвестно, и любой точкой на земной поверхности на удалении от первой не менее одного километра и положение которой известно с точностью, соизмеримой с точностью геодезической привязки точек стояния траекторных средств, которые участвуют в совместных измерениях по цели. Такими точками на земле могут быть геодезические пункты, точки стояния траекторных средств, положение точек стояния которых известно, специальные точки, положение которых известно и фиксируется на земле, и т.д. Измерение расстояния с точки стояния траекторного средства, положение которой неизвестно (определяется), до выбранной точки на земле может быть выполнено с помощью дальномерных измерений, например, радиотехническими или квантово-оптическими средствами.
Дополнительное измеренное расстояние между указанными выше точками включается в общую обработку. При этом процесс вычисления пространственных координат цели и определения широты и долготы точки стояния траекторного средства совмещается в единую процедуру. Дело в том, что при формировании уравнений поправок вида (2) в данном приближении, коэффициенты при неизвестных и расчетные значения координатных параметров вычисляются в том числе и по координатам цели. В свою очередь пространственные координаты цели вычисляются по результатам обработки измерений, полученных со всех траекторных средств, задействованных в работе, в том числе и с траекторного средства, положение точки стояния которой определяется, а значение широты и долготы точки стояния этого траекторного средства задается теми значениями, которые получены в предыдущем приближении. Вычисленные таким образом в данном приближении координаты цели и оценки точности их определения запоминаются и сохраняются.
Что касается дополнительного измеренного расстояния между точками, то в этом случае формируется дополнительное уравнение поправок типа (2), где неизвестными являются поправки к приближенным значениям широты и долготы, а коэффициенты при неизвестных являются частными производными функции расстояния между точками по оцениваемым параметрам. Здесь также в данном приближении при расчетах свободного члена и коэффициентов при неизвестных в качестве значений широты и долготы принимаются такие значения, которые получены по результатам предыдущего приближения.
Вся указанная выше совокупность уравнений поправок решается методом наименьших квадратов. В результате решения вычисляются поправки к приближенным значениям широты и долготы, а значит и определяют уточненные значения широты и долготы в данном приближении. При необходимости продолжают приближения путем формирования всех уравнений поправок с учетом уточненных значений широты и долготы и их решения в следующем приближении. В итоге по результатам последнего приближения вычисляются окончательные значения широты и долготы, пространственные координаты цели и оценки точности их определения. Отметим еще раз, что координаты цели и оценки точности их определения здесь вычисляются по результатам обработки измерений со всех траекторных средств, задействованных в данной работе. Иными словами, измерения с траекторного средства, положение точки стояния которого определяется, используются здесь в том числе и для оценок координат цели и точности их определения. Этим самым увеличивается избыточность измерений, что при обработке обеспечивает повышение точности и достоверности определяемых пространственных координат цели.
Рассмотрим реализацию способа на примере измерений цели с двух точек стояния траекторных средств ( 1 и 2), разнесенных на местности.
Пусть положение точки стояния 2 задается в виде значений геодезических координат, а именно: широты (В2), долготы (L2) и высоты (Н2) с известными средними квадратическими погрешностями (СКП) их определения (соответственно - σB2, σL2, σH2). Что касается точки стояния 1, то значение ее широты и долготы известно, например, грубо (в плане с погрешностью порядка ~1,5...2,0 км), а высота считается известной (т.е. соответственно 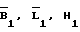 ). Указанные координаты точки стояния 1 могут быть предварительно выбраны, например, с топографической карты (например, как параметры нулевого приближения).
). Указанные координаты точки стояния 1 могут быть предварительно выбраны, например, с топографической карты (например, как параметры нулевого приближения).
Цель находится в зоне видимости с точек стояния 1 и 2, которые ее наблюдают и проводят соответствующие измерения на временном интервале, равном Δt = tk-t1, с известным шагом h, a t1, tk - соответственно время начала и окончания совместных измерений с указанных траекторных средств.
Далее принимается, что траекторное средство 1 выполняет дальномерные измерения (измерения наклонных дальностей D1) с известной СКП ее измерения 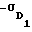 , где нижние индексы подчеркивают принадлежность к измеряемому координатному параметру и номеру средства.
, где нижние индексы подчеркивают принадлежность к измеряемому координатному параметру и номеру средства.
С точки стояния траекторного средства 2 выполняются дальномерно-пеленгационные измерения, а именно - измерения наклонных дальностей (D2) и угловых координат α2, β2 (азимута и угла места) с известными СКП их измерений 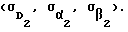 Для упрощения дальнейших рассуждении принимается, что СКП измерения координатных параметров принимается постоянными на всем совместном участке измерений.
Для упрощения дальнейших рассуждении принимается, что СКП измерения координатных параметров принимается постоянными на всем совместном участке измерений.
Таким образом, на совместном участке измерений с траекторных средств 1 и 2 будут получены следующие массивы измерений:
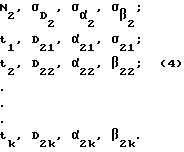
Кроме указанных массивов измерений, дополнительно измеряется расстояние между точками стояния 1 и, например, пунктом геодезической сети (пгс) - S1-пгс и СКП его измерения 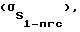 а именно:
а именно: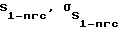 (5)
(5)
При этом известны геодезические координаты этого пункта геодезической сети - B, L, H и оценки точности их определения σB, σL, σH.
Полагаем, что вся обработка результатов измерений будет выполняться в стартовой СК. Это обычная традиционная схема обработки, которая в данном случае и будет использована, хотя, в принципе, не будет никаких отличий, если всю обработку выполнить, например, в СК с началом в точке 2 (A2=0, B2, L2, H2).
Итак, указанные массивы измерений (3), (4), (5), известные координаты точки стояния траекторного средства 2 (В2, L2, H2), координаты точек 1 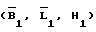 и пункта геодезической сети (B, L, H), а также параметры СК старта - Ао, Во, Lо, Но будут являться тем набором исходных данных, по которым определяются пространственные координаты цели и значения широты (B1) и долготы (L1) точки стояния траекторного средства 1.
и пункта геодезической сети (B, L, H), а также параметры СК старта - Ао, Во, Lо, Но будут являться тем набором исходных данных, по которым определяются пространственные координаты цели и значения широты (B1) и долготы (L1) точки стояния траекторного средства 1.
Пусть 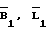 - приближенные значения широты и долготы точки стояния 1. В первом приближении значения
- приближенные значения широты и долготы точки стояния 1. В первом приближении значения 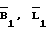 можно интерпретировать как параметры нулевого приближения, в последующем - как значения широты и долготы точки 1, полученные в предыдущем приближении.
можно интерпретировать как параметры нулевого приближения, в последующем - как значения широты и долготы точки 1, полученные в предыдущем приближении.
Используя значения 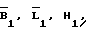 координаты точек 2 и старта, а также массивы измерений (3) и (4) известным способом (см., например, Жданюк Б.Ф. Основы статистической обработки траекторных измерений. - М.: Сов. радио, 1978. - 384 с., ил., с. 57-66) определяются координаты цели и оценки точности их определения на совместном участке измерений:
координаты точек 2 и старта, а также массивы измерений (3) и (4) известным способом (см., например, Жданюк Б.Ф. Основы статистической обработки траекторных измерений. - М.: Сов. радио, 1978. - 384 с., ил., с. 57-66) определяются координаты цели и оценки точности их определения на совместном участке измерений: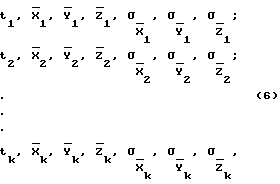
где 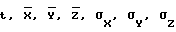 - значения координат цели и оценки точности их определения, вычисленные в данном приближении по результатам всех измерений, в том числе и с траекторного средства, положение точки стояния которого определяется (значок сверху "-" подчеркивает, что это результаты, полученные в данном приближении).
- значения координат цели и оценки точности их определения, вычисленные в данном приближении по результатам всех измерений, в том числе и с траекторного средства, положение точки стояния которого определяется (значок сверху "-" подчеркивает, что это результаты, полученные в данном приближении).
Не является принципиальным, если определение координат цели в каждом приближении будет выполняться поточечно (на каждый очередной момент времени ti(1≤i≤k) на совместном участке измерений), поскольку все последующие расчеты выполняются поточечно. Разница будет лишь в том, что в первом случае координаты цели на очередной момент времени ti выбираются из массива (6), а во втором - вычисляются непосредственно на ti.
Располагая вычисленными значениями координат цели (6), достаточно просто рассчитывается значение наклонной дальности до цели, например, на момент t1(D11p):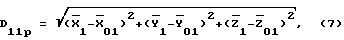
где 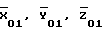 - координаты точки 1 в стартовой СК, вычисленные по известным координатам
- координаты точки 1 в стартовой СК, вычисленные по известным координатам 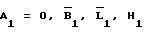 и Ао, Во, Lо, Но и известным соотношениям (см., например, Жданюк Б.Ф. Основы статистической обработки траекторных измерений. - М.: Сов.радио, 1978. - 384 с., ил., с. 193-201);
и Ао, Во, Lо, Но и известным соотношениям (см., например, Жданюк Б.Ф. Основы статистической обработки траекторных измерений. - М.: Сов.радио, 1978. - 384 с., ил., с. 193-201);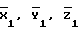 - координаты цели на момент t1 (см. массив (6)).
- координаты цели на момент t1 (см. массив (6)).
Очевидно, что используя значения 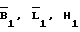 измеренное значение дальности будет отличаться от расчетного значения. Применив ряд Тейлора, напишем уравнение поправок на момент t1:
измеренное значение дальности будет отличаться от расчетного значения. Применив ряд Тейлора, напишем уравнение поправок на момент t1: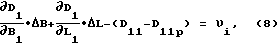
где υ1 - соответствующая невязка;
D11, D11p - измеренное и расчетное значение наклонной дальности.
Неизвестными в этих уравнениях являются поправки к приближенным значениям 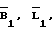 а коэффициенты при неизвестных - частные производные от функции (7) по соответствующим переменным.
а коэффициенты при неизвестных - частные производные от функции (7) по соответствующим переменным.
Коэффициенты при неизвестных (8) проще вычислить методом конечных разностей. Тогда, например, на момент t1 необходимые вычисления можно выполнить следующим образом: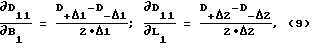
где D+Δ1, D-Δ1, D+Δ2, D-Δ2 - вычисляются с учетом выражения (7).
Например, значение D+Δ1 будет вычисляться следующим образом: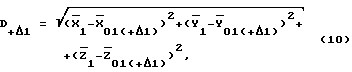
где 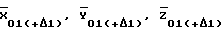 - координаты точки стояния 1 в стартовой СК, вычисленные по известным координатам
- координаты точки стояния 1 в стартовой СК, вычисленные по известным координатам 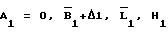 и Ао, Во, Lо, Ho с использованием известных соотношений;
и Ао, Во, Lо, Ho с использованием известных соотношений;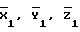 - координаты цели на момент t1 вычисленные по результатам всех измерений, в том числе и с точки 1 и значений
- координаты цели на момент t1 вычисленные по результатам всех измерений, в том числе и с точки 1 и значений 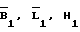 ;
;
Δ1, Δ2 - это вариации по широте и долготе для вычисления частных производных (принимаются равными Δ1 = Δ2 =0,1 угл.сек.).
Аналогичные вычисления по формированию уравнений поправок (8) выполняются по всем измеренным параметрам с траекторного средства 1. Кроме того, массив вида (6) в данном приближении запоминается и сохраняется.
В нашем случае дополнительно измеряется расстояние между точками стояния 1 и пунктом геодезической сети. Если известны координаты точек стояния 1, указанного пункта сети и значений Ао, Во, Lо, Нo, то расчетное значение расстояния может быть вычислено следующим образом (например, в первом приближении)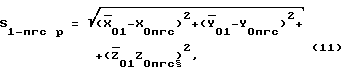
где 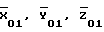 - значение координат точки стояния 1 в стартовой СК, вычисленных по значениям
- значение координат точки стояния 1 в стартовой СК, вычисленных по значениям 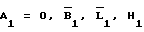 и Ао, Во, Lо, Но.
и Ао, Во, Lо, Но.
XОпгс, YОпгс, ZОпгс - значение координат точки пункта геодезической сети в стартовой СК, вычисленных по значениям А=0, В, L, Н (координаты пункта геодезической сети) и Ао, Во, Lо, Но.
Очевидно, что измеренное значение S1-пгс будет отличаться от расчетного в силу того, что значение 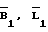 известно приближенно.
известно приближенно.
Применив ряд Тейлора, напишем уравнение поправок: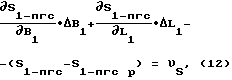
где υS - соответствующая невязка.
В уравнении (12) неизвестными являются поправки к приближенным значениям. 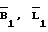 , а коэффициенты при неизвестных - частные производные от функции (11) по соответствующим переменным.
, а коэффициенты при неизвестных - частные производные от функции (11) по соответствующим переменным.
Проще коэффициенты при неизвестных вычислять методом конечных разностей. Тогда будем иметь: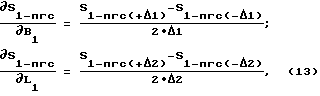
где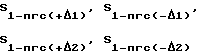
вычисляются с учетом (11).
Например, значение S1-пгс(+Δ1) будет вычисляться следующим образом: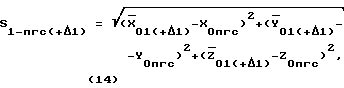
где 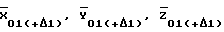 - координаты точки стояния 1 в стартовой СК, вычисленные по известным координатам
- координаты точки стояния 1 в стартовой СК, вычисленные по известным координатам 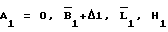 и Ао, Во, Lо, Но с использованием известных соотношений.
и Ао, Во, Lо, Но с использованием известных соотношений.
Значение Δ1 и Δ2 имеет тот же смысл и то же применение, что и при расчетах частных производных вида 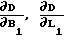 (см. (8).
(см. (8).
Как отмечалось выше, уравнения поправок вида (8) формируются на каждый измеренный параметр с точки 1 и к ним добавляется дополнительное уравнение (12) и вся эта совокупность решается методом наименьших квадратов последовательными приближениями под условием:
[P1•υ2+P2•υ
где [•] - символ Гаусса, означающий суммирование по всем измерениям с точки 1;
P1, P2 - веса измеренных величин D и S1-пгс.
Отметим то обстоятельство, что каждое очередное приближение будет начинаться с вычисления пространственных координат цели по результатам измерений со всех траекторных средств, задействованных в работе, в том числе и с траекторного средства, положение точки стояния которой определяется, а значение широты и долготы этой точки принимается равными тем значениям, которые получены в предыдущем приближении.
По итогам последнего приближения будут вычислены значения широты и долготы точки стояния траекторного средства 1 как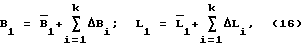
где k - число приближений, а ΔBi, ΔLi - поправки к неизвестным.
Что касается координат цели, то массив (6), полученный (сформированный) в последнем приближении и есть итоговый результат - пространственные координаты цели и оценки точности их определения, вычисленные по результатам совместных измерений со всех траекторных средств, задействованных в данной работе.
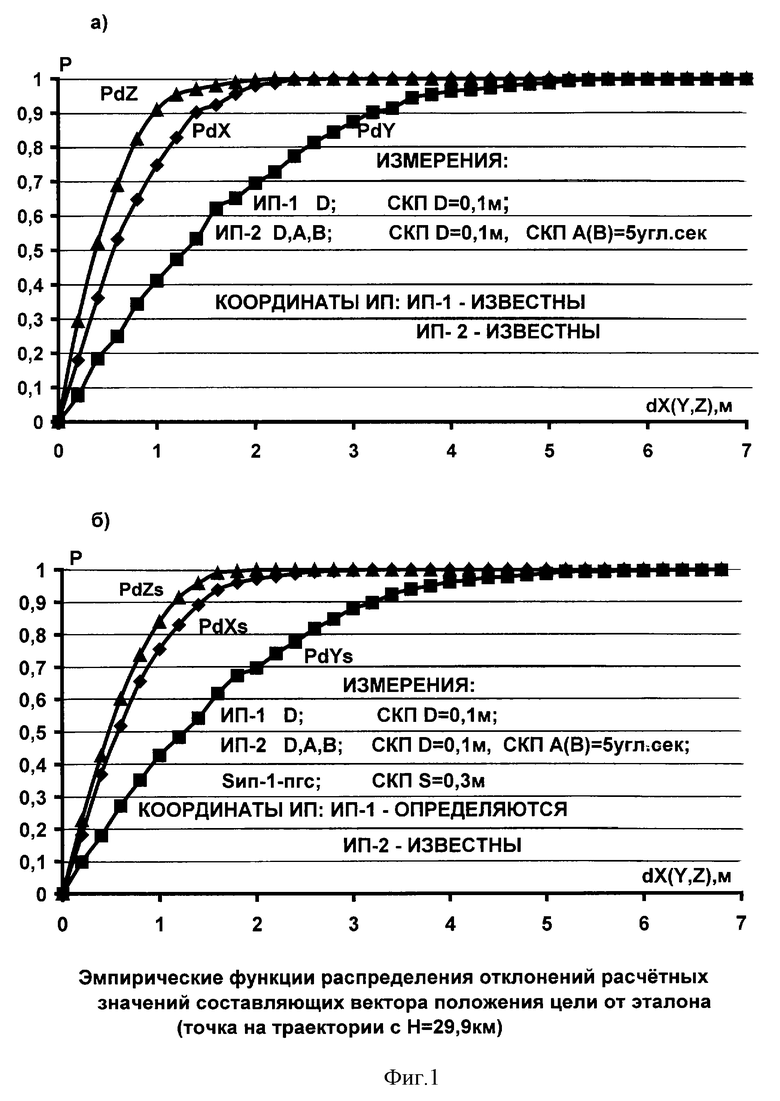
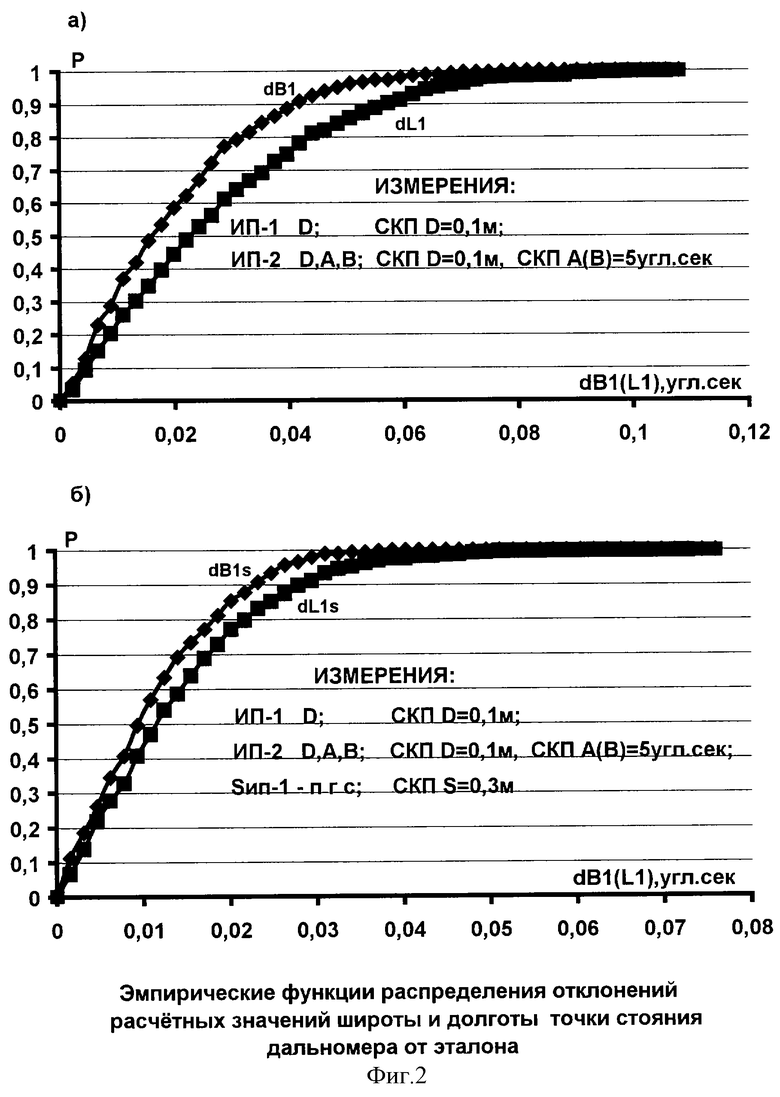
На фиг. 1, 2 приведены эмпирические функции распределения значений отклонений от эталона соответственно составляющих вектора положения цели (dX, dY, dZ и dXs, dYs, dZs - для точки на траектории с Н=29,9 км) и значений dB1, dL1 и dB1s, dL1s, как отклонений расчетных значений широты и долготы, полученных предлагаемым и существующим способами по результатам обработки измерений с траекторных средств 1, 2 (точки стояния 1 и 2). При этом с точки стояния 1 выполняются дальномерные измерения (измерения наклонных дальностей D), а с точки 2 выполняются дальномерно-пеленгационные измерения (измерения дальности и угловых координат D, α, β). Известны СКП измерения координатных параметров. Координаты положения точек стояния (широта, долгота) 2 и точки пгс известны с заданными СКП (в нашем случае она равна 0,01 угл.сек). Координаты положения точки 1 в зависимости от варианта либо известны (с СКП равной 0,01 угл.сек), либо определяются в процессе обработки измерений.
Моделирование измерительной информации выполнялось на интервале Δt=21 с, а по высоте: 8,4...52,8 км. Расстояние между точками 1 и пунктом геодезической сети ~ 1,31 км. Наклонные дальности до цели с точек стояния траекторных средств в соответствии с заданными интервалами высот - с 1: 24...127 км; с 2: 44...145 км. Точки 1 и 2 расположены примерно в створе и перпендикулярно плоскости стрельбы в последовательности (с юга на север) - 1 и 2. Расстояние между точками 1 и 2 равно ~ 53 км. Измерения моделировались с шагом h =1 с и погрешностями:
ΣD∈N(0; 0,1 м);
Δα(β)∈N(0; 5 угл.сек);
ΔS1-пгс∈N(0; 0,3 м),
где N указывает на то, что погрешности измерений распределены по нормальному закону.
Соответственно моделировались и координаты точек стояния 2 и пункта геодезической сети - ΔB(ΔL)∈N(0; 0,01 угл.сек). Число испытаний принималось равным IZ =500.
Итак, на фиг. 1а приводятся эмпирические функции распределения отклонений расчетных значений координат цели от эталона для варианта решения, когда известны координаты точек стояния 1 и 2 и результаты измерений с них, а на фиг. 1б приводятся аналогичные данные при условии, что положение точки 1 определяется предложенным способом по результатам обработки измерений с учетом дополнительно измеренного расстояния между точками 1 и пунктом геодезической сети. При этом с вероятностью Р=1 получены следующие данные (см. фиг. 1б): dХ= 3,2 м (2,8 м); dY=6,8 м (7,0 м); dZ=2,0 м (2,2 м). В скобках приводятся данные, полученные в варианте, когда вся информация считается известной (см. фиг. 1а).
На фиг. 2 приводятся эмпирические функции распределения отклонений расчетных значений широты и долготы точки 1 от эталона, вычисленные существующим (см. фиг. 2а) и предлагаемым (см. фиг. 2б) способами.
Представленные данные на фиг. 1, 2 позволяют сделать вывод о работоспособности предлагаемого способа и его эффективности по сравнению с существующим способом.
Отметим здесь еще раз, что определение широты и долготы точки стояния траекторного средства предлагаемым способом с достаточно высокой точностью позволяет включать измерения с этого траекторного средства как равноценную при обработке измерений, полученных с тех средств, положение точек стояния которых известно. Этим самым обеспечивается повышение точности и достоверности определяемых пространственных координат цели.
Предлагаемый способ упрощает организацию измерений, особенно в труднодоступных и малооборудованных районах за счет вставок в существующую измерительную сеть новых точек стояния траекторных средств при отсутствии их геодезического обеспечения. Этим самым может быть оперативно обеспечена оптимальная геометрия измерений, что позволит в итоге получить наивысшую точность оценок определяемых пространственных координат цели при существующем наборе измерительных траекторных средств.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ЦЕЛИ | 2004 |
|
RU2272254C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ ЦЕЛИ | 1997 |
|
RU2143099C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ЦЕЛИ | 1990 |
|
RU2078309C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНТРОЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ПРОСТРАНСТВЕННО-УГЛОВОЙ ОРИЕНТАЦИИ САМОЛЁТА НА ТРАССАХ И ПРИАЭРОДРОМНЫХ ЗОНАХ ПРИ ЛЁТНЫХ ИСПЫТАНИЯХ ПИЛОТАЖНО-НАВИГАЦИОННОГО ОБОРУДОВАНИЯ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2584368C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ ОБЪЕКТА | 2005 |
|
RU2292526C1 |
| Способ спутникового геодезического нивелирования определения параметров глобальной модели внешнего гравитационного поля Земли (ВГПЗ) | 2021 |
|
RU2783645C1 |
| СПОСОБ ВЫСОКОТОЧНЫХ ИЗМЕРЕНИЙ ТРАЕКТОРНЫХ КООРДИНАТ ЛЕТАТЕЛЬНОГО АППАРАТА В ЛЕТНЫХ ИССЛЕДОВАНИЯХ НА ТРАССАХ БОЛЬШОЙ ПРОТЯЖЕННОСТИ | 2008 |
|
RU2393430C1 |
| Способ коррекции углов визирования на точку | 2020 |
|
RU2758860C1 |
| Способ горизонтирования системы координат угломерного прибора по двум опорным точкам | 2024 |
|
RU2832842C1 |
| СПОСОБ СЪЕМКИ РЕЛЬЕФА ДНА АКВАТОРИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2439614C2 |
Изобретение относится к полигонным испытаниям образцов вооружения и военной техники, контролю за полетом ракетно-космической техники на космодромах и может быть использовано при определении параметров движения цели по результатам обработки данных оптико-электронных и радиотехнических средств траекторных измерений. Способ заключается в дополнительном измерении не менее одного расстояния с точки стояния траекторного средства, положение которой неизвестно, до любой точки на земной поверхности. Положение данной точки на земной поверхности известно с точностью, соизмеримой с точностью геодезической привязки точек стояния траекторных средств, участвующих в измерениях. Указанное дополнительное измерение включается в обработку всей информации, полученной на совместном участке измерений. Технический результат состоит в повышении точности определяемых пространственных координат цели. 2 ил.
Способ определения пространственных координат цели, заключающийся в проведении совместных измерений координатных параметров цели, находящейся в зоне видимости нескольких траекторных средств, разнесенных на местности, у одного из которых неизвестны данные о координатах точки его стояния и с него выполняются измерения наклонных дальностей, а у остальных они известны и задаются в виде геодезических координат (широта, долгота, высота), при этом минимальное число траекторных средств, положение точек стояния которых известно, может быть равно одному, если с него выполняются измерения трех координатных параметров цели, наклонных дальностей и угловых координат, или двум - при измерениях с каждого только угловых координат цели, вычислении с применением метода наименьших квадратов пространственных координат цели и оценок точности их определения по результатам измерений только тех траекторных средств, положение точек стояния которых известно, и, наконец, определении координат точки стояния траекторного средства, положение которого неизвестно, путем решения с применением метода наименьших квадратов и последовательных приближений всех сформированных уравнений поправок, каждое из которых в данном приближении формируется на каждый измеренный параметр на всем совместном участке измерений с точки стояния траекторного средства, положение которой определяется, а неизвестные в каждом из них - поправки к приближенным значениям координат точки стояния траекторного средства, свободный член есть разность между измеренным и расчетным координатным параметрами, а расчетное значение параметра, как и коэффициенты при неизвестных, вычисляются с учетом координат цели и результатов измерений с точки стояния траекторного средства, при этом координаты ее точки стояния задаются теми значениями, которые получены в предыдущем приближении, отличающийся тем, что дополнительно измеряют не менее одного расстояния с точки стояния траекторного средства, положение которой неизвестно, до любой точки на земной поверхности с удалением не менее одного километра и положение которой известно с точностью, сравнимой с точностью геодезической привязки точек стояния траекторных средств, определяют значение широты и долготы точки стояния траекторного средства, а значение высоты этой точки известно, путем решения методом наименьших квадратов и последовательных приближений всех сформированных уравнений поправок и дополнительного уравнения, связанного с измеренным расстоянием между точкой стояния траекторного средства и выбранной точкой на земной поверхности, при этом в каждом уравнении поправок данного приближения неизвестными являются поправки к приближенным значениям широты и долготы, а свободный член и коэффициенты при неизвестных в уравнениях поправок в первом случае определяются в том числе и по пространственным координатам цели, вычисленными в данном приближении последовательно на каждый фиксированный момент времени на всем совместном участке измерений по результатам обработки измерений со всех траекторных средств, в том числе и измерений с траекторного средства, положение точки стояния которой определяется, а значение широты и долготы в этом случае задаются теми ее значениями, которые получены в предыдущем приближении, вычисленные таким образом в данном приближении координаты цели и оценки точности их определения сохраняются и запоминаются, а в дополнительном уравнении поправок коэффициенты при неизвестных, как и расчетное значение расстояния между точками, вычисляются с учетом значений широты и долготы, полученных в предыдущем приближении и, в итоге, по результатам последнего приближения определяют широту и долготу точки стояния траекторного средства и значения пространственных координат цели, вычисленных по результатам обработки измерений со всех задействованных в работе траекторных средств.
| ШЕБШАЕВИЧ B.C | |||
| и др | |||
| Сетевые спутниковые радионавигационные системы | |||
| - М.: Радио и связь, 1982, 272 с., ил | |||
| Топливник с глухим подом | 1918 |
|
SU141A1 |
| Скоропечатный станок для печатания со стеклянных пластинок | 1922 |
|
SU35A1 |
| СПОСОБ ИЗМЕРЕНИЯ СИГНАЛОВ ВЕКТОРНЫМ ИЗМЕРИТЕЛЕМ ПРИ СТРУКТУРНО-ИНФОРМАЦИОННОЙ ИЗБЫТОЧНОСТИ | 1991 |
|
RU2011950C1 |
| US 4134217 A, 16.01.1979 | |||
| US 4675823 А, 23.06.1987 | |||
| US 4700307 А, 13.10.1987. | |||
Авторы
Даты
2003-10-27—Публикация
2002-03-21—Подача