Изобретение относится к области полигонных испытаний образцов вооружения и военной техники и может быть использовано при определении параметров движения цели (объектов наблюдения, испытаний) по данным фоторегистрирующих (оптических) средств траекторных измерений.
Траекторные оптические средства измеряют координатные параметры, которые позволяют непосредственно оценить только положение цели в пространстве, а именно - их пространственные координаты (X, Y, Z). В этом случае для решения задачи определения составляющих вектора скорости цели полученные пространственные координаты, как правило, в функции времени используются в качестве исходных данных.
Например, аппроксимируя отдельно каждую координатную функцию подобранным определенным образом полиномом с последующим дифференцированием вычисляют составляющие вектора скорости. Такой подход имеет больше недостатков, чем преимуществ. Так, при наличии разрывов на интервале измерений можно их восстановить и получить значения полного вектора (координаты и скорости) в каждой точке и с любым шагом. Но вот точность и достоверность получаемых результатов в итоге будет низкой и это может привести к ошибочным выводам при их использовании, например, в анализе движения объекта испытания. В технической литературе подробно рассматриваются подобные способы (см., например, Гудзовский В. А., Худяков С. Т. Баллистика ракет. - М.: МО СССР, 1971).
Более эффективными для решения задачи определения составляющих вектора скорости цели являются способы численного дифференцирования координат.
Ближайшим к заявляемому способу по цели и конечному результату является способ определения составляющих вектора скорости летательного аппарата численным дифференцированием координат (см. Жданюк Б.Ф. Основы статистической обработки траекторных измерений. М. "Советское радио", 1978, с. 253-265).
В этом способе для обеспечения необходимой точности определения производных приходится решать оптимизационную задачу по согласованию шага аргумента и порядка используемых разностей, чтобы уменьшить погрешности, вызываемые случайными ошибками дифференцируемых функций. Кроме этого, для численного дифференцирования координатных функций, как правило, применяют метод скользящего дифференцирования, при котором производная вычисляется только для одной средней точки выбранного интервала обработки. При этом скользящий интервал не должен содержать разрывов по времени. Такой подход в свою очередь затрудняет определение составляющих вектора скорости в нескольких точках как в начале, так и в конце интервала измерений. Имеется в виду, что оценки точности и достоверности получаемых характеристик в этих точках оказываются практически на порядок загрубленными по сравнению с определяемыми в средних точках.
Кроме этого, наличие на интервале измерений разноточных значений координат даже в соседних точках также затрудняет обработку и существенно снижает точностные характеристики получаемых результатов.
Целью изобретения является повышение точности определения составляющих вектора скорости цели по результатам оптических траекторных измерений.
Это достигается тем, что фоторегистрация цели выполняется на фоне опорных точек и дополнительно измеряются скорости изменения ее картинных координат в каждой точке наблюдения. Под опорными точками (звезды, геодезические вехи) здесь понимаются точки с известными координатами (например, задаваемые значениями азимута (α) и угла места (β)) относительно местной измерительной системы координат (СК), начало которой совмещено с точкой стояния оптического средства. Картинные координаты цели (опорных точек) - это координаты цели в СК, две оси которой лежат в плоскости фотоснимка, а третья перпендикулярна этой плоскости и проходит через центр снимка.
При обработке результатов фоторегистрации сначала определяются пространственные координаты цели известным способом (см. Якушин С.М. Заявка на изобретение N4537427 от 17. 12.90 г. "Способ определения пространственных координат цели". Решение о выдаче патента от 18.03.96 г.)
Суть способа определения координат заключается в том, что определяются направляющие косинуса для каждой точки наблюдения между линиями визирования на опорные точки и между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения опорных точек. Полученные значения направляющих косинусов сравнивают между собой и на величину полученной разности компенсируют вычисляемые направляющие косинусы между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения цели и опорных точек. По скомпенсированным таким образом значениям направляющих косинусов и известным направлениям на опорные точки определяют пространственные координаты объекта как точку пересечения прямых круговых конусов, вершина каждого из которых совпадает с точкой наблюдения, а угол полураствора конуса равен углу между направлениями на цель и опорную точку.
Далее, с учетом значений скоростей изменения картинных координат цели и вычисленных значений направляющих косинусов между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения цели и опорных точек вычисляют скорости изменений этих направляющих косинусов. Затем формируют для очередной данной точки наблюдения линейные алгебраические уравнения по каждой опорной точке. Здесь число уравнений для данной точки наблюдения равно числу опорных точек, информация которых привлекается к обработке. При этом в этих уравнениях по каждой опорной точке скорости изменения направляющих косинусов являются правыми частями (свободными членами), неизвестными - определяемые составляющие вектора скорости цели, а коэффициенты при неизвестных вычисляются по известным уже пространственным координатам цели и известным направлениям на соответствующие опорные точки.
Таким образом, каждое уравнение будет содержать три неизвестных - составляющие вектора скорости цели Vx, Vy, Vz.
Число опорных точек, как правило, более трех. Поэтому, используя метод наименьших квадратов, решаем задачу по определению составляющих вектора скорости как задачу по избыточным данным. Аналогичные действия выполняются и для следующих точек наблюдения.
Рассмотрим реализацию способа на примере фотографирования цели на фоне звезд.
Предположим, что фотографирование выполняется на один кадр. В этом случае след движения цели зафиксируется в виде нескольких треков, каждый из которых имеет привязку ко времени. Точно также изобразятся и звезды. Полученные негативы используются для измерения картинных координат изображений цели и звезд на компараторе, например, типа АК-1.
Тогда для одного снимка будем иметь следующие массивы:
массив картинных координат цели
массив картинных координат опорных точек
Согласно известному способу определения пространственных координат цели вначале выполняется сравнение вычисленных направляющих косинусов между линиями визирования на опорные точки и между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения опорных точек. Затем на величину полученной разности компенсируют вычисленные направляющие косинусы (cos Q) между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения цели и опорных точек, и формируют массив, например, на фиксированный момент времени в виде:
где Qi - угол между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения цели и i -опорную точку;
αi, βi - угловые координаты i-опорной точки (1≤i≤n).
Аналогично формируют массивы вида (3) для следующих очередных моментов наблюдения (измерения).
Массивы вида (3) с каждого оптического средства (снимка) на момент t являются основными исходными данными для определения пространственных координат цели. В результате вычислений имеем:
t, X, Y, Z. (4)
Массивы вида (1), (2), (3), (4), а также измеренные значения изменения картинных координат цели в виде: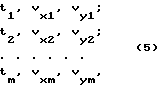
являются исходными данными, используемыми для определения (составляющих вектора скорости цели.
Следует отметить, что массив типа (5) (значения t, Vx, Vy) может быть получен и численным дифференцированием функций картинных координат цели. В этом случае имеем почти идеальные условия - "гладкая" кривая, несложная работа с подбором "оптимального" полинома и, наконец, решение проблемы с начальными и конечными точками на измерительном интервале, что в итоге позволяет по предложенной ниже схеме решения существенно повысить точность определения составляющих вектора скорости цели по сравнению с существующими способами численного дифференцирования пространственных координат.
Представим исходные зависимости для определения составляющих вектора скорости цели (с учетом известного способа определения пространственных координат цели - см. изобретение N 4537427).
Пусть в некоторой системе координат OXYZ известны координаты точек стояния оптических средств. Тогда с учетом данных массива (3) на момент времени t уравнение прямого кругового конуса с вершиной в точке 0λ(λ ≤ j, где j - число оптических средств), углом Qk и осью вращения по линии 0λXkλ запишем следующим образом: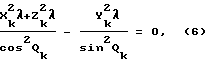
где k - номер опорной точки на кадре λ - оптического средства;
Xkλ, Ykλ, Zkλ - координаты цели в условной СК, в которой 0λXk совпадает с направлением на k-опорную точку;
T - знак транспонирования;
X, Y, Z- координаты цели в СК OXYZ;
X0λ, Y0λ, Z0λ - координаты точки стояния λ - средства в СК OXYZ;
a11k = cosαk•cosβk;
a12k = -cosαk•sinβk;
a13k = -sinαk;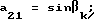
a22k = cosβk;
a23k=0
a31k = sinαk•cosβk;
a32k = -sinαk•sinβk;
a33k = cosαk;
αk, βk - угловые координаты k-опорной точки.
Из выражения (7) следует исходная зависимость:
После несложных преобразований расчетное значение cos Q запишем следующим образом:
где 
Продифференцировав выражение (10) с учетом (9) и после несложных преобразований, получим линейное алгебраическое уравнение вида:
C1k•Vx + C2k•Vy + C3k•Vz = cosQk
где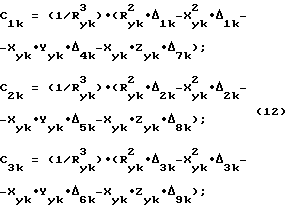
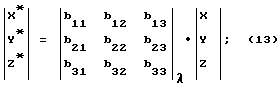



X, Y, Z - координаты цели в СК OXYZ;
Xoo, Yoo, Zoo - координаты точки О СК OXYZ в СК 0λXλYλZλ;
B11, B12, . . . , B33 - направляющие косинусы связи СК в точке стояния оптического средства 0λ и СК OXYZ с началом в точке O (рассчитываются по известным формулам с использованием геодезических координат, характеризующих положение и ориентацию осей соответствующих СК);
Vx, Vy, Vz - составляющие вектора цели в СК OXYZ;
a11k, a12k, ..., a33k - см. (8).
Поскольку коэффициенты при Vx, Vy, Vz в уравнении (11) содержат погрешности (в основном за счет погрешностей определения X, Y, Z цели), значение cos Q также содержит погрешности измерений, то левые и правые части не будут равны, а будут отличаться на некоторую величину поправки ν. Тогда уравнение (11) перепишем в виде уравнения поправок:
С учетом (16) для λ - оптического средства при n-числе опорных точек будем располагать следующей системой уравнений:
Аналогичные системы уравнений типа (17) будем иметь со всех из j-оптических средств на момент t.
Пока нерешенным остается вопрос определения скорости изменения направляющих косинусов при наличии измеренных (или вычисленных) значений скорости изменения картинных координат цели (Vx, Vy - см. массив (5)). В качестве исходной зависимости воспользуемся выражением:
где xц, yц - картинные координаты цели;
fi, yi - картинные координаты i - опорной точки;
f - фокусное расстояние камеры λ - оптического средства;

После дифференцирования и несложных преобразований получим: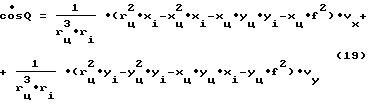
Теперь мы располагаем всеми необходимыми данными для решения системы линейных уравнений типа (17). Поскольку число уравнений типа (16) значительно превосходит число неизвестных (Vx, Vy, Vz на момент t), то решение выполняется с применением метода наименьших квадратов. После решения на момент t будут определены составляющие вектора скорости цели (Vx, Vy, Vz) и оценки точности их определения.
На чертеже приведены эмпирические функции распределения значений ΔVx, ΔVy, ΔVz, полученные предлагаемым способом (первая кривая) и для сравнения - данные, полученные численным дифференцированием координатных функций (т. е. X= f(t), Y=f(t), Z=f(t) - вторая кривая). Моделирование измерительной информации выполнялось на интервале t = 1,0...2,25 с с погрешностями: σxy = 0,005 мм, σf = 0,05 мм, σαβ = 2 угл.с, σxyz = 10 м, σcosQ = 0,0001. Число опорных точек - IM=10. Скорости изменения картинных координат цели vx, vy получены численным дифференцированием их картинных координат с помощью сплайнов первого порядка. Измерения моделировались для 3-х разнесенных в пространстве оптических средств. Информация получена с шагом 0,25 с. Эмпирические функции распределения получены для t= 1,5 с (H=23 км, расстояние до цели - 70...100 км) и числа испытаний IS = 500.
Представленные данные чертежа позволяют сделать вывод о работоспособности предлагаемого способа определения составляющих вектора скорости цели и его эффективности по сравнению с данными, полученными численным дифференцированием координатных функций.
Использование изобретения позволяет в каждой точке наблюдения определять составляющие вектора цели с более высокой точностью и достоверностью по сравнению с существующими способами применительно к оптическим траекторным измерениям.
При этом повышение точности и достоверности определяемых характеристик достигается практически без дополнительных затрат на измерения, а только за счет более полного их использования при обработке.
Кроме этого, с учетом и способа определения пространственных координат цели (см. изобретение N 4537427) обеспечивается возможность упрощения собственно измерений за счет отказа от построения высокоточной системы ориентации для каждого оптического траекторного средства. Иными словами, можно создать сравнительно дешевые измерительные оптические комплексы (в том числе и подвижные) с грубой внутренней системой отсчета (до единиц градусов) для обеспечения измерений в труднодоступных и малооборудованных районах при решении задач оценки полного вектора, характеризующих положение и движение объекта испытаний.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ЦЕЛИ | 1990 |
|
RU2078309C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕМЕНТОВ ОРИЕНТИРОВАНИЯ ФОТОСНИМКА МЕСТНОСТИ | 1995 |
|
RU2101677C1 |
| Способ определения координат объекта по стереопаре его снимков и по снимку летательных аппаратов | 2024 |
|
RU2840058C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЙ КОРОТКОВОЛНОВОГО ДИАПАЗОНА | 2012 |
|
RU2490661C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВ ПРОСТРАНСТВЕННОЙ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2594631C1 |
| НАВИГАЦИОННОЕ УСТРОЙСТВО | 1999 |
|
RU2163352C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЭФФЕКТИВНОЙ ПОВЕРХНОСТИ РАССЕЯНИЯ ОБЪЕКТОВ | 2001 |
|
RU2210789C2 |
| ИЗМЕРИТЕЛЬ РАССТОЯНИЙ НА ЦИФРОВОЙ ВИДЕОКАМЕРЕ | 2018 |
|
RU2689848C1 |
| СПОСОБ ФОРМИРОВАНИЯ ВОЗДУШНО-СКОРОСТНЫХ ПАРАМЕТРОВ МАНЕВРЕННОГО ОБЪЕКТА | 2019 |
|
RU2713585C1 |
| Способ сокращения потерь скорости и времени при осуществлении маневра заданной конфигурации беспилотным летательным аппаратом планирующего типа | 2016 |
|
RU2623361C1 |

Изобретение относится к области полигонных испытаний образцов вооружений и военной техники и может быть использовано при определении параметров движения цели по данным фоторегистрирующих (оптических) средств траекторных измерений. Техническим результатом, достигаемым при реализации данного способа, применительно к траекторным оптическим измерениям, является повышение точности определения составляющих вектора скорости цели в каждой точке наблюдения. Для достижения задачи изобретения выполняется фоторегистрация цели на фоне опорных точек и дополнительно измеряют скорости изменения картинных координат цели в каждой точке наблюдения. С учетом измеренных скоростей картинных координат цели вычисляют скорости изменения направляющих косинусов между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения цели и опорных точек. Затем формируют для точки наблюдения по каждой опорной точке уравнение поправок вида C1k•Vx+C2k•Vy+X3k•Vz-cosQ = νk, где k - номер опорной точки, а νk - соответствующая поправка, Q - угол между направлениями, проходящими через заднюю главную точку фоторегистратора, изображение цели и опорную точку. В этом уравнении неизвестным являются определяемые составляющие вектора скорости цели в точке наблюдения (Vx, Vy, Vz), коэффициенты при неизвестных (C1k, C2k, C3k) вычисляют по известным пространственным координатам цели и известным направлениям на k-опорную точку, а свободным членом - скорость изменения направляющего косинуса между направлением на цель и k-опорную точку. Число аналогичных уравнений равно числу опорных точек, привлекаемых к обработке, их количество, как правило, значительно превосходит число неизвестных. Далее, применяя метод наименьших квадратов, решается задача по определению составляющих вектора скорости цели и выполняется оценка точности их определения в точке наблюдения. 1 ил.
Способ определения составляющих вектора скорости цели, заключающийся в выборе n опорных точек, визировании и фоторегистрации цели и опорных точек из N точек с известными координатами, дешифрировании снимков, идентификации опорных точек, измерении картинных координат цели и опорных точек в системе координат, две оси которой лежат в плоскости фотоснимка, а третья перпендикулярна этой плоскости и проходит через центр фотоснимка, получении значений направляющих косинусов для каждой точки наблюдения между линиями визирования на опорные точки и между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения опорных точек, сравнении их между собой и компенсировании значений направляющих косинусов между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения цели и опорных точек, определении пространственных координат цели по скомпенсированным значениям направляющих косинусов и известным направлениям на опорные точки и вычислении составляющих вектора скорости цели численным дифференцированием ее пространственных координат, отличающийся тем, что дополнительно измеряют скорости изменения картинных координат цели в каждой точке наблюдения, вычисляют, с учетом измеренной скорости изменения картинных координат цели, скорости изменения направляющих косинусов между направлениями, проходящими через заднюю главную точку фоторегистратора и изображения цели и опорных точек, формируют для точки наблюдения уравнения поправок по каждой опорной точке, при этом скорости изменения направляющих косинусов являются в этих уравнениях свободными членами, неизвестными - составляющие вектора скорости цели, а коэффициенты при неизвестных вычисляются по известным пространственным координатам цели и известным направлениям на опорные точки, затем определяют составляющие вектора скорости цели путем решения полученных уравнений поправок с применением метода наименьших квадратов.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Жданюк Б.Ф | |||
| Основы статистической обработки траекторных измерений | |||
| - М.: Советское радио, 1978 | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Способ стереофотограмметрической съемки подвижных объектов | 1974 |
|
SU502222A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Способ стереофотограмметрической съемки подвижного объекта | 1988 |
|
SU1539532A1 |
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ЦЕЛИ | 1990 |
|
RU2078309C1 |
| Кипятильник для воды | 1921 |
|
SU5A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗМЕНЕНИЯ ПОЛОЖЕНИЯ ТОЧЕК ОБЪЕКТА | 1991 |
|
RU2012853C1 |
Авторы
Даты
1999-12-20—Публикация
1997-12-26—Подача