Изобретение относится к области подводной, морской, наземной, и околоземной навигации, в частности осуществляемой с помощью спутниковых радионавигационных систем типа GPS и ГЛОНАСС.
Известен способ определения координат приемника сигнала (см. Андерсон Э. Принципы навигации. - М.: Воениздат, 1968, с.273), заключающийся в измерении двух или более последовательностей разности времени, которые отыскивают непосредственно на карте, на которой нанесены два или больше семейств гипербол в соответствии с разностями времени.
Недостатком данного способа является то, что он применим только в плоском случае и при этом имеет низкую точность как графический способ.
Наиболее близким по технической сущности к заявляемому изобретению является способ разностно-дальномерного определения пространственных координат приемника (см. Соловьев В.А. Системы спутниковой навигации. - М..: Эко-Трендз, 2000, с.35-36), включающий синхронное излучение сигнала в неизвестный момент времени несколькими маяками-излучателями с известными координатами и последующее вычисление координат приемника по моментам приема сигнала при заданной скорости сигнала. При этом для повышения точности используют избыточное число излучателей (например, пять при трехмерном позиционировании) и итеративный метод наименьших квадратов Гаусса-Ньютона.
Недостатком этого способа является неизбежное наличие систематической ошибки, обусловленной априорным назначением скорости сигнала. Сигнал в неоднородной среде проходит от каждого из маяков свой искривленный путь, причем физические условия на каждом из путей свои собственные. Соответственно, любое априорное назначение скорости сигнала содержит в себе неявное усреднение, ориентированное на определенные навигационные условия, необязательно совпадающие с условиями настоящего навигационного сеанса. Это становится источником плохо контролируемой систематической ошибки способа. Для повышения точности для спутниковых систем вводят различные атмосферные поправки, однако многие исследователи отмечают, что они иногда даже ухудшают результаты (см. Серапинас Б.Б. Глобальные системы позиционирования. - М.: ИКФ "Каталог", 2002, с.45).
Задачей настоящего изобретения является повышение точности местоопределения приемника сигнала.
Это достигается тем, что в способе определения декартовых координат приемника, заключающемся в синхронном излучении сигнала в неизвестный момент времени несколькими излучателями с известными координатами с последующим вычислением координат приемника по моментам приема сигнала, в момент приема сигнала от последнего излучателя измеряют квадрат скорости сигнала по моментам времени приема сигнала в текущем навигационном сеансе.
Измеряя квадрат скорости сигнала по моментам времени приема сигнала в текущем навигационном сеансе, фактически, определяют эффективную скорость сигнала. Возможны как плоская (характерная для морской и наземной навигации), так и трехмерная (характерная для подводной и спутниковой навигации) реализации способа. Пусть n - размерность пространства Rn, в котором производится позиционирование, n=2, 3. Для осуществления предлагаемого способа необходимы как минимум n+2 маяка-излучателя. Неизвестный столбец декартовых координат х∈Rn приемника, неизвестный момент τ синхронного излучения и неизвестная скорость сигнала с оказываются связаны n+2 уравнениями
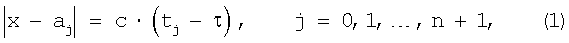
где аj∈Rn - известное местоположение j-го излучателя.
Без ограничения общности положим
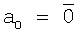 , t0=0,
, t0=0,
где 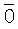 - нулевой столбец. Тогда исходная система запишется в равносильном виде как
- нулевой столбец. Тогда исходная система запишется в равносильном виде как
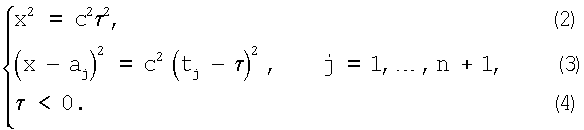
где x2=xTx - скалярный квадрат, (•)T - операция транспонирования.
Вычитая первое уравнение (2) из остальных уравнений (3), получим подсистему
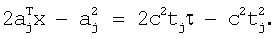
В новых неизвестных переменных
θ=c2τ, x, κ=с2
система (2), (3), (4) равносильна системе
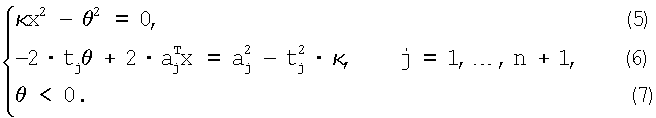
Пусть L - матрица коэффициентов линейной (n+1)×(n+1) системы уравнений (6) относительно столбца X=(θ,xт)т, θ=Х0, столбец u состоит из аj 2, а столбец ν состоит из (-tj 2), j=1, ...,n+1. Тогда из (6) X=U+k·V, где U=L-1·u, V=L-1·ν. Обозначив р=U0, q=V0, Рi=Ui, Qi=Vi, i=1, ..., n, получим

После подстановки (8), (9) в (5) получим кубическое относительно к уравнение
Q2κ3+(2PTQ-q2)κ2+(Р2-2рq)κ-р2=0.
Пусть κ1, κ2, κ3 - его корни. Из этих корней выбирается корень κ*, ближайший к номиналу 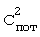 . В итоге искомое х вычисляется по формуле
. В итоге искомое х вычисляется по формуле
х=Р+κ*·Q+a0.
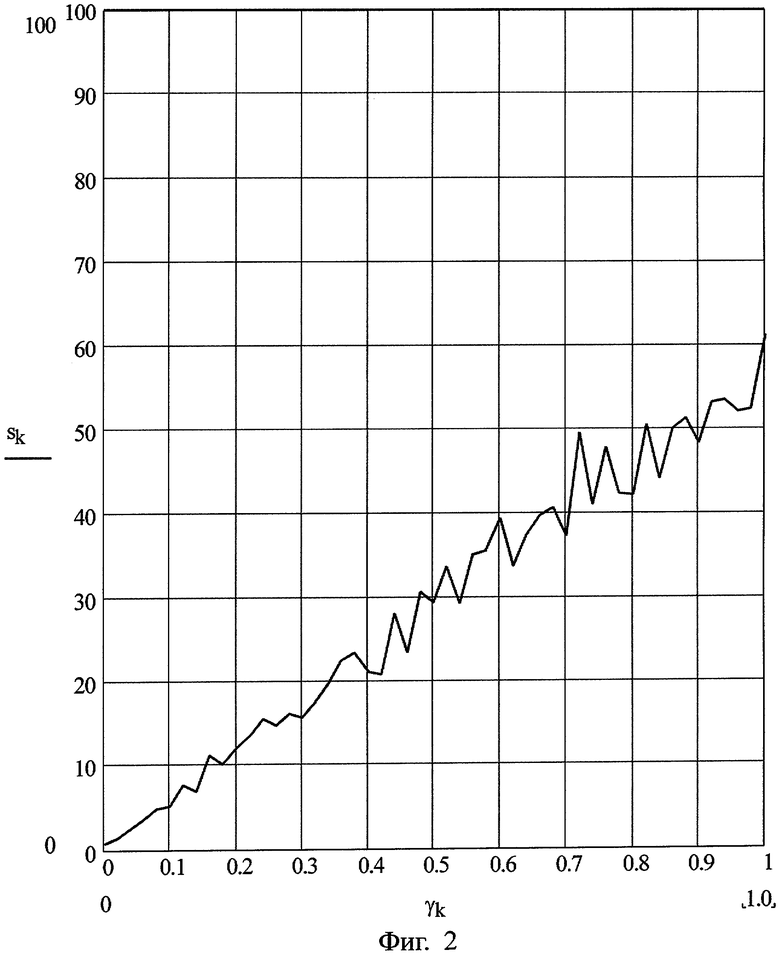
Ниже приводится MathCAD-процедура X(t) обработки столбца t моментов приема сигнала в предлагаемом способе. На фиг.1 изображена модельная конфигурация разностно-дальномерной системы с параметрами, близкими к спутниковой радионавигационной системе. На фиг.2 представлен график отношения точности способа-прототипа к предлагаемому способу в зависимости от отношения точности скорости сигнала к точности часов приемника.
Для сравнения предлагаемого способа с известным способом применялась имитационная модель в среде MathCAD 11 (см. нижеприведенную процедуру SS). В этой модели для произвольной конфигурации 5 маяков-излучателей и приемника в трехмерном пространстве сравнивается работа известного способа с предлагаемым способом при одинаковых входных данных. Для конкретной конфигурации с параметрами, близкими к спутниковой радионавигационной системе, когда пять спутников - вершины шестигранника, два из них находятся в зените, приемник - на поверхности Земли, начало координат в центре Земли (см. фиг.1 и исходные данные), результат сравнения способов оказался следующим. При реальных условиях, что среднеквадратическая ошибка (СКО) измерения времени приемником GPS есть σt=0.001 мкс и СКО скорости света есть σc - 0.0001 м/мкс (см. Берклеевский курс физики. Том 1. Киттель Ч., Найт У., Рудерман М. Механика - М.: Наука, 1975, с.341-342) точность предлагаемого способа превосходит точность известного способа в s=6 раз по результатам 100 имитационных испытаний с помощью процедуры SS.
График зависимости s=s(γ), где
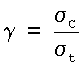
показан на фиг.2. Из этого графика следует, что предлагаемый способ тем точнее известного способа, чем точнее часы приемника относительно точности априорного назначения скорости сигнала.
Для воспроизведения MathCAD-расчета нужно произвести стандартную начальную установку датчика случайных чисел, для чего требуется войти в окно меню Tools/Worksheet options/Built-in Variables и активизировать опцию Restore Defaults.




При пяти маяках в трехмерном пространстве предлагаемый способ приводит к простому конечному алгоритму, тогда как известный способ требует итеративного алгоритма, сходимость которого существенно зависит от начального приближения. Это качество предлагаемого способа обеспечивает ему, дополнительно, более высокие быстродействие и надежность по сравнению с прототипом.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АВИАЦИОННОЙ БЛИЖНЕЙ РАДИОНАВИГАЦИИ | 2021 |
|
RU2778179C1 |
| Способ навигационной поддержки группы специализированных подводных аппаратов, выполняющих общую миссию в мелководной акватории | 2023 |
|
RU2819199C1 |
| Способ навигации с интеграцией систем и средств обеспечения сквозного позиционирования повышенной точности и устойчивости к помехам | 2023 |
|
RU2836625C1 |
| Способ навигации и позиционирования подводных объектов в глубоководном канале на больших дальностях и система для его осуществления | 2018 |
|
RU2674404C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ | 2004 |
|
RU2275650C1 |
| СПОСОБ МНОГОПОЗИЦИОННОЙ БЛИЖНЕЙ РАДИОНАВИГАЦИИ | 2022 |
|
RU2792013C1 |
| Способ, реализующий точную помехоустойчивую синхронизацию опорных станций локальной навигационной системы | 2023 |
|
RU2827095C1 |
| ГИДРОАКУСТИЧЕСКАЯ СИНХРОННАЯ ДАЛЬНОМЕРНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ПОЗИЦИОНИРОВАНИЯ ПОДВОДНЫХ ОБЪЕКТОВ В НАВИГАЦИОННОМ ПОЛЕ ПРОИЗВОЛЬНО РАССТАВЛЕННЫХ ГИДРОАКУСТИЧЕСКИХ МАЯКОВ-ОТВЕТЧИКОВ | 2011 |
|
RU2483326C2 |
| ГИДРОАКУСТИЧЕСКАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2011 |
|
RU2477497C2 |
| СПОСОБ ЛЕТНЫХ ПРОВЕРОК НАЗЕМНЫХ СРЕДСТВ РАДИОТЕХНИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПОЛЕТОВ И УСТРОЙСТВА ДЛЯ ЕГО ПРИМЕНЕНИЯ | 2011 |
|
RU2501031C2 |
Использование: подводная, морская, наземная и околоземная навигация, в частности системы типа GPS и ГЛОНАСС. Сущность способа заключается в том, что в неизвестный для приемника момент времени синхронно излучают сигнал несколькими излучателями с известными координатами. Принимают излученные сигналы приемником, измеряют квадрат скорости сигнала в текущем навигационном сеансе, вычисляют по моментам приема излученных сигналов и измеренному квадрату скорости сигнала декартовы координаты приемника. Достигаемый технический результат - повышение точности местоопределения приемника сигнала. 2 ил.
Способ разностно-дальномерного определения декартовых координат приемника, заключающийся в синхронном излучении сигнала в неизвестный для приемника момент несколькими излучателями с известными координатами и приеме излученных сигналов приемником с последующим вычислением координат приемника, отличающийся тем, что измеряют квадрат скорости сигнала в текущем навигационном сеансе, а декартовы координаты приемника вычисляют по моментам приема излученных сигналов и измеренному квадрату скорости сигнала.
| СОЛОВЬЕВ Ю.А | |||
| Системы спутниковой навигации | |||
| - М.: Эко-Тренз, 2000, с.35-36 | |||
| СПОСОБ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ ПО ИНТЕГРАЛЬНЫМ ПАРАМЕТРАМ | 1997 |
|
RU2125732C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ МЕСТОПОЛОЖЕНИЯ, СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ ФАЗОВЫХ ЦЕНТРОВ АНТЕНН СПУТНИКОВЫХ ИСТОЧНИКОВ НАВИГАЦИОННЫХ СИГНАЛОВ И ФАЗОВЫХ ЦЕНТРОВ АНТЕНН НАВИГАЦИОННОЙ АППАРАТУРЫ ПОЛЬЗОВАТЕЛЕЙ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 2001 |
|
RU2210788C2 |
| JP 6003432, 11.01.1994 | |||
| JP 2002250764, 06.09.2002 | |||
| US 6750814 B1, 15.06.2004. | |||
Авторы
Даты
2007-11-10—Публикация
2005-07-18—Подача