Область техники
Изобретение относится к области авиации, а именно к летным исследованиям ЛА, в которых используются тросовые системы (самолет-буксировщик - трос - буксируемый летательный аппарат), кроме того, результаты оценки положения буксируемого на тросе летательного аппарата используют для определения его аэродинамических характеристик и идентификации его системы управления, для отработки системы дозаправки в воздухе, повышения качества работы транспортировки грузов и сброс их с помощью тросовых систем, отработки систем противовоздушной обороны и средств борьбы с ними в условиях, близких к реальным.
Уровень техники
Существуют разные способы определения динамических параметров поведения тросовых систем (Самолет-буксировщик - Трос - Буксируемый аппарат) для управления буксируемым аппаратом в полнонатурных исследованиях (максимально близких к реальным) их в воздушном потоке. Они используются в известных алгоритмах БЦВМ для вычисления координат буксируемого летательного аппарата. При этом учитывается, что самолет - буксировщик (СБ) может осуществлять разнообразные маневры, а также то, что буксируемый ЛА, имеющий произвольные аэродинамические компоновки и системы управления, может управляться автономно. Требуется при этих условиях определить динамические величины на тросе и у буксируемого аппарата, как в процессе стабилизации движения, так и в переходных процессах.
Использование тросовых систем в летных испытаниях является наименее затратной формой их проведения. Моделирование летно-технических характеристик ЛА с помощью тросовых систем широко используется (например, см. the US patent №5088663, 12/02/1992, «Method launching payload»), но существует значительная область, в которой в настоящее время не существует достоверной информации о поведении буксировочного троса и буксируемого ЛА. Это область касается, прежде всего, переходных процессов во время смены режимов буксирования. Хотя был наработан большой опыт в способах моделирования тросовых систем с помощью различных математических алгоритмов и были даны оценки точности соответствия их истинным значениям к летным испытаниям, в общем, их использование для точного определения динамических параметров и координат троса и буксируемого ЛА в реальном (или близком к нему) масштабе времени практически невозможно вследствие их громоздкости. Появление новых методов, которые позволили бы ввести в режимы реального времени процессы вычисления динамических параметров троса и буксируемого ЛА, как в реальном масштабе времени, так и близком к нему, их координат при различных аэродинамических компоновках и системах управления БЛА, является до настоящего времени задачей нерешенной. Новые методы, обладающие такими характеристиками, необходимы не только при летных испытаниях, но и при проведении прочих работ по буксировке ЛА и грузов. Например, ранее изучаемую задачу о дозаправке самолетов в воздухе с помощью развертываемых в воздушном потоке шлангов можно было бы смоделировать на наземных стендах и использовать для наземной тренировки летчиков с помощью компьютерных тренажеров, экономя при этом значительные материальные средства, а также можно было бы с достаточной точностью отрабатывать десантирование техники с помощью тросовых систем и ее сброс в заданные точки посадки. Рекомендации, основанные на точном знании динамики переходных процессов в режиме реального времени, могли бы упростить системы управления буксируемых ЛА. Более точное определение динамики переходных процессов тросовых систем позволит упростить схему летных испытаний, что, в свою очередь, приведет к снижению материальных затрат по их проведению. Поскольку в настоящее время отсутствуют способы определения с высокой точностью динамических параметров и координат троса и буксируемого летательного аппарата (БЛА), то используется дорогостоящий метод прямого считывания и вычисления этих данных с помощью средств радиолокационного и спутникового слежения.
Существуют сложные способы определения координат тросовой системы, Например, способ, используемый при исследовании систем дозаправки в воздухе (John С.Vassberg, David Т. Yeh, Andrew J. Blair, Jacob M. Evert (The Boeing Company-Phantom Works, Flight Technologies 5301 Bolsa Avenue, Huntington Beach, CA 92647) Dynamic characteristics of а КС-10 wing - pod refueling hose by numerical simulation, AIAA - 2002 - 2712 20 - the AIAA Applied Aerodynamics Conference 24-26 June 2002, St Louis, Missouri). Моделирование движения сложной тросовой системы по такому методу основывается на изучении образования синусоидальных волн переноса энергии и имеет сложный характер, при этом он требует большого количества машинного времени. Метод хорошо себя зарекомендовал в изучении процесса стабилизации движения тросовой системы, а использование его в изучении переходных процессов не отражает реальной физики процессов, происходящих с тросом (шлангом).
Для оценки динамики буксируемого на тросе летательного аппарата используются различные методы моделирования тросовой системы (буксировщик - трос - буксируемое тело). К наиболее известным методам моделирования относится моделирование на основе многостержневой аппроксимации троса, на ее алгоритмах основаны британский коммерческий программный продукт CBAS (Cable - Body - Aircraft - Simulator) (J.F.Henderson, B.Ireland Flight validation of computer program CBAS (cable body airborne simulator)// J Mechanical Engineering, Part G: Journal of Aerospace Engineering, Vol 210, 1996) и российский программный пакет ТАБИ (Трос-Аппарат- Буксировщик - Имитатор) (ФГУП «ЛИИ им. М.М.Громова») для использования в алгоритмах БЦВМ на борту самолета-буксировщика. Кроме того, известен метод приближенного моделирования динамики системы трос-тело в аэродинамических трубах (В.И.Валяев Приближенное моделирование динамики системы трос-тело в аэродинамической трубе, Ученые записки ЦАГИ, 1976, т.7, №3). В этом методе устанавливаются критерии построения модели для динамических испытаний в дозвуковой аэродинамической трубе, производится решение задачи движения системы трос-тело в потоке несжимаемой жидкости в продольной плоскости. Задача решена применительно к испытаниям в аэродинамической трубе при жестком закреплении троса в одной точке. Такое решение непригодно в случае пространственного движения СБ, к которому прикреплен трос.
Однако оценка динамики тросовой системы по методике моделирования многостержневой аппроксимации имеет погрешности в расчете до 30% - по амплитудам и до 25% - по частотам динамических параметров и, соответственно, координат и требует больших затрат машинного времени их расчета.
Наиболее близким способом, принятым за прототип для предлагаемого способа определения динамических параметров и координат тросовой системы, служит способ прямого вычисления текущего положения троса и буксируемого ЛА, который осуществляется с помощью различных датчиков, расположенных на тросе и буксируемом аппарате (Electrodynamic tether control, the US patent №6419191, 16/07/2002). При этом способе считывания и интерактивного вычисления данных используются датчики (сенсоры), которые, будучи расположенными на буксируемом аппарате и тросе, по каналам связи передают свое текущее положение в пространстве относительно буксировщика, а положение буксировщика и буксируемого ЛА определяют относительно земли с помощью системы GPS. При этом существует возможность считывать и вычислять положение буксировщика, троса, буксируемого ЛА с помощью БЦВМ и с наземных передвижных и стационарных радиолокационных комплексов.
К недостаткам подобных систем можно отнести высокую технологическую сложность эксперимента, существование погрешностей измерений, связанных со специфическими для данного метода расчетами (например, поправки на эффект Доплера и т.д.), погрешности спутниковой связи, высокую стоимость эксперимента и сложность универсальной математической модели движения тросовой системы для дальнейшего использования при исследованиях на стендах, а также при математическом моделировании.
Технический результат, на достижение которого направлено изобретение, - повышение точности в определении динамических параметров и координат троса и буксируемого ЛА и уменьшение затрат на обеспечение проведения летного эксперимента с использованием тросовых систем.
Для достижения названного технического результата разработана соответствующая математическая модель движения тросовой системы и метод ее моделирования, которые позволяют определять динамические параметры тросовой системы с минимальной погрешностью в режиме, близком к режиму реального времени, что позволяет прогнозировать положения троса и БЛА относительно самолета - буксировщика в процессе летных исследований. Для этого необходимо включить БЦВМ в систему самолета-буксировщика.
Отличительным признаком предложенного способа является то, что он позволяет отказаться от громоздкой и сложной системы интерактивного слежения с использованием большого количества сигнальных устройств, средств измерений и вычислений.
Предлагаемый способ определения динамических параметров и координат тросовой системы представляет собой способ задания алгоритма вычисления динамических параметров и координат троса и БЛА с высоким уровнем точности для БЦВМ, использующим режим реального времени вычисления параметров и получения из них координат троса и БЛА относительно СБ.
Раскрытие изобретения
Технической задачей предлагаемого способа является повышение точности в определении динамических параметров и координат троса и буксируемого ЛА и уменьшение затрат на обеспечение проведения летного эксперимента с использованием тросовых систем.
В способе управления тросовой системой, состоящей из буксировщика, буксируемого летательного аппарата (ЛА) и соединяющего их троса, включающем определение на коротких временных интервалах координат и скоростей троса и буксируемого ЛА относительно буксировщика, а также параметров движения и ориентации буксировщика, математическое моделирование движения тросовой системы с помощью бортовой цифровой вычислительной машины, определение в результате этого моделирования динамических параметров тросовой системы и их использование для управления данной системой, согласно изобретению, на указанных временных интервалах получают начальные и граничные условия для системы уравнений движения троса, представляемой в форме:
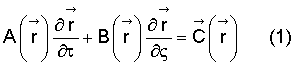
где 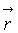 - вектор определяемых динамических параметров, включающий в себя модуль скорости, силу натяжения и углы наклона линии троса в выбранной системе координат,
- вектор определяемых динамических параметров, включающий в себя модуль скорости, силу натяжения и углы наклона линии троса в выбранной системе координат,
А и В - неособые матрицы, зависящие от указанного вектора 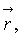 τ - безразмерное время,
τ - безразмерное время,
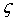 - относительная координата удаления произвольной точки троса от точки крепления троса к буксируемому ЛА, отсчитываемая вдоль линии троса (0<ζ<1),
- относительная координата удаления произвольной точки троса от точки крепления троса к буксируемому ЛА, отсчитываемая вдоль линии троса (0<ζ<1),
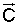 - вектор внешней вынуждающей силы, действующей на тросовую систему. При этом начальные условия получают по параметрам статических (установившихся) положений троса. Граничные условия получают следующим образом: путем измерения параметров движения и ориентации в воздушном потоке буксировщика, в качестве которого используют самолет, а также получают с помощью уравнений динамики буксируемого ЛА, в которых учитывают длину, диаметр сечения, массу и коэффициент растяжения троса, аэродинамические и физические характеристики буксируемого ЛА,
- вектор внешней вынуждающей силы, действующей на тросовую систему. При этом начальные условия получают по параметрам статических (установившихся) положений троса. Граничные условия получают следующим образом: путем измерения параметров движения и ориентации в воздушном потоке буксировщика, в качестве которого используют самолет, а также получают с помощью уравнений динамики буксируемого ЛА, в которых учитывают длину, диаметр сечения, массу и коэффициент растяжения троса, аэродинамические и физические характеристики буксируемого ЛА,
При этом на основе дискретного приращения энергии и динамических параметров тросовой системы формируют и получают эквивалентное (1) упрощенное матричное уравнение в форме:
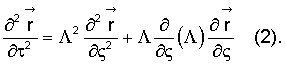
Λ=diag(λ1,...,λn) - диагональная матрица собственных чисел λi=λi(ς,τ) матрицы А-1В,
которое решают в процессе летного эксперимента на борту самолета-буксировщика с использованием указанных начальных условий и совместно с указанными граничными условиями, находя требуемые динамические параметры троса 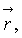 а также координаты троса и буксируемого ЛА, используемые для управления буксируемым ЛА в режиме, близком к режиму реального времени полета тросовой системы.
а также координаты троса и буксируемого ЛА, используемые для управления буксируемым ЛА в режиме, близком к режиму реального времени полета тросовой системы.
Приводимый способ поясняется следующими чертежами:
фиг.1: Схема тросовой системы, состоящей из самолета-буксировщика (14), троса (15), буксируемого летательного аппарата (16),
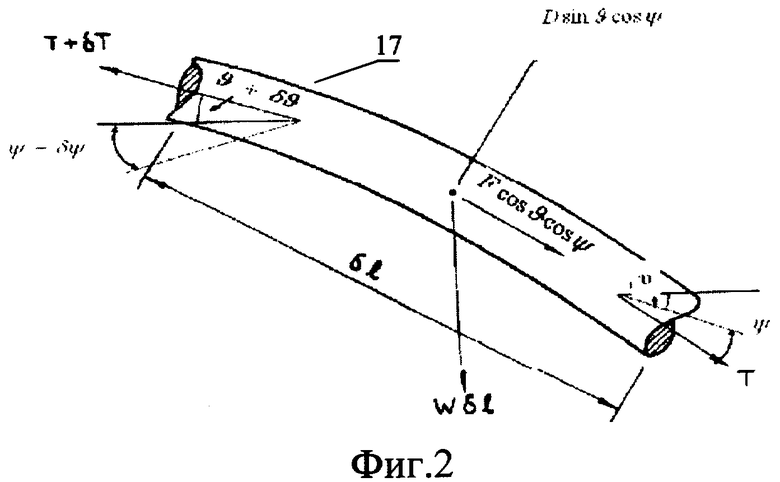
фиг.2: распределение сил на отдельном участке троса (17),
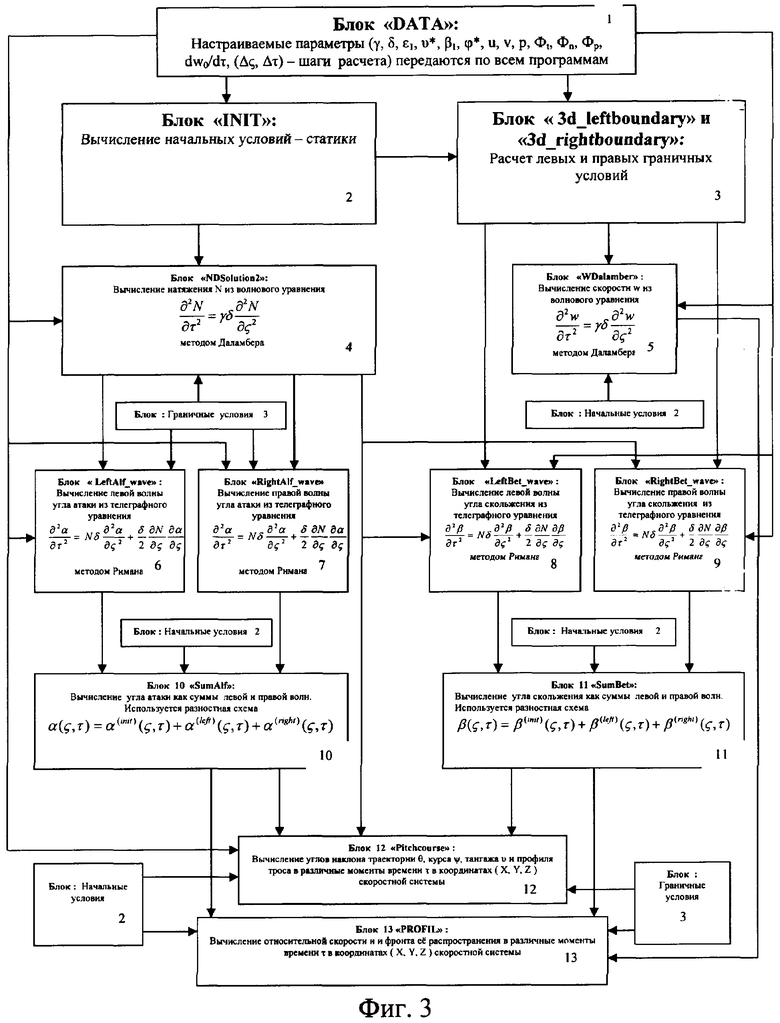
фиг.3: блок-схема программного комплекса расчета динамических параметров и координат тросовой системы,
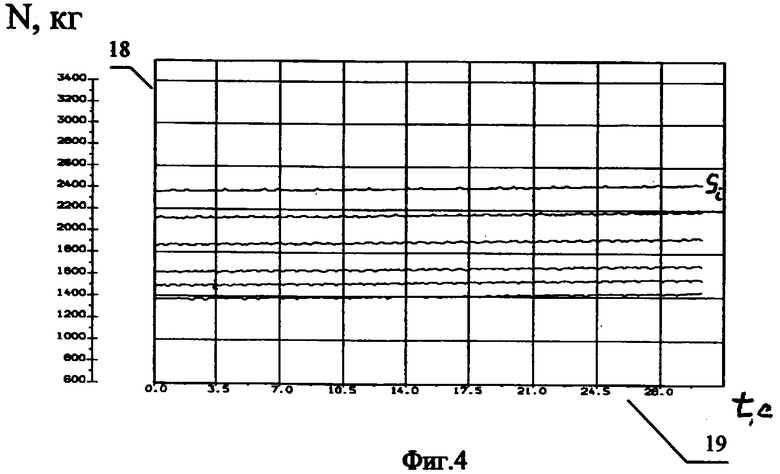
фиг.4: Динамика силы натяжения N(τ) в килограммах (18) на различные участках троса с координатами ς о времени t в секундах (19),
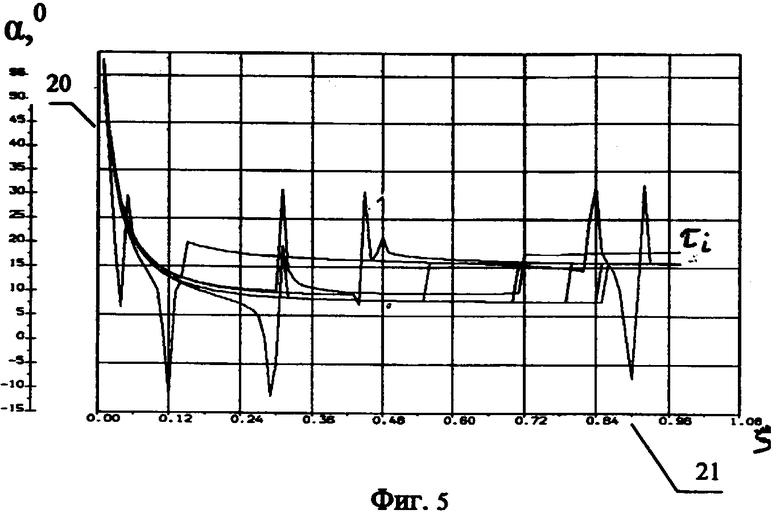
фиг.5: Распределение угла атаки α(ς) в градусах (20) в различные моменты времени τ по координатам троса ς (21),
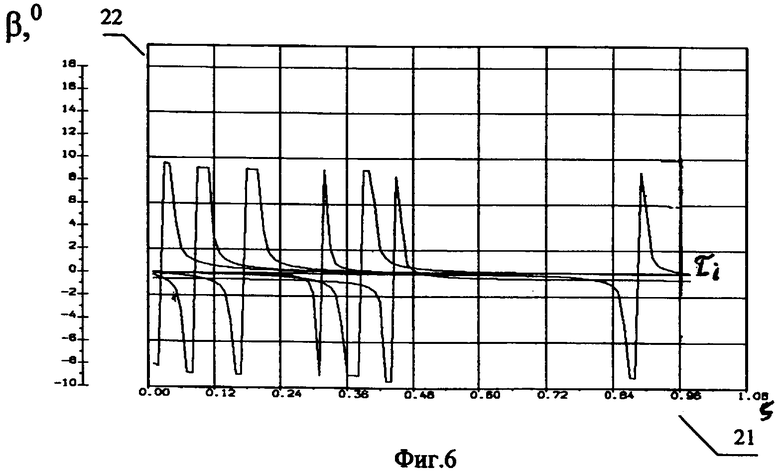
фиг.6: Распределение угла скольжения β(ς) в градусах (22) в различные моменты времени τ по координатам троса ς (21),
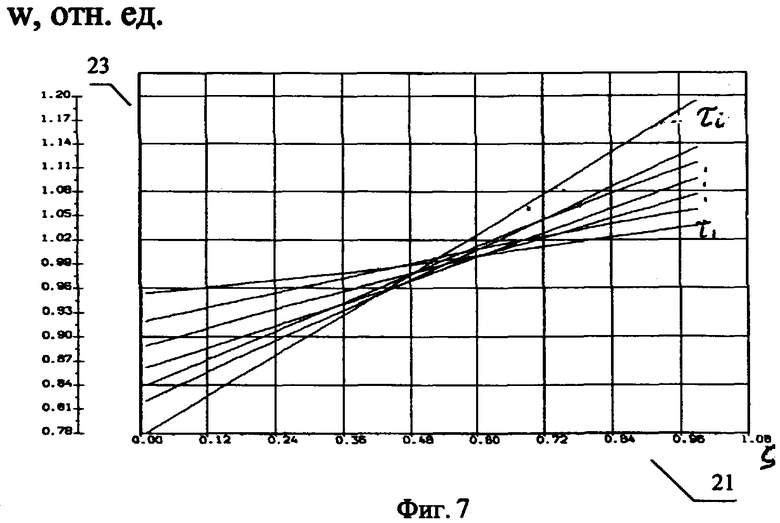
фиг.7: Распределение относительной скорости w(ς) (23), приведенной к скорости буксировки, по тросу в различные моменты времени τ по координатам троса ς (21),
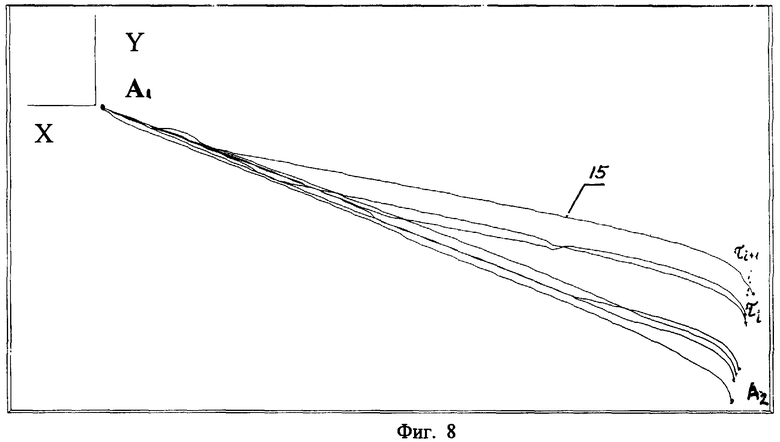
фиг.8: Профили троса при равноускоренном буксировании и попутном ветре в различные моменты времени τ, показанные в продольной плоскости XY относительно точки A1, точки крепления к самолету-буксировщику (СБ).
Способ осуществляется следующим образом.
В качестве входных параметров вводят данные измерений: скорости, высоты, угловых положений СБ, предварительно вводят физические параметры троса: его длину, диаметр, массу и коэффициент растяжения, аэродинамические и физические характеристики БЛА. Исходя из них составляют уравнения динамики СБ и БЛА. Эти системы уравнений представляют собой недоопределенные системы обыкновенных дифференциальных уравнений (ОДУ), поскольку движение буксировщика (14) и буксируемого ЛА (16) наперед неизвестны. Их решают для получения граничных условий для задачи определения динамических параметров и координат тросовой системы.
Определение динамических параметров и координат тросовой системы (см. фиг.1) представляет собой решение системы уравнений динамики и кинематики гибкого и растяжимого троса, описывающее движение троса под действием аэродинамических сил D и F, сил натяжения Т и тяжести Wδ1, которые воздействуют на элементарный участок троса (17) длины δ1 (см. фиг.2). В общем виде система представляет собой систему уравнений в частных производных гиперболического типа вида (1).
Предлагаемый метод решения задачи основывается на использовании физических зависимостей энергии тросовой системы от ее параметров. Предложен дискретный принцип учета распределения энергии и изменения параметров системы. Исходя из его допущений, можно установить, что в переходных процессах вынуждающая сила 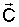 достигает своего экстремального значения и перераспределение энергии в системе происходит дискретно. Изложенные факты лежат в основе дискретно-резонансной теории изменения динамических параметров. Благодаря этому можно осуществить модификацию метода решения системы (1). Модификация системы уравнений заключается в преобразовании уравнения (1) в эквивалентное ему уравнение
достигает своего экстремального значения и перераспределение энергии в системе происходит дискретно. Изложенные факты лежат в основе дискретно-резонансной теории изменения динамических параметров. Благодаря этому можно осуществить модификацию метода решения системы (1). Модификация системы уравнений заключается в преобразовании уравнения (1) в эквивалентное ему уравнение
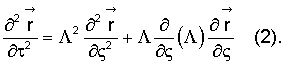
где Λ=diag(λ1,...,λn), λi=λi(ς,τ) - собственные числа матрицы А-1В.
Модификация системы уравнений (1) в систему (2) положено в основу нового численно-аналитического метода определения динамических параметров и координат, который формирует новый метод решения задачи движения тросовой системы. В конечном итоге этот метод позволил разработать предлагаемый способ определения динамических параметров и координат тросовой системы. Численно-аналитический метод решения системы уравнений (1) состоит из нескольких этапов:
1. Определение собственных чисел и собственных векторов системы (1) уравнений гиперболического типа.
2. Определение на их основе вида характеристической системы, эквивалентной системе (1).
3. Доопределение систем уравнений для граничных условий уравнениями эквивалентной характеристической системы и решение полученных систем в численном виде.
4. Определение начальных условий по параметрам статического положения троса, а именно из системы (1), в которой все производные по времени равны нулю.
5. Определение системы уравнений (2) в частных производных, решение которой эквивалентно решению данной системы уравнений (1).
6. Решение новой системы уравнений в аналитическом виде и получение ее численного решения с использованием начальных и граничных условий.
Заявленный способ, включающий определение на коротких временных интервалах координат и скоростей троса и буксируемого ЛА относительно буксировщика, а также параметров движения и ориентации буксировщика, математическое моделирование движения тросовой системы с помощью бортовой цифровой вычислительной машины, динамические параметры определяются в результате этого моделирования и их используют для управления данной системой. На указанных временных интервалах получают начальные и граничные условия для системы уравнений движения троса и решают систему (1), а точнее эквивалентную ей систему (2).
Опишем методологию проведения летных испытаний (ЛИ) с использованием предлагаемого способа. БЦВМ на буксировщике с программным обеспечением, основанном на предлагаемом алгоритме, на выбранных коротких промежутках времени осуществляют вычисление необходимых величин динамических параметров (прогнозные значения). В эти же промежутки времени на буксируемом ЛА измеряют те же динамические параметры. При этом в ходе проведения ЛИ согласно смоделированным данным можно настроить регулируемые в эксперименте параметры на буксируемом ЛА. Данные моделирования (прогнозирования) и измерений вносят на ПЗУ БЦВМ. По необходимости с борта буксировщика они могут быть ретранслированы на сопровождающие данное ЛИ станции слежения.
В ходе послеполетной обработки производят обработку данных ЛИ путем корректировки данных моделирования на имевшиеся внешние возмущения, а также производят обработку измеренных данных стандартными методами и формируют данные для следующих ЛИ. В результате послеполетной обработки производят сравнение прогнозируемой (смоделированной) и измеренной информации. В этом сравнении устанавливают характерные особенности влияния тех или иных факторов на свойства буксируемого ЛА, а также уточняют внутренние особенности его поведения. Например, такое определение может быть важно для корректировки параметров системы управления буксируемым ЛА и быть полезным в выборе ее наиболее удачной схемы.
Предлагаемый способ требует минимального количества машинного времени расчета параметров тросовой системы и координат БЛА, что выводит расчеты параметров в режим, близкий к режиму реального времени. При этом с помощью этого способа их определяют вместе с координатами на коротких интервалах по всей длине тросовой системы с высокой точностью при любых режимах буксировки. Вследствие этого способ можно использовать в алгоритмах БЦВМ самолета-буксировщика, исключив при этом большое количество устройств слежения и вычисления параметров. Для этого можно использовать только параметры, вычисляемые с помощью бортовой БЦВМ. К входным параметрам для решения уравнений вычислений относятся физические параметры троса и аэродинамические данные буксируемого ЛА, а также параметры буксировщика. Благодаря предложенному способу будут сэкономлены значительные материальные средства на летный эксперимент, прежде всего, за счет исключения большой системы измерений, предложенной в прототипе.
В заявленном способе приведен программный комплекс расчетов динамических параметров и координат тросовой системы и показана блок, схема на фиг.3, где изображены:
1 - Блок «DATA»: Настраиваемые параметры γ, δ, ε1, υ*, β1, ϕ*, u, v, p, Фt, Фn, Фр, dw0/dτ, (Δς, Δτ) - шаги расчета передаются по всем блокам.
2 - Блок «INIT»: Вычисление начальных условий - статики.
3 - Блок «3d_leftboundary» и «3d_rightboundary»: Расчет левых и правых граничных условий.
4 - Блок «NDSolution2»: Вычисление натяжения N из волнового уравнения 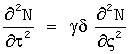 методом Даламбера.
методом Даламбера.
5 - Блок «WDalamber»: Вычисление скорости w из волнового уравнение 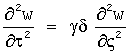 методом Даламбера.
методом Даламбера.
6 - Блок «LeftAlf_wave»:Вычисление левой волны угла атаки из телеграфного уравнения 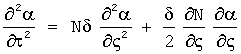 методом Римана.
методом Римана.
7 - Блок «RightAlf_wave»: Вычисление правой волны угла атаки из телеграфного уравнения 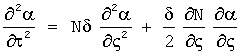 методом Римана.
методом Римана.
8 - Блок «LeftBet_wave»: Вычисление левой волны угла скольжения из телеграфного уравнения 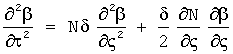 методом Римана.
методом Римана.
9 - Блок «RightBet_wave»: Вычисление правой волны угла скольжения из телеграфного уравнения 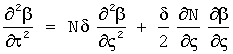 методом Римана.
методом Римана.
10 - Блок «SumAlf»: Вычисление угла атаки как суммы левой и правой волн. Используется формула α(ς,τ)=α(init)(ς,τ)+α(left)(ς,τ)+α(right)(ς,τ)).
11 - Блок «SumBet»: Вычисление угла скольжения как суммы левой и правой волн. Используется формула
β(ς,τ)=β(init)(ς,τ)+β(left)(ς,τ)+β(right)(ς,τ).
12 - Блок «Pitchcourse»: Вычисление углов наклона траектории θ, курса Ψ, тангажа υ и профиля троса в различные моменты времени τ в координатах (X, Y, Z) скоростной системы.
13 - Блок «PROFIL»: Вычисление относительной скорости и фронта ее распространения в различные моменты времени τ в координатах (X, Y, Z) скоростной системы.
Пример
Уравнение движения троса, которое выше представлялось в общем виде матричным уравнением (1), будет выглядеть, в частности, в виде системы безразмерных уравнений для возмущенного ветром движения троса при буксировке ЛА простейшей формы в виде сферы. Летательный аппарат представляет собой не просто полую сферу, а на самом деле устройство этой формы, оборудованное пневматическим двигателем малой мощности (достаточной, чтобы не искажать серьезно движение ЛА). Включение или выключение этого двигателя происходит по команде с буксировщика. Выпуск струи воздуха может происходить через специальные отверстия на корпусе ЛА, ориентированные по осям симметрии ЛА. В рассматриваемом примере для простоты полагают, что реактивное силовое действие струй воздуха 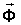 постоянно по времени.
постоянно по времени.
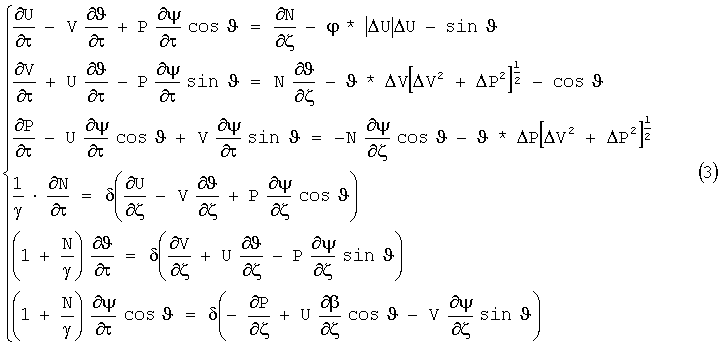
При буксировании аппарата простейшей формы в виде сферы Граничные условия представляются следующим образом:
левое граничное условие (ς=0), описывающее динамику буксируемого летательного аппарата (ЛА) простейшей формы в виде сферы, - в виде:
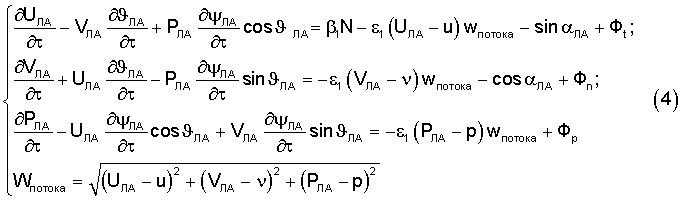
правое граничное условие (ς=1), определяемое движением самолета-буксировщика (СБ), - в виде:
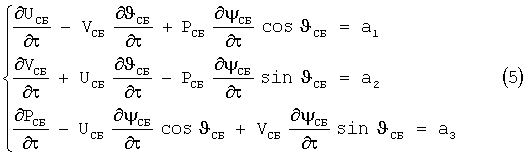
Неизвестными параметрами являются компоненты вектора скорости U, V, Р, приведенные к текущей скорости буксировки, модуль силы натяжения N, углы тангажа υ и курса ψ для элементарных участков троса,
γ - безразмерный модуль эластичности, равный 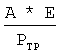 ,
,
где Е - модуль Юнга, А* - площадь сечения троса, Ртр - вес троса;
δ - безразмерный коэффициент, равный 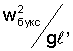
где wбукс - скорость СБ, g - ускорение свободного падения (9,8 м/с2);
ε1 - отношение силы сопротивления к весу буксируемого ЛА;
β1 - коэффициент отношения массы троса к массе буксируемого ЛА;
ϕ*, ϑ* - отношения силы сопротивления к весу троса, подъемной силы к весу троса 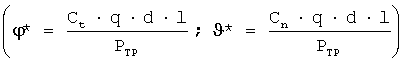 ,
,
где Ct и Cn - коэффициенты поверхностного трения и лобового сопротивления троса, q - величина скоростного напора 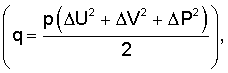 d - диаметр сечения троса;
d - диаметр сечения троса;
ΔU=U-u; ΔV=V-ν, ΔP=P-p - составляющие скорости набегающего потока на участок троса;
(UЛА,VЛА, PЛА) - скорость буксируемого ЛА;
ϑЛА, ψла - углы тангажа и курса для буксируемого ЛА (ϑЛА≈ϑ, ψла≈ψ) - на левой границе);
(UСБ, VСБ, PСБ) - скорость СБ;
ϑСБ, ψсб - углы тангажа и курса для буксируемого ЛА (ϑСБ≈ϑ, ψсб≈ψ) - на правой границе);
u, ν, p - составляющие скорости ветра в системах координат, связанных с буксируемым ЛА, либо тросом, либо СБ;
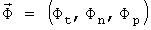 - управляющая сила от пневматического двигателя буксируемого ЛА;
- управляющая сила от пневматического двигателя буксируемого ЛА;
a1,2,3(τ) - известные составляющие ускорения СБ (для простоты рассмотрения постоянны по времени);
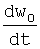 - модуль ускорения СБ, равный
- модуль ускорения СБ, равный 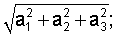
ζ - относительная координата удаления произвольной точки троса от точки крепления троса к буксируемому ЛА (0<ζ<1);
τ - безразмерное время (τ=t×g/wбукс).
Этапы построения решения системы (3) с граничными условиями (4)-(5) имеют следующую последовательность:
1. Определение собственных чисел и собственных векторов системы (3) уравнений гиперболического типа.
В приведенном примере собственные числа системы (3), описывающей динамику и кинематику троса, выглядят так:
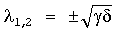
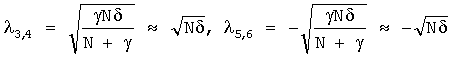
Здесь N<<γ.
2. Была построена характеристическая система, эквивалентная системе (3). Она выглядит так:
Уравнения на положительных характеристиках для корней 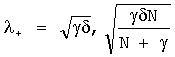 :
:
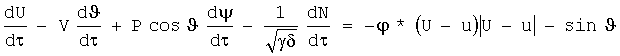
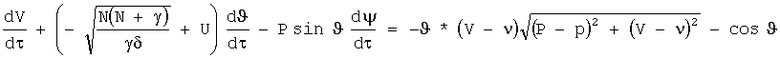
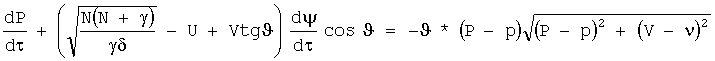
Уравнения на отрицательных характеристиках для корней 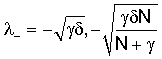 :
:
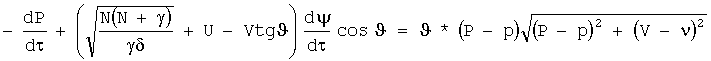
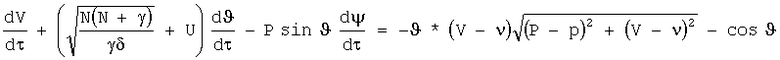
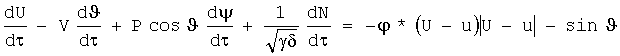
3. Доопределение систем (4)-(5) для граничных условий уравнениями эквивалентной характеристической системы и их решение в численном виде
Для левых граничных условий, описывающих движение буксируемого ЛА, такая система уравнений выглядит так:
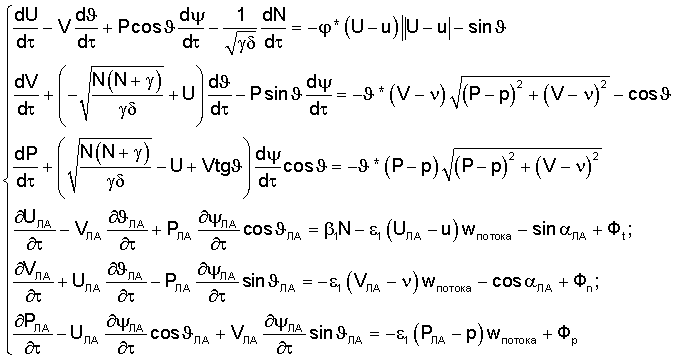
Здесь 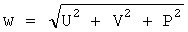 и
и 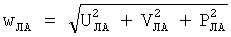 , a связь между ними выражается через соотношение Штайнера.
, a связь между ними выражается через соотношение Штайнера.
Для правых граничных условий, описывающих движение буксировщика, такая система уравнений выглядит так:
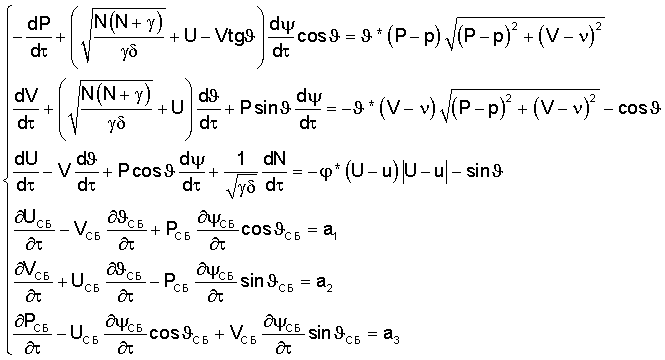
Здесь 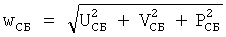 , (а1(τ),а2(τ),а3(τ)) - ускорение буксировщика, которое для примера взято с постоянными составляющими, связь между ними wСБ и
, (а1(τ),а2(τ),а3(τ)) - ускорение буксировщика, которое для примера взято с постоянными составляющими, связь между ними wСБ и 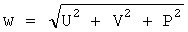 выражается через соотношение Штайнера. Из-за сложного характера эти системы решались численно.
выражается через соотношение Штайнера. Из-за сложного характера эти системы решались численно.
4. Система уравнений для определения начальных условий аналогична по сути (3) и отличается тем, что в ней приравнены к нулю все производные по времени от динамических параметров. При этом для разностной схемы вычисления компонент неизвестного вектора 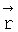 используется в качестве начальной точки значение, которое определяется из уравнений левых граничных условий (для движения буксируемого ЛА), в которых принято также равенство нулю производных динамических параметров. Решение производится численно.
используется в качестве начальной точки значение, которое определяется из уравнений левых граничных условий (для движения буксируемого ЛА), в которых принято также равенство нулю производных динамических параметров. Решение производится численно.
5. Определение новой системы уравнений в частных производных (ее общий вид (2) дан выше), решение которой эквивалентно системе (3).
После перехода от системы (3) к упрощенной системе уравнений при замене переменных U=w cos α cos β, V=w sin α cos β, P=w sin β (w - модуль вектора скорости, α и β - углы атаки и скольжения) и принятых допущениях ϑ≈α, ϑ'τ≈α'τ, ψ'τ≈β'τ была получена новая система уравнений, которая и решалась по новому методу. Эта система уравнений, полученная по формуле (2) с учетом того, что на характеристических направлениях 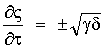 системы вычисляются неизвестные параметры N и w, а на остальных направлениях
системы вычисляются неизвестные параметры N и w, а на остальных направлениях 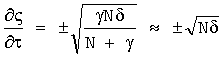 вычисляются соответственно α и β, имеет вид:
вычисляются соответственно α и β, имеет вид:
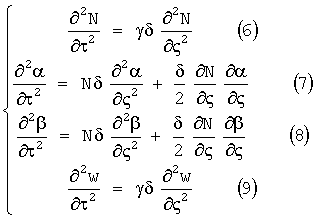
6. Решение новой системы уравнений в аналитическом виде и построение их численного решения с использованием начальных и граничных условий
Аналитическое решение уравнения (6) (для (9) - аналогично) по методу Даламбера:
N(τ,ς)=N(1)(τ,ς)+N(2)(τ,ς)+N(3)(τ,ς)
Здесь:
Решение задачи с начальным условием:
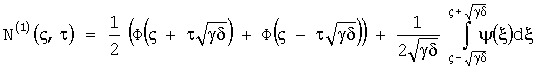
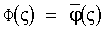 при 0≤ς≤1
при 0≤ς≤1
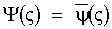 при 0≤ς≤1, где
при 0≤ς≤1, где
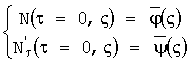 - начальные условия
- начальные условия
Ф(ς), Ψ(ς) - периодические функции с периодом 2l=2, т.е.
Ф(ς)=Ф(ς+2) и Ψ(ς)=Ψ(ς+2)
Решение краевой задачи с нулевыми начальными условиями и левым ненулевым граничным условием (N(τ,ς=0)=N0(τ)):
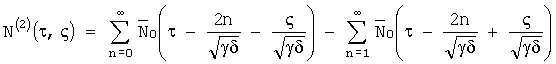
где 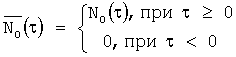
Решение краевой задачи с нулевыми начальными условиями и правым ненулевым граничным условием (N(τ,ς=1)=N1(τ)):
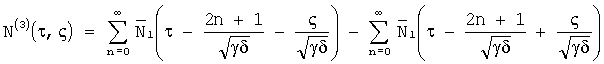
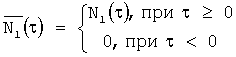
Аналитическое решение уравнения (7) (для (8) - аналогично) по методу Римана:
α(ς,τ)=α(init)(ς,τ)+α(left)(ς,τ)+α(right)(ς,τ)
Здесь
α(init)(ς,τ) - решение, получаемое из начальных условий
Решение для левой краевой задачи:

Решение для правой краевой задачи:
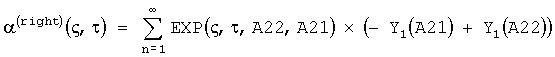
Здесь
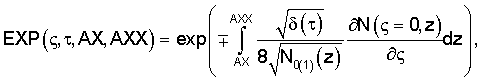
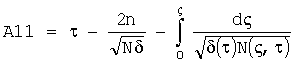 ,
, 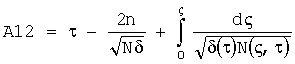 ,
,
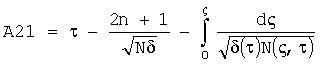 ,
, 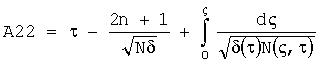 .
.
Если A11, A12, A21, A22<0, то принимаем их равными нулю.
Зная полученные при решении системы уравнений динамические параметры, можно найти неизвестные углы тангажа υ и курса ψ на всей тросовой системе. Затраты времени для расчета неизвестных параметров в одной реализации по новому методу менее 10 минут по сравнению с известными (от 2 часов и более). По предлагаемому способу динамические параметры тросовой системы и координаты БЛА получаются с высоким уровнем достоверности. Результаты расчетов динамических параметров по предлагаемому способу представлены на фиг.4-7, а координаты всей тросовой системы показаны в виде ее профилей (см. фиг.8).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ АВИАЦИОННОЙ БУКСИРОВОЧНОЙ ТРОСОВОЙ СИСТЕМОЙ | 2009 |
|
RU2395430C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ПО КРУГУ АВИАЦИОННОЙ БУКСИРОВОЧНОЙ ТРОСОВОЙ СИСТЕМЫ | 2011 |
|
RU2466062C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЕРЕХЛЕСТА БУКСИРУЕМОЙ ДВУХТРОСОВОЙ САМОЛЕТНОЙ АНТЕННЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2017 |
|
RU2658549C1 |
| Наземный подвижный стенд и способ его применения для испытаний системы автоматического управления дозаправкой в воздухе | 2023 |
|
RU2819151C1 |
| УСТРОЙСТВО ДЛЯ АЭРОГЕОФИЗИЧЕСКОЙ РАЗВЕДКИ (ВАРИАНТЫ) | 2002 |
|
RU2201603C1 |
| Способ формирования управляющего сигнала по углу крена модели гиперзвукового летательного аппарата (ГЛА) для контроля аэродинамической идентичности по числам Рейнольдса траекторий полёта модели и натурного изделия при проведении опережающих лётных исследований аэродинамических характеристик | 2017 |
|
RU2650331C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ВОЗДУШНЫХ СУДОВ | 2011 |
|
RU2460982C1 |
| СПОСОБ АВТОМАТИЗИРОВАННОЙ ОЦЕНКИ В ПОЛЕТЕ СУММАРНОЙ ТЯГИ ДВИГАТЕЛЕЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2008 |
|
RU2364846C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК ШТОПОРА МОДЕЛИ ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2410659C2 |
| Способ обеспечения вихревой безопасности летательного аппарата | 2021 |
|
RU2774083C1 |
Изобретение относится к летным исследованиям летательных аппаратов (ЛА) и может быть использовано для определения аэродинамических характеристик буксируемого ЛА и идентификации его системы управления, для отработки системы дозаправки в воздухе, транспортировки грузов и сброса их с помощью тросовых систем, отработки систем противовоздушной обороны и средств борьбы с ними. Способ включает определение на коротких временных интервалах динамических параметров, координат и скоростей троса и буксируемого ЛА с помощью соответствующих измерений и математического моделирования движения тросовой системы на борту ЛА (самолета-буксировщика). При моделировании исходная система уравнений динамики троса сводится к некоторой упрощенной характеристической системе на основе принципа дискретного приращения энергии и динамических параметров троса. Этот принцип состоит в допущении, что в переходных процессах вынуждающая сила достигает своего экстремального значения, и перераспределение энергии в системе происходит скачкообразно. Граничные условия определяются численно из систем уравнений динамики самолета-буксировщика и буксируемого ЛА. Моделирование и управление буксируемым ЛА (с помощью бортового компьютера) осуществляют в режиме, близком к режиму реального времени полета тросовой системы. Технический результат изобретения состоит в повышении точности определения динамических параметров и координат троса и буксируемого ЛА, а также в уменьшении затрат на проведение летного эксперимента с использованием тросовых систем. 8 ил.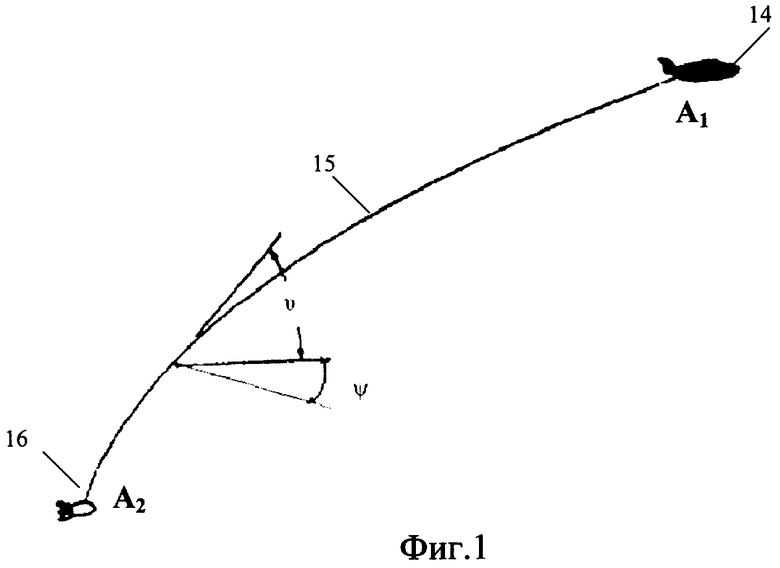
Способ управления тросовой системой, состоящей из буксировщика, буксируемого летательного аппарата (ЛА) и соединяющего их троса, включающий определение на коротких временных интервалах координат и скоростей троса и буксируемого ЛА относительно буксировщика, а также параметров движения и ориентации буксировщика, математическое моделирование движения тросовой системы с помощью бортовой цифровой вычислительной машины, определение в результате этого моделирования динамических параметров тросовой системы и их использование для управления данной системой, отличающийся тем, что на указанных временных интервалах получают начальные и граничные условия для системы уравнений движения троса, представляемой в форме
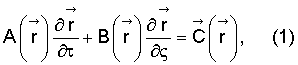
где 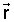 - вектор определяемых динамических параметров, включающий в себя модуль скорости, силу натяжения и углы наклона линии троса в выбранной системе координат,
- вектор определяемых динамических параметров, включающий в себя модуль скорости, силу натяжения и углы наклона линии троса в выбранной системе координат,
А и В - неособые матрицы, зависящие от указанного вектора 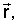
τ - безразмерное время,
ζ - относительная координата удаления произвольной точки троса от точки крепления троса к буксируемому ЛА, отсчитываемая вдоль линии троса (0<ζ<1),
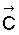 - вектор внешней вынуждающей силы, действующей на тросовую систему,
- вектор внешней вынуждающей силы, действующей на тросовую систему,
причем начальные условия получают по параметрам статических положений троса, а граничные условия получают путем измерения параметров движения и ориентации в воздушном потоке буксировщика, в качестве которого используют самолет, а также с помощью уравнений динамики буксируемого ЛА, в которых учитывают длину, диаметр сечения, массу и коэффициент растяжения троса, аэродинамические и физические характеристики буксируемого ЛА, при этом на основе принципа дискретного приращения энергии и динамических параметров тросовой системы получают эквивалентное (1) упрощенное матричное уравнение в форме
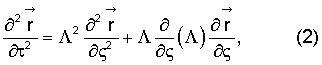
где Λ=diag(λ1,...,λn) - диагональная матрица собственных чисел λi=λi(ς,τ) матрицы А-1В,
которое решают в процессе летного эксперимента на борту самолета-буксировщика с использованием указанных начальных условий и совместно с указанными граничными условиями, находя требуемые динамические параметры троса 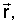 a также координаты троса и буксируемого ЛА, используемые для управления буксируемым ЛА в режиме, близком к режиму реального времени полета тросовой системы.
a также координаты троса и буксируемого ЛА, используемые для управления буксируемым ЛА в режиме, близком к режиму реального времени полета тросовой системы.
| US 6419191 А, 16.07.2002 | |||
| ЭПШТЕЙН Л.А | |||
| О моделировании динамики системы трос-тело, движущейся в воздухе | |||
| Уч | |||
| записки ЦАГИ, т.X, №1, 1979, с.64-67 | |||
| МОСОЛОВ В.Е., ЕЛИСЕЕВ A.M | |||
| Использование интеллектуальных систем в задачах управления движением тросовых систем | |||
| Н.-т | |||
| конф | |||
| проф.-преп., научного и инженерно-технического состава МТУСИ | |||
| Тезисы докладов. |
Авторы
Даты
2009-02-27—Публикация
2007-05-11—Подача