Изобретение относится к космической технике и может быть использовано в системах управления ориентацией спутников связи, снабженных бортовым радиотехническим комплексом (БРК), для выполнения своей целевой задачи.
Известны различные способы управления орбитальной ориентацией космических аппаратов (КА) [см. /1/ стр.39-58, /2/ стр.79-92]. На практике в частности применяется метод, в котором источником используемого в целях определения ориентации КА электромагнитного излучения служат звезды. В этом методе, как и в предлагаемом, по характеру излучения определяют угловое отклонение КА относительно выбранного базиса и с помощью исполнительных органов, например гиродинов, устраняют этот поворот. Практически неизменное положение звезд в инерциальном базисе и их исключительно малые угловые размеры позволяют определять ориентацию относительно инерциального базиса с очень высокой точностью, причем звезды можно найти в большей части пространства, окружающего КА. Однако существуют и проблемы: после сильных вспышек на Солнце летящие от него потоки частиц на несколько суток могут блокировать работу звездных датчиков. Экраны, способные надежно защитить от этого были бы слишком тяжелы. Кроме того, для построения и поддержания орбитальной ориентации знания положения КА относительно звезд не достаточно. Здесь дополнительно требуется знать положение местной орбитальной системы координат КА относительно инерциального базиса, что эквивалентно определению относительно инерциального базиса местной вертикали в точке нахождения КА и плоскости его орбиты. Эта задача может решаться различными путями: либо с помощью регулярных наземных измерений орбиты КА с последующей передачей результатов на борт КА, либо с помощью бортовых приборов автономной навигации, связанных с навигационными спутниковыми группировками ГЛОНАС или GPS. Таким образом, для определения и поддержания трехосной орбитальной ориентации требуется сложная, дорогостоящая специальная аппаратура с длительным непрерывным ресурсом работы. Отказы здесь - не редкость, что, приводит к тяжелым финансово-экономическим потерям. Естественно, это является существенной проблемой для создателей и заказчиков спутников. Существует другой способ построения и поддержания ориентации, использующий датчик местной вертикали и солнечный датчик. Этот способ аналогичен предыдущему, только источниками электромагнитного излучения здесь являются, соответственно, Земля и Солнце. Достоинством этого метода является то, что здесь сразу определяется орбитальная система координат. Недостатком - то, что в периоды, близкие к весеннему и осеннему равноденствию, Солнце раз в сутки находится вблизи Земли и даже прячется за Землю. На это время (до полутора-двух часов) оба датчика теряют работоспособность. Кроме того, современные требования к спутникам связи - автономная непрерывная работа в течение 15 лет, что является серьезной проблемой для любого комплекса бортовой аппаратуры.
Известен также способ управления ориентацией космического аппарата, снабженного бортовым радиотехническим комплексом, наиболее близкий из аналогов, включающий определение, построение и поддержание исходной ориентации космического аппарата, измерение исходных и текущих сигналов, связывающих бортовой радиотехнический комплекс с наземными станциями, определение по текущим и исходным сигналам текущей ориентации космического аппарата коррекцию ориентации космического аппарата. Перед началом определения по текущим и исходным сигналам текущей ориентации КА и ее коррекции определяют закон изменения сигнала путем измерения сигнала при изменении ориентации КА, обеспечивающем приращения исходного сигнала на измерительных станциях, имеющие разные знаки и амплитуды. При поддержании ориентации рассчитывают по определенному закону изменения сигнала положение оси антенны БРК, по измеренному и рассчитанному положению оси антенны БРК определяют текущую ориентацию КА и проводят коррекцию его ориентации [см. /3/].
К недостаткам данного способа следует отнести определение ориентации КА по положению оси антенны, то есть определяется одноосная ориентация КА и не распознаются повороты КА вокруг оси антенны. Так как спутникам, как правило, требуется трехосная ориентация, то для ее коррекции с использованием данного способа в общем случае дополнительно требуется какой-либо датчик, определяющий повороты КА вокруг оси антенны. Кроме того, недостатком данного способа является то, что приведенный в изобретении метод предполагает, что линии одного уровня карты диаграммы направленности должны представлять собой концентрические окружности, что реально редко может встретиться на практике. Лишь в этом случае сигнал станции зависит только от расстояния между станцией и линией визирования антенны БРК, и тогда можно установить определенный закон изменения сигнала при качании станции с разными амплитудами и знаками приращения сигнала.
Задачей предлагаемого способа является построение и поддержание трехосной ориентации КА с помощью БРК в режиме целевого функционирования при отсутствии работающей датчиковой аппаратуры, определяющей ориентацию КА.
Техническим результатом предлагаемого способа управления ориентацией космического аппарата, снабженного бортовым радиотехническим комплексом, является: расширение функциональных возможностей по сравнению с аналогом посредством обеспечения возможности построения и поддержания трехосной ориентацию КА, за счет этого экономия ресурса датчика, определяющего повороты КА вокруг оси антенны БРК, и возможность функционирования при отказах всех датчиков ориентации после определения градиентов диаграммы направленности антенны БРК.
Технический результат достигается тем, что в способе управления ориентацией космического аппарата, снабженного бортовым радиотехническим комплексом, включающем определение, построение и поддержание исходной ориентации космического аппарата, измерение исходных и текущих сигналов, связывающих бортовой радиотехнический комплекс с наземными станциями, определение по текущим и исходным сигналам текущей ориентации космического аппарата, коррекцию ориентации космического аппарата, в отличие от известных способов перед поддержанием ориентации космического аппарата его последовательно поворачивают из исходного положения вокруг трех взаимно перпендикулярных осей в обе стороны, при этом измеряют текущие сигналы наземных станций, определяют, исходя из зависимостей изменения сигналов от поворотов космического аппарата, градиенты диаграммы направленности антенны бортового радиотехнического комплекса в исходных местах нахождения наземных станций в связанном с антенной базисе, при поддержании ориентации космического аппарата определяют разности текущих и исходных сигналов, используя градиенты диаграммы направленности и полученные разности определяют поворот космического аппарата, уменьшающий его угловое отклонение от исходной трехосной ориентации, выполняют определенный поворот, опять определяют разности текущих и исходных сигналов, используя разности текущих и исходных сигналов и градиенты диаграммы направленности определяют поворот космического аппарата и так далее, при этом определяют функцию, характеризующую отклонение космического аппарата от исходной ориентации и представляющую собой сумму квадратов всех определенных разностей, в случае превышения определенной функцией заданной величины, в течение времени, зависящего от скорости приведения космического аппарата к предельной точности поддержания ориентации, определяют текущее количество сигналов станций, если оно меньше заданной величины, то сканируют пространство антенной бортового радиотехнического комплекса и ориентируют космический аппарат так, чтобы улавливать как можно больше сигналов наземных станций, выполняют приведение космического аппарата в область устойчивости процесса поддержания ориентации, для чего измеряют текущие сигналы станций и по ним определяют разности текущих и исходных сигналов, из определенных разностей вычисляют функцию, характеризующую отклонение космического аппарата от исходной ориентации, поочередно поворачивают космический аппарат на заданные углы вокруг осей связанного с ним базиса, после каждого поворота вычисляют функцию, характеризующую отклонение космического аппарата от исходной ориентации, и если она в результате поворота уменьшилась, то следующий поворот вокруг этой оси производят в ту же сторону, в противном случае - в обратную сторону, после каждого поворота вычисляют модуль изменения указанной выше функции, и если он для какой-либо из осей больше заданной величины, то продолжают выполнять определенные повороты космического аппарата, если же он для всех осей меньше заданных величин, что соответствует нахождению космического аппарата либо в минимуме, либо в точке перегиба указанной выше функции, тогда для текущего значения указанной функции выбирают наиболее близкое из предварительно определенных значений функции в точках минимума и перегиба, если это значение - ноль, то переходят к поддержанию ориентации, в противном случае по выбранной величине определяют поворот из текущей ориентации в ориентацию, близкую к исходной, выполняют этот поворот и продолжают приведение космического аппарата в область устойчивости процесса поддержания ориентации, когда модуль изменения функции, характеризующей отклонение космического аппарата от исходной ориентации, для каждой оси становится меньше заданной величины, то переходят к поддержанию ориентации.
Предлагаемый способ целесообразен для поддержания орбитальной ориентации спутников связи на геостационарной орбите с жестко закрепленной на них антенной бортового радиотехнического комплекса (БРК). Такие спутники являются одним из наиболее многочисленных классов функционирующих космических аппаратов. Для поддержания устойчивой связи с абонентами необходимо поддерживать соответствующее направление антенны, чтобы не ослабевали сигналы обмена. Тогда, естественно, возникает стремление использовать изменения этих сигналов, обусловленные отклонением антенны от оптимальной ориентации, для коррекции ориентации антенны.
Суть изобретения поясняется фиг.1-4, на которых приведены: на фиг.1 - схематичный вариант карты диаграммы направленности антенны БРК, на фиг.2 - схематичный типичный график рассчитанного элемента матрицы исходных градиентов в зависимости от величины угла поворота КА из исходного положения вокруг оси связанного с КА базиса, на фиг.3 - схематичный вариант карты диаграммы направленности антенны БРК для оценки ранга матрицы исходных градиентов, на фиг.4 - типичный путь точки, принадлежащей оси антенны БРК, при сканировании пространства, спроектированный на перпендикулярную оси антенны плоскость.
Рассмотрим более детально фиг.1. На ней представлено схематическое изображение карты диаграммы направленности антенны бортового радиотехнического комплекса (БРК) с нанесенными станциями, расположенными в городах. Эллипсы - это линии одного уровня сигнала. Вне внешнего эллипса сигнал близок к нулевому. Для получения качественного сигнала разрабатываются БРК, в диаграммах направленности которых все поверхности одного уровня сигнала охватывают друг друга без включений локальных максимумов и минимумов сигналов. Проекции этих поверхностей на плоскость, перпендикулярную оси антенны БРК, не обязательно представляют собой эллипсы (эллипс приведен здесь для примера, поскольку у российских КА диаграммы направленности имеют вытянутую форму из-за вытянутости территории России), их форма не влияет на решаемую здесь задачу. Есть только одно необходимое условие для возможности определения трехосной ориентации по изменении) сигналов: все станции не должны лежать в областях диаграммы направленности, линии одного уровня которых на карте представляют собой части концентрических окружностей, имеющих единый центр. Иначе не возможно с помощью измерения сигналов почувствовать вращение КА вокруг оси, проходящей через этот центр. Таким образом, поскольку форма линий одного уровня сигнала не играет роли, то она на всех фигурах изображена весьма схематично.
Введем связанный с КА ортонормированный базис с осями x, y, z таким образом, чтобы ось x была направлена вдоль оси антенны БРК. Поскольку здесь рассматриваются КА на геостационарной орбите, и таким образом они висят над выбранными точками экватора, то орбитальный базис можем определить как ортонормированный базис с осями X, Y, Z, у которого одноименные оси совпадают с осями связанного базиса при идеальной ориентации КА относительно поверхности Земли. Эту ориентацию КА будем называть орбитальной или исходной. Для исходной ориентации КА координаты наземных станций могут быть рассчитаны с высокой точностью; назовем эти координаты станций исходными, а положения станций в исходных координатах - исходными положениями.
Рассмотрим диаграмму направленности принимающей антенны БРК КА (фиг.1). Каждой точке диаграммы направленности можно поставить в соответствие градиент сигнала по перемещению в связанном базисе - вектор 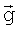 с компонентами {∂u/∂x; ∂u/∂y; ∂u/∂z}, где u - принимаемая мощность радиосигнала (или просто «сигнал») от точечного источника радиосигнала единичной мощности. В дальнейшем будем называть такой вектор градиентом по перемещению. Градиенты по перемещению в исходных координатах станций назовем исходными градиентами по перемещению. Каждой точке диаграммы направленности также можно поставить в соответствие градиент сигнала по повороту КА - вектор с компонентами {∂u/∂φx; ∂u/∂φy; ∂u/∂φz}, где u - принимаемая мощность радиосигнала от неподвижного точечного источника радиосигнала постоянной мощности,
с компонентами {∂u/∂x; ∂u/∂y; ∂u/∂z}, где u - принимаемая мощность радиосигнала (или просто «сигнал») от точечного источника радиосигнала единичной мощности. В дальнейшем будем называть такой вектор градиентом по перемещению. Градиенты по перемещению в исходных координатах станций назовем исходными градиентами по перемещению. Каждой точке диаграммы направленности также можно поставить в соответствие градиент сигнала по повороту КА - вектор с компонентами {∂u/∂φx; ∂u/∂φy; ∂u/∂φz}, где u - принимаемая мощность радиосигнала от неподвижного точечного источника радиосигнала постоянной мощности, 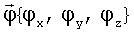 - вектор поворота КА вокруг связанных осей (последовательность поворотов здесь не играет роли). В дальнейшем будем называть такой вектор просто градиентом. Градиенты в исходных положениях станций для конкретных станций назовем исходными градиентами (этот вектор рассчитывается для конкретной мощности источника). Если антенна БРК работает на излучение, то все аналогично.
- вектор поворота КА вокруг связанных осей (последовательность поворотов здесь не играет роли). В дальнейшем будем называть такой вектор просто градиентом. Градиенты в исходных положениях станций для конкретных станций назовем исходными градиентами (этот вектор рассчитывается для конкретной мощности источника). Если антенна БРК работает на излучение, то все аналогично.
Пусть имеются станции в количестве mmax. Каждой из них присвоим номер m (m≤mmax). Обозначим как um сигнал m-й станции. Измерим все um в исходной ориентации КА на геостационарной орбите, назовем их исходными сигналами и обозначим u0m.
Предположим КА находится в требуемой точке геостационарной орбиты, а его ориентация близка к орбитальной (исходной) ориентации.
Запишем приближенное значение вектора перемещения в связанном базисе относительно исходного положения всех m-х станций: 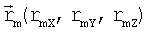 в зависимости от вектора отклонения КА на малый угол:
в зависимости от вектора отклонения КА на малый угол: 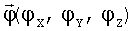 и исходных положений станций:
и исходных положений станций: 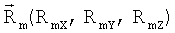 :
:
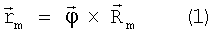
Вычислим все
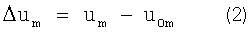
где um - текущий сигнал m-й станции, а u0m - исходный сигнал m-й станции.
Запишем приближенное выражение для Δum:
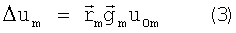
где
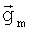 - вектор исходного градиента по перемещению m-й станции
- вектор исходного градиента по перемещению m-й станции
Подставив (1) в (3), получим:
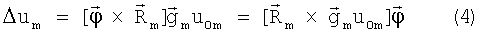
Введем в (4) обозначение: вектор 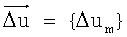 , Q - матрица, у которой m-е строки есть:
, Q - матрица, у которой m-е строки есть: 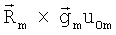 . В результате из (4) получим для всех станций:
. В результате из (4) получим для всех станций:
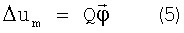
Очевидно, что m-е строки матрицы Q (обозначим Qm) - вектора исходных градиентов m-х станций по повороту КА, или, как было условлено, просто исходные градиенты станций. Поэтому назовем матрицу Q матрицей исходных градиентов.
Покажем как определить матрицу градиентов Q. Повернем КА последовательно на малые углы вокруг осей X, Y, Z. Тогда из (5) получим:
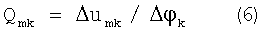
где
Qmk - элементы матрицы Q
Δumk - приращения сигналов m-х станций при повороте вокруг k-х осей от значений угла от -φk до +φk (при φk=0 КА находится в исходной ориентации).
Δφk=(+φk)-(-φk)=2φk (считаем φk>0)
Таким образом (6) преобразуется:
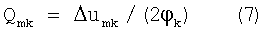
Теперь для каждого Qmk необходимо выбрать оптимальную величину φk такую, чтобы рассчитанное из (7) значение Qmk имело минимальную погрешность. Для этого рассчитаем погрешность Qmk, для чего продифференцировав (7), получим:
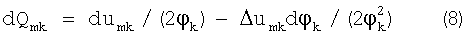
Взяв абсолютную величину от правой и левой частей, и взяв максимальное значение правой части (сумма модулей больше либо равна модулю суммы) получим:
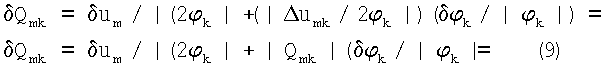
где
δQmk - максимальная абсолютная величина погрешности k-й компоненты исходного градиента m-й станции;
δum - максимальная абсолютная величина погрешности измерения изменения сигнала m-й станции;
δφk - максимальная абсолютная величина погрешности знания φk-го угла поворота КА.
Учитывая, что |2φk||Qmk|=|Δumk|, из (9) получаем выражение для относительной погрешности k-й компоненты исходного градиента m-й станции:
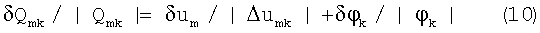
Правая часть (9) с ростом φk, очевидно, уменьшается, то есть уменьшается погрешность вычисления Qmk по формуле (6). Однако с ростом φk начинает изменяться реальная величина Qmk, поскольку градиенты в общем случае Qm меняются. А так как нам нужно измерить Qmk при φk=0, то это означает, что с ростом φk растет систематическая погрешность вычисления Qmk по формуле (6), что не учитывается формулой (9). На фиг.2 дан схематичный график вычисляемой по формуле (6) величины Qmk (на фиг.2 обозначено как q) в зависимости от величины φk (на фиг.2 обозначено как φ). Погрешность вычисления Qmk складывается из случайной и систематической погрешностей. То есть это отклонение измеряемой величины Qmk от реального начального ее значения (на фиг.2 - разность ординат кривой и прямой, параллельной оси абсцисс). При малых φ превалирует случайная погрешность, что на графике условно показано как колебания q, при больших φ превалирует систематическая погрешность, что на графике условно показано, как равномерный уход q от реального значения. Случайные погрешности δum для всех станций можно определить во время измерения исходных сигналов, если измерять их достаточно длительно. Погрешности δφk известны заранее. Таким образом, случайная погрешность δQmk в соответствии с (9) известна при всех измерениях. Встает задача выбора наиболее подходящего с точки зрения минимума погрешности измеренного значения Qmk. Пронумеруем все результаты измерений величины Qmk, тогда (7) приобретет вид:
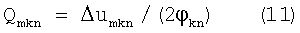
где n - номер измерения (с ростом n растет φkn)
Обозначим:
Qmkn - n-е измеренное значение Qmk;
Qmk - реальное значение при φk=0;
D+ mkn=Qmkn+δQmkn верхний допуск Qmk при n-м измерении;
D- mkn=Qmkn-δQmkn нижний допуск Qmk при n-м измерении
δQmkn - абсолютное значение погрешности Qmkn, рассчитанное из (9) для конкретного φkn.
Если бы не систематическая погрешность, реальное значение Qmk лежало бы между допусками при любом n:
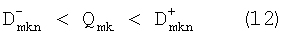
Назовем:
D+c mk и D-c mk - согласованными допусками, формируемыми по алгоритму:
при n=1: D+c mk=D+ mk1; D-c mk=D- mk1 (при этом очевидно, что в силу (12) D-c mk<D+c mk); далее при увеличении n на 1 корректируем D+c mk и D-c mk, исходя из логики:
если D- mkn>D-c mk, то D-c mk=D- mkn;
если D+ mkn<D+c mk, то D+c mk=D+ mkn;
и так до тех пор, пока D-c mk>D+c mk или n станет максимальным; в первом случае обозначаем предыдущее значение n как nmk0 и возвращаем параметрам D+c mk и D-c mk значения при n=nmk0; после этого D+c mk и D-c mk окончательно сформированы.
Когда D+c mk и D-c mk окончательно сформированы вычисляем компоненту матрицы исходных градиентов:
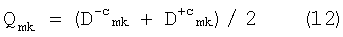
Ясно, что, если систематическая погрешность отсутствует (что в нашем случае не возможно), то в силу (12) момент D-c mk>D+c mk не наступит никогда. Если он все же наступает, то это означает, что при n=nmk0+1 систематическая погрешность Qmk превысила случайную.
Указанным выше путем можно рассчитать матрицу градиентов Q при нахождении КА в требуемой точке геостационарной орбиты в орбитальной (исходной) ориентации.
Теперь предположим, что в процессе поддержания ориентации связанный базис КА отклонился от орбитального на такой малый угол, что матрица градиентов, соответствующая этому положению КА, практически не отличается от матрицы исходных градиентов Q. Обратимся теперь опять к (5). Это избыточная система линейных уравнений mmax-го порядка. Рассчитаем 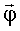 из условия минимума функции (метод наименьших квадратов):
из условия минимума функции (метод наименьших квадратов):
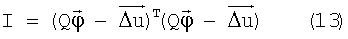
Заметим, что это возможно, когда количество станций (mmax) не меньше трех. Дифференцируя в (13) I по 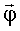 и приравнивая эти частные производные к нулю, получим систему линейных уравнений 3-го порядка:
и приравнивая эти частные производные к нулю, получим систему линейных уравнений 3-го порядка:
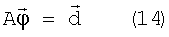
где
- A=QTQ (симметрическая матрица 3×3);
- 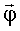 - вектор с компонентами {φx; φy; φz};
- вектор с компонентами {φx; φy; φz};
- 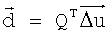 .
.
Если mmax=3, то метод наименьших квадратов вырождается в обычное решение линейной системы уравнений третьего порядка.
Таким образом, вычисляем вектор углового отклонения КА от орбитальной (исходной ориентации):
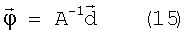
где A-1 - матрица, обратная к А.
Отметим, что для получения (15) связанный с КА ортонормированный базис можно было бы выбрать не так, как это было в начале, а произвольным образом.
Также отметим, что компоненты матрицы A-1 (как и матрицы A) - постоянные величины и могут быть вычислены раз и навсегда.
Более легкая, но аналогично решаемая задача получается, если какие-либо компоненты 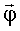 определяются отдельно с помощью каких-либо датчиков и тогда линейные системы (14) и (15) порядка меньше чем 3.
определяются отдельно с помощью каких-либо датчиков и тогда линейные системы (14) и (15) порядка меньше чем 3.
Теперь возьмем скалярное произведение векторов правой и левой частей (5):
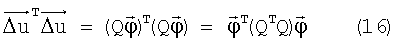
Это согласно обозначениям (14) есть:
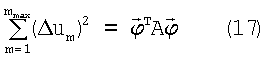
Справа и слева (17) квадратичные формы. Запишем ортогональное преобразование квадратичной формы в правой части (17) с помощью ортогональной матрицы T. Из (17) получаем:
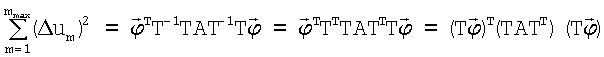
Поскольку матрица A - симметрическая, то, как известно, всегда можно подобрать такую ортогональную матрицу T, которая преобразует матрицу A к диагональному виду. Таким образом, обозначив 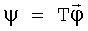 (что есть переход к другому связанному с КА ортонормированному базису, путем поворота, поэтому
(что есть переход к другому связанному с КА ортонормированному базису, путем поворота, поэтому 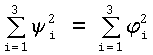 ), преобразуя последнее уравнение, получим:
), преобразуя последнее уравнение, получим:
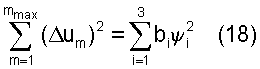
где bi>0 (bi - не отрицательны, поскольку 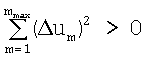 ;
;
bi≠0, поскольку ортогональные преобразования - есть повороты и потому не меняют ранги матриц, а ранг матрицы A равен трем). Из (18) видно, что рост угла отклонения КА от исходного положения приводит к увеличению суммы квадратов Δum. Уменьшение суммы квадратов Δum приводит к уменьшению отклонения КА от исходного положения, а сведение суммы квадратов Δum к нулю приводит КА в исходное положение. Введем обозначение:
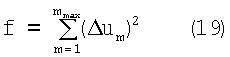
Очевидно, что 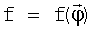 . Таким образом, функция f может служить для оценки величины углового отклонения КА от исходной ориентации.
. Таким образом, функция f может служить для оценки величины углового отклонения КА от исходной ориентации.
Для того чтобы в (15) матрица A-1 существовала, необходимо, чтобы детерминант матрицы A был отличен от нуля (если он в близи нуля, то будут большие вычислительные погрешности при решении системы линейных уравнений (14)), а для этого необходимо, чтобы ранг матрицы A был равен трем. Для этого, прежде всего, количество станций должно быть не меньше трех. Далее поскольку матрица A является квадратом матрицы Q, то ранг матрицы A равен рангу матрицы Q. Поэтому ранг матрицы Q должен быть равен трем. Покажем, что существуют случаи, когда ранг матрицы Q при наличии трех станций равен трем. Рассмотрим систему из трех станций, расположенных относительно диаграммы направленности антенны, как показано на фиг.3 (для простоты и наглядности линии одного уровня сигнала даны как прямоугольники). Положение станций здесь обозначено пронумерованными точками, а стрелки в этих точках обозначают местные градиенты по перемещению 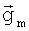 . Выпишем явно матрицу Q (см. (4), (5):
. Выпишем явно матрицу Q (см. (4), (5):
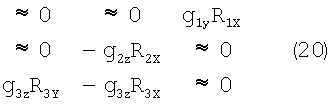
Детерминант этой матрицы есть g1Y R1X g2Z R2X g3Z R3Y≠0, следовательно, ранг равен трем, что и требовалось доказать.
Поскольку в соответствии с обозначением (5) строками матрицы Q являются векторные произведения векторов 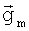 и
и 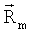 , а вектора
, а вектора 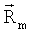 - близки в силу значительности расстояния от Земли до геостационарной орбиты по сравнению с расстоянием от станций до оси X (RmX>>RmY, RmX>>RmZ), то можно считать, что условием минимальности вычислительных погрешностей при решении системы линейных уравнений (5), будет наличие значительно отличающихся по направлению исходных градиентов станций
- близки в силу значительности расстояния от Земли до геостационарной орбиты по сравнению с расстоянием от станций до оси X (RmX>>RmY, RmX>>RmZ), то можно считать, что условием минимальности вычислительных погрешностей при решении системы линейных уравнений (5), будет наличие значительно отличающихся по направлению исходных градиентов станций 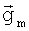 .
.
Кроме того, значительность расстояния от Земли до геостационарной орбиты по сравнению с расстоянием от станций до оси X (RmX>>RmY, RmX>>RmZ) приводит к тому, что, согласно обозначению(5):
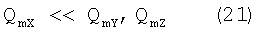
(как пример см. (20)). Запишем теперь погрешность измерения вектора углового поворота по i-й оси δφi, в зависимости от погрешностей измерений сигналов δum. Полагая по другим осям нулевые углы, из (5) получаем:
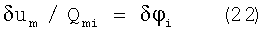
Таким образом, в силу (21) погрешность определения отклонения КА от орбитальной ориентации вокруг оси Х существенно выше в сравнении с погрешностями определения отклонения КА от орбитальной ориентации вокруг осей Y и Z. Уравнение (5) также может быть использовано для расчета изменения сигнала Δum в зависимости от отклонения КА от исходной ориентации на φi. Полагая по другим осям нулевые углы, из (5) получаем:
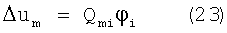
Отсюда видно, что сигналы um, в силу (21) гораздо менее чувствительны к поворотам вокруг оси X, чем вокруг других осей, а, значит, требования пользователей связи к точности ориентации по оси Х гораздо менее жесткие, чем по другим осям. Таким образом, повышенная погрешность в определении углового отклонения КА вокруг оси Х компенсируется соответствующим пониженным требованием к точности ориентации вокруг этой оси.
Итак, предположим, что вектор углового отклонения КА от орбитальной ориентации 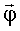 из (15) рассчитан. Повернем КА в соответствии с этим вектором, но в обратную сторону, устраняя таким образом угловое отклонение КА. Так как (1) и (3) носят приближенный характер, то угловое отклонение КА от орбитальной ориентации не будет полностью устранено, однако (если позволяет точность измерений сигналов) квадрат углового отклонения уменьшится. Тогда (1) и (3) станут более точным приближением к реальности и можно будет более точно из (15) рассчитать
из (15) рассчитан. Повернем КА в соответствии с этим вектором, но в обратную сторону, устраняя таким образом угловое отклонение КА. Так как (1) и (3) носят приближенный характер, то угловое отклонение КА от орбитальной ориентации не будет полностью устранено, однако (если позволяет точность измерений сигналов) квадрат углового отклонения уменьшится. Тогда (1) и (3) станут более точным приближением к реальности и можно будет более точно из (15) рассчитать 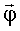 и опять устранить это угловое отклонение КА, и так далее. В результате КА получит орбитальную ориентацию с точностью, определяемой: точностью измерения сигналов станций, конфигурацией диаграммы направленности антенны, расположением станций, точностью исполнительных органов, параметрами системы управления КА.
и опять устранить это угловое отклонение КА, и так далее. В результате КА получит орбитальную ориентацию с точностью, определяемой: точностью измерения сигналов станций, конфигурацией диаграммы направленности антенны, расположением станций, точностью исполнительных органов, параметрами системы управления КА.
До сих пор рассматривался случай, когда матрица градиентов Q для любого текущего положения КА мало отличалась от исходной. Это условие выполняется при небольших отклонениях КА от исходной ориентации. Если отклонение становится достаточно большим, то представленный выше процесс приведения ориентации КА к требуемой (назовем этот процесс поддержанием ориентации) теряет устойчивость. Область векторов поворота КА 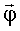 , где описанный процесс поддержания ориентации обладает устойчивостью, назовем областью устойчивости поддержания ориентации или просто областью устойчивости. Эта область определяется областью
, где описанный процесс поддержания ориентации обладает устойчивостью, назовем областью устойчивости поддержания ориентации или просто областью устойчивости. Эта область определяется областью 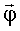 , в которой матрица градиентов Q близка к исходной. При регулярном измерении сигналов станций и штатной работе исполнительных органов выхода КА из области устойчивости не происходит. Однако иногда могут случаться временные перебои с измерениями сигналов станций или возникают иные временные проблемы, из-за которых КА выходит из области устойчивости, и после устранения проблем вернуться в эту область с помощью процесса поддержания ориентации не возможно. Измерение матрицы текущих градиентов Q не помогает, так как уравнение (5) (где Q - матрица текущих градиентов), все равно не верно. Верным является уравнение:
, в которой матрица градиентов Q близка к исходной. При регулярном измерении сигналов станций и штатной работе исполнительных органов выхода КА из области устойчивости не происходит. Однако иногда могут случаться временные перебои с измерениями сигналов станций или возникают иные временные проблемы, из-за которых КА выходит из области устойчивости, и после устранения проблем вернуться в эту область с помощью процесса поддержания ориентации не возможно. Измерение матрицы текущих градиентов Q не помогает, так как уравнение (5) (где Q - матрица текущих градиентов), все равно не верно. Верным является уравнение:
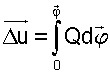
Здесь вычислить интеграл не представляется возможным. В такой ситуации нужна другая последовательность действий (назовем ее построением ориентации), позволяющая КА вернуться в область устойчивости. Опишем эту последовательность.
Предварительно рассмотрим вопрос сканирования пространства антенной БРК, цель которого - привести КА в ориентацию, при которой как можно большее число станций находилось бы в зоне диаграммы направленности антенны. Способы сканирования могут быть различны, приведем один из них. Предположим, нет ни одной станции в зоне диаграммы направленности антенны БРК, то есть сигналы всех станций практически равны нулю. Будем двигать ось x связанного с КА базиса по спирали (примерный типичный путь оси x при сканировании дан на фиг.4, где движение оси x происходит от точки А к точке В). Если шаг спирали достаточно мал, то неизбежно в какой-то момент какая-то станция попадет в зону диаграммы направленности антенны БРК. Тогда будем двигать ось x змейкой в направлении от первоначального положения оси x, при этом амплитуда качания осью x из стороны в сторону нужно делать такой, чтобы при каждом отклонении в сторону все станции выходили из зоны диаграммы направленности. Будем двигаться змейкой до тех пор, пока сигналы станций перестанут появляться (из-за удаления оси x от станций они перестанут попадать в зону диаграммы направленности). При движении змейкой запомним положение оси x, когда количество сигналов от станции было максимальным. После окончания движения змейкой переместим ось x в это положение. Далее будем поворачивать КА вокруг оси x и запомним положение, когда количество сигналов от станции было максимальным. После полного оборота повернем КА вокруг оси x в положение максимума количества получаемых сигналов. Теперь большое количество станций находятся в зоне диаграммы направленности антенны БРК, сканирование окончено.
Если сканирование начинается, когда есть сигнал по крайней мере одной станции, будем двигать ось x связанного с КА базиса по спирали до тех пор, пока при движении по виткам спирали появляются сигналы станций. При движении по спирали запомним положение оси x, когда количество сигналов от станции было максимальным. После окончания движения по спирали переместим ось x в положение, соответствующее максимальному количеству сигналов от станций. Далее будем поворачивать КА вокруг оси x и запомним положение, когда количество сигналов от станции было максимальным. После полного оборота повернем КА вокруг оси x в положение максимума количества получаемых сигналов. Сканирование окончено.
Оптимальные параметры сканирования такие как: скорость, шаг спирали, шаг и амплитуда змейки и др. должны быть выбраны заранее, исходя из конфигурации диаграммы направленности, расположения станций, характеристик системы управления и др. Обычно это делается с помощью наземного компьютерного моделирования.
Рассмотрим теперь функцию, которая уже определялась в (19):
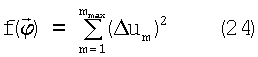
где Δum - разности текущих и исходных значений сигнала. Эта функция однозначна, положительно определена и имеет абсолютный минимум в нуле, равный нулю, то есть f(0)=0. Однако она может иметь и локальные минимумы, максимумы и перегибы, которых, как правило, не много, во всяком случае - счетное число (при количестве станций в зоне диаграммы направленности антенны больше 2). Поскольку диаграмма направленности антенны БРК заранее известна, то не составляет большой проблемы перед полетом КА рассчитать с использованием компьютеров все точки локальных минимумов и перегибов (высокой точности здесь не требуется), обозначим их
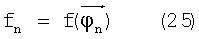
(обозначим за f0 - абсолютный минимум, то есть f0=f(0)=0). Тогда становятся известны и значения обратной функции в этих точках экстремума:
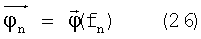
Следует заметить, что в (26), вообще говоря, 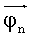 - многозначная функция. Однако отметим, что не следует искать локальных экстремумов, в таких областях
- многозначная функция. Однако отметим, что не следует искать локальных экстремумов, в таких областях 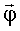 , которым соответствует ситуация, когда в зоне диаграммы направленности антенны БРК меньше трех станций, так как в этих областях бесконечно много точек экстремума (как было показано выше, в этом случае ранг матрицы местных градиентов меньше трех). Более того, как было показано, сканированием пространства можно добиться того, что в зоне диаграммы направленности антенны будут находиться почти все станции, поэтому для поиска fn можно ограничиться только областью
, которым соответствует ситуация, когда в зоне диаграммы направленности антенны БРК меньше трех станций, так как в этих областях бесконечно много точек экстремума (как было показано выше, в этом случае ранг матрицы местных градиентов меньше трех). Более того, как было показано, сканированием пространства можно добиться того, что в зоне диаграммы направленности антенны будут находиться почти все станции, поэтому для поиска fn можно ограничиться только областью 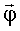 , которой соответствует ситуация, когда в зоне диаграммы направленности антенны БРК находится большая часть станций. Например, если линии одного уровня сигнала на карте диаграммы направленности напоминают эллипс, то в силу инвариантности картинки эллипса относительно поворота на угол π вокруг центра фактически существует только один локальный минимум fn, требующий определения, который получается поворотом КА вокруг оси x из исходного положения на угол, примерно равный π. Это справедливо практически для любой диаграммы направленности вытянутой формы с большим количеством станций. Если в этом локальном минимуме fn близка к нулю, то это означает, что все сигналы станций близки к оптимальным значениям и спутник может хорошо функционировать и в этом положении и, то есть существует два глобальных минимума.
, которой соответствует ситуация, когда в зоне диаграммы направленности антенны БРК находится большая часть станций. Например, если линии одного уровня сигнала на карте диаграммы направленности напоминают эллипс, то в силу инвариантности картинки эллипса относительно поворота на угол π вокруг центра фактически существует только один локальный минимум fn, требующий определения, который получается поворотом КА вокруг оси x из исходного положения на угол, примерно равный π. Это справедливо практически для любой диаграммы направленности вытянутой формы с большим количеством станций. Если в этом локальном минимуме fn близка к нулю, то это означает, что все сигналы станций близки к оптимальным значениям и спутник может хорошо функционировать и в этом положении и, то есть существует два глобальных минимума.
Кроме того, следует заметить, что найденные fn и 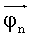 соответствуют только определенному набору станций. Если состав станций меняется, то необходимо пересчитать fn и
соответствуют только определенному набору станций. Если состав станций меняется, то необходимо пересчитать fn и 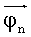 .
.
Реальные диаграммы направленности антенн спутников связи не симметричны, поэтому мало вероятно, особенно при большом количестве станций, что будут очень близкие по значению fn. Если все же такое случиться, то можно исключить из рассмотрения сигнал от одной станции и тогда значения fn изменятся, и еще менее вероятно, что после этого проблема останется. Таким образом, в дальнейшем будем считать, что все значения fn существенно различны, то есть функция 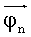 из (26) - однозначна.
из (26) - однозначна.
Теперь вернемся к рассмотрению КА на геостационарной орбите, имеющему некоторое отклонение от исходной ориентации. Повернем КА на некоторый малый угол δφp вокруг оси p связанного с КА базиса (ось p есть либо ось x, либо ось y, либо ось z), при этом функция f изменится на величину δfp. Очевидно, что, повернув теперь КА на угол -δφop, мы вернемся в предыдущее положение и получим изменение -δfp. Запишем выражение для дифференциала δfp:
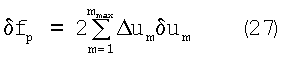
Теперь продифференцируем (23):
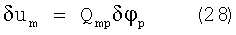
Подставим (28) в (27) и, вынеся δφp за знак суммы, получим:
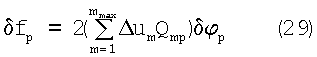
Из (29) видно, что при неизменном δφp знак и величина δfp зависят от знака и величины
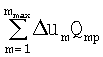 ,
,
которые при достаточно малой по модулю величине δφp меняются достаточно медленно. Поэтому знак и величина δfp имеют определенную консервативность.
На базе вышесказанного, предложим последовательность приведения КА в область устойчивого поддержания ориентации (как уже говорилось, назовем его построением ориентации). Если количество сигналов от станций меньше некоторой величины (из-за того, что большое количество станций находятся вне зоны диаграммы направленности антенны БРК), которая определяется на этапе наземного компьютерного моделирования, то проводим описанное выше сканирование пространства антенной БРК, в результате получаем достаточное количество сигналов от станций. Далее осуществляем приведение к экстремуму функции f, то есть поочередно поворачиваем КА на малые углы δφp (оптимальные величины δφp определяются на этапе наземного компьютерного моделирования и зависят от конфигурации диаграммы направленности антенны БРК, расположения станций, точности измерения сигналов, точности работы исполнительных органов, параметров системы управления и др.) вокруг связанных осей КА по отдельности (p=x, y, z), причем для каждой оси применяется логика: если при повороте на δφp получаем δfp≥0, то в следующие повороты вокруг оси р поворачивать будем на -δφp (как было показано выше, при этом будем получать δfp<0), пока опять не получим при повороте на -δφp изменение δfp≥0, тогда в дальнейшем будем поворачивать вокруг оси р на углы δφp и так далее, до тех пор пока для всех трех осей не станет верным соотношение:
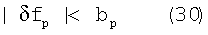
(приход к истинности соотношения (30) в любом случае неизбежен, поскольку функция/положительно определена и не может бесконечно уменьшаться). Величина bp в основном зависит от погрешностей измерения сигналов, конфигурации диаграммы направленности антенны БРК, расположения станций, величины δφp, и определяется при наземном компьютерном моделировании; выполнение соотношения (30), очевидно, означает, что КА пришел в точку экстремума: либо минимум, либо точка перегиба. Определяем ближайшее к f значение из заранее определенных значений fn - (значение функции в точках минимума и перегиба, см. (25)); если fn>0, то делаем поворот на заранее рассчитанный вектор - 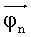 (то есть приводим КА в ближайшую окрестность орбитальной ориентации см. (26)) и продолжаем выполнять приведение к экстремуму функции f (теперь этот экстремум уже будет глобальным минимумом), если fn=0 (это означает, что достигнут глобальный минимум функции f и КА - в орбитальной ориентации), то переходим к поддержанию ориентации (поскольку поддержание ориентации в области устойчивости более точно и быстро приводит КА к орбитальной ориентации).
(то есть приводим КА в ближайшую окрестность орбитальной ориентации см. (26)) и продолжаем выполнять приведение к экстремуму функции f (теперь этот экстремум уже будет глобальным минимумом), если fn=0 (это означает, что достигнут глобальный минимум функции f и КА - в орбитальной ориентации), то переходим к поддержанию ориентации (поскольку поддержание ориентации в области устойчивости более точно и быстро приводит КА к орбитальной ориентации).
Вернемся к поддержанию ориентации. Для него необходимо найти критерий перехода к построению ориентации. Переходить нужно, очевидно, тогда когда отклонение КА от орбитальной ориентации в целом не уменьшается из-за того, что КА вышел из области устойчивости (назовем ситуацией 1), и переходить не нужно, когда КА не вышел из области устойчивости, а отклонение КА от орбитальной ориентации в целом не уменьшается из-за того, что достигнут предел возможности приближения к орбитальной ориентации (назовем ситуацией 2). Заметим, что предел приближения зависит от погрешностей измерения сигналов, погрешностей исполнительных органов, погрешностей измерения ориентации КА при определении матрицы исходных градиентов, упругих колебаний конструкции КА, свойств алгоритмов системы управления КА и т.д.
Проведем сравнение величины функции f в ситуации 1 и ситуации 2. В окрестности своего глобального минимума функция f очевидно близка к нулю, это есть ситуация 2. Согласно (18), если КА выходит из области устойчивости, функция f велика по сравнению с ее значениями в ситуации 2. В локальных минимумах функция f может значительно уменьшиться, но попадание в локальный минимум маловероятно, так как применение поддержания ориентации вне области устойчивости приводит к хаотичному движению. Как уже говорилось выше, как правило, из-за асимметрии диаграммы направленности антенны в локальных минимумах функция f значительно больше, чем в глобальном минимуме. Если же все-таки это не так, то близость f к нулю означает, что все сигналы близки к оптимальным значениям, и ориентацию менять не нужно, то есть КА в другом глобальном минимуме и имеет место ситуация 2.
Таким образом, в ситуации 1 функция f всегда больше, чем в ситуации 2. Значит, для того, чтобы отличать ситуацию 1 от ситуации 2, нужно подобрать некоторую величину fс такую, чтобы в ситуации 1 гарантированно было f>fс, а в ситуации 2 - гарантированно было f<fс. Выше отмечалось, что предел возможности приближения КА к орбитальной ориентации и величины локальных минимумов зависят от множества факторов, поэтому все эти факторы должны быть учтены при выборе fc.
Опишем теперь последовательность действий при поддержании ориентации. Измеряем Δum, где Δum - разность текущего значения сигнала и исходного, из этих значений составляем вектор 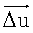 . Зная матрицу исходных градиентов Q (эта матрица должна быть определена перед применением поддержания ориентации, ранее было показано как это сделать, кроме того, перед применением поддержания ориентации необходимо вычислить матрицу А-1=(QTQ)-1), вычисляем
. Зная матрицу исходных градиентов Q (эта матрица должна быть определена перед применением поддержания ориентации, ранее было показано как это сделать, кроме того, перед применением поддержания ориентации необходимо вычислить матрицу А-1=(QTQ)-1), вычисляем 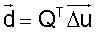 . Из (15) определяем отклонение КА от орбитальной системы координат - вектор поворота
. Из (15) определяем отклонение КА от орбитальной системы координат - вектор поворота 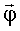 . Поворачиваем КА в соответствии с вектором поворота -
. Поворачиваем КА в соответствии с вектором поворота - 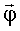 . Опять измеряем Δum и так далее. При этом осуществляем следующую логику: если в течение некоторого времени tc будет f>fс; (ограничения на значение fc обсуждались непосредственно перед описанием последовательности поддержания ориентации), то переходим к построению ориентации (за величину tc можно принять, например, максимальное время приведения КА от границы области устойчивости к предельной точности поддержания ориентации).
. Опять измеряем Δum и так далее. При этом осуществляем следующую логику: если в течение некоторого времени tc будет f>fс; (ограничения на значение fc обсуждались непосредственно перед описанием последовательности поддержания ориентации), то переходим к построению ориентации (за величину tc можно принять, например, максимальное время приведения КА от границы области устойчивости к предельной точности поддержания ориентации).
Таким образом, с помощью использования заявляемого способа после определения градиентов диаграммы направленности антенны БРК при поддержании и построении ориентации решается задача оптимальной ориентации антенны на абонентов без использования для этих целей каких-либо датчиков ориентации. С помощью режима поддержания ориентации осуществляется быстрое и точное приведение антенны к оптимальной ориентации из области устойчивости и далее продолжение поддержания этой ориентации. Кроме того, в этом режиме осуществляется контроль за ориентацией, и в случае выхода из области устойчивости запускается режим построения ориентации. Режим построения ориентации приводит КА в область устойчивости поддержания ориентации и запускает режим поддержания ориентации.
Источники информации
1. И.Ф.Кавинов. Инерциальная навигация в околоземном пространстве. М., Машиностроение, 1988 г.
2. Б.В.Раушенбах, Е.Н.Токарь. Управление ориентацией космических аппаратов. М., Наука, 1974 г.
3. RU 2191721 С1, 2001.02.05.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ ГЕОСТАЦИОНАРНОГО КОСМИЧЕСКОГО АППАРАТА, ОСНАЩЕННОГО РАДИОМАЯКОМ | 2006 |
|
RU2354590C2 |
| Способ управления ориентацией космического аппарата, снабженного бортовым ретрансляционным комплексом | 2021 |
|
RU2761363C1 |
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА, СНАБЖЕННОГО БОРТОВЫМ РАДИОТЕХНИЧЕСКИМ КОМПЛЕКСОМ | 2001 |
|
RU2191721C1 |
| СПОСОБ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА НА ПЛАНЕТУ | 1991 |
|
RU2021173C1 |
| Способ управления космическим аппаратом дистанционного зондирования Земли | 2019 |
|
RU2722598C1 |
| СПОСОБ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ПО МЕСТНОЙ ВЕРТИКАЛИ ПЛАНЕТЫ | 1991 |
|
RU2021174C1 |
| Способ спутниковой гравитационной градиентометрии | 2020 |
|
RU2745364C1 |
| СПОСОБ ПОДДЕРЖАНИЯ ТРЕХОСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА С СИЛОВЫМИ ГИРОСКОПАМИ И ЦЕЛЕВОЙ НАГРУЗКОЙ | 2006 |
|
RU2341419C2 |
| Способ ориентации околоземного орбитального космического аппарата | 2021 |
|
RU2779658C1 |
| УСТРОЙСТВО ДЛЯ ОЦЕНКИ ХАРАКТЕРИСТИК ЗОНЫ НАЧАЛЬНОГО ПОИСКА СВЯЗНЫХ КОСМИЧЕСКИХ АППАРАТОВ | 2003 |
|
RU2242790C1 |
Изобретение относится к космической технике и может быть использовано в системах управления ориентацией спутников связи, снабженных бортовым радиотехническим комплексом, для выполнения своей целевой задачи. Способ управления ориентацией космического аппарата заключается в определении градиентов диаграммы направленности антенны бортового радиотехнического комплекса при поддержании и построении ориентации антенны на абонентов без использования каких-либо датчиков. Достигается расширение функциональных возможностей и возможность функционирования при отказе всех датчиков ориентации после определения градиентов диаграммы направленности антенны бортовым радиотехническим комплексом. 4 ил.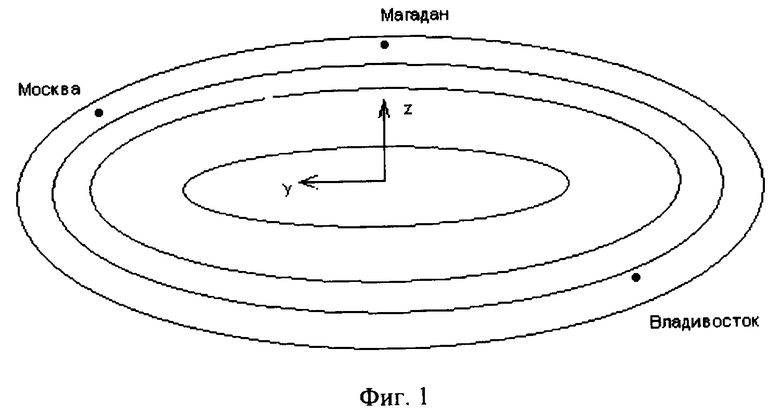
Способ управления ориентацией космического аппарата, снабженного бортовым радиотехническим комплексом, включающий определение, построение и поддержание исходной ориентации космического аппарата, измерение исходных и текущих сигналов, связывающих бортовой радиотехнический комплекс с наземными станциями, определение по текущим и исходным сигналам текущей ориентации космического аппарата, коррекцию ориентации космического аппарата, отличающийся тем, что перед поддержанием ориентации космического аппарата его последовательно поворачивают из исходного положения вокруг трех взаимно перпендикулярных осей в обе стороны, при этом измеряют текущие сигналы наземных станций, определяют, исходя из зависимостей изменения сигналов от поворотов космического аппарата градиенты диаграммы направленности антенны бортового радиотехнического комплекса в исходных местах нахождения наземных станций в связанном с антенной базисе, при поддержании ориентации космического аппарата определяют разности текущих и исходных сигналов, используя градиенты диаграммы направленности и полученные разности определяют поворот космического аппарата, уменьшающий его угловое отклонение от исходной трехосной ориентации, выполняют определенный поворот, опять определяют разности текущих и исходных сигналов, используя разности текущих и исходных сигналов и градиенты диаграммы направленности определяют поворот космического аппарата и так далее, при этом определяют функцию, характеризующую отклонение космического аппарата от исходной ориентации и представляющую собой сумму квадратов всех определенных разностей, в случае превышения определенной функцией заданной величины, в течение времени, зависящего от скорости приведения космического аппарата к предельной точности поддержания ориентации, определяют текущее количество сигналов станций, если оно меньше заданной величины, то сканируют пространство антенной бортового радиотехнического комплекса и ориентируют космический аппарат так, чтобы улавливать как можно больше сигналов наземных станций, выполняют приведение космического аппарата в область устойчивости процесса поддержания ориентации, для чего измеряют текущие сигналы станций и по ним определяют разности текущих и исходных сигналов, из определенных разностей вычисляют функцию, характеризующую отклонение космического аппарата от исходной ориентации, поочередно поворачивают космический аппарат на заданные углы вокруг осей связанного с ним базиса, после каждого поворота вычисляют функцию, характеризующую отклонение космического аппарата от исходной ориентации, и, если она в результате поворота уменьшилась, то следующий поворот вокруг этой оси производят в ту же сторону, в противном случае - в обратную сторону, после каждого поворота вычисляют модуль изменения указанной выше функции, и, если он для какой-либо из осей больше заданной величины, то продолжают выполнять определенные повороты космического аппарата, если же он для всех осей меньше заданных величин, что соответствует нахождению космического аппарата либо в минимуме, либо в точке перегиба указанной выше функции, тогда для текущего значения указанной функции выбирают наиболее близкое из предварительно определенных значений функции в точках минимума и перегиба, если это значение - ноль, то переходят к поддержанию ориентации, в противном случае по выбранной величине определяют поворот из текущей ориентации в ориентацию, близкую к исходной, выполняют этот поворот и продолжают приведение космического аппарата в область устойчивости процесса поддержания ориентации, когда модуль изменения функции, характеризующей отклонение космического аппарата от исходной ориентации, для каждой оси становится меньше заданной величины, то переходят к поддержанию ориентации.
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА, СНАБЖЕННОГО БОРТОВЫМ РАДИОТЕХНИЧЕСКИМ КОМПЛЕКСОМ | 2001 |
|
RU2191721C1 |
| КРАН | 1997 |
|
RU2141400C1 |
| СПОСОБ УПРАВЛЕНИЯ ПЕРЕОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА И СИСТЕМА УПРАВЛЕНИЯ ПЕРЕОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА | 1992 |
|
RU2076833C1 |
| WO 9418073 A1, 18.08.1994. | |||
Авторы
Даты
2009-05-10—Публикация
2006-10-19—Подача