Изобретение относится к космонавтике, а именно к управлению ориентацией космических аппаратов (КА).
Известен способ трехосной ориентации КА в орбитальной системе координат (ОСК) [1] по информации от прибора ориентации на Солнце (ПОС). В этом способе управление ориентацией КА выполняется по информации ПОС и заключается в том, что в бортовую вычислительную машину вводят параметры орбиты КА, рассчитывают положения Солнца в поле обзора ПОС для каждой точки орбиты из условия ориентации КА в орбитальной системе координат. Задают КА поисковую угловую скорость для обеспечения захвата Солнца в поле обзора ПОС, после чего снижают вплоть до нуля угловую скорость, обеспечивая нахождение Солнца в поле обзора ПОС. Затем производят разворот КА таким образом, чтобы Солнце в поле зрения ПОС переместилось в требуемую начальную рассчитанную точку. Далее непрерывно разворачивают КА таким образом, чтобы Солнце в поле зрения ПОС перемещалось по рассчитанным ранее точкам.
Этот способ управления позволяет упростить конструкцию КА при обеспечении условий ориентации КА в ОСК, но не решает задачу трехосной ориентации в инерциальной системе координат (ИСК). Кроме того, из-за ограничения поля зрения ПОС элементами конструкции КА (особенно в сложных конструкциях, например орбитальных станциях) для решения задачи его ориентации на всех участках орбиты понадобится использовать несколько таких приборов. Это затрудняет решение задачи управления ориентацией предлагаемым способом КА. Использование рассматриваемого способа невозможно также на участках орбиты, затененных от Солнца Землей.
Наиболее близким из аналогов является способ управления трехосной ориентацией КА с помощью инерционных исполнительных органов [2], используемый в качестве прототипа. Способ включает в себя математическое моделирование орбиты космического аппарата, измерение параметров его углового движения, измерение кинетического момента в системе силовых гироскопов, определение, построение и поддержание по ним заданной ориентации космического аппарата.
Построение и поддержание ориентации КА производится в ОСК по информации от построителя местной вертикали (ПМВ), прибора планетной ориентации (ППО), ПОС и датчика угловой скорости (ДУС). При этом в качестве исполнительных органов используется двухстепенной силовой гиростабилизатор (ГС) и реактивные двигатели (РД).
В основном режиме система ориентации должна обеспечить постоянное удержание связанных с КА (OX, OY, OZ) и орбитальных осей (ОХо, OYo, OZo) в совмещенном с заданной точностью положении. В качестве осей ориентации выбраны орбитальные оси, начало которых расположено в центре масс КА. Ось ОХо направлена по текущему радиус-вектору КА, ось OYo - по текущему вектору линейной скорости КА, ось OZo дополняет систему координат до правой.
Управление по тангажу θ и крену ϕ осуществляется по сигналам ПМВ.
Отработка внешних возмущающих моментов по тангажу достигается разгоном или торможением маховика гиростабилизатора по сигналу ошибки θ.
Для управления ориентацией по крену ϕ и курсу ψ используется известный метод связывания скрытого кинетического момента СГ с корпусом КА (см. [3], стр.444-522), в соответствии с которым используются свойства вращающегося тела, стремящегося сохранить направление своего вращения в тем большей степени, чем больше его кинетический момент.
Сигнал ошибки по крену измеряется ПМВ и поступает на управляющие обмотки датчика момента СГ, который создает управляющий момент, пропорциональный входному сигналу. Таким образом к гиростабилизатору и к корпусу КА прикладываются разные и противоположно направленные моменты, пропорциональные сигналу ошибки по крену. Под действием датчика момента гиростабилизатор поворачивается относительно корпуса КА на некоторый угол β, оставаясь в инерциальном пространстве неподвижным. Одновременно КА поворачивается в пространстве до полной отработки ошибки по крену ϕ.
Если управление по тангажу и крену ведется идеально, то ось ОХ постоянно сохраняет заданное направление на Землю. Поэтому в инерциальном пространстве спутник вращается вокруг оси OZ с орбитальной угловой скоростью. В то же время при малых возмущающих моментах вектор кинетического момента гиростабилизатора остается в этом пространстве неподвижным. Вектор СГ 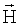 , составляющий с осью OZ(OZo) угол β, должен лежать в плоскости XOZ КА, поскольку СГ может поворачиваться относительно корпуса спутника только в этой плоскости.
, составляющий с осью OZ(OZo) угол β, должен лежать в плоскости XOZ КА, поскольку СГ может поворачиваться относительно корпуса спутника только в этой плоскости.
В случае, если ось OZ не совпадает с осью OZo, имеет место переход отклонения гиростабилизатора β в отклонение корпуса спутника по курсу ψ, поскольку другие отклонения (θ и ϕ) отсутствуют. Таким образом, производится математическое моделирование орбиты и поддержание ОСК, реализуемое по указанным датчикам внешней информации при помощи СГ. При накоплении СГ предельно допустимых значений кинетического момента осуществляется его разгрузка с использованием РД.
В прототипе в качестве КА рассматривается геостационарный спутник связи (ГСС) «Экран», целевой нагрузкой которого являются космические станции (КС) системы спутникового телевещания. Рабочими параметрами КС являются: рабочий диапазон частот, добротность, эквивалентная изотропно излучаемая мощность (ЭИИМ) каждого передатчика, поляризация излучаемого и принимаемого сигналов. Уровень сигнала в «точке прицеливания» (в точке пересечения оси главного лепестка антенны ГСС с земной поверхностью) может служить основным рабочим параметром, подтверждающим штатную ориентацию спутника.
Описанный способ трехосной ориентации имеет минимальный приборный состав и простую высоконадежную аппаратуру, что позволяет рассчитывать на обеспечение значительного полетного ресурса КА. В то же время обеспечивается высокая точность ориентации КА, которая не превышает нескольких угловых минут.
Недостатком способа управления, описанного в прототипе, является то, что отсутствует резерв управления ориентацией КА, позволяющий поддерживать его трехосную ориентации без использования ПМВ, ППО, ПОС и ДУС, что в случаях ограниченного ресурса указанных приборов, их полного или частичного отказа не позволяет увеличить время эксплуатации КА. Кроме этого, невозможность в течение какого-либо интервала времени использовать указанные приборы приведет к потере КА штатной ориентации и, как следствие, к невыполнению им штатной программы полета. Рассматриваемый способ управления не обеспечивает также поддержание ориентации КА в ИСК.
Техническим результатом предлагаемого решения является создание способа поддержания трехосной ориентации КА в ОСК, ИСК, позволяющего сохранить штатную ориентацию в условиях отсутствия информации от приборов, измеряющих параметры углового движения КА. Предлагаемый способ повышает надежность управления ориентацией и увеличивает срок эксплуатации КА.
Технический результат достигается тем, что в предлагаемом способе поддержания трехосной ориентации космического аппарата с силовыми гироскопами и целевой нагрузкой, включающем математическое моделирование орбиты космического аппарата, измерение параметров его углового движения, определение, построение и поддержание по ним заданной ориентации космического аппарата, измерение кинетического момента в системе силовых гироскопов, в отличие от известного способа по измеренным параметрам углового движения и значениям кинетического момента силовых гироскопов определяют параметры действующих на космический аппарат возмущающих моментов, определяют номинальные рабочие параметры целевой нагрузки при штатной ориентации космического аппарата, определяют интервалы времени (ti0, tik), на которых измерение параметров углового движения не производится, где i=1, 2, ..., n - указанные интервалы времени, по измеренным на момент времени начала i-го интервала параметрам углового движения космического аппарата и кинетического момента его силовых гироскопов, а также с учетом внешних возмущающих моментов, рассчитанных с использованием определенных ранее параметров возмущающих моментов, прогнозируют на i-м интервале изменения кинетического момента в системе силовых гироскопов, соответствующие поддержанию заданной ориентации на i-м интервале, далее для поддержания заданной ориентации космического аппарата воздействуют на силовые гироскопы таким образом, чтобы их кинетический момент в каждый момент времени i-го интервала соответствовал спрогнозированному, измеряют рабочие параметры целевой нагрузки и сравнивают их с номинальными параметрами, в случае соответствия сравниваемых параметров продолжают управление ориентацией космического аппарата по спрогнозированному кинетическому моменту, в противном случае с момента времени ti1 взаимного несоответствия указанных параметров целевой нагрузки повторно измеряют параметры углового движения, определяют по ним текущую ориентацию космического аппарата, строят заданную ориентацию на интервале времени (ti1, ti') и повторно определяют параметры возмущающих моментов, действующих на космический аппарат, далее при выполнении условия (ti1, ti')∈(ti0, tik) с использованием измеренных на момент времени ti1 значений вектора кинетического момента силовых гироскопов и параметров углового движения прогнозируют изменение кинетического момента силовых гироскопов на оставшейся части i-го интервала, учитывая при этом внешние возмущающие моменты, рассчитанные с использованием повторно определенных ранее параметров возмущающих моментов, и продолжают управлять ориентацией космического аппарата на указанном i-м интервале по вновь спрогнозированному кинетическому моменту для системы силовых гироскопов, в противном случае продолжают управление ориентацией космического аппарата по измеряемым параметрам углового движения до очередного (i+1)-го интервала, далее повторяют управление космическим аппаратом вышеуказанным образом на (i+1)-м интервале по спрогнозированным значениям вектора кинетического момента для системы силовых гироскопов с последующим переходом на управление ориентацией космического аппарата по измеряемым параметрам его углового движения и заканчивают процесс управления поддержанием трехосной ориентации космического аппарата по спрогнозированным значениям вектора кинетического момента силовых гироскопов по истечению n-го интервала.
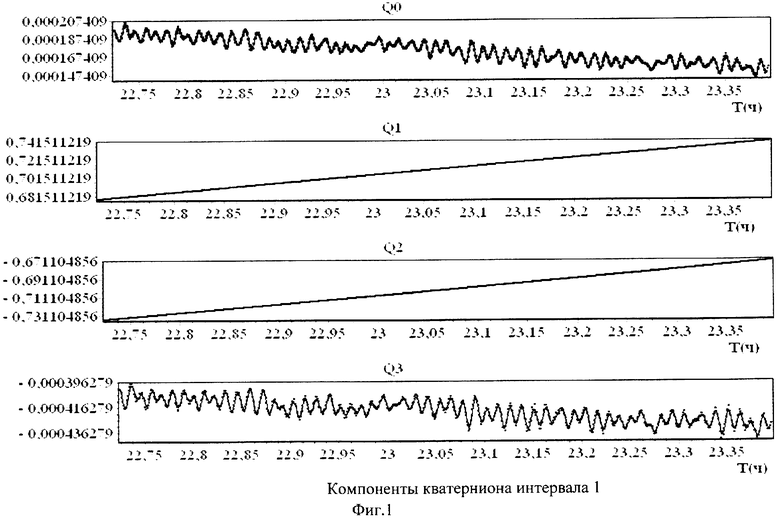
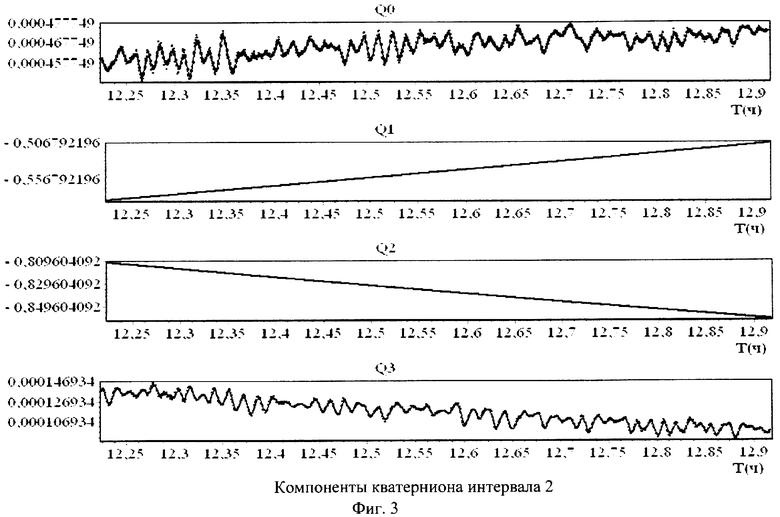
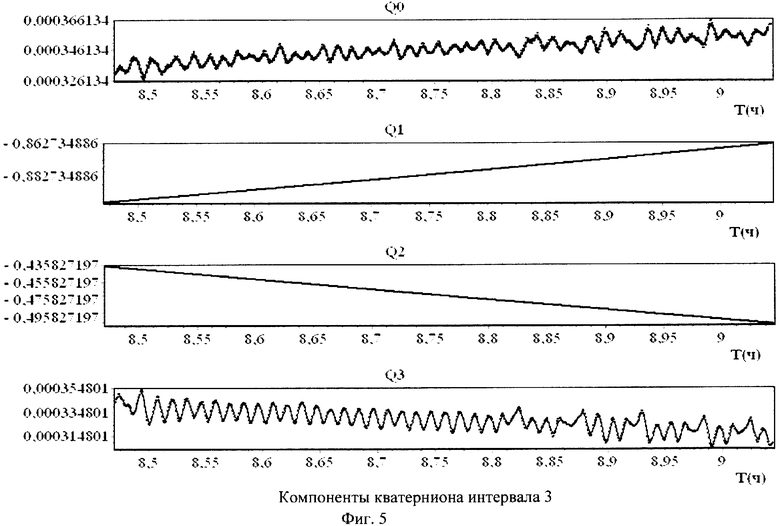
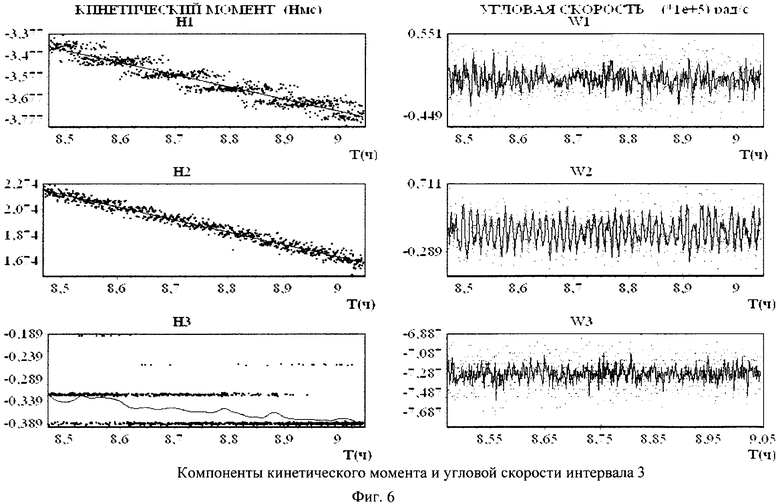
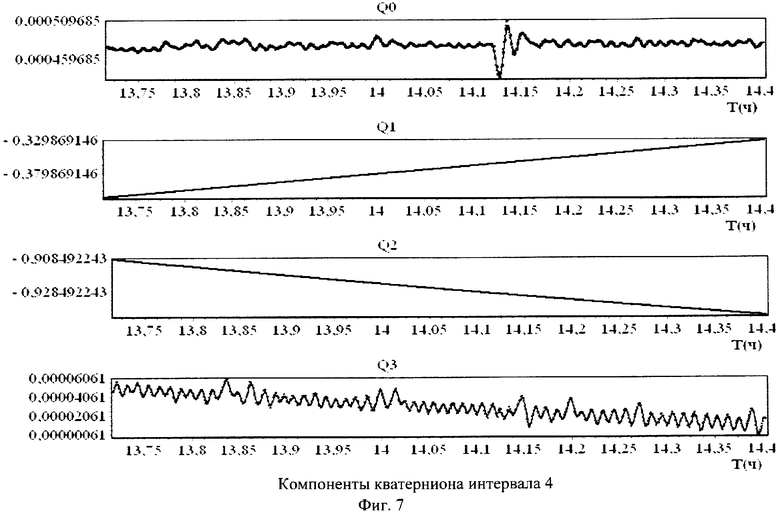
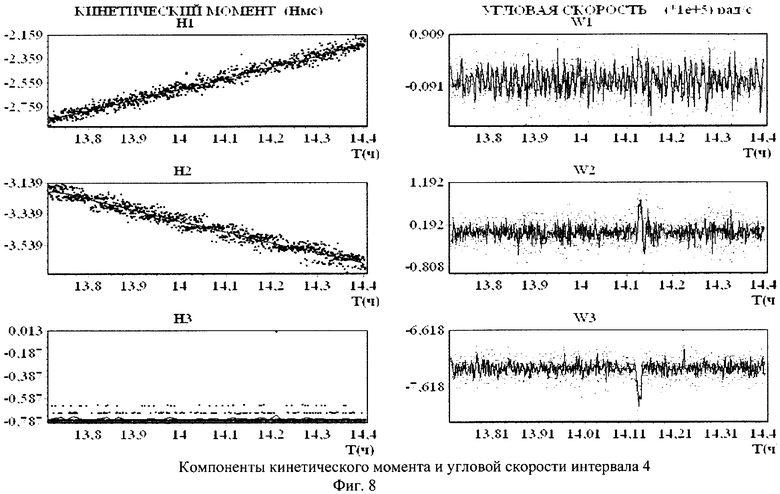
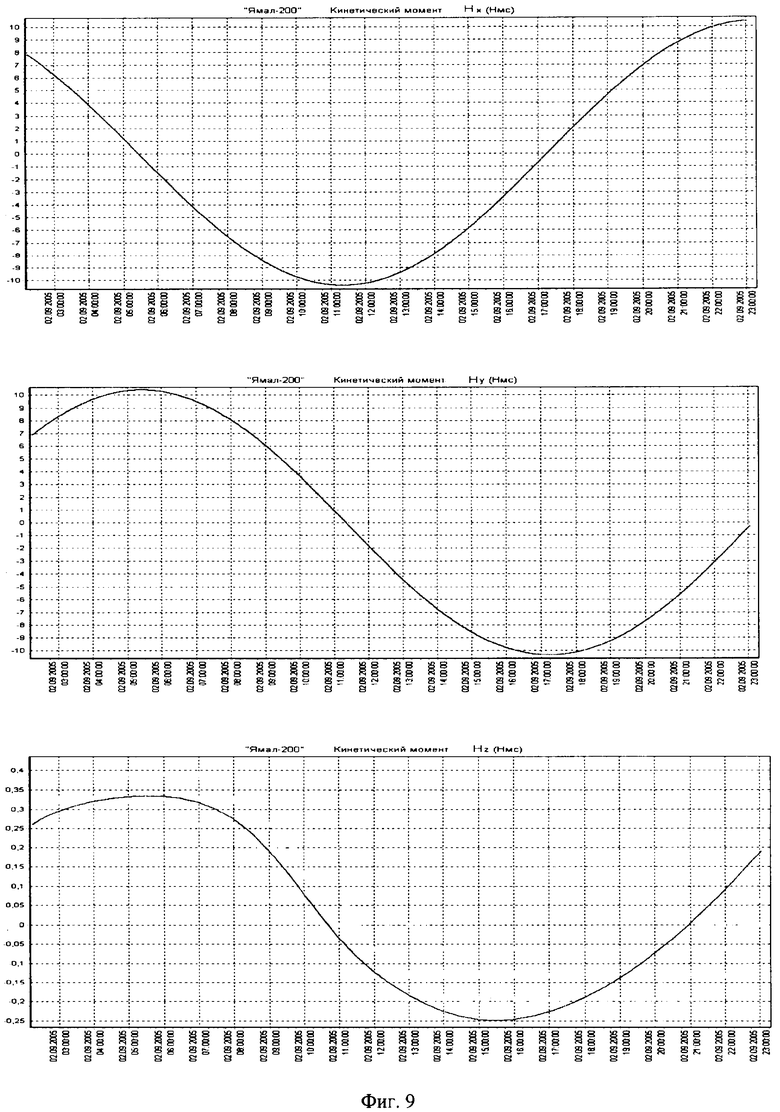
Для пояснения сущности предлагаемого способа приводятся фиг.1-10 и таблицы 1, 2. На фиг.1-4 маркеры указывают точки, отвечающие телеметрическим данным, а кривые изображают сглаживающие эти данные сплайны. На фиг.5-8 точками обозначены измеренные значения компонентов вектора угловой скорости, а сплошными линиями - результат аппроксимации. На фиг.9 точками обозначены измеренные значения кинетического момента силовых гироскопов, а сплошная линия - закон изменения кинетического момента силовых гироскопов, полученный расчетным путем. Аналогично, на фиг.10 точками обозначены измеренные значения компонент угловой скорости ГСС, а сплошными линиями - расчетные значения. В таблицах 1 и 2 представлены полученные значения тензора инерции КА и параметров возмущающих моментов.
Суть предлагаемого способа состоит в том, чтобы определить закон изменения кинетического момента силовых гироскопов, при котором угловая скорость КА будет соответствовать угловой скорости аппарата, соответствующей поддержанию заданной ориентации. Следовательно, меняя кинетический момент силовых гироскопов по определенному закону, получим заданную ориентацию КА. При этом для контроля правильности решения поставленной задачи используется информация, подтверждающая получение сигнала от целевой нагрузки КА с параметрами, соответствующими номинальным рабочим параметрам. Значения этих параметров напрямую зависят от ориентации аппарата. В качестве целевой нагрузки, по рабочим параметрам которой будет оцениваться точность ориентации, могут выступать, например, бортовой ретрансляционный комплекс (рабочий параметр - мощность сигнала, принимаемого на контрольных измерительных станциях) или бортовые телескопы, предназначенные для наблюдения и съемки заданных участков звездного неба (рабочий параметр - распознанный наблюдаемый участок звездного неба) и др.
Рассмотрим решение задачи поддержания трехосной ориентации КА в ОСК предлагаемым способом на примере геостационарного спутника связи "Ямал". Для управления ориентацией этих спутников используются установленные на борту ПОС, звездные датчики, датчик определения координат центра Земли (ДОКЦЗ), аналог ПМВ, гироскопический измеритель вектора угловой скорости (ГИВУС). В качестве исполнительных органов выступают одностепенные силовые гироскопы - маховики. На базе бортовой цифровой вычислительной машины построены динамический и кинематический контуры системы управления движением и навигации (СУДН). При этом используются принципы бескарданной системы управления ориентацией КА (см. [3], стр.101-103).
Для решения поставленной задачи, прежде всего, требуется определить параметры возмущающих моментов, действующих на КА. В общем случае при решении задачи определения параметров возмущающих моментов, зависящих от орбиты и конструктивных особенностей КА, требуется определять параметры различных возмущающих моментов. Для низкоорбитальных КА преобладающими возмущающими моментами являются гравитационный и аэродинамический. Для высокоорбитальных КА, например геостационарных, требуется учитывать, как правило, гравитационный момент и момент от силы светового давления. Кроме того, конструктивные особенности как низкоорбитальных, так и высокоорбитальных аппаратов могут привести к появлению существенных собственных магнитных моментов, которые также необходимо учитывать при их взаимодействии с магнитным полем Земли.
Методика определения параметров возмущающих моментов зависит от формы представления этих моментов. Например, в [4] при моделировании аэродинамического момента, действующего на международную космическую станцию (МКС), предполагалось, что атмосфера вращается вместе с Землей и что станция имеет форму сферы, центр которой смещен относительно центра масс. Аэродинамический момент аппроксимировался следующими выражениями:
Ma1=ρV(P3V2-P2V3), Ma2=ρV(P1V3-P3V1),
Ma3=ρV(P2V1-P1V2), 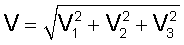
где ρ - плотность набегающего на МКС аэродинамического потока, Vi - компоненты скорости центра масс станции относительно поверхности земли, Pi - постоянные коэффициенты (параметры аэродинамического момента).
В качестве параметров гравитационного момента, действующего на аппарат, могут выступать компоненты тензора инерции. В [4], [5] и [6] описан способ оценки этих параметров. Компоненты гравитационного момента задавались формулами
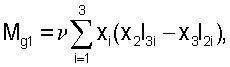
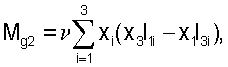
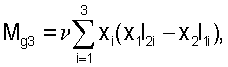
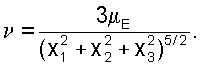
Здесь хi - компоненты геоцентрического радиуса-вектора центра масс станции, Iij - компоненты тензора инерции станции в строительной системе координат, Iij=Iji (i, j=1, 2, 3), μЕ - гравитационный параметр Земли.
В [4], [5], [6] предложены разные способы определения описанных параметров возмущающих моментов. Способы определения различаются между собой, но основу определения во всех случаях составляет решение динамических уравнений Эйлера при использовании измеренных на борту параметров углового движения - кватернионов ориентации КА и угловых скоростей, а также результатов моделирования орбиты КА и измерений кинетического момента в системе силовых гироскопов.
В рассматриваемом случае на ГСС действуют следующие возмущающие моменты - гравитационные от Земли, Луны и Солнца, магнитный момент, от взаимодействия собственного магнитного момента КА с магнитным полем Земли и момент от силы светового давления. Учитывая то, что порядок гравитационных моментов от Луны и Солнца, а также магнитный момент существенно меньше гравитационных моментов от Земли и момента от силы светового давления (на 5 порядков), влиянием указанных моментов можно пренебречь.
Определение параметров внешних возмущающих моментов выполняется следующим образом. Предполагается, что ГСС является гиростатом. Центр масс спутника движется по геостационарной орбите. Элементы этого движения определяются по данным радиоконтроля орбиты. В качестве исполнительных органов, используемых на ГСС для управления ориентацией, применяются маховики. Для записи уравнений изменения собственного кинетического момента системы маховиков вводятся две правые декартовы системы координат. Начала обеих систем помещены в центр масс - точку О.
В качестве базовой системы координат принимается система OY1Y2Y3, плоскость OY1Y2 которой параллельна среднему земному экватору эпохи 2000.0. Ось OY1 направлена в точку весеннего равноденствия указанной эпохи, ось OY3 направлена в соответствующий северный полюс мира. Под ориентацией спутника понимается ориентация жестко связанной с его корпусом строительной системы координат Oy1y2y3. В режиме поддержания штатной ориентации ГСС ось Oy1 направлена по текущему радиус-вектору, ось Oy2 - по текущему вектору линейной скорости.
Положение системы Oy1y2y3 относительно системы OY1Y2Y3 задается с помощью нормированного кватерниона Q=(q0, q1, q2, q3), 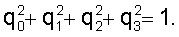 Матрица перехода от системы Oy1y2y3 к системе OY1Y2Y3 обозначается
Матрица перехода от системы Oy1y2y3 к системе OY1Y2Y3 обозначается 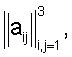 где aij - косинус угла между осями OYi и Oyj. Элементы этой матрицы выражаются через компоненты Q с помощью известных формул:
где aij - косинус угла между осями OYi и Oyj. Элементы этой матрицы выражаются через компоненты Q с помощью известных формул:
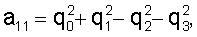 а12=2(q1q2-q0q3), а21=2(q1q2+q0q3) и т.п. Ниже компоненты векторов и координаты точек указываются в системе Oy1y2y3.
а12=2(q1q2-q0q3), а21=2(q1q2+q0q3) и т.п. Ниже компоненты векторов и координаты точек указываются в системе Oy1y2y3.
Оценка тензора инерции спутника выполнялась на освещенных Солнцем интервалах орбиты. Из моментов внешних сил, приложенных к спутнику, учитывались гравитационный и момент от силы светового давления. Компоненты гравитационного момента задавались формулами
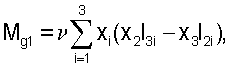
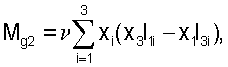
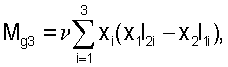
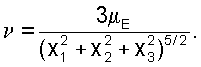
Здесь хi - компоненты геоцентрического радиуса-вектора центра масс станции, Iij - компоненты тензора инерции станции в строительной системе координат, Iij=Iji (i, j=1, 2, 3), μЕ - гравитационный параметр Земли. Момент от силы светового давления аппроксимируется выражениями
Ms1=k(p2es3- p3es2), Ms2=k(p3es1- p1es3), Ms1=k(p1es2- p2es2).
Здесь k=(r*/Δ)2, r* - средний радиус орбиты Земли; Δ - расстояние от КА до Солнца; рi - постоянные коэффициенты; еsi - компоненты орта направления ГСС - Солнце. При выводе этих выражений предполагалось, что на интервалах оценки площадь поверхности ГСС, на которую воздействует набегающий световой поток, неизменна и отражающие свойства поверхности спутника во всех его точках одинаковы.
Компоненты кинетического момента спутника в его движении относительно центра масс имеют вид
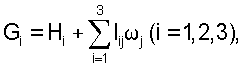
где Нi и ωj - компоненты собственного кинетического момента системы маховиков и угловой скорости ГСС. Теорема об изменении кинетического момента ГСС под действием указанных выше внешних моментов выражается соотношениями
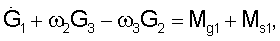
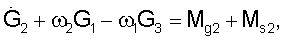
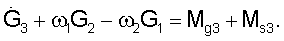
Здесь точкой обозначено дифференцирование по времени t.
Подставив в эти соотношения выписанные выше выражения для величин Кi, Мgi и Мsi, можно получить уравнения
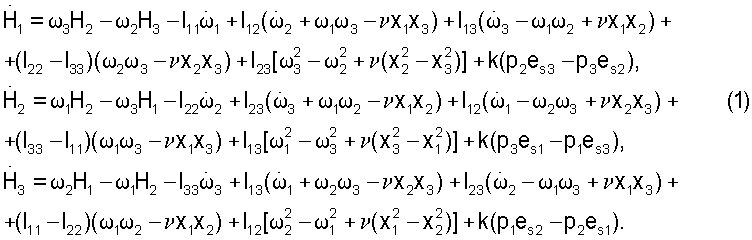
С помощью соотношений Iij=Iji из этих уравнений исключены компоненты тензора инерции Iij при i>j.
Ниже выписанные уравнения используются следующим образом. На некотором отрезке времени, длиной несколько часов, по телеметрической информации восстанавливается фактическое движение спутника относительно центра масс, в том числе его угловая скорость и угловое ускорение. В результате уравнения (1) станут замкнутой системой относительно переменных Нi (i=1, 2, 3). В этой системе величины Iij, рi будут рассматриваться как искомые параметры возмущающих моментов (гравитационного и от силы светового давления соответственно). Общее решение этих уравнений с явно однозначной его зависимостью от параметров и начальных условий представлено следующим образом
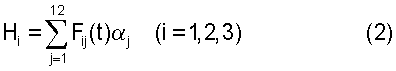
где αi=Hi(t0) - начальные условия, t0 - заданный момент времени, α4=I11, α5=I12, α7=I22, α8=I23, α9=I33, α10=p1, α11=p2, α12=p3. Функции Fij(t) определяются начальными задачами, для линейных дифференциальных уравнений, не содержащих параметров.
Телеметрическое обеспечение системы маховиков позволяет в некоторые моменты времени tn (n=1, 2, ..., N) измерять значения Hi(tn) компонентов ее собственного кинетического момента. Точность измерения кинетического момента маховиков ГСС "Ямал-200" составляет 0.1 Нмс. Результаты измерений этих величин обозначаются соответственно 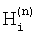 . Если указанные измерения приходятся на отрезок времени, для которого имеются значения кватерниона ориентации, то с помощью соотношений (2) их можно обработать каким-либо статистическим методом и определить вектор α=(α1, α2, ..., α12)Т. Поскольку вычисляемые по формулам (2) величины Hi(tn) зависят от α линейно, наиболее подходящим в данном случае методом обработки является метод наименьших квадратов. В рамках этого метода оценкой вектора α служит его значение, минимизирующее функцию
. Если указанные измерения приходятся на отрезок времени, для которого имеются значения кватерниона ориентации, то с помощью соотношений (2) их можно обработать каким-либо статистическим методом и определить вектор α=(α1, α2, ..., α12)Т. Поскольку вычисляемые по формулам (2) величины Hi(tn) зависят от α линейно, наиболее подходящим в данном случае методом обработки является метод наименьших квадратов. В рамках этого метода оценкой вектора α служит его значение, минимизирующее функцию
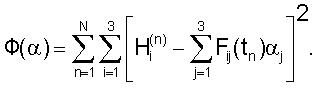
Это значение определяется так называемыми нормальными уравнениями, которые в данном случае имеют вид:
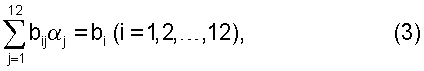
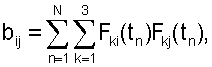
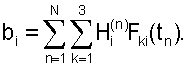
Если ошибки в измерениях величин 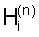 (i=1, 2, 3; n=1, 2, ..., N) независимы и имеют одинаковое нормальное распределение с нулевым средним значением и стандартным отклонением σ, то оценка
(i=1, 2, 3; n=1, 2, ..., N) независимы и имеют одинаковое нормальное распределение с нулевым средним значением и стандартным отклонением σ, то оценка 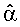 вектора α, определяемая системой (3), является несмещенной с ковариационной матрицей σ2B-1, где В - матрица системы (3). Поскольку значение σ- неизвестно, его квадрат - дисперсию ошибок измерений - при расчете ковариационной матрицы можно заменить оценкой
вектора α, определяемая системой (3), является несмещенной с ковариационной матрицей σ2B-1, где В - матрица системы (3). Поскольку значение σ- неизвестно, его квадрат - дисперсию ошибок измерений - при расчете ковариационной матрицы можно заменить оценкой
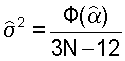
Чтобы реализовать описанный подход к оцениванию тензора инерции спутника, необходимо располагать методом восстановления его фактического движения по телеметрической информации. Ниже используется метод, основанный на аппроксимации вращательного движения спутника сплайнами.
Телеметрическая информация собирается на временном интервале не более часа, содержит последовательность моментов времени, кватернионов и угловых скоростей
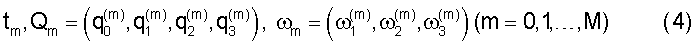
Здесь t0<t1<...<tM, Qm - значение кватерниона Q, вычисленное на момент времени tm, ωm - значение угловой скорости, определенное на этот же момент времени. Как правило, tm+1-tm≅2 с. Кватернион, задающий ориентацию спутника, определен с точностью до знака. Знаки Qm и момент t0 в (2) выбираются из условия
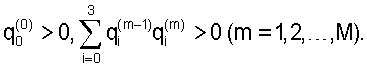
Сглаживание последовательности кватернионов (4) выполняется покомпонентно с использованием решения следующей задачи. Пусть для моментов времени tm (m=0, 1, ..., M), tm<tm+1, известны приближенные значения хm≈f(tm) некоторой гладкой функции f(t). Требуется восстановить эту функцию на отрезке t0≤t≤tM.
Если предположить, что эта функция дважды непрерывно дифференцируема, то решение сводится к решению вариационной задачи
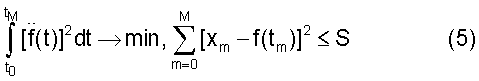
Здесь S - заданное положительное число. Решением задачи (5) является кубический сплайн.
Норма кватерниона, который образован сплайнами, сглаживающими компоненты кватернионов (4), уже не равна единице, но мало отличается от нее. Полученная кватернионная функция нормируется на единицу и служит аппроксимацией вращения системы Oy1y2y3 относительно системы OY1Y2Y3 на отрезке t0≤t≤tM.
Для уменьшения случайных ошибок при определении значений угловой скорости спутника используется процесс сглаживания, основанный на применении метода наименьших квадратов. Предполагается, что измеренные значения угловой скорости имеют одинаковую точность и функция ω(t) на участке измерений может быть достаточно хорошо описана многочленом третьей степени. В результате по наблюдаемым значениям функции в точках измерений методом наименьших квадратов построен многочлен третьей степени, описывающий функцию 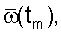 и значениями этой функции считают значения
и значениями этой функции считают значения 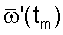 полученного многочлена в точках tm. Вычисление выполняется по четырем точкам с использованием следующего выражения
полученного многочлена в точках tm. Вычисление выполняется по четырем точкам с использованием следующего выражения
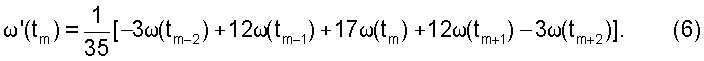
Такое определение угловой скорости спутника позволяет уменьшить влияние ошибок измерений при последующей аппроксимации функции 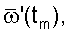 которая выполняется для получения значений угловой скорости в требуемые моменты времени. Методика аппроксимации та же, что и для кватернионов. Аналогичный подход используется при вычислении значений кинетического момента маховиков.
которая выполняется для получения значений угловой скорости в требуемые моменты времени. Методика аппроксимации та же, что и для кватернионов. Аналогичный подход используется при вычислении значений кинетического момента маховиков.
Примеры аппроксимации вращательного движения ГСС описанным способом приведены на фиг.1-8. Эти чертежи иллюстрируют стабилизацию спутника в орбитальной системе координат при движении ГСС по освещенной Солнцем части орбиты.
На фиг.1-4 маркеры указывают точки 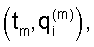 отвечающие телеметрическим данным (4), а кривые изображают сглаживающие эти данные сплайны.
отвечающие телеметрическим данным (4), а кривые изображают сглаживающие эти данные сплайны.
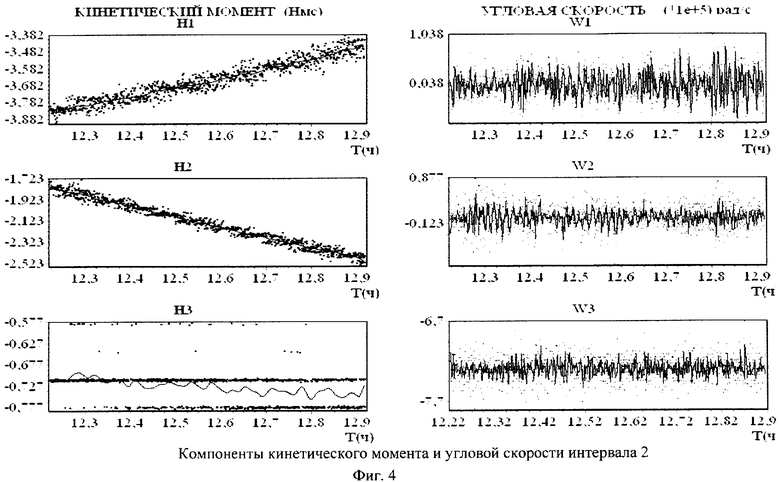
Детали движения спутника на соответствующих интервалах времени представлены на фиг.5-6. Здесь точками представлены измеренные значения кинетического момента и угловой скорости, а сплошные линии - результат аппроксимации.
В приведенных примерах ориентация спутника поддерживалась одними лишь маховиками. Реактивные двигатели системы управления движением ГСС не включались. Это обстоятельство позволило использовать полученные на соответствующих временных интервалах данные измерений кинетического момента маховиков для оценки тензора инерции спутника. В таблицах 1 и 2 приведены результаты оценки этого тензора, а также параметров светового давления ГСС при движении по освещенной Солнцем части орбиты на четырех таких интервалах (инт.1-4). В таблице указаны номер интервала, дата и время, на которые этот интервал приходится, оценка 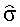 стандартного отклонения ошибок в данных измерениях кинетического момента маховиков, оценки параметров Iij и рi, а также стандартные отклонения этих оценок
стандартного отклонения ошибок в данных измерениях кинетического момента маховиков, оценки параметров Iij и рi, а также стандартные отклонения этих оценок 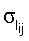 и
и 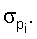
Проведенные расчеты показывают высокую степень точности полученных значений динамических параметров спутника.
В соответствии с программой полета определяют интервал времени, на котором использование датчиков ориентации не производится. Например, (t10, t1k)=(02.09.05 02:30:00, 02.09.05 23:10:00).
Следующий шаг решения поставленной задачи состоит в формировании на заданном временном интервале закона изменения кинетического момента маховиков, при котором будет обеспечиваться поддержание заданной ориентации КА в орбитальной системе координат. Сделать это можно следующим образом.
Используя измеренные на момент времени начала интервала параметры углового движения и кинетического момента силовых гироскопов, учитывая внешние возмущающие моменты, рассчитанные с использованием определенных ранее параметров возмущающих моментов, определяется закон изменения кинетического момента в системе силовых гироскопов 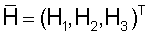 (1, 2, 3 обозначают оси ОХ, OY и OZ), соответствующий поддержанию заданной ориентации на этом интервале. Для рассматриваемого случая управления ориентацией геостационарного спутника прогноз ведут, решая систему динамических уравнений Эйлера, учитывая влияние на спутник гравитационного момента
(1, 2, 3 обозначают оси ОХ, OY и OZ), соответствующий поддержанию заданной ориентации на этом интервале. Для рассматриваемого случая управления ориентацией геостационарного спутника прогноз ведут, решая систему динамических уравнений Эйлера, учитывая влияние на спутник гравитационного момента 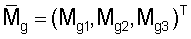 и момента от силы светового давления
и момента от силы светового давления 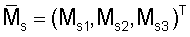
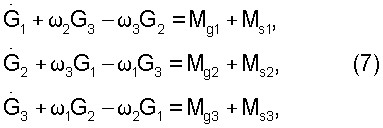

Для определения вектора угловой скорости, соответствующего заданной ориентации КА (в данном случае - орбитальной) на рассматриваемом временном интервале, используются рассчитанные на заданные моменты времени интервала (зависящие от шага интегрирования динамических уравнений) значения текущего радиус-вектора КА 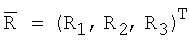 и вектора линейной скорости КА
и вектора линейной скорости КА 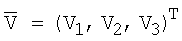 . Для расчета вектора угловой скорости может использоваться следующее выражение:
. Для расчета вектора угловой скорости может использоваться следующее выражение:
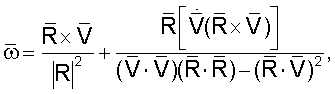
здесь точкой обозначено дифференцирование по времени. На фиг.5, 6, 7, 8 точками обозначены измеренные значения компонентов вектора угловой скорости, а сплошной линией - рассчитанные по указанному выражению.
Поддержание заданной ориентации ГСС выполняют, управляя системой силовых гироскопов, изменяя их кинетический момент в соответствии с определенным законом изменения кинетического момента силовых гироскопов. В рассматриваемом случае для системы из трех маховиков, оси вращения которых расположены вдоль осей связанного базиса, в каждый k-й момент времени, используя известные на (k+1) моменты времени из определенного ранее закона (по (8)) значения кинетического момента маховиков 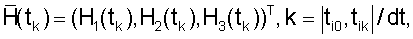 (dt - шаг решения задачи на борту КА) и известные моменты инерции маховиков Jm1, Jm2, Jm3, определяется требуемое значение угловой скорости каждого маховика (ωmi, i=1, 2, 3, i - номер маховика) на каждый последующий момент времени (k+1) в соответствии с выражениями
(dt - шаг решения задачи на борту КА) и известные моменты инерции маховиков Jm1, Jm2, Jm3, определяется требуемое значение угловой скорости каждого маховика (ωmi, i=1, 2, 3, i - номер маховика) на каждый последующий момент времени (k+1) в соответствии с выражениями
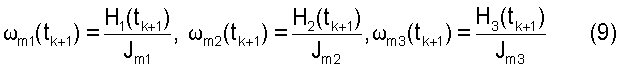
Полученные значения (9) в бортовой вычислительной машине (БЦВМ) сравниваются с текущими значениями угловой скорости маховиков ωm1(tk), ωm2(tk), ωm3(tk)
Δωmi=ωmi(tk+1)-ωmi(tk), i=1, 2, 3.
На основании результатов сравнения, в соответствии со штатным алгоритмом управления скоростью вращения маховиков, БЦВМ формирует на интервале времени dt управляющие воздействия по осям (каналам) управления, направленные на изменение угловой скорости маховиков, выдавая на приводы роторов маховиков серию импульсов, пропорциональных Δωmi.
Анализируя представленные графики изменения кинетического момента в СГ КА на рассматриваемом интервале, нетрудно сделать вывод, что в данном случае задача поддержания ориентации КА в орбитальной системе координат будет решена успешно, если кинетический момент силовых гироскопов изменять в соответствии с определенным законом (фиг.9). На фиг.9 точками обозначены измеренные значения кинетического момента силовых гироскопов Hx, Hy, Hz, а сплошная линия - закон изменения кинетического момента силовых гироскопов, полученный расчетным путем и предназначенный для использования при управлении ориентацией предлагаемым способом. Но при этом необходимо учитывать, что во время управления ориентацией КА предлагаемым способом нельзя исключать возможность появления какого-либо неучтенного возмущающего момента, который может быть вызван как внешними факторами, например вспышкой на Солнце, так и внутренними, например незапланированное включение какой-либо аппаратуры, создающей дополнительный собственный магнитный момент КА.
Во избежание потери ориентации из-за действия неучтенных моментов для контроля ориентации КА в таких случаях может быть использована информация, характеризующая значения рабочих параметров целевой нагрузки. Например, для геостационарного спутника связи это могут быть рабочие сигналы от бортового ретрансляционного комплекса.
Для получения эталонного сигнала, т.е. сигнала, с которым при движении по прогнозируемым значениям суммарного вектора кинетического момента СГ КА будет сравниваться текущий сигнал, необходимо при заданной ориентации аппарата выполнить на наземных пунктах измерение рабочих параметров принимаемого сигнала (например, его мощности). В процессе поддержания ориентации КА по прогнозу изменения кинетического момента в системе силовых гироскопов на наземных пунктах выполняется штатное измерение текущих параметров принимаемого сигнала и сравнение этого сигнала с эталонным его значением. Например, можно использовать сигнал от радиомаяка, диапазон которого при штатной ориентации КА составляет 20±0.5 дБ, см.[7].
Если измеренный сигнал находится внутри диапазона, то продолжают управление ориентацией КА, меняя кинетический момент силовых гироскопов по определенному закону. В противном случае с момента времени t11 несовпадения эталонного и измеренного сигналов для управления ориентацией КА включают датчики ориентации. При этом необходимо отметить, что может происходить лишь ухудшение рабочих характеристик в пределах допустимых значений без потери функциональности целевой нагрузки.
По измерениям датчиков ориентации на интервале (t11, t1')∈(t10, t1k) определяют параметры углового движения (текущую ориентацию КА и его угловую скорость) и выполняют построение и последующее поддержание заданной ориентации КА. Одновременно производят повторное определение параметров возмущающих моментов, действующих на КА. Для продолжения поддержания ориентации КА по указанному прогнозу, используя измерения кинетического момента силовых гироскопов и измерения угловой скорости КА, выполняют определение новых параметров возмущающих моментов.
Если к моменту завершения определения параметров возмущающих моментов в соответствии с программой полета интервал поддержания ориентации КА по прогнозу изменения кинетического момента в системе СГ не завершен, то переходят на управление ориентацией КА по новому определенному закону изменения кинетического момента силовых гироскопов. Далее управляют ориентацией КА до завершения выбранного интервала. Сравнение спрогнозированного (эталонного для последующего управления) значения кинетического момента с текущим его значением выполняется непрерывно, на всем протяжении интервала (t10, t1k) реализации предлагаемого способа только таким образом можно контролировать соответствие текущей ориентации КА требуемой.
В случае необходимости, вызванной ухудшением значений рабочих параметров целевой нагрузки, управление по указанному прогнозу прерывают и переходят на управление по датчикам-измерителям параметров углового движения. Далее уточняют значения параметров главного вектора возмущающего момента, действующего на КА, и с учетом их, в свою очередь, вновь прогнозируют значения вектора кинетического момента в системе СГ. И по уточненным данным производят последующее управление КА вплоть до момента времени завершения интервала (t10, t1k).
Приведенный пример моделирования орбиты КА и прогноза изменений вектора кинетического момента в системе СГ для режима поддержания трехосной ориентации в ОСК показывает необходимую последовательность действий, которую можно воспроизвести и для режимов поддержания ориентации в ИСК. Отличаются только спрогнозированные значения вектора кинетического момента в системе СГ, зависящие от положения осей связанного базиса в инерциальном пространстве.
По завершении 1-го интервала продолжают поддержание ориентации КА по измеренным параметрам его углового движения. При дальнейшем выполнении программы полета КА может возникать планируемая или вынужденная необходимость в использовании рассмотренного способа поддержания его трехосной ориентации на i-x интервалах, где i=1, 2, ..., n - число указанных интервалов, на которых измерения параметров углового движения не выполняются. Планируемый (детерминированный) переход на предлагаемый способ управления КА может быть вызван, например, необходимостью экономии ресурса датчиков контроля и управления углового движения КА, технологической необходимостью, связанной с предотвращением «засветки» оптических датчиков Солнцем и т.д. Управление поддержанием трехосной ориентации КА по прогнозируемым значениям вектора кинетического момента заканчивают по истечении n-го полетного интервала.
Вынужденная (вероятностная) необходимость перехода на управление КА с использованием предлагаемого способа может быть вызвана частичным или полным отказом датчиков, связанным, например, с воздействием на них частиц высоких энергий (протонов и электронов) в периоды высокой активности Солнца.
Предлагаемый способ позволяет повысить отказоустойчивость КА при поддержании трехосной ориентацией, т.к. может использоваться и в случаях незапланированного отключения датчиков ориентации при нештатных ситуациях и в случаях, когда использование датчиков невозможно (например, в результате засветки их Солнцем). Кроме того, применение предлагаемого способа может увеличить срок эксплуатации КА за счет экономии ресурса по числу включений и продолжительности работы датчиков ориентации.
Список литературы
1. Способ трехосной ориентации космического аппарата в орбитальной системе координат. Патент RU 2247684 С2.
2. Л.А.Мирошниченко, В.А.Раевский, Г.М.Маркелов. Система ориентации и стабилизации спутника телевизионного вещания "Экран". Техническая кибернетика, №4, 1977 г.
3. Б.В.Раушенбах, Е.Н.Токарь. Управление ориентацией космических аппаратов. М.: Наука, 1974 г.
4. Ю.Р.Банит, М.Ю.Беляев, Т.А.Добринская, Н.И.Ефимов, В.В.Сазонов, В.М.Стажков. Определение тензора инерции международной космической станции по телеметрической информации. Препринт №57, ИПМ им. М.В. Келдыша, 2002 г.
5. Способ определения инерционных характеристик космического аппарата в процессе управления с помощью силовых гироскопов и реактивных двигателей. Патент RU 2208559 С1.
6. Н.Н.Севастьянов, В.Н.Бранец, Ю.Р.Банит, М.Ю.Беляев, В.В.Сазонов. Определение тензора инерции геостационарных спутников "Ямал" по телеметрической информации. ИПМ им. М.В.Келдыша, 2006 г.
7. Способ управления ориентацией космического аппарата, снабженного бортовым радиотехническим комплексом. Патент RU 2191721 С1.
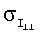
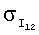
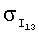
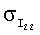
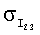
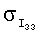
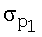
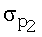
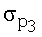

Изобретение относится к управлению ориентацией космического аппарата (КА). Предлагаемый способ включает математическое моделирование орбиты КА, измерение кинетического момента силовых гироскопов и - на определенных полетных интервалах - параметров углового движения КА. По этим измерениям поддерживают заданную ориентацию КА и определяют действующие на КА возмущающие моменты. На интервале, когда не производится измерение параметров углового движения КА, прогнозируют изменения кинетического момента силовых гироскопов, требуемые для поддержания заданной ориентации КА. В соответствии с прогнозом воздействуют на эти гироскопы и одновременно измеряют рабочие параметры целевой нагрузки. С момента несоответствия данных параметров их номинальным значениям при штатной ориентации КА повторно измеряют параметры углового движения КА, определяют действующие на КА возмущающие моменты и строят заданную ориентацию КА. Затем на оставшейся части указанного интервала прогнозируют, как и ранее, изменение кинетического момента силовых гироскопов и поддерживают заданную ориентацию КА в соответствии с прогнозом. Если же указанный интервал уже исчерпан, то продолжают управление ориентацией КА по измеряемым параметрам его углового движения до очередного интервала, на котором не производится измерение параметров углового движения КА. Техническим результатом изобретения является сохранение штатной ориентации КА в условиях отсутствия информации от приборов, измеряющих параметры углового движения КА. 10 ил., 2 табл.
Способ поддержания трехосной ориентации космического аппарата с силовыми гироскопами и целевой нагрузкой, включающий математическое моделирование орбиты космического аппарата, измерение параметров его углового движения, измерение кинетического момента силовых гироскопов, определение, построение и поддержание по измеренным величинам заданной ориентации космического аппарата, отличающийся тем, что по измеренным параметрам углового движения и значениям кинетического момента силовых гироскопов определяют параметры действующих на космический аппарат возмущающих моментов, определяют номинальные рабочие параметры целевой нагрузки при штатной ориентации космического аппарата, определяют интервалы времени (ti0, tik), на которых измерение параметров углового движения не производится, где i=1, 2, ...n - указанные интервалы времени, по измеренным на момент начала i-го интервала параметрам углового движения космического аппарата и кинетического момента его силовых гироскопов, а также с учетом возмущающих моментов, рассчитанных с использованием определенных ранее параметров этих моментов, прогнозируют на данном i-м интервале изменения кинетического момента силовых гироскопов, соответствующие поддержанию заданной ориентации космического аппарата на этом интервале, а для поддержания этой ориентации воздействуют на силовые гироскопы так, чтобы их кинетический момент в каждый момент времени данного i-го интервала соответствовал спрогнозированному, измеряют рабочие параметры целевой нагрузки и сравнивают их с номинальными параметрами, в случае соответствия сравниваемых параметров продолжают управление ориентацией космического аппарата по спрогнозированному кинетическому моменту, а в случае взаимного несоответствия указанных параметров целевой нагрузки с момента til повторно измеряют параметры углового движения космического аппарата, определяют по ним его текущую и строят заданную ориентацию, повторно определяя на интервале необходимой длительности (til, ti') параметры возмущающих моментов, действующих на космический аппарат, при выполнении условия принадлежности (til,ti')∈(ti0, tik) с использованием измеренных на момент времени til значений вектора кинетического момента силовых гироскопов и параметров углового движения космического аппарата вновь прогнозируют изменение кинетического момента силовых гироскопов на оставшейся части i-го интервала, учитывая при этом возмущающие моменты, рассчитанные с использованием повторно определенных ранее параметров возмущающих моментов и продолжают управлять ориентацией космического аппарата на указанном i-м интервале по вновь спрогнозированному кинетическому моменту силовых гироскопов, а при невыполнении указанного условия принадлежности продолжают управление ориентацией космического аппарата по измеряемым параметрам его углового движения до очередного (i+1)-го интервала, далее повторяют управление космическим аппаратом вышеуказанным образом на (i+1)-м интервале по спрогнозированным значениям вектора кинетического момента силовых гироскопов, с последующим переходом на управление ориентацией космического аппарата по измеряемым параметрам его углового движения и заканчивают процесс управления поддержанием трехосной ориентации космического аппарата по спрогнозированным значениям вектора кинетического момента силовых гироскопов по истечении n-го интервала.
| МИРОШНИЧЕНКО Л.А., РАЕВСКИЙ В.А | |||
| и др | |||
| Система ориентации и стабилизации спутника телевизионного вещания "Экран" | |||
| - Техническая кибернетика, №4, 1977 | |||
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ ПРИ ПОДДЕРЖАНИИ ЗАДАННОЙ ОРИЕНТАЦИИ С ПОМОЩЬЮ РЕАКТИВНЫХ МАХОВИКОВ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2281232C2 |
| СПОСОБ ФОРМИРОВАНИЯ УПРАВЛЯЮЩИХ МОМЕНТОВ НА КОСМИЧЕСКИЙ АППАРАТ С СИЛОВЫМИ ГИРОСКОПАМИ И ПОВОРОТНЫМИ СОЛНЕЧНЫМИ БАТАРЕЯМИ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2196710C2 |
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ С ПОМОЩЬЮ РЕАКТИВНЫХ ИСПОЛНИТЕЛЬНЫХ ОРГАНОВ ПРИ ПОДДЕРЖАНИИ ЗАДАННОЙ ОРИЕНТАЦИИ | 1996 |
|
RU2112713C1 |
| US 6089508 A, 18.07.2000. | |||
Авторы
Даты
2008-12-20—Публикация
2006-06-23—Подача