Текст описания приведен в факсимильном виде.





























Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств. Техническим результатом является расширение повышение быстродействия. Устройство содержит сумматор, на выходе которого формируется текущая сумма ±[SΣ]f(Δt)↓ и результирующая сумма ±[SΣ] в формате позиционно-знаковой системы счисления, два регистра встречного сдвига, две структуры логических элементов И, логический элемент И, устройство памяти. 1 ил.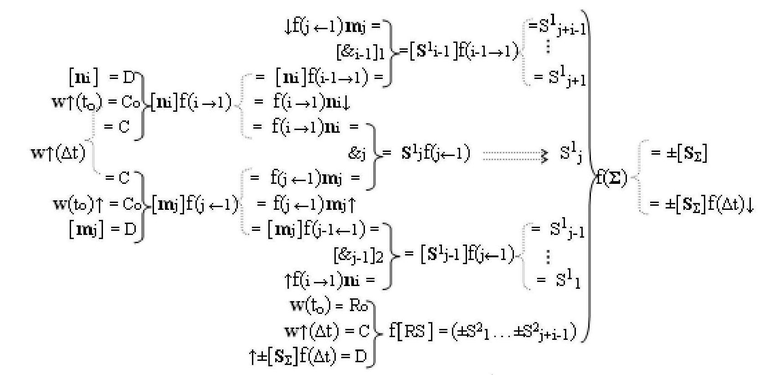
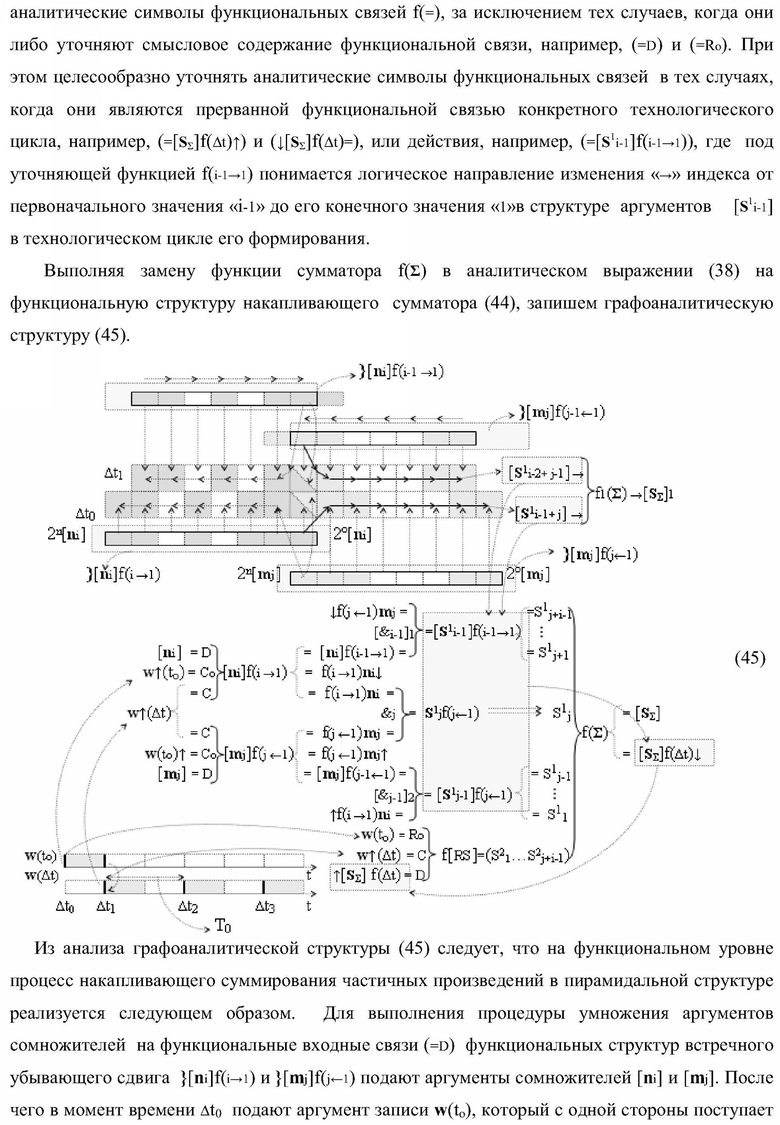
Функциональная структура умножителя, в котором входные аргументы имеют формат двоичной системы счисления f(2n), а выходные аргументы сформированы в формате позиционно-знаковой системы счисления f(+/-), которая включает функциональную структуру сумматора f(Σ), в которой функциональная выходная связь структуры аргументов суммы [SΣ] и структуры аргументов текущей суммы [SΣ]f(Δt)↓, является соответственно функциональной выходной связью умножителя, а первая группа функциональных входных связей S1 1-S1 j+i+1 приема частичных произведений [S1 i-1]f(i-1→1), S1 jf(j←i) и [S1 j-1]f(j←1), где S1 - аргумент частичного произведения; i и j - индексы разряда соответствующих сомножителей [ni] и [mj]; f(i-1→1) и f(j←i) - функциональное действие, которое выполняется над индексами i и j частичных произведений, является функциональными выходными связями структуры логических функций f([&i-1]1)-И, f(&j)-И и f[&j-1]2)-И, в которой логические функции f([&i-1]1)-И и f[&j-1]2)-И представляют собой «i-1» и «j-1» логических функций f(&)-И, в которых первая и вторая соответственно функциональные входные связи функционально объединены для приема аргумента множимого, при этом вторая группа функциональных входных связей S2 1-S2 j+i-1 является соответствующими функциональными выходными связями функциональной структуры памяти f[RS], в которой функциональные входные связи D приема текущей суммы аргументов частичных произведений ↑[SΣ]f(Δt) является функциональными выходными связями функциональной структуры сумматора f(Σ), а функциональные входные связи С и Ro приема соответствующих аргументов w↑(Δt) и w(to), которые выполняют соответственно функцию записи текущих структур аргументов суммы [SΣ]f(Δt)↓, и функцию исключения активизации выходных связей функциональной структуры памяти f[RS] перед новым циклом умножения аргументов сомножителей [ni] и [mj] являются функциональными входными связями умножителя, который включает функциональную структуру сдвига }[ni]f(i→1), в которой функциональные входные связи D приема структуры аргументов [ni] и функциональная входная связь С приема аргумента w↑(to) для исключения активизации выходных связей функциональной структуры сдвига }[ni]f(i→1) перед очередным циклом сдвига и функциональная входная связь Со приема аргумента w↑(Δt) записи структуры аргументов [ni] в функциональную структуру сдвига }[ni]f(i→1) является функциональными входными связями умножителя, который включает также функциональную структуру сдвига }[mj]f(j←1), отличающаяся тем, что функциональная структура сумматора f(Σ) выполнена с процедурой логического дифференцирования первой промежуточной суммы аргументов частичных произведений и с формированием текущей суммы ±[SΣ]f(Δt)↓ и результирующей суммы ±[SΣ] в формате позиционно-знаковой системы счисления f(+/-), и функциональная структура памяти f[RS] также выполнена с возможностью приема текущих структур аргументов суммы ↑±[SΣ]f(Δt) в формате позиционно-знаковой системы счисления f(+/-), при этом в функциональной структуре сдвига }[mj]f(j←1) функциональные входные связи D приема структуры аргументов сомножителя [mj] являются функциональными входными связями умножителя, а функциональные входные связи С и Со приема аргумента w↑(Δt) и w(tо)↑ соответственно являются функциональными одноименными входными связями функциональной структуры сдвига }[ni]f(i→1), при этом функциональные структуры сдвига }[ni]f(i→1) и }[mj]f(j←1) одновременно выполняют функцию убывающего сдвига f(i→1) и f(j←1), при этом сдвиг структуры аргументов сомножителя [ni] в функциональной структуре сдвига }[ni]f(i→1) выполняют с убыванием младших разрядов, а сдвиг структуры аргументов сомножителя [mj] в функциональной структуре сдвига }[mj]f(j←1) выполняют с убыванием старших разрядов, в которой функциональные выходные связи аргументов }[mj]f(j-1←1) и f(j←1)mj↑ являются первыми функциональными входными связями линейной структуры логических функций f[&j-1]2)-И и общими функциональными связями линейной структуры логических функций f([&i-1]1)-И, в которой вторые функциональные входные связи приема аргументов [ni]f(i-1→1) являются функциональные выходные связи функциональной структуры убывающего сдвига }[ni]f(i→1), в которой функциональная выходная связь аргумента f(i→1)ni является общей функциональной связью линейной структуры логических функций f[&j-1]2)-И и первой функциональной входной связью логической функции f(&j)-И, в которой вторая функциональная входная связь приема аргумента f(j←1)mj является функциональной выходной связью функциональной структуры убывающего сдвига }[mj]f(j←1), при этом математическая модель функциональной структуры умножителя в аналитической форме имеет вид
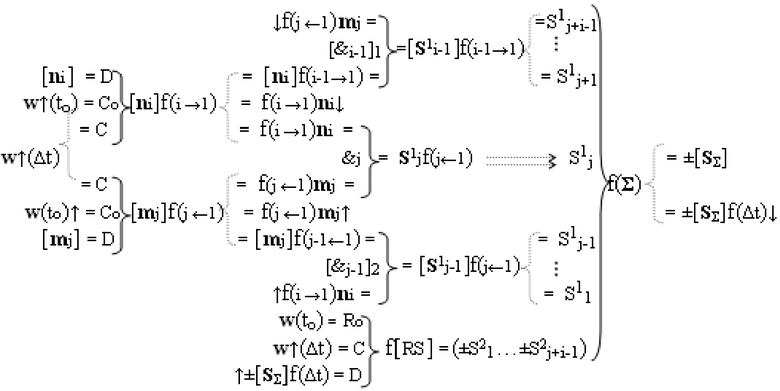

| КАРЦЕВ М.А., БРИК В.А | |||
| Вычислительные системы и синхронная арифметика | |||
| - М.: «Радио и связь», 1981, с.164, рис.4.1.1 | |||
| УСТРОЙСТВО УМНОЖЕНИЯ | 1998 |
|
RU2148270C1 |
| СПОСОБ УМНОЖЕНИЯ ДВУХ ЦИФРОВЫХ СИГНАЛОВ | 1993 |
|
RU2065201C1 |
| Устройство для умножения | 1984 |
|
SU1226447A1 |
| US 5986587 A, 16.11.1999 | |||
| US 6816877 B2, 09.11.2004. | |||
Авторы
Даты
2009-11-20—Публикация
2008-04-29—Подача