Текст описания приведен в факсимильном виде.













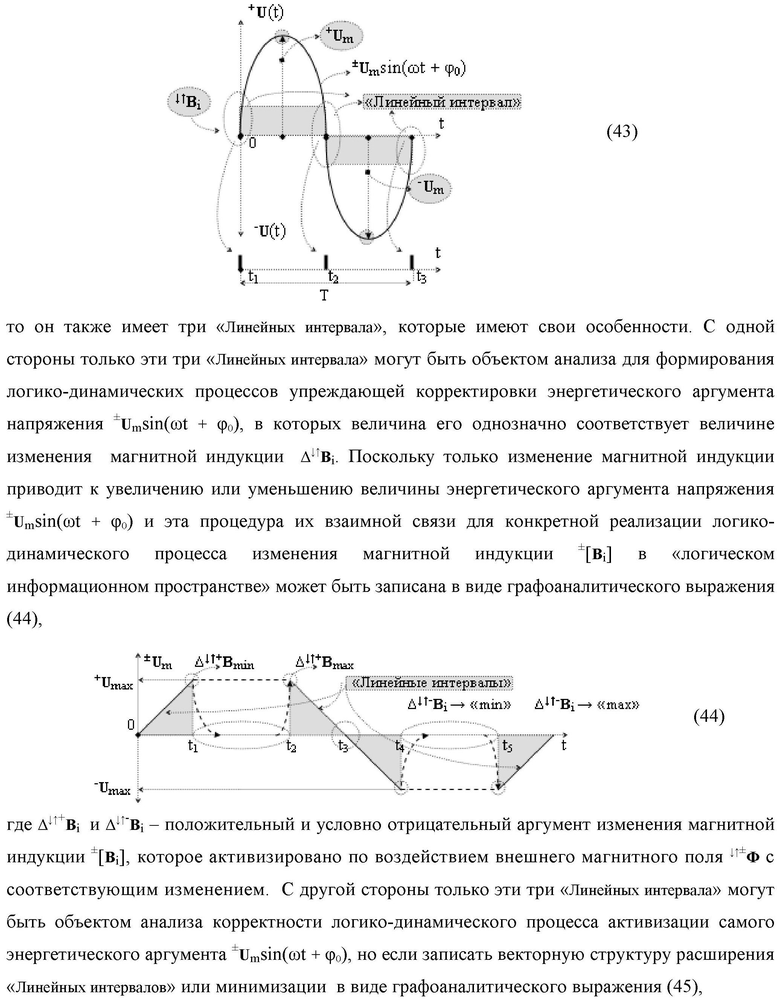











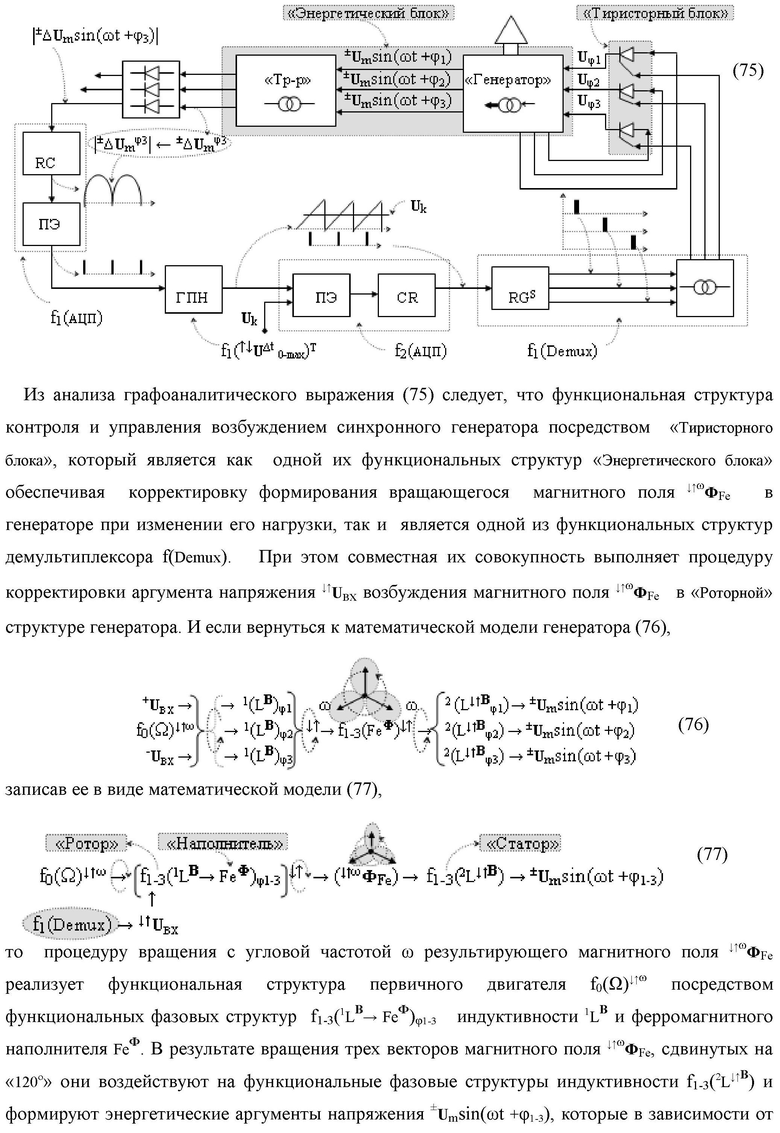

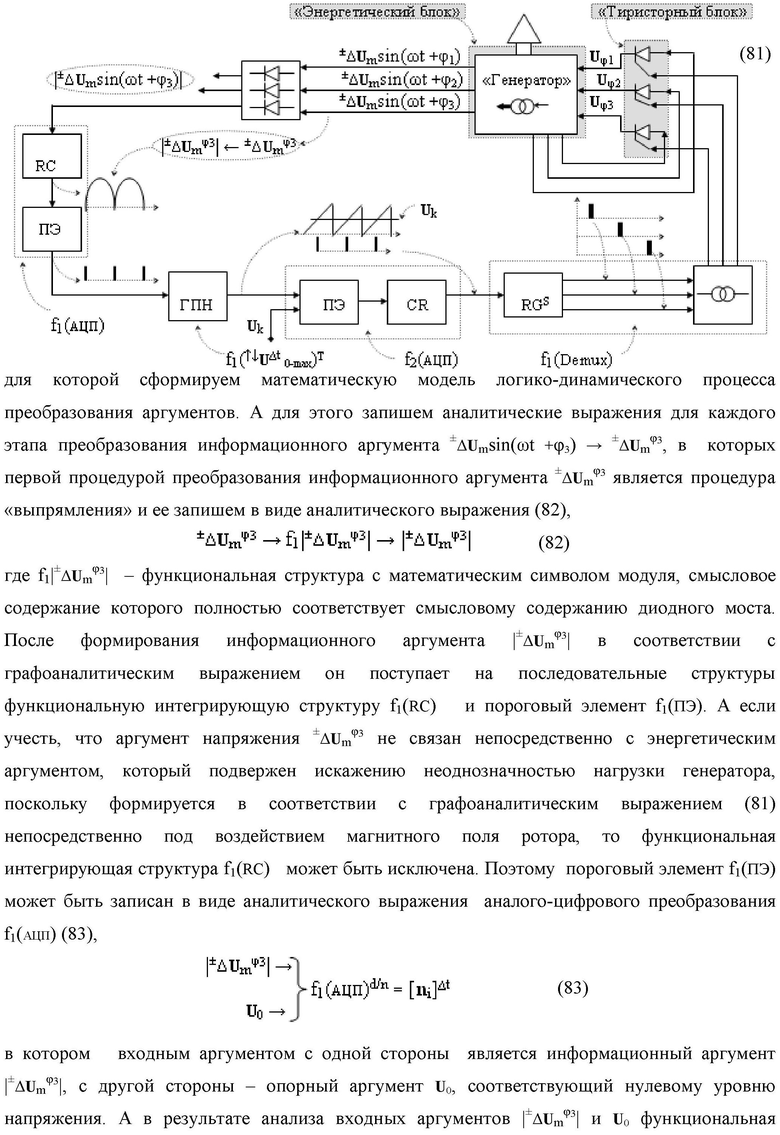

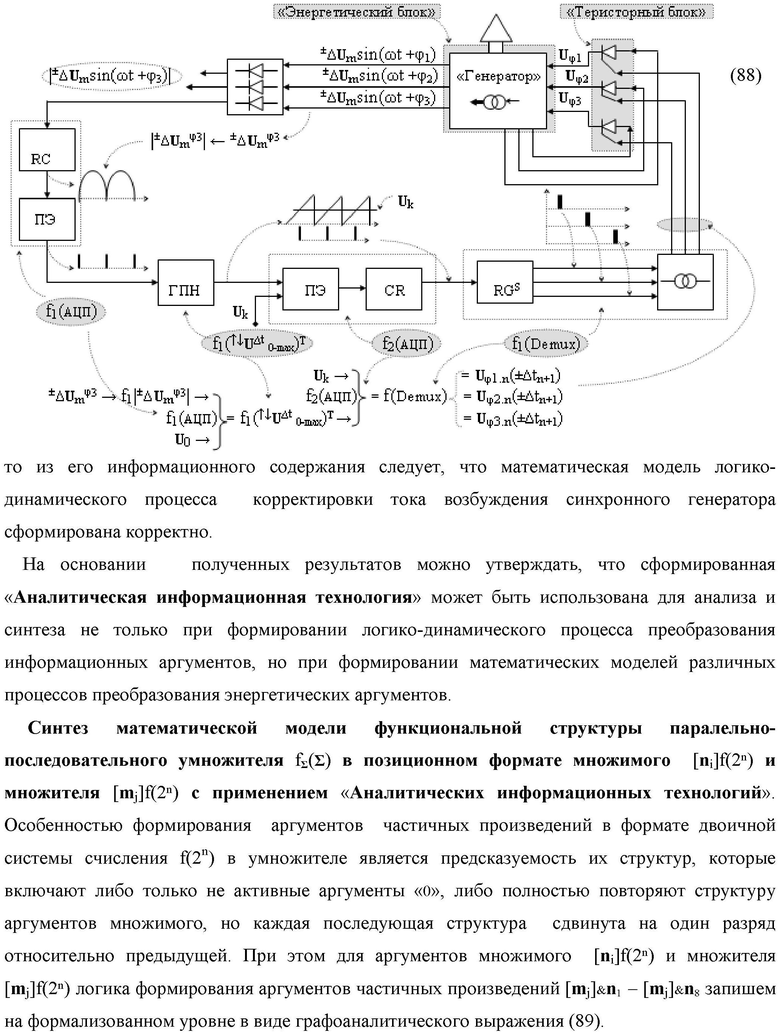





Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройствах для выполнения арифметических операций умножения аргументов множимого [mj]f(2n) и множителя [ni]f(2n) в позиционном формате. Техническим результатом является упрощение структуры и повышение быстродействия параллельно-последовательного умножителя. Умножитель выполнен в виде двух эквивалентных по структуре каналов для формирования промежуточной суммы младших и старших разрядов, каждый из которых содержит логические функции И для формирования аргументов частичных произведений, и сумматоры.
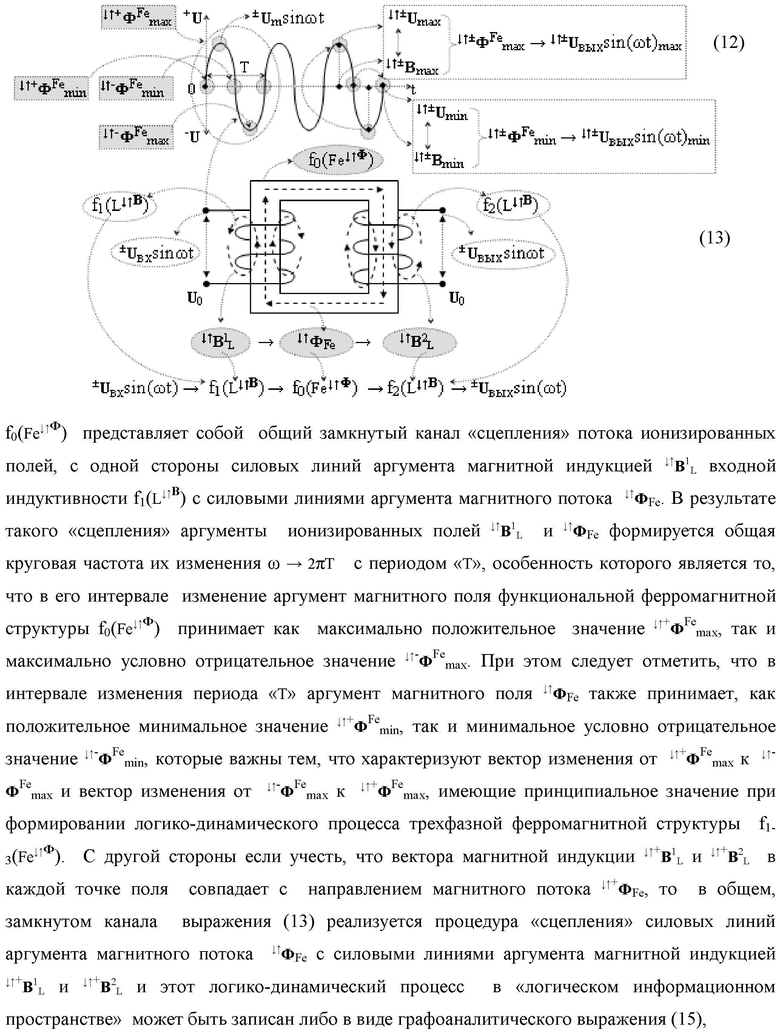
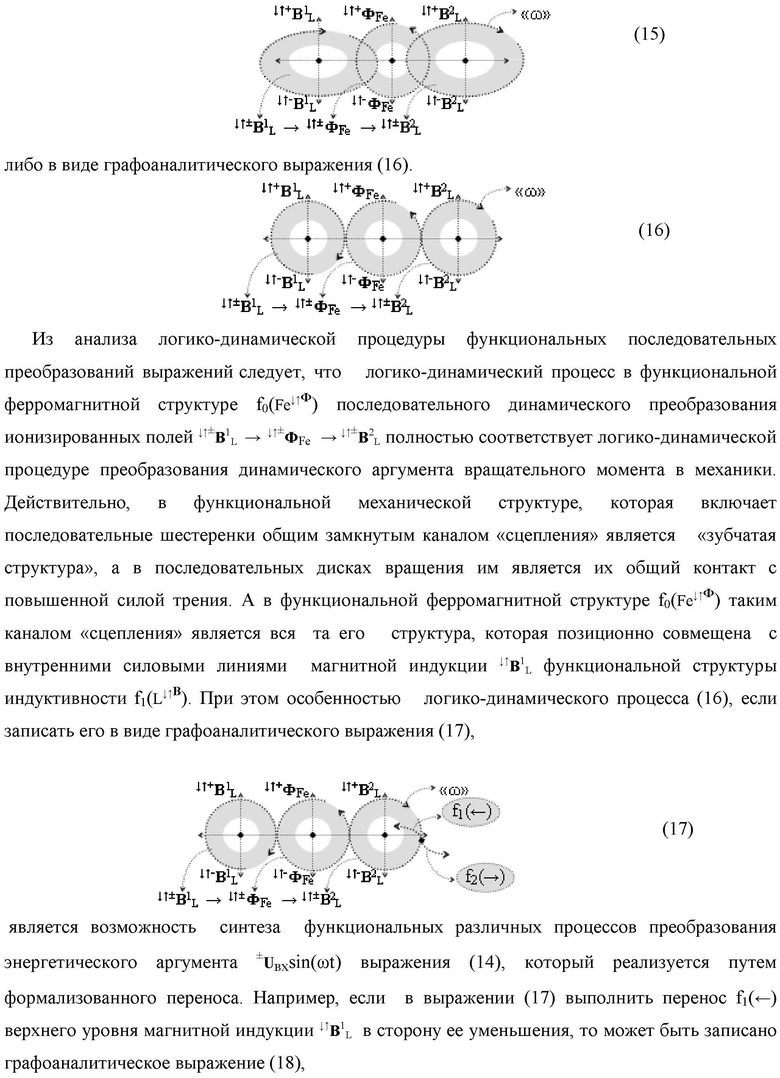
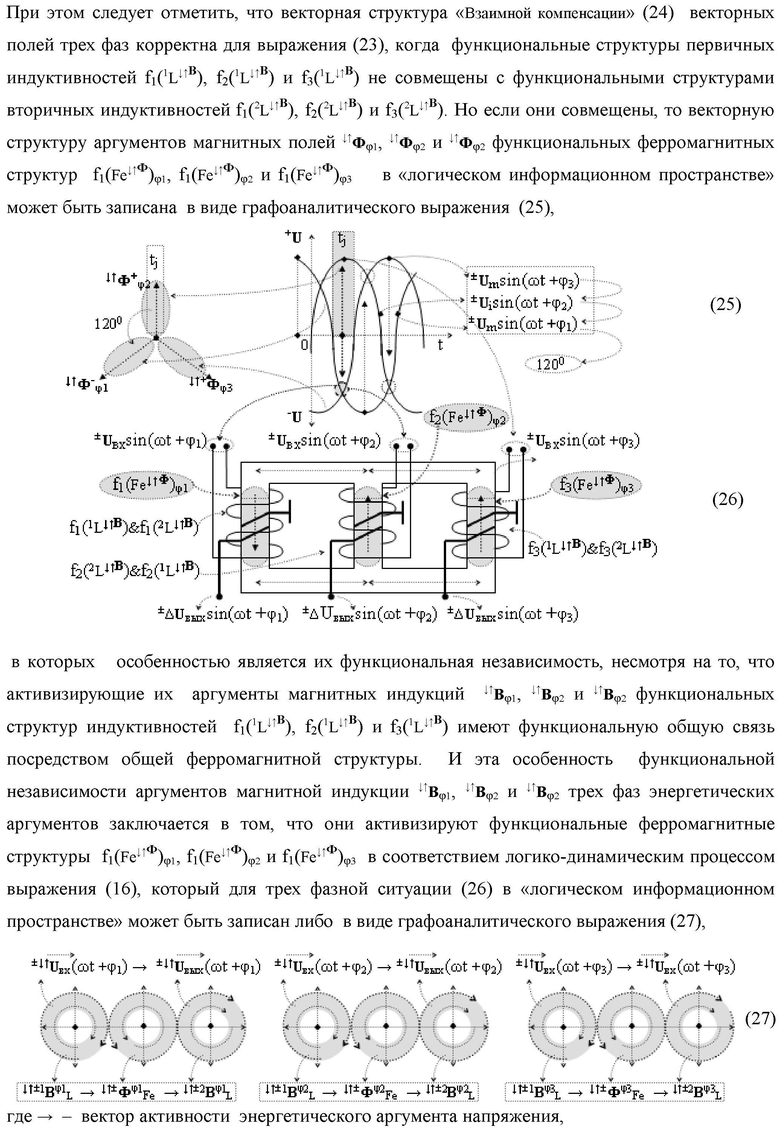
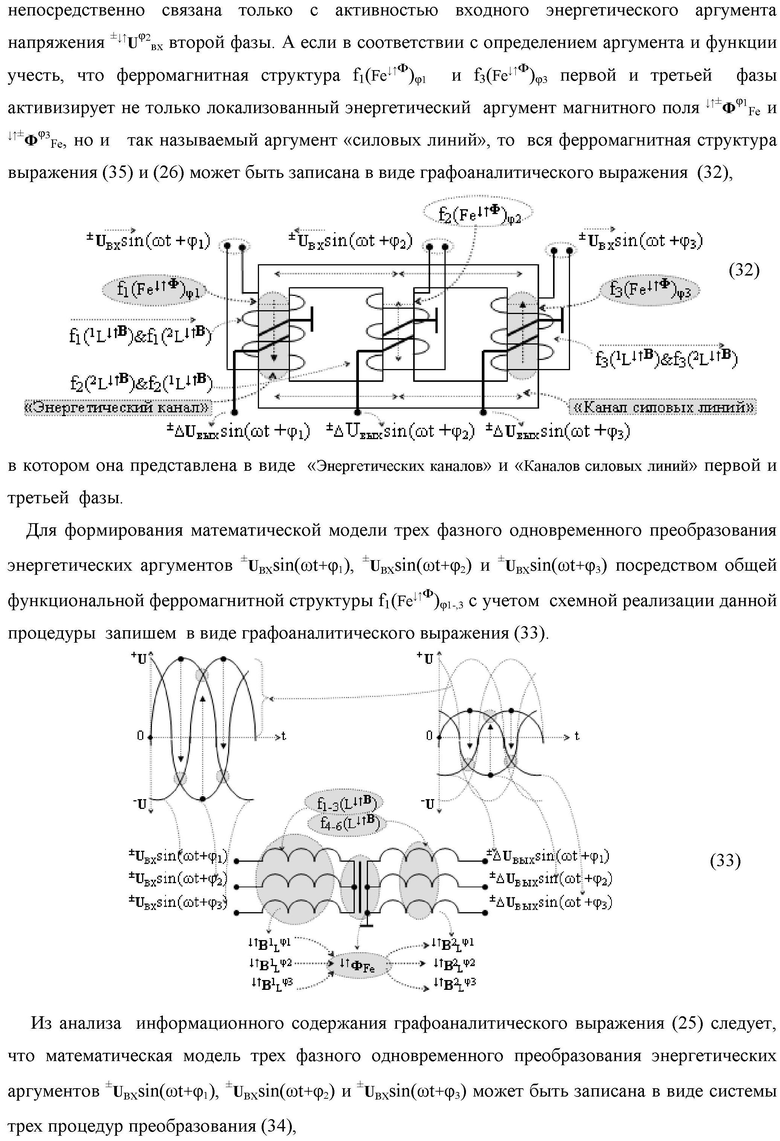
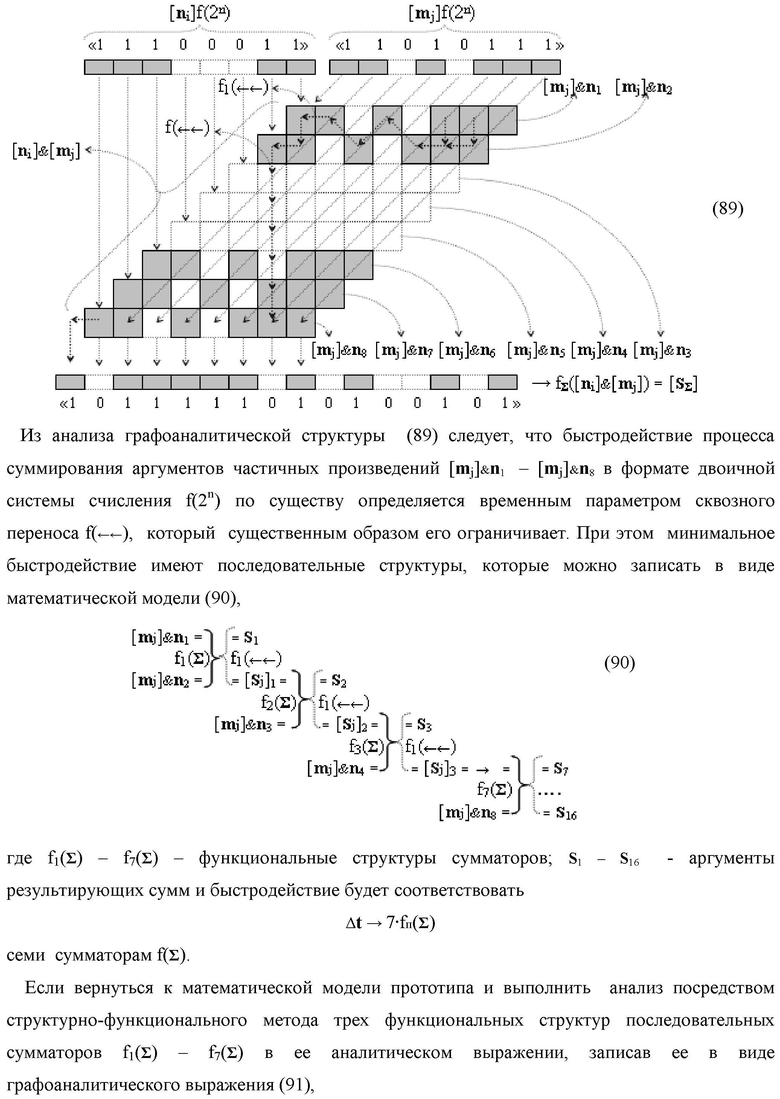
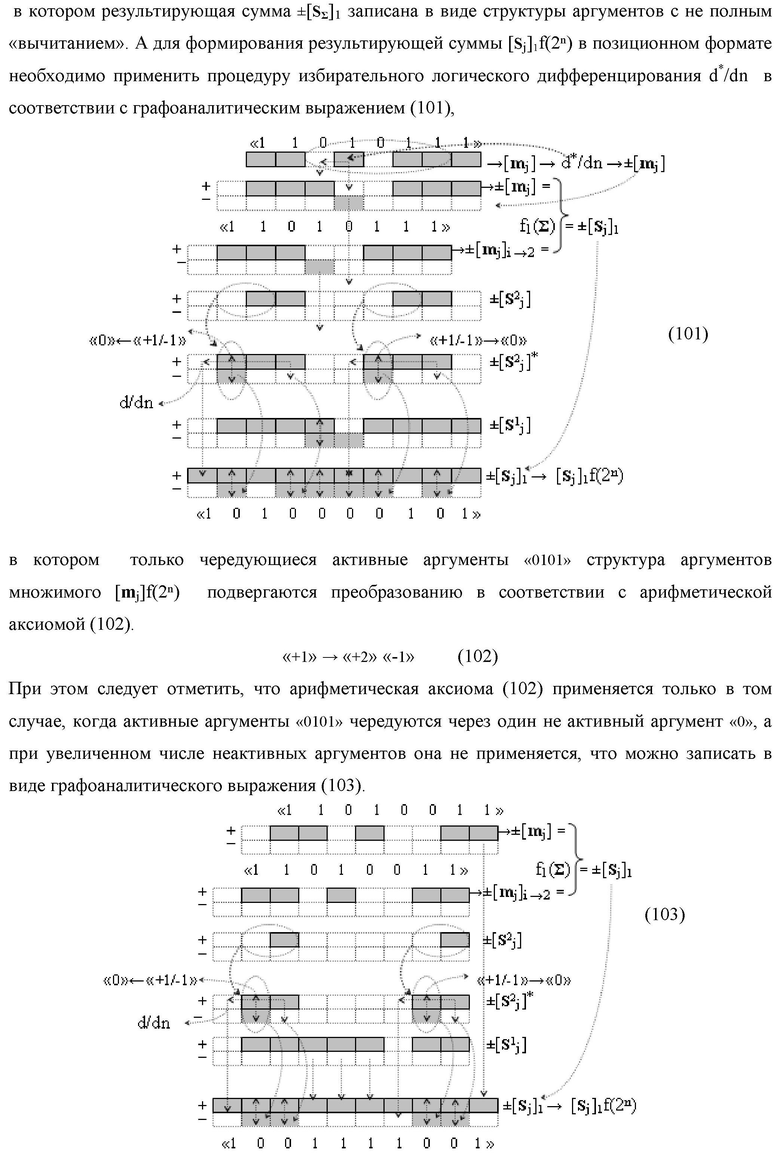
Функциональная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [mj]f(2n) и множителя [ni]f(2n), включающая линейные логические функции f1-8[&j]-И и каждая из них включает «j» логических функций fj(&)-И, в которых первые функциональные связи являются функциональной входной связью функциональной структуры умножителя для приема аргументов n1-n8 множителя [ni]f(2n), вторые функциональные входные связи в каждой линейной логической функции f1-8[&j]-И являются функциональными входными связями функциональной структуры умножителя fΣ(Σ) для приема соответствующих аргументов множимого [mj]f(2n), при этом функциональная выходная связь линейной логической функции f1[&j]-И, формирующая аргумент младшего разряда S1 1 результирующей суммы [SΣ], является функциональной выходной связью функциональной структуры умножителя fΣ(Σ), а остальные ее функциональные выходные связи и функциональные выходные связи линейной логической функции f2[&j]-И являются первыми и вторыми функциональными входными связями (S1 1…j) и (S2 1…j) функциональной структуры сумматора f1(Σ), в котором функциональная выходная связь, формирующая аргумент второго младшего разряда S1 2 результирующей суммы [SΣ], является функциональной выходной связью функциональной структуры умножителя fΣ(Σ), a остальные ее функциональные выходные связи являются первыми функциональными входными связями (S1 1…j) функциональной структуры сумматора f5(Σ), в котором функциональные выходные связи, формирующие аргументы младших разрядов S1 3 и S1 4 результирующей суммы [SΣ], является функциональной выходной связью функциональной структуры умножителя fΣ(Σ), а остальные функциональные выходные связи являются первыми функциональными входными связями (S1 1…j) функциональной структуры сумматора f7(Σ), при этом функциональные выходные связи линейной логической функции f6[&j]-И и f8[&j]-И являются вторыми функциональными входными связями (S2 1…j) функциональных структур сумматоров f3(Σ) и f4(Σ), в которых функциональные выходные связи одного являются функциональными входными связями другого, за исключением функциональной связи младшего разряда функциональной структуры сумматора f3(Σ), формирующая аргумент S2 1 результирующей суммы [SΣ], отличающаяся тем, что входная структура умножителя fΣ(Σ) выполнена в виде двух каналов эквивалентных по структуре для формирования промежуточной суммы [SΣ]5 младших разрядов и промежуточной суммы [SΣ]6 старших разрядов, первый из которых включает линейные логические функции f1-4[&j]-И и функциональные структуры сумматоров f1(Σ), f2(Σ) и f5(Σ) для формирования результирующей промежуточной суммы [SΣ]5, при этом функциональные связи в первом канале младших разрядов промежуточных сумм выполнены в соответствии с математической моделью вида

а второй канал включает линейные логические функции f5-8[&j]-И и функциональные структуры сумматоров f3(Σ), f4(Σ) и f6(Σ) для формирования результирующей промежуточной суммы S2 1, S2 2, S2 3, S2 4 и [SΣ]6, при этом функциональные связи во втором канале старших разрядов промежуточных сумм выполнены в соответствии с математической моделью вида

где 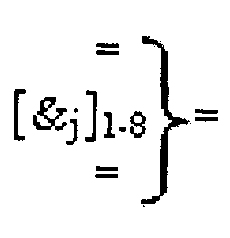 - линейные логические функции f1-8[&j]-И.
- линейные логические функции f1-8[&j]-И.
| УЭЙКЕРЛИ ДЖ | |||
| Проектирование цифровых устройств, т.1 | |||
| - М.: Постмаркет, 2002, с.519-521, рис.5.98 | |||
| ФУНКЦИОНАЛЬНАЯ ВХОДНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО УМНОЖИТЕЛЯ ФОРМАТА ПОЗИЦИОННО-ЗНАКОВОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+/-) | 2008 |
|
RU2378684C1 |
| US 5907499 A, 25.05.1999 | |||
| US 5986587 A, 16.11.1999. | |||
Авторы
Даты
2012-01-10—Публикация
2010-03-04—Подача