ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПРЕДВАРИТЕЛЬНОГО СУММАТОРА f(Σ) УСЛОВНО "j" РАЗРЯДА ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО УМНОЖИТЕЛЯ f(Σ), РЕАЛИЗУЮЩАЯ ПРОЦЕДУРУ "ДЕШИФРИРОВАНИЯ" АРГУМЕНТОВ ЧАСТИЧНЫХ ПРОИЗВЕДЕНИЙ СО СТРУКТУРАМИ АРГУМЕНТОВ МНОЖИМОГО [m]f(2) И МНОЖИТЕЛЯ [n]f(2) В ПОЗИЦИОННОМ ФОРМАТЕ "ДОПОЛНИТЕЛЬНОГО КОДА" И ФОРМИРОВАНИЯ ПРОМЕЖУТОЧНОЙ СУММЫ [Sj]f(2) В ПОЗИЦИОННОМ ФОРМАТЕ "ДОПОЛНИТЕЛЬНОГО КОДА RU" (ВАРИАНТЫ РУССКОЙ ЛОГИКИ) Российский патент 2016 года по МПК G06F7/505 

Текст описания приведен в факсимильном виде.

Группа изобретений относится к вычислительной технике и может быть использована при построении параллельно-последовательного умножителя с входными аргументами слагаемых [m_j]f(2ⁿ) и [n_i]f(2ⁿ) в формате «дополнительный код». Техническим результатом является повышение быстродействия преобразования входных аргументов. В одном из вариантов структура реализована с использованием логических элементов И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ. 2 н.п. ф-лы.

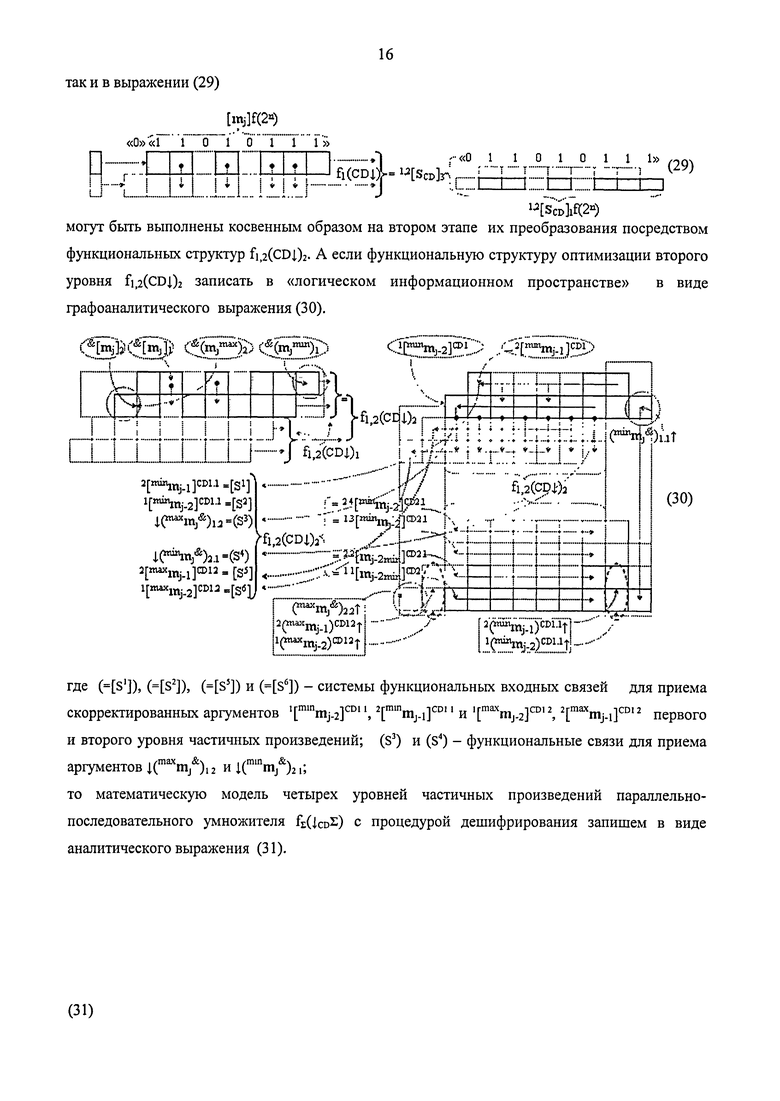
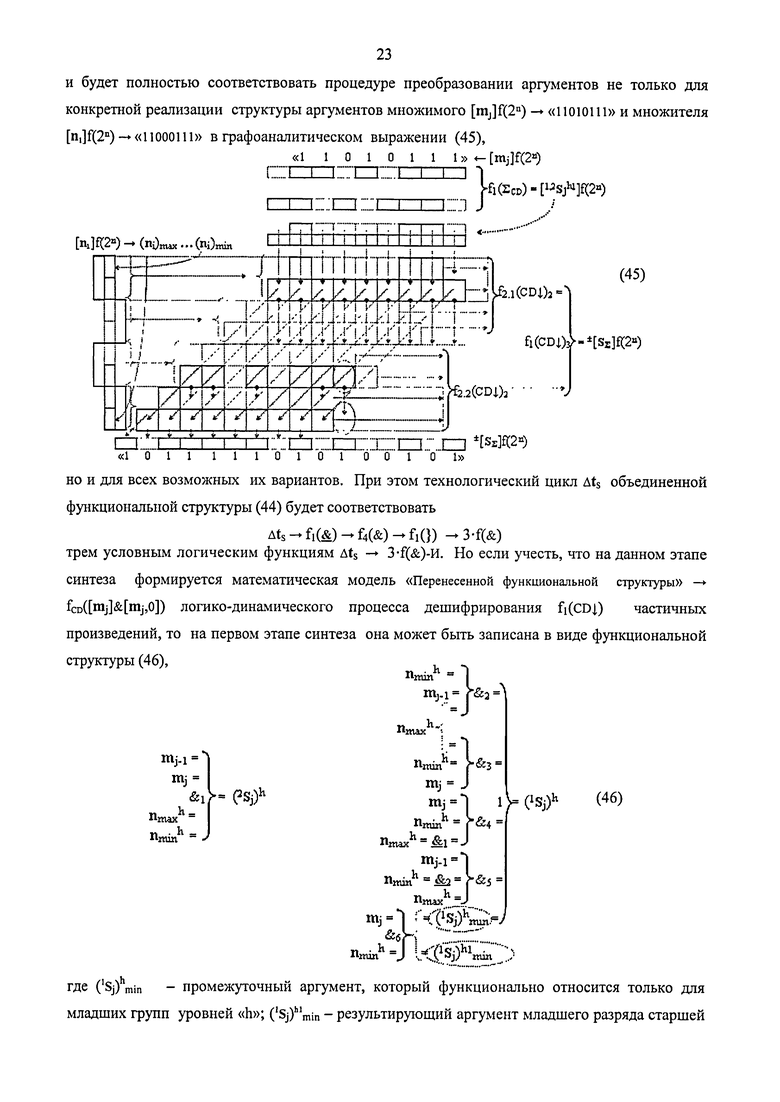
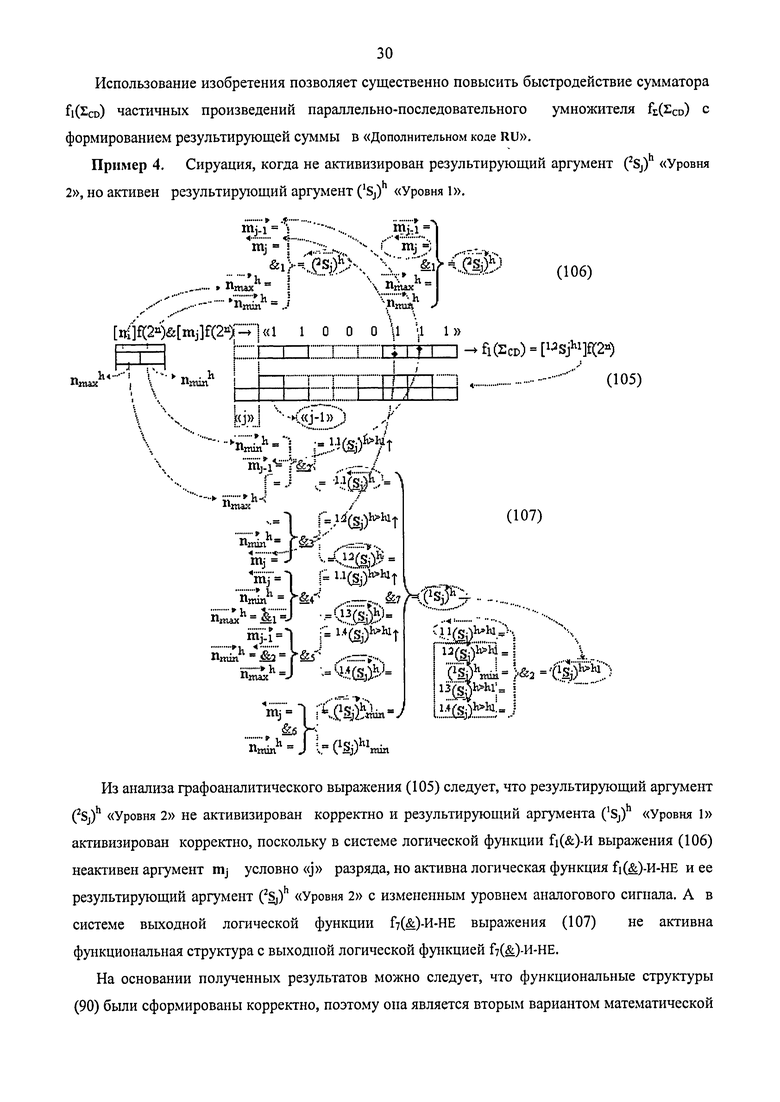
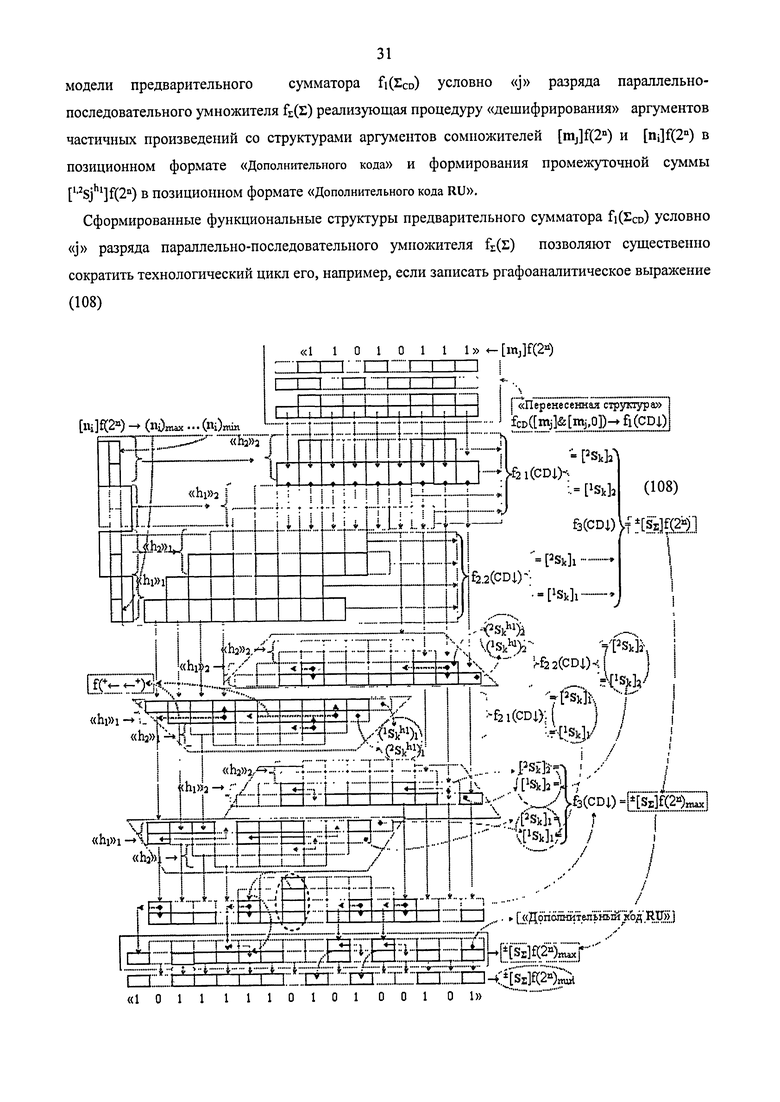
1. Функциональная структура предварительного сумматора f₁(Σ_CD) условно «j» разряда параллельно-последовательного умножителя f_Σ(Σ) реализующая процедуру «дешифрирования» аргументов частичных произведений со структурами аргументов множимого [m_j]f(2ⁿ) и множителя [n_i]f(2ⁿ) в позиционном формате «Дополнительного кода» и формирования промежуточной суммы [^1,2Sj^h1]f(2ⁿ) в позиционном формате «Дополнительного кода RU», включающая входную логическую функцию f₃(&)-И, в которой функциональная связь является функциональной входной связью функциональной структуры для приема аргумента m_j множимого условно «j» разряда, включает также логическую функцию f₄(&)-И с входной логической функцией f₁( & )-НЕ, а также логическую функцию f₁(})-ИЛИ, отличающаяся тем, что для активизации результирующего аргумента (¹ S _j)^h «Уровня 1» без изменения уровня аналогового сигнала введены логические функции f₂(&)-И, f₅(&)-И, f₆(&)-И и f₂( & )-НЕ, а для активизации результирующего аргумента (¹ S _j)^h «Уровня 1» с измененным уровнем аналогового сигнала введена логическая функция f₁(}& )-ИЛИ-НЕ, при этом для активизации результирующего аргумента (² S _j)^h без изменения уровня аналогового сигнала и результирующего аргумента (² S _j)^h с измененным уровнем аналогового сигнала «Уровня 2» введены логические функции f₁(&)-И и f₁(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

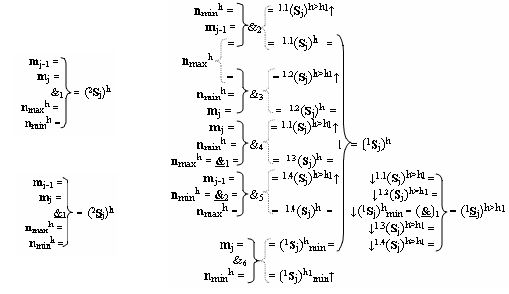
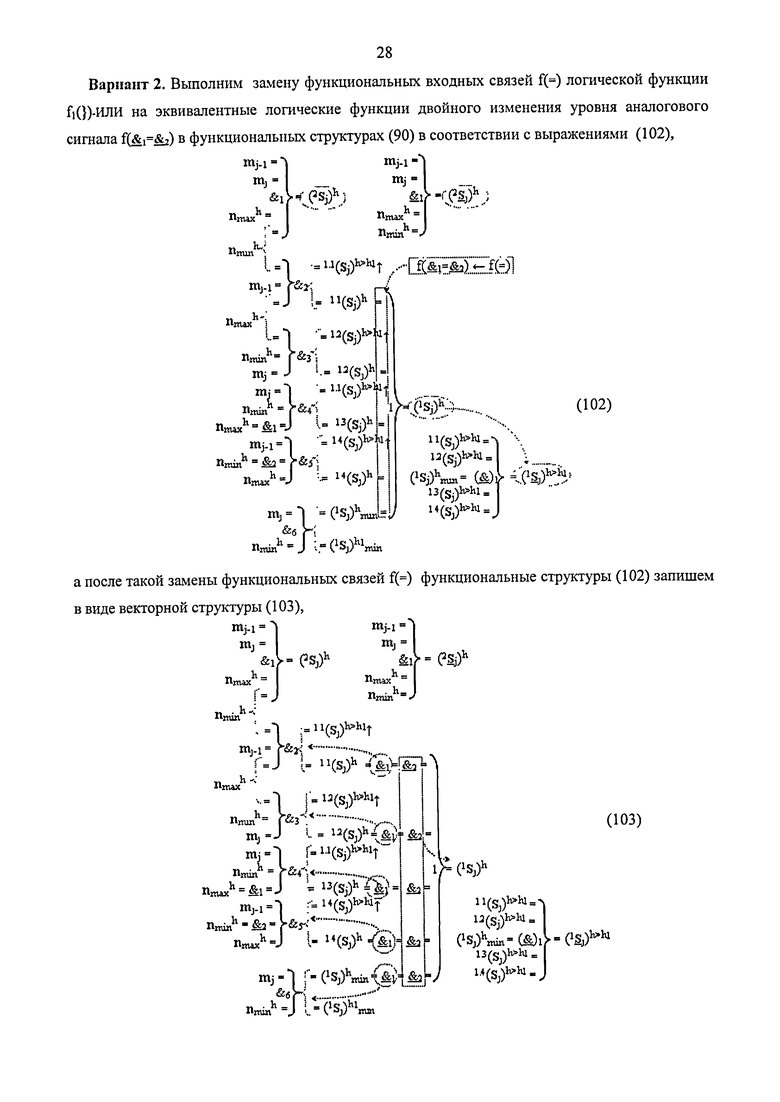
где ^1.1(S _j)^h>h1↑ … ^1.4(S _j)^h>h1↑ - дополнительные преобразованные аргументы логических функций f₂(&)-И - f₅(&)-И, включаемые в систему дополнительной логической функции f₁(}& )-ИЛИ-НЕ для всех уровней «h»>«h₁»,
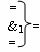
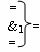- логическая функция f₁(&)-И;

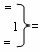
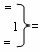
- логическая функция f₁(})-ИЛИ;

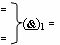
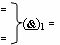
- логическая функция f₁(}& )-ИЛИ-НЕ;

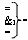
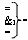
- логическая функция f₁(&)-И-НЕ;
«= & ₁=» - логическая функция f₁( & )-НЕ изменения активности входных аналоговых сигналов.

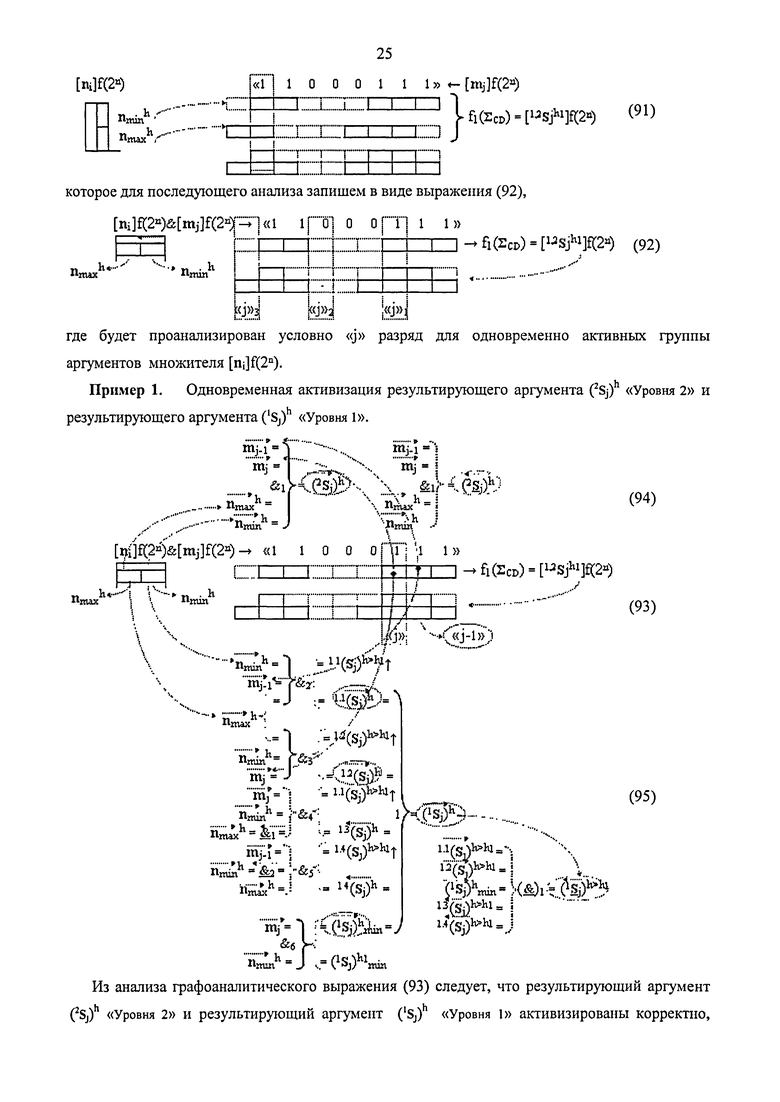
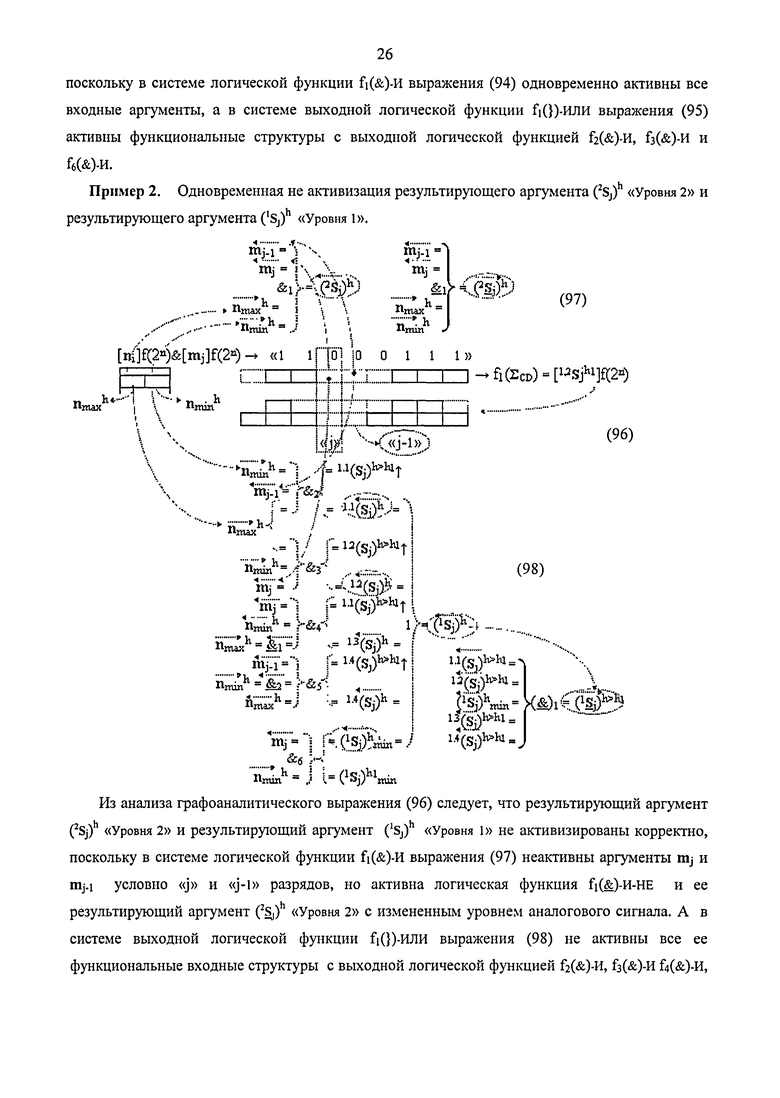
2. Функциональная структура предварительного сумматора f₁(Σ_CD) условно «j» разряда параллельно-последовательного умножителя f_Σ(Σ) реализующая процедуру «дешифрирования» аргументов частичных произведений со структурами аргументов сомножителей [m_j]f(2ⁿ) и [n_i]f(2ⁿ) в позиционном формате «Дополнительного кода» и формирования промежуточной суммы [^1,2Sj^h1]f(2ⁿ) и [^1,2Sj^h2]f(2ⁿ) в позиционном формате «Дополнительного кода RU», включающая логическую функцию f₁(&)-И, в которой функциональная связь является функциональной входной связью функциональной структуры для приема аргумента m_j множимого условно «j» разряда, включает также логическую функцию f₂(&)-И, отличающаяся тем, что для активизации результирующего аргумента (¹ S _j)^h «Уровня 1» без изменения уровня аналогового сигнала введены логические функции f₂(&)-И-НЕ, f₃(&)-И-НЕ, f₄(&)-И-НЕ, f₅(&)-И-НЕ, f₆(&)-И-НЕ и f₇(&)-И-НЕ, а для активизации результирующего аргумента (¹ S _j)^h «Уровня 1» с измененным уровнем аналогового сигнала введена логическая функция f₂(&)-И, при этом для активизации результирующего аргумента (² S _j)^h с измененным уровнем аналогового сигнала «Уровня 2» введена логическая функция f₁(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

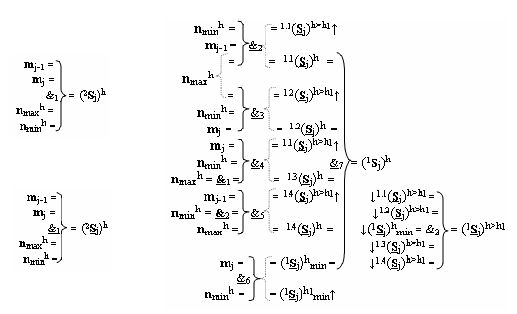
где ^1.1( S _j)^h>h1↑ … ^1.4( S _j)^h>h1↑ и (¹ S _j)^h _min - дополнительные преобразованные аргументы логических функций f₂(&)-И-НЕ - f₆(&)-И-НЕ, включаемые в систему дополнительной логической функции f₂(&)-И для всех уровней «h»>«h₁».