Текст описания приведен в факсимильном виде































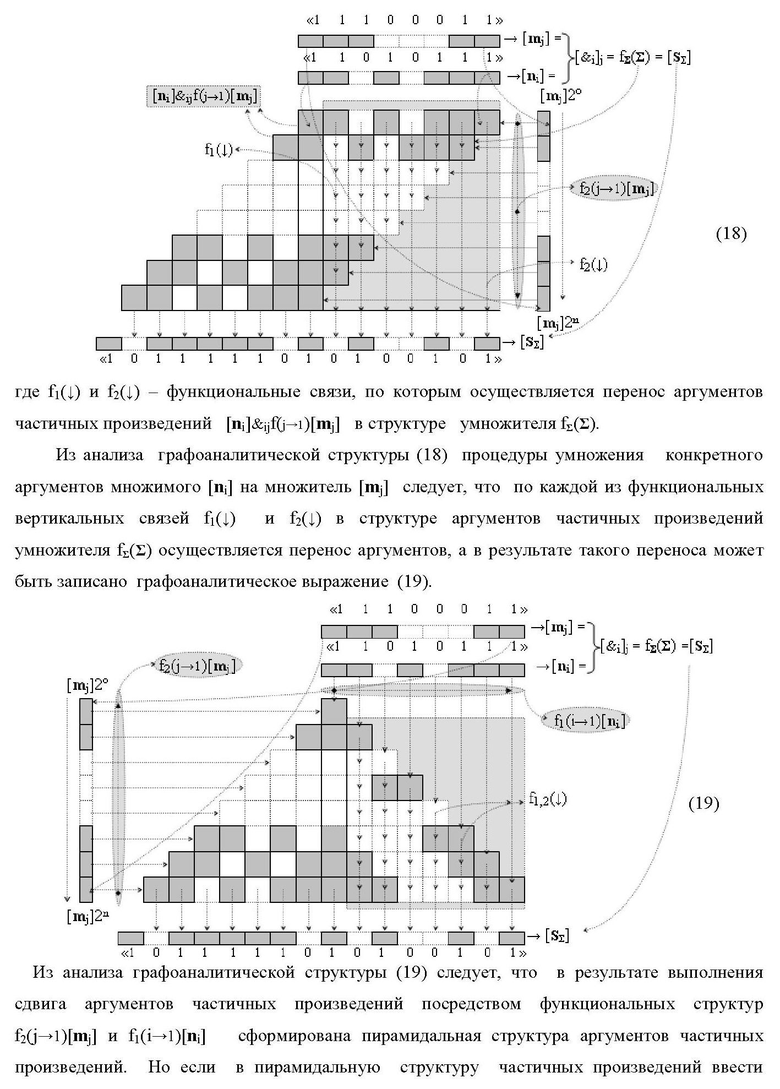

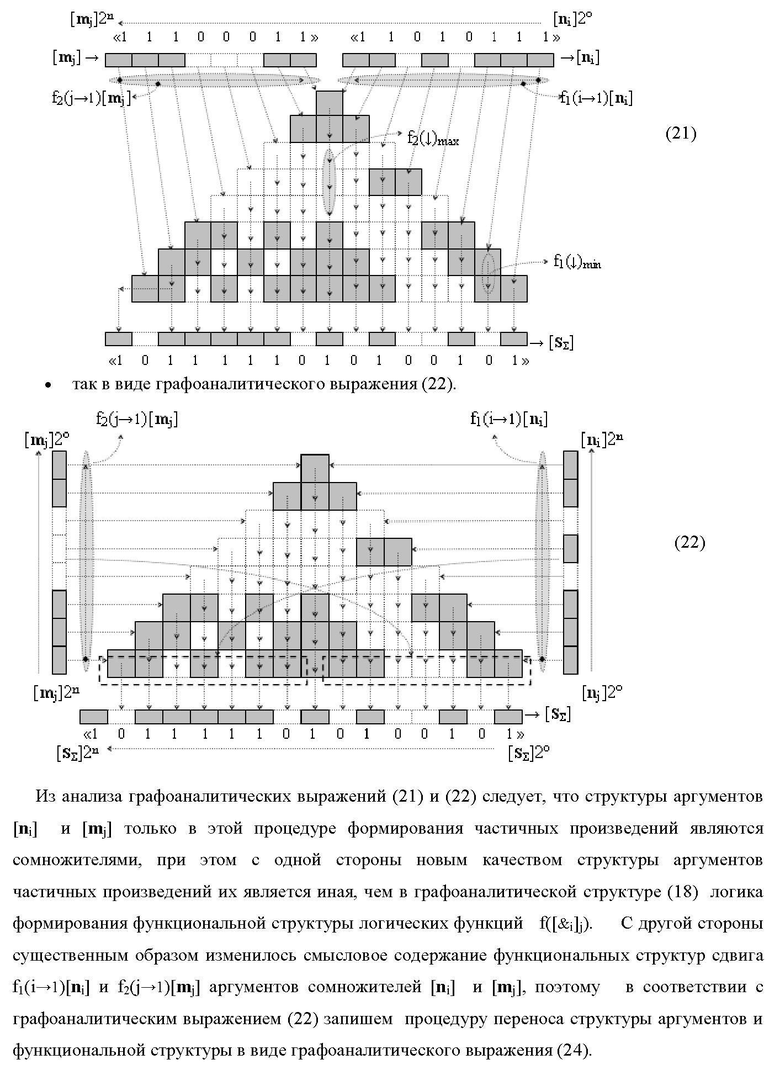



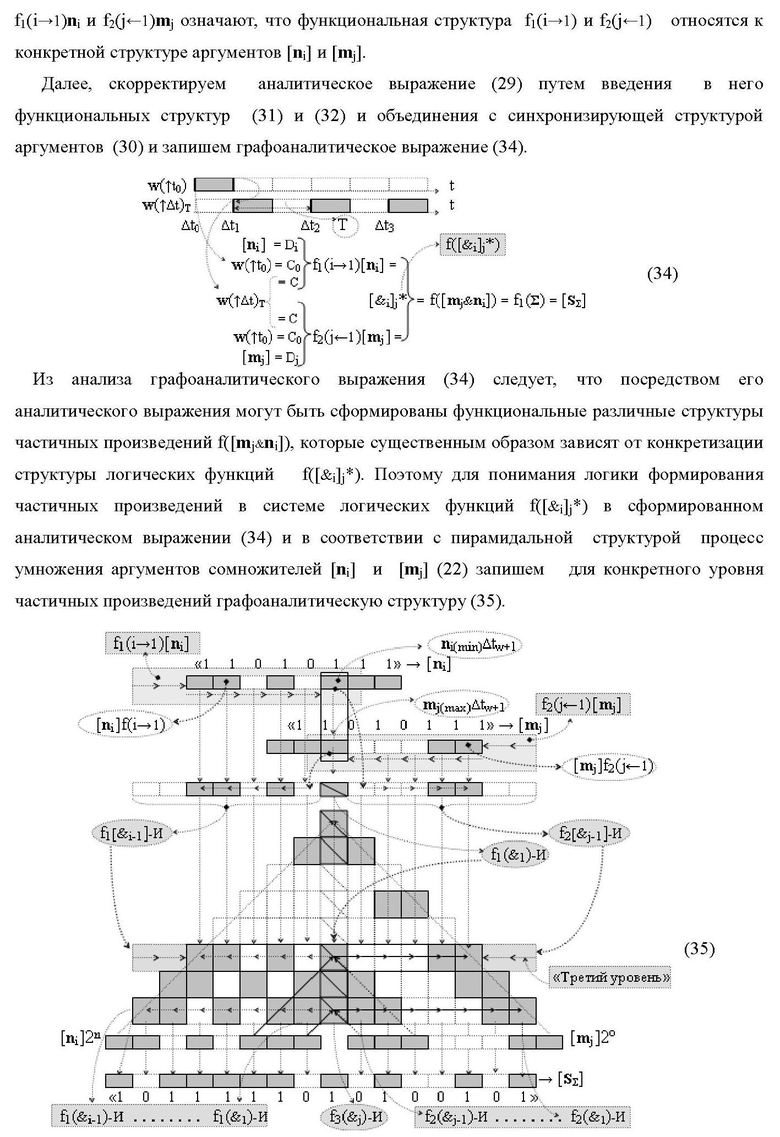















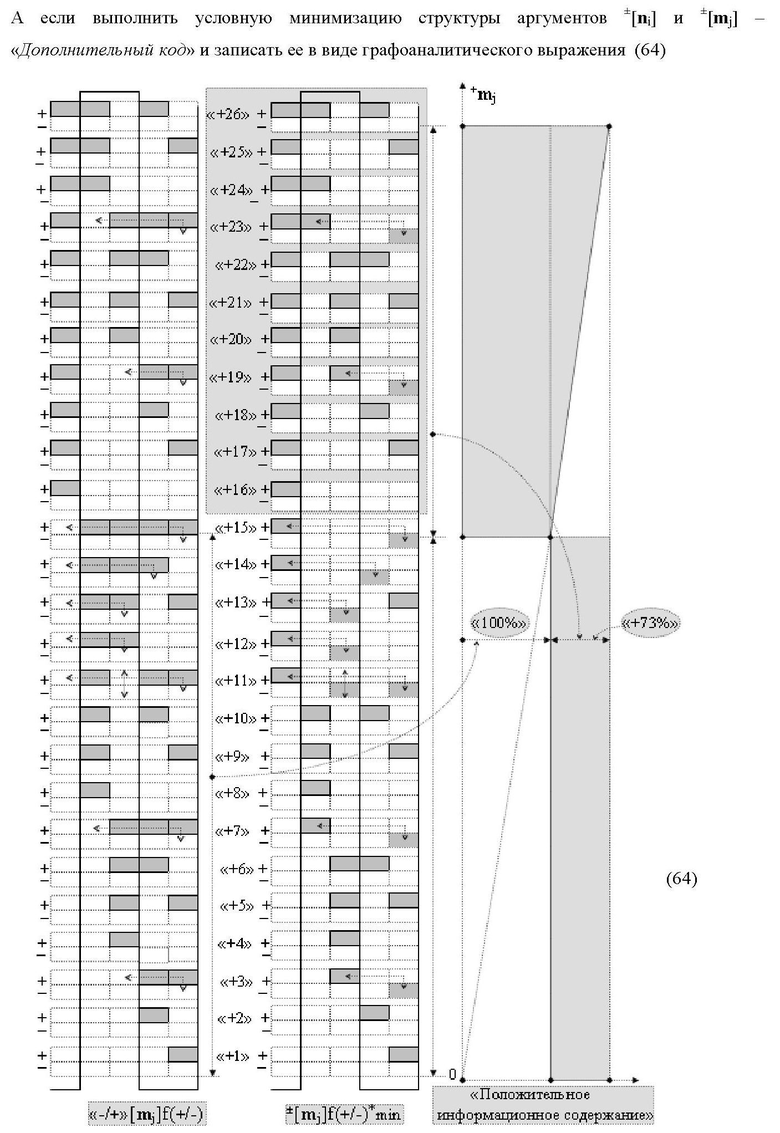


Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических операций умножения аргументов сомножителей. Техническим результатом является повышение быстродействия процесса преобразования аргументов при формировании результирующей суммы частичных произведений. В одном из вариантов структура реализована с использованием логических элементов И. 8 н.п. ф-лы.
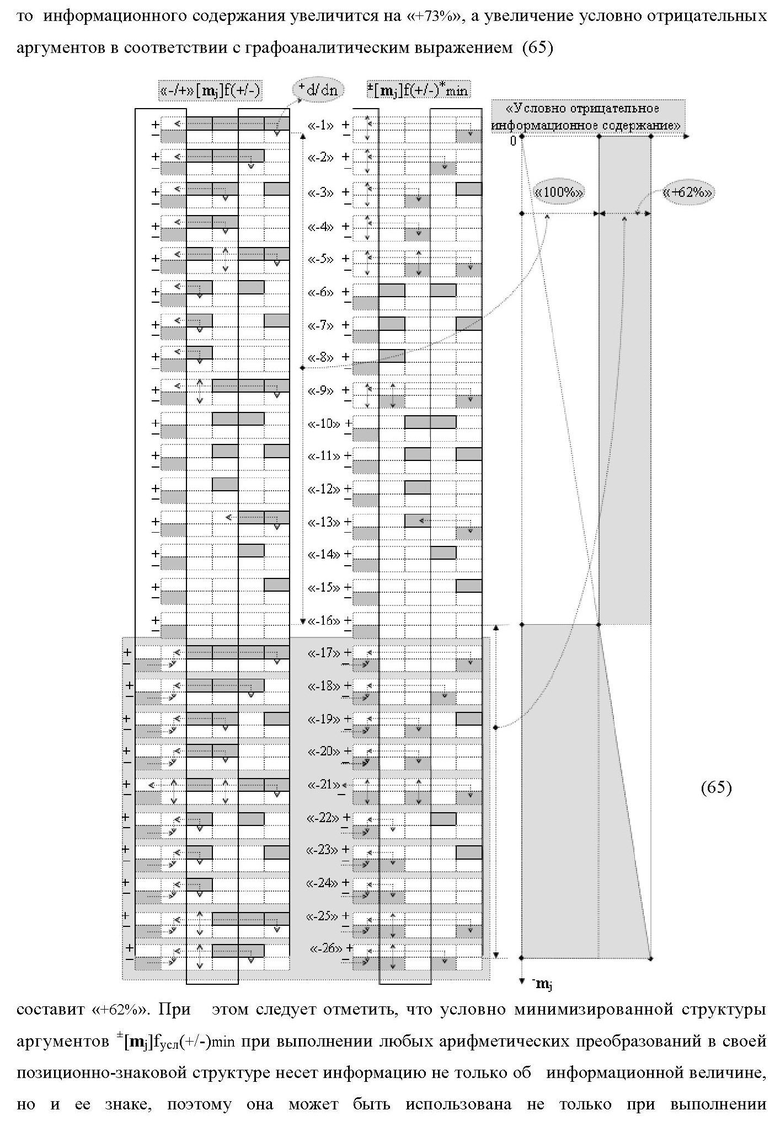
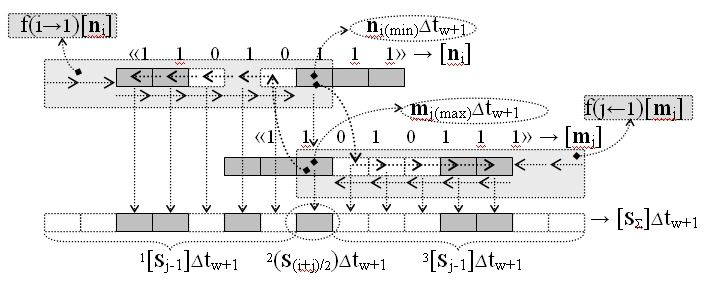
1. Способ логико-динамического процесса формирования информационных аналоговых сигналов частичных произведений аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) для последующего накапливающего суммирования в сумматоре f1(±
Σ), в котором одновременно выполняют дискретный сдвиг аргументов аналоговых сигналов сомножителей ±[n
i] и ±[m
j], при этом посредством функциональной структуры сдвига f2(j←1)[m
j] дискретный сдвиг f2(j←1) структуры аргументов ±[m
j] выполняют в позиционное положение старшего разряда, а посредством функциональной структуры убывающего сдвига f1(i→1)[n
i] дискретный сдвиг f1(i→1) структуры аргументов ±[n
i] выполняют в позиционное положение первого младшего «imin» разряда, а его текущим аргументом аналогового сигнала множителя n
i(min)∆tw после выполненных сдвигов f2(j←1)∆tw и f1(i→1)∆tw структур аргументов сомножителей ±[n
i] и ±[m
j] посредством функциональной логической структуры f2(&j-1)-И реализуют логическое умножение n
i(min)∆tw(&j-1)±[m
j-1] → 2[S
j-1]∆tw текущего аргумента аналогового сигнала множителя n
i(min)∆tw на структуру аргументов аналоговых сигналов множимого ±[m
j-1] и формируют аргументы аналоговых сигналов второй половины частичного произведения 2[S
j-1]∆tw, которые через функциональную структуру сумматора f1(±
Σ) и функциональную структуру памяти f1(RSΣ) подают на вторые функциональные связи (=[SΣ]2) того же сумматора f1(±
Σ) в виде структуры аргументов ↓[S
Σ]∆tw и посредством их общей функциональной структуры, эквивалентной математической модели вида
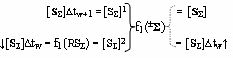
выполняют логическое суммирование аргументов частичных произведений [S
Σ]∆tw и [S
Σ]∆tw+1, которые подают на вторые и первые функциональные входные связи (=[SΣ]2) и (=[SΣ]1) функциональной структуры сумматора f1(±
Σ), и формируют как структуру позиционных аргументов результирующей суммы [S
Σ] результата умножения, так и структуру промежуточной суммы аргументов [S
Σ]∆tw↑, отличающийся тем, что в функциональной структуре сдвига f2(j←1)[m
j] дискретный сдвиг структуры аргументов ±[m
j] выполняют с убыванием ее старшего «jmax» разряда, формируют в «jmax» разряде текущий аргумент аналоговый сигнал аргумента множителя m
j(max)∆tw и посредством функциональной логической структуры f1(&i-1)-И реализуют логическое умножение m
j(max)∆tw(&i-1)±[n
i-1] → 1[S
i-1]∆tw текущего аргумента аналогового сигнала множителя m
j(max)∆tw на структуру аргументов аналоговых сигналов множимого ±[n
i-1] и формируют структуру аргументов аналоговых сигналов первой половины частичного произведения 1[S
i-1]∆tw, а посредством функциональной логической структуры f1(&1)-И реализуют логическое умножение m
j(max)∆tw(&i)n
i(min)∆tw → (S
(i+j)/2)∆tw+1 текущего аргумента аналогового сигнала множителя m
j(max)∆tw на текущий аргумент аналогового сигнала множителя n
i(min)∆tw и формируют аргумент аналогового сигнала (S
(i+j)/2)∆tw среднего частичного произведения, который включают в структуру аргументов 1±[S
i-1]∆tw и 2±[S
j-1]∆tw в соответствии с аналитическим выражением вида
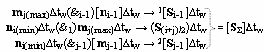
и формируют структуру аргументов аналоговых сигналов предыдущего частичного произведения [S
Σ]∆tw, при этом формирование последующих аргументов частичных произведений [S
Σ]∆tw+1 выполняют также в соответствии с аналитическим выражением вида
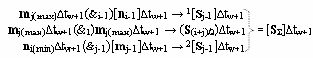
и в соответствии с логико-динамическим процессом вида
где  и
и  - положительный активный и неактивный формализованный позиционный аргумент аналогового сигнала, соответствующий логическому аргументу «1» и логическому аргументу «0», формируют последующую структуру аргументов частичных произведений [S
Σ]∆tw+1.
- положительный активный и неактивный формализованный позиционный аргумент аналогового сигнала, соответствующий логическому аргументу «1» и логическому аргументу «0», формируют последующую структуру аргументов частичных произведений [S
Σ]∆tw+1.
2. Способ логико-динамического процесса формирования информационных аналоговых сигналов частичных произведений аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) для последующего накапливающего суммирования в сумматоре f1(±
Σ), в котором одновременно выполняют дискретный сдвиг аргументов аналоговых сигналов сомножителей ±[n
i] и ±[m
j], при этом посредством функциональной структуры сдвига f2(j←1)[m
j] дискретный сдвиг f2(j←1) структуры аргументов ±[m
j] выполняют в позиционное положение старшего (±jmax) разряда, а посредством функциональной структуры убывающего сдвига f1(i→1)[n
i] дискретный сдвиг f1(i→1) структуры аргументов ±[n
i] выполняют в позиционное положение первого младшего «imin» разряда, а его текущим аргументом аналогового сигнала множителя n
i(min)∆tw после выполненных сдвигов f2(j←1)∆tw и f1(i→1)∆tw структур аргументов сомножителей ±[n
i] и ±[m
j] функциональной логической структуры f2(&j-1)-И реализуют логическое умножение n
i(min)∆tw(&j-1)±[m
j-1] → 2[S
j-1]∆tw текущего аргумента аналогового сигнала множителя n
i(min)∆tw на структуру аргументов аналоговых сигналов множимого ±[m
j-1] и формируют аргументы аналоговых сигналов второй половины частичного произведения 2[S
j-1]∆tw, которые через функциональную структуру сумматора f1(±
Σ) и функциональную структуру памяти f1(RSΣ) подают на вторые функциональные связи (=[SΣ]2) того же сумматора f1(±
Σ) в виде структуры аргументов ↓[S
Σ]∆tw и посредством их общей функциональной структуры, эквивалентной математической модели вида
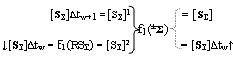
выполняют логическое суммирование аргументов частичных произведений [S
Σ]∆tw и [S
Σ]∆tw+1, которые подают на вторые и первые функциональные входные связи (=[SΣ]2) и (=[SΣ]1) функциональной структуры сумматора f1(±
Σ) и формируют как структуру аргументов результирующей суммы ±[S
Σ] результата умножения, так и структуру промежуточной суммы аргументов ±[S
Σ]∆tw↑, отличающийся тем, что в функциональной структуре сдвига f2(j←1)[m
j] дискретный сдвиг структуры аргументов ±[m
j] выполняют с убыванием ее старшего «jmax» разряда и формируют в «jmax» разряде текущий аргумент аналоговый сигнал аргумента множителя m
j(max)∆tw и посредством логических функций f2(&i-1)-И реализуют логическое умножение m
j(max)∆tw(&i-1)±[n
i-1] → 1[S
i-1]∆tw текущего аргумента аналогового сигнала множителя m
j(max)∆tw на структуру аргументов аналоговых сигналов множимого ±[n
i-1] и формируют структуру аргументов аналоговых сигналов первой половины частичного произведения 1[S
i-1]∆tw, а посредством функциональной логической структуры f1(&1)-И реализуют логическое умножение m
j(max)∆tw(&i)n
i(min)∆tw → (S
(i+j)/2)∆tw+1 текущего аргумента аналогового сигнала множителя m
j(max)∆tw на текущий аргумент аналогового сигнала множителя n
i(min)∆tw и формируют аргумент аналогового сигнала (S
(i+j)/2)∆tw среднего частичного произведения, который включают в последовательную структуру аргументов 1[S
i-1]∆tw и 2[S
j-1]∆tw в соответствии с аналитическим выражением вида
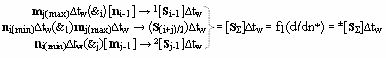
аргументов аналоговых сигналов частичного произведения [S
Σ]∆tw и посредством функциональной структуры избирательного логического дифференцирования f1(d/dn*) позиционную структуру предыдущего частичного произведения [S
Σ]∆tw преобразуют в позиционно-знаковую структуру аргументов ±[S
Σ]∆tw, при этом формирование последующих аргументов частичных произведений [S
Σ]∆tw+1 выполняют также в соответствии с аналитическим выражением вида
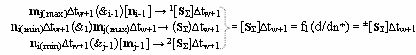
и в соответствии с логико-динамическим процессом вида
где  и
и  - положительный и условно отрицательный формализованный позиционно-знаковый аргумент аналогового сигнала, соответствующий положительному аргументу «+1» и условно отрицательному аргументу «-1» соответственно, при этом накапливающее суммирование скорректированных предыдущих и последующих аргументов частичных произведений ±[S
Σ]∆tw и ±[S
Σ]∆tw+1 выполняют посредством функциональной позиционно-знаковой структуры, эквивалентной математической модели вида
- положительный и условно отрицательный формализованный позиционно-знаковый аргумент аналогового сигнала, соответствующий положительному аргументу «+1» и условно отрицательному аргументу «-1» соответственно, при этом накапливающее суммирование скорректированных предыдущих и последующих аргументов частичных произведений ±[S
Σ]∆tw и ±[S
Σ]∆tw+1 выполняют посредством функциональной позиционно-знаковой структуры, эквивалентной математической модели вида
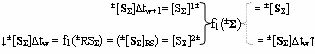
где ±[S
Σ]∆tw↑ и ↓±[S
Σ]∆tw - аргументы обратной связи;
в которой первые и вторые функциональные входные связи (=[SΣ]1±) и (=[SΣ]±2) выполняют в виде положительного канала суммирования и условно отрицательного канала суммирования.
3. Способ логико-динамического процесса формирования информационных аналоговых сигналов частичных произведений аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) для последующего накапливающего суммирования в сумматоре f1(±
Σ), в котором одновременно выполняют дискретный сдвиг аргументов аналоговых сигналов сомножителей ±[n
i] и ±[m
j], при этом посредством функциональной структуры сдвига f2(±j←1)[m
j] дискретный сдвиг f2(±j←1) структуры аргументов ±[m
j] выполняют в позиционное положение старшего «jmax» разряда, а посредством функциональной структуры убывающего сдвига f1(±i→1)[n
i] дискретный сдвиг f1(±i→1) структуры аргументов ±[n
i] выполняют в позиционное положение младшего «imin» разряда и текущими аргументами аналогового сигнала множителя ±
n
i(min)∆tw после выполненных сдвигов f2(±j←1)∆tw и f1(±i→1)∆tw структур аргументов сомножителей ±[n
i] и ±[m
j] посредством функциональной логической структуры f2(±&j-1)-И реализуют логическое умножение ±
n
i(min)∆tw(&j-1)±[m
j-1] → 2±[S
j-1]∆tw текущего аргумента аналогового сигнала множителя ±
n
i(min)∆tw на структуру аргументов аналоговых сигналов множимого ±[m
j-1] и формируют аргументы аналоговых сигналов второй половины частичного произведения 2±[S
j-1]∆tw, а посредством функциональной структуры памяти f1(±RSΣ) и функциональной структуры сумматора f1(±
Σ) выполняют накапливающее логическое суммирование промежуточной структуры аргументов суммы ±[S
Σ]∆tw↑ с последующей структурой аргументов аналоговых сигналов частичного произведения ±[S
Σ]∆tw+1, отличающийся тем, что в функциональной структуре сдвига f2(±j←1)[±
m
j] дискретный сдвиг структуры аргументов ±[m
j] выполняют с убыванием ее старшего «jmax» разряда и формируют текущий аргумент аналогового сигнала множителя ±
m
j(max)∆tw и посредством функциональной логической структуры f1(&i-1)-И реализуют логическое умножение ±
m
j(max)∆tw(±&i)±[n
i-1] → 1±[S
i-1]∆tw текущего аргумента аналогового сигнала множителя ±
m
j(max)∆tw на структуру аргументов аналоговых сигналов множимого ±[n
i-1] и формируют структуру аргументов аналоговых сигналов первой половины частичного произведения 1±[S
i-1]∆tw, а посредством функциональной логической структуры f1(±&1)-И реализуют логическое умножение ±
m
j(max)∆tw(&1)±
n
i(min)∆tw → ±(S
(i+j)/2)∆tw текущего аргумента аналогового сигнала множителя ±
m
j(max)∆tw на текущий аргумент аналогового сигнала множителя ±
n
i(min)∆tw и формируют аргумент аналогового сигнала среднего частичного произведения ±(S
(i+j)/2)∆tw, который включают в позиционно-знаковую структуру аргументов аналоговых сигналов 1±[S
i-1]∆tw и 2±[S
j-1]∆tw в соответствии с аналитическим выражением вида
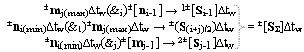
предыдущего позиционно-знакового частичного произведения ±[S
Σ]∆tw и аналогичным образом формируют позиционно-знаковую структуру последующих аргументов частичного произведения ±[S
Σ]∆tw+1 в соответствии с аналитическим выражением вида

при этом логико-динамический процесс формирования информационных аналоговых сигналов частичных произведений позиционно-знаковых аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) выполняют в соответствии с векторной структурой графоаналитического выражения вида
при этом накапливающее суммирование позиционно-знаковых аргументов частичных произведений ±[S
Σ]∆tw и ±[S
Σ]∆tw+1 выполняют посредством функциональной структуры, эквивалентной математической модели вида
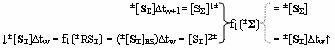
где ±[S
Σ]∆tw↑ и ↓±[S
Σ]∆tw - аргументы обратной связи; (±[S
Σ]RS)∆tw - аргументы промежуточной суммы частичных произведений функциональной структуры памяти f1(±RSΣ), которую реализуют в виде положительного и условно отрицательного канала.
4. Способ логико-динамического процесса формирования информационных аналоговых сигналов частичных произведений аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) для последующего накапливающего суммирования в сумматоре f1(±
Σ), в котором одновременно выполняют дискретный сдвиг аргументов аналоговых сигналов сомножителей ±[n
i] и ±[m
j], при этом посредством функциональной структуры сдвига f(j←1)[m
j], эквивалентной математической модели вида
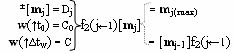
предварительно посредством переднего фронта входного аргумента w(↑t0), подаваемого на функциональную входную связь (=C0), выполняют сброс структуры аргументов сомножителя ±[m
j] предыдущей процедуры умножения, и по переднему фронту входного аргумента w(↑∆tw), который подают на функциональную входную связь (=C), выполняют ввод очередной структуры аргументов сомножителя ±[m
j], подаваемую на функциональные связи (=Dj), и выполняют дискретный сдвиг f2(j←1) этой структуры в позиционное положение старшего разряда «jmax» для формирования текущего аргумента m
j(max) и структуры аргументов множимого [m
j-1]f2(j←1), а посредством функциональной структуры убывающего сдвига f1(i→1)[n
i], эквивалентной математической модели вида
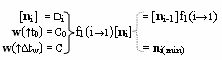
выполняют аналогичные действия, но сдвиг f1(i→1) структуры аргументов сомножителя ±[n
i] выполняют в позиционное положение первого младшего разряда (imin), а его текущим аргументом аналогового сигнала n
i(min)∆tw после выполненных сдвигов f2(j←1)∆tw и f1(i→1)∆tw структур аргументов сомножителей ±[n
i] и ±[m
j] посредством функциональной структуры f2(&j-1)-И, эквивалентной математической модели вида
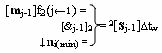
реализуют логическое умножение n
i(min)∆tw(&j-1)±[m
j-1] → 2[S
j-1]∆tw текущего аргумента аналогового сигнала множителя n
i(min)∆tw на структуру аргументов аналоговых сигналов множимого ±[m
j-1] и формируют аргументы аналоговых сигналов частичного произведения 2[S
j-1]∆tw, которые подают через функциональную структуру сумматора f1(±
Σ) и функциональную структуру памяти f1(RSΣ), эквивалентной математической модели вида
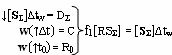
на вторые функциональные связи (=[SΣ]2) того же сумматора f1(±
Σ) в виде структуры аргументов ↓[S
Σ]∆tw и посредством их общей функциональной структуры, эквивалентной математической модели вида
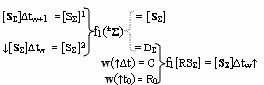
выполняют логическое суммирование аргументов частичных произведений [S
Σ]∆tw и [S
Σ]∆tw+1, которые подают на первых и вторых функциональных входных связях (=[SΣ]2) и (=[SΣ]1) сумматора f1(±
Σ) и формируют как структуру позиционных аргументов результирующей суммы [S
Σ] результата умножения структур аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код», так и структуру промежуточной суммы аргументов [S
Σ]∆tw↑, отличающийся тем, что в функциональной структуре сдвига f2(j←1)[m
j] дискретный сдвиг структуры аргументов множимого ±[m
j] выполняют с убыванием старших разрядов, а его текущими аргументом аналогового сигнала m
j(max)∆tw и посредством функциональной логической структуры f1(&i-1)-И, эквивалентной математической модели вида
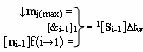
реализуют логическое умножение m
j(max)∆tw(&i-1)±[n
i-1] → 1[S
i-1]∆tw текущего аргумента аналогового сигнала m
j(max)∆tw на структуру аргументов аналоговых сигналов множимого ±[n
i-1] и формируют структуру аргументов аналоговых сигналов частичного произведения 1[S
i-1]∆tw, а посредством функциональной логической структуры f1(&1)-И, эквивалентной математической модели вида
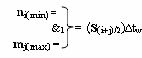
реализуют логическое умножение m
j(max)∆tw(&i)n
i(min)∆tw → (S
(i+j)/2)∆tw текущего аргумента аналогового сигнала множителя m
j(max)∆tw на текущий аргумент аналогового сигнала множителя n
i(min)∆tw и формируют аргумент аналогового сигнала частичного произведения (S
(i+j)/2)∆tw, который включают в позиционную структуру аргументов 1[S
i-1]∆tw и 2[S
j-1]∆tw в соответствии с аналитическим выражением вида
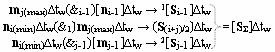
аргументов аналоговых сигналов частичного произведения [S
Σ]∆tw, при этом формирование последующих аргументов частичных произведений [S
Σ]∆tw+1 выполняют также в соответствии с аналитическим выражением вида
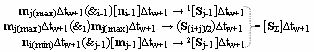
и в соответствии с логико-динамическим процессом вида
где  и
и  - положительный активный и неактивный формализованный позиционный аргумент аналогового сигнала, соответствующий логическому аргументу «1» и логическому аргументу «0», формируют последующие аргументы частичных произведений [S
Σ]∆tw+1, которые в функциональной структуре пирамидального умножителя fΣ(Σ), эквивалентной математической модели вида
- положительный активный и неактивный формализованный позиционный аргумент аналогового сигнала, соответствующий логическому аргументу «1» и логическому аргументу «0», формируют последующие аргументы частичных произведений [S
Σ]∆tw+1, которые в функциональной структуре пирамидального умножителя fΣ(Σ), эквивалентной математической модели вида
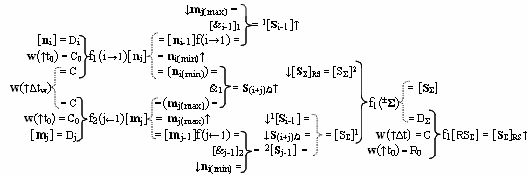
выполняют накапливающее суммирование.
5. Способ логико-динамического процесса формирования информационных аналоговых сигналов частичных произведений аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) для последующего накапливающего суммирования в сумматоре f1(±
Σ), в котором одновременно выполняют дискретный сдвиг аргументов аналоговых сигналов сомножителей ±[n
i] и ±[m
j], при этом посредством функциональной структуры сдвига f2(j←1)[m
j] эквивалентной математической модели вида
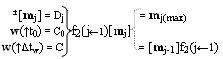
предварительно посредством переднего фронта входного аргумента w(↑t0), подаваемого на функциональную входную связь (=C0), выполняют сброс структуры аргументов сомножителя ±[m
j] предыдущей процедуры умножения и по переднему фронту входного аргумента w(↑∆tw), который подают на функциональную входную связь (=C), выполняют ввод очередной структуры аргументов сомножителя ±[m
j], которую подают на функциональные связи (=Dj) и выполняют дискретный сдвиг f2(j←1) этой структуры в позиционное положение старшего разряда «jmax» для формирования текущего аргумента m
j(max) и структуры аргументов сомножителя [m
j-1]f2(j←1), а посредством функциональной структуры убывающего сдвига f1(i→1)[n
i] эквивалентной математической модели вида
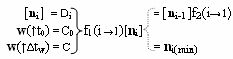
выполняют аналогичные действия, но сдвиг f1(i→1) структуры аргументов сомножителя ±[n
i] выполняют в позиционное положение первого младшего разряда (imin), а его текущим аргументом аналогового сигнала n
i(min)∆tw после выполненных сдвигов f2(j←1)∆tw и f1(i→1)∆tw структур аргументов сомножителей ±[n
i] и ±[m
j] реализуют посредством функциональной логической структуры f2(&j-1)-И, эквивалентной математической модели вида

логическое умножение n
i(min)∆tw(&j-1)±[m
j-1] → 2[S
j-1]∆tw текущего аргумента аналогового сигнала множителя n
i(min)∆tw на структуру аргументов аналоговых сигналов множимого ±[m
j-1] и формируют аргументы аналоговых сигналов второй половины частичного произведения 2[S
j-1]∆tw, которые через функциональную структуру сумматора f1(±
Σ) и функциональную структуру памяти f1(RSΣ), эквивалентной математической модели вида
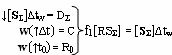
подают на вторые функциональные связи (=[SΣ]2) того же сумматора f1(±
Σ) в виде структуры аргументов ↓[S
Σ]∆tw и посредством их общей функциональной структуры, эквивалентной математической модели вида
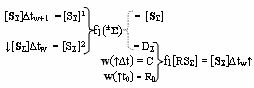
выполняют логическое суммирование аргументов частичных произведений [S
Σ]∆tw и [S
Σ]∆tw+1, которые подают на первых и вторых функциональных входных связях (=[SΣ]2) и (=[SΣ]1) сумматора f1(±
Σ) и формируют как структуру позиционных аргументов результирующей суммы [S
Σ] результата умножения структур аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код», так и структуру промежуточной суммы аргументов [S
Σ]∆tw↑, отличающийся тем, что в функциональной структуре сдвига f2(j←1)[m
j] дискретный сдвиг структуры аргументов ±[m
j] выполняют с убыванием ее старшего (±jmax) разряда, а его текущими аргументом аналогового сигнала формируют как аргумент множителя m
j(max)∆tw и посредством функциональной логической структуры f1(&i-1)-И, эквивалентной математической модели вида
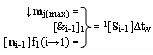
реализуют логическое умножение m
j(max)∆tw(&i-1)±[n
i-1] → 1[S
i-1]∆tw текущего аргумента аналогового сигнала m
j(max)∆tw на структуру аргументов аналоговых сигналов множимого ±[n
i-1] и формируют аргументы аналоговых сигналов частичного произведения 1[S
i-1]∆tw, а посредством функциональной логической структуры f1(&)-И, эквивалентной математической модели вида
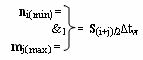
реализуют логическое умножение m
j(max)∆tw(&1)n
i(min)∆tw → (S
(i+j)/2)∆tw+1 текущего аргумента аналогового сигнала m
j(max)∆tw на текущий аргумент аналогового сигнала n
i(min)∆tw и формируют аргумент частичного произведения (S
(i+j)/2)∆tw, который включают в последовательную позиционную структуру аргументов 1[S
i-1]∆tw и 2[S
j-1]∆tw в соответствии с аналитическим выражением вида
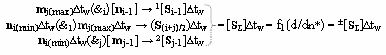
аргументов аналоговых сигналов частичного произведения [S
Σ]∆tw и посредством функциональной структуры избирательного логического дифференцирования f1(d/dn*) позиционную структуру как предыдущего частичного произведения [S
Σ]∆tw преобразуют в позиционно-знаковую структуру ±[S
Σ]∆tw, так и последующие аргументы частичного произведения [S
Σ]∆tw+1 также преобразуют в позиционно-знаковую структуру частичного произведения ±[S
Σ]∆tw+1 в соответствии с аналитическим выражением вида
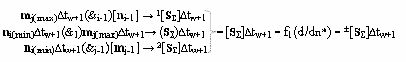
и в соответствии с логико-динамическим процессом вида
где  и
и  - положительный и условно отрицательный формализованный позиционно-знаковый аргумент аналогового сигнала, соответствующий положительному аргументу «+1» и условно отрицательному аргументу «-1» соответственно,
- положительный и условно отрицательный формализованный позиционно-знаковый аргумент аналогового сигнала, соответствующий положительному аргументу «+1» и условно отрицательному аргументу «-1» соответственно,
при этом накапливающее суммирование скорректированных предыдущих и последующих аргументов частичных произведений ±[S
Σ]∆tw и ±[S
Σ]∆tw+1 выполняют посредством функциональной позиционно-знаковой структуры эквивалентной математической модели вида
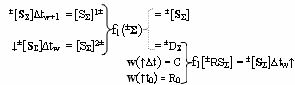
где ±[S
Σ]∆tw↑ и ↓±[S
Σ]∆tw - аргументы обратной связи;
в которой первые и вторые функциональные входные связи (=[SΣ]1±) и (=[SΣ]2±) выполняют в виде положительного канала суммирования и условно отрицательного канала суммирования в функциональной структуре пирамидального умножителя fΣ(Σ), эквивалентной математической модели вида
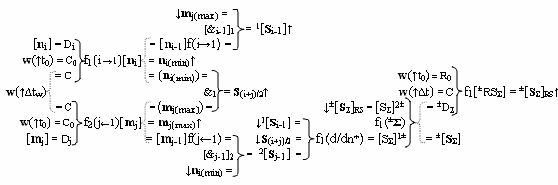
где ±[S
Σ]RS↑ и ↓±[S
Σ]RS - аргументы обратной связи накапливающего сумматора (f1(±
Σ) = f1[±RSΣ]).
6. Способ логико-динамического процесса формирования информационных аналоговых сигналов частичных произведений аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) для последующего накапливающего суммирования в сумматоре f1(±
Σ), в котором одновременно выполняют дискретный сдвиг аргументов аналоговых сигналов сомножителей ±[n
i] и ±[m
j], при этом посредством функциональной структуры сдвига f2(±j←1)[m
j] дискретный сдвиг f2(±j←1) структуры аргументов ±[m
j] выполняют в позиционное положение старшего «±jmax» разряда, а посредством функциональной структуры убывающего сдвига f1(±i→1)[n
i] дискретный сдвиг f1(±i→1) структуры аргументов ±[n
i] выполняют в позиционное положение первого младшего «imin» разряда, а его текущими аргументами аналогового сигнала ±
n
i(min)∆tw после выполненных сдвигов f2(±j←1)∆tw и f2(±i→1)∆tw структур аргументов сомножителей ±[n
i] и ±[m
j] реализуют посредством логических функций f2(±&j-1)-И логическое умножение ±
n
i(min)∆tw(&j-1)±[m
j-1] → 2±[S
j-1]∆tw текущего аргумента аналогового сигнала ±
n
i(min)∆tw на структуру аргументов аналоговых сигналов множимого ±[m
j-1] и формируют аргументы аналоговых сигналов частичного произведения ±2[S
j-1]∆tw, посредством функциональной структуры памяти f1(±RSΣ) и функциональной структуры сумматора f1(±
Σ) выполняют накапливающее логическое суммирования результирующей его структуры аргументов ±[S
Σ]∆tw↑ с последующей структурой аргументов ±[S
Σ]∆tw+1 аналоговых сигналов частичного произведения, отличающийся тем, что в качестве аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» используют их позиционно-знаковую структуру аргументов, которая включает как логическую последовательность аналоговых сигналов положительного информационного содержания +[n
i] и +[m
j], так и последовательность аналоговых сигналов условно отрицательного информационного содержания -[n
i] и -[m
j], и в функциональной структуре сдвига f1(±i→1)[n
i], эквивалентной математической модели вида
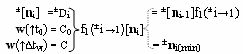
сдвиг их выполняют одновременно с формированием позиционно-знакового аргумента множителя ±
n
i(min) в «±imin» разряде и аргументов множимого ±[n
i-1]f(±i→1) и посредством функциональной структуры сдвига f2(±j←1)[±
m
j], эквивалентной математической модели вида
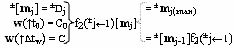
также выполняют дискретный сдвиг f(±j←1) всей позиционно-знаковой структуры аргументов сомножителя ±[m
j], но с убыванием ее аргумента старшего «±jmax» разряда с формированием в нем текущего позиционно-знакового аргумента множителя ±
m
j(max) и посредством положительной и условно отрицательной функциональной структуры f1(±&i-1)-И, эквивалентной математической модели вида
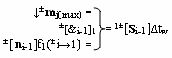
реализуют логическое умножение ±
m
j(max)∆tw(±&i)±[n
i-1] → 1±[S
i-1]∆tw позиционно-знакового аргумента аналогового сигнала множителя ±
m
j(max)∆tw на структуру позиционно-знаковых аргументов аналоговых сигналов множимого ±[n
i-1] и формируют позиционно-знаковую структуру аргументов аналоговых сигналов первой половины частичного произведения ±1[S
i-1]∆tw, а посредством положительной и условно отрицательной функциональной структуры f2(±&j-1)-И, эквивалентной математической модели вида
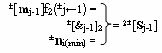
реализуют логическое умножение ±
n
i(min)∆tw(&j-1)±[m
j-1] → 2±[S
j-1]∆tw позиционно-знакового аргумента аналогового сигнала множителя ±
n
i(min) на структуру позиционно-знаковых аргументов аналоговых сигналов множимого ±[m
j-1] и формируют позиционно-знаковую структуру аргументов аналоговых сигналов второй половины частичного произведения 2±[S
j-1], при этом посредством положительной и условно отрицательной функциональной структуры f1(±&1)-И, эквивалентной математической модели вида
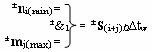
реализуют логическое умножение ±
m
j(max)∆tw(±&1)±
n
i(min)∆tw → ±(S
(i+j)/2)∆tw текущего аргумента аналогового сигнала множителя ±
m
j(max)∆tw на текущий аргумент аналогового сигнала множителя ±
n
i(min)∆tw и формируют позиционно-знаковый аргумент аналогового сигнала среднего частичного произведения ±(S
(i+j)/2)∆tw, который включают в общую позиционно-знаковую структуру аргументов аналоговых сигналов 1±[S
i-1]∆tw и 2±[S
j-1]∆tw в соответствии с аналитическим выражением вида
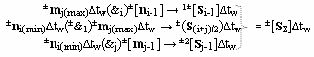
формируют предыдущее частичное позиционно-знаковое произведения ±[S
Σ]∆tw и аналогичным образом формируют позиционно-знаковую структуру аргументов последующего частичного произведения ±[S
Σ]∆tw+1 в соответствии с аналитическим выражением вида
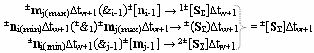
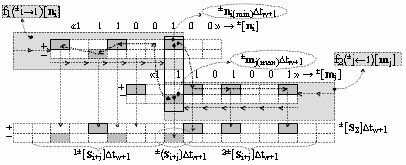
при этом логико-динамический процесс формирования информационных аналоговых сигналов частичных произведений позиционно-знаковых аргументов сомножителей ±[n
i] и ±[m
j] усеченной пирамидальной структуры умножителя fΣ(Σ) выполняют в соответствии с векторной структурой графоаналитического выражения вида
а накапливающее суммирование позиционно-знаковых предыдущих и последующих аргументов частичных произведений ±[S
Σ]∆tw и ±[S
Σ]∆tw+1 выполняют посредством функциональной позиционно-знаковой структуры, которая эквивалентна математической модели вида
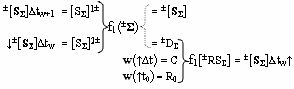
где ±[S
Σ]∆tw↑ и ↓±[S
Σ]∆tw - аргументы обратной связи;
в которой первые и вторые функциональные входные связи (=[SΣ]1±) и (=[SΣ]2±) выполняют в виде положительного канала суммирования и условно отрицательного канала суммирования в функциональной структуре пирамидального умножителя fΣ(Σ), эквивалентной математической модели вида
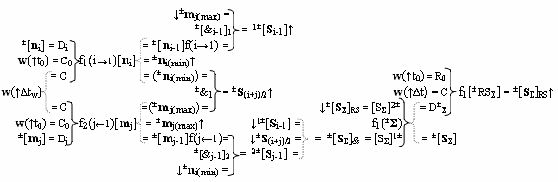
где ±[S
Σ]RS↑ и ↓±[S
Σ]RS - аргументы обратной связи накапливающего сумматора (f1(±
Σ) = f1[±RSΣ]); ±[S
Σ]& - позиционно-знаковая структура аргументов частичных произведений.
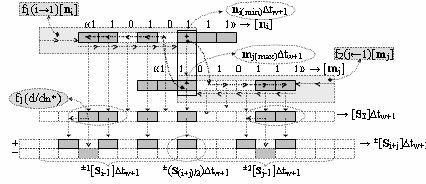
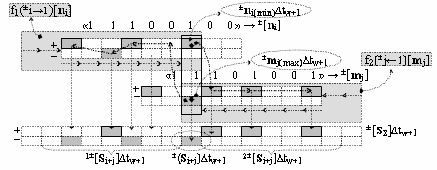
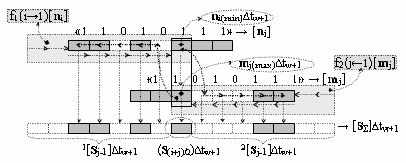
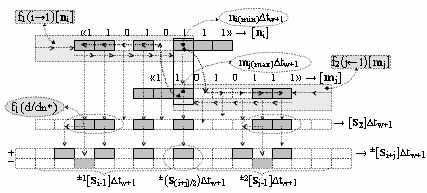
7. Функциональная структура логико-динамического процесса формирования информационных аналоговых сигналов частичных произведений аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) для последующего накапливающего суммирования в сумматоре f1(±
Σ), включающая функциональную структуру f2(j←1)[m
j] дискретного сдвига f2(j←1) структуры аргументов ±[m
j] в позиционное положение старшего (±jmax) разряда и функциональную структуру убывающего сдвига f1(i→1)[n
i] дискретный сдвиг f1(i→1) структуры аргументов ±[n
i] в которых функциональные входные связи (=Di), (=Dj), (=C0) и (=C) являются функциональными входными связями функциональной усеченной пирамидальной структуры умножителя fΣ(Σ) для приема аргументов сомножителей ±[n
i] или ±[m
j] и управляющего по переднему фронту аналогового сигнала аргумента сброса w(↑∆to) и аргумента сдвига w(↑∆tw), а функциональные выходные связи являются функциональными входными связями функциональной логической структуры f2(&j-1)-И, в которой функциональные выходные связи являются функциональными первыми входными связями (=[SΣ]1±) функциональной структуры сумматора f1(±
Σ), а его вторые функциональные связи (=[SΣ]2±) являются функциональными выходными связями функциональной структуры памяти f1(RSΣ), в которой функциональные входные связи (=R0) и (=C) являются функциональными входными связями функциональной усеченной пирамидальной структуры умножителя fΣ(Σ) для приема аргументов управляющих аналоговых сигналов сброса w(↑t0) и аргумента сдвига w(↑∆tw) соответственно, а входные функциональные информационные связи (=±DΣ) являются функциональными выходными связями функциональной структуры сумматора f1(±
Σ) и выходными функциональными связями функциональной усеченной пирамидальной структуры умножителя fΣ(Σ) результирующей суммы ±[S
Σ] аргументов частичных произведений, отличающаяся тем, что в структуру дополнительно введены функциональная логическая структура f1(±&i-1)-И, функциональная логическая структура f1(±&1)-И и функциональная структура избирательного логического дифференцирования f1(d/dn*), и все функциональные структуры выполнены в виде положительного и условно отрицательного канала, при этом функциональные связи в функциональной структуре выполнены в соответствии с математической моделью вида
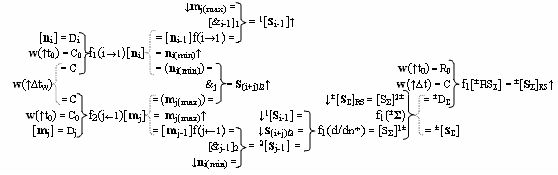
8. Функциональная структура логико-динамического процесса формирования информационных аналоговых сигналов частичных произведений аргументов сомножителей ±[n
i] и ±[m
j] - «Дополнительный код» усеченной пирамидальной структуры умножителя fΣ(Σ) для последующего накапливающего суммирования в сумматоре f1(±
Σ), включающая функциональную структуру f2(±j←1)[m
j] дискретный сдвиг f2(±j←1) структуры аргументов ±[m
j] в позиционное положение старшего (±jmax) разряда и функциональную структуру убывающего сдвига f1(±i→1)[n
i] дискретный сдвиг f1(±i→1) структуры аргументов ±[n
i], в которых функциональные входные связи (=Di), (=Dj), (=C0) и (=C) являются функциональными входными связями функциональной усеченной пирамидальной структуры умножителя fΣ(Σ) для приема аргументов сомножителей ±[n
i] или ±[m
j] и управляющих по переднему фронту аналоговых сигналов сброса w(↑∆tw) и сдвига w(↑∆tw), а функциональные выходные связи являются функциональными входными связями функциональной логической структуры f2(±&j-1)-И, в которой функциональные выходные связи являются функциональными первыми входными связями (=[SΣ]1±) функциональной структуры сумматора f1(±
Σ), а его вторые функциональные связи (=[SΣ]2±) являются функциональными выходными связями функциональной структуры памяти f1(±RSΣ), в котором функциональные входные связи (=R0) и (=C) являются функциональными входными связями функциональной усеченной пирамидальной структуры умножителя fΣ(Σ) для приема аргументов аналоговых сигналов сброса w(↑t0) и аргумента сдвига w(↑∆tw) соответственно, а входные функциональные информационные связи (=±DΣ) являются функциональными выходными связями функциональной структуры сумматора f1(±
Σ) и выходными функциональными связями функциональной усеченной пирамидальной структуры умножителя fΣ(Σ) результирующей суммы ±[S
Σ] аргументов частичных произведений, отличающаяся тем, что в структуру дополнительно введены функциональная логическая структура f1(±&i-1)-И и функциональная логическая структура f1(±&1)-И и все функциональные структуры выполнены в виде положительного и условно отрицательного канала, при этом функциональные связи в функциональной структуре умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида
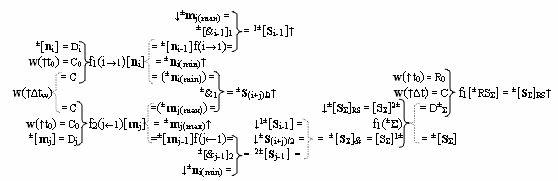
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА УМНОЖИТЕЛЯ, В КОТОРОМ ВХОДНЫЕ АРГУМЕНТЫ ИМЕЮТ ФОРМАТ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(2), А ВЫХОДНЫЕ АРГУМЕНТЫ СФОРМИРОВАНЫ В ФОРМАТЕ ПОЗИЦИОННО-ЗНАКОВОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+/-) | 2008 |
|
RU2373563C9 |
| ФУНКЦИОНАЛЬНАЯ ВХОДНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО УМНОЖИТЕЛЯ ФОРМАТА ПОЗИЦИОННО-ЗНАКОВОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+/-) | 2008 |
|
RU2378684C1 |
| JP 7141148 A, 02.06.1995 | |||
| JP 56094435 A, 30.07.1981. | |||
Авторы
Даты
2013-02-20—Публикация
2011-04-01—Подача