Изобретение относится к области машиностроения, а именно к созданию композиционных алмазосодержащих материалов (КАМ) и инструментов на их основе, предназначенных для качественного и экономичного шлифования и полирования поверхностей различных материалов: сталей, сплавов, драгоценных металлов, а также минералов различной твердости и обрабатываемости.
В число основных задач при разработке режущих инструментов входит необходимость повышения основных технических характеристик и улучшения эксплуатационных параметров работоспособности инструмента. Работоспособность абразивных инструментов определяется их износостойкостью, эффективностью работы, качеством обработанной поверхности и характеризуется такими основными эксплуатационными параметрами, как удельный расход абразива, производительность и шероховатость обработанной поверхности. Производительность шлифования и качество обработки существенно зависят от стабильности режущих свойств инструмента, т.е. стабильности количества активных абразивных зерен в процессе его эксплуатации, позволяющих инструменту работать в режиме самозатачивания. Поэтому при разработке композиционных материалов абразивного назначения особенно важным является определение изменения количества активных зерен (AЗ) при трении и изнашивании. Существующие методы расчета дают возможность вычислять количество активных (режущих) зерен в исходном состоянии исследуемых образцов, однако не позволяют определить ее изменение в процессе работы инструмента. Между тем, располагая данными о стабильности режущих микроклинов в композиционном материале, можно от экспериментального подбора алмазно-абразивного инструмента для различных условий работы перейти к его теоретическому расчету с определением всех необходимых параметров, обуславливающих наиболее эффективное его использование для конкретных условий обработки.
Большинство исследователей определяет количество активных (режущих) зерен различными способами. В.Н.Бакуль определяет число зерен (частиц) алмаза, содержащихся в одном карате в зависимости от зернистости, концентрации и марки алмаза, уподобляя форму зерна эллипсоиду [Бакуль В.Н. Работоспособность алмазных кругов на органической связке отечественного и зарубежного производства. - Киев, 1969. - 25 с.]. Попытки других различных исследователей теоретически определить число зерен, приходящихся на единицу поверхности алмазоносного слоя, основаны на трудах Бакуля. Так, в работе [Верещагин В.А. Определение количества зерен, приходящихся на единицу поверхности. / Верещагин В.А., Журавлев В.В. Композиционные алмазосодержащие материалы и покрытия. Минск: «Нувука i Тэхнiка», 1991 г. - 208 с.] предлагается зависимость для расчета количества зерен на любом фиксированном уровне рабочего поверхностного слоя на основе квазистатической модели износа матрицы. Данная модель не учитывает условий работы и закрепления зерен в матрице.
Наиболее близкий аналог изобретения - способ расчета количества зерен в однослойных алмазно-гальванических покрытиях, где определяется количество алмазов на единице площади поверхности при допущении, что алмазные зерна имеют форму эллипсоида или шара [А.Г.Щиголев, Б.И.Полупан, В.В.Коломиец. Определение количества зерен по глубине рабочего поверхностного слоя алмазного инструмента. // Синтетические алмазы. - 1979. - №3. - С.19-25].
Описанные методы расчета количества зерен являются не универсальными, они разработаны для частных случаев исследований с учетом особенностей изготовления рассматриваемых объектов и материалов. Анализ существующих работ показал, что эффективность, качество обработки и долговечность инструмента во многом зависит от количества AЗ в рабочем слое. Проведенный анализ современного состояния важной научно-прикладной задачи расчета количества активных зерен в абразивных композиционных материалах явился обоснованием для цели и технического результата изобретения.
Техническим результатом является разработка и реализация расчетно-экспериментального способа определения количества активных AЗ в композиционном материале, который позволяет оценить стабильность режущих свойств инструмента.
Раскрытие изобретения. Разработан и реализован способ определения количества активных абразивных зерен (AЗ) шлифпорошка со статистически равномерным распределением их в объеме композиционного материала, основанный на данных микроскопического анализа приповерхностного слоя композиционного материала, включающий выбор геометрической модели AЗ в форме куба, проведено измерение линейных размеров случайных сечений AЗ в приповерхностном слое композиционного материала и вычисление их количества в этом слое на основе вероятностного распределения площадей случайных сечений AЗ кубической формы.
Объекты исследования: В качестве абразивного материала использовались шлифпорошки из технических синтетических и природных алмазов (по три разновидности) различных зернистостей. Шлифпорошки изначально принимались за «безымянные» (марка, зернистость, стандарт, по которому велась их классификация, считались неизвестными), и им присваивались буквенно-цифровые обозначения: С или П (шлифпорошки из синтетических/природных алмазов), цифры I, II, III (номера в порядке возрастания зернистости). В качестве основы композиционного материала был выбран ПТФЭ - полимер, который обладает необходимыми свойствами, предъявляемыми к связке алмазно-абразивного инструмента [Шиц Е.Ю. Исследование и разработка полимерных композиционных материалов с использованием природных алмазных порошков. Дис. …канд. техн. наук: - 05.02.01 / Е.Ю.Шиц; ОИФТПС СО РАН. - Якутск, 2000. - 180 с.]. Образцы для испытаний изготавливались из композиций с 40 мас.% содержанием алмазного порошка по технологии холодного прессования при давлении 50 МПа с последующим свободным спеканием при температуре 375±5°С.
Разработка и реализация способа. Алгоритм способа определения количества AЗ в композиционном материале приведен на фиг.1.
Этап 1. Выбор геометрической модели AЗ. В качестве модели зерна шлифпорошков из технических синтетических алмазов разными авторами принимались правильные многогранники и тела вращения. Геометрическое моделирование зерен шлифпорошков из природных алмазов ранее не проводилось.
На фиг.2. приведены электронные снимки зерен и исследованных алмазных шлифпорошков. Видно, что алмазные зерна являются совокупностью осколочных частиц неправильной формы, произвольное сечение которых в подавляющем большинстве случаев можно считать четырех- или пятиугольниками, как и в других несферических порошках [М.М.Цымбалист, Н.А.Руденская, Б.П.Кузьмин, В.А.Паньков. Учет фактора формы при ситовом анализе несферических порошков. // Физика и химия обработки материалов. - 2003. - №6. - С. 61-63].
В качестве геометрической модели зерна абразивного наполнителя выбирался такой вариант модели, при котором параметр D, характеризующий величину отклонения объема реального зерна Vr от объема его модельного аналога Vm, принимает минимальное значение:

где i, Р - порядковый номер и количество исследованных зерен соответственно. Совокупность линейных измерений, необходимых для вычисления Vr и Vm, определяется формой AЗ. Всего было изучено по 250-300 зерен каждой разновидности исследованных алмазных шлифпорошков. Значения D для различных геометрических моделей зерен приведены в таблице 1.
В соответствии с выбранным критерием (1) в качестве геометрической модели зерен для всех исследованных шлифпорошков был принят куб.
Этап 2. Расчет количества активных AЗ в композиционном материале проводился с применением метода количественной металлографии, основанного на изучении размерного распределения микрочастиц в объеме материала по исследованию распределения площадей их случайных сечений Fi. Совокупность линейных измерений, необходимых для вычисления Fi, определяется видом случайного сечения.
Вычисление количества частиц k - й размерной группы Nk проводилось по формуле, полученной с использованием вероятностного распределения Fi для кубических частиц [С.А.Салтыков. Стереометрическая металлография. - М.: Металлургия, 1970. - 376 с.].
Если известно распределение площадей сечений микрочастиц данной формы, а также число сечений какой-либо одной размерной группы, то можно легко определить количество сечений для всех остальных размерных групп. Это положение является основой метода расчета количества и распределения размеров микрочастиц в объеме по распределению площадей сечений на плоскости шлифа.
Так как площади сечений микрочастиц пропорциональны квадратам их линейных размеров, с целью соблюдения единообразия в методиках, выбираем для образования размерных групп площадей сечений микрочастиц убывающий геометрический ряд с множителем (10-0,1)2=10-0,2=0,63096. Такой ряд дает более тонкую, дифференцированную оценку площадей, чем ряд стандартной шкалы оценки величины зерна по ГОСТ 5639-65: в стандартной шкале средняя площадь зерна каждой последующей группы (балла) составляет половину площади зерна предыдущей группы, а в принятой шкале - примерно 2/3.
В распределении площадей случайных сечений куба, полученном экспериментально, принята линейная шкала значений F/Fmax по оси абсцисс, тогда как нам необходимо иметь распределение площадей случайных сечений куба F/Fmax по размерным группам, основывающимся на геометрическом ряде. Путем соответствующего перерасчета данных получено распределение площадей случайных сечений куба, приведенное в табл.2.
Рассмотрим систему, состоящую из микрочастиц кубической формы: наибольшие микрочастицы имеют ребро а1; следующие по размера a2=0,7943a1 и т.д. На случайной плоскости, пересекающей систему кубических микрочастиц, образуются их сечения со следующими размерами:
Сечение F1 является максимальным сечением наибольших по размеру микрочастиц, F2=0,6310 F1, F3=0,3981 F2 и т.д. (см. табл.2).
Сечения наибольшего размера (F1-F2) могут принадлежать только наибольшим микрочастицам 1-й размерной группы. Количество таких сечений, равное n1, составляет 41,1% от общего количества сечений микрочастиц 1-й размерной группы. Поэтому общее количество сечений микрочастиц этой группы определится отношением
n1100/41,1=2,433n1,
а количество микрочастиц 1-й размерной группы в единице объема будет равно:
N1=2,433n1/H1
Сечения 2-й размерной группы принадлежат микрочастицам как 1-й, так и 2-й групп. В соответствии с распределением площадей случайных сечений куба (см. табл.3.2) количество сечений 2-й размерной группы, принадлежащее микрочастицам наибольших размеров, определится отношением
n1(100/41,1)(100/16,4)=0,399n1
Поэтому количество сечений 2-й размерной группы, принадлежащих только микрочастицам той же группы, определится разностью:
n2-0,399n1
Это количество сечений составляет 41,1% всех сечений микрочастиц 2-й размерной группы. Поэтому количество всех сечений микрочастиц 2-й группы будет равно:
n2-0,399n1(100/41,1)=2,433n2-0,971n1.
Количество микрочастиц 2-й размерной группы в единице объема определится равенством:
N2=1/H1(2,433n2-0,971n1).
Продолжая описанным способом последовательный расчет микрочастиц остальных размерных групп, приходим к общей формуле, которая позволяет рассчитывать количество микрочастиц любой размерной группы:

Подсчет частиц в размерных группах начинают от k=1, в нашем случае k заключен в интервале от [1…10]. При k=0 количество частиц равно 0.
При подстановке k=1 в упомянутую формулу /2/ получаем:
N1=2,433n1/H1,
т.е. в первой размерной группе коэффициент 2,433 нужно умножить на количество сечений, штук первой размерной группы.
При k=2
N2=1/Н2(2,433n2-0,971n1),
при k=3
N3=1/Н3(2,433n3-0,971n2-0,270n1)
и т.д., расчет количества микрочастиц какой-либо из размерных групп ведут до тех пор, пока индекс очередного количества сечений микрочастиц n не превратится в нуль. Так, например, при расчете микрочастиц 5-й размерной группы используются первые пять членов многочлена, заключенного в скобки, так как индекс шестого члена оказывается равным нулю.
Hk=1,5 h - так называемая средняя высота куба, если h - ребро куба (h определялась как полусумма сторон прямоугольника, описанного вокруг проекции случайного сечения зерна). nk=n /S, где n
/S, где n - количество сечений, штук частиц в размерных группах, S - площадь исследованной поверхности. Количество активных AЗ в композиционном материале, равное
- количество сечений, штук частиц в размерных группах, S - площадь исследованной поверхности. Количество активных AЗ в композиционном материале, равное  (К - количество размерных групп), вычислялось на основании измерений площадей случайных сечений 100-150 зерен.
(К - количество размерных групп), вычислялось на основании измерений площадей случайных сечений 100-150 зерен.
Этап 3. Проверка достоверности результатов проводилась путем сравнения no и значения количества AЗ в исходном состоянии, определенного исходя из показателей зернового состава шлифорошка nисх. Определение зернистости и показателей зернового состава шлифпорошков проводилось с применением так называемого компьютерного диагностического сита (КДС) - косвенной диагностики шлифпорошков, основанной на данных микроскопического анализа [Новиков Н.В., Никитин Ю.И., Петасюк Г.А. Компьютерное диагностическое сито для идентификации зернистости и зернового состава микроскопических проб алмазных шлифпорошков. // Сверхтвердые материалы. - 2003. - №3. - С.71-83].
Значение nисх вычислялось по формуле:

где j, J - порядковый номер и количество фракций в зерновом составе алмазного шлифпорошка; νотн - относительное объемное содержание зерен алмаза в композиционном материале (при 40 мас.% алмаза νотн=40ρс/(60ρа+40ρс), ρс, ρа - плотности ПТФЭ и алмаза);  (dj - длина стороны ячейки сита, в которую проходит зерно).
(dj - длина стороны ячейки сита, в которую проходит зерно).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОРТИРОВКИ АЛМАЗОСОДЕРЖАЩЕГО МАТЕРИАЛА | 2016 |
|
RU2625640C1 |
| СПОСОБ ПОЛУЧЕНИЯ АБРАЗИВНЫХ ЗЕРЕН | 1997 |
|
RU2132268C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СИЛЫ УДАРА ЗЕРЕН О ПРЕГРАДУ | 2015 |
|
RU2603224C1 |
| Способ изготовления сложнопрофильного абразивного инструмента | 1990 |
|
SU1754430A1 |
| СПОСОБ ПОЛУЧЕНИЯ ПОЛИКРИСТАЛЛИЧЕСКОГО МАТЕРИАЛА НА ОСНОВЕ КУБИЧЕСКОГО НИТРИДА БОРА, СОДЕРЖАЩЕГО АЛМАЗЫ | 2011 |
|
RU2484888C1 |
| СТРУКТУРИРОВАННЫЙ АЛМАЗНЫЙ ИНСТРУМЕНТ И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2017 |
|
RU2650459C1 |
| ИНСТРУМЕНТ ДЛЯ ПРАВКИ ШЛИФОВАЛЬНЫХ КРУГОВ | 2006 |
|
RU2334609C1 |
| Абразивная проволока | 2015 |
|
RU2612112C2 |
| СПОСОБ ИЗГОТОВЛЕНИЯ АБРАЗИВНОГО ИНСТРУМЕНТА | 1996 |
|
RU2104856C1 |
| АБРАЗИВНОЕ ИЗДЕЛИЕ (ВАРИАНТЫ) И СПОСОБ ЕГО ФОРМИРОВАНИЯ | 2010 |
|
RU2508968C2 |

Изобретение относится к созданию композиционных алмазосодержащих материалов, а именно к способам определения относительного изменения активных абразивных зерен в композиционном материале при трении и изнашивании на основе данных микроскопического анализа приповерхностного слоя композиционного материала. В качестве геометрической модели абразивных зерен выбирают форму куба. Определяют количество активных абразивных зерен в композиционном материале в его исходном состоянии (nо) и после испытания на трение и изнашивание (nэ). Определяют относительное изменение количества активных абразивных зерен по соотношению: С=(n0-nэ/n0)×100%. Количество активных абразивных зерен определяют путем суммирования абразивных зерен в каждой из размерных групп. Количество размерных групп определяют на основе вероятностного распределения площадей случайных сечений кубической формы в объеме приповерхностного слоя композиционного материала. В результате повышается эффективность шлифования, а также износостойкость и работоспособность абразивных инструментов. 2 ил., 3 табл.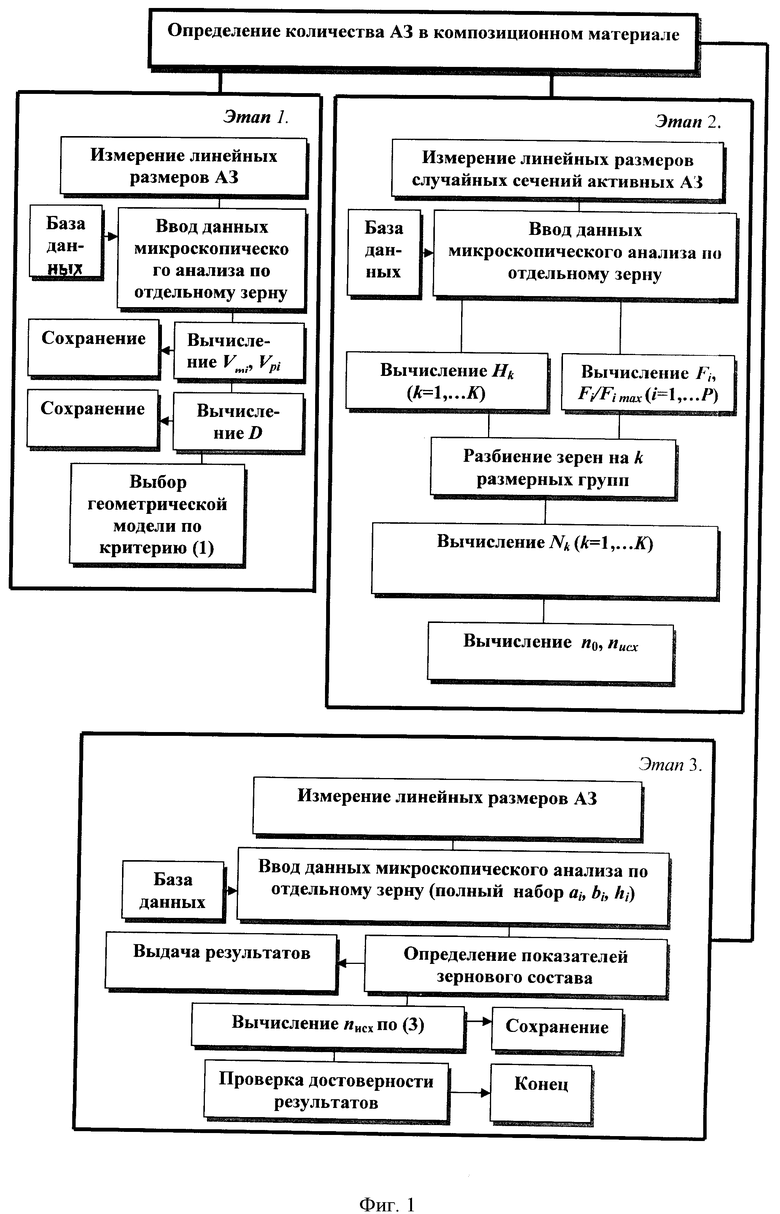
Способ определения относительного изменения активных абразивных зерен в композиционном материале при трении и изнашивании на основе данных микроскопического анализа приповерхностного слоя композиционного материала, при этом в качестве геометрической модели абразивных зерен выбирают форму куба, определяют количество активных абразивных зерен в композиционном материале в его исходном состоянии (n0) и после испытания на трение и изнашивание (nэ), и определяют относительное изменение количества активных абразивных зерен по соотношению: С=(n0-nэ/n0)·100%, причем количество активных абразивных зерен определяют путем суммирования абразивных зерен в каждой из размерных групп, количество которых определяют на основе вероятностного распределения площадей случайных сечений кубической формы в объеме приповерхностного слоя композиционного материала.
| Щиголев А.Г | |||
| и др | |||
| Определение количества зерен по глубине рабочего поверхностного слоя алмазного инструмента | |||
| Синтетические алмазы, №3, 1979, с.19-25 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ИСПОЛЬЗОВАНИЯ АБРАЗИВНЫХ ЗЕРЕН | 2001 |
|
RU2191678C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОЧНОСТИ АБРАЗИВНЫХ ЗЕРЕН | 0 |
|
SU170730A1 |
| MX 9702267 A, 28.06.1997. | |||
Авторы
Даты
2011-06-27—Публикация
2008-01-21—Подача