Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических процедур суммирования и умножения условно минимизированных аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min.
Известен способ, реализованный посредством функциональных входных структур сумматора с избирательным логическим дифференцированием d*/dn первой промежуточной суммы ±[S1 i] минимизированных структур аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min (см. Патент № 2 424 548 от 10.11.2009 г.), в соответствии с которым введена процедура избирательного логического дифференцирования d*/dn, которая, по существу, является процедурой предварительного введения сквозного переноса f1(±←←). При этом условно «i» разряд в функциональной структуре по первому варианту выполнен в виде положительного и условно отрицательного каналов суммирования слагаемых, которые эквивалентны по структуре логических функций, и положительный канал реализован в соответствии с математической моделью вида
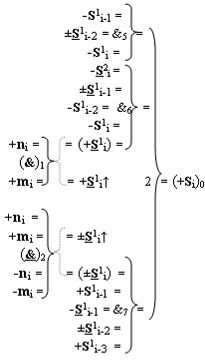
где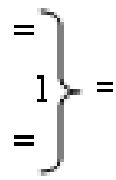 
- логическая функция f1(})-ИЛИ; 
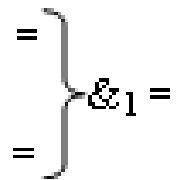- логическая функция f1(&)-И;
где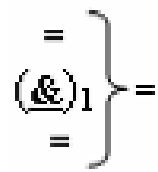 
- логическая функция f1(}&)-ИЛИ-НЕ; 
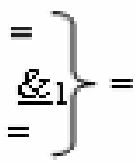- логическая функция f1(&)-И-НЕ;
«=&1=» - логическая функция f1(&)-НЕ изменения активности аргумента аналогового сигнала, а условно отрицательный канал реализован в соответствии с математической моделью вида
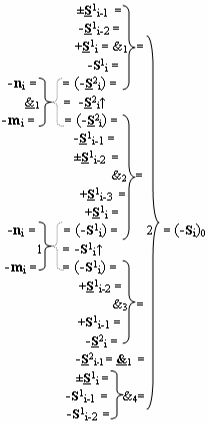
При этом по второму варианту функциональная структура параллельного сумматора выполнена также в виде положительного и условно отрицательного каналов суммирования слагаемых, которые эквивалентны по структуре логических функций, и положительный канал реализован в соответствии с математической моделью вида
а в условно отрицательном канале сумматора выполнен в соответствии с математической моделью вида
При этом по третьему варианту функциональная структура параллельного сумматора выполнена также в виде положительного и условно отрицательного каналов суммирования слагаемых, которые эквивалентны по структуре логических функций, и положительный канал реализован в соответствии с математической моделью вида
а условно отрицательный канал реализован в соответствии с математической моделью вида
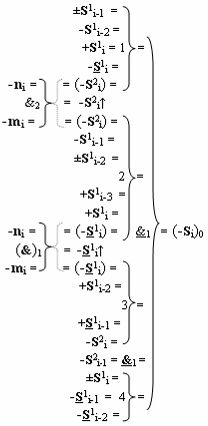
При этом по четвертому варианту функциональная структура параллельного сумматора выполнена также в виде положительного и условно отрицательного каналов суммирования слагаемых, которые эквивалентны по структуре логических функций, и положительный канал реализован в соответствии с математической моделью вида
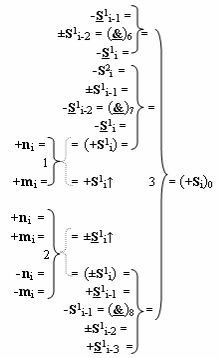
а условно отрицательный канал реализован в соответствии с математической моделью вида
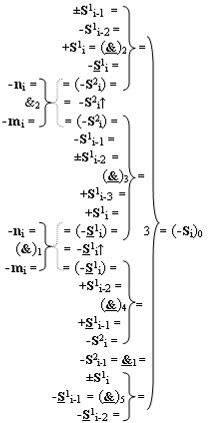
в которых логическая функция f3(})-ИЛИ в положительном и условно отрицательном канале функциональной структуры сумматора является выходной логической (прототип).
Известный прототип имеет технологические возможности, которые заключаются в том, что для решения задачи повышения быстродействия арифметических преобразований аргументов аналоговых сигналов слагаемых в качестве их использованы позиционно-знаковые структуры слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min.
Недостатком прототипа является то, что результирующая структура аргументов суммы ±[S3 i], которая сформирована с чередующимися положительными и условно отрицательными активными аргументами, не всегда позволяет первый уровень суммирования частичных произведений в параллельно-последовательном умножителе ±fΣ(ΣRU)min выполнить посредством совокупности логических функций ±[f1-4(})-ИЛИ], например, в графоаналитическом выражении вида
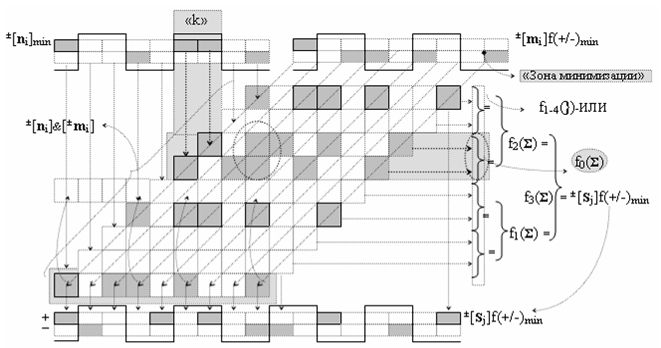
что не приводит к существенному сокращению его технологического цикла tΣ преобразования аргументов частичных произведений. Поскольку функциональная структура сумматора не обеспечивает формирование результирующей структуры суммы аргументов ±[Sj]f(+/-)min, в которой активен только один аргумент в условно «k» «Зоне минимизации» множителя ±[ni]min, а при реализации такой условно минимизированной структуры аргументов множителя ±[ni]min процедуру суммирования частичных произведений в умножителе ±fΣ(ΣRU)min можно записать в виде графоаналитического выражения вида
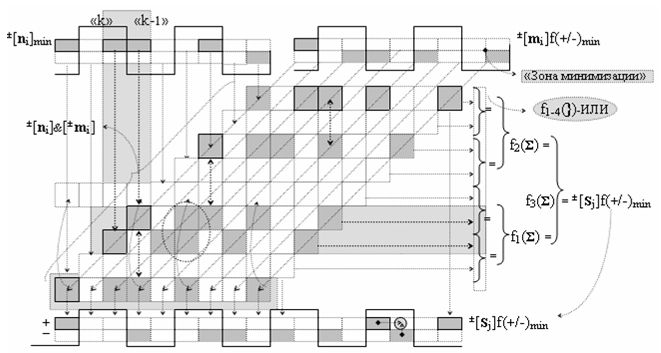
При этом следует отметить, что при использовании в функциональных арифметических структурах условно минимизированных структур аналоговых сигналов сомножителей ±[ni]f(+/-)min и ±[mi]f(+/-)min, в которых два последовательных активных аргумента множителя ±[ni]min, позиционно расположенные между «Зонами минимизации», активизируют аргументы частичных произведений, и они распределены между двумя последовательными функциональными структурами логических функций ±[f1-4(})-ИЛИ], что приводит к существенному упрощению функциональной структуры сумматоров первого уровня умножителя ±fΣ(ΣRU)min, а последующие функциональные структуры сумматоров могут быть выполнены без сквозного переноса.
Техническим результатом предложенного изобретения является минимизация технологического цикла tΣ функциональных арифметических структур.
Указанный технологический результат достигается следующим способом формирования логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), который реализован посредством функциональных различных структур.
Способ формирования логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованный с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1) (Русская логика), в соответствии с которым в «Положительном канале сумматора «i» разряда» и «Условно отрицательном канале сумматора «i» разряда» условно «k» «Зоны минимизации» выполняют одновременный анализ аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min посредством функциональных структур
с выходными логическими функциями f5(})-ИЛИ и f6(})-ИЛИ, в систему которых включают положительные аргументы аналоговых сигналов (+ni)k и (+mi)k и условно отрицательные аргументы аналоговых сигналов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», активизирующие положительный «Комплексный аргумент» (+nVmi)k и условно отрицательный «Комплексный аргумент» (-nVmi)k и посредством функциональных структур с выходными логическими функциями f1(}&)-ИЛИ-НЕ, f3(}&)-ИЛИ-НЕ и f1(&)-И-НЕ вида
в «Положительном канале сумматора «i» разряда», в систему которых включают положительные аргументы аналоговых сигналов (+ni)k и (+mi)k и условно отрицательные аргументы аналоговых сигналов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» и активизируют обобщенный «Комплексный аргумент» (-Comp)Si+1 i)k и +(±Comp)Si+1 i)k и положительный «Комплексный аргумент» (+n&mi)k с измененным уровнем аналогового сигнала, а посредством функциональных структур с выходными логическими функциями f2(}&)-ИЛИ-НЕ , f4(}&)-ИЛИ-НЕ и f2(&)-И-НЕ вида
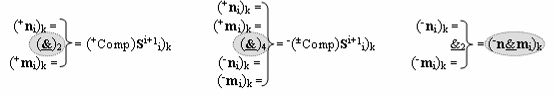
в «Условно отрицательном канале сумматора «i» разряда», в систему которых также включают положительные аргументы аналоговых сигналов (+ni)k и (+mi)k и условно отрицательные аргументы аналоговых сигналов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», активизируют обобщенный «Комплексный аргумент» (+Comp)Si+1 i)k и -(±Comp)Si+1 i)k, которые подают на соответствующие функциональные входные связи входных логических функций f1(&)-И - f6(&)-И в «Положительном канале сумматора «i» разряда» и подают на соответствующие функциональные входные связи входных логических функций f11(&)-И - f16(&)-И в «Условно отрицательном канале сумматора «i» разряда» условно «k» «Зоны минимизации», которые включают в систему выходных логических функций f1(})-ИЛИ и f3(})-ИЛИ в соответствии с аналитическим выражением вида
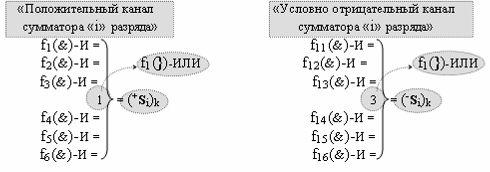
и посредством которых активизируют положительный аргумент результирующей суммы (+Si)k и условно отрицательный аргумент результирующей суммы (-Si)k, отличающийся тем, что для одновременного анализа аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в соответствии с графоаналитическим выражением вида
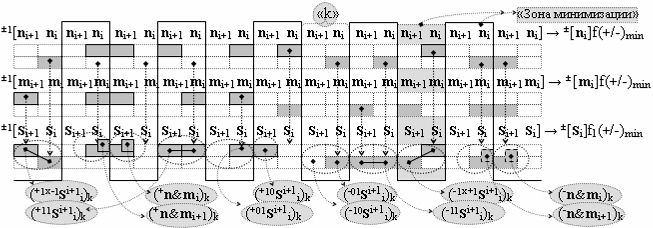
где 
и 
- положительный аргумент и условно отрицательный аргумент соответственно;
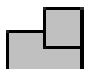и 
- положительный двойной аргумент и условно отрицательный двойной аргумент в условно «i» и «i+1» разряда соответственно;
в каждой условно «k» «Зоне минимизации», в которую включают по два последовательных разряда - условно «i» разряд и условно «i+1» разряд и активизируют следующие «Комплексные аргументы»:
▶ «+Комплексный аргумент» (+01Si+1 i)k активизируют посредством функциональной структуры графоаналитического выражения вида
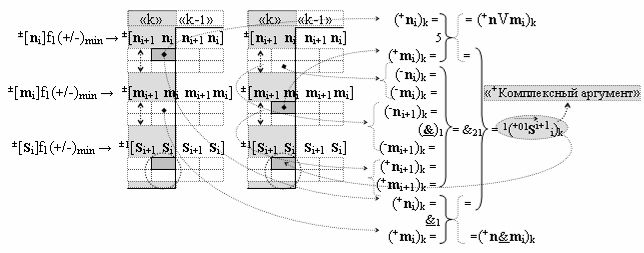
с входными логическими функциями f5(})-ИЛИ, f1(}&)-ИЛИ-НЕ и f1(&)-И-НЕ и выходной логической функцией f21(&)-И;
▶ «-Комплексный аргумент» (-01Si+1 i)k активизируют посредством функциональной структуры вида
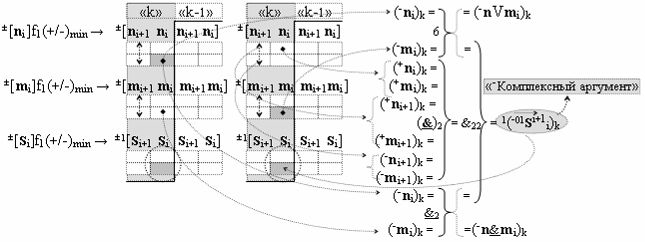
с входными логическими функциями f6(})-ИЛИ, f2(}&)-ИЛИ-НЕ и f2(&)-И-НЕ и выходной логической функцией f22(&)-И;
▶ «+Комплексный аргумент» (+10Si+1 i)k активизируют посредством функциональной структуры графоаналитического выражения вида
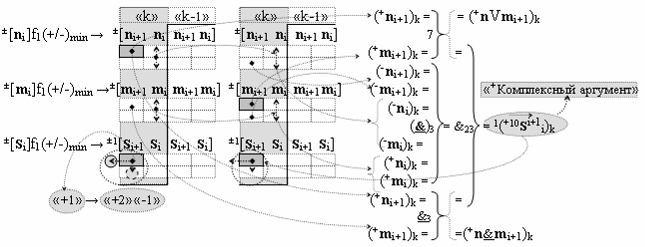
с входными логическими функциями f7(})-ИЛИ, f3(}&)-ИЛИ-НЕ и f3(&)-И-НЕ и выходной логической функцией f23(&)-И;
где 
и 
- преобразованный положительный и условно отрицательный результирующие аргументы, которые активизированы посредством применения арифметических аксиом троичной системы счисления fRU(+1,0,-1);
▶ «-Комплексный аргумент» (-10Si+1 i)k активизируют посредством функциональной структуры графоаналитического выражения вида
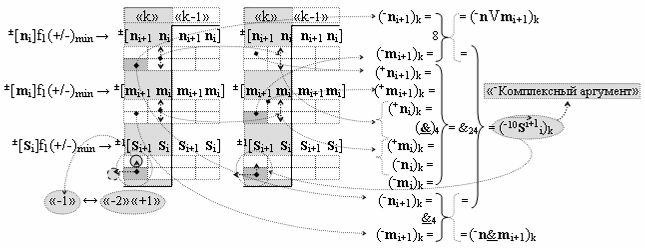
с входными логическими функциями f8(})-ИЛИ, f4(}&)-ИЛИ-НЕ и f4(&)-И-НЕ и выходной логической функцией f24(&)-И;
▶ «+Комплексный аргумент» (+11Si+1 i)k без изменения уровня аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
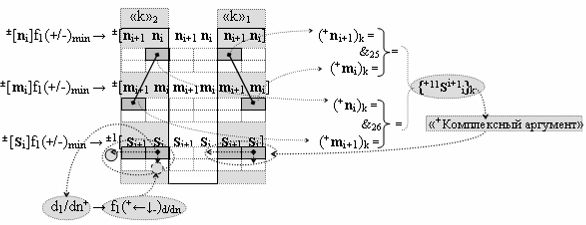
с входными логическими функциями f25(&)-И и f26(&)-И;
▶ «+Комплексный аргумент» (+11Si+1 i)k с измененным уровнем аналогового сигнала активизируют посредством функциональных структур вида
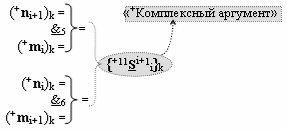
с входными логическими функциями f5(&)-И-НЕ и f6(&)-И-НЕ;
▶ «-Комплексный аргумент» (-11Si+1 i)k → {-11Si+1 i}k без изменения уровня аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
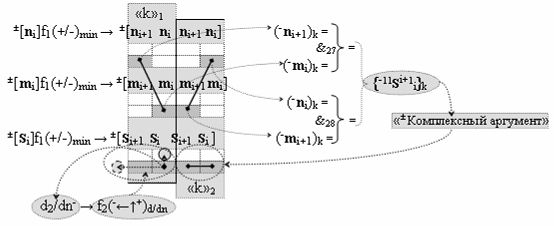
с входными логическими функциями f27(&)-И и f28(&)-И;
▶ «-Комплексный аргумент» (-11Si+1 i)k → {-11Si+1 i}k с измененным уровнем аналогового сигнала активизируют посредством функциональных структур вида
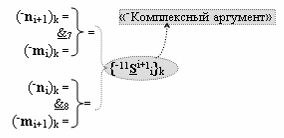
с входными логическими функциями f7(&)-И-НЕ и f7(&)-И-НЕ;
▶ «+Комплексный аргумент» (+n&mi)k активизируют посредством функциональной структуры графоаналитического выражения вида
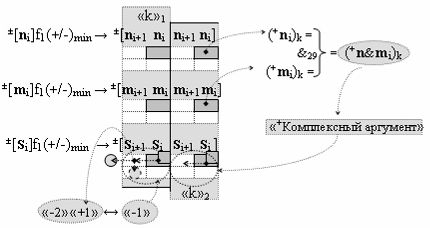
с выходной логической функцией f29(&)-И;
▶ «-Комплексный аргумент» (-n&mi)k активизируют посредством функциональной структуры графоаналитического выражения вида
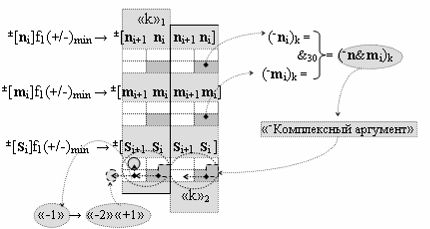
с выходной логической функцией f30(&)-И;
▶ «+Комплексный аргумент» (+n&mi+1)k активизируют посредством функциональной структуры графоаналитического выражения вида
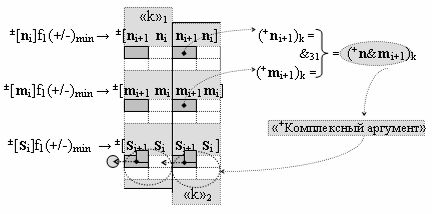
с выходной логической функцией f31(&)-И;
▶ «-Комплексный аргумент» (-n&mi+1)k активизируют посредством функциональной структуры графоаналитического выражения вида
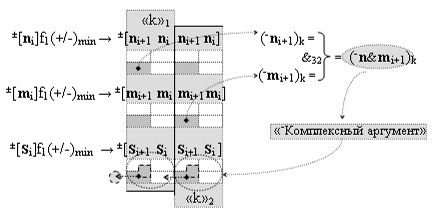
с выходной логической функцией f32(&)-И;
▶ «±Комплексный аргумент» (+1х-1Si+1 i)k → {+1х-1Si+1 i}k активизируют посредством функциональных структур графоаналитического выражения вида
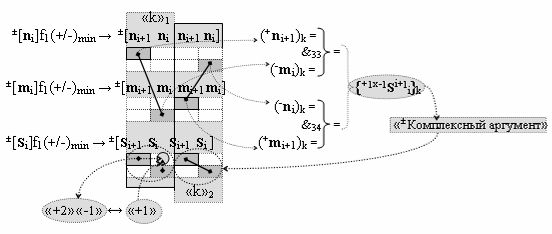
с входными логическими функциями f33(&)-И и f34(&)-И;
▶ «±Комплексный аргумент» (-1х+1Si+1 i)k → {-1х+1Si+1 i}k активизируют посредством функциональных структур графоаналитического выражения вида
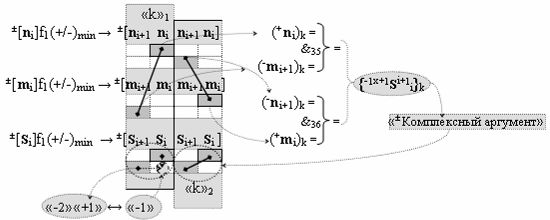
с входными логическими функциями f35(&)-И f36(&)-И;
при этом «±0Комплексный аргумент» (±0х0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» активизируют посредством функциональной структуры графоаналитического выражения вида
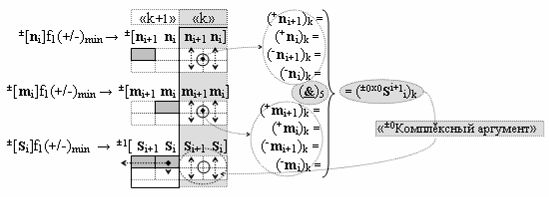
с входной логической функцией f5(}&)-ИЛИ-НЕ;
и «±Комплексный аргумент» (±11.0,±1,±0х0Si+1 i)k одновременной активности положительных и условно отрицательных аргументов в условно «k» «Зоне минимизации», которые соответствуют арифметической аксиоме «+1»«-1» → «±01» и неактивности аргументов в условно «k» «Зоне минимизации» активизируют посредством функциональной структуры графоаналитического выражения вида
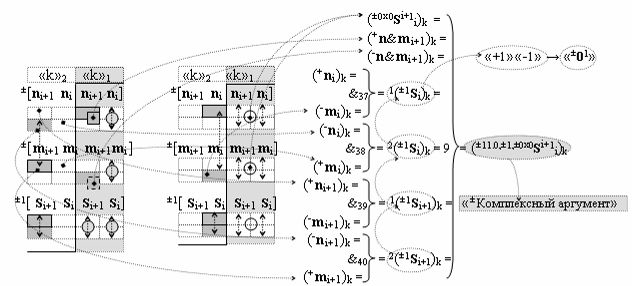
с входными логическими функциями f37(&)-И, f38(&)-И, f39(&)-И, f40(&)-И и выходной логической функцией f9(})-ИЛИ;
после чего выполняют одновременный анализ активных «Комплексных аргументов» аналоговых сигналов слагаемых в соответствующих условно «k» «Зонах минимизации» в соответствии с графоаналитическим выражением вида
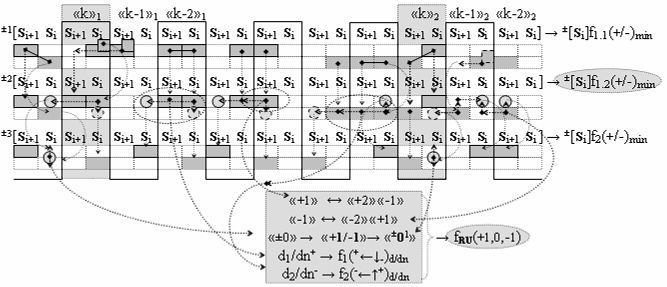
и активизируют возможные дополнительные «Комплексные аргументы»:
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k активизируют посредством функциональных структур графоаналитического выражения вида
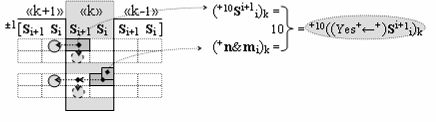
с выходной логической функцией f10(})-ИЛИ;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k активизируют посредством функциональных структур графоаналитического выражения вида
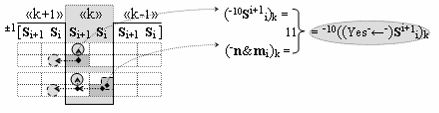
с выходной логической функцией f11(})-ИЛИ;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k активизируют посредством совокупности преобразованных положительных аргументов {+11Si+1 i}k графоаналитического выражения вида
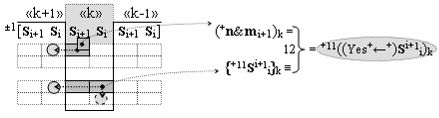
с выходной логической функцией f12(})-ИЛИ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k активизируют посредством совокупности преобразованных условно отрицательных аргументов {-11Si+1 i}k графоаналитического выражения вида
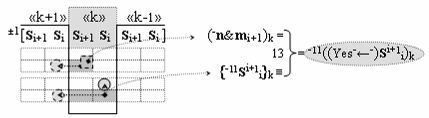
с выходной логической функцией f13(})-ИЛИ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k активизируют посредством функциональных структур графоаналитического выражения вида
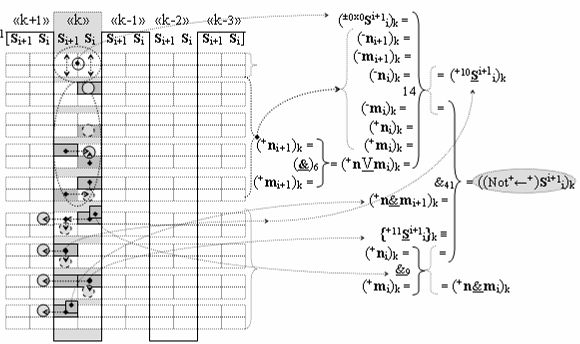
с входными логическими функциями f6(}&)-ИЛИ-НЕ, f14(})-ИЛИ и f9(&)-И-НЕ и с выходной логической функцией f41(&)-И;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k активизируют посредством функциональных структур графоаналитического выражения вида
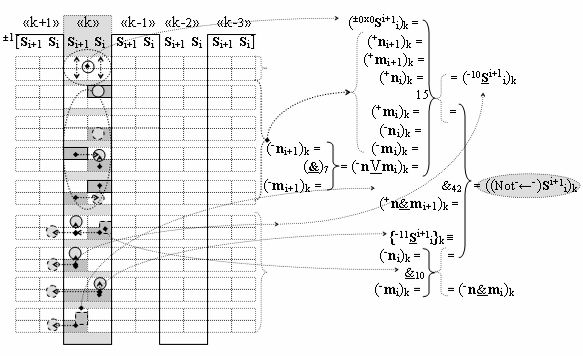
с входными логическими функциями f7(}&)-ИЛИ-НЕ, f15(})-ИЛИ и f10(&)-И-НЕ и с выходной логической функцией f42(&)-И;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
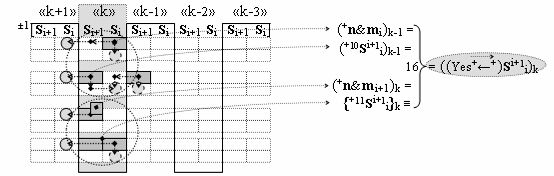
с выходной логической функцией f16(})-ИЛИ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
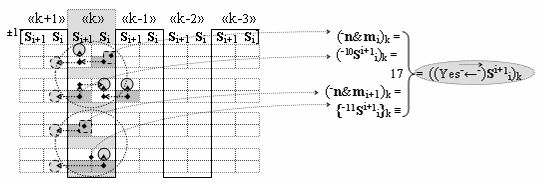
с выходной логической функцией f17(})-ИЛИ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f43(&)-И;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
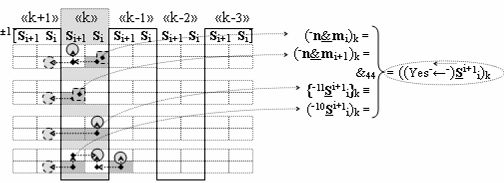
с выходной логической функцией f44(&)-И;
▶ «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k посредством функциональных структур графоаналитического выражения вида
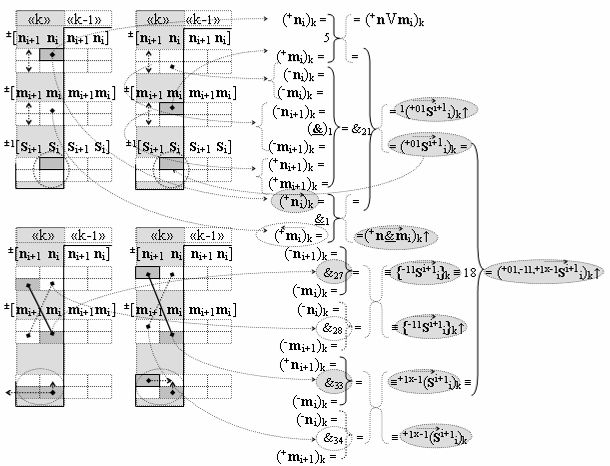
с выходной логической функцией f18(})-ИЛИ и входными логическими функциями f5(})-ИЛИ, f1(}&)-ИЛИ-НЕ, f21(&)-И, f1(&)-И-НЕ, f27(&)-И, f28(&)-И, f33(&)-И и f34(&)-И;
▶ «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k посредством функциональных структур графоаналитического выражения вида
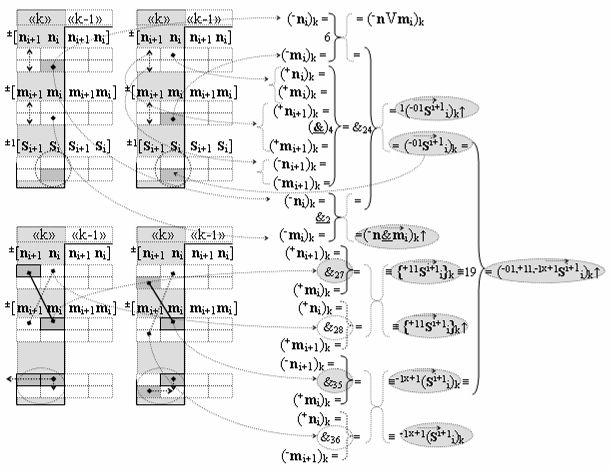
с выходной логической функцией f19(})-ИЛИ и входными логическими функциями f6(})-ИЛИ, f4(}&)-ИЛИ-НЕ, f24(&)-И, f2(&)-И-НЕ, f27(&)-И, f28(&)-И, f35(&)-И и f36(&)-И;
затем посредством выходной функциональной структуры «Положительного канала сумматора «i» разряда» вида
с общей выходной логической функцией f1(})-ИЛИ и в соответствии с графоаналитическим выражением вида
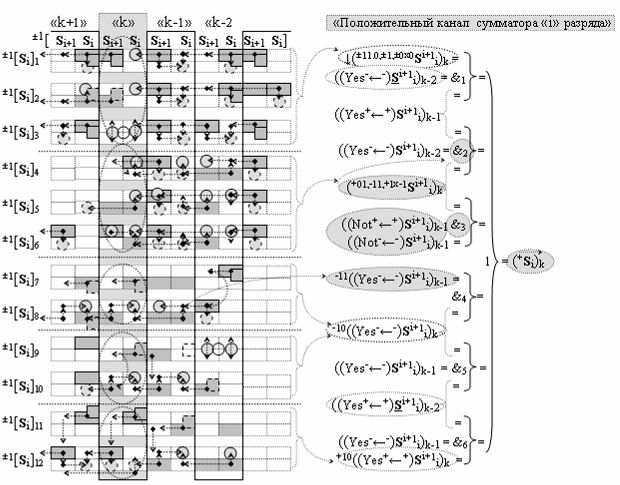
выполняют одновременный анализ активных «Комплексных аргументов» аналоговых сигналов слагаемых в соответствующих условно «k» «Зонах минимизации» и активизируют положительный результирующий аргумент суммы (+Si)k,
где ((Yes+←+)Si+1 i)k-1 и ((Yes-←-)Si+1 i)k-2 - «Комплексные аргументы» условно «k-1» «Зоны минимизации» и условно «k-1» «Зоны минимизации» соответственно;
а также посредством выходной функциональной структуры «Условно отрицательный канал сумматора «i» разряда» вида
с общей выходной логической функцией f3(})-ИЛИ и в соответствии с графоаналитическим выражением вида
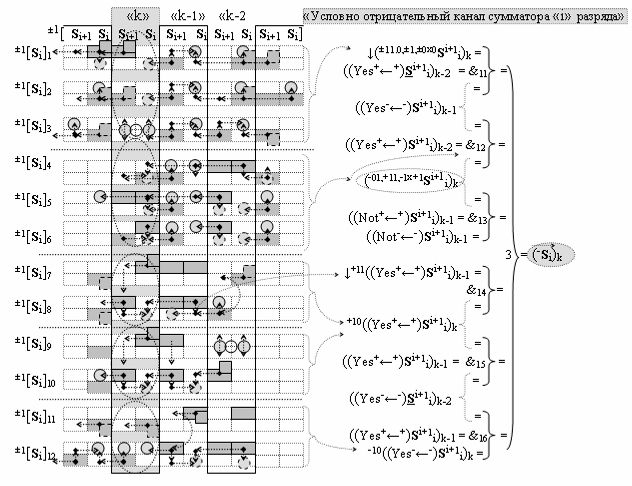
выполняют одновременный анализ активных «Комплексных аргументов» аналоговых сигналов слагаемых в соответствующих условно «k» «Зонах минимизации» и активизируют результирующий условно отрицательный аргумент суммы (-Si)k, при этом посредством дополнительной выходной функциональной структуры с выходной логической функцией f2(})-ИЛИ «Положительного канала сумматора «i+1» разряда» в соответствии с графоаналитическим выражением вида
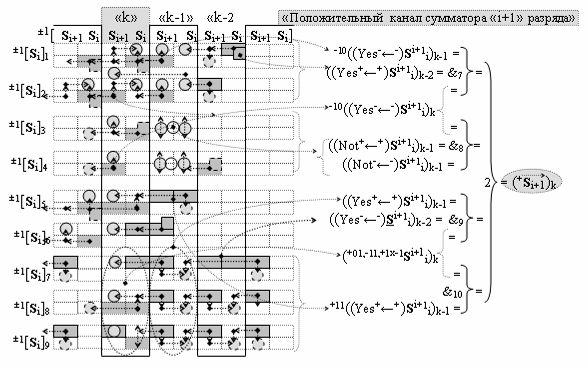
и дополнительной выходной функциональной структуры с выходной логической функцией f2(})-ИЛИ «Условно отрицательного канала сумматора «i+1» разряда» в соответствии с графоаналитическим выражением вида
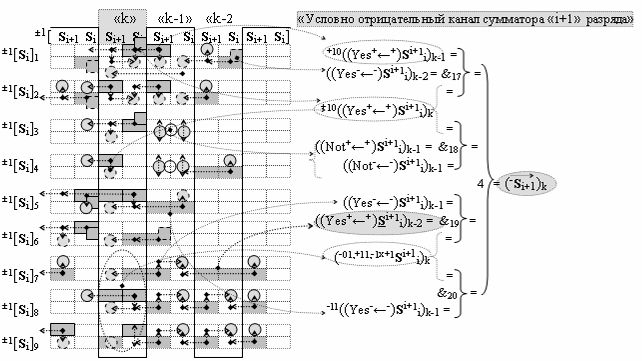
выполняют одновременный анализ активных «Комплексных аргументов» аналоговых сигналов слагаемых в соответствующих условно «k» «Зонах минимизации» и активизируют положительный результирующий аргумент результирующей суммы (+Si+1)k и условно отрицательный аргумент результирующей суммы (-Si+1)k условно «i+1» разряда.
Вариант 1. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), включающая «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации», которые включают выходную структуру логических функций, реализованную в соответствии с математической моделью вида
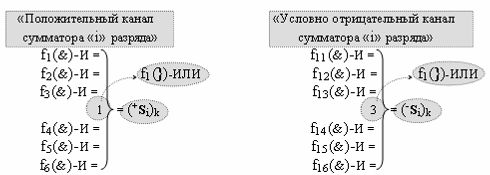
и с входными логическими функциями f1(&)-И - f6(&)-И и с входными логическими функциями f11(&)-И - f16(&)-И, функциональные выходные связи (=) которых являются функциональными входными связями выходной логической функции f1(})-ИЛИ и f3(})-ИЛИ для активизации положительного аргумента суммы (+Si)k условно «i» разряда и для активизации условно отрицательного аргумента (-Si)k условно «i» разряда, при этом «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации» также включает функциональную входную структуру, сформированную в соответствии с математической моделью вида
и с выходными логическими функциями f5(})-ИЛИ и f6(})-ИЛИ, функциональные входные связи которых являются функциональными входными связями для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», для активизации положительного «Комплексного аргумента» (+nVmi)k и условно отрицательного «Комплексного аргумента» (-nVmi)k, при этом «Положительный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
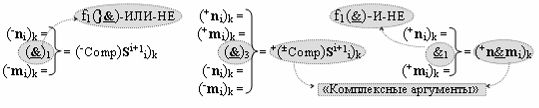
и с выходными логическими функциями f1(}&)-ИЛИ-НЕ, f3(}&)-ИЛИ-НЕ и f1(&)-И-НЕ, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для активизации «Комплексных аргументов» (-Comp)Si+1 i)k, +(±Comp)Si+1 i)k и «Комплексного аргумента» (+n&mi)k с измененным уровнем аналогового сигнала, при этом «Положительный канал сумматора «i» разряда» также включает логическую функцию f21(&)-И, а «Условно отрицательный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
и с выходными логическими функциями f2(}&)-ИЛИ-НЕ, f4(}&)-ИЛИ-НЕ и f2(&)-И-НЕ, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для активизации «Комплексных аргументов» (+Comp)Si+1 i)k, -(±Comp)Si+1 i)k и «Комплексного аргумента» (-n&mi)k с измененным уровнем аналогового сигнала, при этом «Условно отрицательный канал сумматора «i» разряда» также включает логическую функцию f22(&)-И, при этом в условно «k» «Зону минимизации» введены в соответствии с аналитическим выражением вида
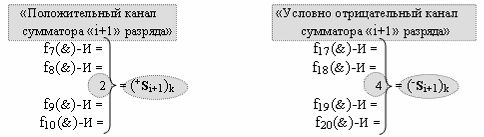
дополнительная структура логических функций с входными логическими функциями f7(&)-И - f10(&)-И, функциональные выходные связи которых являются функциональными входными связями логической функции f2(})-ИЛИ, которая активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда в «Положительном канале сумматора «i+1» разряда», и дополнительная структура логических функций с входными логическими функциями f17(&)-И - f20(&)-И, функциональные выходные связи которых являются функциональными входными связями логической функции f4(})-ИЛИ, которая активизирует условно отрицательный результирующий аргумент (-Si+1)k условно «i+1» разряда в «Условно отрицательном канале сумматора «i+1» разряда», при этом в систему входных логических функций f1(&)-И - f10(&)-И «Положительного канал сумматора «i» разряда» и «Положительного канал сумматора «i+1» разряда», которые сформированы в соответствии с математической моделью вида
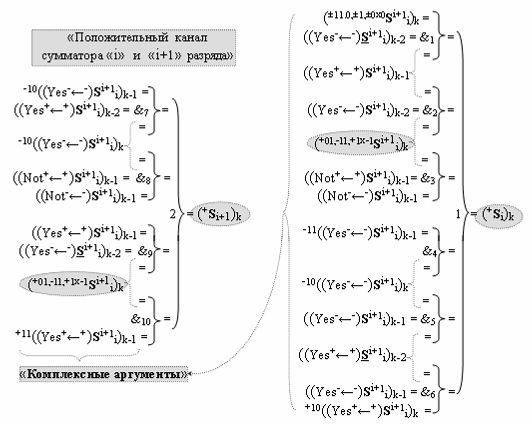
с входными «Комплексными аргументами», которые включены также и в «Условно отрицательный канал сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k функциональной входной структуры, которая сформирована в соответствии с математической моделью вида
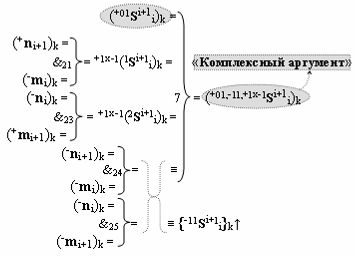
и с выходной логической функцией f18(})-ИЛИ и входными логическими функциями f45(&)-И, f46(&)-И, f47(&)-И и f48(&)-И, в которой «+Комплексный аргумент» (+01Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
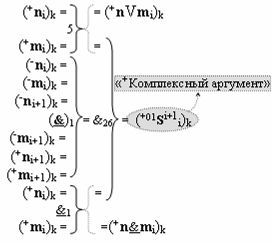
с входными логическими функциями f5(})-ИЛИ, f1(}&)-ИЛИ-НЕ и f1(&)-И-НЕ и выходной логической функцией f26(&)-И;
а в систему входных логических функций f1(&)-И - f10(&)-И «Условно отрицательного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i+1» разряда», которые сформированы в соответствии с математической моделью вида
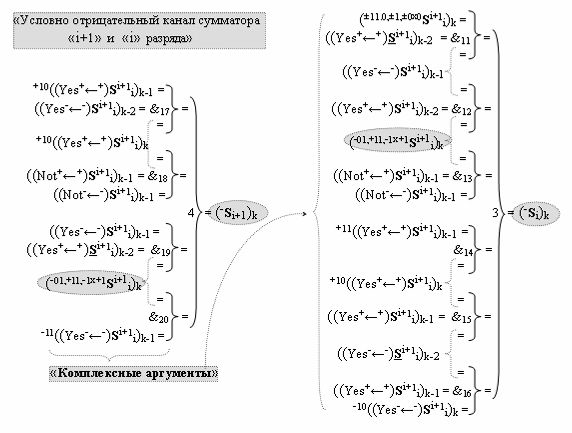
включены «Комплексные аргументы», которые являются общими аргументами с «Положительным каналом сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k функциональной входной структуры, которая сформирована в соответствии с математической моделью вида
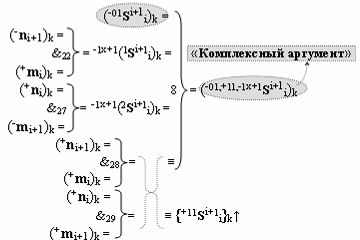
с выходной логической функцией f8(})-ИЛИ и входными логическими функциями f22(&)-И, f27(&)-И, f28(&)-И и f29(&)-И, в которой «-Комплексный аргумент» (-01Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
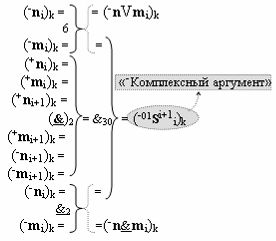
с входными логическими функциями f6(})-ИЛИ, f2(}&)-ИЛИ-НЕ и f2(&)-И-НЕ и выходной логической функцией f30(&)-И;
при этом «Комплексные аргументы» в выходных функциональных структурах, которые реализованы в соответствии с математической моделью «Положительного канала сумматора «i+1» и «i» разряда» и математической моделью «Условно отрицательного канала сумматора «i+1» и «i» разряда», сформированы посредством следующих функциональных структур:
▶ «±Комплексный аргумент» (±11.0,±1,±0х0Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f31(&)-И, f32(&)-И, f33(&)-И, f34(&)-И и выходной логической функцией f9(})-ИЛИ, в которой «±0Комплексный аргумент» (±0х0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
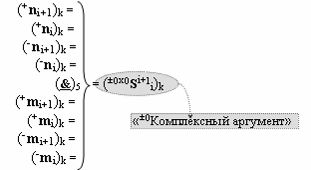
с входной логической функцией f5(}&)-ИЛИ-НЕ, «+Комплексный аргумент» (+n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f35(&)-И, а «-Комплексный аргумент» (-n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
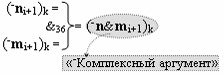
с выходной логической функцией f36(&)-И;
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
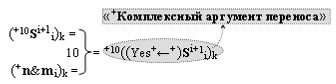
с выходной логической функцией f10(})-ИЛИ, в которой «+Комплексный аргумент» (+10Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
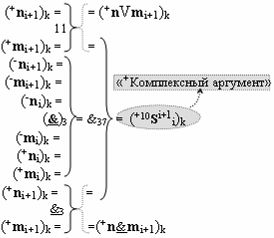
с входными логическими функциями f11(})-ИЛИ, f3(}&)-ИЛИ-НЕ и f3(&)-И-НЕ и выходной логической функцией f37(&)-И, а «+Комплексный аргумент» (+n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f38(&)-И;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
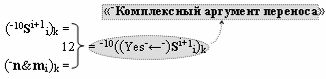
с выходной логической функцией f12(})-ИЛИ, в которой «-Комплексный аргумент» (-10Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
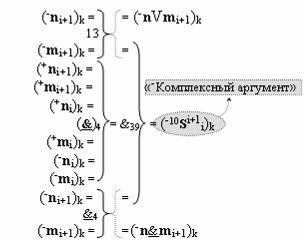
с входными логическими функциями f13(})-ИЛИ, f4(}&)-ИЛИ-НЕ и f4(&)-И-НЕ и выходной логической функцией f39(&)-И, а «-Комплексный аргумент» (-n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
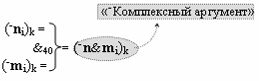
с выходной логической функцией f40(&)-И;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f14(})-ИЛИ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
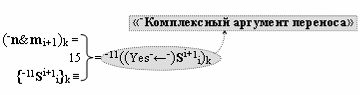
с выходной логической функцией f15(})-ИЛИ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
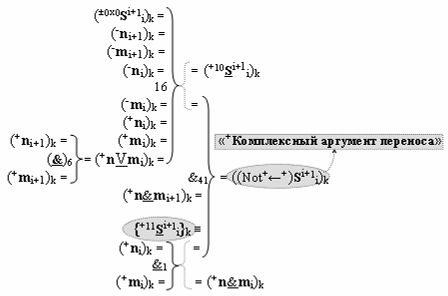
с входными логическими функциями f6(}&)-ИЛИ-НЕ, f16(})-ИЛИ и f1(&)-И-НЕ и с выходной логической функцией f41(&)-И, в которой «+Комплексный аргумент» {+11Si+1 i}k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
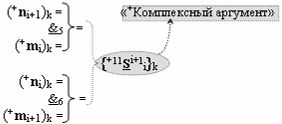
с входными логическими функциями f5(&)-И-НЕ и f6(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
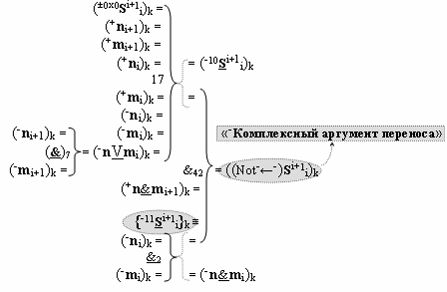
с входными логическими функциями f7(}&)-ИЛИ-НЕ, f17(})-ИЛИ и f2(&)-И-НЕ и с выходной логической функцией f42(&)-И, в которой «-Комплексный аргумент» (-11Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
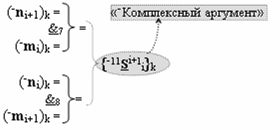
с входными логическими функциями f7(&)-И-НЕ и f8(&)-И-НЕ;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
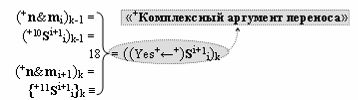
с выходной логической функцией f18(})-ИЛИ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f119(})-ИЛИ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
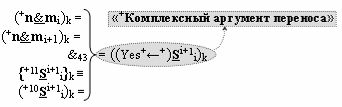
с выходной логической функцией f43(&)-И;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
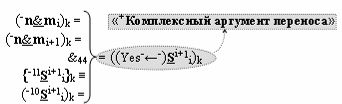
с выходной логической функцией f44(&)-И.
Вариант 2. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), включающая «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации», которые включают выходную структуру логических функций, реализованную в соответствии с математической моделью вида
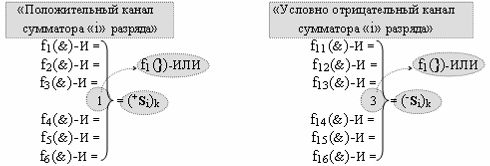
и с входными логическими функциями f1(&)-И-НЕ - f6(&)-И-НЕ и с входными логическими функциями f13(&)-И-НЕ - f18(&)-И-НЕ, функциональные выходные связи (=) которых являются функциональными входными связями выходной логической функции f11(&)-И-НЕ и f23(&)-И-НЕ для формирования положительного аргумента суммы (+Si)k условно «i» разряда и для активизации условно отрицательного аргумента (-Si)k условно «i» разряда, при этом «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации» также включает функциональную входную структуру, сформированную в соответствии с математической моделью вида
и с выходными логическими функциями f1(})-ИЛИ и f2(})-ИЛИ, функциональные входные связи которых являются функциональными входными связями для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», для активизации положительного «Комплексного аргумента» (+nVmi)k и условно отрицательного «Комплексного аргумента» (-nVmi)k, при этом «Положительный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
и с выходными логическими функциями f1(}&)-ИЛИ-НЕ, f3(}&)-ИЛИ-НЕ и f25(&)-И-НЕ, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для формирования обобщенного «Комплексного аргумента» (-Comp)Si+1 i)k и +(±Comp)Si+1 i)k и положительного «Комплексного аргумента» (+n&mi)k с измененным уровнем аналогового сигнала, при этом «Положительный канал сумматора «i» разряда» также включает логическую функцию f26(&)-И-НЕ и f5(}&)-ИЛИ-НЕ;
а «Условно отрицательный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
и с выходными логическими функциями f2(}&)-ИЛИ-НЕ, f4(}&)-ИЛИ-НЕ и f27(&)-И-НЕ, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для формирования обобщенного «Комплексного аргумента» (+Comp)Si+1 i)k и -(±Comp)Si+1 i)k и условно отрицательного «Комплексного аргумента» (-n&mi)k с измененным уровнем аналогового сигнала, при этом «Условно отрицательный канал сумматора «i» разряда» также включает логическую функцию f28(&)-И-НЕ и f6(}&)-ИЛИ-НЕ; при этом в условно «k» «Зону минимизации» введены в соответствии с аналитическим выражением вида
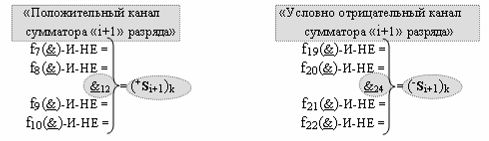
дополнительная структура логических функций с входными логическими функциями f7(&)-И-НЕ - f10(&)-И-НЕ, функциональные выходные связи которых являются функциональными входными связями логической функции f12(&)-И-НЕ, которая активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда в «Положительном канале сумматора «i+1» разряда», и дополнительная структура логических функций с входными логическими функциями f19(&)-И-НЕ - f22(&)-И-НЕ, функциональные выходные связи которых являются функциональными входными связями логической функции f24(&)-И-НЕ, которая активизирует условно отрицательный результирующий аргумент (-Si+1)k условно «i+1» разряда в «Условно отрицательном канале сумматора «i+1» разряда», при этом в систему входных логических функций f1(&)-И-НЕ - f10(&)-И-НЕ «Положительного канал сумматора «i» разряда» и «Положительного канал сумматора «i+1» разряда», реализованные в соответствии с математической моделью вида
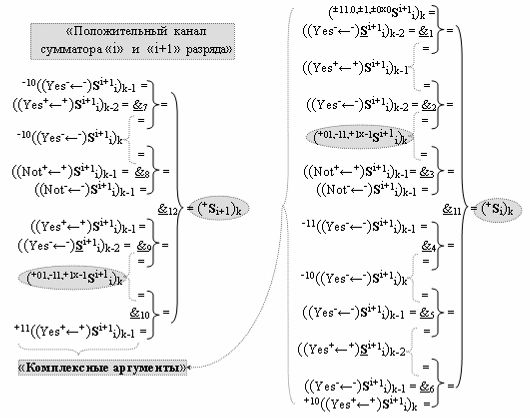
с входными «Комплексными аргументами», которые включены также и в «Условно отрицательный канал сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k функциональной входной структуры, которая сформирована в соответствии с математической моделью вида
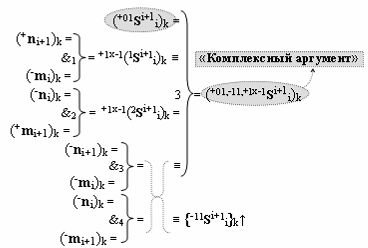
и с выходной логической функцией f3(})-ИЛИ и входными логическими функциями f1(&)-И, f2(&)-И, f3(&)-И и f4(&)-И, в которой «+Комплексный аргумент» (+01Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
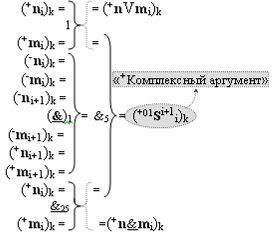
с входными логическими функциями f1(})-ИЛИ, f1(}&)-ИЛИ-НЕ и f25(&)-И-НЕ и выходной логической функцией f5(&)-И;
а в систему входных логических функций f11(&)-И-НЕ - f20(&)-И-НЕ «Условно отрицательного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i+1» разряда», сформированные в соответствии с математической моделью вида
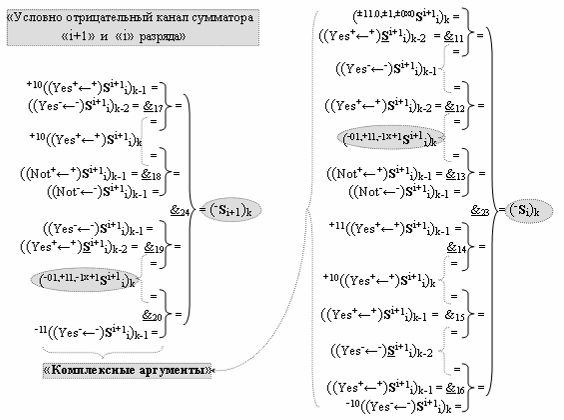
с входными «Комплексными аргументами», которые являются общими аргументами с «Положительным каналом сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k функциональной входной структуры, которая сформирована в соответствии с математической моделью вида
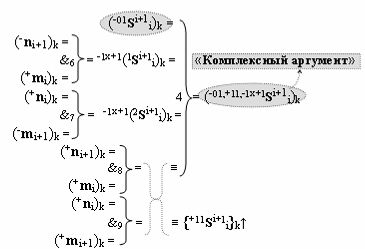
с выходной логической функцией f4(})-ИЛИ и входными логическими функциями f6(&)-И, f7(&)-И, f8(&)-И и f9(&)-И, в которой «-Комплексный аргумент» (-01Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
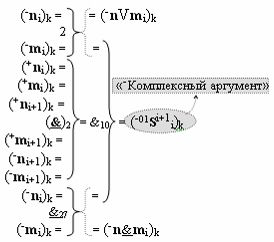
с входными логическими функциями f2(})-ИЛИ, f2(}&)-ИЛИ-НЕ и f27(&)-И-НЕ и выходной логической функцией f10(&)-И;
при этом «Комплексные аргументы» в выходных функциональных структурах, которые реализованы в соответствии с математической моделью «Положительного канала сумматора «i+1» и «i» разряда» и математической моделью «Условно отрицательного канала сумматора «i+1» и «i» разряда», сформированы посредством следующих функциональных структур:
▶ «±Комплексный аргумент» (±11.0,±1,±0х0Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f11(&)-И, f12(&)-И, f13(&)-И, f14(&)-И и выходной логической функцией f5(})-ИЛИ, в которой «±0Комплексный аргумент» (±0х0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
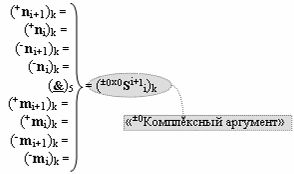
с входной логической функцией f5(}&)-ИЛИ-НЕ, «+Комплексный аргумент» (+n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
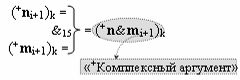
с выходной логической функцией f15(&)-И, а «-Комплексный аргумент» (-n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
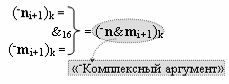
с выходной логической функцией f16(&)-И;
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f6(})-ИЛИ, в которой «+Комплексный аргумент» (+10Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
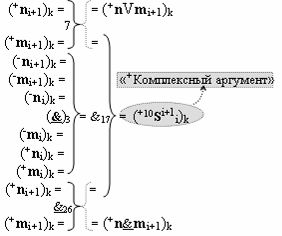
с входными логическими функциями f7(})-ИЛИ, f3(}&)-ИЛИ-НЕ и f26(&)-И-НЕ и выходной логической функцией f17(&)-И, а «+Комплексный аргумент» (+n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
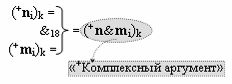
с выходной логической функцией f18(&)-И;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
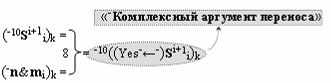
с выходной логической функцией f8(})-ИЛИ, в которой «-Комплексный аргумент» (-10Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f9(})-ИЛИ, f4(}&)-ИЛИ-НЕ и f28(&)-И-НЕ и выходной логической функцией f19(&)-И, а «-Комплексный аргумент» (-n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
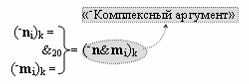
с выходной логической функцией f20(&)-И;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
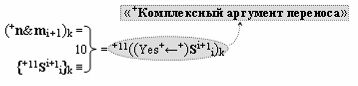
с выходной логической функцией f10(})-ИЛИ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
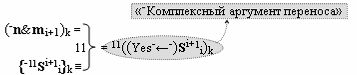
с выходной логической функцией f11(})-ИЛИ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
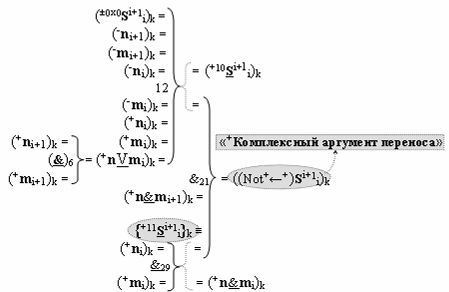
с входными логическими функциями f6(}&)-ИЛИ-НЕ, f12(})-ИЛИ и f29(&)-И-НЕ и с выходной логической функцией f21(&)-И, в которой «+Комплексный аргумент» {+11Si+1 i}k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f30(&)-И-НЕ и f31(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
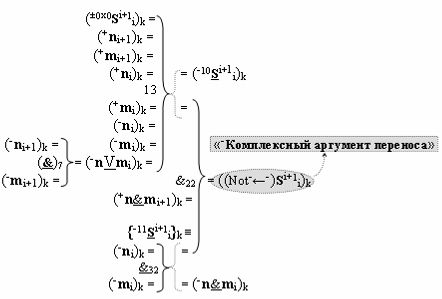
с входными логическими функциями f7(}&)-ИЛИ-НЕ, f13(})-ИЛИ и f32(&)-И-НЕ и с выходной логической функцией f22(&)-И, в которой «-Комплексный аргумент» (-11Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
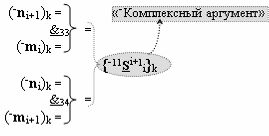
с входными логическими функциями f33(&)-И-НЕ и f34(&)-И-НЕ;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f14(})-ИЛИ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
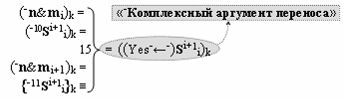
с выходной логической функцией f15(})-ИЛИ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
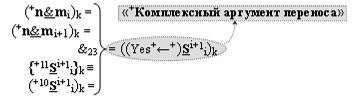
с выходной логической функцией f23(&)-И;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
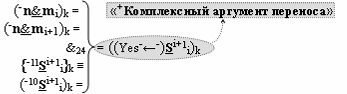
с выходной логической функцией f24(&)-И.
Вариант 3. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) с процедурой одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1).
Вариант 4. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), включающая «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации», которые включают выходную структуру логических функций, реализованную в соответствии с математической моделью вида
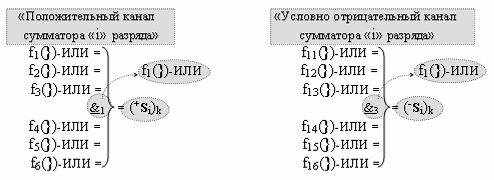
и с входными логическими функциями f1(})-ИЛИ - f6(})-ИЛИ и с входными логическими функциями f11(})-ИЛИ - f16(})-ИЛИ, функциональные выходные связи (=) которых являются функциональными входными связями выходной логической функции f1(&)-И-НЕ и f3(&)-И-НЕ для формирования положительного аргумента суммы (+Si)k условно «i» разряда и для активизации условно отрицательного аргумента (-Si)k условно «i» разряда, при этом «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации» также включает функциональную входную структуру, которая сформирована в соответствии с математической моделью вида
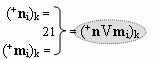
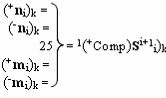
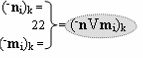
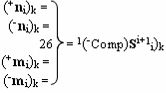
с выходной логической функцией f21(})-ИЛИ и f22(})-ИЛИ, в которых функциональные входные связи являются функциональными входными связями для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», для формирования положительного «Комплексного аргумента» (+nVmi)k и условно отрицательного «Комплексного аргумента» (-nVmi)k, при этом «Положительный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
с выходной логической функцией f1(}&)-ИЛИ-НЕ и f1(&)-И, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k условно «i» разряда «k» «Зоны минимизации» для активизации обобщенного «Комплексного аргумента» (+Comp)Si+1 i)k и положительного «Комплексного аргумента» (+n&mi)k без изменения уровня аналогового сигнала, при этом «Положительный канал сумматора «i» разряда» также включает логическую функцию f23(})-ИЛИ, а «Условно отрицательный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
с выходными логическими функциями f2(}&)-ИЛИ-НЕ и f2(&)-И, функциональные входные связи которых являются функциональными входными связями сумматора для приема условно отрицательных аргументов аналоговых сигналов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для формирования обобщенного «Комплексного аргумента» (-Comp)Si+1 i)k и условно отрицательного «Комплексного аргумента» (-n&mi)k без изменения уровня аналогового сигнала, при этом «Условно отрицательный канал сумматора «i» разряда» включает также логическую функцию f24(})-ИЛИ, при этом в условно «k» «Зону минимизации» введены в соответствии с аналитическим выражением вида
дополнительная структура логических функций с входными логическими функциями f7(})-ИЛИ - f10(})-ИЛИ, функциональные выходные связи которых являются функциональными входными связями логической функции f2(&)-И-НЕ, которая активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда в «Положительном канале сумматора «i+1» разряда» и дополнительная структура логических функций с входными логическими функциями f17(})-ИЛИ - f20(})-ИЛИ, функциональные выходные связи которых являются функциональными входными связями логической функции f4(&)-И-НЕ, которая формирует условно отрицательный результирующий аргумент (-Si+1)k условно «i+1» разряда в «Условно отрицательном канале сумматора «i+1» разряда», при этом в систему входных логических функций f1(})-ИЛИ - f10(})-ИЛИ «Положительного канал сумматора «i» разряда» и «Положительного канал сумматора «i+1» разряда», реализованные в соответствии с математической моделью вида
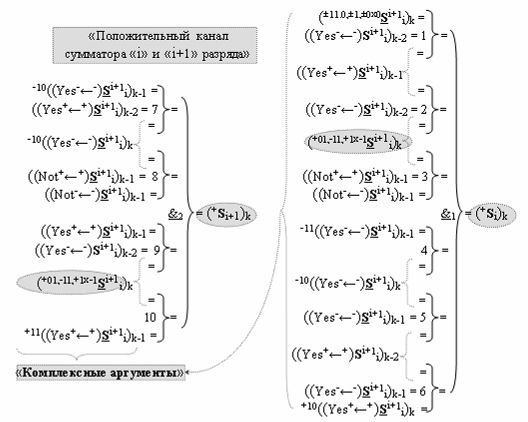
с входными «Комплексными аргументами», которые включены также и в «Условно отрицательный канал сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
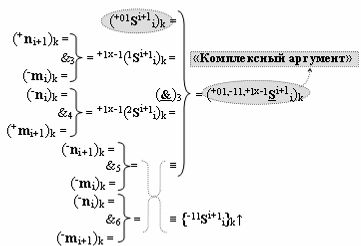
и с выходной логической функцией f3(}&)-ИЛИ-НЕ и входными логическими функциями f3(&)-И, f4(&)-И, f5(&)-И и f6(&)-И, в которой «+Комплексный аргумент» (+01Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
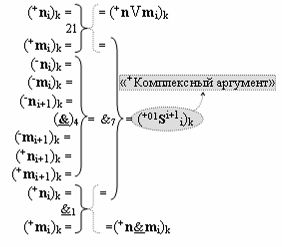
с входными логическими функциями f21(})-ИЛИ, f4(}&)-ИЛИ-НЕ и f1(&)-И-НЕ и выходной логической функцией f7(&)-И;
а в систему входных логических функций f11(})-ИЛИ - f20(})-ИЛИ «Условно отрицательного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i+1» разряда», сформированных в соответствии с математической моделью вида
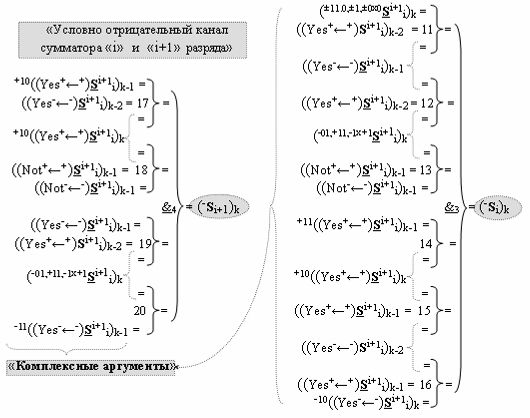
включены «Комплексные аргументы», которые являются общими аргументами с «Положительным каналом сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
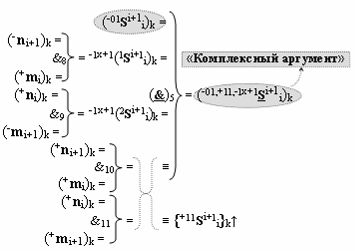
с выходной логической функцией f5(}&)-ИЛИ-НЕ и входными логическими функциями f8(&)-И, f9(&)-И, f10(&)-И и f11(&)-И, в которой «-Комплексный аргумент» (-01Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f22(})-ИЛИ, f6(}&)-ИЛИ-НЕ и f2(&)-И-НЕ и выходной логической функцией f12(&)-И;
при этом «Комплексные аргументы» в выходных функциональных структурах, которые реализованы в соответствии с математической моделью «Положительного канала сумматора «i+1» и «i» разряда» и математической моделью «Условно отрицательного канала сумматора «i+1» и «i» разряда», сформированы посредством следующих функциональных структур:
▶ «±Комплексный аргумент» (±11.0,±1,±0х0Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f13(&)-И, f14(&)-И, f15(&)-И, f16(&)-И и выходной логической функцией f7(}&)-ИЛИ-НЕ, в которой «±0Комплексный аргумент» (±0х0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
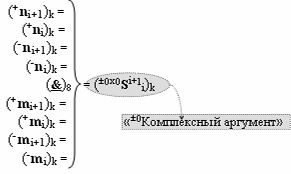
с входной логической функцией f8(}&)-ИЛИ-НЕ, «+Комплексный аргумент» (+n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f17(&)-И, а «-Комплексный аргумент» (-n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
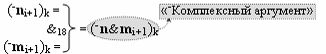
с выходной логической функцией f18(&)-И;
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
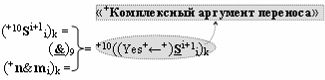
с выходной логической функцией f9(}&)-ИЛИ-НЕ, в которой «+Комплексный аргумент» (+10Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
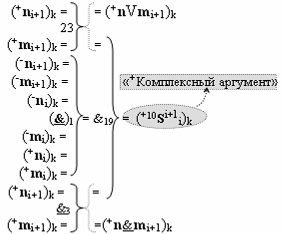
с входными логическими функциями f23(})-ИЛИ, f1(}&)-ИЛИ-НЕ и f3(&)-И-НЕ и выходной логической функцией f19(&)-И, а «+Комплексный аргумент» (+n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
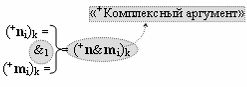
с выходной логической функцией f1(&)-И;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f10(}&)-ИЛИ, в которой «-Комплексный аргумент» (-10Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
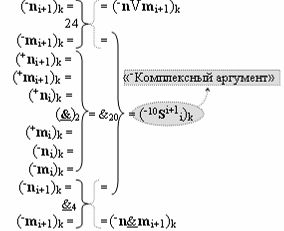
с входными логическими функциями f24(})-ИЛИ, f2(}&)-ИЛИ-НЕ и f4(&)-И-НЕ и выходной логической функцией f20(&)-И, а «-Комплексный аргумент» (-n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
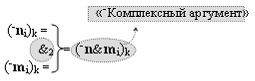
с выходной логической функцией f2(&)-И;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f11(}&)-ИЛИ-НЕ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f12(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
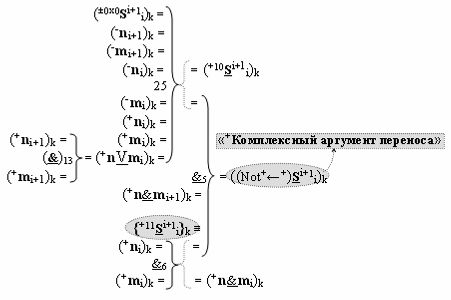
с входными логическими функциями f13(}&)-ИЛИ-НЕ, f25(})-ИЛИ и f6(&)-И-НЕ и с выходной логической функцией f5(&)-И-НЕ, в которой «+Комплексный аргумент» {+11Si+1 i}k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
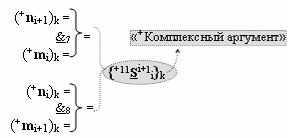
с входными логическими функциями f7(&)-И-НЕ и f8(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
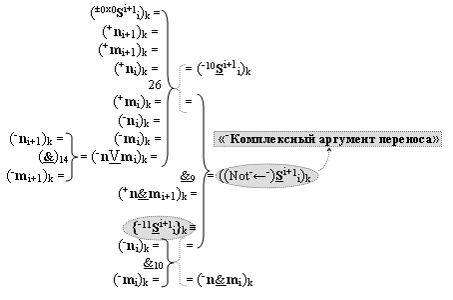
с входными логическими функциями f14(}&)-ИЛИ-НЕ, f26(})-ИЛИ и f10(&)-И-НЕ и с выходной логической функцией f9(&)-И-НЕ, в которой «-Комплексный аргумент» (-11Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
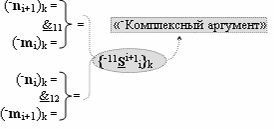
с входными логическими функциями f11(&)-И-НЕ и f12(&)-И-НЕ;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
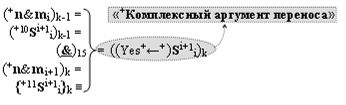
с выходной логической функцией f15(}&)-ИЛИ-НЕ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f16(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
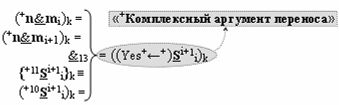
с выходной логической функцией f13(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
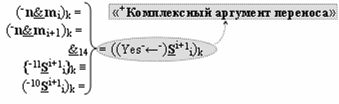
с выходной логической функцией f14(&)-И-НЕ.
Вариант 5. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), включающая «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации», включающие выходную структуру логических функций, которая реализована в соответствии с математической моделью вида
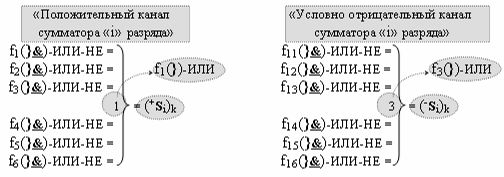
и с входными логическими функциями f1(}&)-ИЛИ-НЕ - f6(}&)-ИЛИ-НЕ и с входными логическими функциями f11(}&)-ИЛИ-НЕ - f16(}&)-ИЛИ-НЕ, функциональные выходные связи (=) которых являются функциональными входными связями выходной логической функции f1(})-ИЛИ и f3(})-ИЛИ для активизации положительного аргумента суммы (+Si)k условно «i» разряда и для активизации условно отрицательного аргумента (-Si)k условно «i» разряда, при этом «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации» также включает функциональную входную структуру, сформированную в соответствии с математической моделью вида
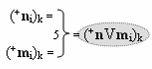
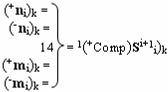
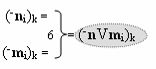
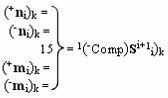
и с выходными логическими функциями f5(})-ИЛИ и f6(})-ИЛИ, функциональные входные связи которых являются функциональными входными связями для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», для активизации положительного «Комплексного аргумента» (+nVmi)k и условно отрицательного «Комплексного аргумента» (-nVmi)k, при этом «Положительный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
с выходными логическими функциями f21(}&)-ИЛИ-НЕ и f1(&)-И, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k условно «i» разряда «k» «Зоны минимизации» для активизации обобщенного «Комплексного аргумента» (+Comp)Si+1 i)k «Комплексного аргумента» (+n&mi)k, при этом «Положительный канал сумматора «i» разряда» также включает логическую функцию f22(}&)-ИЛИ-НЕ, а «Условно отрицательный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
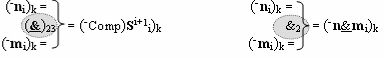
с выходными логическими функциями f4(}&)-ИЛИ-НЕ и f2(&)-И, функциональные входные связи которых являются функциональными входными связями сумматора для приема условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для активизации обобщенного «Комплексного аргумента» (-Comp)Si+1 i)k и «Комплексного аргумента» (-n&mi)k, при этом «Условно отрицательный канал сумматора «i» разряда» также включает логическую функцию f26(}&)-ИЛИ-НЕ, при этом в условно «k» «Зону минимизации» введены в соответствии с аналитическим выражением вида
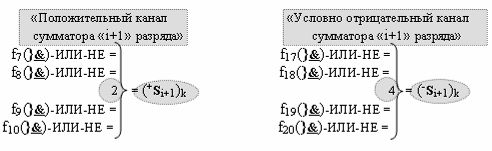
дополнительная структура логических функций с входными логическими функциями f7(}&)-ИЛИ-НЕ - f10(}&)-ИЛИ-НЕ, функциональные выходные связи которых являются функциональными входными связями логической функции f2(})-ИЛИ и которая активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда в «Положительном канале сумматора «i+1» разряда» и дополнительная структура логических функций с входными логическими функциями f17(}&)-ИЛИ-НЕ - f20(}&)-ИЛИ-НЕ, функциональные выходные связи которых являются функциональными входными связями логической функции f4(})-ИЛИ и которая активизирует условно отрицательный результирующий аргумент (-Si+1)k условно «i+1» разряда в «Условно отрицательном канале сумматора «i+1» разряда», при этом в систему входных логических функций f1(}&)-ИЛИ-НЕ - f10(}&)-ИЛИ-НЕ «Положительного канал сумматора «i» разряда» и «Положительного канал сумматора «i+1» разряда», которые реализованы в соответствии с математической моделью вида
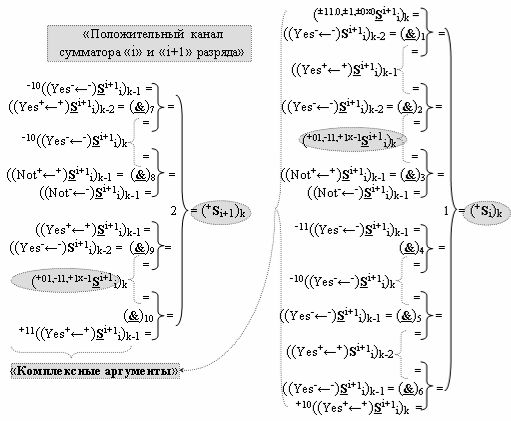
включены «Комплексные аргументы», которые также включены и в «Условно отрицательный канал сумматора «i+1» и «i» разряда», а также включен «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k с измененным уровнем аналогового сигнала и он является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
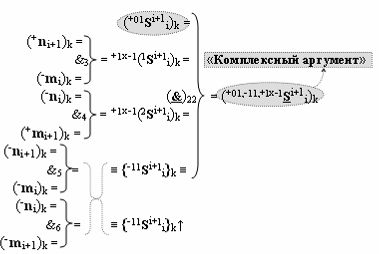
с выходной логической функцией f22(}&)-ИЛИ-НЕ и входными логическими функциями f3(&)-И, f4(&)-И, f5(&)-И и f6(&)-И, в которой «+Комплексный аргумент» (+01Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
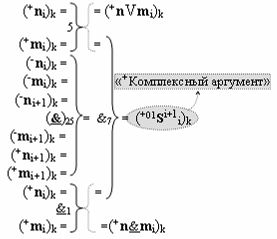
с входными логическими функциями f5(})-ИЛИ, f25(}&)-ИЛИ-НЕ и f1(&)-И-НЕ и выходной логической функцией f7(&)-И;
а в систему входных логических функций f1(})-ИЛИ - f10(})-ИЛИ «Условно отрицательного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i+1» разряда», сформированных в соответствии с математической моделью вида
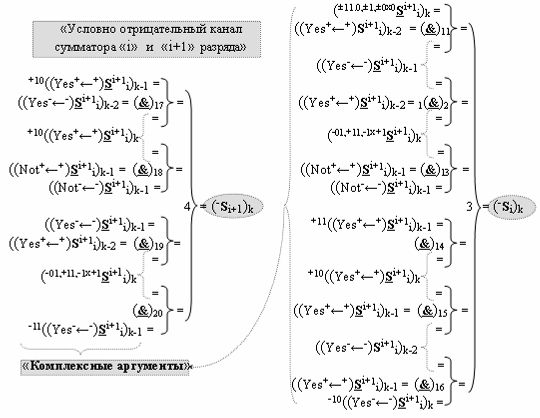
включены «Комплексные аргументы», которые являются общими аргументами с «Положительным каналом сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
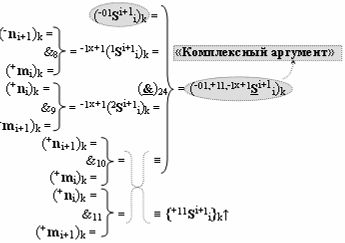
с выходной логической функцией f24(}&)-ИЛИ-НЕ и входными логическими функциями f8(&)-И, f9(&)-И, f10(&)-И и f11(&)-И, в которой «-Комплексный аргумент» (-01Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
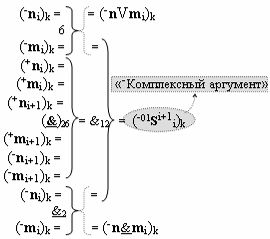
с входными логическими функциями f6(})-ИЛИ, f21(}&)-ИЛИ-НЕ и f2(&)-И-НЕ и выходной логической функцией f12(&)-И;
при этом «Комплексные аргументы» в выходных функциональных структурах, которые реализованы в соответствии с математической моделью «Положительного канала сумматора «i+1» и «i» разряда» и математической моделью «Условно отрицательного канала сумматора «i+1» и «i» разряда», сформированы посредством следующих функциональных структур:
▶ «±Комплексный аргумент» (±11.0,±1,±0х0Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
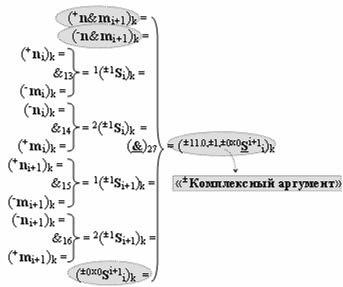
с входными логическими функциями f13(&)-И, f14(&)-И, f15(&)-И, f16(&)-И и выходной логической функцией f27(}&)-ИЛИ-НЕ, в которой «+Комплексный аргумент» (+n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
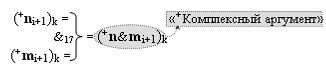
с выходной логической функцией f17(&)-И, «-Комплексный аргумент» (-n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
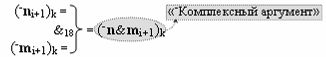
с выходной логической функцией f18(&)-И, а «±0Комплексный аргумент» (±0х0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
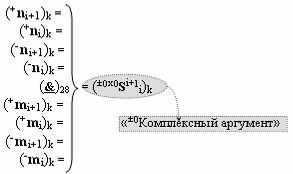
с входной логической функцией f28(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
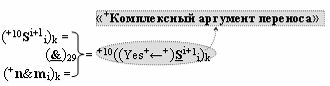
с выходной логической функцией f29(}&)-ИЛИ-НЕ, в которой «+Комплексный аргумент» (+10Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
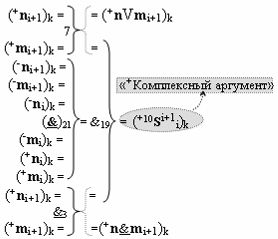
с входными логическими функциями f7(})-ИЛИ, f21(}&)-ИЛИ-НЕ и f3(&)-И-НЕ и выходной логической функцией f19(&)-И, а «+Комплексный аргумент» (+n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
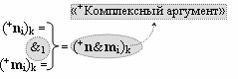
с выходной логической функцией f1(&)-И;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
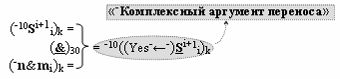
с выходной логической функцией f30(}&)-ИЛИ, в которой «-Комплексный аргумент» (-10Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
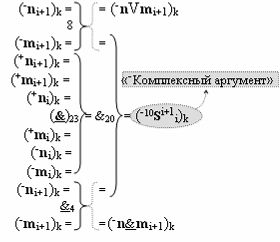
с входными логическими функциями f8(})-ИЛИ, f23(}&)-ИЛИ-НЕ и f4(&)-И-НЕ и выходной логической функцией f20(&)-И, а «-Комплексный аргумент» (-n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
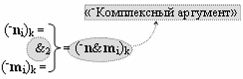
с выходной логической функцией f2(&)-И;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
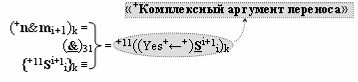
с выходной логической функцией f31(}&)-ИЛИ-НЕ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
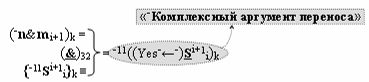
с выходной логической функцией f32(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
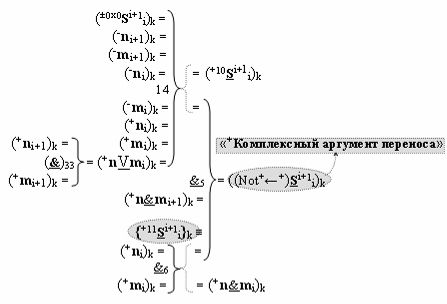
с входными логическими функциями f33(}&)-ИЛИ-НЕ, f14(})-ИЛИ и f6(&)-И-НЕ и с выходной логической функцией f5(&)-И-НЕ, в которой «+Комплексный аргумент» {+11Si+1 i}k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
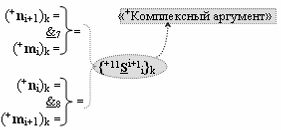
с входными логическими функциями f7(&)-И-НЕ и f8(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
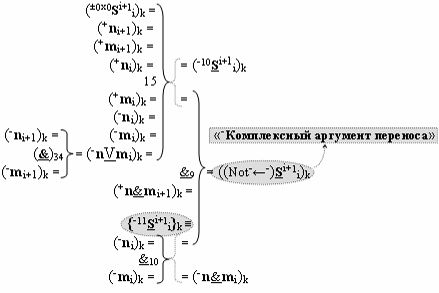
с входными логическими функциями f34(}&)-ИЛИ-НЕ, f15(})-ИЛИ и f10(&)-И-НЕ и с выходной логической функцией f9(&)-И-НЕ, в которой «-Комплексный аргумент» (-11Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
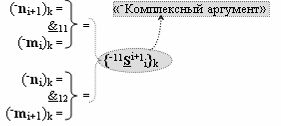
с входными логическими функциями f11(&)-И-НЕ и f12(&)-И-НЕ;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
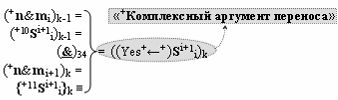
с выходной логической функцией f34(}&)-ИЛИ-НЕ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f35(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
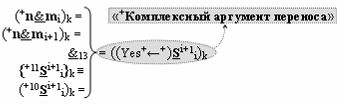
с выходной логической функцией f13(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
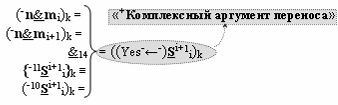
с выходной логической функцией f14(&)-И-НЕ.
Сущность логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) с процедурой одновременного преобразования аргументов аналоговых сигналов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1) и ее различных вариантов функциональных структур будет пояснена в процессе синтеза математических моделей предложенного технологического решения.
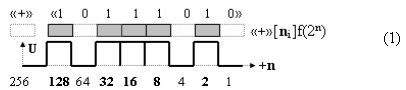
Предварительный анализ возможности формирования логико-динамического процесса преобразования условно минимизированных структур аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(+←←↓-) с процедурой одновременного преобразования аргументов посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1). Если проанализировать на формализованном уровне позиционную структуру положительных активных аргументов слагаемых «+»[ni]f(2n) в виде формализованного выражения (1)
и позиционную структуру условно отрицательных аргументов слагаемых «-»[mi]f(2n) в виде формализованного выражения (2),
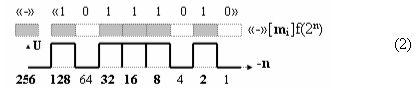
то по уровню аналогового сигнала «+»[Ui], за исключением аргумента знака «+» и «-» они эквивалентны. Поэтому выполнение каких либо арифметических действий над аргументами слагаемых «+»[ni]f(2n) и «-»[mi]f(2n) на формализованном уровне вызывает определенную проблему, которая связана с необходимостью учета знакового разряда «+» и «-», и он в данной ситуации представляет собой какой-то символ или «метку» о принадлежности структуры одной или другой категории информационного содержания. И только позиционное положение может исключить неоднозначность, поэтому положительная структура аргументов слагаемого (1) может быть записана в виде выражения (3),
а условно отрицательная структура аргументов слагаемого (2) может быть записана в виде выражения (4)
и только в такой интерпретации не только исключается необходимость введения в выражениях (1) и (2) дополнительных символов «+» и «-», но и возникает возможность выполнения арифметических действий над аргументами без перевода структуры аргументов «-»[mi]f(+/-) в так называемый «Дополнительный код». При этом следует особо отметить, что если структуру аргументов (4) перевести в «Дополнительный код», а эту арифметически корректно можно реализовать только с применением арифметических аксиом троичной системы счисления f(+1,0,-1) (5),
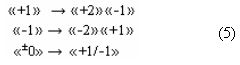
к которым относится и процедура логического дифференцирования ±d/dn как условно отрицательной последовательности активных аргументов, так и положительной последовательности аргументов, которую запишем в виде графоаналитического выражения (6).
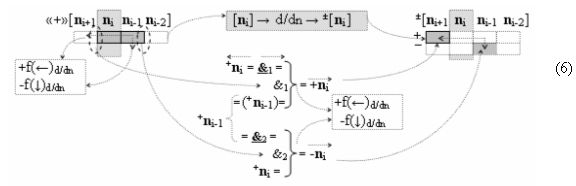
И она, по существу, представляет собой процедуру предварительного введения сквозного переноса, но выполняется на локальном уровне, в котором логическая функция f1(&)-И формирует положительный аргумент +ni локального переноса +f(←)d/dn активного аргумента из предыдущего старшего разряда непрерывной последовательности в последующий неактивный старший разряд. А логическая функция f2(&)-И формирует условно отрицательный аргумент -ni локального переноса -f(↓)d/dn, и этот перенос выполняется в условно «i» разряде, который соответствует младшему аргументу непрерывной последовательности, и при его переносе положительный аргумент преобразуется в условно отрицательный аргумент. При этом следует отметить, что применение арифметических аксиом троичной системы счисления f(+1,0,-1) (5) позволяют на научно обоснованном уровне выполнять любые процедуры преобразования аргументов, например процедуру формирования «Дополнительного кода» можно записать в виде графоаналитического выражения (7),
в котором неактивные аргументы после первого активного условно отрицательного аргумента в исходной структуре «-»[mi]f(+/-) преобразуют в соответствии с арифметической аксиомой «±0» → «+1/-1» и выполняют процедуру логического дифференцирования d/dn условно отрицательных аргументов. В результате формируется позиционно-знаковая структура «-/+»[mi]f(+/-) с тем же информационным содержанием «-»«186», но с максимальным числом положительных аргументов в младших разрядах, число которых может быть минимизировано, и в данной ситуации с применением процедуры логического дифференцирования d/dn положительных аргументов в структуре, которая выполняется в соответствии с графоаналитическим выражением (8).
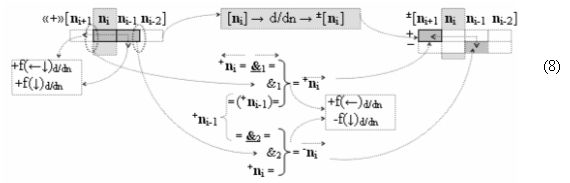
И она, по существу, представляет собой процедуру предварительного введения сквозного переноса, но выполняется на локальном уровне, в которой логическая функция f1(&)-И формирует положительный аргумент +ni локального переноса +f(←)d/dn активного аргумента из предыдущего старшего разряда непрерывной последовательности в последующий неактивный старший разряд. А логическая функция f2(&)-И формирует условно отрицательный аргумент -ni локального переноса -f(↓)d/dn, и этот перенос выполняется в условно «i» разряде, который соответствует младшему аргументу непрерывной последовательности, и при его переносе положительный аргумент преобразуется в условно отрицательный аргумент. И если применить процедуру логического дифференцирования d/dn, но только к последовательности как минимум двух активных аргументов в результирующей структуре «-/+»[mi]f(+/-) выражения (7), то может быть записано графоаналитическое выражение (9),
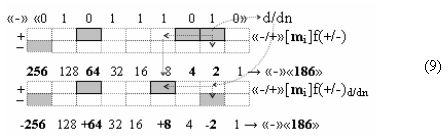
в котором активные как положительные аргументы, так и условно отрицательные аргументы чередуются как минимум через один не активный аргумент. В результате применения арифметической аксиомы «±0» → «+1/-1» и выполнения процедуры логического дифференцирования d/dn позиционную систему счисления «+»f(2n) положительных аргументов (10)
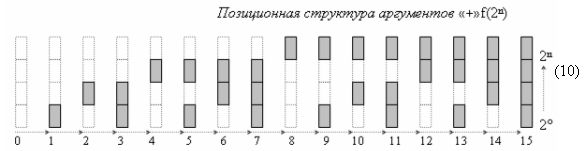
можно преобразовать в минимизированную систему счисления «+»f(+/-)min (11)
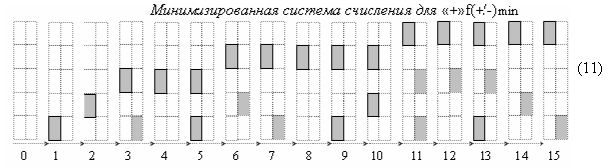
и такие структуры аргументов позволяет существенно повысить быстродействие процедуры умножения. Поскольку первый этап суммирования частичных произведений, если записать процедуру параллельно-последовательного умножения fΣ(Σ) в виде графоаналитического выражения (12),
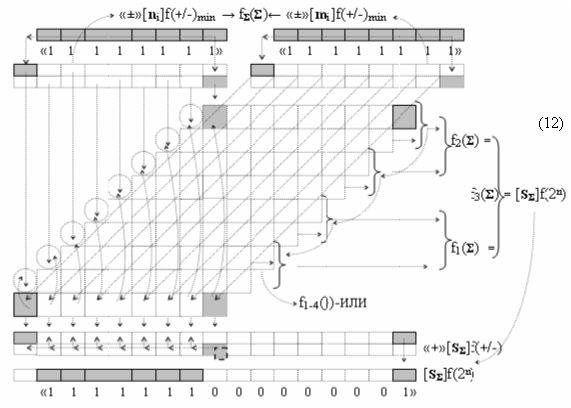
то становится вполне корректная возможность замены первого уровня функциональных структур сумматоров f1(Σ) - f4(Σ) на соответствующие последовательности логических функций f1-4(})-ИЛИ. А для того, чтобы сформировать минимизированную структуру результирующей суммы «+»[SΣ]f(+/-)min достаточно выполнить перенос двух активных условно отрицательных аргументов в условно «i» разряде в соответствии с графоаналитическим выражением (13).
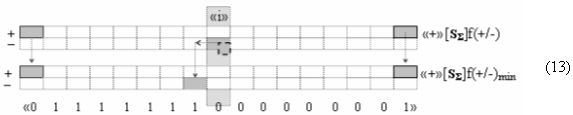
Поскольку в графоаналитическом выражении (12) первый этап суммирования сводится к объединению групп частичных произведений посредством логической функции f1(})-ИЛИ, то, например, 16-разрядный параллельно последовательный умножитель fΣ(Σ) преобразуется в 8-разрядный, что, как минимум, приводит к уменьшению технологического цикла умножения в два раза. А поскольку процессор преобразования аргументов в параллельно-последовательном умножителе fΣ(Σ) включает функциональную структуру сумматора f(Σ), поэтому имеет смысл проанализировать и технологический цикл преобразования в нем, но не в том, в котором все действия над аргументами слагаемых «+»[ni]f(+/-) и «+»[mi]f(+/-) выполняются по «Правилам», по которым процедуру, например, суммирования аргументов слагаемых с одинаковыми знаками «+»[ni]f(2n) → «10111010» и «+»[mi]f(2n) → «10101101» можно записать посредством графоаналитического выражения (12),
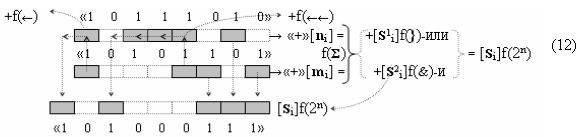
а по арифметическим аксиомам (5). И если проанализировать процедуру преобразования, например, аргументов слагаемых с разными знаками «+»[ni]f(2n) → «101000111» и «-»[mi]f(2n) → «010001101» в графоаналитическом выражении(13),
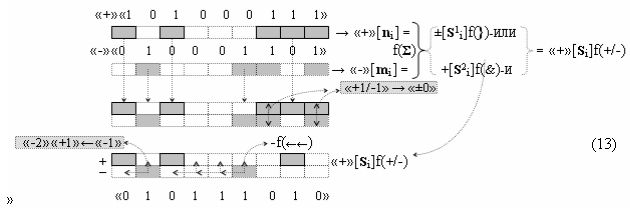
в которой выполнена только процедура удаления активного логического нуля «+1/-1» → «±0», то в результате преобразования аргументов или их минимизации формируется результирующая позиционно-знаковая сумма «+»[Si]f(+/-). При этом следует отметить, что если в выражении (12) очередная процедура суммирования результирующей суммы [Si]f(2n) невозможна без выполнения сквозного переноса +f(←←), то в выражении (13) сквозной перенос -f(←←) условно отрицательного аргумента может быть отложен, который выполняется в соответствии с арифметической аксиомой «-1» → «-2»«+1» . Поскольку при очередной процедуре суммирования условно отрицательные аргументы не реализованных переносов могут сформировать активные логические нули «+1/-1» → «±0» с активными положительными аргументами очередного слагаемого. При этом следует также отметить, что особенностью результирующей суммы «+»[Si]f(+/-) в выражении (13) является то, что она может быть минимизирована по числу активных аргументов в своей структуре с применением обратной арифметической аксиомы «-2»«+1» → «-1», и эту процедуру можно записать в виде графоаналитического выражения (14).
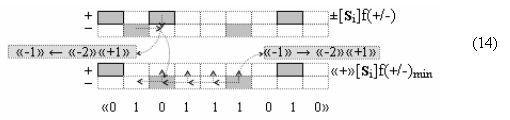
И если совместить позиционную структуру аргументов «+»[Si]f(2n) → «10111010» с минимизированной позиционно-знаковой структурой аргументов «+»[Si]f(+/-)min в выражении (15),
то можно констатировать, что она была сформирована с применением арифметической аксиомы «0» → «+1/-1» троичной системы счисления f(+1,0,-1) (5) и процедуры логического дифференцирования d/dn. В результате логико-динамический процесс формирования положительно минимизированной структуры аргументов «+»[Si]f(+/-)min может быть записан в виде графоаналитического выражения (16),
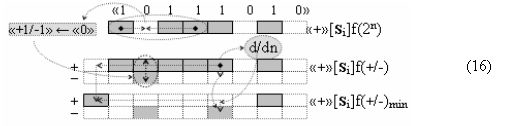
а логико-динамический процесс формирования условно отрицательной структуры аргументов «-»[ni]f(+/-)min можно быть записан в виде графоаналитического выражения (17).
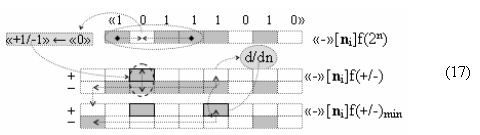
А функциональную структуру этой процедуры логического дифференцирования d/dn для положительных и условно отрицательных позиционно-знаковых аргументов ±[ni]f(+/-) после объединения функциональных структур (6) и (8) посредством логической функции f1(})-ИЛИ и f2(})-ИЛИ можно записать в виде аналитических выражений (18) и (19).
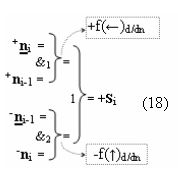
В результате аналитические выражения (17) и (18) являются математическими моделями условно «i» разряда процедуры логического дифференцирования d/dn как структуры с одним активным аргументом «010», так и структуры с непрерывной последовательностью активных аргументов «0111…10». Но если вернуться к анализу логико-динамического процесса преобразования аргументов в выражении (16), записав его в виде графоаналитического выражения (20),
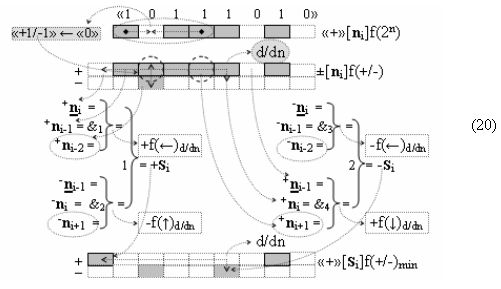
то процедура логического дифференцирования d/dn (18) и (19) должна включать дополнительные условия активности предыдущего аргумента +ni-2 и -ni-2 в системе логических функций f1(&)-И и f3(&)-И, а также дополнительные условия активности последующего аргумента -ni+1 и +ni+1 и система логических функций f2(&)-И и f4(&)-И, что позволяет исключить из процедуры логического дифференцирования d/dn структуры «010» как положительных аргументов, так и условно отрицательных аргументов. Но в этой ситуации с одной стороны активные аргументы структуры «010» как положительных аргументов, так и условно отрицательных аргументов должны быть результирующими аргументами. Поэтому введем в аналитическое выражение (20) функциональные дополнительные структуры и запишем графоаналитическое выражение (21),
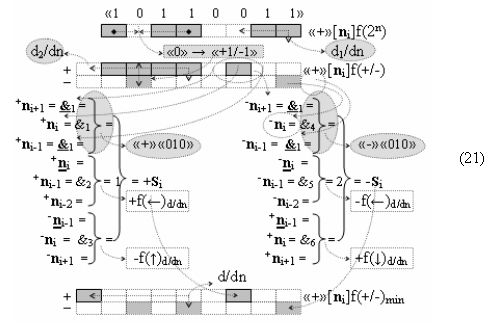
в котором введены логические функции f1(&)-И и f4(&)-И в систему логической функции f1(})-ИЛИ и f2(})-ИЛИ и их результирующие аргументы +Si и -Si активизируются и в том случае, если активны логические функции f1(&)-И и f4(&)-И. При этом из анализа логико-динамического процесса преобразования аргументов (19) следует, что логические функции f1(})-ИЛИ и f2(})-ИЛИ должны активизироваться не только когда в структуре «+»[ni]f(+/-) сформирована последовательность активных и неактивных аргументов, но и в случае активизации неактивных аргументов посредством применения арифметической аксиомы «0» → «+1/-1», а условно отрицательный аргумент в данной конкретной ситуации также является результирующим аргументом. Следует также отметить, что с одной стороны как процедура логического дифференцирования d2/dn с активизацией аргумента структуры «010», так и активизация неактивных аргументов в структуре «01011» должны выполняться в выражении (21) одновременно, поскольку их преобразованные аргументы являются аргументами результирующей минимизированной структуры «+»[Si]f(+/-)min. С другой стороны на первом этапе перед применением процедуры логического дифференцирования d2/dn в исходной структуре «+»[ni]f(2n) должны быть активизированы неактивные аргументы, которые чередуются с активными аргументами, но при условии, что первый неактивный аргумент «0» позиционно расположен после как минимум двух последовательно активных аргументов «11» как, например, в выражении (22).
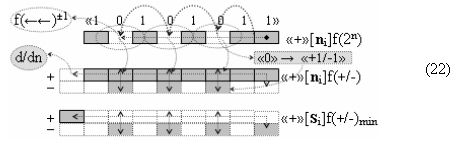
И такая активизация неактивных аргументов «0» → «+1/-1», по существу, представляет собой сквозную активизацию f(←←)±1, которая в какой-то степени соответствует сквозному переносу f(←←) при выполнении процедуры суммирования аргументов слагаемых «+»[ni]f(2n) и «+»[mi]f(2n), но имеет особенность. И эта особенность заключается в том, что сквозная активизация f(←←)±1 имеет две реализации при условии, если аргументы «+»[ni]f(2n) функционально разделить на группы, в которые входили бы только два последовательных аргумента. В результате такого деления структуры аргументов «+»[ni]f(2n) могут быть сформированы две функциональные структуры сквозной активизации f1(←←)±1 и f2(←←)±1, например, для выражения (22) логико-динамический процесс сквозной активизации f1(←←)±1 может быть записан в виде графоаналитического выражения (23),
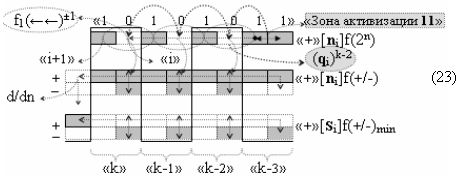
в котором аргумент (qi)k-2 сквозной активизации f1(←←)±1 неактивных аргументов «0» → «+1/-1» формируется в условно «i» разряде «k-2» группы «Зоны активизации 11». А для структуры, например, аргументов «+»[ni]f(2n) → «01010110» логико-динамический процесс сквозной активизации f2(←←)±1 неактивных аргументов 0» → «+1/-1» может быть в графоаналитическом выражении (24),
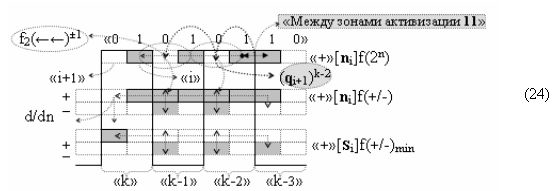
в котором аргумент (qi+1)k-2 сквозной активизации f2(←←)±1 формируется «Между зонами активизации 11» в условно «i+1» разряде «k-2» группы. И если записать математическую модель формирования аргумента ±1(←)kqi сквозной активизации f1(←←)±1 и аргумента ±1(←)kqi+1 сквозной активизации f2(←←)±1 для положительной структуры аргументов «+»[ni]f(2n) → «10110111» в виде графоаналитического выражения (25),
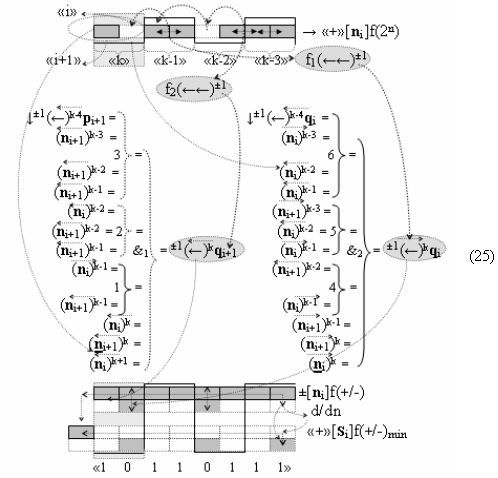
то из него следует, что технологический цикл ΔtΣ для 8-разрядной структуры позиционных аргументов [ni]f(2n) будет соответствовать
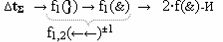
двум условным логическим функциям f(&)-И. При этом, если проанализировать логику формирования функциональной, например, сквозной активизации f2(←←)±1, записав ее в виде графоаналитического выражения (26) и (27),
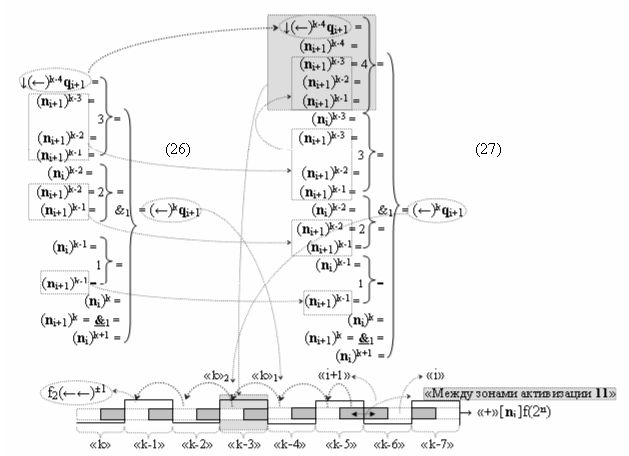
то из нее следует, что с каждой последующей дополнительной «k» группой аргументов должна быть введена дополнительная логическая функция f4(})-ИЛИ, в которой помимо входных аргументов (ni+1)k - (ni+1)k-3 условно «i» разряда логической функции f4(})-ИЛИ должен быть введен дополнительный аргумент (ni+1)k-4 условно «i+1» разряда «k-4» группы. При этом из системы логической функции f3(})-ИЛИ выражения (26) аргумент активизации ↓(←)k-4qi+1 уменьшают на единицу и вводят в систему дополнительной логической функции f4(})-ИЛИ выражения (27), а вместо него в системе логической функции f3(})-ИЛИ вводят входной аргумент (ni)k-4 условно «i» разряда «k-4» группы. В результате для 16-разрядной структуры позиционных аргументов [ni]f(2n) в системе логической функции f1(&)-И должно быть включено четыре дополнительных логических функций f5-8(})-ИЛИ, в последней из которых система будет включать восемь входных аргументов. Поэтому технологический цикл ΔtΣ функциональной структуры активизации f1(←←)±1 и f2(←←)±1 процедуры преобразования позиционной структуры аргументов «+»[ni]f(2n) в минимизированную позиционно-знаковую структуру аргументов «+»[Si]f(+/-)min для 32-разрядной структуры [ni]f(2n) будет соответствовать
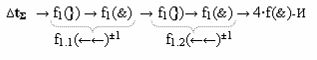
четырем условным логическим функциям f(&)-И. В результате может быть сформирована функциональная 32-разрядная параллельная структура сумматора ±f(Σ)min. При этом следует особо отметить, что минимизированные структуры позиционно-знаковых аргументов сомножителей ±[ni]f(+/-)min и ±[mi]f(+/-)min в параллельно-последовательном умножителе ±fΣ(Σ)min также позволяют существенно сократить и его технологический цикл формирования результирующей суммы. Поскольку если для конкретной реализации аргументов сомножителей ±[ni]f(+/-)min → «11101011»f(2n) и ±[mi]f(+/-)min → «11010111»f(2n) записать процедуру формирования частичных произведений в параллельно-последовательном умножителе ±fΣ(Σ)min в виде графоаналитического выражения (28),
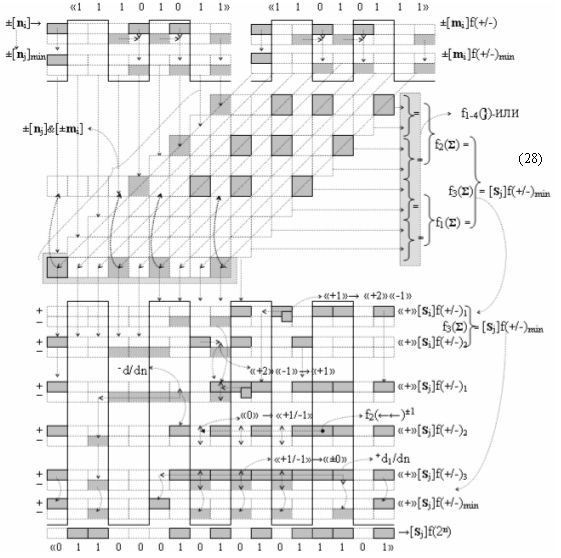
то первый уровень суммирования аргументов частичных произведений может быть реализован посредством линейных логических функций f1-4(})-ИЛИ, что приведет к существенному сокращению технологического цикла ΔtΣ в параллельно-последовательном умножителе ±fΣ(Σ)min. При этом во втором уровне сумматоров f1(Σ) и f2(Σ) все преобразования активных аргументов выполняют как в «Зонах минимизации», как это было реализовано в графоаналитическом выражении (29), так и между «Зонами минимизации», как эта процедура реализована в графоаналитическом выражении (30).
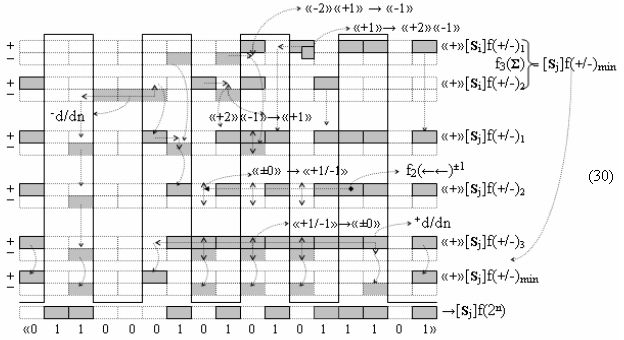
И все преобразования аргументов выполняются в соответствии с прямыми аксиомами, например, «+1»→ «+2»«-1», «-1» → «-2»«+1» и «+1/-1»→«±0» и обратными арифметическими аксиомами, например, «+2»«-1»→«+1», «-2»«+1» → «-1» и «0» → «+1/-1», а также с применением процедуры логического дифференцирования -d/dn и +d/dn последовательностей активных условно отрицательных аргументов и положительных аргументов. При этом особенностью логико-динамических процессов преобразования аргументов в сумматоре f3(Σ) как в выражении (29), так и в выражении (30) является процедура сквозной активизации f2(←←)±1 неактивных аргументов «±0» → «+1/-1» при минимизации структуры аргументов «+»[Sj]f(+/-)2, которая, по существу, эквивалентна сквозному переносу f(←←) в позиционном сумматоре. Поскольку если сформировать графоаналитическое выражение для 32-разрядного сумматора,
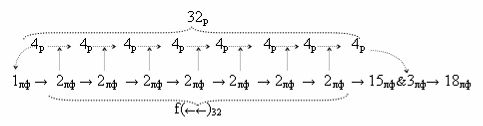
то последовательность условных логических функций f(&)-И в логико-динамическом процессе ускоренного сквозного переноса f(←←)32 будет соответствовать 1лф&14лф→ 15лф, когда как в процедуре сквозной активизации f2(←←)±1 неактивных аргументов «±0» → «+1/-1» выражения (26) и (27) последовательность условных логических функций f(&)-И будет соответствовать 1лф&4лф→ 5лф. А если учесть, что технологический цикл tΣ в 8-разрядном комбинационном умножителе fΣ(Σ) включает 14·fп(Σ) полных сумматоров, а каждый из них эквивалентен 6лф, то он будет соответствовать 94лф. В результате, если выполнить замену позиционных структур аргументов сомножителей [ni]f(2n) и [mi]f(2n) в умножителе fΣ(Σ) на минимизированные структуры аргументов сомножителей ±[ni]f(+/-)min и ±[mi]f(+/-)min, то быстродействие его может быть увеличено как минимум на порядок. И это обстоятельство формирует необходимость в синтезе математической модели сумматора ±f(Σ)min, реализующего процедуру преобразования минимизированных структур позиционно-знаковых аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min. При этом следует отметить, что в параллельно-последовательном умножителе ±fΣ(Σ)min графоаналитического выражения (28) минимизированные структуры позиционно-знаковых аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min были сформированы неформализованным методом, поскольку в структуре множимого ±[mi]f(+/-) активные аргументы были преобразованы между «Зонами минимизации», а в структуре аргументов множителя ±[ni] активные аргументы были преобразованы в «Зоне минимизации». И если выполнить эту процедуру неформализованным методом и записать процедуру формирования частичных произведений в параллельно-последовательном умножителе ±fΣ(Σ)min либо вида,
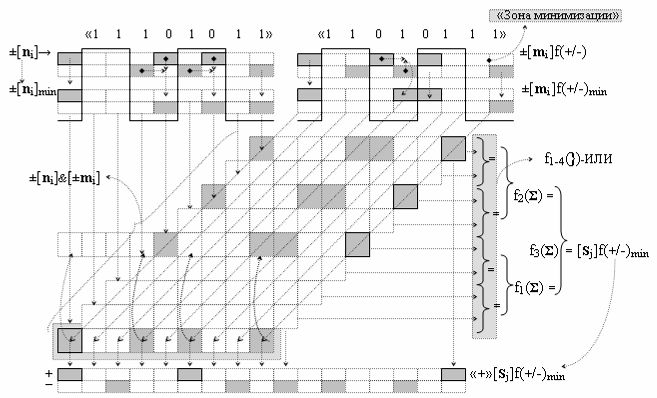
где преобразование структур аргументов сомножителей выполнено в «Зоне минимизации», либо формализованным методом, в котором преобразования аргументов сомножителей ±[ni]min и ±[mi]f(+/-) выполняют только между «Зонами минимизации», и эту процедуру запишем в виде графоаналитического выражения (32).
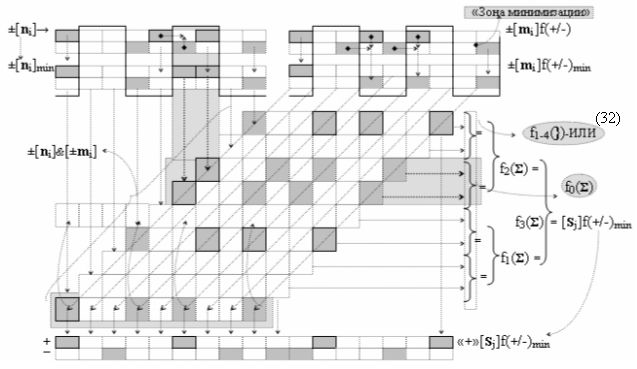
При этом следует отметить, что особенностью структуры аргументов множимого ±[ni]f(+/-)min является одновременная активность двух аргументов в «Зоне минимизации», и в этой ситуации входная структура сумматора f3(Σ) не может быть выполнена в виде системы логических функций f2(})-ИЛИ, поскольку необходима функциональная входная структура сумматора f0(Σ). Но если записать графоаналитическое выражение (33),
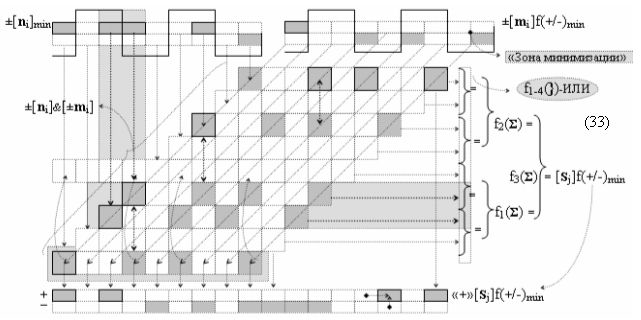
в котором последовательно активные аргументы позиционно расположены между «Зонами минимизации», то соответствующие частичные произведения функционально принадлежат двум разным группам логических функций f2(})-ИЛИ. Поэтому структуры аргументов множителя ±[ni]f(+/-)min перед формированием частичных произведений должны быть логически преобразованы, и это преобразование необходимо выполнять только в «Зонах минимизации». А если вернуться к логико-динамическому процессу (30) и записать его в виде графоаналитического выражения (34),
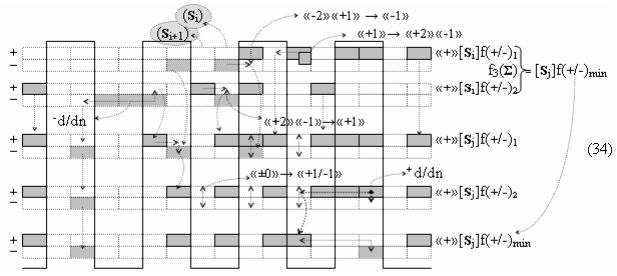
то, если с одной стороны при формировании промежуточной суммы не выполнять преобразования между «Зонами минимизации», а только в «Зонах минимизации», поскольку структура активных аргументов относится к условно минимизированной категории, а выполнять преобразования аргументов только в «Зонах минимизации» в соответствии с арифметическими аксиомами «+2»«-1»→«+1» и «-2»«+1» → «-1», то может быть сформирован корректный логико-динамический процесс преобразования частичных произведений в сумматоре f3(Σ). С другой стороны в промежуточной структуре суммы «+»[Sj]f(+/-)1 необходимо выполнять активизацию неактивных логических нулей «±0»→ «+1/-1» только в условно «i» разряде, поскольку если записать логико-динамический процесс преобразования аргументов (35),
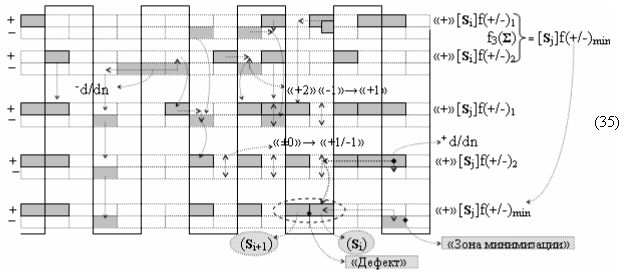
то в результате неактивизации неактивных логических нулей «±0» → «+1/-1» в условно «i» разряде результирующая структура аргументов будет сформирована с «Дефектом», поскольку в «Зоне минимизации» сформированы два последовательно активных аргумента. Но если записать графоаналитическое выражение (36)
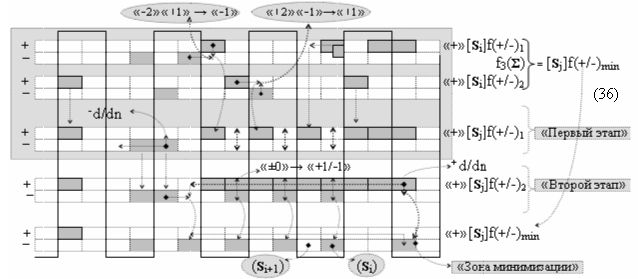
и активизировать неактивные логические нули «±0» → «+1/-1» в условно «i» разряде, то после выполнения процедуры логического дифференцирования +d/dn → f1(+←↓-)d/dn будет сформирована корректная условно минимизированная структура аргументов«+»[Sj]f(+/-)min. И все преобразования аргументов выполняются в соответствии с прямыми аксиомами, например, «+1»→ «+2»«-1», «-1» → «-2»«+1» и «+1/-1»→«±0» и обратными арифметическими аксиомами, например, «+2»«-1»→«+1», «-2»«+1» → «-1» и «0» → «+1/-1», а также с применением процедуры логического дифференцирования -d/dn и +d/dn последовательностей активных условно отрицательных аргументов и положительных аргументов. При этом особенностью логико-динамических процессов преобразования аргументов в сумматоре f3(Σ) как в выражении (29), так и в выражении (30) является процедура сквозной активизации f2(←←)±1 неактивных аргументов «±0» → «+1/-1» при минимизации структуры аргументов «+»[Sj]f(+/-)2, которая, по существу, эквивалентна сквозному переносу f(←←) в позиционном сумматоре. Поскольку если сформировать графоаналитическое выражение для 32-разрядного сумматора,
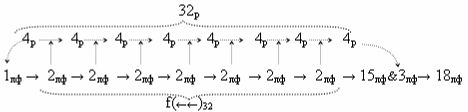
то последовательность условных логических функций f(&)-И в логико-динамическом процессе ускоренного сквозного переноса f(←←)32 будет соответствовать 1лф&14лф→ 15лф, когда как в процедуре сквозной активизации f2(←←)±1 неактивных аргументов «±0» → «+1/-1» выражения (26) и (27) последовательность условных логических функций f(&)-И будет соответствовать 1лф&4лф→ 5лф. А если учесть, что технологический цикл tΣ в 8-разрядном комбинационном умножителе fΣ(Σ) включает 14·fп(Σ) полных сумматоров, а каждый из них эквивалентен 6лф, то он будет соответствовать 94лф. В результате, если выполнить замену позиционных структур аргументов сомножителей [ni]f(2n) и [mi]f(2n) в умножителе fΣ(Σ) на минимизированные структуры аргументов сомножителей ±[ni]f(+/-)min и ±[mi]f(+/-)min, то быстродействие его может быть увеличено как минимум на порядок. И это обстоятельство формирует необходимость в синтезе математической модели сумматора ±f(Σ)min, реализующего процедуру преобразования минимизированных структур позиционно-знаковых аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min.
Синтез математической модели входного логико-динамического процесса преобразования условно минимизированных структур аргументов слагаемых «+»[ni]fRU(+/-)min и «+»[mi]fRU(+/-)min троичной системы счисления f(+1,0,-1)RU сумматора ±f1(ΣRU). Поскольку из предварительного анализа логико-динамического процесса преобразования минимизированных структур аргументов слагаемых «+»[ni]fRU(+/-)min и «+»[mi]fRU(+/-)min в сумматоре ±f1(ΣRU)min следует, что процедура формирования результирующей суммы «+»[Si]fRU(+/-)min в том же формате может быть реализована без функциональной структуры сквозного переноса ±f(←←). Поэтому проведем обобщающий анализ процедур преобразования активных аргументов и определимся с функциональной структурой сумматора ±f1(ΣRU)min, в которой особенностью является наличие в ней двух аналитических выражений условно «i+1» разряда и условно «i» разряда условно «k» «Зоны минимизации». А для этого запишем графоаналитическое выражение (37).
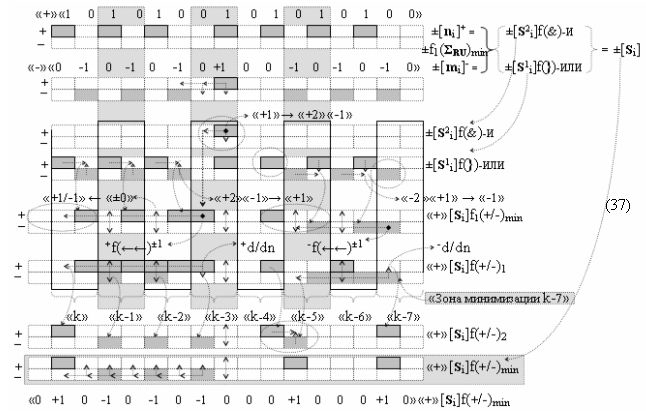
Из анализа процедуры преобразования аргументов на «Первом этапе» выражения (37) следует, что в условно «k» «Зоне минимизации» на предварительном этапе выполняют формирование аргументов второй предварительной суммы (±[S2 i]f(&)-И и аргументов первой предварительной суммы ±[S1 i]f(})-ИЛИ) и их активизируют посредством функциональных структур «Положительного канала суммирования», которые запишем в виде аналитических выражений (38),
а для «Условно отрицательного канала суммирования» запишем в виде аналитических выражений (39),
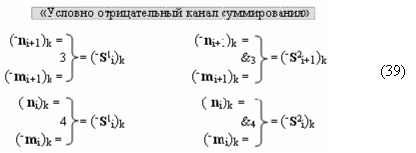
в результате формируем структуру аргументов (40).
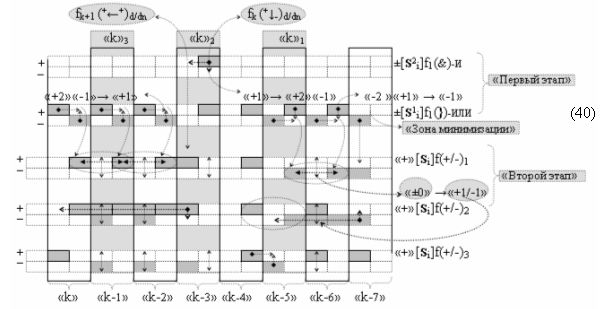
При этом следует отметить, что особенностью «Первого этапа» преобразования аргументов предварительной суммы (±[S2 i]f(&)-И и аргументов первой предварительной суммы ±[S1 i]f(})-ИЛИ) является преобразование только в «Зонах минимизации». Поскольку если сформировать логико-динамический процесс преобразования минимизированных аргументов слагаемых «+»[ni]fRU(+/-)min → «+»«0100110010110011» и «+»[mi]fRU(+/-)min → «+»«0110101101110100» в виде графоаналитического выражения (41)
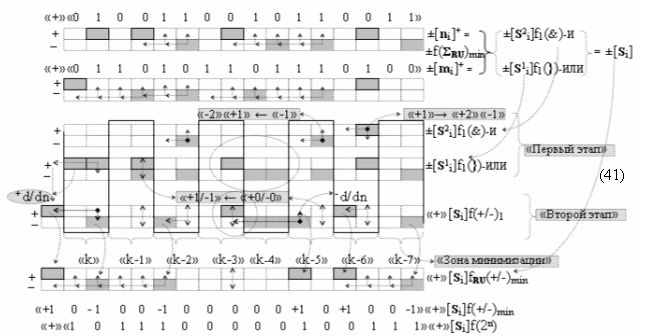
или минимизированных аргументов слагаемых «+»[ni]f(+/-)min → «+»«0010101001010110»f(2n) и «+»[mi]f(+/-)min → «+»«0011100100011010»f(2n) в виде графоаналитического выражения (42),
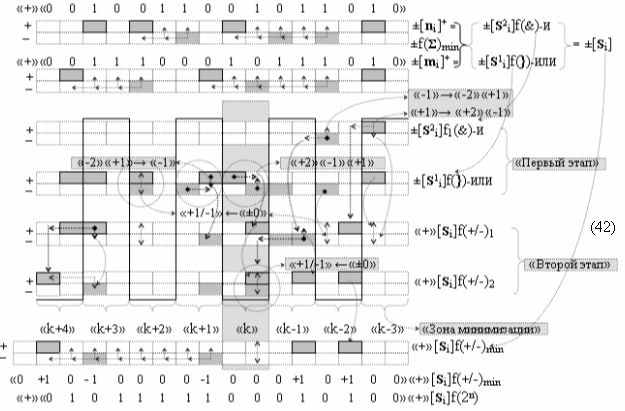
то такая процедура позволяет минимизировать число активных аргументов в «Зонах минимизации». Поскольку если преобразование аргументов в структуре второй промежуточной суммы ±[S2 i]f1(&)-И выполняется в соответствии с прямыми арифметическими аксиомами «+1» → «+2»«-1» и «-1» → «-2»«+1» с одновременным удалением активного логического нуля «+1/-1» → «±0», то преобразование аргументов в структуре первой промежуточной суммы ±[S1 i]f(})-ИЛИ выполняется в соответствии с обратными арифметическим аксиомам «+2»«-1» → «+1» и «-2»«+1» → «-1», что приводит также к минимизации числа активных аргументов в структуре аргументов «+»[Si]f(+/-)1. При этом если сформировать логико-динамический процесс преобразования минимизированных аргументов слагаемых «+»[ni]fRU(+/-)min → «+»«0100110010110011» и «+»[mi]fRU(+/-)min → «+»«01110001101 0100» в виде графоаналитического выражения (43),
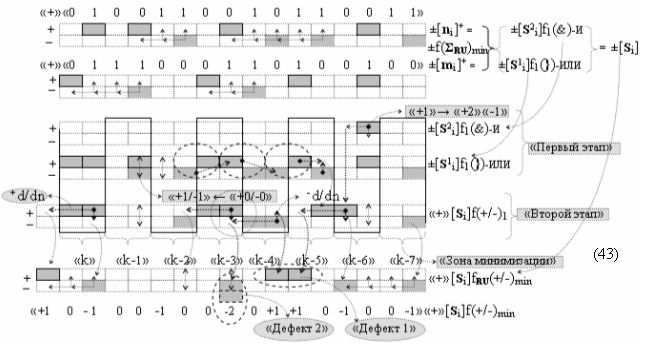
то из анализа результирующая сумма «+»[Si]fRU(+/-)min следует, что в ее структуре сформированы «Дефектом 1» и «Дефектом 2» непосредственно связаны с нереализованной процедурой преобразования активных аргументов между «Зонами минимизации». И эту процедуру преобразования необходимо выполнять для условно отрицательного аргумента в соответствии с графоаналитическим выражением (44)
при условии активности положительного одноименного аргумента S1 i в условно «k-1» «Зоне минимизации», при этом следует отметить, что в результате применения арифметической аксиомы «-2»«+1» → «-1» выполнен «Разрыв последовательности» положительных аргументов, что исключает формирование «Дефект 2» в выражении (43), и функциональную структуру такого преобразования запишем в виде аналитического выражения (45),
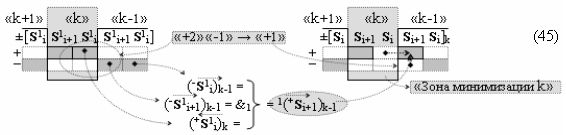
а для условно «k» «Зоны минимизации» его запишем в виде функциональной структуры (46).
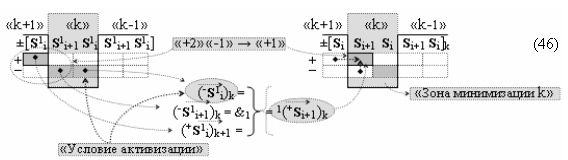
Аналогичную процедуру преобразования аргументов с применением арифметической аксиомы «-2»«+1» → «-1» запишем и для другой последовательности аргументов (47),
а для условно «k» «Зоны минимизации» функциональную структуру запишем в виде аналитического выражения (48).
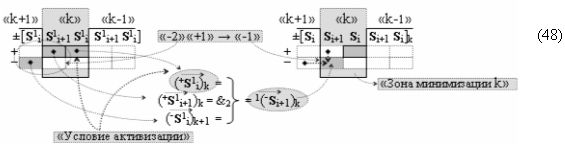
При этом следует отметить, что в системе логической функции f1(&)-И и f2(&)-И функциональных структур (46) и (48) введен дополнительный условно отрицательный аргумент (-S1 i)k и дополнительный положительный аргумент (+S1 i)k, который в соответствующей функциональной структуре является «Условием активизации» для исключения неоднозначности преобразования активных аргументов как в структуре аргументов (49),
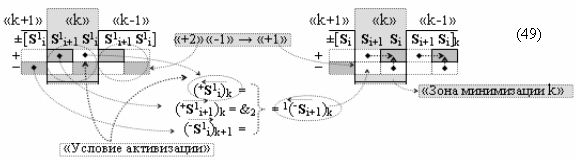
так и в структуре аргументов (50),
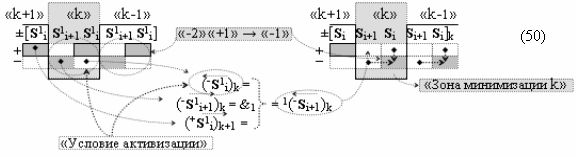
где преобразования аргументов посредством арифметических аксиом и выполняется в условно «k» «Зонах минимизации». И если с учетом логико-динамического процесса функциональных структур (48) и (50) скорректировать процедуру преобразования промежуточной структуры аргументов суммы в выражении (43), записав эту процедуру в виде графоаналитического выражения (51),
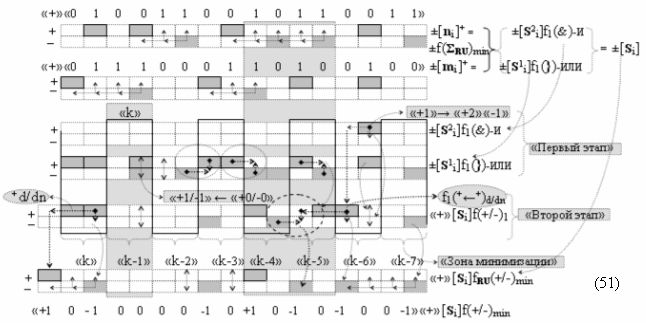
то на «Втором этапе» преобразования структуры аргументов промежуточной суммы «+»[Si]f(+/-)1 аргумент локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn в «k-5» «Зоне минимизации» может быть скорректирован. При этом преобразование в «k-4» «Зоне минимизации» должно выполняться в соответствии с арифметической аксиомой «+2»«-1» → «+1» при условии неактивности аргумента локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn в «k-4» «Зоне минимизации». При этом следует отметить, что корректировка структуры аргументов первой промежуточной суммы ±[S1 i]f1(})-ИЛИ в графоаналитическом выражении (51) может быть выполнена на этапе ее формирования, поскольку если записать графоаналитическое выражение (52),
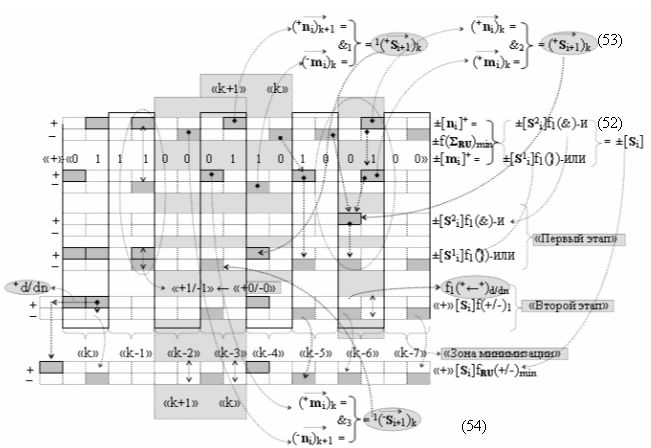
то предварительный анализ активности аргументов слагаемых ±[ni]+ и ±[mi]+, которые позиционно расположены между «Зонами минимизации», позволяет посредством функциональных структур (53), (54) существенно минимизировать промежуточную сумму ±[S1 i]f1(})-ИЛИ.
Из анализа графоаналитического выражения (52) следует, что удаление активных логических нулей «+1/-1» → «±0» в условно «k» «Зоне минимизации» выражения (55)
должно выполняться в «Зонах минимизации» косвенным образом при активизации аргументов промежуточной суммы ±[S1 i]f1(})-ИЛИ и такая процедура может быть реализована при преобразовании аргументов слагаемых ±[ni]+ и ±[mi]+. Аналогичная процедура должна быть реализована и при активизации активного аргумента второй промежуточной суммы ±[S2 i]f1(&)-И в соответствии с графоаналитическими выражениями (56)
или графоаналитическими выражениями (57).
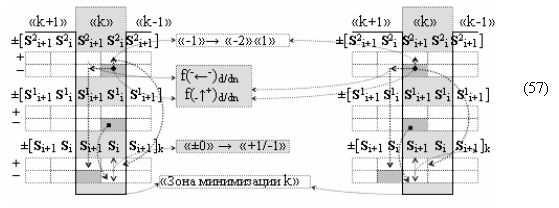
При этом особенностью аргумента локального переноса f(+←+)d/dn и f(-←-)d/dn в данной ситуации является реализация его посредством арифметической аксиомы «+1»→ «+2»«-1» и «-1» → «-2»«+1» и посредством функциональных структур (58),
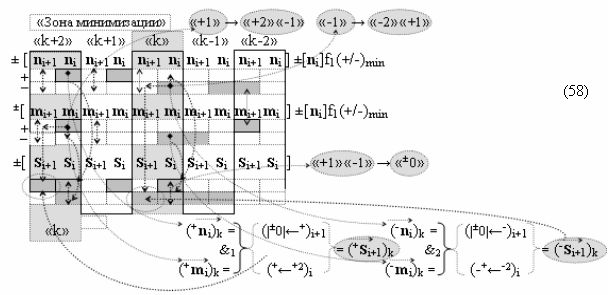
в которой функциональные структуры активизируют положительный результирующий аргумент (+Si+1)k и условно отрицательный результирующий аргумент (-Si+1)k в условно «i+1» разряде. При этом следует особо отметить логику формирования условно минимизированной структуры слагаемого ±[ni]f1(+/-)min и ±[ni]f1(+/-)min, в соответствии с которой, если в условно «k» «Зоне минимизации» одновременно активны аргументы слагаемых (+ni)k и (+mi)k или (-ni)k и (+mi)k, то в этой «Зоне минимизации» в условно «i+1» разряде должен быть неактивен логический ноль «±0i+1». Но если между «Зонами минимизации» одновременно активны аргументы слагаемых (+ni+1)k и (+mi+1)k или (-ni+1)k и (+mi+1)k, то преобразование этих аргументов неоднозначное и зависит от конкретной активности аргументов в условно «k+1» «Зоне минимизации». Поэтому функциональные аналогичные структуры, которые активизируют результирующий аргумент (+Si)k и (-Si)k условно «i+1» разряда в условно «k» «Зоне минимизации» запишем в виде аналитических выражений (59),
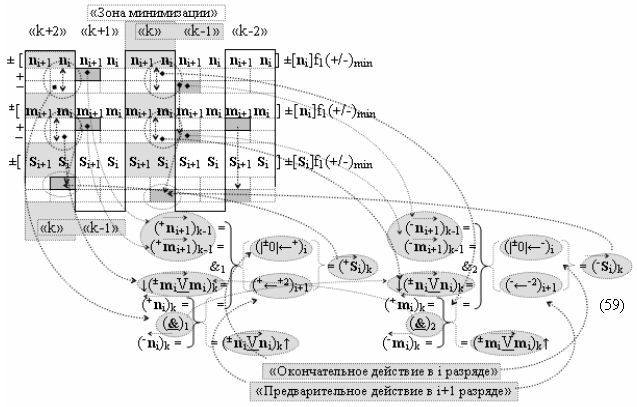
но в данной ситуации в систему логической функции f1(&)-И и f2(&)-И введены преобразованный аргумент (±niVmi)k и (±niVmi)k функциональной дополнительной структуры с выходной логической функцией f1(}&)-ИЛИ-НЕ и f1(}&)-ИЛИ-НЕ, которые является «Условиями активизации», поскольку возможны другие ситуации. При этом следует отметить, что на выходе системы логических функций f1(&)-И и f2(&)-И, которые записаны в виде выражения вида
введена уточняющая информация о действиях, которые, по существу, выполняет конкретная функциональная структура, и если нижняя совокупность информационных символов (+←+2)i+1 и (-←-2)i+1 соответствует тому, что «Предварительное действие в i+1 разряде» соответствует локальному переносу двух положительных и условно отрицательных аргументов из условно «i+1» разряда в условно «i» разряда, где активизируется только один положительный аргумент, то верхняя совокупность информационных символов (|±0|←+)i и (|±0|←-)i соответствует «Окончательному действию в i разряде». И оно заключается в том, что активность аргументов в условно «i» разряде соответствует абсолютному нулю (|±0|), поскольку в этом разряде аргументы двух слагаемых не активны, поэтому в нем активизируется положительный (+) или условно отрицательный (-) аргумент локального переноса, который был сформирован в результате «Предварительного действия в i+1 разряде». При этом следует отметить, что введение уточняющих информационной последовательности символов на выходе системы логической функции позволяет однозначно понимать логико-динамический процесс преобразования такой функциональной структуры.
Ситуация 1. Возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min между «Зонами минимизации», в которых активные аргументы формируют активный логический ноль «+1»«-1» → «±0» и он возможен в двух вариантах.
Вариант 1. Активный логический ноль «+1»«-1» → «±0» в совместной структуре аргументов слагаемых ±[ni]f1(+/-)min → «0-1,+10» и ±[mi]f1(+/-)min → «00,+10» или ±[ni]f1(+/-)min → «0+1,-10» и ±[mi]f1(+/-)min → «00,-10» и преобразование аргументов в этой ситуации запишем либо в виде графоаналитического выражения (60),
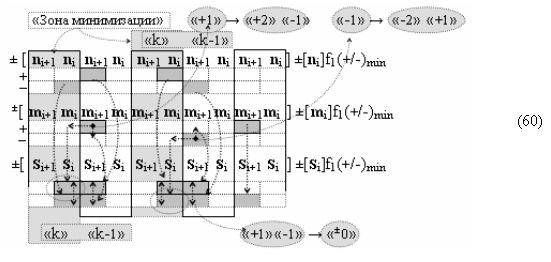
либо в виде графоаналитического выражения (61),
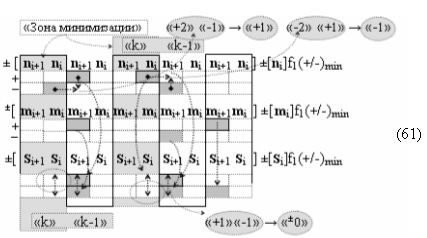
а функциональную структуру для положительного аргумента (+Si)k и функциональную структуру для условно отрицательного аргумента (-Si)k запишем в виде аналитических выражений (62).
Но возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, которую запишем в виде графоаналитического выражения (63),
и в виде графоаналитического выражения (64),
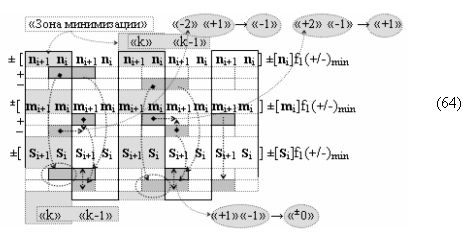
в которой в условно «i» разряде активизирован аргумент результирующей суммы, поскольку в результате преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min посредством обратных арифметических аксиом «+2» «-1» → «+1» и «-2» «+1» → «-1» между «Зонами минимизации» в условно «k-1» «Зоне минимизации» активизирован активный логический ноль «+1»«-1» → «±0». При этом следует отметить, что особенностью структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min является то, что между «Зонами минимизации» в условно «k-1» «Зоне минимизации» одновременно активизирован аргумент одного знака условно «i-1» разряда, в результате активность аргумента того же знака в условно «i» разряда «k» «Зоны минимизации» является результирующим аргументом, при активном аргументе противоположного знака в этом разряде, поэтому функциональную структуру для данной ситуации запишем в виде аналитического выражения (65).
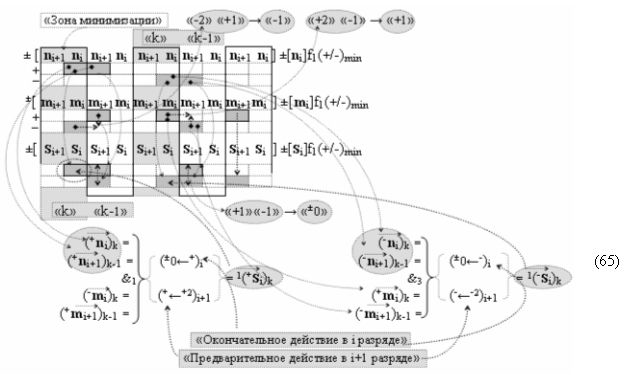
Что касается информационного содержания «Окончательного действия в i разряде», которое записано в виде выражений (±0←+)i и (±0←-)i, то в данной ситуации в условно «i» разряде активность аргументов соответствует не абсолютному нулю (|±0|), а в соответствии с обратной арифметической аксиомой «+1»«-1» → «±0» активность аргументов эквивалентна логическому нулю (±0) и только поэтому в функциональных структурах (65) активизирован результирующий аргумент 1(+Si)k и 1(-Si)k.
Функциональную аналогичную структуру запишем и для структуры аргументов (63) в виде аналитического выражения (66).
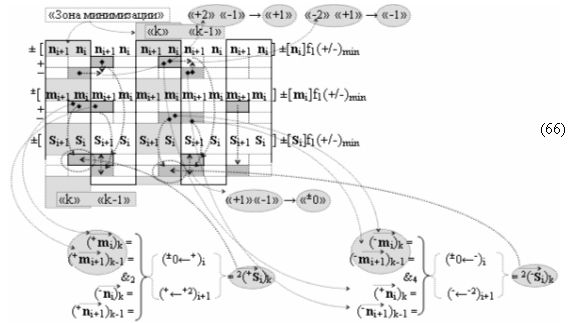
И если аналитические выражения (59), (65) и (66) ввести в систему логической функции f3(})-ИЛИ и f4(})-ИЛИ, то объединенные функциональные структуры запишем в виде аналитических выражений (67),
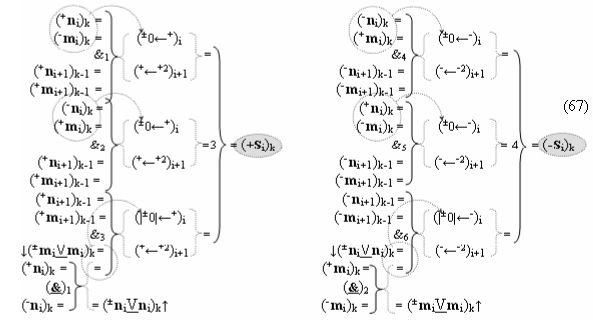
которые активизируют результирующие положительный аргумент (+Si)k и условно отрицательный аргумент (-Si)k условно «i» разряда.
Ситуация 2. Возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min между «Зонами минимизации», в результате преобразования которой одновременно активны аргументы разных знаков, и если активные аргументы преобразовать в соответствии с обратными арифметическими аксиомами «+2» «-1» → «+1» и «-2» «+1» → «-1», то процедуру их преобразования запишем в виде графоаналитического выражения (68),
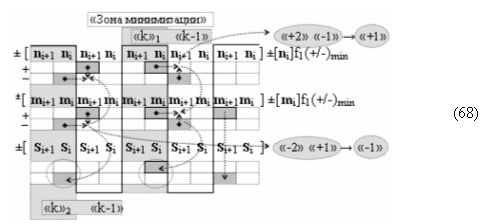
в котором после преобразования аргументов двух слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в соответствии с обратной арифметической аксиомой «+2» «-1» → «+1» в условно «i+1» разряде «k-1» «Зоны минимизации» одновременно активизированы два положительных аргумента, соответствующие одному положительному аргументу в условно «i» разряде «k»1 «Зоны минимизации». Аналогичная ситуация и после преобразования аргументов в соответствии обратной арифметической аксиомой «-2» «+1» → «-1» в условно «i» разряде «k»2 «Зоны минимизации». При этом функциональную структуру для положительного аргумента (+Si)k и функциональную структуру для условно отрицательного аргумента (-Si)k запишем в виде аналитического выражения (69),
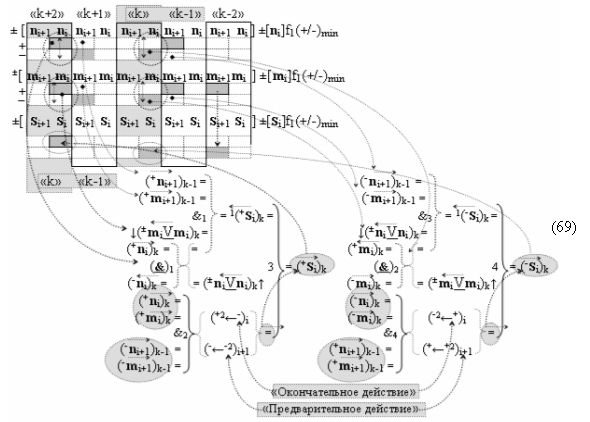
с выходной логической функцией f2(&)-И и f4(&)-И, которые введены в систему выходной логической функции f3(})-ИЛИ и f4(})-ИЛИ соответственно. При этом следует отметить, что выходные логические функции f3(})-ИЛИ и f4(})-ИЛИ, которые активизируют положительный результирующий и условно отрицательный аргумент (+Si)k и (-Si)k, являются выходной функциональной структурой математической модели входной структуры сумматора ±f(ΣRU)min условно «i» разряда. И если функциональные структуры с выходной логической функцией f2(&)-И и f4(&)-И ввести в систему логической функции f3(})-ИЛИ и f4(})-ИЛИ аналитического выражения (70),
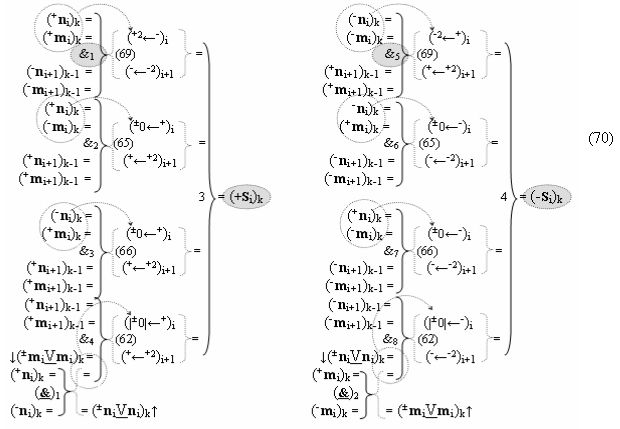
которая является математической моделью входной структуры сумматора ±f(ΣRU)min условно «i» разряда на данном этапе ее синтеза.
Ситуация 3. Возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, в которой активизируют положительный и условно отрицательный аргумент одного локального переноса в результате преобразования аргументов посредством процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn и d1/dn → f1(-←↑+)d/dn и функциональную структуру такого преобразования запишем либо в виде аналитического выражения (71),
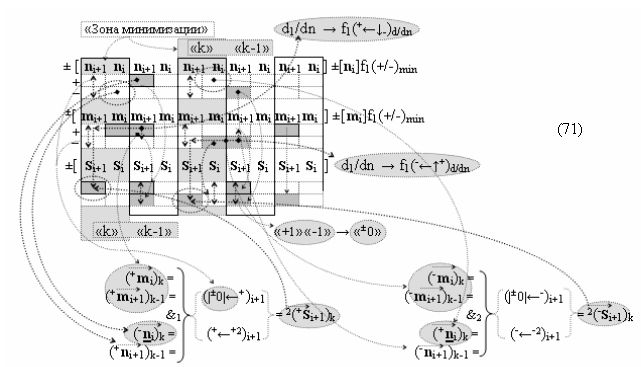
либо в виде аналитического выражения (72),
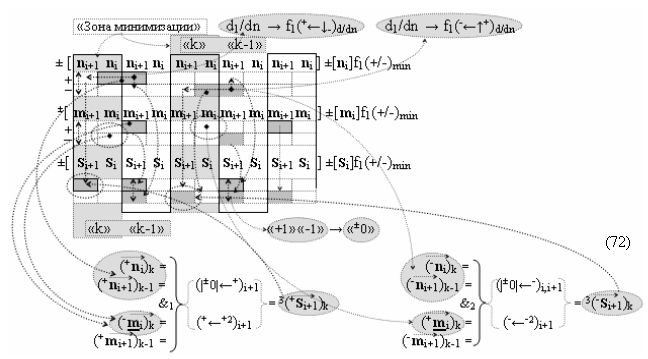
которые активизируют положительный результирующий и условно отрицательный аргумент (+Si+1)k и (-Si+1)k, являются функциональной входной структурой математической модели сумматора ±f(ΣRU)min условно «i+1» разряда. И если функциональные структуры с выходной логической функцией f1(&)-И и f2(&)-И выражений (58), (71) и (72) ввести в систему логической функции f1(})-ИЛИ и f2(})-ИЛИ, то запишем аналитические выражения (73)
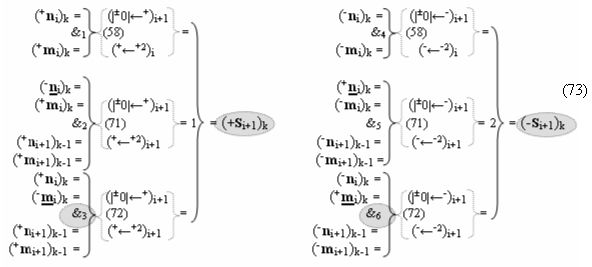
математической модели функциональной входной структуры сумматора ±f(ΣRU)min на данном этапе ее синтеза.
Ситуация 4. Возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, в которой активизируют положительный и условно отрицательный аргумент в результате преобразования аргументов посредством процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn и d1/dn → f1(-←↑+)d/dn с формированием двух локальных переносов, и функциональную структуру такого преобразования запишем либо в виде аналитического выражения (74),
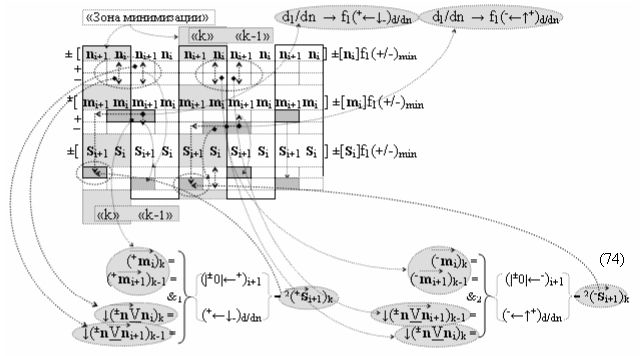
и в виде аналитического выражения (75),
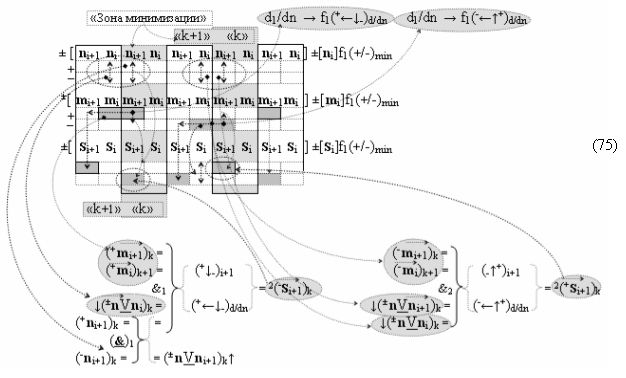
либо в виде аналитического выражения (76),
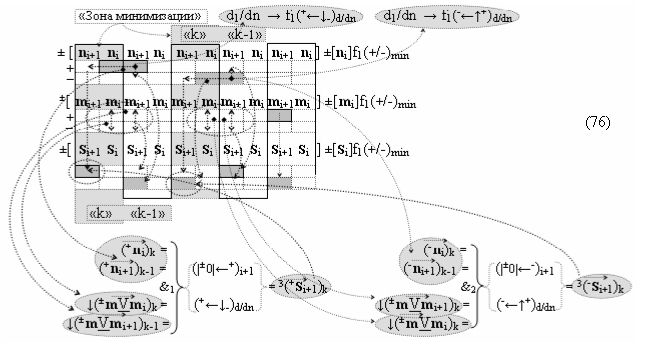
и в виде аналитического выражения (77),
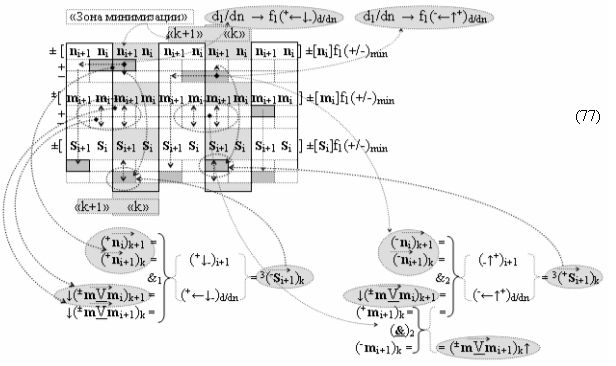
которые активизируют положительный результирующий и условно отрицательный аргумент (+Si+1)k и (-Si+1)k, являются функциональной входной структурой математической модели сумматора ±f(ΣRU)min условно «i+1» разряда. Поэтому введем функциональные структуры (74) - (77) в соответствующие системы логических функций f1(})-ИЛИ и f2(})-ИЛИ выражения (73) и структуру логических функций положительного результирующего аргумента (+Si+1)k условно «i+1» разряда запишем в виде аналитического выражения (78),
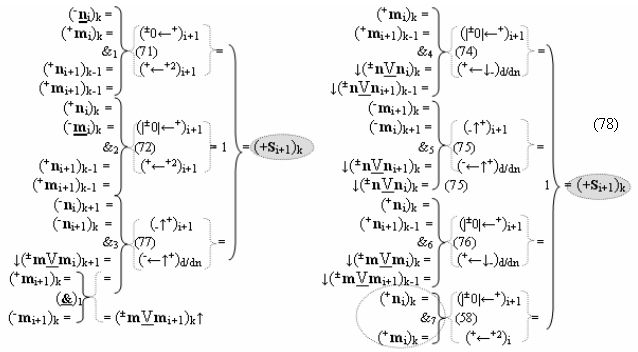
и структуру логических функций условно отрицательного результирующего аргумента (+Si+1)k условно «i+1» разряда запишем в виде аналитического выражения (79).
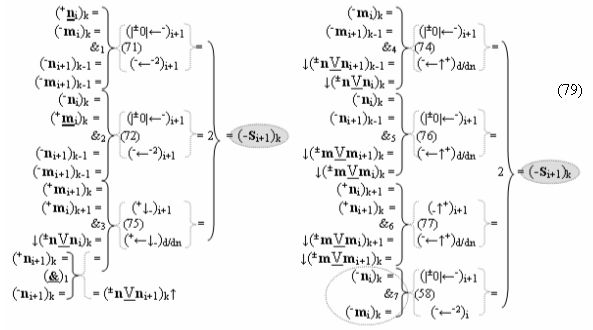
А структуру логических функций (70) положительного результирующего аргумента (+Si)k условно «i» разряда запишем в виде аналитического выражения (80)
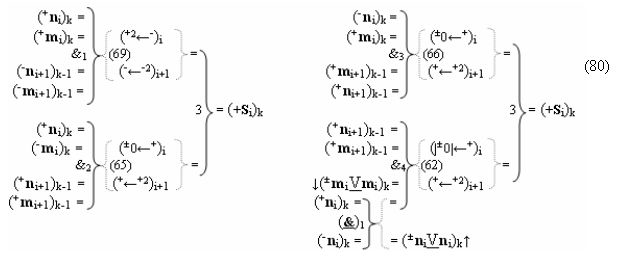
и структуру логических функций (70) условно отрицательного результирующего аргумента (+Si)k условно «i» разряда запишем в виде аналитического выражения (81).
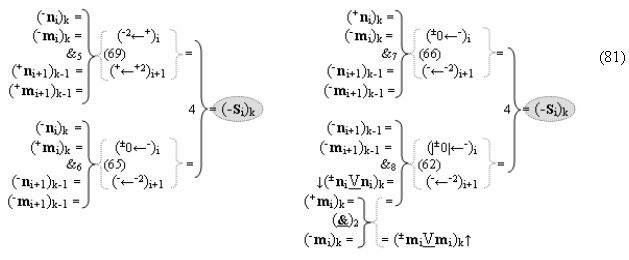
Ситуация 5. Возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, в которой активизируют положительный и условно отрицательный аргумент двух локальных переносов в результате преобразования аргументов посредством процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn и d1/dn → f1(-←↑+)d/dn и функциональные структуры такого преобразования запишем в виде аналитических выражений (82).
При этом следует отметить, что посредством функциональных структур (82) активизируют только результирующий аргумент 1(+Si)k и 1(-Si)k условно «i» разряда, поскольку в аналитических выражениях (80) и (81) активизацию результирующих аргументов 1(+Si+1)k и 1(-Si+1)k условно «i+1» разряда активизируют посредством функциональных структур, которые включают выходную логическую функцию f7(&)-И и которые запишем в виде аналитических выражений (83)
с преобразованными аргументами (+n&mi)k и (-n&mi)k, и они могут быть введены в систему логических функций f1(&)-И и f2(&)-И выражения (82). При этом если вернуться к анализу функциональных структур (78) и (79), активизирующих положительный и условно отрицательный аргумент (+Si+1)k и (-Si+1)k условно «i+1» разряда, записав их в виде выражения (84)
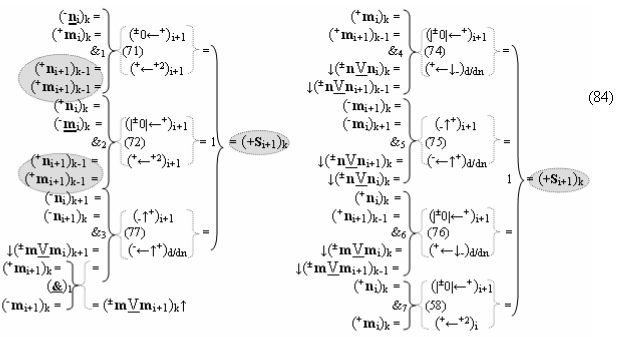
и выражения (85),
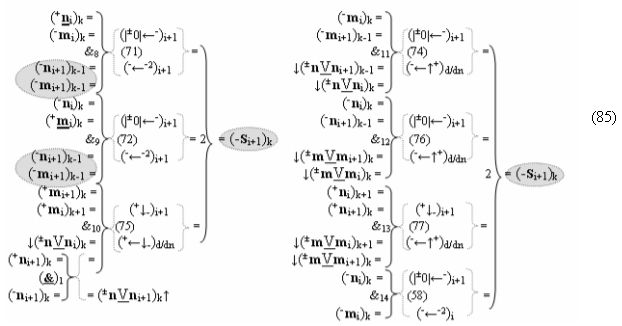
в которых в системы логических функций f1(&)-И, f2(&)-И и f8(&)-И, f9(&)-И включены как положительные аргументы (+ni+1)k-1 и (+mi+1)k-1, так и условно отрицательные аргументы (-ni+1)k-1 и (-mi+1)k-1, то в этой ситуации целесообразно функциональные структуры (82) скорректировать. И если вернуться к анализу функциональных структур (80) и (81), активизирующие положительный и условно отрицательный аргумент (+S)k и (-Si)k условно «i» разряда, записав их в виде выражения (86)
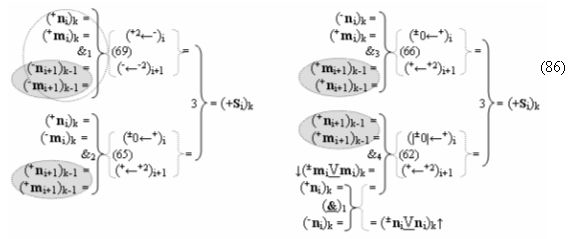
и выражения (87),
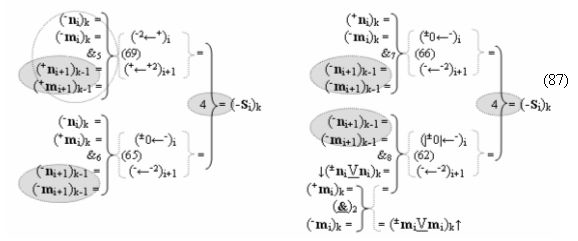
в которых в системы логических функций f1(&)-И - f8(&)-И включены как положительные аргументы (+ni+1)k-1 и (+mi+1)k-1, так и условно отрицательные аргументы (-ni+1)k-1 и (-mi+1)k-1, то в этой ситуации целесообразно функциональные структуры (86) и (87) с выходными логическими функциями f1(&)-И и f5(&)-И скорректировать в соответствии с выражением (88)
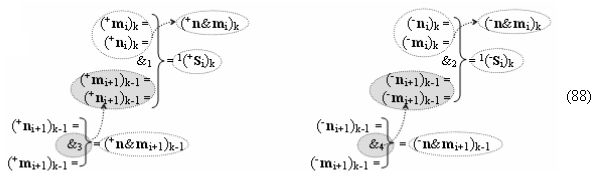
и записать в виде структуры логических функций (89).
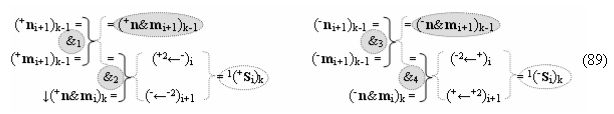
И если ввести скорректированную соответствующую функциональную структуру (89) в систему логической функции f3(})-ИЛИ выражения (86), то с учетом скорректированной функциональной структуры (82)
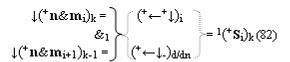
запишем аналитическое выражение (90),
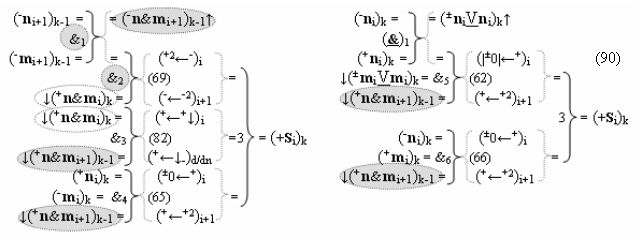
которое активизирует положительный аргумент (+S)k условно «i» разряда. А если ввести скорректированную соответствующую функциональную структуру (89) в систему логической функции f3(})-ИЛИ выражения (87), то с учетом скорректированной функциональной структуры (82)
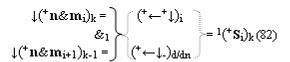
запишем аналитическое выражение (91),
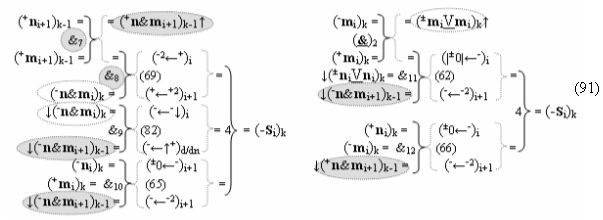
которое активизирует условно отрицательный аргумент (-Si)k условно «i» разряда. При этом функциональные структуры условно «i+1» разряда (84) и (85) с учетом преобразованных аргументов (+n&mi+1)k и (-n&mi+1)k положительного канала запишем в виде аналитического выражения (92),
а для условно отрицательного канала запишем в виде аналитического выражения (93),
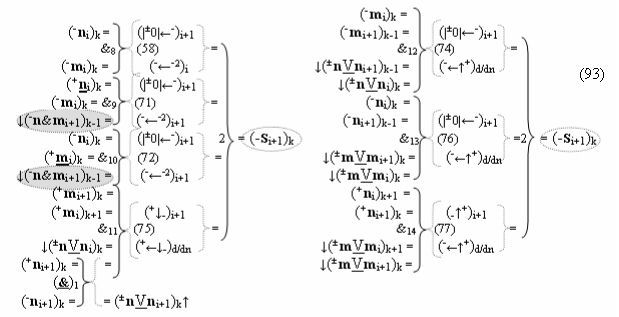
Ситуация 5. Возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (94),
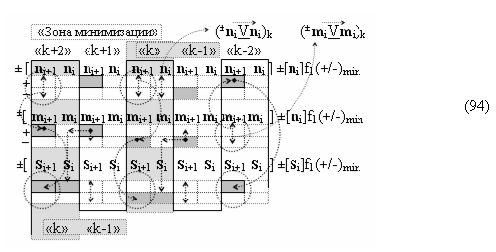
в которой активизация результирующих аргументов промежуточной суммы реализуется при активных преобразованных аргументов (±niVni)k и (±miVmi)k «Условия активизации» и возможна структура аргументов слагаемых (95),
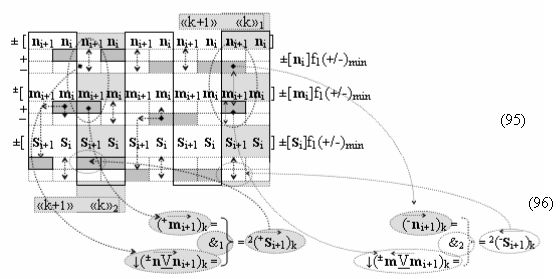
в которой в условно «k»2 «Зоне минимизации» структура аргументов слагаемых посредством функциональной структуры с выходной логической функцией f1(&)-И активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда. Поскольку в структуре аргументов слагаемого ±[ni]f1(+/-)min в условно «i+1» разряде одновременно не активен как положительный аргумент (+ni+1)k, так и условно отрицательный аргумент (-ni+1)k и в этой ситуации активен преобразованный аргумент (±nVni+1)k. А в условно «k»1 «Зоне минимизации» структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min исключает активизацию условно «i+1» разряде результирующего условно отрицательного аргумента (-Si+1)k, поскольку в этом разряде не активен преобразованный аргумент (±mVmi+1)k логического нуля. Но если записать структуру аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (97),
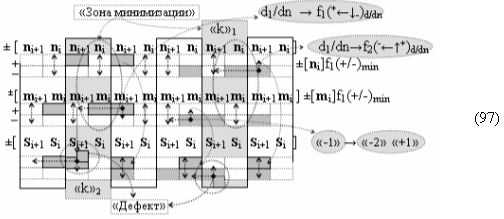
и выполнить преобразования в соответствии с процедурой логического дифференцирования d1/dn → f1(+←↓-)d/dn и d1/dn → f2(-←↑+)d/dn и арифметической аксиомы «-1» → «-2» «+1», а также преобразования в соответствии с логикой функциональных структур (96), то будет сформирован «Дефект», который может быть исключен только после применения очередного преобразования. При этом следует отметить, что если записать графоаналитическое выражение (98),
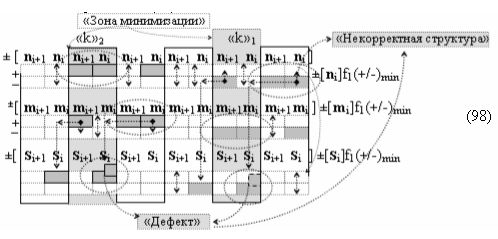
в котором аргумент в условно «i» разряде был активизирован в соответствии с логикой функциональных структур (99),
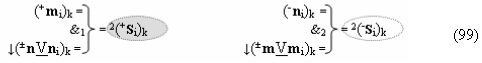
то в условно «i» разряде аналогичный «Дефект» сформированным быть не может, поскольку в «Зоне минимизации» не могут быть активизированы два последовательных аргумента.
Возвращаясь к анализу графоаналитического выражения (97), записав его в виде графоаналитического выражения (100)
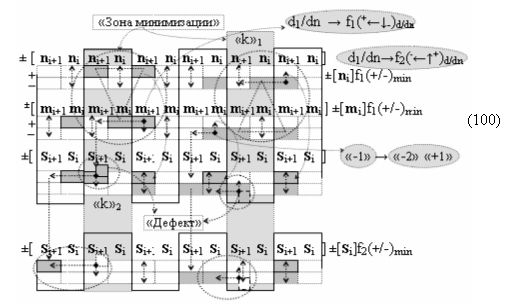
можно отметить, что если в условно «k»1 «Зоне минимизации» преобразование аргументов носит локальный характер, то в условно «k»1 «Зоне минимизации» преобразование аргументов может сформировать сквозной перенос f1(+←←+)d/dn. При этом следует отметить, что структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min выражения (100) имеет особенность позиционной последовательности активных аргументов, поскольку если записать логико-динамический процесс преобразования аргументов (101),
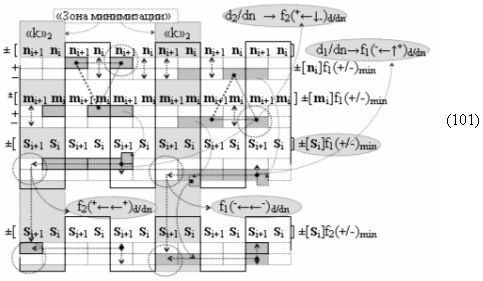
то после формирования объединенной структуры аргументов ±[Si]f1(+/-)min в ней активные аргументы расположены в последовательности, и она соответствует условно отрицательному сквозному переносу f1(-←←-)d/dn и положительному сквозному переносу f2(+←←+)d/dn, которые в данной ситуации реализуют посредством процедуры логического дифференцирования d1/dn → f1(-←↑+)d/dn и d2/dn → f2(+←↓-)d/dn. А если проанализировать позиционную последовательность активных аргументов в структуре аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, то особенность заключается в последовательной активности как минимум двух аргументов условно «i+1» разряда в структуре одного из слагаемых и активности аргумента условно «i» разряда в структуре другого слагаемого, который позиционно расположен между активными аргументами условно «i+1» разряда. При этом следует отметить, что такая особенность, если записать графоаналитическое выражение (102)
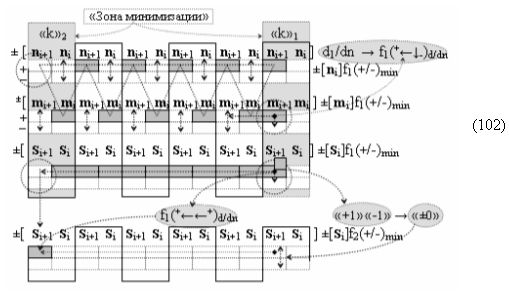
или графоаналитическое выражение (103),
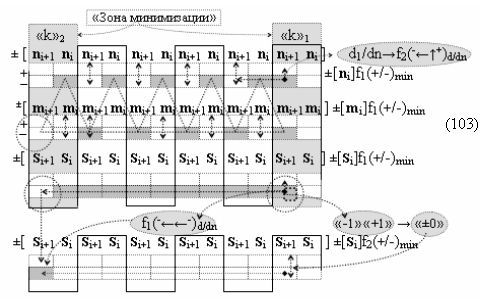
то она может быть в «Зонах минимизации» в неограниченной их последовательности. Также следует отметить, что сквозной перенос f1(+←←+)d/dn или f1(-←←-)d/dn формируется только в одноименной по знаку структуре аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min и активный аргумент такого переноса может быть активизирован на локальном уровне. Поэтому проанализируем структуру аргументов слагаемых (104),
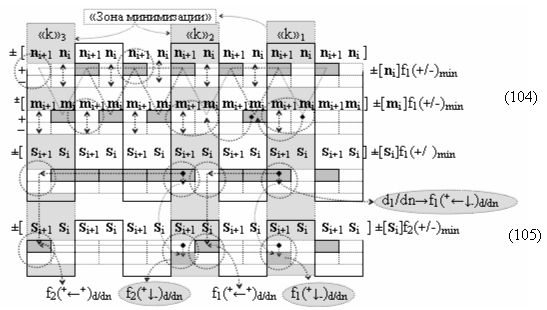
в которой активные аргументы не формируют сквозной перенос f1(+←←+)d/dn, но если логически продифференцировать d1/dn → f1(-←↑+)d/dn результирующую сумму ±[Si]f1(+/-)min, то будет сформирована скорректированная результирующая сумма ±[Si]f2(+/-)min (105), где активизирован в условно «i+1» разряде условно отрицательный аргумент (-Si+1)k локальных переносов f1(+↓-)d/dn и f2(+↓-)d/dn. При этом следует отметить, что если сформировать функциональные структуры (106),
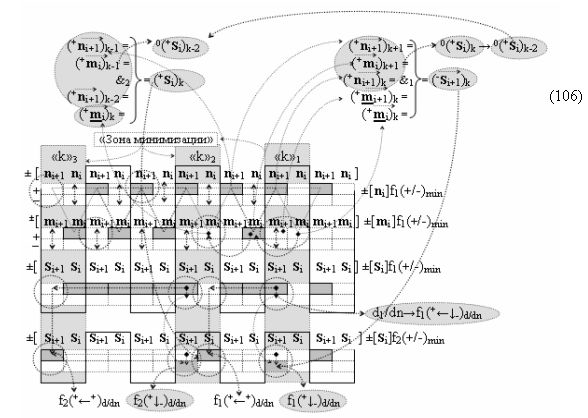
то условно отрицательный аргумент (-Si+1)k локального переноса f1(+↓-)d/dn активизирует функциональная структура с выходной логической функцией f1(&)-И, в которой три входных аргумента (+ni+1)k+1, (+mi)k+1 и (+ni+1)k могут быть включены в систему отдельной логической функцию f0(&)-И для формирования преобразованного аргумента 0(+Si)k. И этот преобразованный аргумент 0(+Si)k → 0(+Si)k-2 для условно «k»2 «Зоны минимизации» будет являться входным аргументом 0(+Si)k-2 условно «k-2» «Зоны минимизации» для функциональной структуры (106) с выходной логической функцией f2(&)-И. И если записать скорректированные функциональные структуры (107),
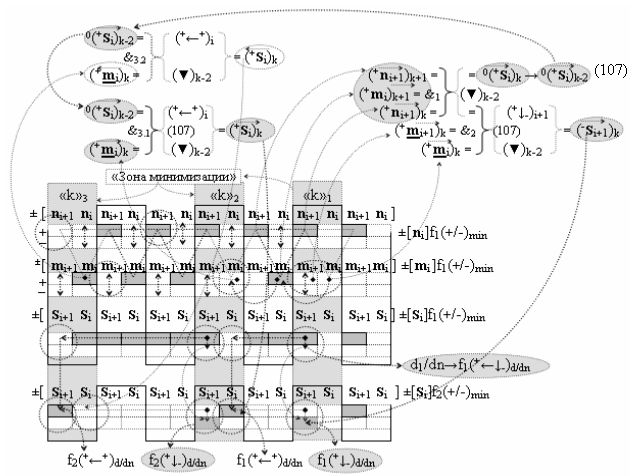
то функциональная структура с выходной логической функцией f3.1(&)-И, активизирующая положительный аргумент локального переноса f1(+←+)d/dn существенно минимизирована по числу входных аргументов, при этом она корректно активизирует положительный результирующий аргумент (+Si)k условно «i» разряда в условно «k»2 «Зоне минимизации». А в условно «k»3 «Зоне минимизации» эта функциональная структура с выходной логической функцией f3.2(&)-И не активна, поскольку в ее системе не активен входной аргумент (+mi)k с измененным уровнем аналогового сигнала, поэтому в этой «Зоне минимизации» должен быть активизирован в условно «i+1» разряде аргумент (+Si+1)k локального переноса f2(+←+)d/dn. И если для условно «k»3 «Зоны минимизации» записать функциональные структуры (108),
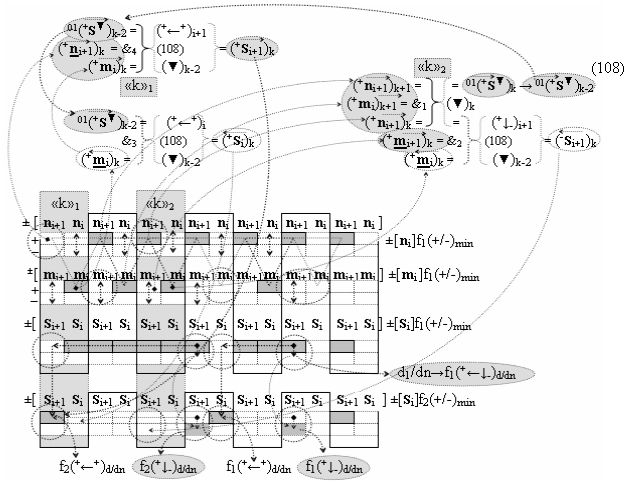
то функциональная структура с выходной логической функцией f4(&)-И корректно активизирует результирующий аргумент (+Si+1)k в условно «i+1» разряде «k» «Зоны минимизации», когда как результирующий аргумент (+Si)k условно «i» разряда в этой «Зоне минимизации» корректно не активен. При этом результирующий условно отрицательный аргумент (-Si+1)k условно «i+1» разряда в «k»2 «Зоне минимизации» логической функции f2(&)-И также корректно не активен, поскольку не активен в этой «Зоне минимизации» аргумент второго слагаемого (+mi)k условно «i» разряда с измененным уровнем аналогового сигнала. Поэтому функциональные структуры (108) являются функциональными структурами математической модели входной структуры сумматора ±f1(ΣRU)min, поскольку если записать логико-динамический процесс преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, в совместной структуре которых активен сквозной перенос f1(+←←+) в виде выражения (109),
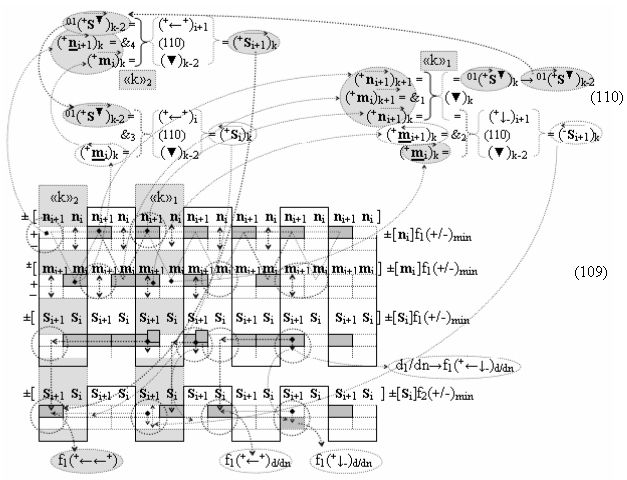
то функциональные структуры (110) также корректны, поскольку условно отрицательный аргумент (-Si+1)k функциональной структуры с выходной логической функцией f2(&)-И в «k»1 «Зоне минимизации» не активен, а в «k»2 «Зоне минимизации» активизирован положительный аргумент сквозного переноса f1(+←←+). В этой связи вернемся к дополнительному анализу процедуры преобразования аргументов слагаемых (71), записав ее в виде выражения (111),
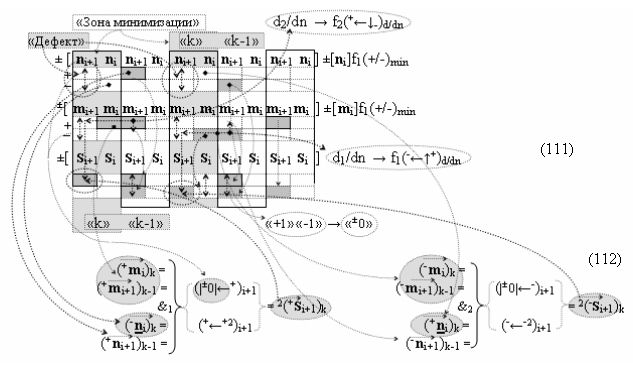
в котором функциональные структуры (112) имеют «Дефект», поскольку с одной стороны не учитывают возможную активность положительного аргумента (+ni+1)k условно «i+1» разряда, поскольку его активность приводит к сквозному переносу f1(+←←+) и f2(-←←-). С другой стороны функциональные структуры (112) не учитывают возможную активность условно отрицательного аргумента (-ni+1)k условно «i+1» разряда, который исключает активизацию положительного аргумента 2(+Si+1)k или условно отрицательного аргумента 2(-Si+1)k в условно «k» «Зоне минимизации». Поэтому в систему логических функций f1(&)-И и f2(&)-И необходимо ввести преобразованный аргумент ↓(±nVni+1)k неактивности аргументов в условно «i+1» разряде, и функциональные структуры (112) запишем в виде аналитических выражений (113),
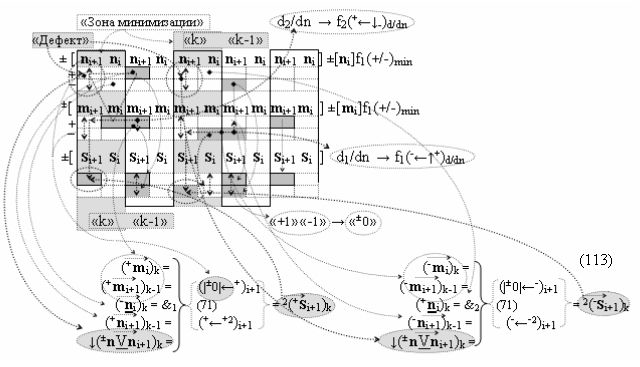
а с учетом входного преобразованного аргумента (+n&mi+1)k-1 функциональные структуры (113) запишем в виде аналитических выражений (114).
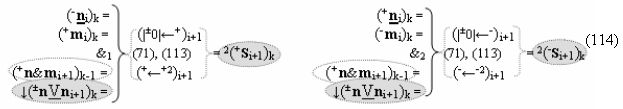
Аналогичную корректирову выполним и в аналитических выражениях (72), которые запишем в виде скорректированных функциональных структур (115),
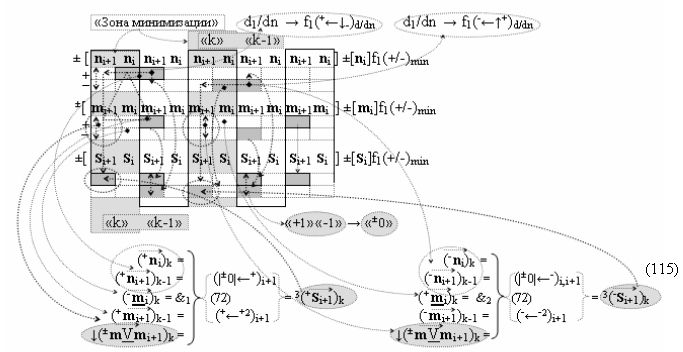
с дополнительным преобразованным аргументом (±mVmi+1)k неактивности аргументов в условно «i+1» разряде, а с учетом входного преобразованного аргумента (-n&mi+1)k-1 функциональные структуры (115) запишем в виде аналитических выражений (116).
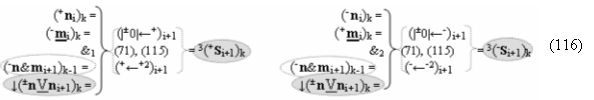
Поскольку функциональные структуры (114) и (116) включают дополнительные входные преобразованные аргументы ↓(±nVni+1)k, поэтому положительный канал функциональной структуры условно «i+1» разряда (92) запишем в виде аналитического выражения (117),
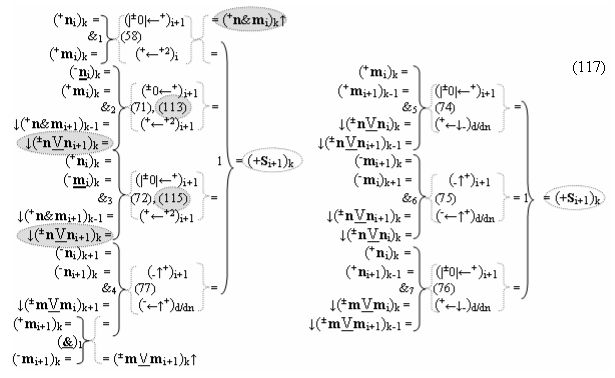
а для условно отрицательного канала (93) запишем в виде аналитического выражения (118).
При этом следует отметить, что в аналитических выражениях (117) и (118) введены преобразованные аргументы (+n&mi)k↑ и (-n&mi)k↑, поскольку если вернуться к анализу структуры логических функций положительного канала условно «i» разряда (90), записав его в виде аналитического выражения (119)
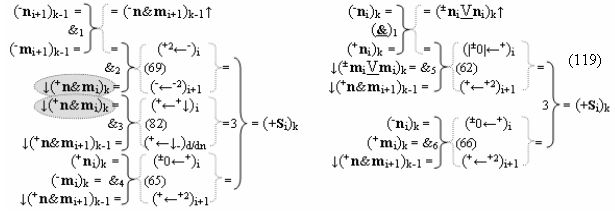
и вернуться к анализу структуры логических функций условно отрицательного канала условно «i» разряда (91), записав его в виде аналитического выражения (120),
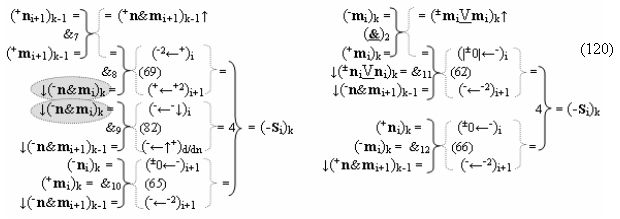
то положительные преобразованные аргументы (+n&mi)k↑ включены в систему логических функций f2(&)-И и f3(&)-И выражения (119), а условно отрицательные аргументы (-n&mi)k↑ включены в систему логических функций f8(&)-И и f9(&)-И выражения (120).
Далее, учитывая равную вероятность активных аргументов в структуре аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, запишем для этой ситуации функциональные структуры (121),
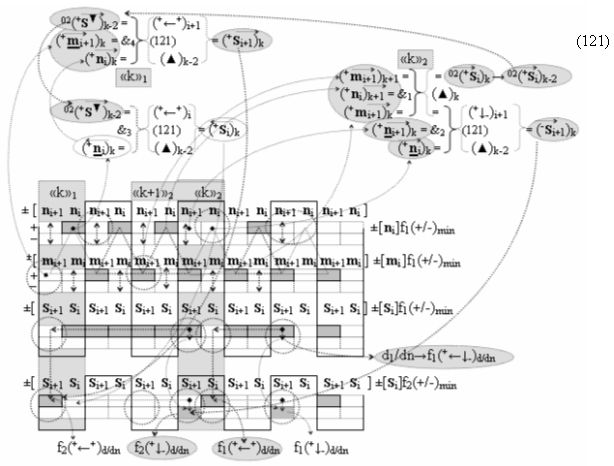
которые также являются функциональными корректными структурами математической модели входной структуры сумматора ±f1(ΣRU)min. А поскольку равная вероятность относится и к знакам аргументов, поэтому сформирует функциональные дополнительные структуры для условно отрицательных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, и запишем структуры логических функций (122)
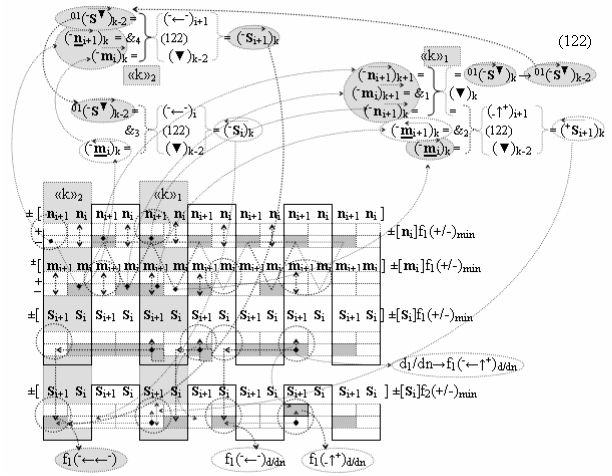
структуры логических функций (123),
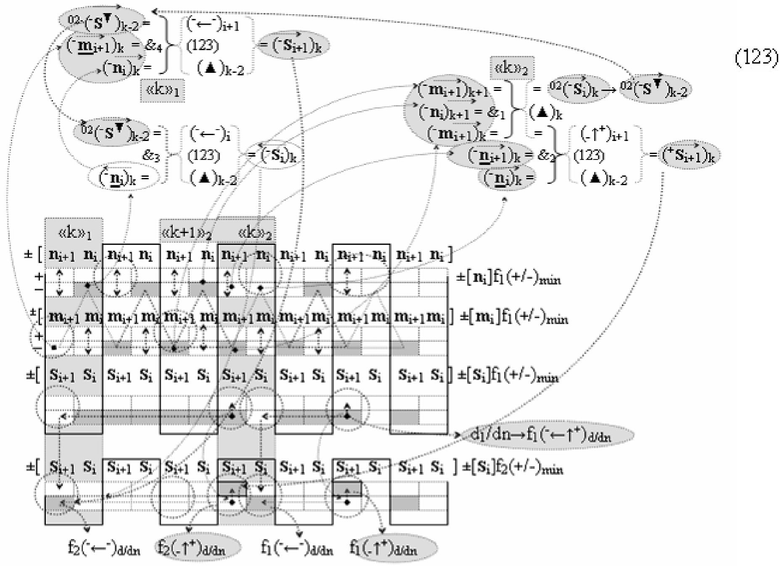
которые адекватно отражают логико-динамический процесс преобразования аргументов слагаемых, поэтому они также являются функциональными структурами математической модели входной структуры сумматора ±f1(ΣRU)min. Поскольку если записать процедуру преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (124),
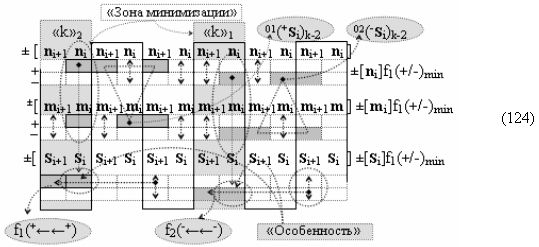
или процедуру преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (125),
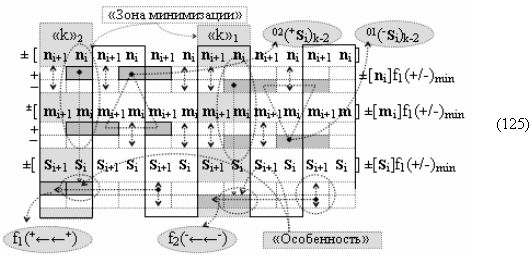
то с одной стороны аргумент (+Si+1)k и (-Si+1)k сквозного переноса f1(+←←+) и f2(-←←-) посредством функциональных структур (114) и (117) активизирован корректно, но с другой стороны в условно «k» «Зоне минимизации» сформирована «Особенность», и она непосредственно связана с активизацией результирующих аргументов (+Si)k и (-Si)k в условно «i» разряде. При этом следует отметить, что активность результирующих аргументов (+Si)k и (-Si)k в условно «i» разряде возможна только при одновременной активности положительных аргументов (+ni)k и (+mi)k, так и условно отрицательных аргументов (-ni)k, (-mi)k двух слагаемых этого разряда и активности преобразованных аргументов 01(+Si)k-2, 02(+Si)k-2 и 02(+Si)k-2, 01(+Si)k-2 условно «i-2» разряда. А если учесть, что в структуре логических функций (117) и (118) сформирован преобразованный положительный аргумент (+n&mi)k и условно отрицательный аргумент (-n&mi)k,
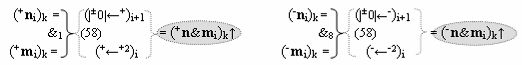
то результирующий аргумент (+Si)k и (-Si)k в условно «i» разряде выражения (124) может быть активизирован посредством функциональной структуры (126),
а результирующий аргумент (+Si)k и (-Si)k в условно «i» разряде выражения (125) может быть активизирован посредством функциональной структуры (127)
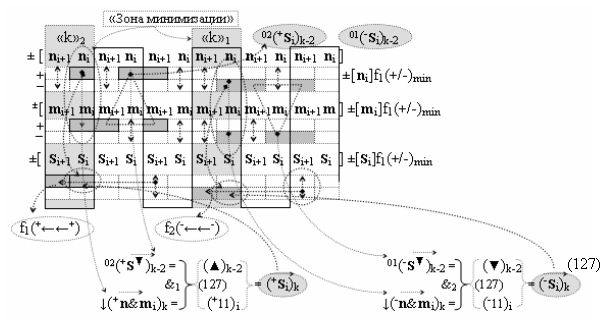
и на данном этапе синтеза входной структуры сумматора ±f1(ΣRU)min аналитические выражения (126) и (127) являются математическими моделями конкретных структур аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min.
На основании полученных результатов после объединения сформированных функциональных структур (110), (121), (122), (123), (126) и (127), которые активизируют аргументы сквозных переносов f1(+←←+) и f2(-←←-) для положительного канала условно «i» разряда, запишем в виде структуры логических функций (128)
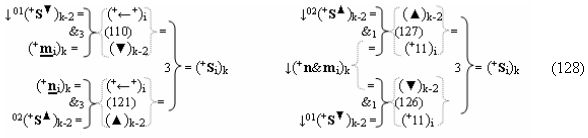
для условно отрицательного канала условно «i» разряда запишем в виде структуры логических функций (129),
а функциональные структуры условно «i+1» разряда запишем для положительного канала в виде структуры логических функций (130)
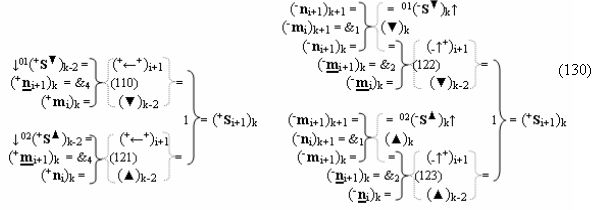
для условно отрицательного канала в виде структуры логических функций (131).
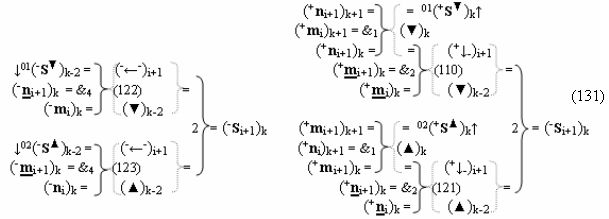
Поскольку функциональные структуры (128) - (131) были сформированы в результате анализа конкретных структур аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, поэтому проанализируем корректность их логико-динамического процесса активизации результирующих аргументов для других возможных структур слагаемых.
Версия 1. Если вернуться к анализу логико-динамического процесса преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (121), которое запишем в виде выражения (132),
то в условно «k» «Зоне минимизации» в структуре аргументов первого слагаемого ±[ni]f1(+/-)min возможна активность с учетом логики формирования условно минимизированной структуры аргументов ±[Si]f2(+/-)min условно отрицательного аргумента либо в условно «i+1» разряде, либо в условно «i» разряде, поэтому в систему логических функций f3(&)-И и f2(&)-И необходимо ввести «Дополнительное условие» активизации результирующего аргумента (+Si)k и (-Si+1)k, а функциональные структуры (133) записать в виде аналитических выражений (134).
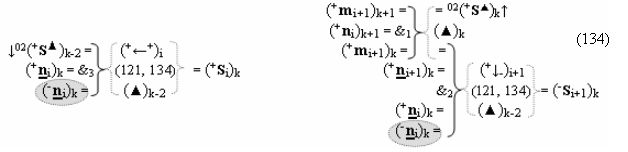
В результате если записать для скорректированной структуры аргументов первого слагаемого ±[ni]f1(+/-)min в виде графоаналитического выражения (135),
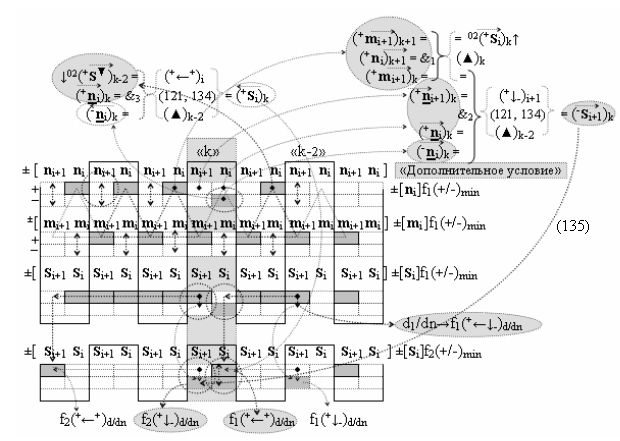
то в условно «i» разряде будет сформирован активный логический ноль «+1»«-1» → «±0», поэтому функциональная структура с выходной логической функцией f2(&)-И исключает активизацию положительного аргумента сквозного переноса f1(+←+)d/dn.
Из предварительного анализа возможности формирования логико-динамического процесса преобразования условно минимизированных структур аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min следует, что функциональная структура сумматора ±f1(ΣRU)min без сквозного переноса f1(+←←↓-) с процедурой одновременного преобразования аргументов первой промежуточной суммы ±[S1 i]f(})-ИЛИ посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1) может быть сформирована, если исключить активизацию последовательно активных аргументов в «Зоне минимизации», что позволит существенно упростить функциональную структуру первого уровня суммирования частичных произведений в параллельно последовательном умножителе ±fΣ(ΣRU)min.
Синтез математической модели сумматора ±f1(ΣRU)min условно минимизированных структур аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min с процедурой одновременного преобразования аргументов первой промежуточной суммы ±[S1 i]f(})-ИЛИ в соответствии с арифметическими аксиомами троичной системы счисления fRU(+1,0,-1). Если повторно вернуться к анализу логико-динамического процесса преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (132), которое запишем в виде выражения (136),
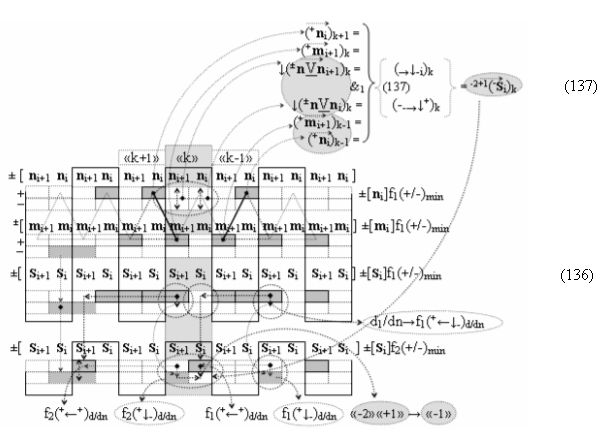
то посредством функциональной структуры (137), которая, по существу, активизирует результирующий условно отрицательный аргумент -2+1(-Si)k в соответствии с обратной арифметической аксиомой «-2»«+1» → «-1» и это действие логической функции f1(&)-И может быть записано как (-→↓+)k, а в результате такого преобразования в условно «k» «Зоне минимизации» будет активизирован (→↓-i)k условно отрицательный аргумент в условно «i» разряде минимизированной структуре результирующей суммы ±[Si]f2(+/-)min. При этом функциональную структуру (137) целесообразно записать в виде аналитического выражения (138)
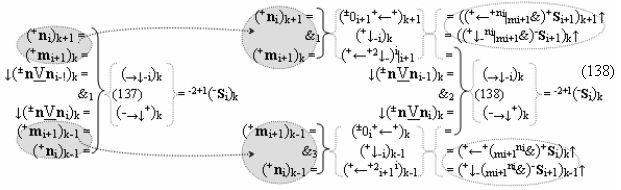
с двумя функциональными входными структурами с выходной логической функцией f1(&)-И и f3(&)-И. И если функциональная структура с выходной логической функцией f1(&)-И, записав ее в виде аналитического выражения (139)
выполняет анализ {(+←+2↓-)i|i+1} активности положительных аргументов в соответствии с индексом «i|i+1» между «Зонами минимизации» и активизирует как положительный аргумент (+←+(ni|mi+1&)+Si+1)k+1↑, функционально принадлежащий{(±0i+1 +←+)k+1} условно «i+1» разряду «k+1» «Зоны минимизации», так и условно отрицательный аргумент (+↓-(ni|mi+1&)-Si+1)k↑, функционально принадлежащий {(+↓-i)k} условно «i» разряду «k» «Зоны минимизации», то функциональная структура с выходной логической функцией f2(&)-И, записав ее в виде аналитического выражения (140)
выполняет анализ (+←+2 i+1 i)k-1 активности положительных аргументов в соответствии с индексом «i+1 i» в «k-1» «Зоне минимизации» и активизирует как положительный аргумент (+←+(mi+1 ni&)+Si)k↑, функционально принадлежащий условно «i» разряду «k» «Зоны минимизации», так и условно отрицательный аргумент (+↓-(mi+1 ni&)-Si+1 i)k-1↑, функционально принадлежащий {(+↓-i)k-1} условно «i» разряду «k-1» «Зоны минимизации». При этом следует отметить, что в структуре логических функций (138) введены функциональные дополнительные структуры (139) и (140), поскольку возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, в которой процедуру активизации результирующего аргумента -2+1(-Si)k запишем посредством либо в виде не минимизированной функциональной структуры (141),
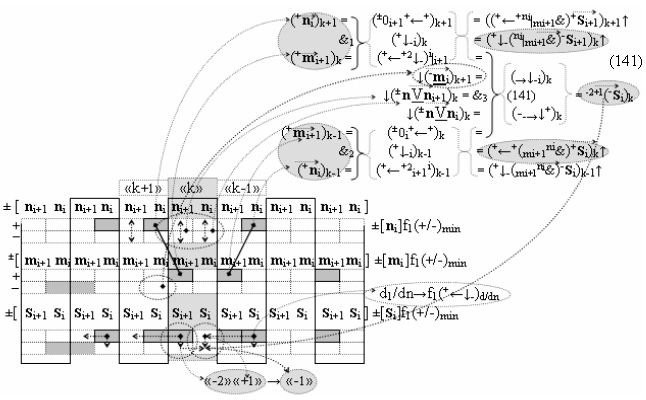
либо с учетом преобразованных аргументов (+↓-(ni|mi+1&)-Si+1)k↑ и (+←+(mi+1 ni&)+Si)k↑ функциональных структур (139) и (140) запишем в виде минимизированной функциональной структуры (142),
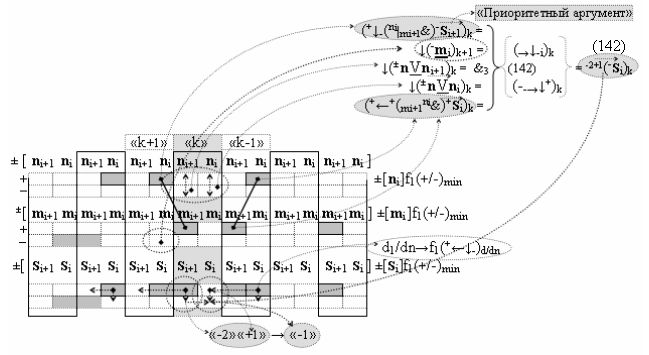
в которой также в соответствии с обратной арифметической аксиомой «-2»«+1» → «-1» в условно «k» «Зоне минимизации» активизирован условно отрицательный аргумент -2+1(-Si)k в результирующей структуре аргументов суммы ±[Si]f2(+/-)min. При этом следует отметить, что в систему логической функции f3(&)-И введен преобразованный аргумент ↓(-mi)k+1 с измененным уровнем аналогового сигнала условно «i+1» разряда, поскольку возможна структура аргументов второго слагаемого ±[mi]f1(+/-)min с активными аргументами между «Зонами минимизации».
Вариант 1. Активен условно отрицательный аргумент (-mi)k+1 в «k+1»«Зоне минимизации», который в логико-динамическом процессе преобразования аргументов слагаемых (143),
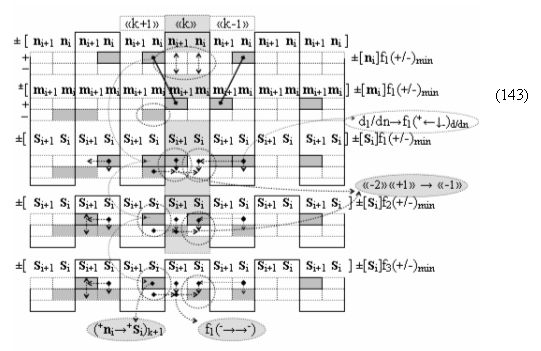
который в структуре промежуточной суммы ±[Si]f1(+/-)min был посредством обратной арифметической аксиомы «-2»«+1» → «-1» предварительно преобразован в условно отрицательный аргумент (-mi+1)k условно «i+1» разряда в «k»«Зоне минимизации», после чего посредством той же обратной арифметической аксиомы был активизирован в условно «i» разряда в той же «Зоне минимизации». В результате был выполнен локальный двойной обратный перенос f1(-→→-), при этом в «k+1»«Зоне минимизации» активизирован положительный результирующий аргумент (+ni→+Si)k+1. А для формирования его функциональной структуры необходимо проанализировать условия его активизации, а для этого запишем возможные ситуации.
Ситуация 1. Структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, при которых сформирована последовательность активных аргументов, и они в своей последовательности соответствуют процедуре формализованного сквозного переноса f1(+←←+) и при его выполнении в структуре промежуточной суммы ±[Si]f1(+/-)min выражения (144)
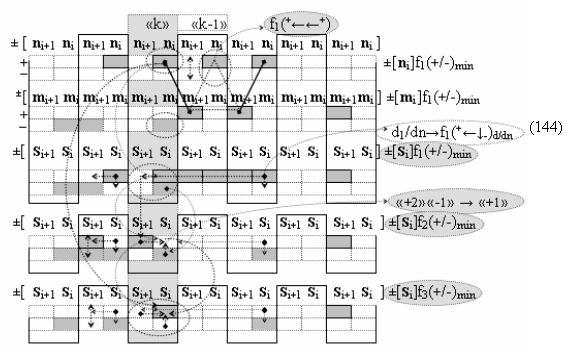
формируем структуру аргументов промежуточной суммы ±[Si]f2(+/-)min. И если в условно «k» «Зоне минимизации» выполнить преобразования активных аргументов в соответствии с обратной арифметической аксиомой «+2»«-1» → «+1», то будет активизирован положительный результирующий аргумент (+ni→+Si)k, который формально соответствует активному положительному аргументу (+ni)k первого слагаемого ±[ni]f1(+/-)min.
Ситуация 2. Структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, при которых сформирована последовательность активных положительных аргументов с условно отрицательным аргументом между ними, и они в своей последовательности соответствуют процедуре локального переноса f1(+←+), а при его выполнении в структуре промежуточной суммы ±[Si]f1(+/-)min выражения (145)
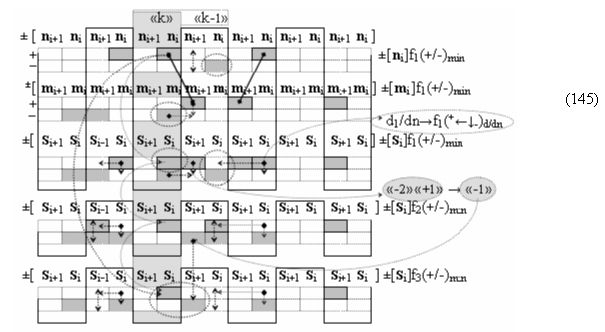
формируем структуру аргументов промежуточной суммы ±[Si]f2(+/-)min. И если в условно «k» «Зоне минимизации» выполнить преобразования активных аргументов в соответствии с обратной арифметической аксиомой «-2»«+1» → «-1», то будет активизирован в условно «k-1» «Зоне минимизации» условно отрицательный аргумент (-mi→-Si+1)k-1, который формально соответствует активному условно отрицательному аргументу (-mi)k условно «k» «Зоны минимизации» второго слагаемого ±[mi]f1(+/-)min. При этом в условно «k» «Зоне минимизации» также будет активен положительный аргумент (+ni→+Si)k, который формально соответствует активному положительному аргументу (+ni)k первого слагаемого ±[ni]f1(+/-)min.
Из полученных результатов следует, что активизация положительного аргумента (+ni)k → (+Si)k первого слагаемого ±[ni]f1(+/-)min в результирующей сумме ±[Si]f3(+/-)min не зависит от активности аргументов в условно «i» разряде «k-1» «Зоны минимизации», а условием его активизации в условно «Зоне минимизации» вида,
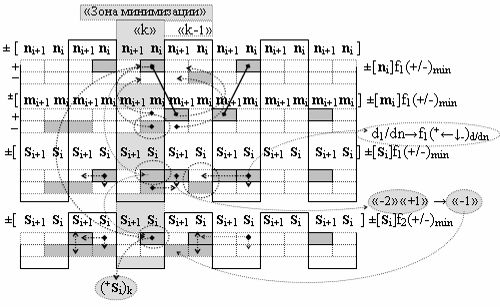
если записать функциональную структуру (146)
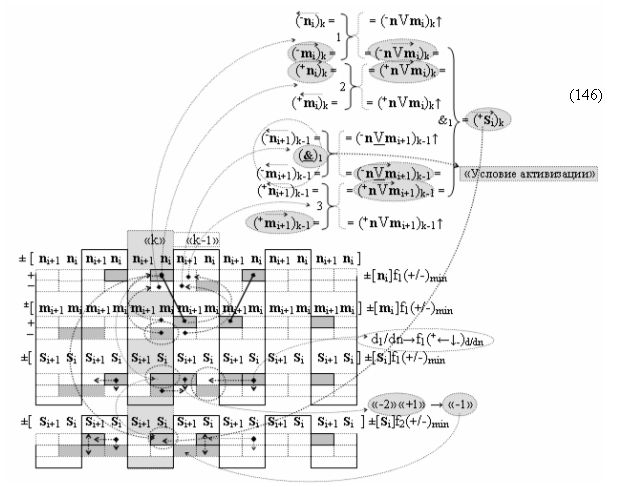
является активность преобразованного условно отрицательного аргумента (-nVmi+1)k-1 условно «i+1» разряда «k-1» «Зоны минимизации», который активизирует логическая функция f1(}&)-ИЛИ-НЕ, и ее активная функциональная структура является «Условием активизации». При этом следует отметить, что активные аргументы условно «k» и «k-1» «Зоны минимизации» введены в систему логических функций f1(})-ИЛИ, f2(})-ИЛИ и f3(})-ИЛИ в связи с тем, что результирующий аргумент (+Si)k в условно «i» разряде активизируется в следующих возможных вариантах слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, которые запишем в виде графоаналитический выражений (146) - (148).
Вариант 1.
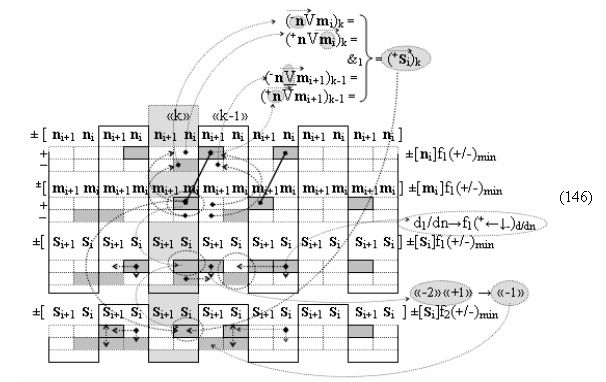
Вариант 2.
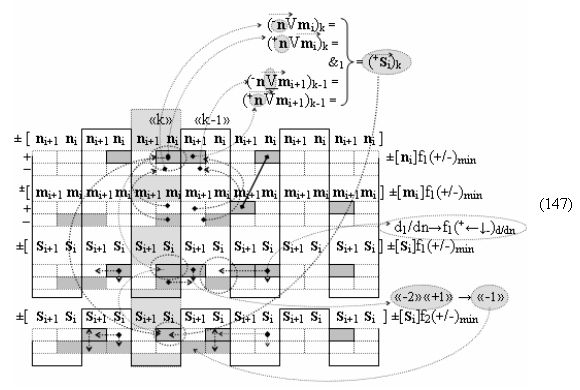
Вариант 3.
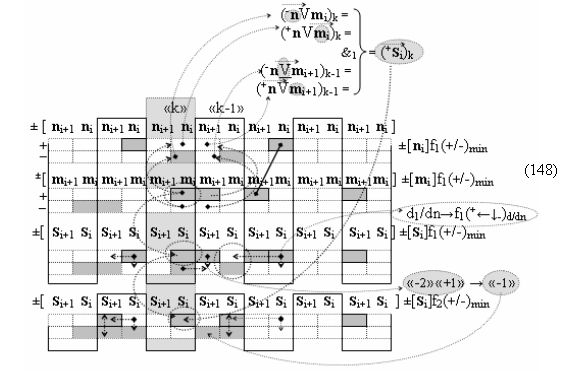
А если учесть, что в структуре результирующей суммы ±[Si]f2(+/-)min в условно «i+1» разряде «k-1» «Зоны минимизации» активизирован условно отрицательный аргумент (-Si+1)k-1, то функциональную структуру для его активизации в условно «k» «Зоне минимизации» запишем в виде аналитического выражения (149),
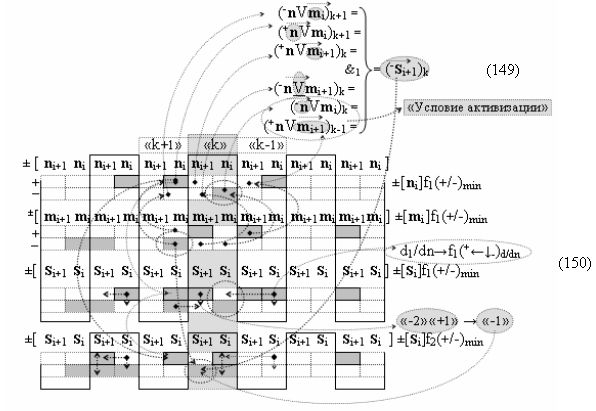
в котором «Условием активизации» является преобразованный условно отрицательный аргумент (-nVmi)k условно «i» разряда «k» «Зоны минимизации» и преобразованный положительный аргумент (+nVmi+1)k-1 условно «i+1» разряда «k-1» «Зоны минимизации». И если в структуре аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, например, выражения (150) не активен преобразованный аргумент «Условия активизации», то логико-динамических процесс преобразования запишем в виде графоаналитического выражения (151),
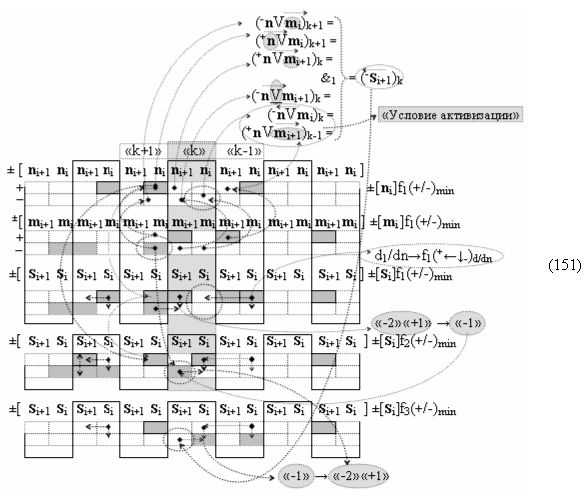
в котором не активен преобразованный условно отрицательный аргумент (-nVmi)k условно «i» разряда в «k» «Зоне минимизации» и для формирования результирующей суммы ±[Si]f3(+/-)min преобразование в структуре аргументов ±[Si]f2(+/-)min выполняют в соответствии с обратной арифметической аксиомой «-2»«+1» → «-1». В результате в условно «k» «Зоне минимизации» активизирован условно отрицательный аргумент (-Si)k условно «i» разряда, а функциональную структуру для его активизации запишем в виде аналитического выражения (152),
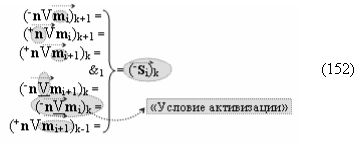
в котором «Условием активизации» является преобразованный условно отрицательный аргумент (-nVmi)k условно «i» разряда с измененным уровнем аналогового сигнала «k-1» «Зоны минимизации».
А если в структуре аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min выражения (150) не активен преобразованный положительный аргумент (+nVmi+1)k-1 «Условия активизации», то логико-динамических процесс преобразования запишем в виде графоаналитического выражения (153),
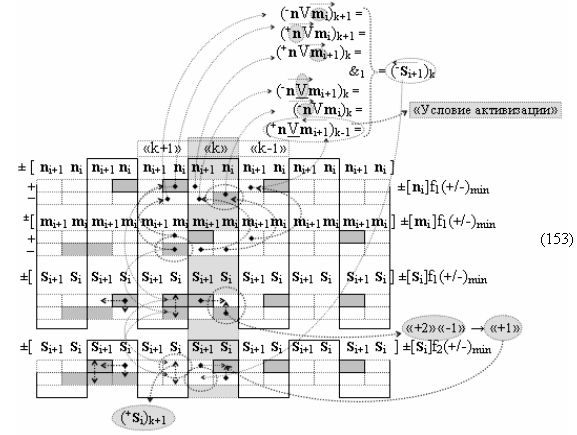
в котором не активен преобразованный положительный аргумент (+nVmi+1)k-1 условно «i+1» разряда в «k-1» «Зоне минимизации», и для формирования результирующей суммы ±[Si]f2(+/-)min преобразование в структуре аргументов ±[Si]f1(+/-)min выполняют в соответствии с обратной арифметической аксиомой «+2»«-1» → «+1». В результате в условно «k» «Зоне минимизации» активизирован положительный аргумент (+Si)k условно «i» разряда, а функциональную структуру для его активизации запишем в виде аналитического выражения (154),
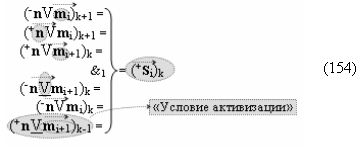
в котором «Условием активизации» является преобразованный положительный аргумент (-nVmi+1)k-1 условно «i+1» разряда с измененным уровнем аналогового сигнала «k-1» «Зоны минимизации». При этом следует отметить, что в данной ситуации в условно «k+1» «Зоне минимизации» логико-динамического процесса преобразования аргументов не активизируют положительный результирующий аргумент (+Si)k+1 условно «i» разряда. И если вернуться к анализу функциональной структуры (146), посредством которой активизируют в условно «k+1» «Зоне минимизации» положительный результирующий аргумент (+Si)k условно «i» разряда, записав ее в виде аналитического выражения (155),
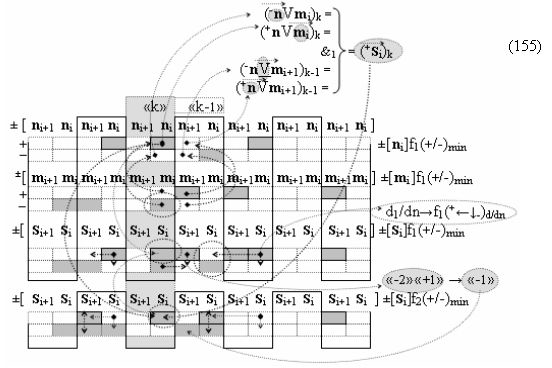
то в него не введены ограничения на активизацию данного аргумента. Поскольку если записать для структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min выражения (153) графоаналитическое выражение (156),
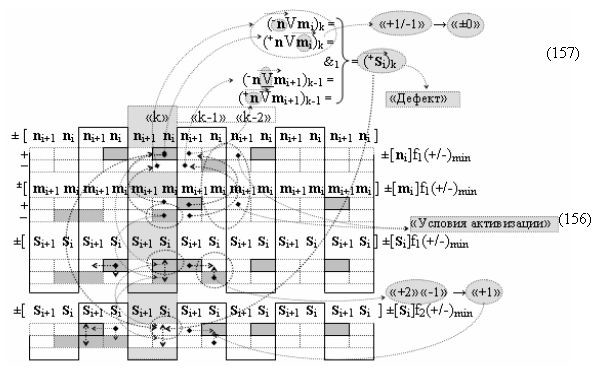
то положительный аргумент (+Si)k условно «i» разряда в функциональной структуре (157) активизирован не корректно. Поэтому определимся с возможными входными преобразованными аргументами «Условия активизации» функциональной структуры (157) с выходной логической функцией f1(&)-И, в систему которой включены преобразованные аргументы (-nVmi)k и (+nVmi)k, соответствующие активному логическому нулю «+1/-1» → «±0», и это было связано с тем, чтобы исключить предварительный этап суммирования, включающий процедуру удаления его из структуры промежуточной суммы ±[Si]f1(+/-)min, что приведет к сокращению технологического цикла ∆tΣ в функциональной структуре сумматора ±f(ΣRU)min. И если записать результирующую сумму ±[Si]f2(+/-)min выражения (156) в виде графоаналитического выражения (158),
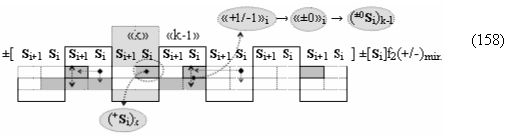
то из его анализа следует, что для активизации положительного аргумента (+Si)k условно «i» разряда в условно «k» «Зоне минимизации» необходимо, чтобы в условно «k-1» «Зоне минимизации» был активизирован активный логический ноль («+1/-1»i → «±0»i)k-1. А такая ситуация исключена в логико-динамическом процессе преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min выражения (156), поскольку если записать графоаналитическое выражение (159),
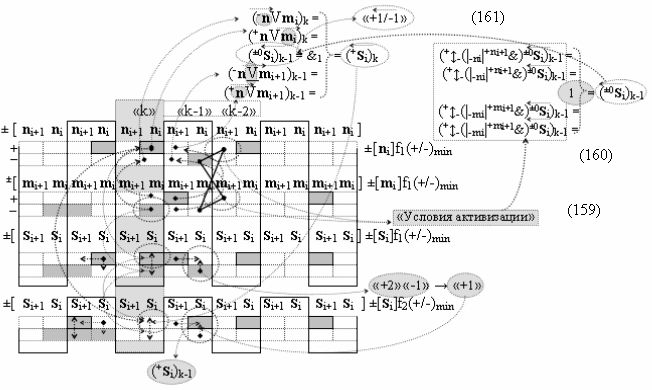
то не активизированные логические нули («+1/-1»i → «±0»i)k-1 могут быть объединены посредством функциональной структуры с выходной логической функцией f1(})-ИЛИ в выражении (160) с входными преобразованными аргументами (+↕-(-ni|+ni+1&)±0Si)k-1, (+↕-(-ni|+ni+1&)±0Si)k-1, (+↕-(-mi|+mi+1&)±0Si)k-1 и (+↕-(-mi|+mi+1&)±0Si)k-1, которые были сформированы между «Зонами минимизации» посредством логической функции f(&)-И и активизируют результирующий аргумент (±0Si)k-1, и он введен в систему логической функции f1(&)-И (161), исключая активизацию ее в графоаналитическом выражении (159). В результате после объединения функциональных структур (160) и (161) запишем аналитическое выражение (162),
посредством которого активизируют положительный результирующий аргумент (+Si)k условно «i» разряда в условно «k» «Зоне минимизации». При этом следует отметить, что функциональная структура (162) может быть минимизирована, если учесть, что активные входные аргументы (-nVmi)k и (+nVmi)k в функциональной структуре (157), которую запишем в виде аналитического выражения (163)
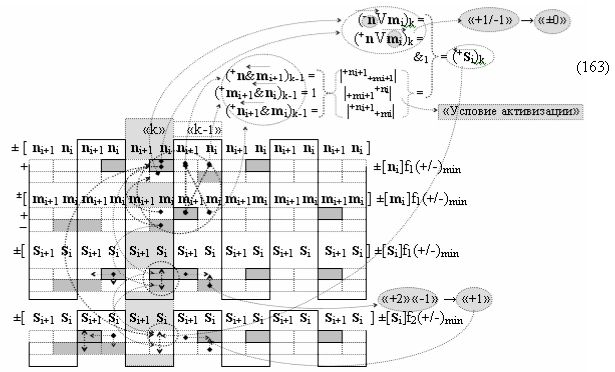
в своей совокупности соответствуют активному логическому нулю «+1/-1» → «±0», а в этой ситуации результирующий аргумент может быть активизирован только посредством положительного аргумента локального переноса f1(+|←+) из условно «k-1» «Зоны минимизации», а это возможно в этой «Зоне минимизации» только в трех ситуациях активности аргументов |+ni+1 +mi+1|, |+mi+1 +ni| и |+ni+1 +mi|, которого активизирует логическая функция f1(})-ИЛИ. Действительно, если записать логико-динамический процесс преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в виде графоаналитического выражения (164)
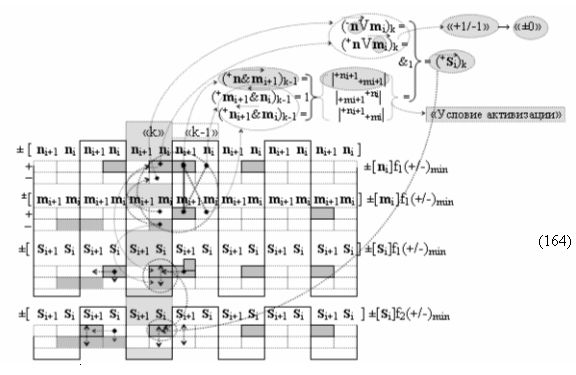
или в виде графоаналитического выражения (165)
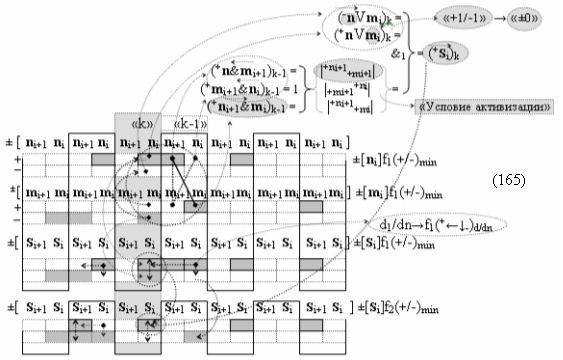
то положительный результирующий аргумент (+Si)k условно «i» разряда корректно активизирован. При этом в условно «k-1» «Зоне минимизации» активизируют условно отрицательный результирующий аргумент (-Si)k условно «i» разряда локального переноса f1(+↓-)d/dn процедуры логического дифференцирования d1/dn→f1(+←↓-)d/dn при тех же входных аргументах «Условия активизации», не преобразованных посредством логической функции f1(}&)-ИЛИ-НЕ, а функциональную структуру этой процедуры запишем в виде аналитического выражения (166).
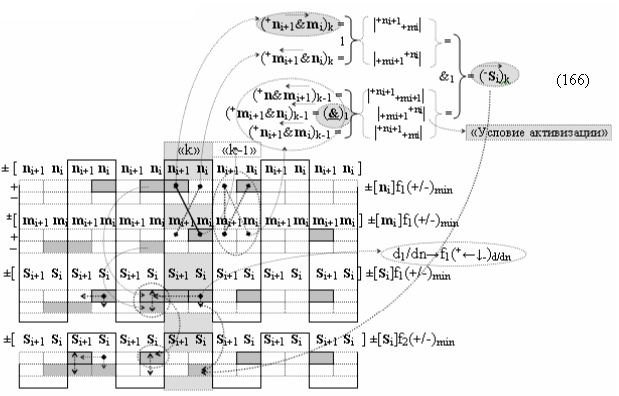
в котором необходима активность в условно «k» «Зоне минимизации» одного из входных преобразованных аргументов (+ni+1&mi)k или (+mi+1&ni)k, который посредством логической функции f1(})-ИЛИ и f1(&)-И активизирует результирующий условно отрицательный аргумент (-Si)k. Но возможны еще две структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, активные положительные аргументы которых также исключают в условно «k» «Зоне минимизации» активизацию результирующего условно отрицательного аргумента (-Si)k, и их запишем в виде графоаналитического выражения (167)
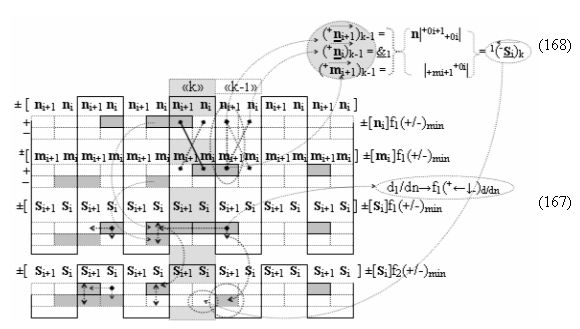
и в виде графоаналитического выражения (169),
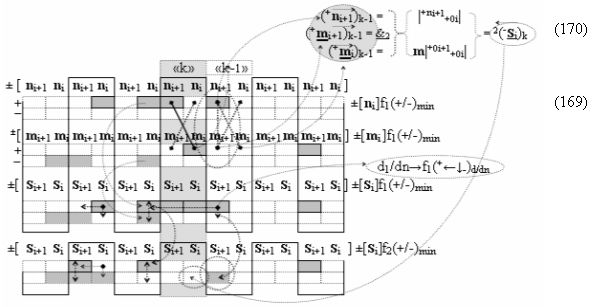
в которых функциональные структуры (168) и (170) с выходными логическими функциями f1(&)-И-НЕ и f2(&)-И-НЕ после введения в систему логических функций (166), записав ее в виде аналитического выражения (171),
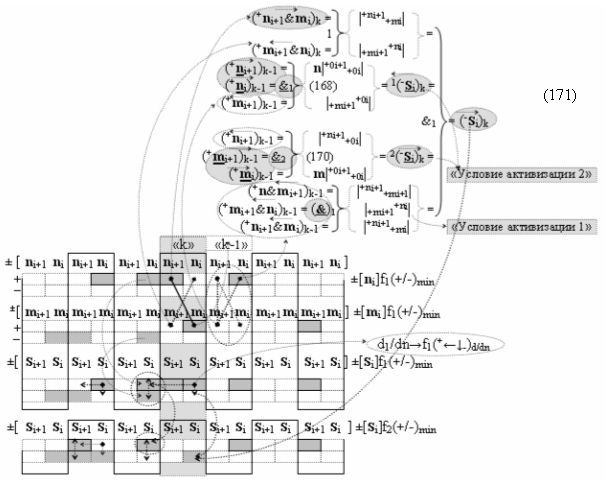
при их активности будут являться «Условием активизации 2» для положительной последовательности аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min. В результате функциональная структура (169) является корректной функциональной структурой, которая активизирует результирующий условно отрицательный аргумент (-Si)k в условно «i» разряде в структуре положительных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min. Но условно отрицательный аргумент (-Si)k в условно «i» разряде в структуре положительных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min может быть сформирован не только в результате локального переноса f1(+↓-)d/dn процедуры логического дифференцирования d1/dn→f1(+←↓-)d/dn, но и при его локальном переносе f1(+|←+)d/dn из условно «k-1» «Зоны минимизации». Поскольку если вернуться к анализу логико-динамического процесса преобразования аргументов слагаемых (151), записав его с учетом функциональной структуры (152) в виде графоаналитического выражения (172),
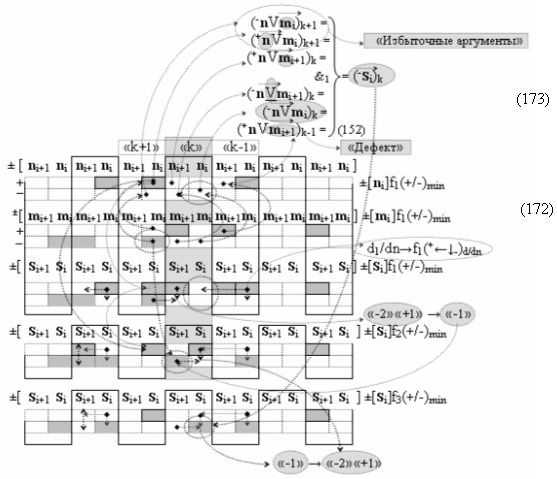
в котором результирующий условно отрицательный аргумент (-Si)k в условно «i» разряде в положительной структуре аргументов слагаемых активизирован в результате преобразования аргументов в условно «k» «Зоне минимизации» посредством применения обратной арифметической аксиомы «-2»«+1» → «-1», а ее применение в промежуточной сумме возможно только при активном положительном аргументе локального переноса f1(+|←+)d/dn из условно «k-1» «Зоны минимизации». А локальный перенос f1(+|←+)d/dn в данной ситуации возможен только при последовательной активности положительных аргументов в промежуточной сумме ±[Si]f1(+/-)min, которая не учтена в функциональной структуре (173), поэтому она сформирована с «Дефектом» и «Избыточными аргументами». Поскольку с одной стороны введенный в систему логической функции f1(&)-И преобразованный положительный аргумент (+nVmi+1)k-1не соответствует условию активизации положительного аргумента локального переноса f1(+|←+)d/dn, с другой стороны для применения обратной арифметической аксиомы «-2»«+1» → «-1» достаточно анализ активности аргументов в условно «k» «Зоне минимизации», поэтому функциональную структуру (173) запишем в виде аналитического выражения (174).
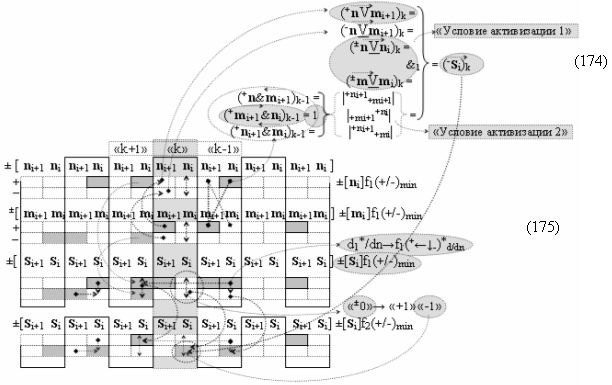
Из анализа логико-динамического процесса преобразования аргументов в структуре промежуточной суммы ±[Si]f1(+/-)min выражения (175) следует, что для формирования в данном случае минимизированной структуры аргументов результирующей суммы ±[Si]f2(+/-)min необходимо выполнить процедуру избирательного логического дифференцирования d1 */dn+→f1(+←↓-)* d/dn со следующей логикой преобразования аргументов, которую запишем в виде графоаналитического выражения (176)
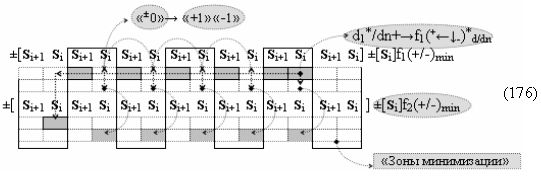
с формированием результирующей минимизированной суммы ±[Si]f2(+/-)min и в виде графоаналитического выражения (177)
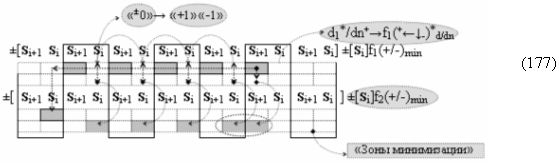
с формированием результирующей условно минимизированной суммы ±[Si]f2(+/-)min и активными аргументами между «Зонами минимизации». При этом следует отметить, что преобразование неактивных аргументов в чередующей последовательности одноименных аргументов выполняют в соответствии с арифметической аксиомой «±0»→ «+1»«-1», только если они позиционно расположены в условно «i» разряде. Поскольку если записать графоаналитическое выражение (178),
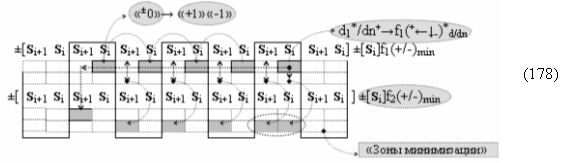
в котором активизированы неактивные аргументы в соответствии с арифметической аксиомой «±0»→ «+1»«-1», позиционно расположенные в условно «i+1» разряде, то структура результирующей суммы ±[Si]f2(+/-)min не относится к категории условно минимизированной суммы, поскольку два последовательно активных аргумента позиционно расположены в «Зоне минимизации». Аналогичные преобразования выполняют посредством процедуры избирательного логического дифференцирования d1 */dn-→f1(-←↑+)* d/dn и в структуре промежуточной суммы ±[Si]f1(+/-)min с чередующейся последовательностью условно отрицательных аргументов
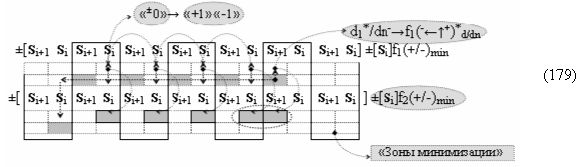
в результате также структуру результирующей суммы ±[Si]f2(+/-)min формируют в условно минимизированном виде, поскольку последовательные активные аргументы позиционно расположены между «Зонами минимизации». При этом следует отметить, что активизацию условно отрицательных аргументов в выражении (177) и положительных аргументов в выражении (179) в соответствии с арифметической аксиомой «±0»→ «+1»«-1» выполняют в чередующей последовательности, в которой отсутствует положительный аргумент локального переноса f1(+|←+)d/dn из предыдущей «Зоны минимизации». И функциональную структуру такого преобразования для положительной структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min запишем в виде аналитического выражения (180),
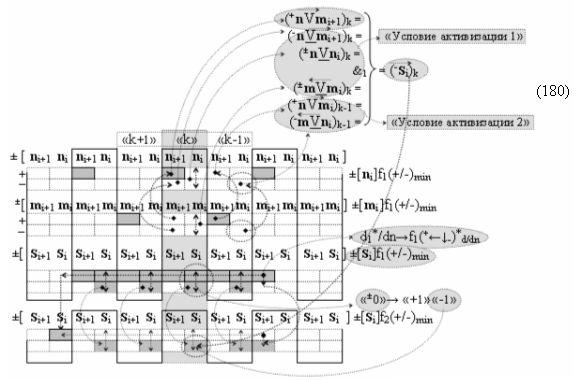
а для условно отрицательной структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min запишем в виде аналитического выражения (181),
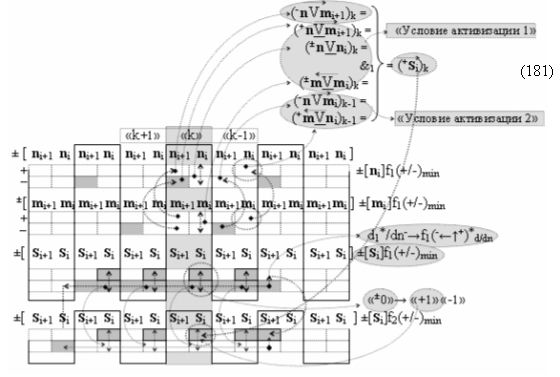
в котором посредством функциональной структуры с выходной логической функцией f1(&)-И активизирован положительный результирующий аргумент (+Si)k условно «i» разряда. И если вернуться к повторному анализу функциональной структур (174), записав ее в виде аналитического выражения (182),
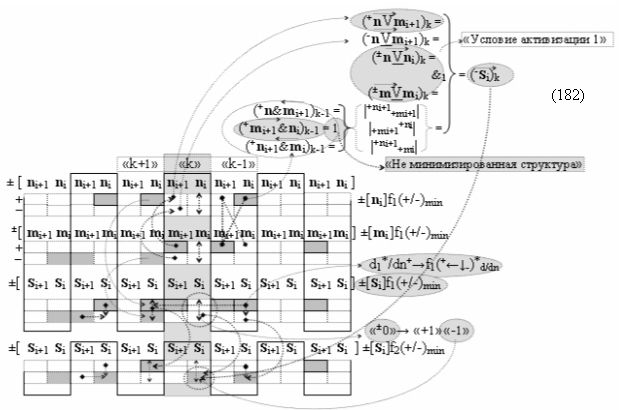
то с учетом функциональной структуры (181) в аналитическом выражении (182) в систему выходной логической функции f1(&)-И включена «Не минимизированная структура» с выходной логической функцией f1(})-ИЛИ и она может быть исключена, и скорректированное аналитическое выражение запишем в виде функциональной структуры (183),
в которой включены два условия активизации. Но функциональная структура с выходной логической функцией f1(})-ИЛИ в выражении (182), если ее записать в виде аналитического выражения (184),
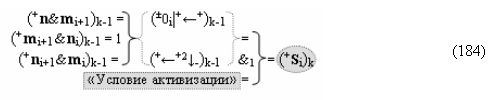
активизирует аргумент локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn и активизирует также положительный аргумент (+Si)k условно «i» разряда, но при соответствующих «Условиях активизации». Поэтому определимся с этими условиями, а для этого запишем для аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min логико-динамический процесс формирования условно минимизированной результирующей суммы в виде графоаналитического выражения (185),
в котором для активизации положительного аргумента (+←+)d/dn(+Si)k-1 условно «k-1» «Зоны минимизации» локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn введено «Условие активизации», и оно заключается в том, что в условно «k» «Зоне минимизации» должны быть неактивные все аргументы слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, и только в этой ситуации активизируют результирующий положительный аргумент (+Si)k функциональной структуры (186). Но поскольку положительный аргумент (+←+)d/dn(+Si)k-1 является аргументом условно «k-1» «Зоны минимизации», а в этой «Зоне минимизации» активизируют условно отрицательный аргумент (+↓-)d/dn(-Si)k-1 локального переноса f1(+↓-)d/dn. Поэтому функциональную структуру (186) запишем в виде аналитического выражения (187)
с входным преобразованным аргументом ↓(+←+)d/dn(+Si)k-1 условно «k-1» «Зоны минимизации», а активизацию условно отрицательного аргумента (+↓-)d/dn(-Si)k-1 локального переноса f1(+↓-)d/dn в этой зоне с учетом синтеза математической модели условно «k» «Зоны минимизации» запишем в виде функциональной структуры (188),
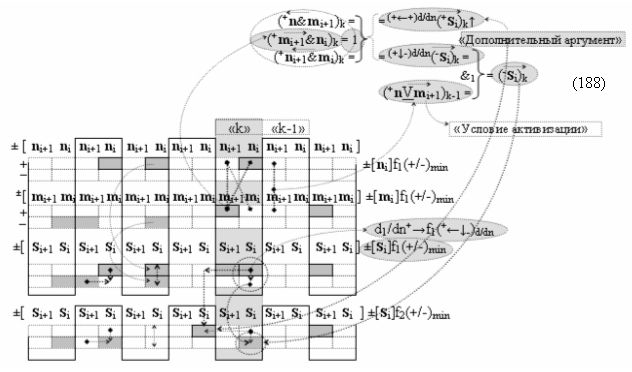
в которой введен преобразованный дополнительный аргумент (+←+)d/dn(+Si)k↑ для очередной «Зоны минимизации». При этом следует отметить, что в систему выходной логической функции f1(&)-И в качестве «Условия активизации» введен только один преобразованный положительный аргумент (+nVmi+1)k-1, поскольку только неактивность его исключает активизацию условно отрицательного результирующего аргумента (-Si)k, а его неактивность непосредственно связана с активностью положительного аргумента одного из слагаемых ±[ni]f1(+/-)min или ±[mi]f1(+/-)min
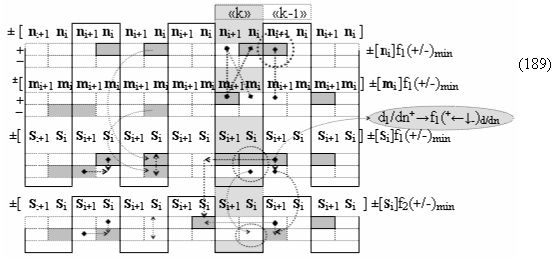
или с одновременно активностью положительного аргумента двух слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min.
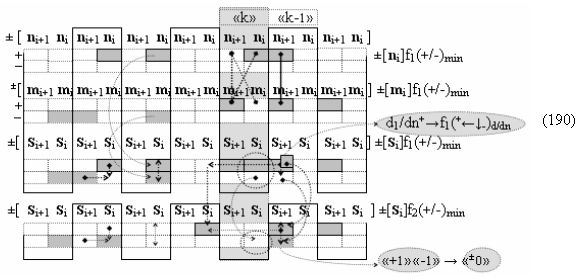
И если в логико-динамическом процессе преобразования аргументов (189) в результате процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn в условно «k-1» «Зоне минимизации» активизируется результирующий условно отрицательный аргумент, то в процедуре преобразования аргументов (190) этот условно отрицательный аргумент с положительным аргументом формирует активный логический ноль «+1»«-1» → «±0», поэтому в функциональной структуре (188) преобразованный положительный аргумент (+nVmi+1)k-1 введен в систему логической функции f1(&)-И корректно. Возможна также структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, которую запишем в виде графоаналитического выражения (191),
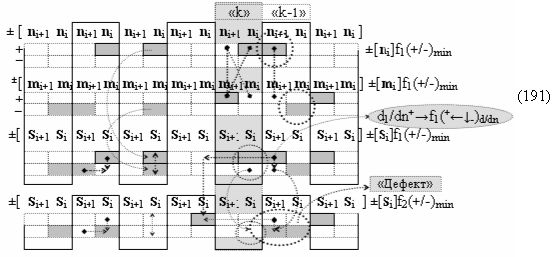
в котором результирующая структура суммы ±[Si]f2(+/-)min имеет «Дефект», поскольку преобразование аргументов для исключения должно выполняться в соответствии с логико-динамическим процессом (192).
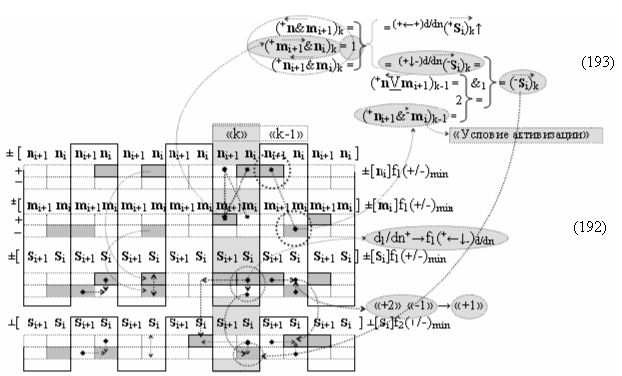
И для данной структуры аргументов слагаемых в функциональной структуре (193) введена дополнительная логическая функция f2(})-ИЛИ, в систему которой включен преобразованный аргумент (+ni+1&-mi)k-1 условно «k-1» «Зоны минимизации», являющийся в данной ситуации аргументом «Условия активизации» результирующего условно отрицательного аргумента (-Si)k локального переноса f1(+↓-)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn в «k» «Зоне минимизации». И возможна также структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, которую запишем в виде графоаналитического выражения (193),
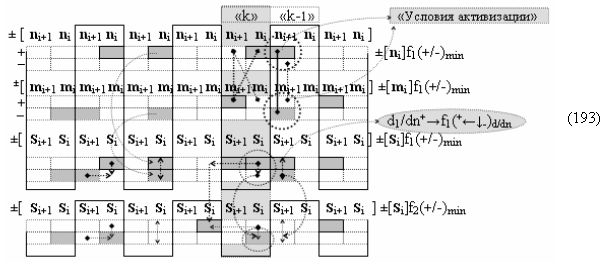
в которой также в условно «k» «Зоне минимизации» активен результирующий условно отрицательный аргумент (-Si)k локального переноса f1(+↓-)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn. Поэтому в систему дополнительной логической функции f2(})-ИЛИ выражения (193) необходимо ввести два преобразованных аргумента (+ni+1&-mi+1)k-1 и (-ni+1&+mi+1)k-1 «k-1» «Зоны минимизации» дополнительного «Условия активизации», и функциональную структуру для этой ситуации запишем в виде аналитического выражения (194),
которое и является математической моделью функциональной структуры для активизации результирующего условно отрицательного аргумента (-Si)k локального переноса f1(+↓-)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn. При этом следует отметить, что в функциональной структуре (194) в системе входной логической функции f1(})-ИЛИ включен «Избыточный аргумент» (+n&mi+1)k, который в логико-динамическом процессе преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (195)
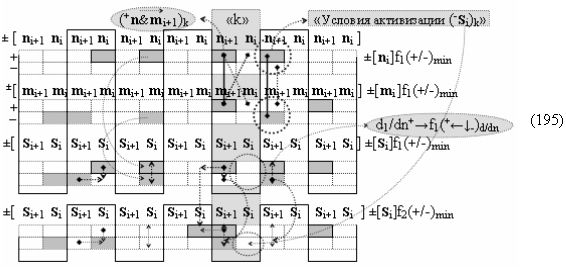
активен при активном «Условии активизации (-Si)k», что приведет к формированию «Дефекта». Поэтому функциональную структуру (194) запишем в виде аналитического выражения (196),
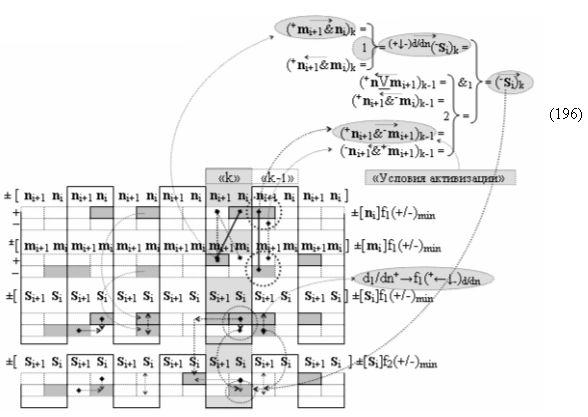
в котором логическая функция f1(})-ИЛИ выполняет только функцию активизации условно отрицательного аргумента (+↓-)d/dn(-Si)k локального переноса f1(+↓-)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn, а функциональную структуру, активизирующую положительный аргумент (+←+)d/dn(+Si)k локального переноса f1(+←+)d/dn запишем в виде аналитического выражения (197).
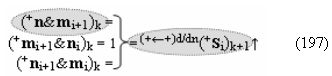
Далее, если вернуться к анализу функциональной структуры (166), которая также выполняет только функцию активизации условно отрицательного аргумента (+↓-)d/dn(-Si)k локального переноса f1(+↓-)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn, записав ее в виде аналитического выражения (198),
и провести сравнительный анализ со структурой логических функций (196), то они имеют разные функциональные структуры «Условия активизации». Поэтому проведем дополнительный анализ корректности активизации результирующего условно отрицательного аргумента (-Si)k, а для этого сформируем графоаналитическое выражение (199),
в котором функциональная структура (200) корректно активизирует результирующий условно отрицательный аргумент (-Si)k. Но возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (201),
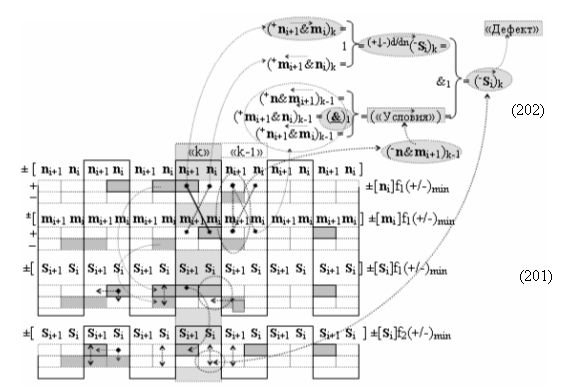
в котором результирующий условно отрицательный аргумент (-Si)k функциональной структуры (202) активизирован с «Дефектом», поскольку в систему логической функции f1(}&)-ИЛИ-НЕ не включен преобразованный условно отрицательный аргумент (-n&mi+1)k-1, который в данной ситуации является «Условием активизации». Поэтому функциональную структуру (202) запишем либо в виде аналитического выражения (203),
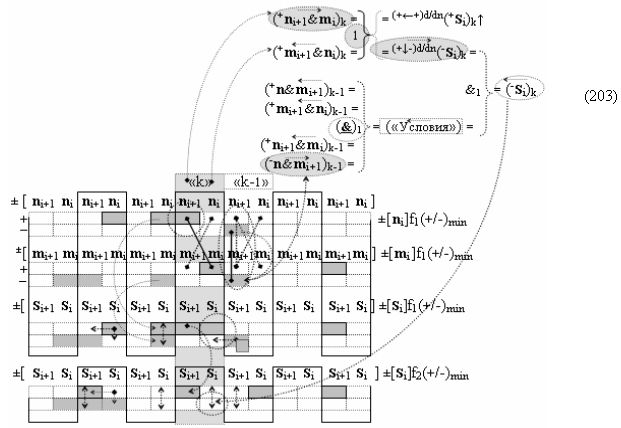
либо в виде аналитического выражения (204),
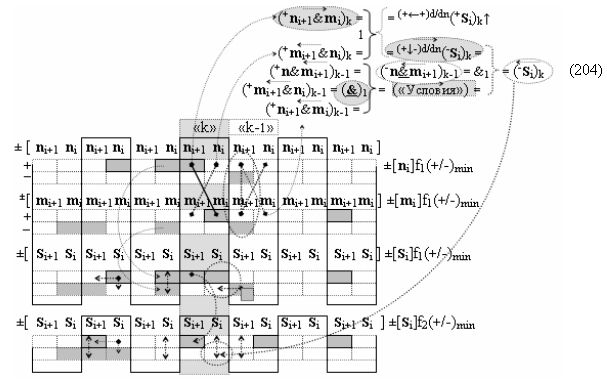
которые корректно исключают активизацию результирующего условно отрицательного аргумента (-Si)k, поскольку в систему логической функции f1(}&)-ИЛИ-НЕ выражения (203) включен преобразованный условно отрицательный аргумент (-n&mi+1)k-1, сформированный посредством логической функции f(&)-И. А в выражении (204) корректный результат получен в связи с неактивностью преобразованного условно отрицательного аргумента (-n&mi+1)k-1, сформированного посредством логической функции f(&)-И-НЕ, который включен в систему выходной логической функции f1(&)-И. Но при этом в условно «k» «Зоне минимизации» должен быть активизирован положительный результирующий аргумент (+Si+1)k условно «i+1» разряда и его активизируют посредством функциональной структуры (205),
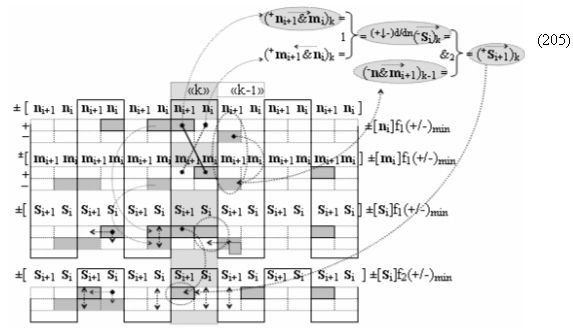
а если учесть, что она будет включена в выходную систему логической функции общей математической модели сумматора ±f1(ΣRU)min, то выполним ее минимизацию, поскольку в данной реализации ее технологический цикл ∆tΣ преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min соответствует
∆tΣ → f(&) → f1(}) → f2(&) → f(})вых → 4∙f(&)
четырем условным логическим функциям f(&)-И. А для этого запишем векторную структуру (206)
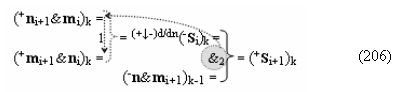
переноса выходной логической функции через систему логической функции и запишем структуру логических функций (207),
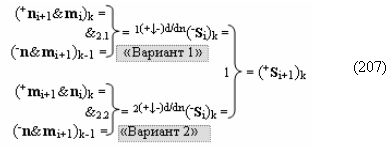
в которой сформированы «Вариант 1» и «Вариант 2» функциональной структуры, активизирующей положительный результирующий аргумент (+Si+1)k условно «i+1» разряда с технологическим циклом ∆tΣ
∆tΣ → f(&) → f2(&) → f1(})вых → 3∙f(&)
равным трем условным логическим функциям f(&)-И.
Далее, если вернуться к анализу функциональной структуры (203), записав ее в виде аналитического выражения (208)
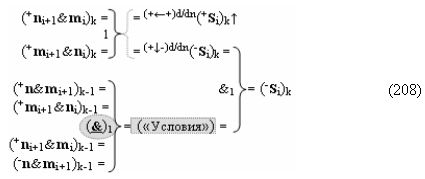
и к анализу функциональной структуры (204), записав ее в виде аналитического выражения (209)
то они также могут быть минимизированы. Поскольку если записать функциональную структуру («Условия») с выходной логической функцией f1(}&)-ИЛИ-НЕ ↔ f2(})-ИЛИ = f1(&)-НЕ выражения (203) в скорректированном виде
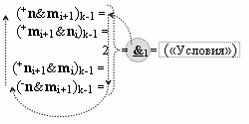
и выполнить перенос логической функции f1(&)-НЕ через систему логической функции f2(})-ИЛИ, то ее свойства изменятся на свойства логической функции f2(&)-И, а дальнейший перенос логической функции f1(&)-НЕ через преобразованные входные аргументы изменят логическую функцию f(&)-И → f(&)-И-НЕ, посредством которой они были сформированы, в результате запишем скорректированную функциональную структуру (210).
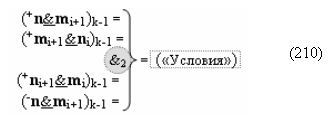
А если учесть, что скорректированная функциональная структура (210) («Условия») с выходной логической функцией f2(&)-И должна быть включена в систему логической функции f1(&)-И выражения (208), то после объединения одноименных логических функций запишем аналитическое выражение (211),
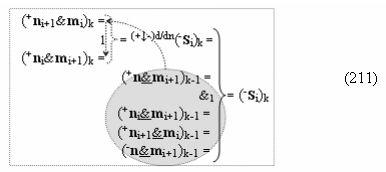
в которой выполним перенос функциональной структуры с выходной логической функцией f1(&)-И через систему логической функции f1(})-ИЛИ и запишем аналитическое выражение (212)
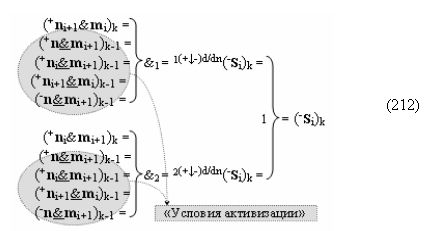
с технологическим циклом ∆tΣ
∆tΣ → f(&)Vf(&) → f2(&) → f1(})вых → 3∙f(&)
равным трем условным логическим функциям f(&)-И. При этом следует отметить, что «Условия активизации» выражения (212) должны быть введены и в функциональную структуру (197), активизирующую положительный аргумент (+←+)d/dn(+Si)k+1 локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn в условно «k-1» «Зоне минимизации»,
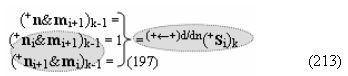
но это «Условие активизации» (213) непосредственно касается только преобразованных входных аргументов (+ni&mi+1)k-1 и (+ni+1&mi)k-1, поскольку если записать логико-динамический процесс преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (214),
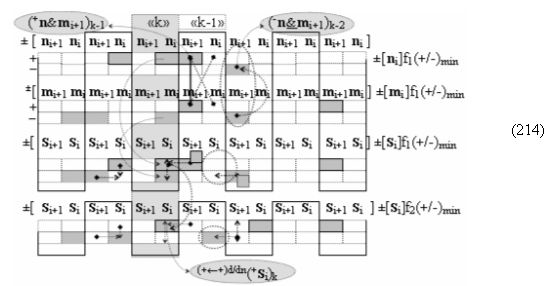
то активность положительного преобразованного аргумента (+n&mi+1)k-1 не зависит от активности преобразованного условно отрицательного аргумента (-n&mi+1)k-2 условно «k-2» «Зоны минимизации». Поэтому функциональную структуру (213) для очередной «k» «Зоны минимизации» запишем в виде аналитического выражения (215),
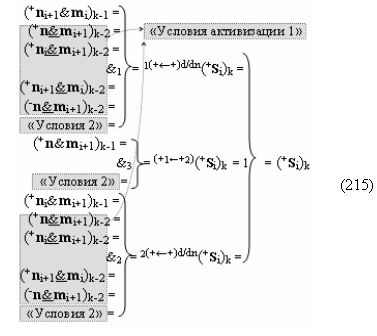
в котором в систему логических функций f1(&)-И - f2(&)-И введены общие «Условия 2» для активизации положительного результирующего аргумента (+Si)k в этой «Зоне минимизации» в результате выполнения как локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn+→f1(+←↓-)d/dn, активизирующего положительный преобразованный аргумент 1(+←+)d/dn(+Si)k и 2(+←+)d/dn(+Si)k посредством логических функций f1(&)-И и f2(&)-И, так и локального переноса f1(+1←+2) двойного аргумента из предыдущего разряда, активизирующего положительный преобразованный аргумент (+1←+2)(+Si)k посредством логических функций f3(&)-И. При этом следует отметить, что для всех логических функций f1(&)-И - f3(&)-И «Условия 2» является общим «Условием активизации», поэтому сформируем те логико-динамические процессы преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, в которых активизирован положительный преобразованный аргумент (+1←+2)(+Si)k и определимся со всеми возможными условиями его активизации.
Версия 1, 2 и 3. Активизация положительного преобразованного аргумента (+1←+2)(+Si)k в условно «k» «Зоне минимизации» возможна в графоаналитическом выражении (216)
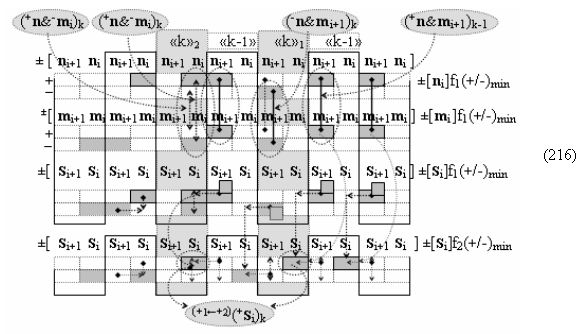
в условно «k»1 «Зоне минимизации» при одновременной активности в условно «i+1» разряде как положительных аргументов, так и условно отрицательных аргументов двух слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, а в условно «k»2 «Зоне минимизации» при активном аргументе нуля «+1»«-1» → «±0» в условно «i» разряде и «Условия активизации» в данной ситуации введем в систему логической функции f3(&)-И выражения (215). В результате функциональную структуру запишем в виде аналитического выражения (217),
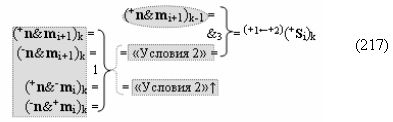
в котором «Условия 2» представляют собой функциональную структуру с выходной логической функцией f3(&)-И с входными преобразованными аргументами (+n&mi+1)k, (-n&mi+1)k, (+n&-mi)k и (-n&+mi)k , активность одного из них активизирует, при активном преобразованном аргументе (+n&mi+1)k-1 активизирует положительный результирующий аргумент (+1←+2)(+Si)k. При этом следует отметить, что технологический цикл ∆tΣ «Условия 2» соответствует
∆tΣ → f(&) → f1(}) → 2∙f(&)
двум условным логическим функциям f(&)-И, и если ввести «Условия 2» в систему логических функций f1(&)-И и f2(&)-И выражения (215), записав аналитическое выражение (218),
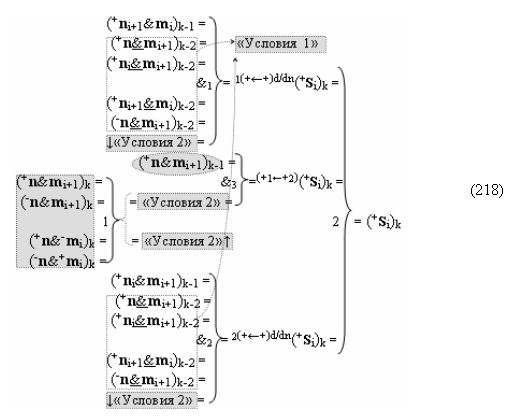
то технологический цикл ∆tΣ активизации промежуточных аргументов 1(+←+)d/dn(+Si)k и 2(+←+)d/dn(+Si)k будет соответствовать
∆tΣ → f(&) → f1(}) → f1(&) → f2(}) → 4∙f(&)
четырем условным логическим функциям f(&)-И. Но если функциональную структуру (218) записать в виде скорректированного аналитического выражения (219)
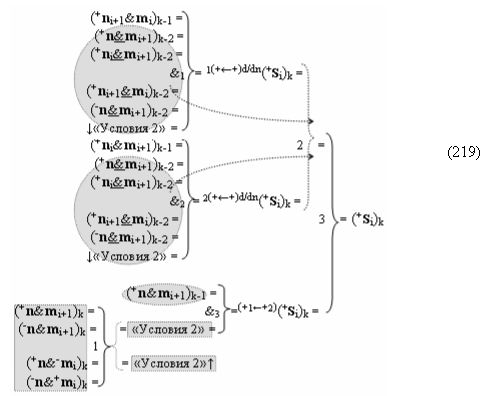
и выполнить перенос функциональных структур с выходными логическими функциями f1(&)-И и f2(&)-И с одноименными аргументами через систему логической функции f2(})-ИЛИ, то запишем скорректированную структуру логических функций (220),
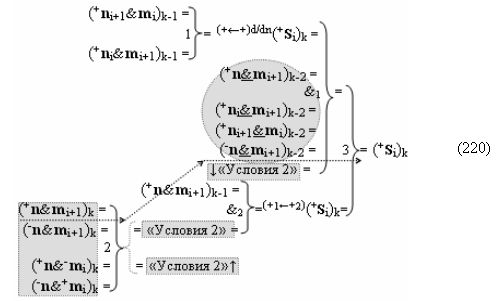
в которой технологический цикл ∆tΣ активизации промежуточных аргументов 1(+←+)d/dn(+Si)k и 2(+←+)d/dn(+Si)k будет также соответствовать
∆tΣ → f(&) → f2(}) → f1(&) → f3(}) → 4∙f(&)
четырем условным логическим функциям f(&)-И, но с минимальным числом логических функций, поэтому она является оптимизированной структурой логических функций. А если записать графоаналитическое выражение (221)
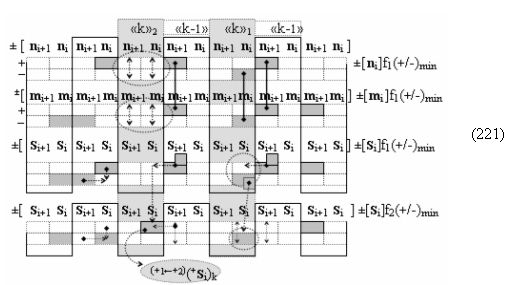
то «Условием 3» в условно «k»2 «Зоне минимизации» является преобразованный аргумент (±n,±mi+1)V(±n,±mi)k функциональной структуры (222),
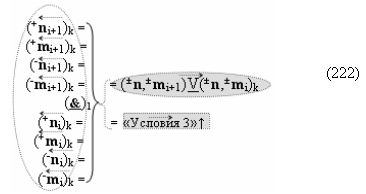
при этом следует отметить, что «Условие 2» выражения (220) и «Условие 3» выражения (222) функционально не совместимы, поскольку активность одного исключает активность другого. Действительно, для активизации преобразованного аргумента (±n,±mi+1)V(±n,±mi)k Условия 3»↑ необходимо, чтобы в системе логической функции f1(}&)-ИЛИ-НЕ выражения (222) неактивными были все входные аргументы, а в этой ситуации, если активизировать входные аргументы в соответствии со структурой аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (223),
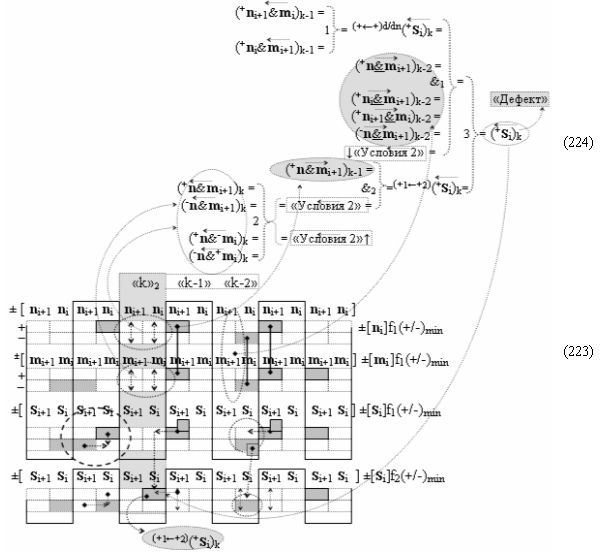
то положительный результирующий аргумент (+Si)k в функциональной структуре (224) не будет активизирован. Поэтому необходимо в систему логической функции f2(})-ИЛИ выражения (224) ввести функциональную дополнительную структуру «Условия 3» выражения (222) и записать в виде аналитического выражения (225),
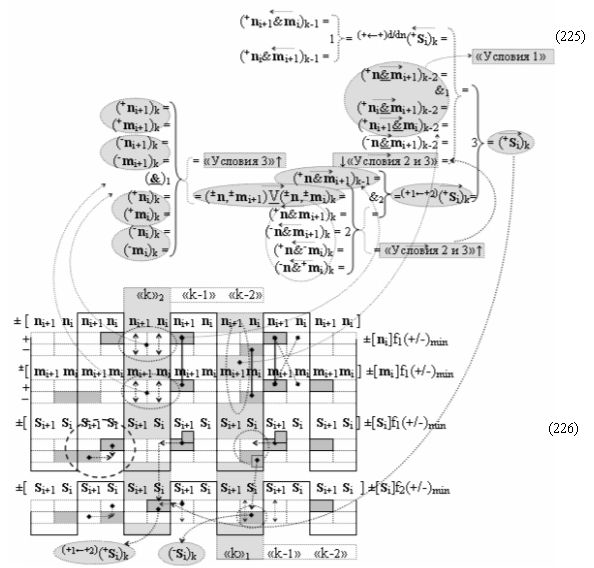
в которой положительный результирующий аргумент (+Si)k корректно активизирован при активном положительным аргументе (+n&mi+1)k-1 локального переноса f1(+←+2), поскольку активен в системе логической функции f1(}&)-ИЛИ-НЕ ее преобразованный аргумент (±n,±mi+1)V(±n,±mi)k в условно «k»2 «Зоне минимизации». Но если проанализировать процедуру активизации условно отрицательного результирующего аргумента (-Si)k в условно «k»1 «Зоне минимизации» графоаналитического выражения (226), то он активизируется при активном положительном аргументе (+n&mi+1)k-1 локального переноса f1(+←+2) и активном положительном аргументе (+←+)d/dn(+Si)k локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn. А для этого необходима одновременная активность в «i» разряде одновременно двух условно отрицательных аргументов (-n&mi)k слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, при этом следует отметить, что при активном положительном аргументе (+←+)d/dn(+Si)k локального переноса f1(+←+)d/dn «Условия 1» структуры логических функций (225) должны быть соблюдены. Поэтому эти «Условия 1» целесообразно записать в виде отдельной функциональной структуры с выходной логической функцией f1(&)-И в аналитическом выражении (227),
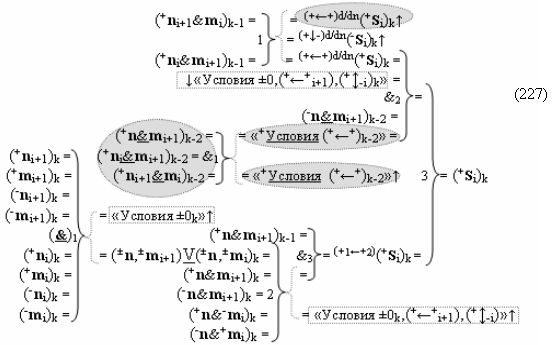
в котором введены дополнительные преобразованные положительные аргументы (+←+)d/dn(+Si)k↑ и «+Условия (+←+)k-2»↑. В результате функциональную структуру, посредством которой активизируют условно отрицательный результирующий аргумент (-Si)k, запишем в виде аналитического выражения (228)
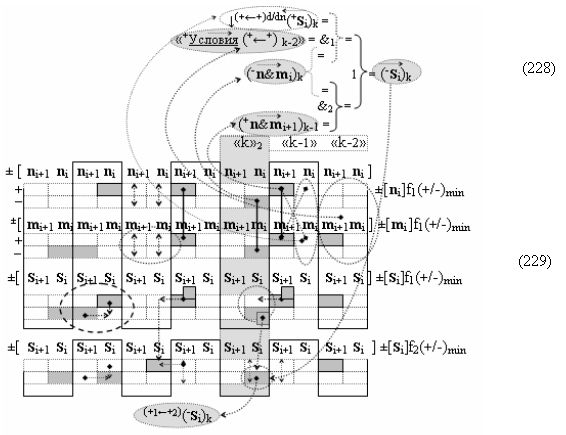
с выходной логической функцией f1(})-ИЛИ и в ее систему может быть введена неоптимизированная функциональная структура (211), записав ее в виде выражения (230),
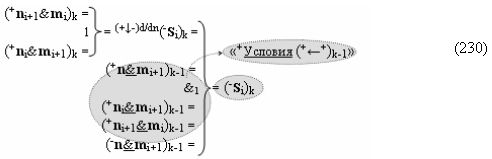
активизирующая также условно отрицательный результирующий аргумент (-Si). При этом следует отметить, что особенностью в системе выходной логической функции f1(&)-И выражения (230) является совокупность преобразованных аргументов, сформированных посредством логической функции f1(&)-И-НЕ, которые в системе этой функции активизируют аргумент «Условия 1»k-1 условно «k-1» «Зоны минимизации», и этот преобразованный аргумент включают в систему других логических функций. Поэтому функциональную структуру (230) целесообразно записать в виде аналитического выражения (231)
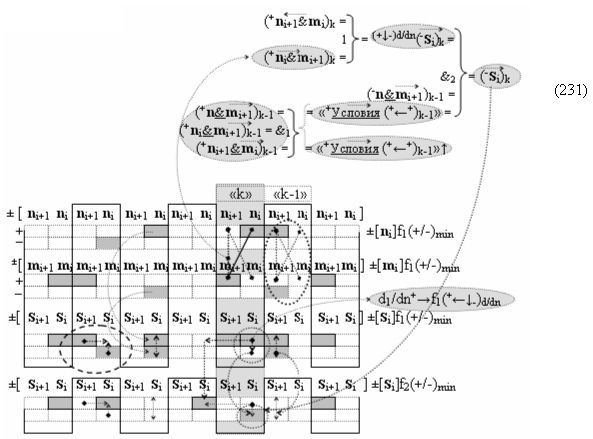
с преобразованным положительным аргументом «+Условия (+←+)k-1» условно «k-1» «Зоны минимизации», при этом из функциональной структуры (231) может быть исключена логическая функция f1(})-ИЛИ, поскольку она включена в структуру логических функций выражения (227).
В результате после объединения функциональных структур (228) и (231) запишем аналитическое выражение (232),
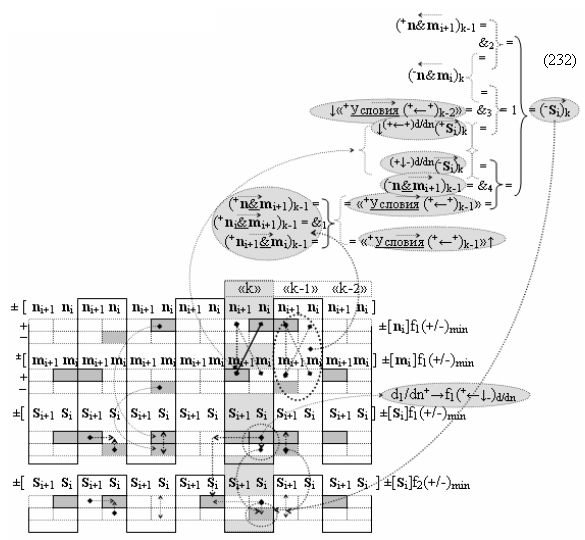
где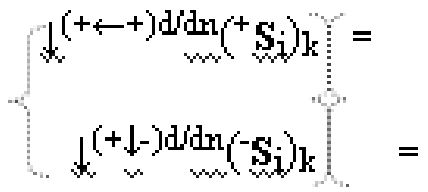 
- система преобразованных аргументов, которые формирует одна функциональная структура, активизирующая положительный аргумент (+←+)d/dn(+Si)k↑ локального переноса f1(+←+)d/dn и условно отрицательный аргумент (+↓-)d/dn(-Si)k↑
локального переноса f1(+↓-)d/dn процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn. А, учитывая то, что в структуре логических функций выражения (232) включена функциональная структура преобразованного положительного аргумента «+Условия (+←+)k-1»↑ условно «k-1» «Зоны минимизации», поэтому функциональную структуру (227) запишем в виде аналитического выражения (233)
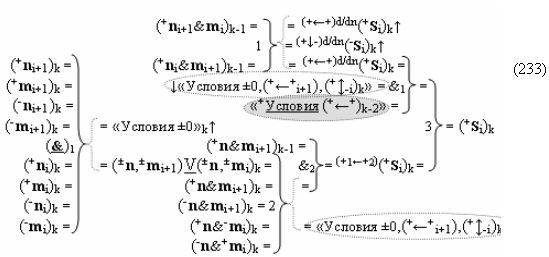
с преобразованным положительным аргументом «+Условия (+←+)k-2» условно «k-2» «Зоны минимизации».
Далее, если вернуться к анализу функциональной структуры (205), записав ее в виде аналитического выражения (234),
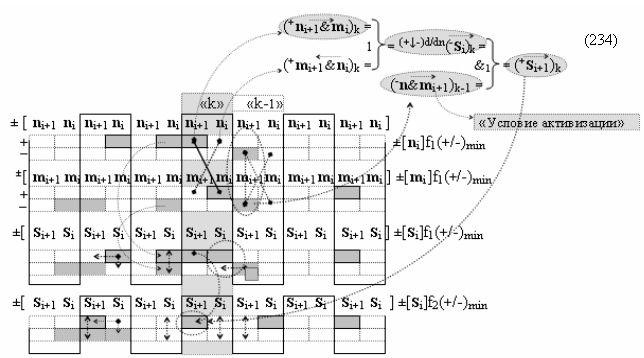
то для активизации положительного результирующего аргумента (+Si+1)k условно «i+1» разряда преобразованный аргумент (-n&mi+1)k-1 является недостаточым «Условием активизации», поскольку возможны еще две структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, при преобразовании которых также активизируется этот аргумент. Поэтому функциональную структуру (234) запишем в виде аналитического выражения (235),
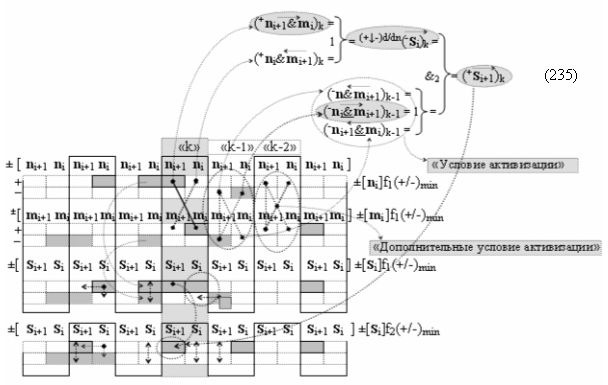
в которое необходимо ввести «Дополнительные условие активизации» условно «k-2» «Зоны минимизации», и они непосредственно относятся только к преобразованным условно отрицательным аргументам (-ni&mi+1)k-1 и (-ni+1&mi)k-1. Поэтому функциональную структуру (235) с учетом функциональной структуры (233) запишем в виде аналитического выражения (236),
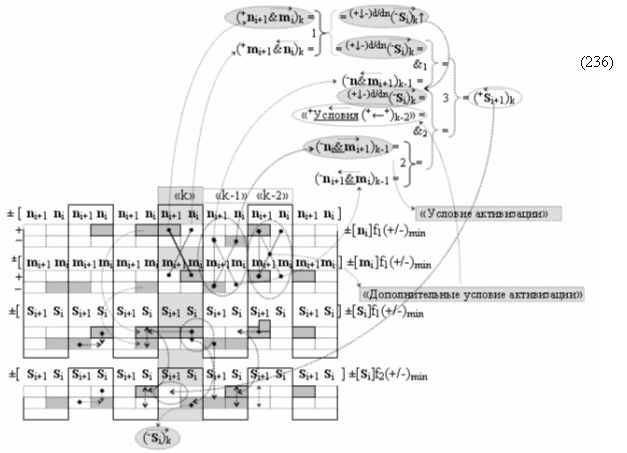
в котором в качестве «Дополнительного условия активизации» в систему логической функции введен положительный неактивный преобразованный аргумент «+Условия (+←+)k-2» условно «k-2» «Зоны минимизации», сформированный в функциональной структуре (231). В результате функциональная структура (236) корректно не активизирует результирующий условно отрицательный аргумент (-Si+1)k условно «i+1» разряда, но при этом в условно «k-2» «Зоне минимизации» активен условно отрицательный аргумент (-Si)k условно «i» разряда, а для его активизации сформирована функциональная структура (231). Поэтому проанализируем ее корректность активизации этого аргумента, а для этого запишем векторную структуру активизации аргументов (237).
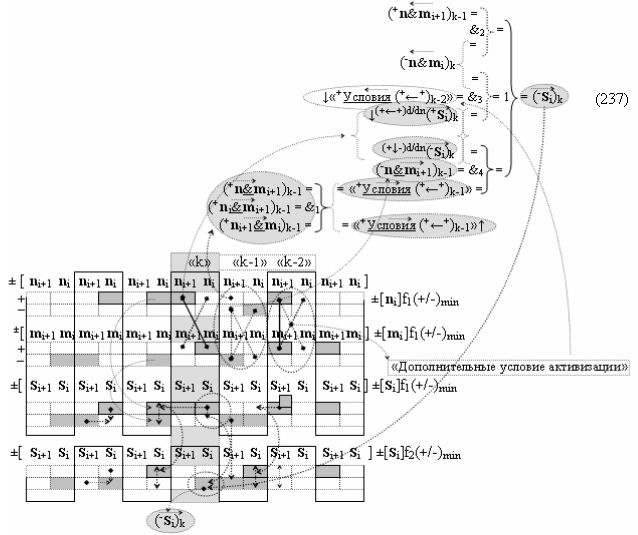
Из анализа векторной структуры активизации аргументов в функциональной структуре (237) следует, что результирующий условно отрицательный аргумент (-Si)k условно «i» разряда активизирован корректно, но если записать структуру аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (238),
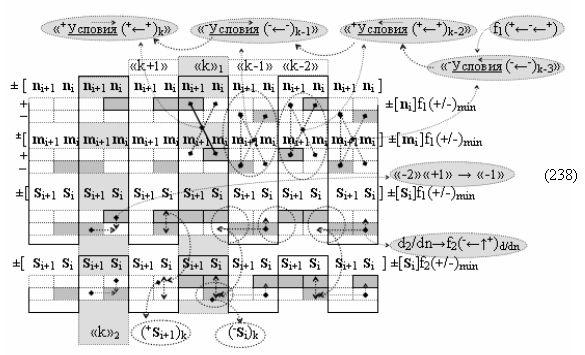
то активизация этого аргумента зависит от последовательной активности преобразованных положительных и условно отрицательных аргументов «+Условия (+←+)k» → «-Условия (-←-)k-1» → «+Условия (+←+)k-2» → «-Условия (-←-)k-3» «Зон минимизации», которые, по существу, относятся к категории сквозного переноса f1(+←-←+). И в этой ситуации возникает неоднозначность в активизации как результирующего условно отрицательного аргумента (-Si)k в условно «k»1 «Зоне минимизации», так и положительного результирующего аргумента (+Si+1)k в условно «k+1» «Зоне минимизации», поскольку необходим анализ предыдущих «Зон минимизации». Аналогичная ситуация возможна и в условно «k»2 «Зоне минимизации», если записать графоаналитическое выражение (239),
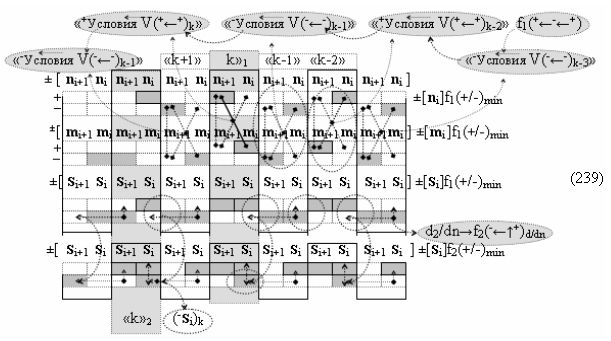
где «+Условия V(+←+)k» и «-Условия V(-←-)k» - положительный и условно отрицательный преобразованный аргумент возможных локальных переносов процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn d2/dn→f2(-←↑+)d/dn, который сформирован посредством функциональной структуры (240)
и посредством функциональной структуры (241),
которые сформированы посредством логической функции f1(})-ИЛИ и f2(})-ИЛИ в условно «k» «Зоне минимизации», и в систему включают два положительных преобразованных аргумента (+ni+1&mi)k и (+ni&mi+1)k и условно отрицательных аргумента (-ni+1&mi)k и (-ni&mi+1)k соответственно. При этом следует отметить, что в систему логических функций f1(})-ИЛИ и f2(})-ИЛИ не введен преобразованный аргумент (+mi+1&ni)k и (-mi+1&ni)k , поскольку их активность не приводит к неоднозначности при преобразовании аргументов слагаемых в условно «k+1» «Зоне минимизации». При этом следует отметить, что такая неоднозначность в активизации результирующего условно отрицательного аргумента (-Si)k, так и положительного результирующего аргумента (+Si)k в условно «k» «Зоне минимизации» непосредственно связана с чередующейся структурой положительных двойных и условно отрицательных аргументов в объединенной структуре слагаемых ±[Si]f1(+/-)min. И если сформировать графоаналитическое выражение (242),
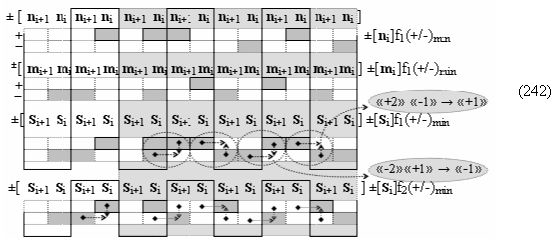
то преобразование объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min может быть выполнено либо посредством процедуры логического дифференцирования условно отрицательных последовательно активных аргументов, как в выражении (239),
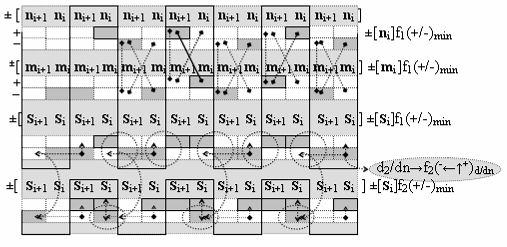
либо посредством применения обратных арифметических аксиом «+2» «-1» → «+1» и «-2»«+1» → «-1», в результате будет сформирована в «Зонах минимизации» с чередующейся структурой положительных двойных и условно отрицательных аргументов условно минимизированная структура результирующей суммы ±[Si]f2(+/-)min. При этом следует отметить, что преобразование таких структур на локальном уровне может быть выполнено для положительного преобразованного аргумента «+Условия V(+←+)k» посредством функциональной структуры (243)
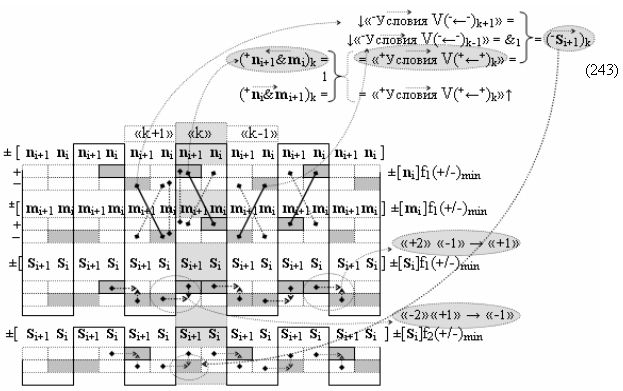
и преобразование может быть выполнено для условно отрицательного преобразованного аргумента «-Условия V(-←-)k» посредством функциональной структуры (244),
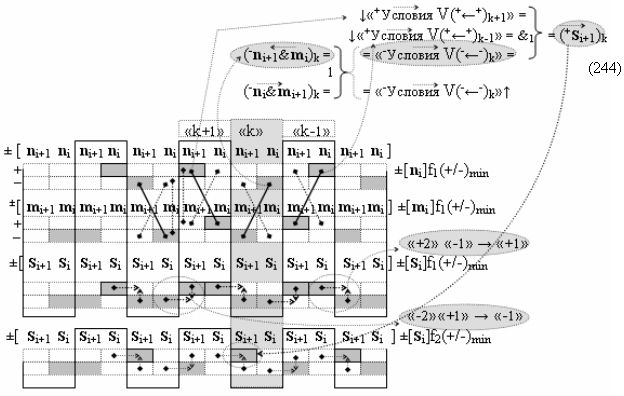
в результате преобразованный положительный аргумент «+Условия V(+←+)k в функциональной структуре (243) активизирует результирующий условно отрицательный аргумент (-Si+1)k условно «i+1» разряда, а условно отрицательный аргумент «+Условия V(+←+)k в функциональной структуре (244) активизирует положительный результирующий аргумент (+Si+1)k в том же разряде. При этом следует отметить, что все преобразования аргументов в объединенной структуре слагаемых ±[Si]f1(+/-)min в выражениях (244) и (245) выполняют между «Зонами минимизации» с применением обратных арифметических аксиом «+2» «-1» → «+1» и «-2»«+1» → «-1». Аналогичные преобразования выполняют, когда структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min формирует либо один положительный преобразованный аргумент «+Условия V(+←+)k» и активизирует в этой ситуации функциональная структура (245)
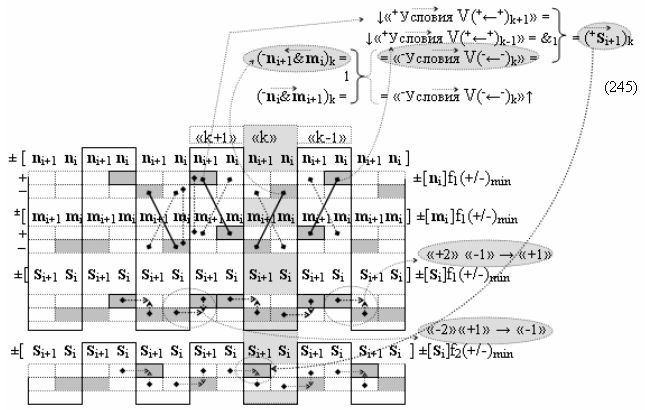
условно отрицательный аргумент (-Si+1)k, либо один условно отрицательный преобразованный аргумент «-Условия V(-←-)k», и в этой ситуации функциональная структура (246)
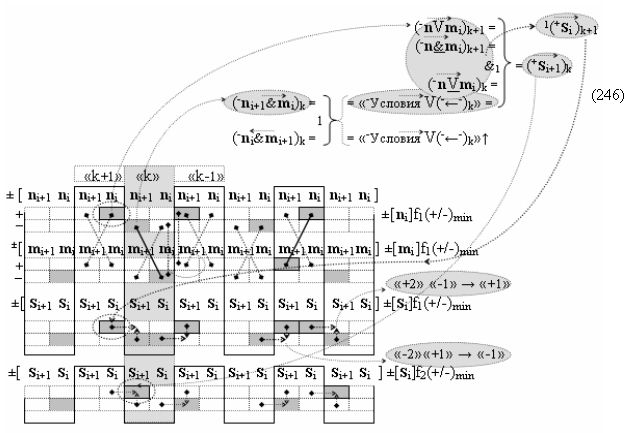
активизирует положительный аргумент (+Si+1)k условно «i+1» разряда. При этом особенностью функциональных структур (245) и (246) является совокупность преобразованных аргументов, и если записать их для условно «k» «Зоны минимизации» в виде аналитического выражения (247)
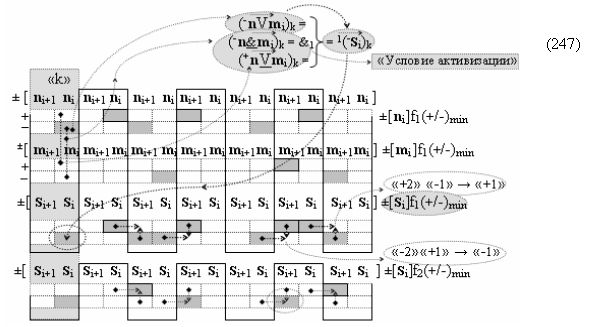
и в виде аналитического выражения (248)
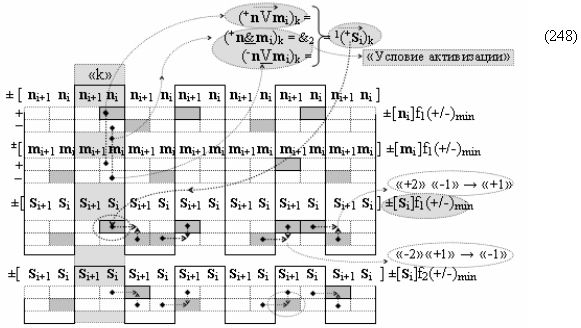
то функциональные структуры (247) и (248) являются математическими моделями активизации условно отрицательного аргумента 1(-Si)k и положительного аргумента 1(+Si)k в объединенной структуре слагаемых ±[Si]f1(+/-)min, а для их активизации необходимо только два «Условия». С одной стороны в условно «k» «Зоне минимизации» не должно быть двух одноименных аргументов, поэтому в систему логических функций f2(&)-И f1(})-ИЛИ введен преобразованный аргумент (+nVmi)k и (-nVmi)k соответственно, которые сформированы посредством логической функции f(&)-И-НЕ. С другой стороны в условно «k» «Зоне минимизации» не должно быть активного логического нуля «+1»«-1» → «±0», поэтому в систему логических функций f2(&)-И f1(})-ИЛИ введен преобразованный аргумент (-n&mi)k и (+n&mi)k соответственно, которые сформированы посредством логической функции f(}&)-ИЛИ-НЕ → (V). И если записать функциональные структуры в виде аналитического выражения (249)
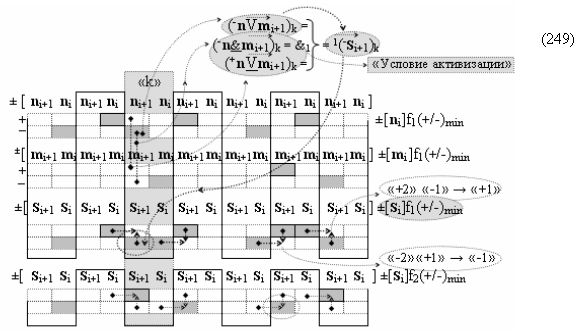
и в виде аналитического выражения (250)
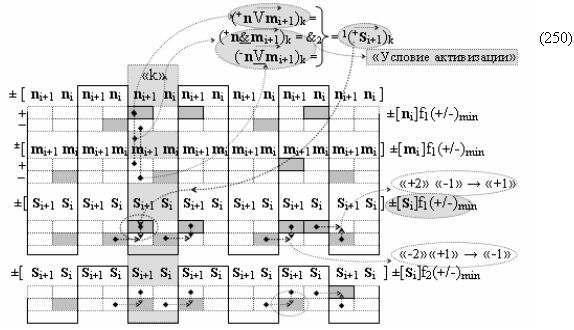
то функциональные структуры (249) и (250) являются математическими моделями активизации условно отрицательного аргумента 1(-Si+1)k и положительного аргумента 1(+Si+1)k в объединенной структуре слагаемых ±[Si]f1(+/-)min условно «i+1» разряда. В результате математическая модель сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» может быть сформирована при анализе объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min, что существенно ускорит ее синтез. Поэтому вернемся к процедуре активизации результирующего условно отрицательного аргумента (-Si+1)k условно «i+1» разряда в графоаналитическом выражении (243) и для условно «k» «Зоны минимизации» запишем скорректированную функциональную структуру (251),
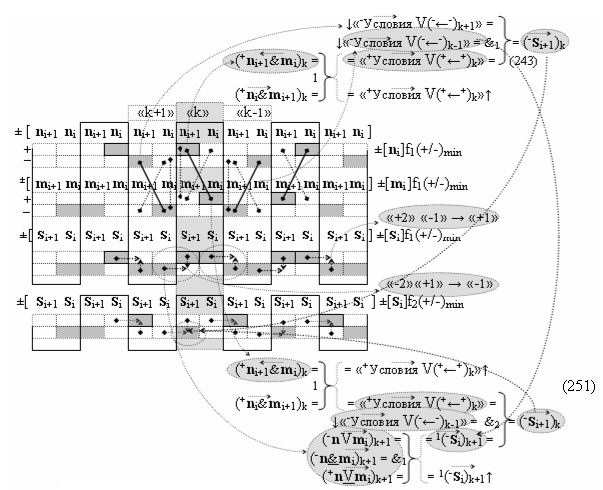
в которой особенностью является преобразованный условно отрицательный аргумент (-Si)k+1 условно «i» разряда условно «k+1» «Зоны минимизации» и его активность достаточна для активизации результирующего аргумента. При этом следует отметить, что в функциональной исходной структуре (243) условно отрицательный аргумент ↓«-Условия V(-←-)k+1» в системе выходной логической функции f1(&)-И ограничивает активизацию результирующего аргумента, поскольку возможна структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в условно «k+1» «Зоне минимизации», процедуру преобразования которых запишем в виде графоаналитического выражения (252),
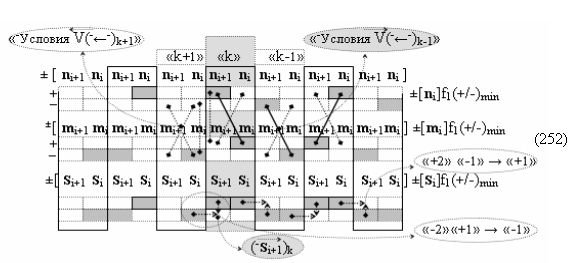
в которой условно отрицательный аргумент ↓«-Условия V(-←-)k+1» условно «k+1» «Зоны минимизации» является неактивным, но результирующий аргумент (-Si+1)k в этой ситуации в условно «k» «Зоне минимизации» активизирован корректно и его активизирует функциональная структура (251). Аналогичный результат будет получен и в графоаналитическом выражении (253),
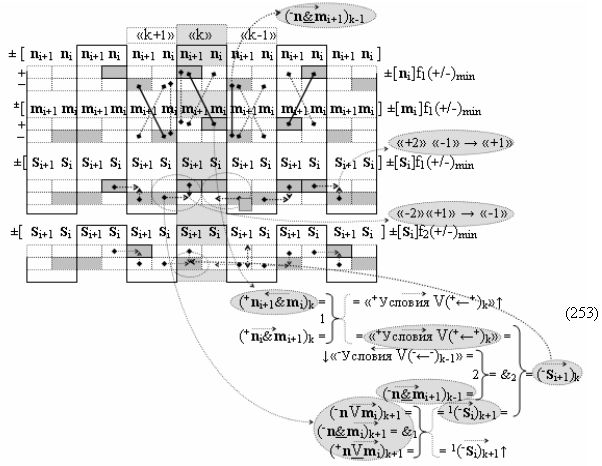
когда в условно «k-1» «Зоне минимизации» активен условно отрицательный аргумент (-n&mi+1)k-1, который включен в функциональной структуре (253) в систему дополнительной логической функции f2(})-ИЛИ и в которую включен и условно отрицательный аргумент ↓«-Условия V(-←-)k-1» условно «k-1» «Зоны минимизации», поскольку только при их активности может быть активизирован результирующий аргумент (-Si+1)k, а во всех остальных ситуациях он активизирован быть не может.
Ситуация 1. В объединенной структуре аргументов слагаемых ±[Si]f1(+/-)min в условно «k-1» «Зоне минимизации» активен условно отрицательный аргумент (-Si)k-1.
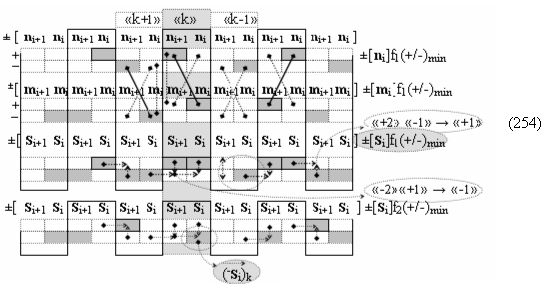
Ситуация 2. В объединенной структуре аргументов слагаемых ±[Si]f1(+/-)min в условно «k-1» «Зоне минимизации» активен положительный аргумент (+Si)k-1.
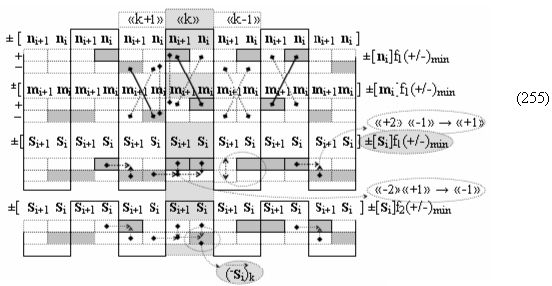
Ситуация 3. В объединенной структуре аргументов слагаемых ±[Si]f1(+/-)min в условно «k-1» «Зоне минимизации» активны два условно отрицательных аргумента (-Si)k-1.
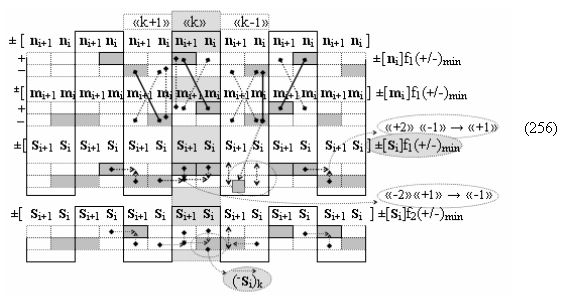
Ситуация 4. В объединенной структуре аргументов слагаемых ±[Si]f1(+/-)min в условно «k-1» «Зоне минимизации» активны два положительных аргумента (+Si)k-1.
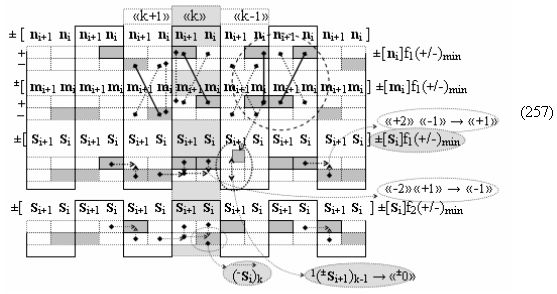
Поскольку в графоаналитических выражениях (254) - (257) в условно «k» «Зоне минимизации» активизирован условно отрицательный аргумент (-Si)k условно «i» разряда и условием его активизации в функциональной структуре (237) является условно отрицательный аргумент (-n&mi+1)k-1 и положительный преобразованный аргумент «+Условия (+←+)k-1»,
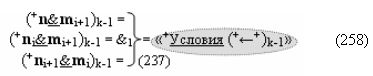
но если проанализировать условия активности условно отрицательного аргумента (-Si)k в условно «i» разряде на уровне объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min, то таким одним и единственно корректным «Условием активизации» является неактивность объединенного аргумента 1(±Si+1)k-1 → «±0» «i+1» разряда в условно «k-1» «Зоне минимизации», и его запишем в виде аналитического выражения (259),
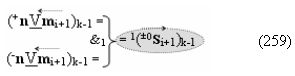
в котором по сравнению с функциональной структурой (258) минимизировано число входных преобразованных аргументов и включены в систему выходной логической функции f1(&)-И только два преобразованных аргумента (+nVmi+1)k-1 и (-nVmi+1)k-1, сформированы посредством логической функции f(}&)-ИЛИ-НЕ. В результате объединенный аргумент 1(±0Si+1)k-1 «i+1» разряда в условно «k-1» «Зоне минимизации» может быть активным только в том случае, когда в функциональной структуре (259) одновременно не активны положительный преобразованный аргументы (+nVmi+1)k-1 и условно отрицательный преобразованный аргумент (-nVmi+1)k-1. И если вернуться к анализу логико-динамических процессов преобразования аргументов слагаемых (254) - (257) и активизации в условно «k» «Зоне минимизации» условно отрицательного аргумента (-Si)k условно «i» разряда, то функциональную структуру для его активизации запишем в виде аналитического выражения (260).
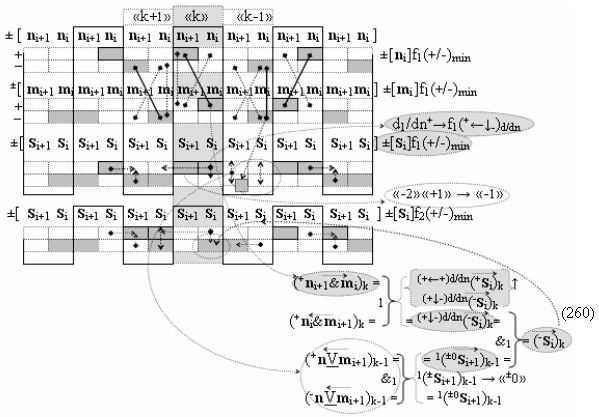
И оно включает функциональную входную структуру с выходной логической функцией f1(})-ИЛИ для активизации одновременно преобразованного условно отрицательного преобразованного аргумента (+↓-)d/dn(-Si)k локального переноса f1(+↓-)d/dn и положительного аргумента (+←+)d/dn(+Si)k локального переноса (+←+)d/dn(+Si)k процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn и включает функциональную входную структуру с выходной логической функцией f1(&)-И для активизации преобразованного аргумента 1(±0Si+1)k-1 «i+1» разряда условно «k-1» «Зоны минимизации», который в объединенной структуре слагаемых ±[Si]f1(+/-)min является неактивным аргументом. При этом следует отметить, что функциональная структура (260) является одной из функционально законченной математической моделью, которая в условно «k» «Зоне минимизации» активизирует условно отрицательный аргумент (-Si)k «i» разряда, являющийся, по существу, аргументом (+↓-)d/dn(-Si)k локального переноса f1(+↓-)d/dn и независит от активности аргументов условно «k-2» «Зоны минимизации». Поскольку в объединенной структуре слагаемых ±[Si]f1(+/-)min в условно «k-1» «Зоне минимизации» аргумент 1(±Si+1)k-1 → «±0» «i+1» разряда является неактивным и возможные активные структуры аргументов в условно «k-2» «Зоне минимизации» могут активизировать результирующий аргумент суммы только в условно «i+1» разряде условно «k-1» «Зоны минимизации» и такая активизация не нарушает логики формирования результирующей условно минимизированной структуры суммы ±[Si]f2(+/-)min, которая допускает активные аргументы только между «Зонами минимизации». При этом следует отметить, однозначность активизации аргумента результирующей суммы ±[Si]f2(+/-)min в условно «k» «Зоне минимизации» возможна не только при неактивном аргументе 1(±Si+1)k-1 → «±0» «i+1» разряда «k-1» «Зоны минимизации», но и при его активном аргументе 1(±Si+1)k-1 → «±1», поскольку если вернуться к процедуре преобразования слагаемых (229), записав ее для положительных аргументов 1(+Si+1)k-1 → «+1» в виде выражения (261),
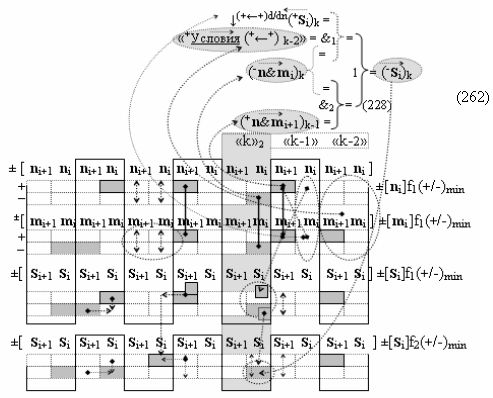
а для условно отрицательных аргументов 1(-Si+1)k-1 → «-1» в виде выражения (263),
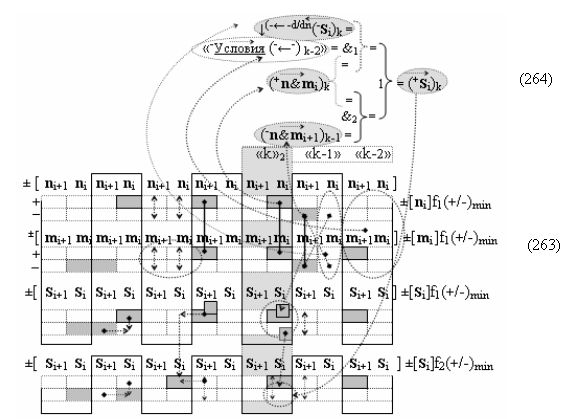
и вернуться к процедуре преобразования слагаемых в выражении (265),
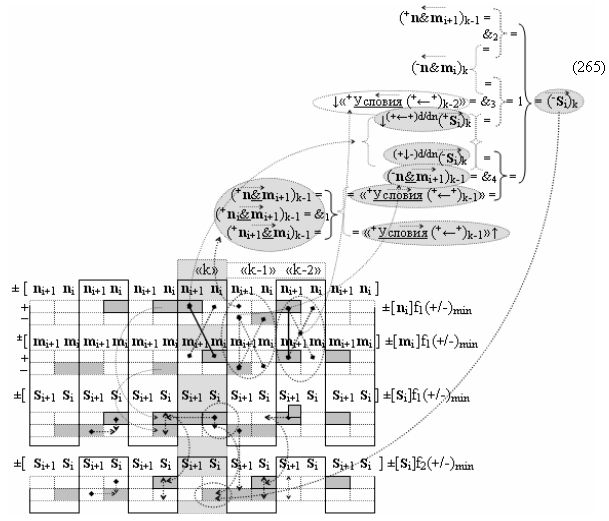
то для последующего формализованного синтеза результирующей математической модели условно «k» «Зоны минимизации» сумматора ±f(ΣRU)min необходимо проанализировать только все структуры положительных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в условно «k» «Зоне минимизации» и записать общее аналитическое выражение, а общее аналитическое выражение для всех структур условно отрицательных аргументов слагаемых может быть записано путем изменения знаков у аргументов в аналитическом выражении положительных структунр слагаемых. Поскольку аргументы разных знаков равно вероятны, поэтому из функциональной структуры (265) могут быть временно исключены функциональные входные структуры с выходными логическими функциями f1(&)-И и f2(&)-И, и ее запишем в виде аналитического выражения (266)
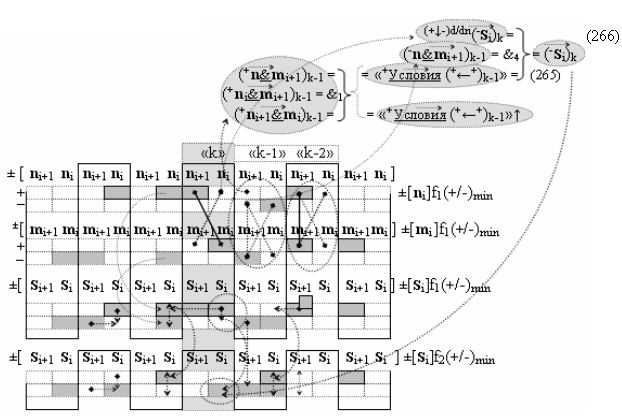
в связи с их принадлежностью к активизации условно отрицательного аргумента (-n&mi)k и в результате преобразования этого аргумента была сформирована функциональная структура (262), которую запишем в виде аналитического выражения (266).
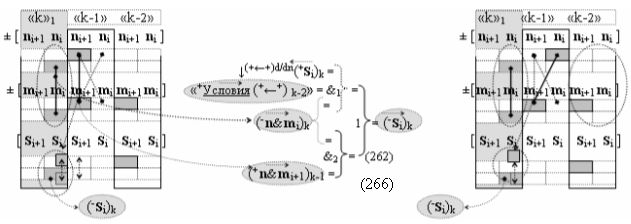
А преобразование положительного преобразованного аргумента (+n&mi)k было выполнено в функциональной структуре (264), и если записать ее в виде аналитического выражения (267),
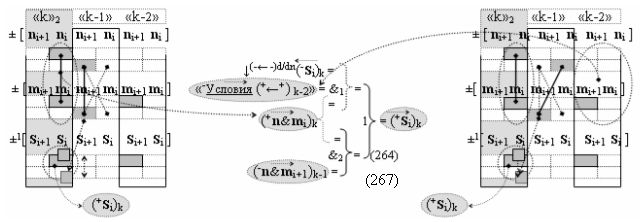
то из сравнительного анализа функциональных структур (266) и (267) следует, что они эквивалентны за исключением знаков аргументов. Поэтому дальнейший синтез математической модели условно «k» «Зоны минимизации» сумматора ±f(ΣRU)min выполним анализ только всех возможных структур положительных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в условно «k» «Зоне минимизации». А для этого, учитывая логику формирования условно минимизированной структуры аргументов результирующей суммы ±[Si]f1(+/-)min, запишем все возможные структуры слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, которые могут активизировать как положительный результирующий аргумент суммы (+Si)k и условно отрицательный аргумент (-Si)k условно «i» разряда, так и положительный результирующий аргумент суммы (+Si+1)k и условно отрицательный аргумент (-Si+1)k условно «i+1» разряда, и определимся с условиями их активизации. При этом «Условия активизации» всех результирующих аргументов (±Si)k и (±Si+1)k целесообразно ограничить, учитывая активные аргументы только в предыдущих условно «k-1» и «k-2» «Зонах минимизации», поскольку для некоторых структур аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min только аргументы условно «k-1» и «k-2» «Зон минимизации» являются «Условиями активизации».
Ситуация 1. Активизация положительного результирующего аргумента суммы (+Si)k условно «i» разряда и «Условие активизации» в условно «k» «Зоне минимизации» в функциональной структуре (268)
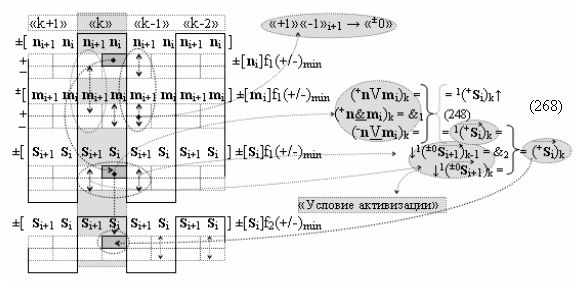
запишем в виде двух преобразованных аргументов ↓1(±0Si+1)k условно «k» «Зоны минимизации» и преобразованного аргумента ↓1(±0Si+1)k+1 условно «k-1» «Зоны минимизации». При этом следует отметить, что если вернуться к анализу функциональной структуры (259), которую запишем в виде аналитического выражения (269),
то ее преобразованный аргумент 1(±0Si+1)k-1 может быть использован в качестве «Условия активизации» только как преобразованный аргумент 1(±0Si+1)k-1 условно «k» «Зоны минимизации» с функциональной структурой (270).
Поскольку не возможн в условно «i+1» разряде активный логический ноль «+1»«-1»i+1 → «±0» в условно «k» «Зоне минимизации» при активном положительном аргументе (+n)k или (+mi)k условно «i» разряда одного из слагаемых и это связано с условиями формирования условно минимизированной структуры аргументов. При этом в условно «k-1» «Зоне минимизации», если записать графоаналитические выражения (271),
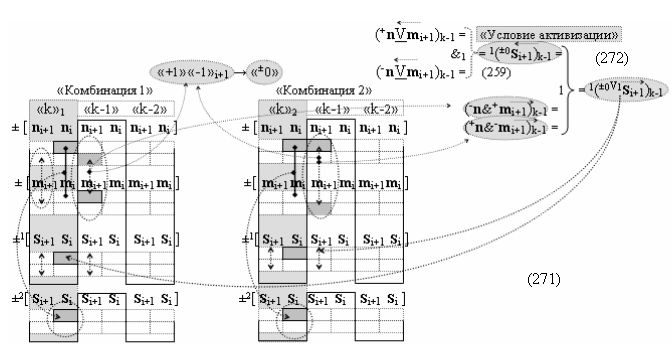
возможен как активный логический ноль «+1»«-1»i+1 → «±0», так и неактивный логический ноль, а функциональную структуру такой активизации запишем в виде аналитического выражения (273), в которой, по существу, в систему логической функции f1(})-ИЛИ включены три возможных «Условия активизации», когда не активен логический ноль «+1»«-1»i+1 → «±0» (функциональная структура с выходной логической функцией f1(}&)-ИЛИ-НЕ) и когда он активен, и в этой ситуации активны либо преобразованный аргумент (-n&+mi+1)k-1, либо преобразованный аргумент (+n&-mi+1)k-1. А если учесть, что функциональная структура (272) будет включена в систему логической функции f2(&)-И выражения (268) с выходной логической функцией f1(})-ИЛИ, записав общую структуру логических функций с учетом функциональной структуры (270) первого «Условия активизации» в виде либо аналитического выражения (273),
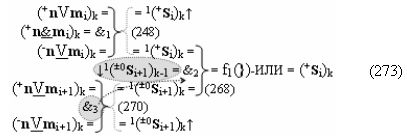
либо после объединения одноименных логических функций f3(&)-И и f2(&)-И запишем структуру логических функций (274),
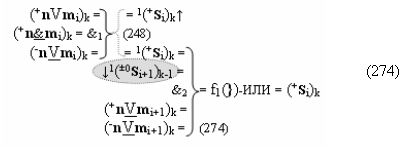
то общий технологический цикл ∆tΣ активизации результирующего аргумента суммы будет увеличен до ∆tΣ → 5∙f(&) пяти условных логических функций f(&)-И. А для минимизации технологического цикла ∆tΣ → 4∙f(&) до четырех условных логических функций f(&)-И функциональную структуру (272) запишем в виде выражения (275),
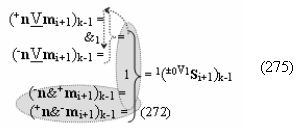
в котором выполним перенос функциональной структуры с выходной логической функцией f1(})-ИЛИ через систему логической функции f1(&)-И и запишем структуру логических функций (276).
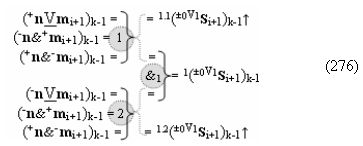
При этом особенностью функциональной структуры (276) является выходная логическая функция f1(&)-И, которую введем в систему выходной логической функции f2(&)-И выражения (274) и запишем структуру логических функций (277),
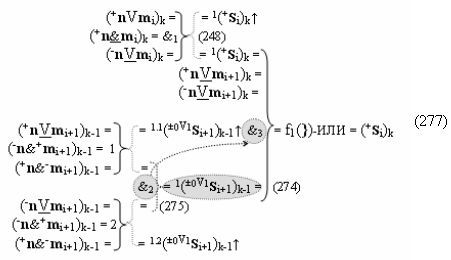
а после объединения одноименных логических функций f2(&)-И и f3(&)-И запишем скорректированное аналитическое выражение (278).
Из анализа структуры логических функций (278) следует, что в систему выходной логической функции f2(&)-И включен как преобразованный положительный аргумент (+nVmi+1)k и условно отрицательный аргумент (-nVmi+1)k условно «k» «Зоны минимизации», так и посредством логической функции f1(})-ИЛИ и f2(})-ИЛИ включен преобразованный положительный аргумент (+nVmi+1)k-1 и условно отрицательный аргумент (-nVmi+1)k-1 условно «k-1» «Зоны минимизации». А поскольку формируем математическую модель сумматора ±f(ΣRU)min условно «k» «Зоны минимизации», поэтому запишем скорректированную структуру логических функций (279),
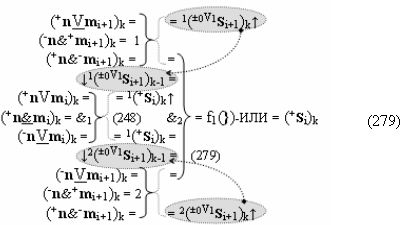
в которой функциональные структуры с выходной логической функцией f1(})-ИЛИ и f2(})-ИЛИ функционально принадлежат условно «k» «Зоне минимизации», а преобразованные аргументы (+nVmi+1)k и (-nVmi+1)k выражения (278) записаны в системе выходной логической функции f2(&)-И посредством преобразованных аргументов ↓1(±0V1Si+1)k-1 и ↓1(±0V1Si+1)k-1, сформированные в условно «k-1» «Зоне минимизации». И если для структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min двух «Комбинация» записать графоаналитическое выражение (280),
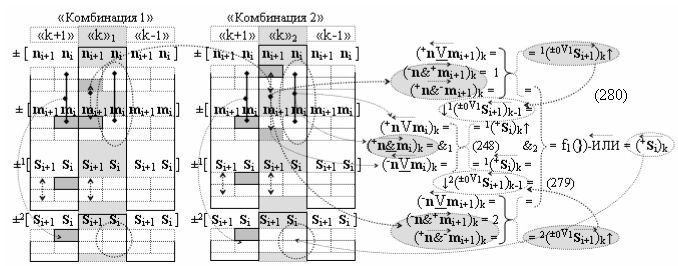
то активные преобразованные аргументы 1(±0V1Si+1)k↑ и 2(±0V1Si+1)k↑, активизированные в условно «k» «Зоне минимизации» в условно «k+1» «Зоне минимизации», которая при анализе в ней аргументов слагаемых будет условно «k» «Зоной минимизации», являются активными аргументами условно «k-1» «Зоне минимизации». В результате функциональная структура (279) представляет собой одну из функциональных структур математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации», которая активизирует положительный аргумент (+Si)k результирующей суммы.
Ситуация 2. Активизация положительного результирующего аргумента суммы (+Si)k условно «i» разряда в условно «k» «Зоне минимизации» и его «Условия активизации», которые включают анализ активных аргументов в условно «k+1», «k», «k-1» и «k-2» «Зонах минимизации»,
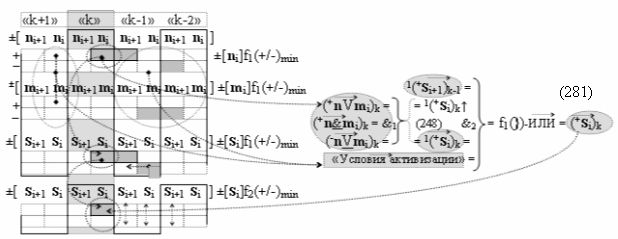
при активном аргументе 1(+Si+1)k-1 условно «i+1» разряда, функциональная структура которого будет включена в структуру логических функций, активизирующая положительный результирующий аргумент (+Si+1)k условно «i+1» разряда. При этом следует отметить, что если записать графоаналитическое выражение (282),
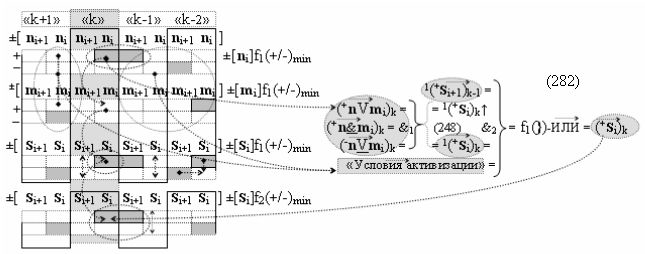
то последовательно активные положительные аргументы в объединенной структуре аргументов слагаемых ±[Si]f1(+/-)min, позиционно расположенные между «Зонами минимизации» при определенных «Условиях активизации», являются результирующими аргументами. Но возможны структуры аргументов слагаемых (283) - (285),
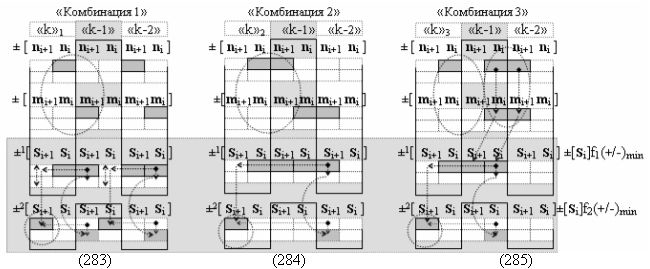
в которых однозначность преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min имеет только объединенная структура аргументов ±[Si]f1(+/-)min, но в ней активные аргументы с учетом графоаналитического выражения (285), активизированы функциональными двойными структурами. С одной стороны, например, в графоаналитических выражениях (283) и (284) активизированы в условно «i» разряде посредством функциональной структуры (248),
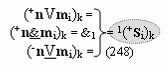
с другой стороны в графоаналитическом выражении (285) тот же положительный результирующий аргумент 1(+Si)k активизирован в условно «i» разряде посредством преобразованного аргумента (+n&mi+1)k-1 условно «k-1» «Зоны минимизации». И если их объединить в системе логической функции f1(})-ИЛИ, то запишем функциональную структуру (286),
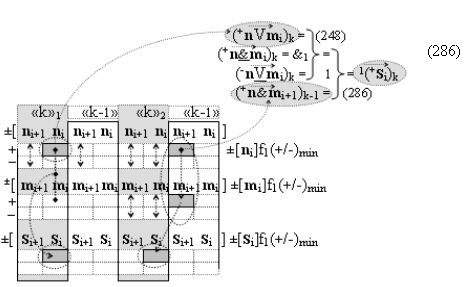
в которой результирующий аргумент 1(+Si)k условно «i» разряда активизирован в двух ситуациях. А поскольку объединенная структура аргументов ±[Si]f1(+/-)min в условно «i» разряде результирующий аргумент 1(+Si)k условно «i» разряда может быть не активен, поэтому запишем функциональную структуру (287),
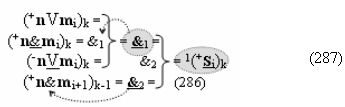
в которой выполним объединение логической функции f1(&)-НЕ с логической функцией f1(&)-И и с логическим символом (&) преобразованного аргумента (+n&mi+1)k-1. В результате запишем минимизированную функциональную структуру (288)
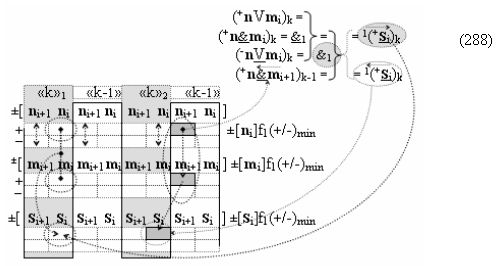
с выходной логической функцией f1(&)-И. И если записать графоаналитическое выражение (289),
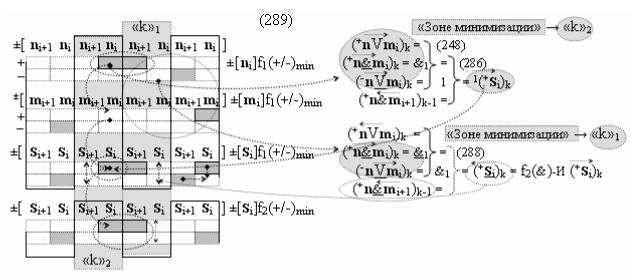
1(+Si)k функциональной структуры (286) корректно активизирован в «Зоне минимизации» → «k»2, а объединенный аргумент 1(+Si)k с измененным уровнем сигнала функциональной структуры (288) корректно не активизирован в «Зоне минимизации» → «k»1. При этом следует отметить, что объединенный аргумент 1(+Si)k был сформирован с измененным уровнем сигнала для активизации выходной логической функции f2(&)-И, которая активизирует результирующий аргумент суммы (+Si)k в условно «i» разряде.
Функциональную аналогичную структуру запишем и для объединенного аргумента 1(+Si+1)k условно «i+1» разряда без измененного уровня аналогового сигнала в виде функциональной структуры (290)
и для объединенного аргумента 1(+Si)k условно «i+1» разряда с измененным уровнем аналогового сигнала в виде функциональной структуры (291),
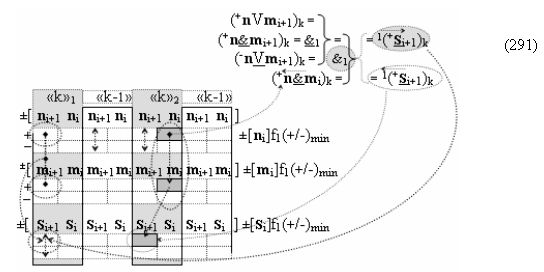
в которых дополнительные преобразованные аргументы (+n&mi)k и (+n&mi)k сформированы в условно «k» «Зоне минимизации».
Далее, если вернуться к анализу процедуры активизации результирующего аргумента суммы (+Si)k в графоаналитическом выражении (280), записав ее функциональную структуру в виде аналитического выражения (292),
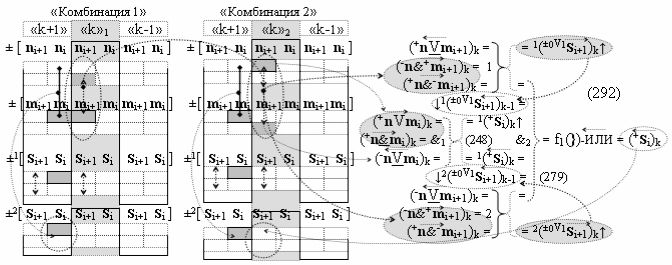
а для сопоставительного анализа корректности функциональной структуры запишем скорректированную функциональную структуру (293),
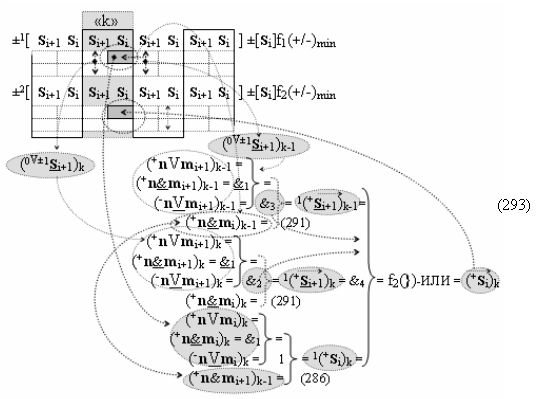
или после объединения одноименных логических функций f2(&)-И - f4(&)-И запишем оптимизированную функциональную структуру (294),
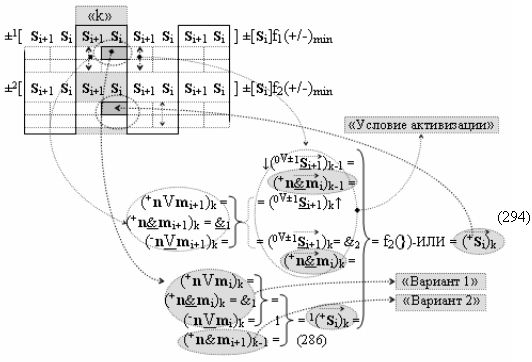
то оптимизированная функциональная структура (294) включает два «Варианта» активизации результирующего аргумента (+Si)k, когда как функциональная структура (292) включает только «Вариант 1». При этом в структуру логических функций (294) включена только одна функциональная структура «Условия активизации» с выходной логической функцией f1(&)-И-НЕ, и входные преобразованные аргументы в ее системе соответствуют преобразованным входным аргументам «Варианта 1», когда как в структуру логических функций (292) включены две функциональные структуры «Условия активизации» с выходной логической функцией f1(})-ИЛИ и f2(})-ИЛИ с иными входными преобразованными аргументами. Но технологический цикл ∆tΣ преобразования аргументов в функциональной структуре (294) по сравнению с технологическим циклом ∆tΣ преобразования аргументов в функциональной структуре (292) увеличен ∆tΣ → 5∙f(&)-И до пяти условных логических функций f(&)-И, но он может быть минимизирован, если выполнить перенос функциональной структуры с «Условиями активизации» через систему логической функции f1(})-ИЛИ.
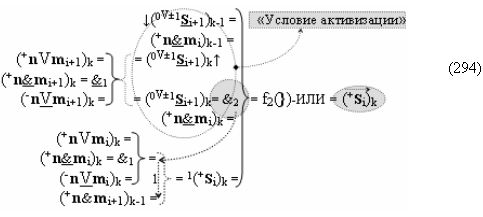
В результате такого переноса запишем аналитическое выражение (295)
с технологическим циклом ∆tΣ → 4∙f(&)-И преобразования аргументов, который соответствует четырем условным логическим функциям f(&)-И. Но если в функциональную структуру с «Условиями активизации» с выходной логической функцией f1(&)-И-НЕ выражения (294), а она соответствует последовательности f1(&)-И → f1(&)-НЕ, то запишем оптимизированную структуру логических функций (296)
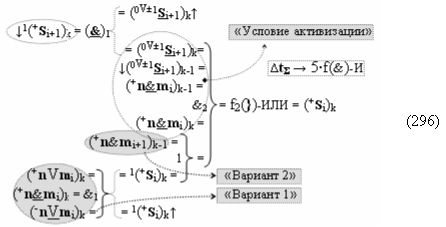
с технологическим циклом ∆tΣ → 5∙f(&)-И преобразования аргументов, который соответствует пяти условным логическим функциям f(&)-И. Поскольку структура логических функций (296) включает преобразованный объединенный аргумент ↓1(+Si+1)k условно «i+1» разряда условно «k» «Зоны минимизации», поэтому сформирует его функциональную структуру, а для этого запишем аналитическое выражение, которое активизирует результирующий аргумент (+Si+1)k условно «i+1» разряда «k» «Зоны минимизации» в виде неоптимизированной структуры логических функций (297).
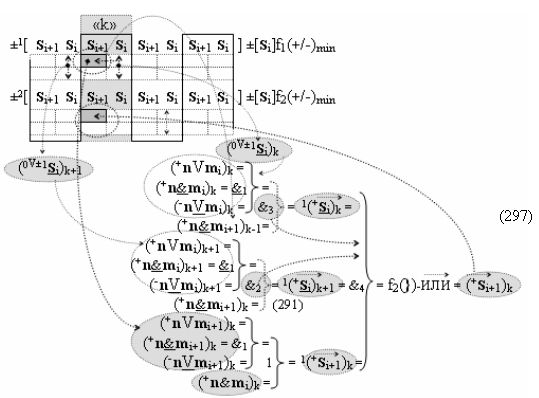
А после объединения одноименных логических функций f2(&)-И - f4(&)-И запишем оптимизированную структуру логических функций (298),
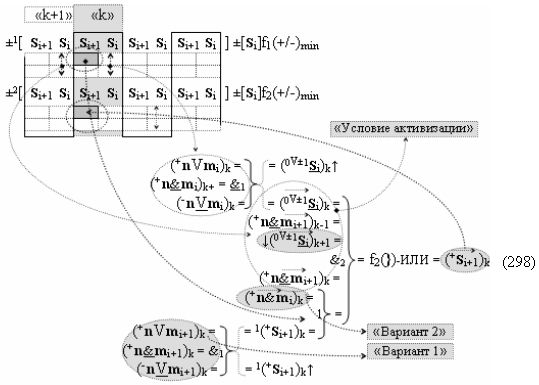
в которой функциональная структура с выходной логической функцией f1(&)-И-НЕ может быть скорректирована, поскольку она соответствует последовательности f1(&)-И → f1(&)-НЕ с входным преобразованным аргументом 1(+Si)k условно «i» разряда условно «k» «Зоны минимизации». И если функциональную структуру (296), активизирующую результирующий аргумент (+Si)k условно «i» разряда записать в виде аналитического выражения (299)
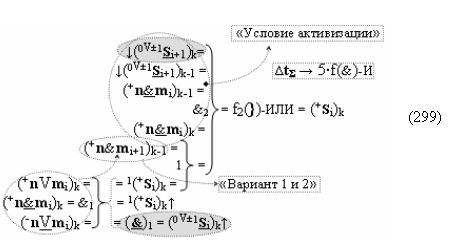
с преобразованным аргументом (0V±1Si)k↑ с измененным уровнем аналогового сигнала условно «i» разряда, то структуру логических функций (298) запишем в виде функциональной структуры (300)
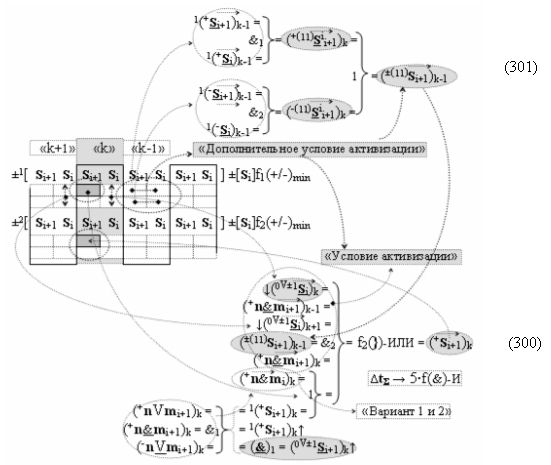
с преобразованным аргументом (0V±1Si+1)k↑ с измененным уровнем аналогового сигнала условно «i+1» разряда. При этом следует отметить, что для активизации преобразованного аргумента (+Si+1)k условно «i+1» разряда необходимо в систему логической функции f2(&)-И ввести «Дополнительное условие активизации», которым является неактивность двух аргументов в условно «k-1» «Зоне минимизации» как положительных аргументов 1(+Si+1)k-1 и 1(+Si)k-1, так и условно отрицательных аргументов 1(-Si+1)k-1 и 1(-Si)k-1. И аргумент «Дополнительного условия активизации» на уровне объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min запишем в виде структуры логических функций (301), и если ее ввести в систему логической функции f2(&)-И выражения (300), то технологический цикл ∆tΣ преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-) существенно будет увеличен. Поэтому вернемся к анализу функциональной структуры (205), записав ее в виде графоаналитического выражения (302),
со структурой логических функций (303), которая активизирует положительный аргумент (+Si+1)k условно «i+1» разряда и в которой с одной стороны технологический цикл ∆tΣ преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min соответствует
∆tΣ → f(&) → f1(}) → f2(&) → f(})вых → 4∙f(&)
четырем условным логическим функциям f(&)-И. С другой стороны функциональная структура с выходной логической функцией f1(})-ИЛИ, которая активизирует как условно отрицательный аргумент (+↓-)d/dn(-Si)k, так и положительный аргумент (+←+)d/dn(+Si)k процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn, по существу, является функциональной структурой для активизации положительного преобразованного аргумента (+(11)Si i+1)k. Но в системе этой функциональной структуры только два преобразованных аргумента (+ni+1&mi)k и (-ni+1&mi)k, и она не учитывает два других возможных варианта преобразованного аргумента ((+ni+1)k&(+ni+1&mi+1)k-1)k и ((+mi+1)k&(+ni+1&mi+1)k-1)k,
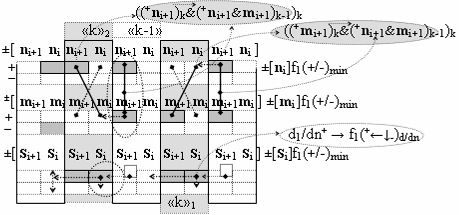
которые формирует функциональная структура с выходной логической функцией f(&)-И с тремя входными аргументами в своей системе. В результате структуру логических функций (303) запишем в виде аналитического выражения (304),
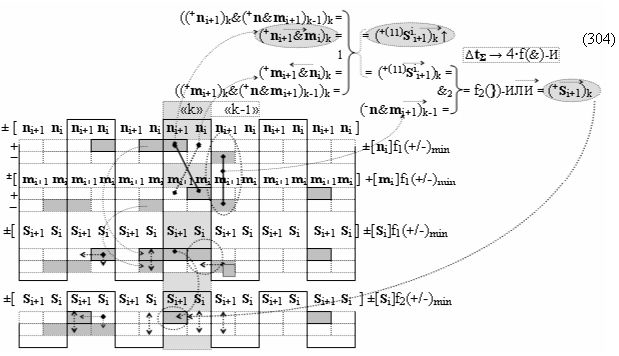
в которой функциональная структура с выходной логической функцией f1(})-ИЛИ активизирует преобразованный аргумент (+(11)Si i+1)k в условно «k» «Зоне минимизации» без изменения уровня аналогового сигнала с технологическим циклом ∆tΣ → 2∙f(&)-И с двумя условными логическими функциями f(&)-И. А функциональную структуру условно «k» «Зоны минимизации», посредством которой активизируют преобразованный аргумент «Дополнительное условие активизации» (±(11)Si i+1)k-1 после переноса логической функции f1(&)-НЕ в выражении (305)
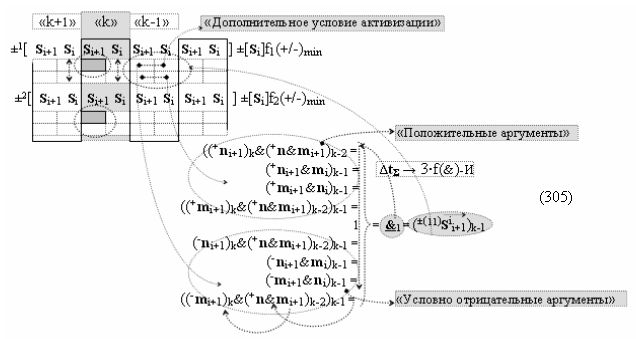
через систему логической функции f1(})-ИЛИ, что приведет к изменению ее логических свойств на свойства логической функции f1(&)-И. А дальнейшее объединение перенесенной логической функции f1(&)-НЕ с логическим символом (&) входных преобразованных аргументов приведет к изменению логического символа (&) → (&) на символ логической функции f1(&)-И-НЕ. В результате запишем скорректированную функциональную структуру с выходной логической функцией f1(&)-И в виде аналитического выражения (306),
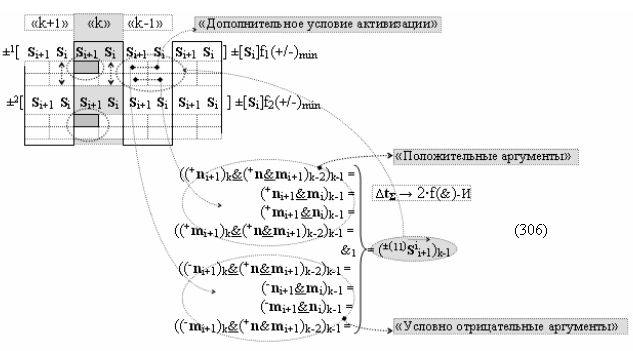
в которой технологический цикл ∆tΣ → 2∙f(&)-И преобразования аргументов соответствует двум условным логическим функциям f(&)-И, но если учесть, что функциональная структура с выходной логической функцией f1(&)-И включена в систему логической функцией f2(&)-И (307),
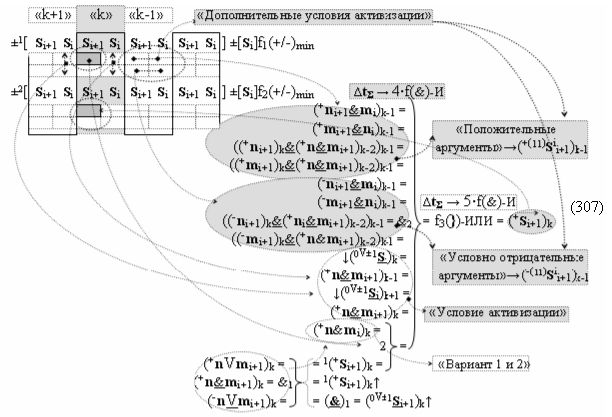
то технологический цикл ∆tΣ → 1∙f(&)-И «Дополнительных условий активизации» соответствует одной условной логической функции f(&)-И, а технологический цикл ∆tΣ «Дополнительных условий активизации» с учетом логических функций f2(&)-И f2(})-ИЛИ соответствует ∆tΣ → 3∙f(&)-И трем условным логическим функциям f(&)-И. При этом следует отметить, что для минимизации аналитической записи структуры логических функций (307) технологический цикл ∆tΣ → 4∙f(&)-И «Дополнительных условий активизации» может быть увеличен до четырех условных логических функций f(&)-И, а для этого скорректируем функциональную структуру (306) и запишем ее в виде параллельно последовательных одноименных логических функций f1(&)-И ║ f2(&)-И → f3(&)-И (308),
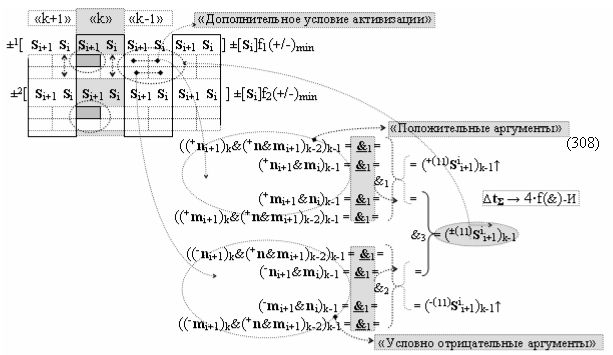
а после переноса логических функций f1(&)-НЕ через систему логической функции f1(&)-И и f2(&)-И, что приведет к изменению логических их свойств на свойства логической функции f1(})-ИЛИ и f1(})-ИЛИ. А после объединения их с перенесенной логической функцией f1(&)-НЕ запишем оптимизированное аналитическое выражение (309),
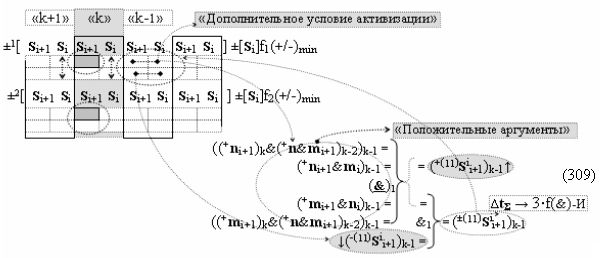
в котором только «Положительные аргументы», включеные в систему логической функции f1(}&)-ИЛИ-НЕ активизируют преобразованный положительный аргумент (+(11)Si i+1)k-1↑, являющийся входным аргументом функциональной структуры условно отрицательного канала сумматора ±f(ΣRU)min условно «k» «Зоны минимизации». И такое перераспределение функциональных структур «Положительных аргументов» и «Условно отрицательных аргументов» структуры логических функций (308) позволяет оптимизировать аналитическое выражение (307) и записать его в виде функциональной структуры (310),
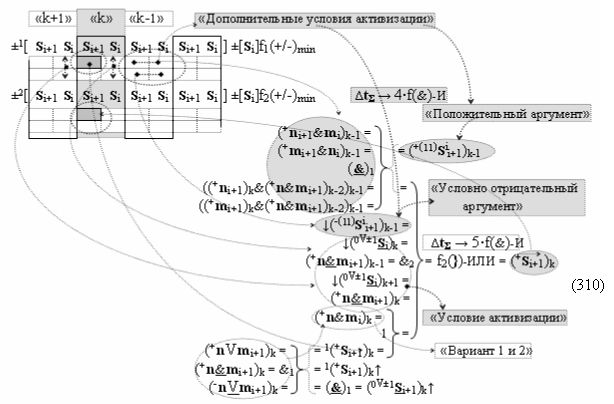
в которой положительное «Дополнительное условие активизации» включено в систему логической функции f2(&)-И в виде функциональной структуры с выходной логической функцией f1(}&)-ИЛИ-НЕ и преобразованного условно отрицательного аргумента ↓(-(11)Si i+1)k-1. Поскольку «Условие активизации» включает преобразованный аргумент ↓(0V±1Si)k с измененным уровнем аналогового сигнала, который для активизации положительного результирующего аргумента суммы (+Si+1)k включает последовательность логических функций f1(&)-И → f1(&)-НЕ, и она приводит к увеличению технологического цикла ∆tΣ → 5∙f(&)-И преобразования аргументов, поэтому выполним объединение их f1(&)-И + f1(&)-НЕ → f1(&)-И-НЕ и запишем минимизированную функциональную структуру в виде аналитического выражения (311).
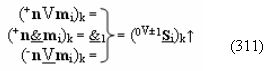
При этом последовательность логических функций f1(&)-И → f1(})-ИЛИ → 1(+Si+1)k↑ в выражении (310), которая, по существу, формирует объединенный аргумент слагаемого 1(+Si+1)k, также скорректируем в соответствии с векторной структурой переноса функциональных структур (312)
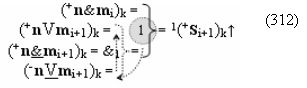
и запишем структуру логических функций (313)
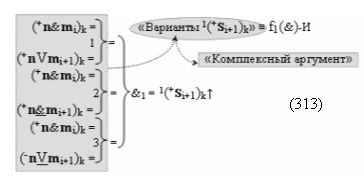
с тремя входными логическими функциями f1(})-ИЛИ - f3(})-ИЛИ, формирующими «Комплексный аргумент», и выходной логической функцией f1(&)-И. В результате структуру логических функций (310) запишем в виде аналитического выражения (314),
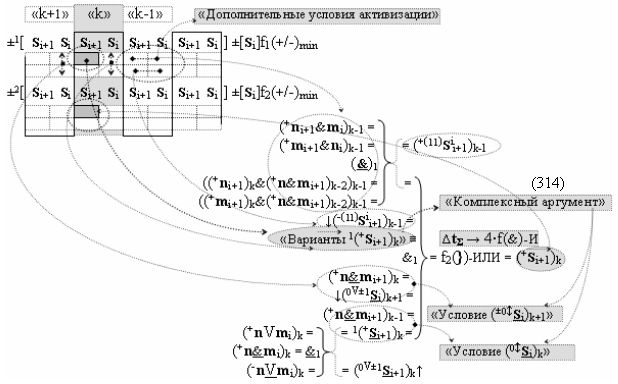
в котором «Комплексный аргумент» «Варианты 1(+Si+1)k» введен в систему логической функции f1(&)-И с символом (≡) - совокупности функциональных цифровых связей. Для минимизации аналитической формы записи математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» посредством «Комплексного аргумента» в функциональной структуре (314) запишем совокупность преобразованных аргументов
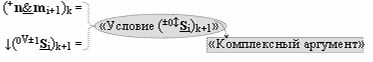
и совокупность преобразованных аргументов,
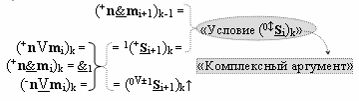
в результате ее запишем в виде аналитического выражения (315).
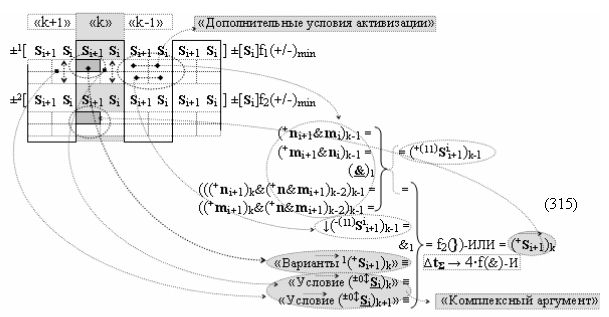
Далее, если вернуться к анализу процедуры преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в выражении (304),
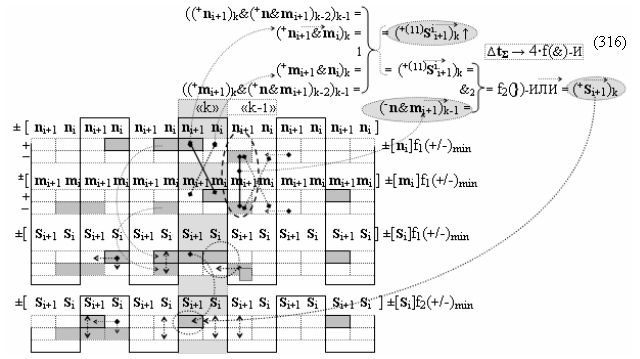
в которой также активизирован положительный результирующий аргумент суммы (+Si+1)k, то он посредством функциональной структуры (316) активизирован только для одного из возможных вариантов активных условно отрицательных аргументов (-n&mi+1)k-1, а остальные четыре варианта, которые активизирует функциональная структура (317)
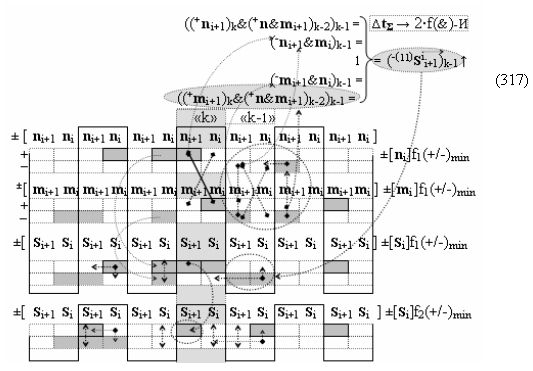
условно отрицательного канала сумматора f(ΣRU)min в «k-1» «Зоне минимизации» не включены в функциональную структуру (316). Но если посредством логической функции f3(})-ИЛИ ввести в функциональную структуру (317) преобразованный условно отрицательный аргумент (-(11)Si i+1)k и записать структуру логических функций (318),
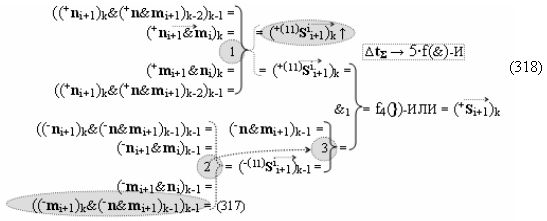
в которой выполним объединение одноименных логических функций f1(})-ИЛИ и f2(})-ИЛИ, то в результате запишем аналитическое выражение (319).
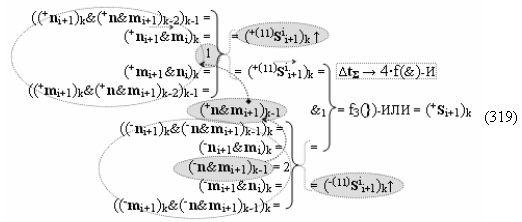
с технологическим циклом ∆tΣ → 4∙f(&)-И четыре условные логические функции f(&)-И. При этом из анализа положительной и функциональной структур с выходными логическими функциями f1(})-ИЛИ и f2(})-ИЛИ следует, что если в систему логической функции f1(})-ИЛИ ввести дополнительный преобразованный положительный аргумент (+n&mi+1)k-1, то из системы логической функции f1(&)-И может быть исключена функциональная структура с выходной логической функцией f2(})-ИЛИ, а вместо нее в минимизированное аналитическое выражение (320)
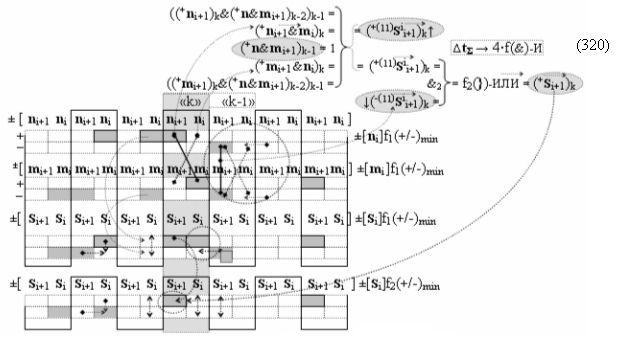
преобразованный условно отрицательный аргумент ↓(-(11)Si i+1)k.
Поскольку функциональная структура преобразованного условно отрицательного аргумента (-(11)Si i+1)k↑ в выражении (319) и функциональная структура преобразованного положительного аргумента (+(11)Si i+1)k ↑ в выражении были скорректированы, которые сформированы на уровне анализа аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, поэтому вернемся к функциональной структуре (310), записав ее в виде графоаналитического выражения (321).
Из анализа структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (322) следует, что в систему логической функции f1(}&)-ИЛИ-НЕ необходимо ввести дополнительный преобразованный аргумент (+n&mi+1)k-1, а из системы логической функции f2(&)-И необходимо исключить положительный «Избыточный аргумент» (+n&mi+1)k, поскольку он включен в систему логической функции f1(&)-И для активизации объединенного аргумента 1(+Si+1)k. При этом следует отметить, что если в системе логической функции f1(})-ИЛИ активен преобразованный аргумент (+n&mi)k без изменения уровня аналогового сигнала, то условно «k» «Зоне минимизации» преобразованный аргумент (+n&mi+1)k с измененным уровнем аналогового сигнала всегда активен. В результате после объединения функциональных структур (220) и (221), активизирующие результирующий аргумент (+Si+1)k «i-1» разряда запишем в виде аналитического выражения (323),
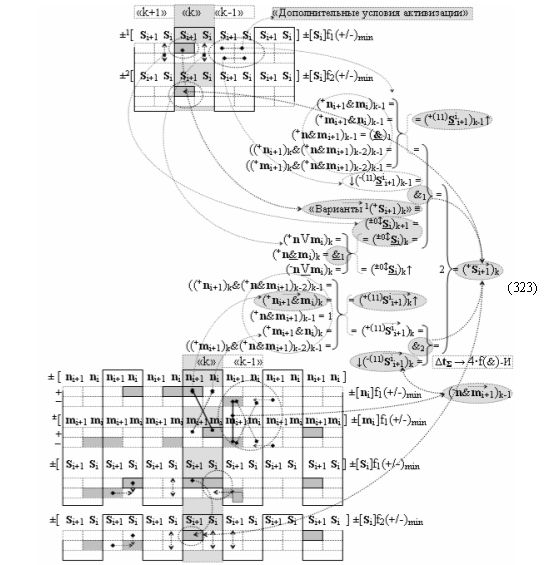
где «Варианты 1(+Si+1)k» - «Комплексный аргумент» структуры логических функций (313), которую запишем в виде аналитического выражения (324).
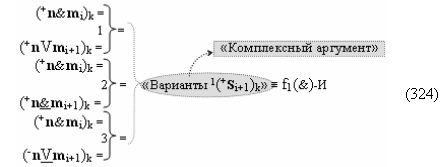
При этом следует отметить, что поскольку в структуру логических функций выражения (323) включены функциональная структура с выходной логической функцией f1(})-ИЛИ и функциональная структура с выходной логической функцией f1(}&)-ИЛИ-НЕ с одноименными преобразованными аргументами. Поэтому их преобразованные аргументы записаны в виде аргумента (+(11)Si i+1)k↑ условно «k» «Зоны минимизации» без изменения уровня аналогового сигнала и в виде аргумента (+(11)Si i+1)k-1↑ условно «k-1» «Зоны минимизации» с измененным уровнем аналогового сигнала соответственно. А, учитывая то, что формируют математическую модель условно «k» «Зоны минимизации», поэтому из структуры логических функций (323) функциональная структура с выходной логической функцией f1(}&)-ИЛИ-НЕ должна быть исключена и представлена в виде преобразованного аргумента ↓(+(11)Si i+1)k-1 условно «k-1» «Зоны минимизации». При этом в систему логической функции f1(&)-И выражения (323) включен «Комплексный аргумент» «Варианты 1(+Si+1)k» условно «i+1» разряда, который включает три функциональные структуры и при его активности активизирует положительный результирующий аргумент суммы (+Si+1)k, поэтому проанализируем возможность при его активизации ввести преобразованный аргумент (+(11)Si i+1)k↑ условно «k» «Зоны минимизации» с измененным уровнем аналогового сигнала. А для этого вернемся к дополнительному анализу скорректированной функциональной структуры (321), записав ее в виде структуры логических функций (325),
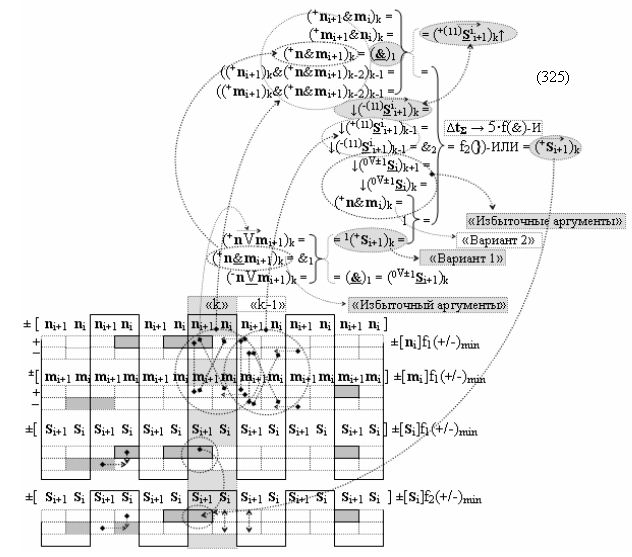
в которой введена положительная функциональная структура, формирующая преобразованный аргумент (+(11)Si i+1)k↑ и условно отрицательный преобразованный аргумент ↓(-(11)Si i+1)k условно «k» «Зоны минимизации» с измененным уровнем аналогового сигнала. В результате с одной стороны в системе логической функции f1(&)-И при скорректированных «Условиях активизации» результирующего аргумента суммы (+Si+1)k преобразованный аргумент (+n&mi+1)k с измененным уровнем аналогового сигнала является «Избыточнымй аргументом», поскольку его функции выполняет преобразованный аргумент (+n&mi+1)k без изменения уровня аналогового сигнала в системе логической функции f1(}&)-ИЛИ-НЕ. С другой стороны в систему логической функции f2(&)-И включены «Избыточные аргументы» ↓(0V±1Si)k+1 и ↓(0V±1Si)k условно «i» разряда «k+1» «Зоны минимизации» и «k» «Зоны минимизации» соответственно, а в систему логической функции f1(})-ИЛИ включен избыточный преобразованный аргумент (+n&mi)k «Варианта 2» активизации результирующего аргумента суммы (+Si+1)k. И если входной аргумент ↓(0V±1Si)k+1 условно «i» разряда «k+1» «Зоны минимизации» может быть исключен в связи с тем, что это условие является избыточным, поскольку аргумент 1(+Si+1)k «Вариант 1» удовлетворяет логике формирования условно минимизированной суммы, то входной аргумент ↓(0V±1Si)k условно «i» разряда «k» «Зоны минимизации» может быть исключен в связи с тем, что изменена его функциональная структура, которую запишем в виде аналитического выражения (326)
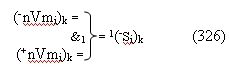
с выходной логической функцией f1(&)-И-НЕ, которую введем в скорректированную функциональную структуру (325). В результате скорректированную структуру логических функций (325) запишем в виде аналитического выражения (327).
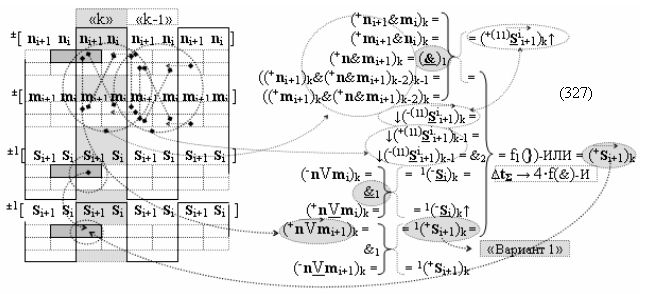
При этом функциональную структуру, посредством которой активизируют преобразованноый аргумент (+n&mi)k «Вариант 2», запишем в виде аналитического выражения (328),
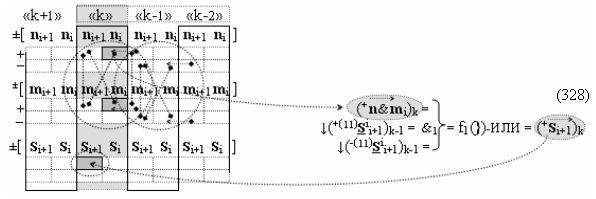
в котором условием активизации результирующего аргумента суммы (+Si+1)k условно «i+1» разряда являются только два преобразованных аргумента ↓(+(11)Si i+1)k-1 и ↓(-(11)Si i+1)k-1. И эта функциональная структура корректно не активна, если структура аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min включает активный положительный аргумент (+(11)Si i+1)k-1 условно «k-1» «Зоны минимизации» (329),
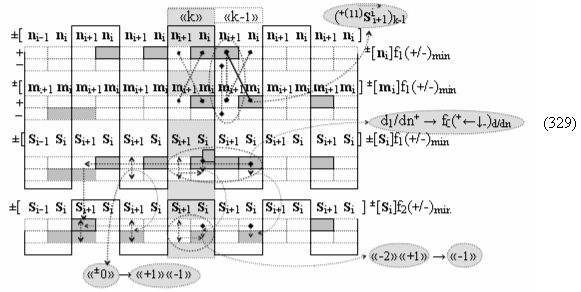
то для формирования минимизированной структуры аргументов суммы ±[Si]f2(+/-)min выполняют процедуру логического дифференцирования d1/dn+ → f0(+←↓-)d/dn положительной последовательности аргументов с учетом арифметической аксиомы «±0» → «+1»«-1». При этом в условно «k» «Зоне минимизации» активизируют результирующий условно отрицательный аргумент суммы (-Si)k условно «i+1» разряда с учетом обратной арифметической аксиомы «-2»«+1» → «-1». Но может быть исключена процедура активизации условно отрицательных аргументов активизированных посредством применения арифметической аксиомы «±0» → «+1»«-1». Поскольку в условно «k» «Зоне минимизации» второй положительный аргумент может быть преобразован посредством арифметической аксиомы «+1» → «+2»«-1» и в этой ситуации графоаналитическое выражение (329) запишем в виде выражения (330),
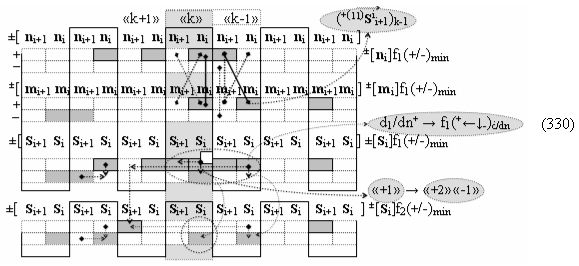
в котором также активизацию аргументов выполняют в соответствии с процедурой логического дифференцирования d1/dn+ → f1(+←↓-)d/dn и активизируют его посредством функциональной структуры (331).
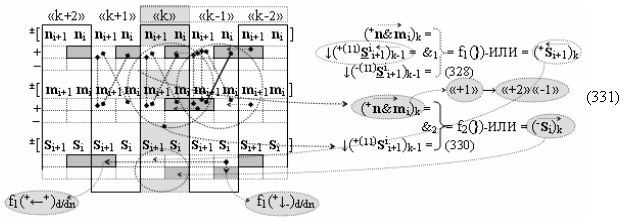
И если активность условно отрицательного аргумента (-Si)k условно «i» разряда однозначна, то активность аргументов локальных переносов f1(+←+)d/dn и f1(+↓-)d/dn процедуры логического дифференцирования d1/dn+ → f1(+←↓-)d/dn существенно зависит от активных аргументов в условно «k+1» и «k-2» «Зонах минимизации», поэтому сформируем все возможные варианты активизации результирующих аргументов суммы в этих «Зонах минимизации». А поскольку результирующий аргумент суммы локальных переносов f1(+←+)d/dn и f1(+↓-)d/dn может быть активизирован в условно «i» разряде, поэтому функциональную структуру положительного аргумента (+Si)k этого разряда в условно «k» «Зоне минимизации», когда его активизируют без преобразования, и такую структуру логических функций запишем в виде аналитического выражения (332).
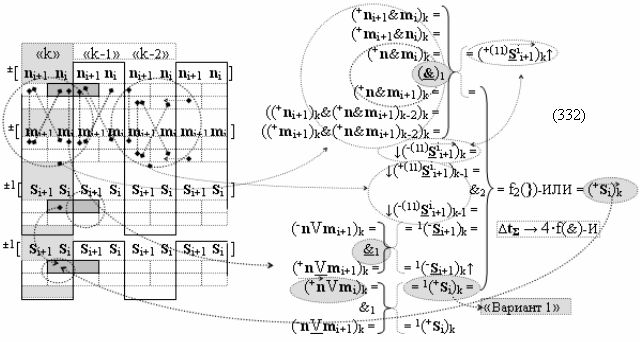
дополнительно введен положительный аргумент (+n&mi+1)k для формирования промежуточного аргумента (+(11)Si i+1)k↑, общего для двух условных разряда в «k» «Зоне минимизации». Поскольку если вернуться к анализу функциональной структуры (327), которая активизирует результирующий аргумент суммы (+Si+1)k условно «i+1» разряда, записав ее в виде аналитического выражения (333),
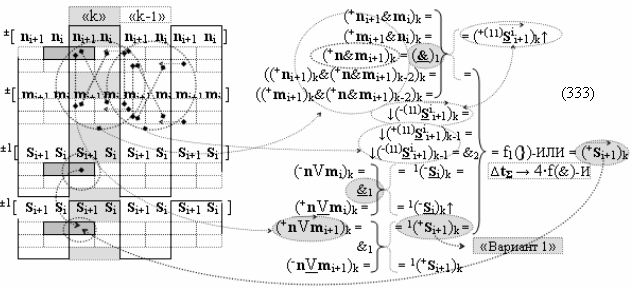
то в систему логической функции f1(}&)-ИЛИ-НЕ введен положительный входной аргумент (+n&mi+1)k, а для минимизации математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» функциональная структура в выражении (333) с логической функцией f1(}&)-ИЛИ-НЕ может быть заменена на промежуточный аргумент (+(11)Si i+1)k, в результате скорректированную структуру логических функций (333) запишем в виде минимизированного аналитического выражения (334)
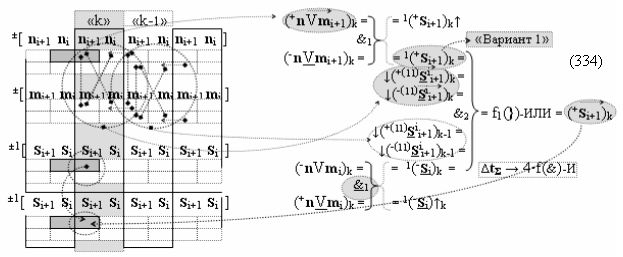
и структуру логических функций (332) также запишем с преобразованным положительным аргументом ↓(+(11)Si i+1)k в системе логической функции f2(&)-И в виде аналитического выражения (335).
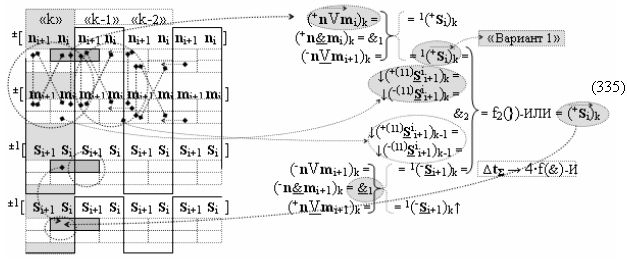
При этом функциональную структуру с выходной логической функцией f1(}&)-ИЛИ-НЕ выражения (332) для формирования положительных аргументов (+(11)Si i+1)k↑ и (+(11)Si i+1)k↑ без изменения уровня аналогового сигнала и с измененным уровнем аналогового сигнала соответственно запишем в виде структуры логических функций (336).
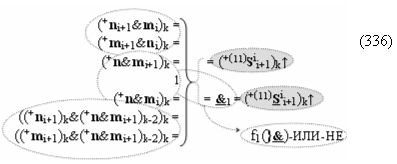
А если учесть, что при анализе активных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в условно «k» «Зоне минимизации» также возможны преобразованные аргументы (+n&mi+1)k и (+n&mi)k, а также преобразованные аргументы функциональной структуры (337),
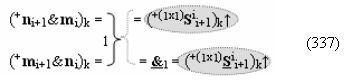
которые формируют в этой зоне аргументы (+(1х1)Si i+1)k↑ и (+(1х1)Si i+1)k↑ локальных переносов с неизменным уровнем аналогового сигнала и с измененным уровнем аналогового сигнала, поэтому для минимизации аналитической записи анализируемых структур логических функций, активизирующих результирующие аргументы, будем использовать только преобразованные аргументы.
И если записать структуру аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (338),
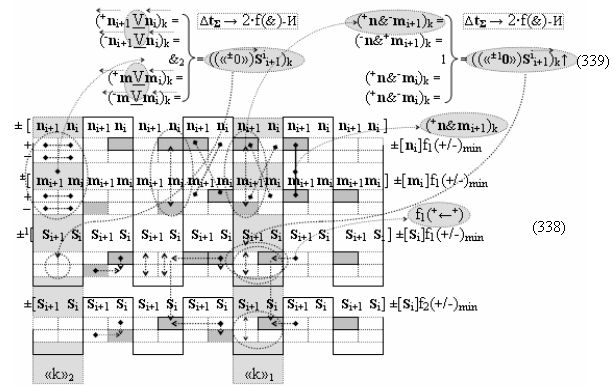
то для синтеза математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» с технологическим циклом ∆tΣ → 4∙f(&)-И необходимо сформировать дополнительные преобразованные аргументы, в которых технологический цикл ∆tΣ → 2∙f(&)-И не должен превышать двух условных логических функций f(&)-И. И такими функциональными структурами являются аналитические выражения (339), которые активизируют как преобразованный аргумент ((«±10»)Si i+1)k↑ активных логических нулей «+1»«-1» → «±10»iV«±10»i+1, так и преобразованный аргумент неактивных логических нулей «±0»i&«±0»i+1 в условно «i+1» и «i» разрядах в «k» «Зоне минимизации» и которые являются необходимым и достаточным условием активизации положительного аргумента (+n&mi+1)k-1 и положительного аргумента (+(1х1)Si i+1)k-1 выражения (337) «k-1» «Зоны минимизации» в условно «k» «Зоне минимизации». При этом следует отметить, что поскольку преобразованные аргументы ((«±10»)Si i+1)k и ((«±0»)Si i+1)k на уровне объединенной структуры аргументов ±[Si]f1(+/-)min, например, в структуре аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (340)
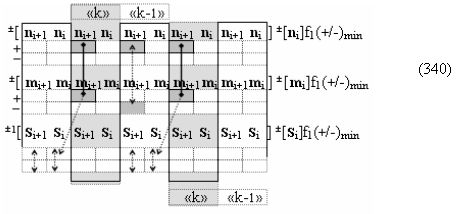
равновероятны, а их объединение приведет к увеличению технологического цикла ∆tΣ → 4∙f(&)-И преобразования аргументов слагаемых, но существенно упростит синтез математической модели сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации», поэтому на предварительном этапе ее синтеза сформирует функциональную структуру (341)
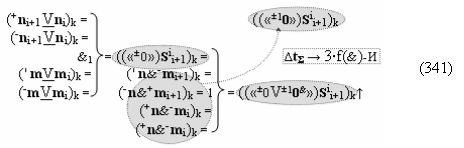
с комплексным аргументом ((«±0V±10»)Si i+1)k, объединяющую пять возможных входных аргументов, которые позволяют однозначно активизировать результирующие аргументы суммы. При этом если проанализировать технологический цикл ∆tΣ, например, 32-разрядного сумматора f1(Σ) с ускоренным переносом, записав его в виде выражения (342),
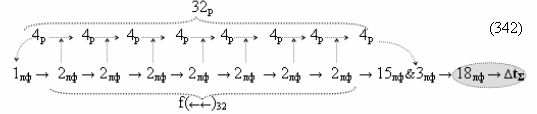
то последовательность условных логических функций (лф) → f(&)-И с учетом процедуры ускоренного сквозного переноса f(←←)32 будет соответствовать 15лф&3лф → 18лф или ∆tΣ → 18∙f(&)-И восемнадцати условным логическим функциям f(&)-И. А технологический цикл сумматора ±f1(ΣRU)min с ∆tΣ → 4∙f(&)-И и с ∆tΣ → 5∙f(&)-И минимизирован в 4,5 и 3,5 раз по сравнению с технологическм циклом выражения (342), при этом увеличение функциональной структуры сумматора ±f1(ΣRU)min на одну условную логическую функцию f(&)-И приводит к увеличению ↑∆tΣ → на 25%, что приводит к достаточно существенному увеличению его. Поэтому после синтеза математической модели сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации» проанализируем практическую целесообразность сформировать функциональную структуру (341) с технологическим циклом ∆tΣ → 4∙f(&)-И, который соответствует четырем условным логическим функциям f(&)-И. И такая возможность есть, поскольку если в структуре логических функций (341) выполнить перенос в соответствии с векторной структурой (343),
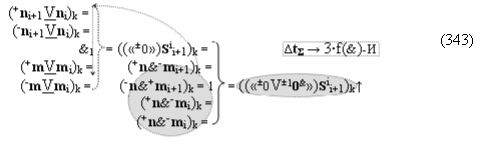
функциональной структуры с выходной логической функцией f1(})-ИЛИ через систему логической функции f1(&)-И, то запишем структуру логических функций (344),
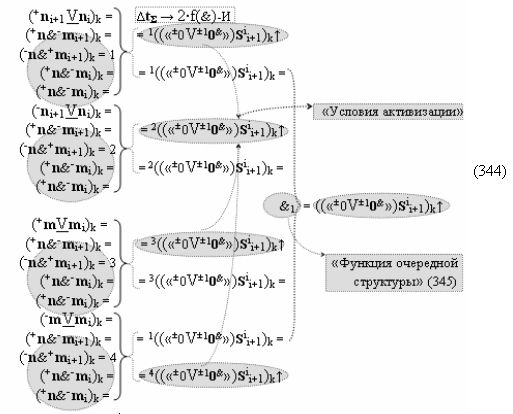
которая включает четыре функциональные входные структуры с выходными логическими функциями f1(})-ИЛИ - f4(})-ИЛИ, которые активизируют совокупность комплексных аргументов 1-4((«±0V±10&»)Si i+1)k↑, являются «Условиями активизации» активизируемой структуры аргументов «Активизируемый аргумент» слагаемых в аналитическом выражении (345).
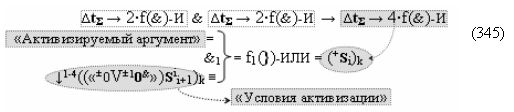
В результате технологический цикл ∆tΣ → 4∙f(&)-И формирования результирующего аргумента суммы в функциональной структуре (345) с комплексным «Условием активизации» ↓1-4((«±0V±10&»)Si i+1)k будет соответствовать четырем условным логическим функциям f(&)-И.
Далее, если вернуться к анализу структуры аргументов слагаемых (104), записав их логико-динамический процесс преобразования в виде графоаналитического выражения (343),
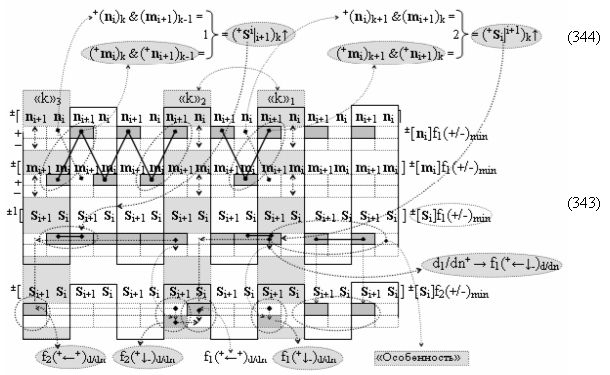
то для активизации аргумента локального переноса f1(+↓-)d/dn, f2(+↓-)d/dn и f2(+←+)d/dn процедуры логического дифференцирования d1,2/dn+ → f1,2(+←↓-)d/dn должны быть сформированы функциональные структуры (344) с преобразованными положительными аргументами (+Si|i+1)k и (+Si|i+1)k, которые активизированы между «Зонами минимизации» и в которых верхний индекс (i|i+1) и (i|i+1) разряда объединенного аргумента соответствует условно «k» «Зоны минимизации». При этом следует отметить, что ранее был сформирован преобразованный положительный аргумент (+Si i+1)k условно «k» «Зоны минимизации» и он активен, когда активны два последовательных аргумента в «Зоне минимизации». В результате введения промежуточных или «Комплексных аргументов», функционально принадлежащих объединенной структуре ±[Si]f1(+/-)min, а она позволит существенно упростить синтез математической модели сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации». Но для этого необходимо проанализировать логико-динамический процесс преобразования аргументов слагаемях ±[ni]f1(+/-)min и ±[mi]f1(+/-)min и сформировать дополнительные «Комплексные аргументы» на уровне объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min, которые учитывали характерные структурные «Особенности» слагаемых и позволяли косвенным образом выполнить процедуру сквозного переноса с одновременным формированием аргументов условно минимизированной суммы ±[Si]f2(+/-)min. Так, например, в графоаналитическом выражении (343) «Особенностью» является чередующаяся последовательность положительных аргументов в объединенной структуре слагаемых ±[Si]f1(+/-)min, которая имеет однозначно корректное преобразование только при косвенной процедуре логического дифференцирования d0/dn+ → f0(+←↓-)d/dn, например, в графоаналитическом выражении (345),
в котором посредством функциональной структуры (346) с выходной логической функцией f3(&)-И активизирован «Комплексный аргумент» 1(+10Si+1 &)k «i+1» разряда в условно «k» «Зоне минимизации». При этом следует отметить, что особенностью функциональной структуры (346) является выходная логическая функция f3(&)-И, которая, если записать ее в виде аналитического выражения (347),
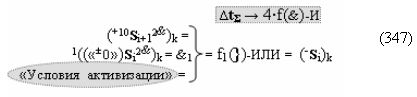
может включать комплексный аргумент «Условия активизации» для активизации результирующего условно отрицательного аргумента суммы (-Si)k условно «i» разряда «k» «Зоны минимизации». Результирующий условно отрицательный аргумент суммы (-Si)k условно «i» разряда в графоаналитическом выражении (345) также активизируют и в ситуации, когда перед последовательностью положительных аргументов в объединенной структуре слагаемых ±[Si]f1(+/-)min в непрерывной последовательности активизированы как минимум два условно отрицательных аргумента. Действительно, если записать структуру логических функций (348),
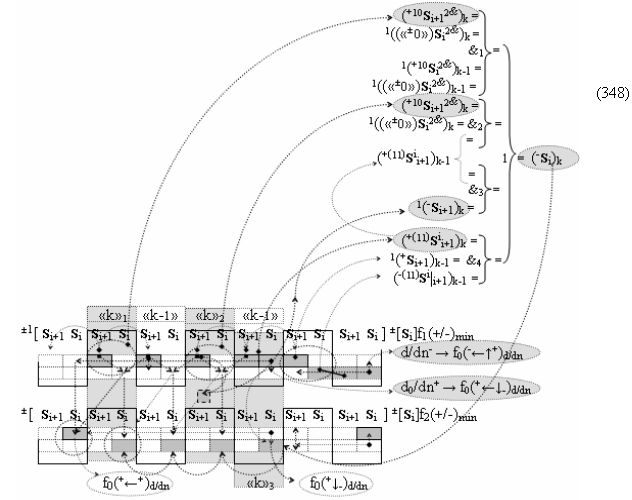
которая активизирует результирующий условно отрицательный аргумент суммы (-Si)k условно «i» разряда в различных ситуациях и которые для однозначности запишем в виде графоаналитического выражения (349),
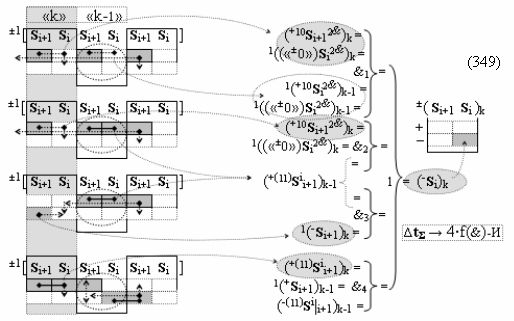
то переход на уровень «Комплексных аргументов» активизированных в объединенной структуре слагаемых ±[Si]f1(+/-)min, функционально связанных с конкретной анализируемой структурой, позволит корректно сформировать математическую модель сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации».
Поскольку сформирована функциональная структура, активизирующая условно отрицательный аргумент суммы (-Si)k условно «i» разряда в «k» «Зоне минимизации» при преобразовании положительных аргументов, поэтому запишем для других возможных «Комбинаций» положительных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (350)
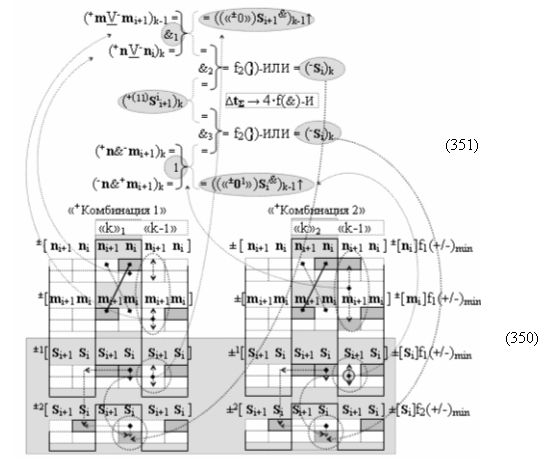
функциональные дополнительные структуры (351), которые активизируют тот же условно отрицательный аргумент суммы (-Si)k. При этом в систему логических функций f2(&)-И и f3(&)-И введена функциональная структура с выходной логической функцией f1(&)-И, активизирующая преобразованный аргумент неактивного логического нуля «±0» в условно «i+1» разряде и функциональная структура с выходной логической функцией f1(})-ИЛИ, активизирующая преобразованный аргумент активного логического нуля «±01» в условно «i+1» разряде. И если эти функциональные структуры записать в виде соответствующих преобразованных аргументов ((«±0»)Si+1 &)k-1 и ((«±01»)Si &)k-1 условно «i-1» разряда с соответствующей объединенной структурой аргументов слагаемых ±[Si]f1(+/-)min, то запишем графоаналитическое выражение (352),
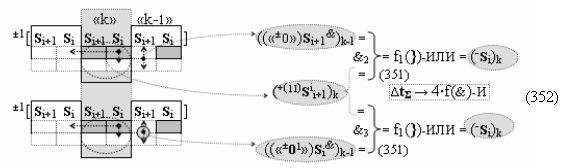
которое затем объединим с графоаналитическим выражением (348) и запишем объединенную структуру логических функций (353).
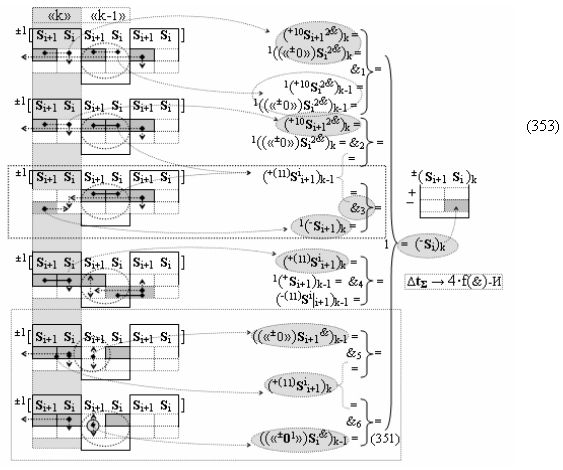
В результате условно отрицательный аргумент суммы (-Si)k условно «i» разряда при преобразовании положительных аргументов объединенных слагаемых ±[mi]f1(+/-)min может быть активизирован в шести различных ситуациях. При этом из анализа процедуры преобразования аргументов условно «k» «Зоне минимизации» следует, что функциональная структура с выходной логической функцией f3(&)-И включена в выходную систему логической функции f1(})-ИЛИ не корректно. Поскольку в «k» «Зоне минимизации» преобразуют условно отрицательный аргумент 1(-Si+1)k в связи с активным положительным аргументом локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn+ → f1(+←↓-)d/dn, поэтому он функционально относится к структуре условно отрицательного канала сумматора ±f(ΣRU)min и поэтому функциональную структуру с выходной логической функцией f3(&)-И (354)
необходимо исключить из системы выходной логической функции f1(})-ИЛИ выражения (353) и записать в виде структуры логических функций (355).
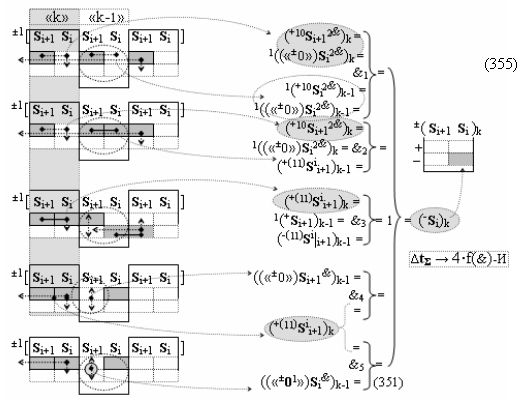
В результате условно отрицательный аргумент суммы (-Si)k условно «i» разряда при преобразовании положительных аргументов объединенных слагаемых ±[mi]f1(+/-)min может быть активизирован на первом этапе синтеза в пяти различных ситуациях. Но существуют структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min (356),
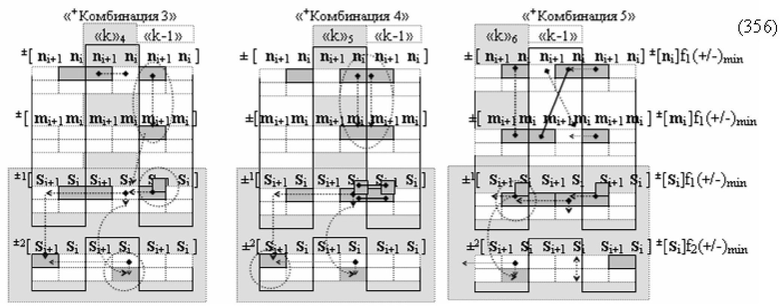
в которых также активизирован условно отрицательный аргумент суммы (-Si)k условно «i» разряда. Поэтому для положительной «+Комбинации 3» запишем функциональную структуру (357),
для положительной «+Комбинации 4» запишем функциональную структуру (358),
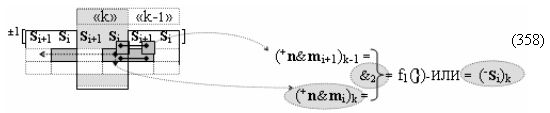
для положительной «+Комбинации 5» запишем функциональную структуру (359),
которые могут быть записаны в виде объединенного выражения (360)(360)
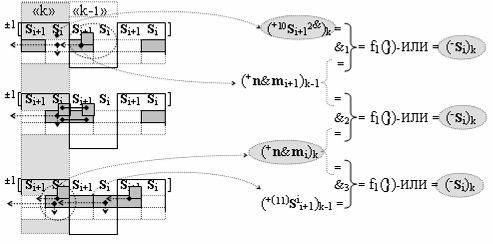
И если функциональные объединенные структуры (360) ввести в систему выходной логической функции f1(})-ИЛИ выражения (355), то функционально законченную структуру логической функции запишем в виде аналитического выражения (361).
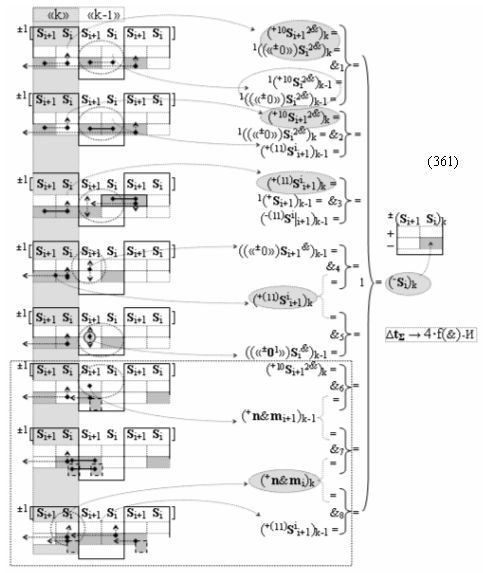
При этом следует отметить, что структура логических функций (361), которая активизирует условно отрицательный аргумент суммы (-Si)k условно «i» разряда и сформирована в результате преобразования положительных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, функционально относится к структуре условно отрицательного канала сумматора ±f(ΣRU)min. А при преобразовании условно отрицательных ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в аналогичных структурных ситуациях будет активизирован положительный аргумент суммы (+Si)k условно «i» разряда, и такая функциональная структура может быть записана формализованным методом посредством изменения знаков аргументов в выражении (362).
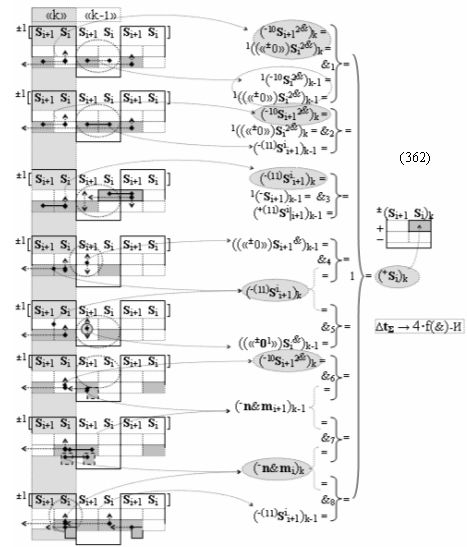
Из анализа процедуры активизации положительного аргумента суммы (+Si)k условно «i» разряда в условно «k» «Зоне минимизации» выражения (362) следует, что все функциональные структуры с выходными логическими функциями f1(&)-И - f8(&)-И корректно его активизируют. При этом следует отметить, что поскольку формализованный метод записи функциональной структуры, которая активизирует аргумент результирующей суммы противоположного знака, является корректным, поэтому продолжим анализ и формирование дополнительных структур для «Положительного канала сумматора «i» разряда» и для «Условно отрицательного канала сумматора «i» разряда». А для этого вернемся к анализу выражения (345, записав его в виде графоаналитического выражения (363)
и дополнительному анализу функциональной структуры с выходной логической функцией f1(&)-И, активизирующей результирующий условно отрицательный аргумент суммы (-Si)k. Поскольку если записать возможные аргументы слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в виде графоаналитического выражения (364),
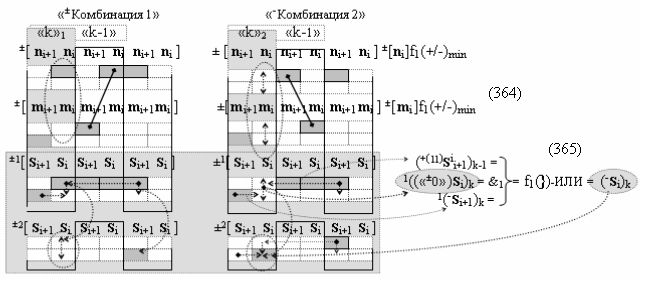
то в систему логической функции (363) необходимо ввести дополнительный преобразованный аргумент 1((«±0»)Si)k неактивного логического нуля, а функциональную структуру в этой ситуации запишем в виде аналитического выражения (365), и только она может корректно активизировать результирующий условно отрицательный аргумент суммы (-Si)k. Поэтому введем эту функциональную структуру в структуру логических функций «Условно отрицательного канала сумматора «i» разряда» (361), которую запишем в виде выражения (366).
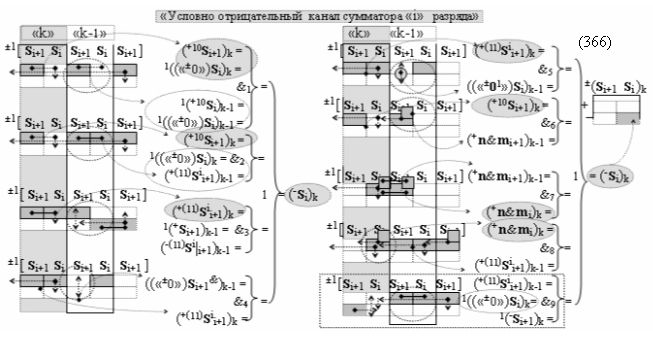
А функциональную структуру, активизирующую положительный аргумент суммы (+Si)k в «Положительном канале сумматора «i» разряда», запишем в виде аналитического выражения (367)
и введем ее в структуру логических функций «Положительного канала сумматора «i» разряда» (362), которую запишем в виде аналитического выражения (368).
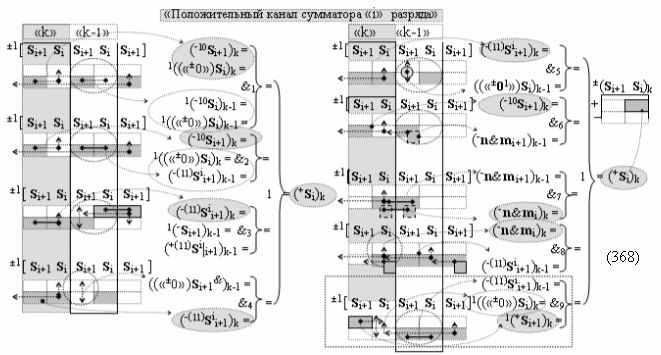
Далее, для формирования функционально законченного «Положительного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i» разряда» необходимо сформировать функциональные дополнительные структуры локальных переносов в следующих ситуациях.
Ситуация 1. Активны аргументы противоположного знака в условно «k» «Зоне минимизации» и активны «Условия активизации», которые запишем в виде графоаналитического выражения (369)
и которые преобразуют в соответствии с арифметическими аксиомами «+2» «-1» → «+1» и «-2» «+1» → «-1», но с конкретными «Условиями активизации», и эти условия запишем в виде различных вариантов. А для формирования аналитических дополнительных структур для «Положительного и условно отрицательного канала сумматора «i» разряда» первой ситуации запишем преобразованные аргументы, технологический цикл которых ∆tΣ → 2∙f(&)-И минимизирован до двух условных логических функций f(&)-И, а такой «+Комплексный аргумент» ((±1х1)+Si+1 i)k в условно «k» «Зоне минимизации» активизируют посредством функциональной структуры (370).
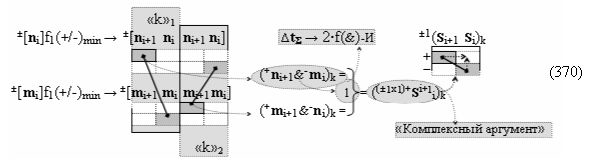
А «-Комплексный аргумент» ((±1х1)-Si+1 i)k в условно «k» «Зоне минимизации» активизируют посредством функциональной структуры (371),
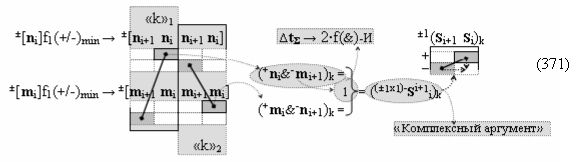
в которой технологический цикл ∆tΣ → 2∙f(&)-И минимизирован до двух условных логических функций f(&)-И. При этом следует отметить, что в условно «k» «Зоне минимизации» равновероятен как «+Комплексный аргумент» ((±1х1)+Si+1 i)k, так и «-Комплексный аргумент» ((±1х1)-Si+1 i)k, а возможна ситуация, когда в условно «k» «Зоне минимизации» активен аргумент ((±1х1)+Si+1 i)k или ((±1х1)-Si+1 i)k, и в условно «k-1» «Зоне минимизации» также активен аргумент ((±1х1)+Si+1 i)k-1 или ((±1х1)-Si+1 i)k-1, которые могут быть объединены в системе логической функции f1(})-ИЛИ выражения (372),
в котором технологический цикл ∆tΣ → 3∙f(&)-И увеличен до трех логических функций f(&)-И. А если учесть, что ((±1х1)+Si+1 i)k-1 или ((±1х1)-Si+1 i)k-1 формируют также посредством логической функции f1(})-ИЛИ в выражениях (370) и (371), то «Комплексный аргумент» (1х1|+ -|Si+1 i)k-1 в условно «k-1» «Зоне минимизации» необходимо сформировать посредством функциональной структуры (373),
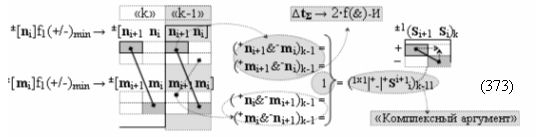
в которой технологический цикл ∆tΣ → 2∙f(&)-И минимизирован до двух условных логических функций f(&)-И. В результате первый вариант функциональной дополнительной структуры запишем либо в виде аналитического выражения (374),
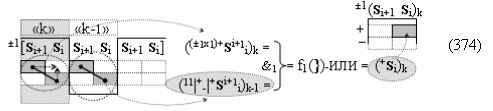
либо в виде аналитического выражения (375),
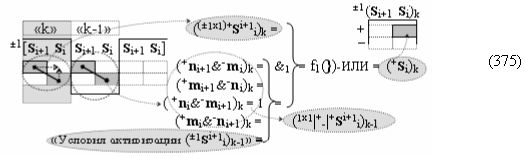
в котором в систему логической функции f1(&)-И включена функциональная структура (372). При этом следует отметить, что функциональная структура (375) с входной логической функцией f1(})-ИЛИ позволяет в свою систему включать дополнительное «Условие активизации (±1Si+1 i)k-1», которые активно в условно «k-1» «Зоне минимизации» и такими условием является активный логический ноль «+1»«-1» → «±01» и его в графоаналитическом выражении (376)
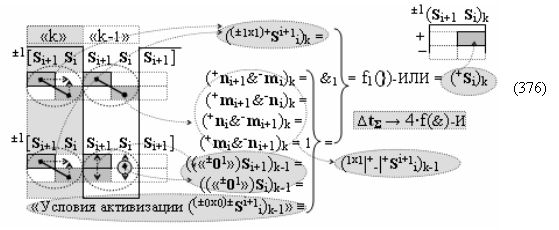
в системе логической функции запишем в виде двух преобразованных аргументов ((«±01»)Si+1)k-1 условно «i-1» разряда и ((«±01»)Si)k-1 условно «i» разряда. При этом в систему входной логической функции 1(})-ИЛИ выражения (376) может быть включен и «Комплексный аргумент» неактивные логические нули «±0»k условно «k-1» «Зоны минимизации», функциональную структуру которого запишем в виде аналитического выражения (377),
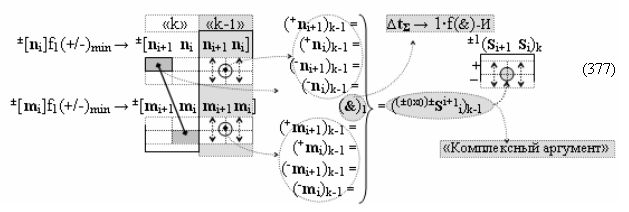
в котором логическая функция f1(}&)-ИЛИ-НЕ будет активна только в случае одновременной неактивности всех входных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min. Но если учесть логику формирования условно минимизированной структуры аргументов, то для активизации преобразованного аргумента в условно «k» «Зоне минимизации» необходимым и достаточным условием является неактивность «Комплексного аргумента» ((±0)±Si+1)k-1 функциональной структуры (378),
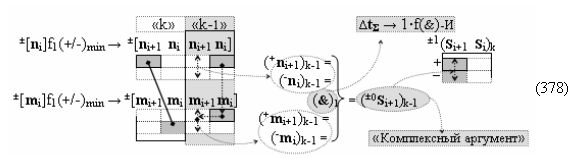
поскольку любые преобразования в условно «k-1» «Зоне минимизации» приводят к формированию условно минимизированной структуры аргументов. При этом следует отметить, что технологический цикл ∆tΣ → 1∙f(&)-И минимизирован до одной условной логической функции f(&)-И, в результате «Комплексный аргумент» ((±0х0)±Si+1 i)k-1 выражения (378) может быть записан в одной системе логической функции f1(})-ИЛИ, выражение (376) совместно с аргументами ((«±01»)Si+1)k-1 и ((«±01»)Si)k-1 активого логического нуля «+1»«-1» → «±01» и объединенное выражение в данной ситуации запишем в виде графоаналитического выражения (379).
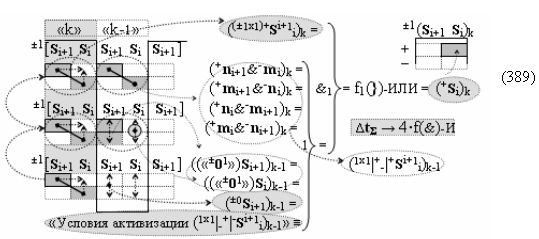
При этом в систему входной логической функции f1(})-ИЛИ выражения (379) может быть включен и «Комплексный аргумент» (1х1|- +|Si+1 i)k-1 функциональной структуры (380),
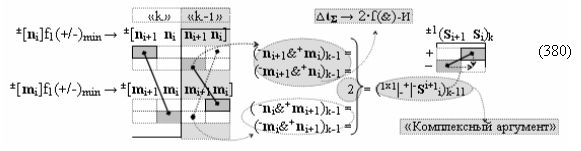
который также является «Условием активизации» положительного результирующего аргумента суммы (+Si)k в условно «k» «Зоне минимизации», в результате структуру логических функций (379) после объединения логической функции f2(})-ИЛИ выражения (380) и логической функции f1(})-ИЛИ выражения (379) запишем в виде аналитического выражения (381).
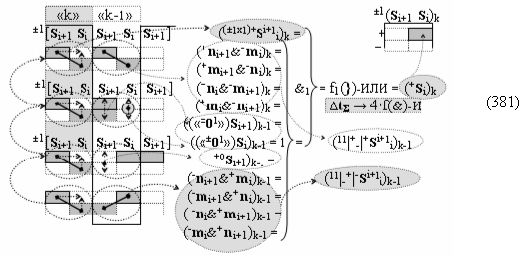
При этом если в системе логической функции f1(})-ИЛИ выражения (381) совокупность входных преобразованных аргументов (382)
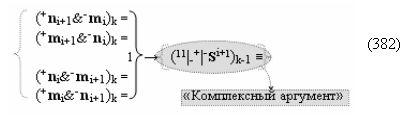
и совокупность входных преобразованных аргументов (383)
записать посредством «Комплексных аргументов», то структуру логических функций (381) запишем в виде минимизированного аналитического выражения (384).
Вариант 1.
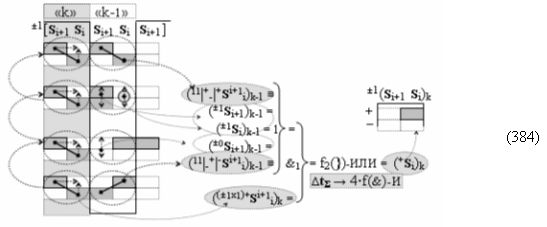
При этом следует отметить, что функциональная структура (380) была сформирована в ситуации, когда в условно «k-1» «Зоне минимизации» были либо не активны все аргументы объединенной структуры слагаемых ±[Si]f1(+/-)min, либо активны в ней одновременно два аргумента. Но возможны структуры аргументов, когда в условно «k-1» «Зоне минимизации» активен только один положительный аргумент 1(+Si+1)k-1 или условно отрицательный аргумент 1(1Si+1)k-1, а активизацию аргумента в условно «k» «Зоне минимизации» выполняют и для этой ситуации, поэтому сформируем функциональную структуру (385).
Вариант 2.
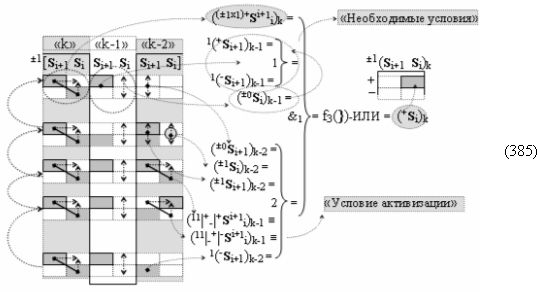
Из анализа функциональной структуры (385) следует, что «Необходимые условия» для активизации результирующего аргумента суммы (+Si)k в ней представлены посредством логической функции f1(})-ИЛИ как положительный аргумент 1(+Si+1)k-1, так и условно отрицательный аргумент 1(-Si+1)k-1 условно «k-1» «Зоны минимизации», которая включена в систему логической функции f1(&)-И совместно с входным аргументом активизированного нуля (±0Si)k-1. При этом в систему логической функции f1(&)-И также включена логическая функция f2(})-ИЛИ с входными аргументами «Условие активизации», но в нее могут быть включены два возможных варианта аргументов слагаемых (386),
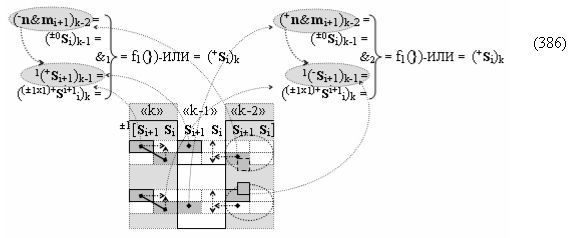
поскольку активный условно отрицательный аргумент (-n&mi+1)k-2 условно «i-2» разряда может быть включен в систему логической функции f1(&)-И только с положительным аргументом 1(+Si+1)k-1, а положительный аргумент (+n&mi+1)k-2 условно «i-2» разряда может быть включен в систему логической функции f2(&)-И только с условно отрицательным аргументом 1(-Si+1)k-1. Поэтому в функциональную структуру двух возможных вариантов (384) и (385), которые запишем в виде графоаналитического выражения (387)
необходимо ввести две дополнительные структуры (386) для того, чтобы процедура преобразования аргументов в соответствии с обратной арифметической аксиомой «+2» «-1» → «+1» была корректно реализована. В результате будет сформирована функционально законченная структура логических функций с возможными вариантами активизации аргумента результирующей суммы (+Si)k и она будет включать четыре возможных варианта комбинаций возможных аргументов слагаемых, которые не могут быть объединены, поскольку была проанализирована «Разрешительная ситуация». А возможна «Запретительная ситуация», когда процедуру преобразования аргументов в условно «k» «Зоне минимизации» выполняют с учетом возможных «Запретительных аргументов», а такие аргументы непосредственно связаны с возможными локальными переносами аргументов из условно «k-1» «Зоны минимизации». Поэтому запишем возможные структуры аргументов слагаемых ±[Si]f1(+/-)min, в которых активизирован локальный перенос и для них запишем структуру логических функций (388),
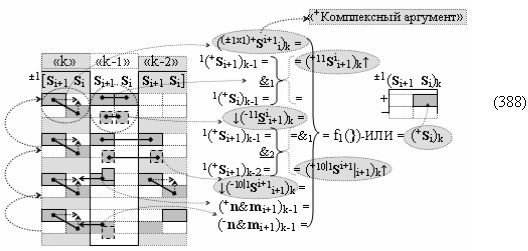
в которой в систему логической функции f1(&)-И введены две функциональные структуры с выходными логическими функциями f1(&)-И-НЕ и f2(&)-И-НЕ с положительными входными аргументами. А функциональные аналогичные структуры с условно отрицательными входными аргументами в выражении (388) записаны в виде преобразованных аргументов ↓(-11Si i+1)k и ↓(+10|1Si+1 i+1)k, поскольку их функциональные структуры являются структурами «Условно отрицательного канала сумматора «i» разряда», и их запишем в виде выражения (389).
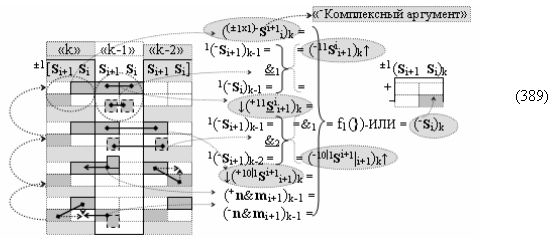
При этом следует отметить, что функциональная структура «+Комплексного аргумента» ((±1х1)+Si+1 i)k и «-Комплексного аргумента» ((±1х1)-Si+1 i)k в условно «k» «Зоне минимизации» также может быть минимизирована, поскольку если вернуться к анализу функциональной структуры (370), записав ее в виде выражения (390)
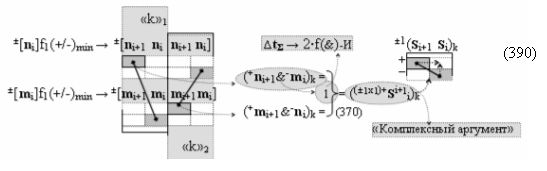
и функциональной структуры (371), записав ее в виде выражения (391),
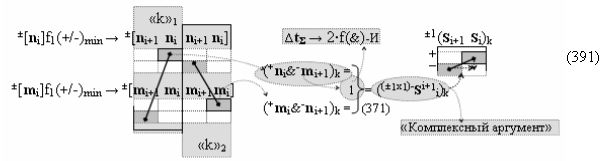
то для активизации этих аргументов необходимо включить в математическую модель сумматора ±f(ΣRU)min четыре функциональные дополнительные структуры для активизации преобразованных аргументов (+ni+1&-mi)k, (+mi+1&-ni)k, (+ni&-mi+1)k и (+mi&-ni+1)k, а также логическую функцию f1(})-ИЛИ. А если учесть, что в математическую модель сумматора ±f(ΣRU)min должны быть включены функциональные структуры (247) и (248), записав их в виде аналитических выражений (292),
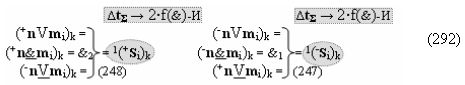
и включены функциональные структуры (249) и (250), записав их в виде аналитических выражений (293)
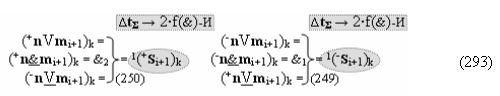
с технологическим циклом ∆tΣ → 2∙f(&)-И, равным двум условным логическим функциям f(&)-И, то функциональные структуры (390) и (391) могут быть исключены из математической модели сумматора ±f(ΣRU)min, а «+Комплексный аргумент ((±1х1)+Si+1 i)k» в структуре логических функций (388) может быть записан посредством двух преобразованных аргументов 1(+Si+1)k условно «i+1» разряда и 1(-Si)k условно «i» разряда выражений (292) и (293). В результате скорректированную структуру логических функций (388) запишем в виде аналитического выражения (294),
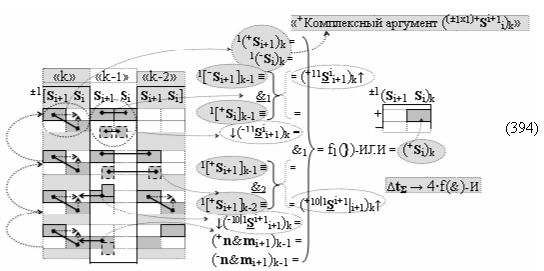
а скорректированную структуру логических функций (389) запишем в виде аналитического выражения (295),
в которых в систему логических функций f1(&)-И-НЕ и f1(&)-И-НЕ включены преобразованные аргументы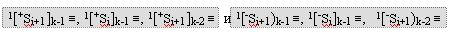 
с функциональной цифровой связью (≡), под которой будем понимать функциональную цифровую связь либо непосредственно самих преобразованных аргументов функциональных структур (292) и (293) и в этом случае технологический цикл ∆tΣ → 5∙f(&)-И структуры логических функций (394) и (395) будет соответствовать пяти условным логическим функциям f(&)-И. Либо под входным аргументом и функциональной цифровой связью (≡) будем понимать совокупность самих входных аргументов функциональных структур (292) и (293), и в этом случае технологический цикл ∆tΣ → 4∙f(&)-И структуры логических функций (394) и (395) будет соответствовать четырем условным логическим функциям f(&)-И. Поэтому функциональные структуры (394) и (395) запишем в виде аналитических выражений (396)
и в виде аналитических выражений (397)
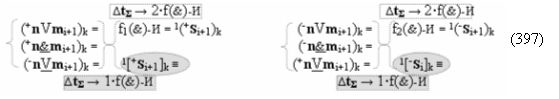
На основании полученных результатов следует, что оптимальная структура логических функций математической модели сумматора ±f1(ΣRU)min может быть сформирована на уровне символики объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min, что позволит существенно минимизировать число функциональных входных структур в аналитическом выражении математической модели сумматора ±f1(ΣRU)min. Поскольку если вернуться к повторному анализу предварительно сформированной структуре логических функций «Положительного канала сумматора «i» разряда» (368), записав ее с учетом скорректированной символики входного аргумента 1((«±0»)Si+1)k → 1(±0Si+1)k и 1((«±0»)Si)k → 1(±0Si)k в виде графоаналитического выражения (398),
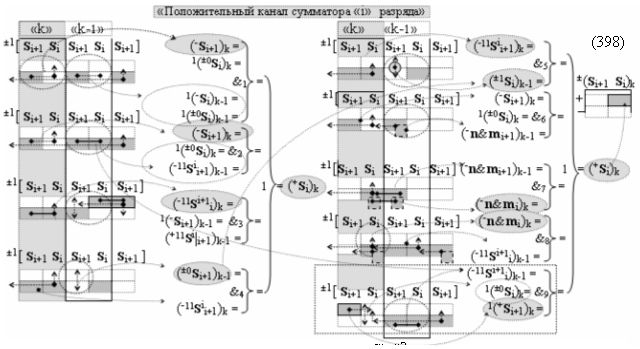
где входные аргументы (-10Si+1)k и 1(±0Si)k в условно «k» «Зоне минимизации» сформированы посредством функциональных структур (399),
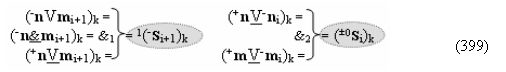
а входной аргумент (-11Si i+1)k сформирован посредством функциональной структуры (400),
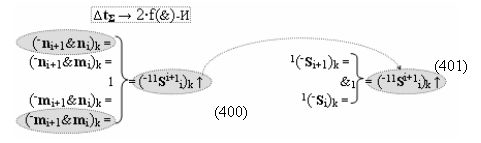
которая на уровне объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min полностью соответствует минимизированной структуре (401) с выходной логической функцией f1(&)-И, то структура логических функций (398) может быть существенно минимизирована. И эта минимизация связана с тем, что как входные аргументы (-10Si+1)k и 1(±0Si)k в выражении (399), так и входной аргумент в выражении (401) сформированы посредством логической функции f(&)-И, которые могут быть объединены с логической функцией f(&)-И, формирующей результирующий аргумент (+Si)k. Но для того, чтобы минимизировать структуру логических функций (398), необходимо ввести объединяющую входную логическую функцию f2(})-ИЛИ для объединения соответствующих «Условий активизации», «Комплексный аргумент» которых позиционно расположен в условно «k-1» «Зоне минимизации» и их технологический цикл ∆tΣ → 1∙f(&)-И не должен превышать одной условной логической функции f(&)-И. Поэтому с одной стороны функциональную структуру (400) запишем в виде аналитического выражения (402),
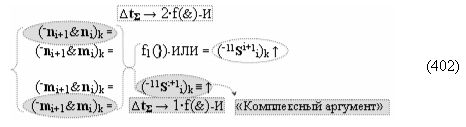
в котором введен «Комплексный аргумент» (-11Si+1 i)k ≡ ↑ и который представляет совокупность входных аргументов логической функции f1(})-ИЛИ, с другой стороны сформируем функциональную структуру (403)
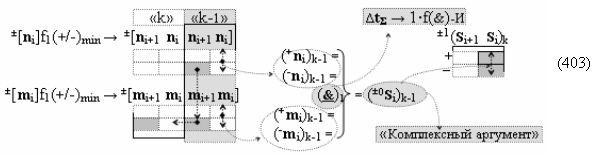
посредством которой в условно «k-1» «Зоне минимизации» неактивные аргументы нуля «±0»→«+1»«-1» условно «i-1» разряда преобразуют в активный аргумент (±0Si)k-1 активного логического нуля «±0»«+1»«-1» → «±0» и в этой функциональной структуре технологический цикл ∆tΣ → 1∙f(&)-И не превышает одной условной логической функции f(&)-И. В результате структуру логических функций (398) с активными одноименными аргументами условно «k» «Зоне минимизации» с учетом функциональной структуры (399) запишем в виде двух функциональных структур (404) и (405),
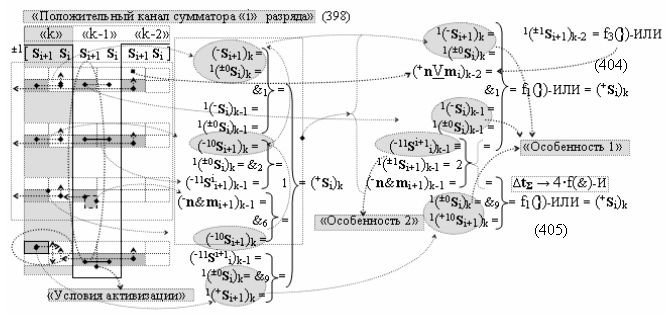
в которых «Особенностью 2» являются одновременная последовательность условно отрицательных аргументов в условно «k» «Зоне минимизации» и результирующий аргумент (-11Si+1 i)k активизирует функциональная структура (406)
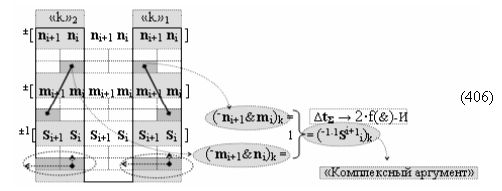
с технологическим циклом ∆tΣ → 2∙f(&)-И, который соответствует двум условным логическим функциям f(&)-И, но с выходной логической функцией f1(})-ИЛИ. А «Особенностью 1» является последовательность активного и неактивного аргумента 1(-Si+1)k и 1(±0Si)k в условно «k» «Зоне минимизации», и результирующие аргументы 1(-Si+1)k и (±0Si)k активизируют функциональные структуры выражения (399),
которые для результирующего объединенного условно отрицательного аргумента 1(-10Si+1 i)k запишем в виде аналитического выражения (407),
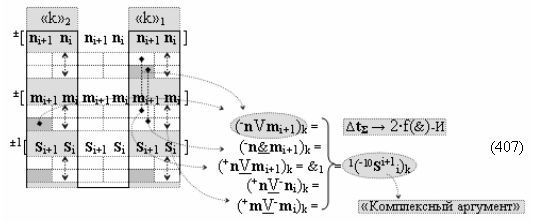
с технологическим циклом ∆tΣ → 2∙f(&)-И, который также соответствует двум условным логическим функциям f(&)-И, но с выходной логической функцией f1(&)-И. При этом в объединенной структуре аргументов слагаемых ±[Si]f1(+/-)min в условно «k» «Зоне минимизации» возможен «Комплексный аргумент» 1(-01Si+1 i)k и 1(-1+1Si+1 i)k, поэтому запишем функциональную структуру, активизирующую условно отрицательный аргумент 1(-01Si+1 i)k в виде аналитического выражения (308)
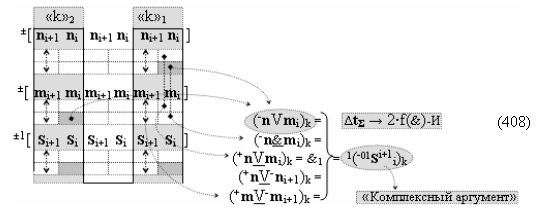
и функциональную структуру (391), активизирующую аргумент в виде аналитического выражения (409).
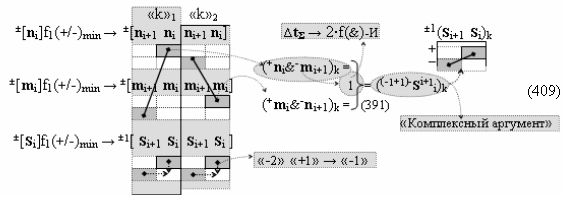
Функциональные аналогичные структуры имеют и положительные «Комплексные аргументы» (+11Si+1 i)k, 1(+10Si+1 i)k, 1(+01Si+1 i)k и 1(+1-1Si+1 i)k, которые запишем в виде аналитического выражения (409),
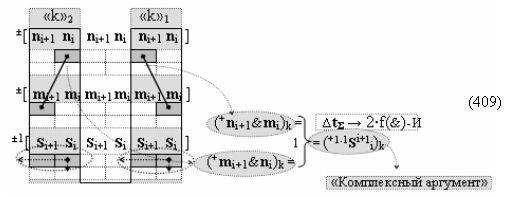
функциональную структуру, активизирующую положительный аргумент (+10Si+1 i)k, запишем в виде аналитического выражения (410),
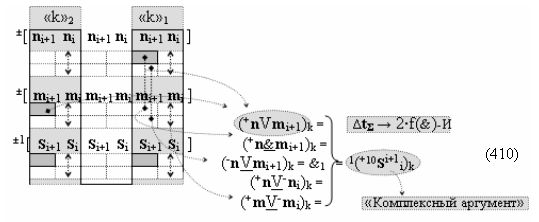
и функциональную структуру, активизирующую положительный аргумент (+01Si+1 i)k, запишем в виде аналитического выражения (411),
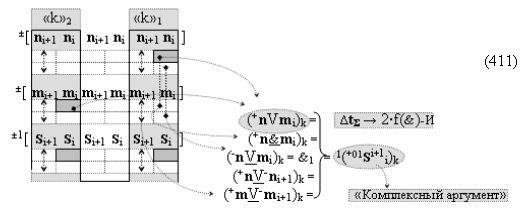
а функциональную структуру (390), активизирующую аргумент (+1-1Si+1 i)k, запишем в виде аналитического выражения (412).
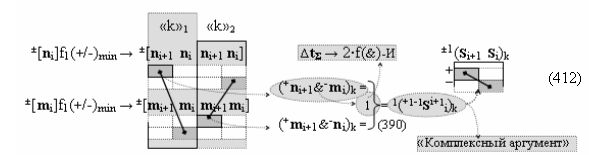
Необходимым аналогичным и достаточным «Условием активизации» одного из слагаемых или аргумента их преобразования в условно «k» «Зоне минимизации» является и «Комплексный аргумент» (±1Si+1)k-1 «i+1» разряда или аргумент (±1Si)k-1 «i» разряда в условно «k-1» «Зоны минимизации», которые соответствуют аргументу активного логического нуля «+1»«-1» → «±01», и функциональные структуры их запишем в виде аналитических выражений (413).
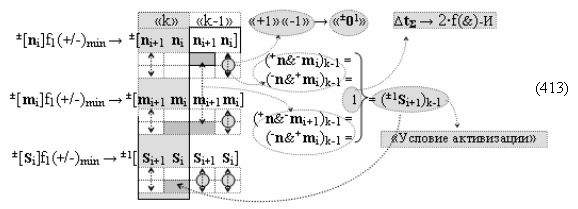
При этом следует отметить, что как аргумент (±1Si+1)k-1 активного логического нуля «+1»«-1» → «±01» выражения (413), так и аргумент (±0Si+1)k-1 неактивного логического нуля «±0» выражения (403) равновероятны в структуре аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, а они являются необходимым и достаточным «Условием активизации» либо одного из аргументов слагаемых, либо аргумента процедуры их преобразования в условно «k» «Зоне минимизации». А если учесть, что аргумент (±0Si+1)k-1 неактивного логического нуля «±0» выражения (403) имеет технологический цикл ∆tΣ → 1∙f(&)-И, равным одной условной логической функции 1∙f(&)-И, поэтому он может быть включен в систему логической функции f1(})-ИЛИ выражения (413), которое запишем в виде аналитического выражения (414).
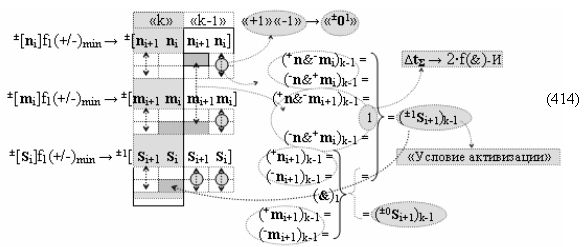
При этом следует отметить, что к категории необходимого и достаточного «Условия активизации» аргументов в условно «k» «Зоне минимизации» также могут быть отнесены следующие функциональные структуры.
1. Функциональная структура (415),
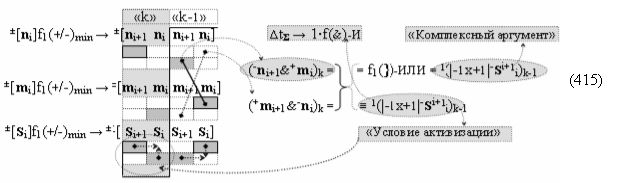
активизирующая условно отрицательный «Комплексный аргумент» 1(|-1х+1|-Si+1 i)k-1 в условно «k-1» «Зоне минимизации», в которой входные аргументы
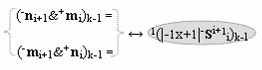
могут быть введены в выходную систему логической функции f1(})-ИЛИ выражения (414) в виде аргумента 1(|-1х+1|-Si+1 i)k-1 «Условия активизации». Поскольку структура аргументов в условно «k-1» «Зоне минимизации» минимизирована с активизацией результирующего аргумента в условно «i-1» разряде, в результате функциональную структуру (414) запишем в виде аналитического выражения (416)
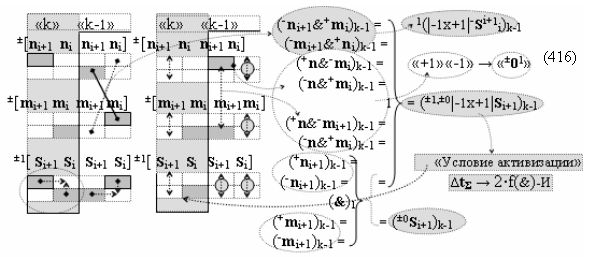
2. Функциональная структура (417),
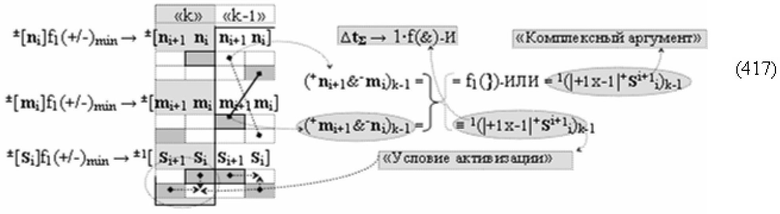
активизирующая положительный «Комплексный аргумент» 1(|+1х-1|+Si+1 i)k-1 в условно «k-1» «Зоне минимизации», в которой входные аргументы
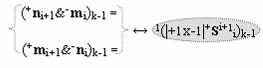
могут быть введены в выходную систему логической функции f1(})-ИЛИ выражения (416) в виде аргумента 1(|+1х-1|+Si+1 i)k-1 «Условия активизации». Поскольку структура аргументов в условно «k-1» «Зоне минимизации» минимизирована с активизацией результирующего аргумента в условно «i-1» разряде, в результате функциональную структуру (416) запишем в виде аналитического выражения (418).
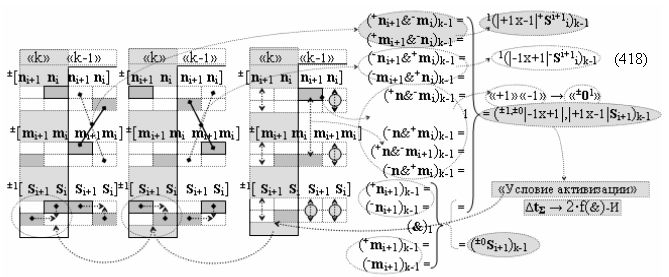
3. Функциональная структура (376), которую запишем в виде в виде аналитического выражения (419),
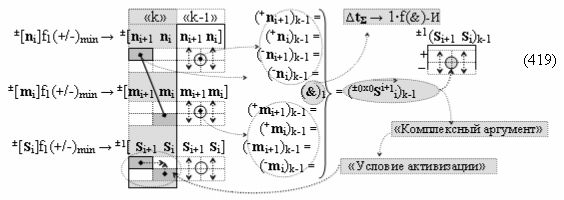
активизирующая посредством логической функции f1(}&)-ИЛИ-НЕ «Комплексный аргумент» ((±0х0)±Si+1 i)k-1 неактивности всех слагаемых в условно «k-1» «Зоне минимизации», которую также введем в структуру логических функций (418), в результате ее запишем в виде аналитического выражения (420).
При этом следует отметить, что сформированная функциональная структура (420) является «Условием активизации» как положительных аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, так и условно отрицательных аргументов слагаемых, когда в условно «k» «Зоне минимизации» одновременно активны два аргумента и их преобразуют в соответствии с процедурой логического дифференцирования d1/dn+ → f1(+←↓-)d/dn или d2/dn- → f2(-←↑+)d/dn или в соответствии с обратными арифметическими аксиомами «+2» «-1» → «+1» и «-2» «+1» → «-1». А также в ситуациях активности одного из аргументов в условно «k» «Зоне минимизации», но при активности аргумента (±1,±0,±0х0|-1х+1|,|+1х-1|Si+1 i)k+1 «Условия активизации» в условно «k+1» «Зоне минимизации».
Ситуация 1. В условно «k» «Зоне минимизации» активен только положительный аргумент 1(+01Si+1 i)k условно «i» разряда с технологическим циклом ∆tΣ → 2∙f(&)-И в системе логической функции f1(&)-И функциональной структуры (421),
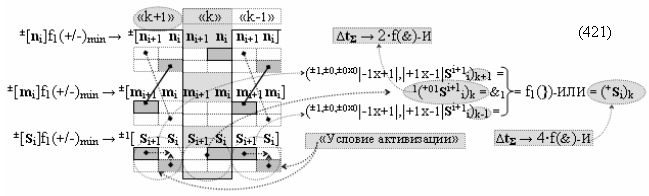
в которой технологический цикл ∆tΣ → 4∙f(&)-И соответствует четырем условным логическим функциям f(&)-И. При этом следует отметить, что если вернуться в анализу функциональной структуры (411) положительный аргумент 1(+01Si+1 i)k, записав ее в виде аналитического выражения (422),
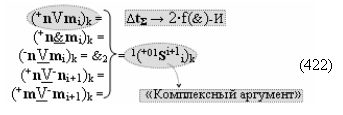
то для минимизации аналитического выражения сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» целесообразно не объединять одноименные логические функции f2(&)-И выражения (422) с логической функцией f1(&)-И выражения (421), поскольку это объединение не приведет к минимизации технологического циклы ∆tΣ → 4∙f(&)-И общей функциональной структуры, посредством которой активизируют положительный результирующий аргумент суммы (+Si)k условно «i» разряда.
Ситуация 2. В условно «k» «Зоне минимизации» активен только положительный аргумент 1(+10Si+1 i)k условно «i+1» разряда с технологическим циклом ∆tΣ → 2∙f(&)-И в системе логической функции f1(&)-И функциональной структуры (423).
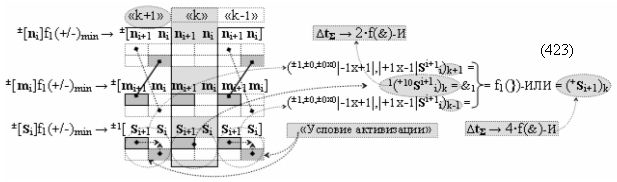
Ситуация 3. В условно «k» «Зоне минимизации» активен только условно отрицательный аргумент 1(-01Si+1 i)k условно «i» разряда с технологическим циклом ∆tΣ → 2∙f(&)-И в системе логической функции f1(&)-И функциональной структуры (424),
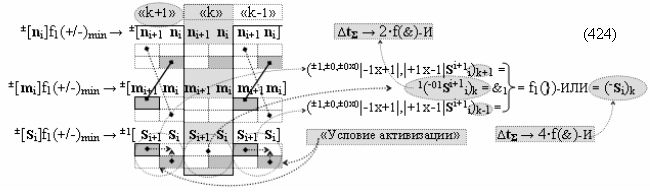
которая активизирует условно отрицательный аргумент результирующей суммы (-Si)k условно «i» разряда.
Ситуация 4. В условно «k» «Зоне минимизации» активен только условно отрицательный аргумент 1(-10Si+1 i)k условно «i+1» разряда с технологическим циклом ∆tΣ → 2∙f(&)-И в системе логической функции f1(&)-И функциональной структуры (425),
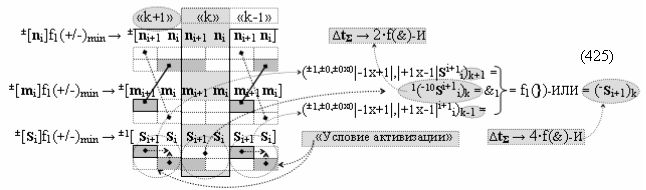
которая активизирует условно отрицательный аргумент результирующей суммы (-Si+1)k условно «i+1» разряда.
Далее, если вернуться к функциональной структуре (420) «Условия активизации», записав ее с учетом функциональной структуры (423) в виде графоаналитического выражения (426),
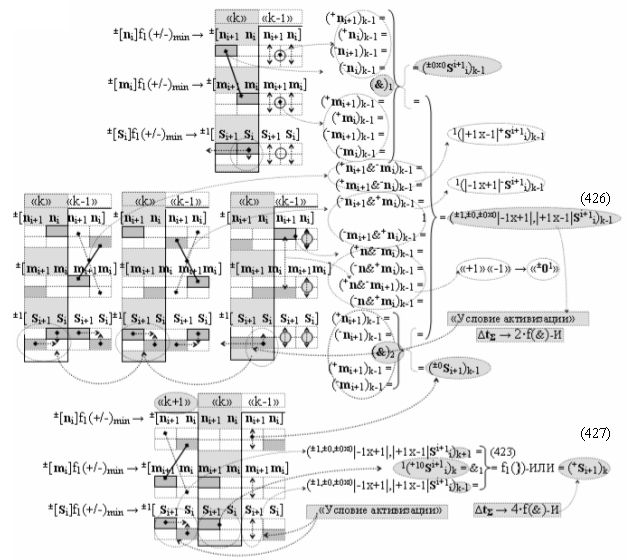
то функциональная входная структура «Условия активизации» с выходной логической функцией f1(}&)-ИЛИ-НЕ корректно активизирует в условно «k» «Зоне минимизации» результирующий положительный аргумент суммы (+Si+1)k условно «i+1» разряда. Поскольку даже если в предыдущих «Зонах минимизации» возможен локальный перенос, то аргумент его будет активизирован в условно «i+1» разряде условно «k-1» «Зоны минимизации». Но если записать структуру аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min в виде графоаналитического выражения вида (429)
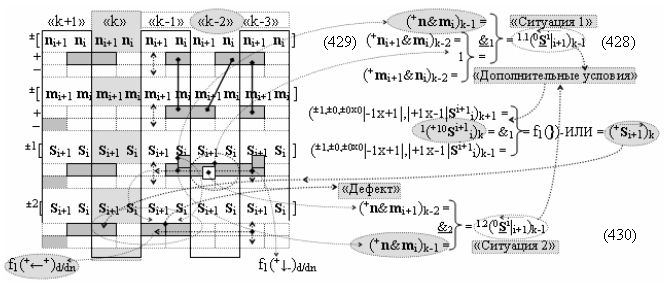
и активизировать функциональную структуру выражения (428), то структура аргументов в условно «k-1» «Зоне минимизации» имеет «Дефект», поскольку не соответствует логике формирования структуры условно минимизированных аргументов. Поэтому в систему логической функции f1(&)-И выражения (428) необходимо ввести «Дополнительные условия» активизации результирующего аргумента суммы (+Si+1)k и их формирует функциональная структура (429) и (430) с выходными логическими функциями f1(&)-И-НЕ и f2(&)-И-НЕ, в систему которых включены аргументы «Ситуация 1» и «Ситуация 2», а поскольку они равновероятны, поэтому эти функциональные структуры введем в систему логической функции f2(})-ИЛИ и запишем структуру логических функций (431)
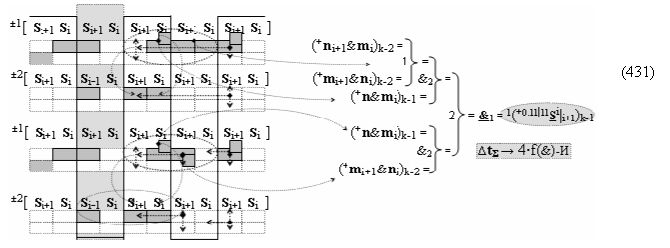
и она имеет технологический цикл ∆tΣ → 4∙f(&)-И, соответствующий четырем условным логическим функциям f(&)-И. Но если записать векторную структуру (432)
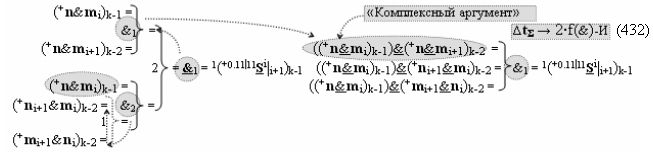
переноса функциональной структуры с выходной логической функцией f2(&)-И через систему логической функции f1(})-ИЛИ и перенос логической функции f1(&)-НЕ через систему логической функции f2(})-ИЛИ, то запишем функциональную структуру (432) с выходной логической функцией f1(&)-И, в системе которой «Комплексные аргументы» ((+n&mi)k-1)&(+n&mi+1)k-2, ((+n&mi)k-1)&(+ni+1&mi)k-2 и ((+n&mi)k-1)&(+mi+1&ni)k-2 также сформированы посредством одной логической функции f0(&)-И-НЕ. В результате минимизированная функциональная структура (432) имеет технологический цикл ∆tΣ → 2∙f(&)-И, который соответствует двум условным логическим функциям f(&)-И.
На основании полученных результатов из структуры логических функций (420), которую запишем в виде аналитического выражения (433)
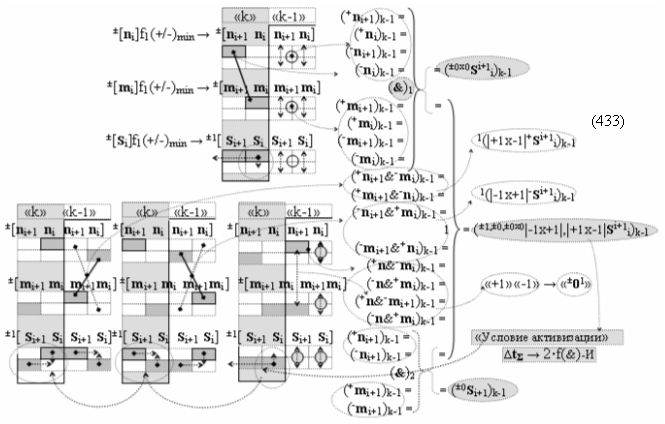
необходимо исключить функциональную структуру с выходной логической функцией f1(}&)-ИЛИ-НЕ, поскольку она не соответствует категории необходимого и достаточного «Условия активизации» аргумента в условно «k» «Зоне минимизации» и записать ее в виде аналитического выражения (434).
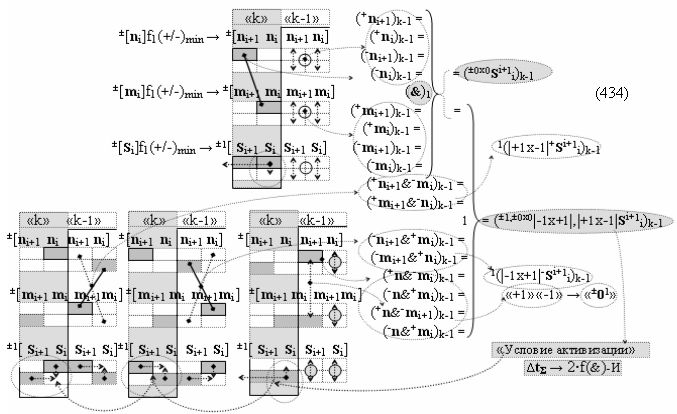
А если вернуться к векторной структуре (432), записав ее без выходной логической функции f1(&)-НЕ в виде выражения (435)
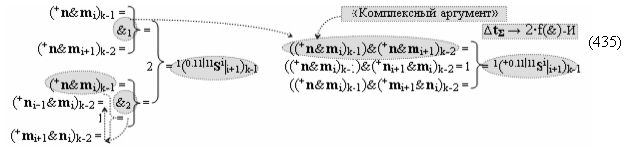
и выполнить перенос функциональной структуры с выходной логической функцией f2(&)-И через систему логической функции f1(})-ИЛИ, то запишем функциональную структуру (435) с выходной логической функцией f1(})-ИЛИ, в системе которой «Комплексные аргументы» ((+n&mi)k-1)&(+n&mi+1)k-2, ((+n&mi)k-1)&(+ni+1&mi)k-2 и ((+n&mi)k-1)&(+mi+1&ni)k-2 сформированы посредством функциональной структуры (436).
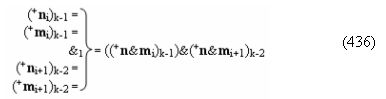
и функциональных структур (437).
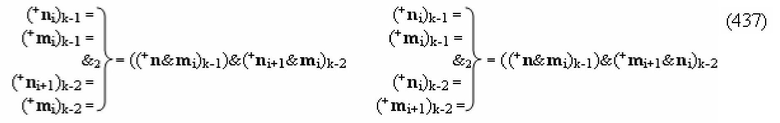
В результате процедуру преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min выражения (428) запишем в виде графоаналитического выражения (437),
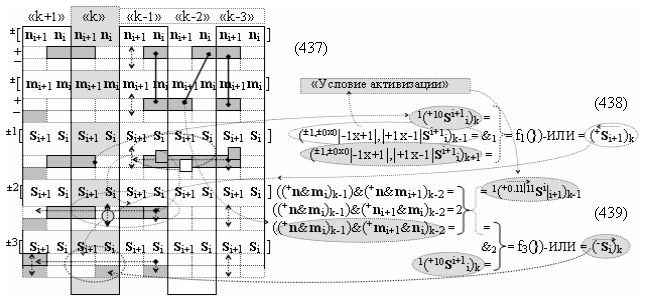
в котором в условно «k» «Зоне минимизации» не активен положительный аргумент результирующей суммы (+Si+1)k условно «j+1» разряда функциональной структуры (438), поскольку в системе логической функции f1(&)-И не активен аргумент (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1 необходимого и достаточного «Условия активизации» выражения (434). Но активен условно отрицательный аргумент результирующей суммы (-Si)k условно «j» разряда функциональной структуры (439), поскольку в системе логической функции f2(&)-И активен как входной положительный аргумент 1(+10Si+1 i)k, так и активна функциональная структура с выходной логической функцией f2(})-ИЛИ, поскольку в ее системе активен «Комплексный аргумент» ((+n&mi)k-1)&(+mi+1&ni)k-2 условно «k-1» «Зоне минимизации». При этом следует отметить, что функциональная структура с выходной логической функцией f2(})-ИЛИ выражения (439), которая активизирует аргумент 1(+0.11|11Si|i+1)k-1 «Условия активизации» может быть сформирована и в условно «k» «Зоне минимизации» в виде выражения (440),
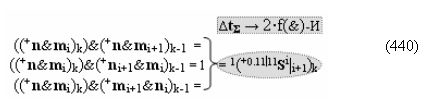
результирующий аргумент 1(+0.11|11Si|i+1)k которого является условно отрицательным аргументом результирующей суммы (-Si)k условно «i» разряда. Поскольку если записать графоаналитическое выражение (441),
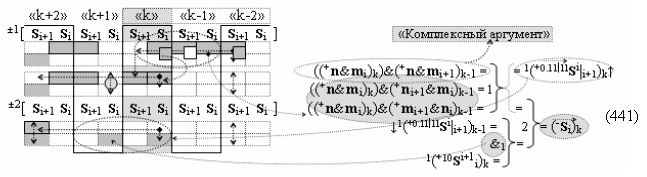
то положительный аргумент 1(+0.11|11Si|i+1)k↑ функциональной структуры с выходной логической функцией f1(})-ИЛИ посредством выходной логической функции f2(})-ИЛИ активизирует условно отрицательный аргумент результирующей суммы (-Si)k условно «i» разряда. При этом в систему логической функции f1(&)-И, которая активизирует в условно «k+1» «Зоне минимизации», включен входной аргумент ↓1(+0.11|11Si|i+1)k-1 условно «k-1» «Зоны минимизации», при этом следует отметить, что если «Комплексный аргумент» ((+n&mi)k)&(+n&mi+1)k-1 в системе логической функции f1(})-ИЛИ выражения (441) однозначно активизирует преобразованный аргумент 1(+0.11|11Si|i+1)k↑, то «Комплексные аргументы» одновременной активности двух последовательных положительных аргументов ((+n&mi)k)&(+ni+1&mi)k-1 и ((+n&mi)k)&(+ni+1&mi)k-1 в условно «k-1» «Зоне минимизации» должны быть дополнительно проанализированы. Поскольку их логика преобразования существенно зависит от активности аргументов в условно «k-2» «Зоне минимизации» и одной из возможных структур аргументов в этой зоне является структура локального переноса условно отрицательных аргументов, которую запишем в виде графоаналитического выражения (442).
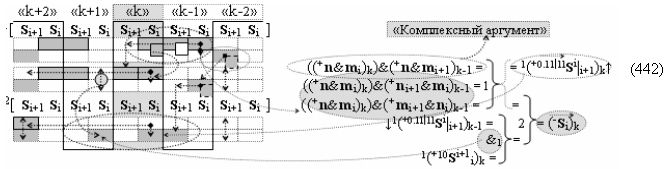
Из анализа логико-динамического процесса преобразования аргументов в объединенной структуре слагаемых ±[Si]f1(+/-)min выражения (442) следует, что если в условно «k» «Зоне минимизации» активизировать результирующий условно отрицательный аргумент суммы (-Si)k при активном аргументе 1(+0.11|11Si|i+1)k↑ логической функции f1(})-ИЛИ, то преобразование в условно «k-1» «Зоне минимизации» необходимо выполнять с учетом возможной активности условно отрицательного аргумента локального переноса из условно «k-2» «Зоны минимизации».
Поскольку в условно «k-1» «Зоне минимизации» выражения (442) сформирована «нестандартная» структура условно отрицательных аргументов с необходимостью локального переноса аргумента из условно «i» разряда в условно «i+1» разряд, поэтому сформирует функциональную структуру, посредством которой активизируют условно отрицательный аргумент суммы (-Si+1)k. При этом следует отметить, что этот аргумент может быть активизирован в следующих ситуациях:
Ситуация 1. Активен условно отрицательный аргумент (-n&mi+1)k-1 и 1(-11Si+1 i)k-1, и эту ситуацию запишем в виде графоаналитического выражения (443).
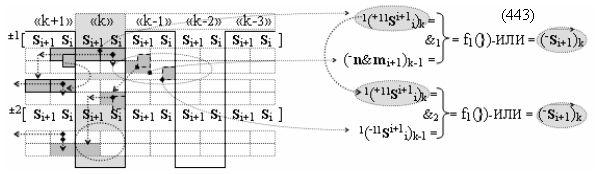
Ситуация 2. Активен условно отрицательный аргумент 1(-10Si+1 i)k-1 и активен условно отрицательный аргумент (-n&mi+1)k-2 или 1(-11Si+1 i)k-2 в условно «k-2» «Зоне минимизации», и эту ситуацию запишем в виде графоаналитического выражения (444).
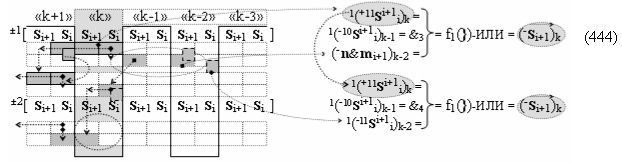
Ситуация 3. Активен условно отрицательный аргумент 1(-10Si+1 i)k-1 и 1(-10Si+1 i)k-2 и активен условно отрицательный аргумент (-n&mi+1)k-2 или 1(-11Si+1 i)k-2 в условно «k-2» «Зоне минимизации», и эту ситуацию запишем в виде графоаналитического выражения (445).
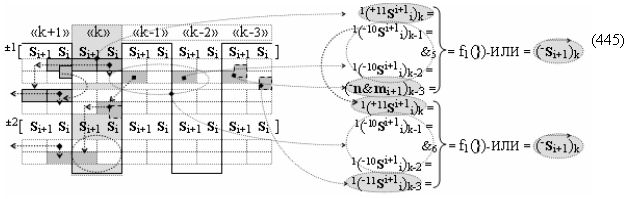
Ситуация 4. Активны три последовательных условно отрицательных аргумента 1(-10Si+1 i)k-1, 1(-10Si+1 i)k-2 и 1(-10Si+1 i)k-3, и эту ситуацию запишем в виде графоаналитического выражения (446),
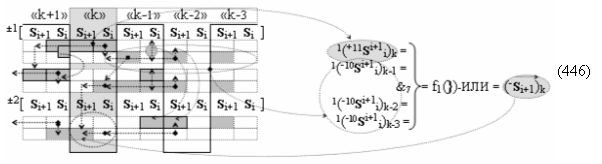
при этом следует отметить, что активность трех последовательных условно отрицательных аргументов 1(-10Si+1 i)k-1, 1(-10Si+1 i)k-2 и 1(-10Si+1 i)k-3 является необходимым и достаточным условием активизации условно отрицательного аргумента суммы (-Si+1)k условно «i+1» разряда. Поскольку если сформировать графоаналитическое выражение (447),
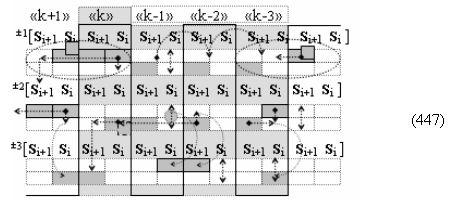
то из него следует, что для формирования условно отрицательного аргумента локального переноса в условно «k-1» «Зоне минимизации» необходимо и достаточно активности трех последовательных условно отрицательных аргументов 1(-10Si+1 i)k-1, 1(-10Si+1 i)k-2 и 1(-10Si+1 i)k-3, поскольку такая последовательность непредсказуема.
Ситуация 5. Активны два последовательных условно отрицательных аргумента 1(-10Si+1 i)k-1 и 1(-10Si+1 i)k-2 и активен аргумент (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k-3 в условно «k-3» «Зоне минимизации», и эту ситуацию запишем либо в виде графоаналитического выражения (448),
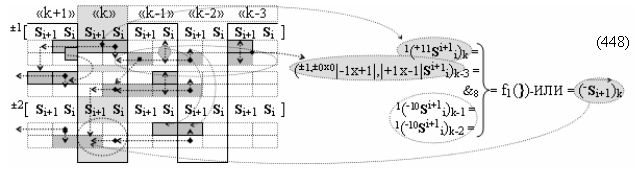
либо в виде графоаналитического выражения (449).
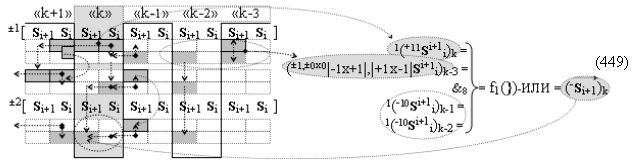
Из сопоставительного анализа логико-динамических процессов преобразования объединенной структуры аргументов слагаемых (448) и (449) следует, что функциональная структура активизации условно отрицательного аргумента суммы (-Si+1)k с учетом процедуры преобразования в условно «k-1» «Зоне минимизации» выражения (449) может быть минимизирована. И эта минимизация на первом этапе может включать функциональную структуру первой ситуации (443) и функциональную дополнительную входную структуру с входной логической функцией f3(&)-И выражения (450),
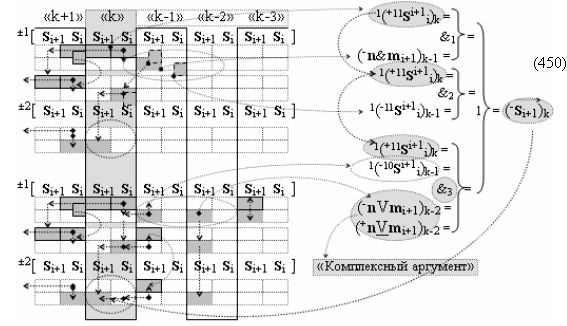
в систему которой включены два «Комплексных аргумента» (-nVmi+1)k-2 и (+nVmi+1)k-2, и их совокупность соответствует тому, что в условно «k-2» «Зоне минимизации» активен условно отрицательный аргумент условно «i+1» разряда и не активен положительный аргумент в этом разряде. А если учесть объединяющую особенность входных аргументов (-n&mi+1)k-1 и 1(-11Si+1 i)k-1, и эту особенность запишем в виде функциональной структуры (451)
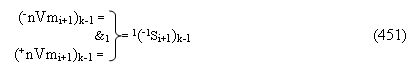
то структуру логических функций (450) в минимизированном виде запишем в виде аналитического выражения (452),
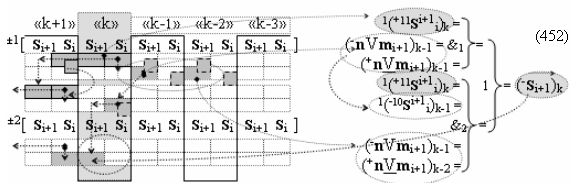
в котором в систему логической функции f1(&)-И включены два «Комплексных аргумента» (-nVmi+1)k-1 и (+nVmi+1)k-1 и их совокупность также соответствует тому, что в условно «k-1» «Зоне минимизации» активен условно отрицательный аргумент условно «i+1» разряда и не активен положительный аргумент в этом разряде. При этом следует отметить, что входные функциональные структуры с выходными логическими функциями f1(&)-И и f2(&)-И объединяют «Комплексный аргумент» 1(-10Si+1 i)k-1, и он позволяет структуру логических функций (452) записать в виде минимизированной функциональной структуры (453)
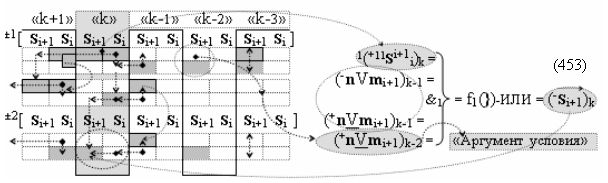
для активизации условно отрицательного аргумента результирующей суммы (-Si+1)k с «Аргументом условия» (+nVmi+1)k-2, который в ситуации активного логического нуля «+1»«-1» → «±01» выражения (454)
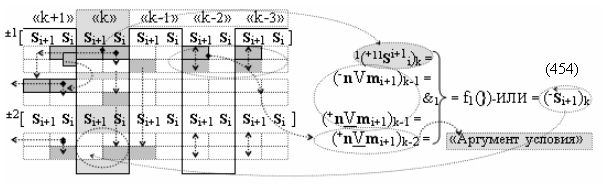
исключает активизацию аргумента результирующей суммы (-Si+1)k, поскольку в системе логической функции f1(&)-И не активен положительный входной аргумент (+nVmi+1)k-2 в условно «k-2» «Зоне минимизации». Аналогичная ситуация и в графоаналитическом выражении (455),
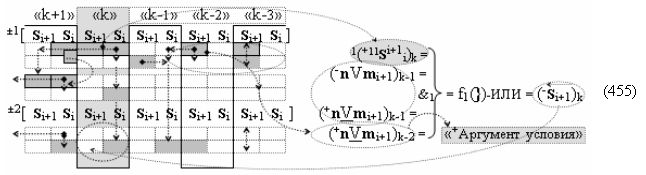
в котором также неактивный «Аргумент условия» (+nVmi+1)k-2 исключает активизацию аргумента результирующей суммы (-Si+1)k. Но если активизирован аргумент результирующей суммы (-Si+1)k, а он активизирован в соответствии с арифметической аксиомой «-1» → «-2» «+1» в условно «k-1» «Зоне минимизации», должен быть активизирован положительный аргумент результирующей суммы (+Si+1)k-1. И эту ситуацию запишем в виде графоаналитического выражения (456),
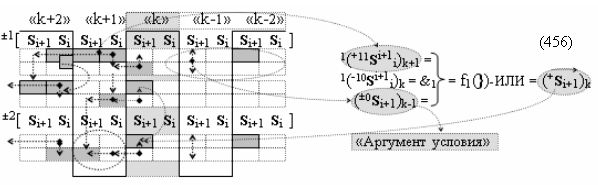
в котором в систему логической функции f1(&)-И включен «Аргумент условия» (±0Si)k-1, сформированный посредством функциональной структуры (457).
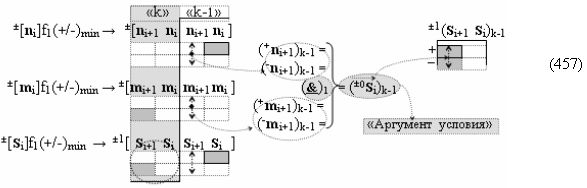
А если вернуться к анализу функциональной структуры (423), записав ее в виде выражения (458),
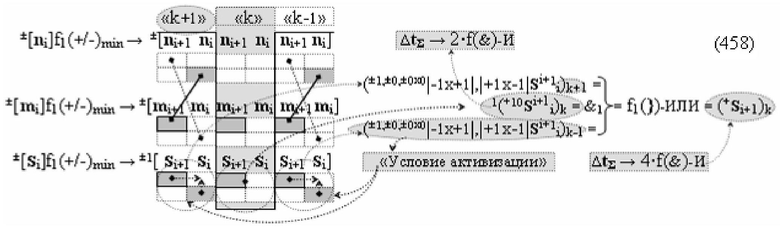
в котором при активизации положительного результирующего аргумента суммы (+Si+1)k условно «i+1» разряда в качестве «Условия активизации» является «Комплексный аргумент» (±1,±0,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1, сформированный посредством функциональной структуры (420), которую запишем в виде аналитического выражения (459).
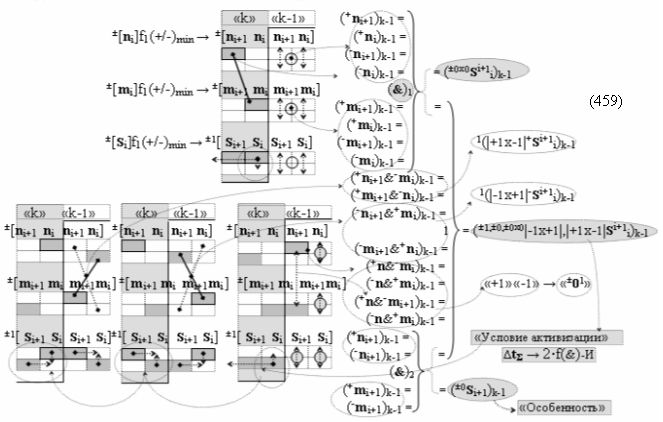
При этом следует отметить, что «Особенность» структуры логических функций (459) является функциональная входная структура с выходной логической функцией f2(}&)-ИЛИ-НЕ, и ее преобразованный аргумент (±0Si+1)k-1 включен в систему логической функции f1(&)-И выражения (456), которое совместно с функциональной структурой (458) запишем в виде аналитического выражения (460),
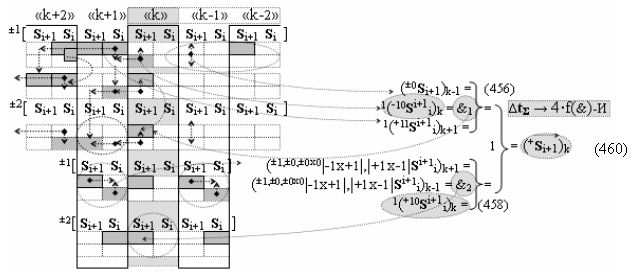
посредством которого активизируют положительный результирующий аргумент суммы (+Si+1)k условно «i+1» разряда в условно «k» «Зоне минимизации». При этом следует также отметить, что «Особенность» структуры логических функций (459) с выходной логической функцией f2(}&)-ИЛИ-НЕ и является функциональная принадлежность в условно «k» «Зоне минимизации» ее только условно «i+1» разряду. А если учесть, что в структуре аргументов слагаемых ±[Si]f1(+/-)min положительные и условно отрицательные аргументы равновероятны, то функциональную структуру (453),
которая активизирует условно отрицательный аргумент суммы (-Si+1)k условно «i+1» разряда в условно «k» «Зоне минимизации», то для аналогичной структуры аргументов противоположного знака функциональную структуру запишем в виде аналитического выражения (461)
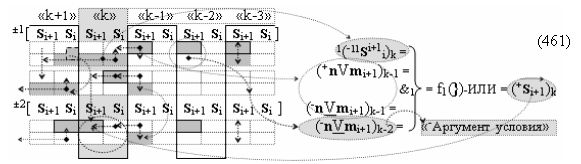
и введем ее в систему логической функции f1(})-ИЛИ выражения (460). А если вернуться к анализу графоаналитического выражения (437), записав его в виде выражения (462),
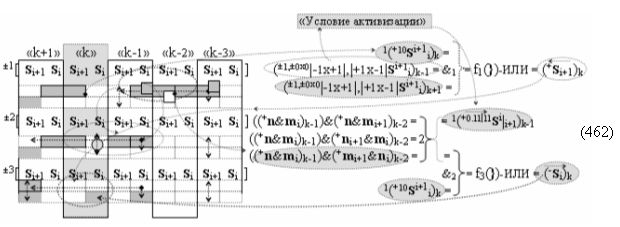
в котором «Условием активизации» аргумента 1(+10Si+1 i)k в системе логической функции f1(&)-И является входной аргумент (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1, в котором по сравнению с аргументом (±1,±0,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1 исключена одна из возможных ситуаций (±0i+1)k-1 неактивности аргументов в условно «i+1» разряде. И это исключение привело к необходимости формирования дополнительной функциональной структуры (434),
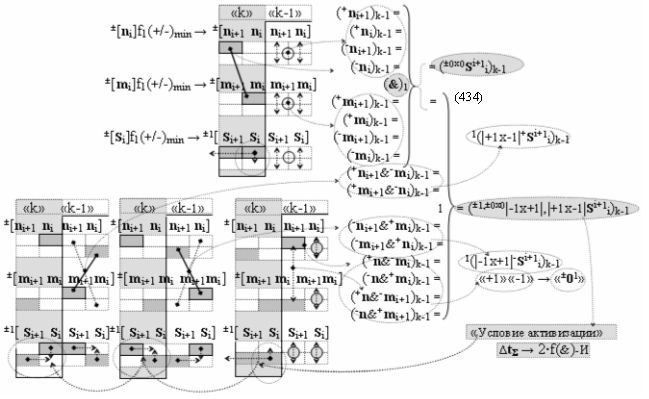
в результате в структуру логических функций математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» необходимо включать и функциональную структуру (433), которую запишем в виде аналитического выражения (463)
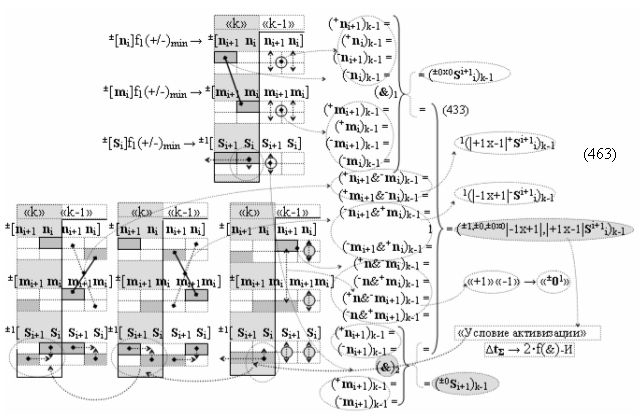
с входной логической функцией f2(}&)-ИЛИ-НЕ. Но если в систему логической функции f1(&)-И выражения (462) ввести функциональную структуру (432),
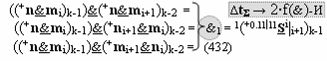
то эта логическая функция в выражении (464)
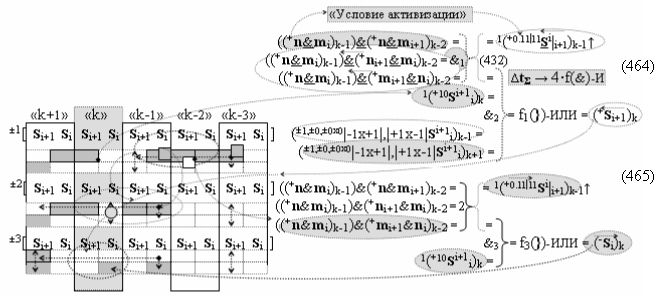
корректно не активизирована, поскольку в ее системе не активен либо входной аргумент ((+n&mi)k-1)&(+ni+1&mi)k-2, либо входной аргумент ((+n&mi)k-1)&(+mi+1&ni)k-2 «Условия активизации», которые сформированы посредством логической функции f1(&)-И-НЕ. При этом входные аргументы (±1,±0,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1 и (±1,±0,±0х0|-1х+1|,|+1х-1|Si+1 i)k+1 логической функции f2(&)-И исключают одну из возможных ситуаций (±0i+1)k-1 неактивности аргументов в условно «i+1» разряде «k-1» «Зоны минимизации». В результате в структуру логических функций математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» включена только одна функциональная структура (463). При этом функциональная структура с выходной логической функцией f1(&)-И выражения (464) записана с преобразованным аргументом 1(+0.11|11Si|i+1)k-1↑ с измененным уровнем аналогового сигнала, поскольку возможна структура аргументов слагаемых ±[Si]f1(+/-)min выражения (456),
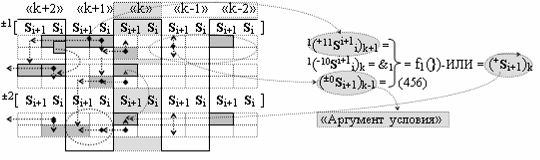
которую запишем либо в виде графоаналитического выражения (466),
либо в виде графоаналитического выражения (467),
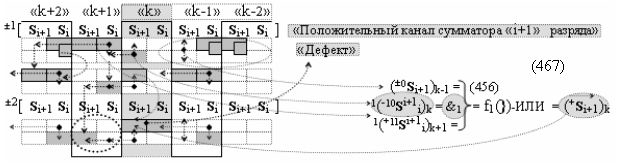
А если аналогично функциональной структуре (432),
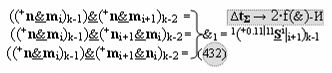
которая активизирует сформировать преобразованный положительный аргумент 1(+0.11|11Si|i+1)k-1↑ с измененным уровнем аналогового сигнала записать функциональную структуру (468)
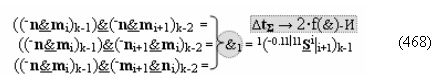
с преобразованным условно отрицательным аргументом 1(+0.11|11Si|i+1)k-1↑ с измененным уровнем аналогового сигнала и ввести условно отрицательный аргумент 1(-0.11|11Si|i+1)k-1↑ и положительный аргумент 1(+0.11|11Si|i+1)k-1↑ с измененным уровнем аналогового сигнала выражения (464) в систему логической функции f1(&)-И выражений (466) и (467) соответственно, то корректную функциональную структуру (466) запишем в виде аналитического выражения (469),
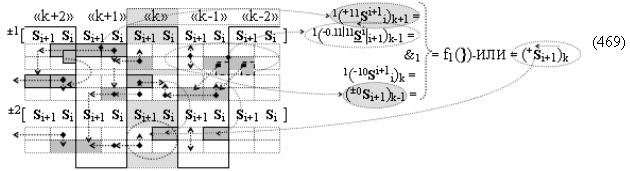
а корректную функциональную структуру (467) запишем в виде аналитического выражения (470).
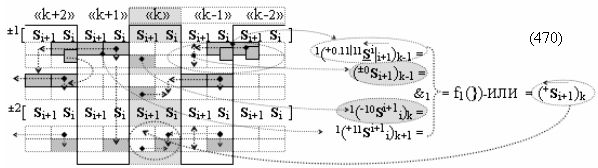
А если учесть логику формирования условно минимизированной структуры аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min, в соответствии с которой в «Зоне минимизации» может быть активизирован только один аргумент, то при формировании объединенной структуры слагаемых ±[Si]f1(+/-)min в каждой «Зоне минимизации» могут быть активные только два аргумента. И в этой ситуации при активности в условно «k-1» «Зоне минимизации» выражения (469) и (470) одновременно двух аргументов условно «i» разряда приводит к тому, что в системе логической функции f1(&)-И этих выражений входной аргумент (±0Si+1)k-1 избыточен. Но поскольку формируется математическая модель сумматора ±f(ΣRU)min условно «k» «Зоны минимизации», поэтому ее структура логических функций должна включать только функциональные структуры, посредством которых активизируют аргументы результирующей суммы. И в этой связи запишем процедуру активизации результирующих аргументов суммы слагаемых (469) в виде аналитических выражений (471) и (472),
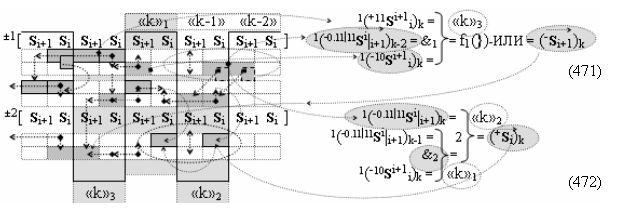
в которых условно отрицательный аргумент 1(-0.11|11Si|i+1)k активизирует функциональная структура (473),
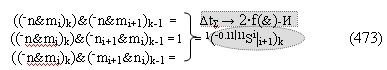
и аналогичные аналитические выражения (474) и (475)
для аргументов слагаемых противоположного знака.
Из сопоставительного анализа логико-динамических процессов преобразования аргументов слагаемых ±[Si]f1(+/-)min выражений (472) и (475) следует, что активный аргумент 1(-10Si+1 i)k и 1(+10Si+1 i)k в условно «k»1 «Зоне минимизации» корректно преобразован только с применением арифметических аксиом «-1» → «-2» «+1» и «+1» → «+2»«-1», при этом «Условием активизации» в данной ситуации является активность аргумента 1(+0.11|11Si|i+1)k-1 в «k-1» «Зоне минимизации» двойного локального переноса. Но возможны и другие ситуации, в которых активный аргумент 1(-10Si+1 i)k и 1(+10Si+1 i)k в условно «k» «Зоне минимизации» корректно преобразован только с применением тех же арифметических аксиом. Так для условно отрицательного аргумента 1(-10Si+1 i)k преобразование с применением арифметической аксиомы «-1» → «-2» «+1» запишем в виде графоаналитического выражения (476),
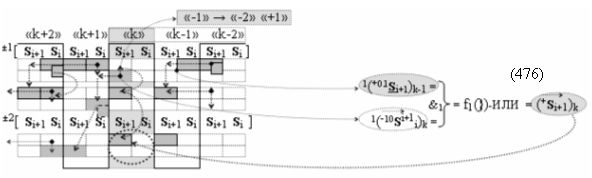
и в виде графоаналитического выражения (477).
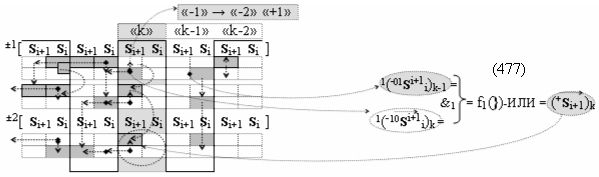
А для положительного аргумента 1(+10Si+1 i)k преобразование с применением арифметической аксиомы «+1» → «+2»«-1» запишем в виде графоаналитического выражения (478),
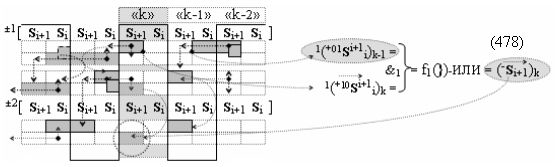
и в виде графоаналитического выражения (479).
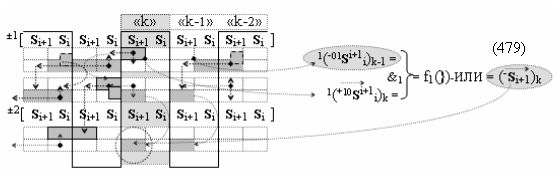
Но если вернуться к анализу процедуры преобразования аргументов слагаемых и (282)
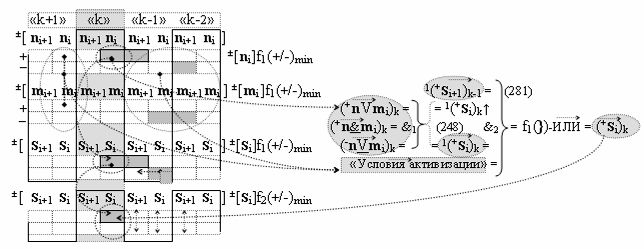
и с учетом скорректированной логики формирования функциональных структур записать графоаналитическое выражение (480)
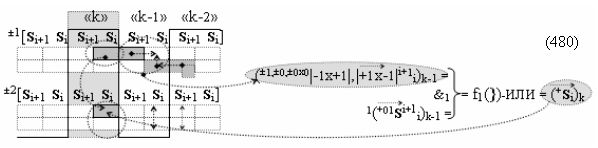
для активизации положительного аргумента суммы (+Si)k условно «i» разряда или графоаналитическое выражение (481)
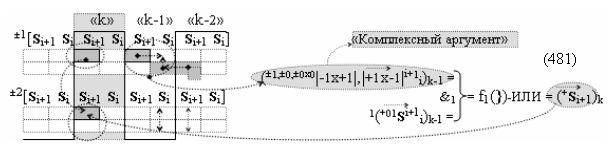
для активизации положительного аргумента суммы (+Si+1)k условно «i+1» разряда, то с одной стороны с учетом логико-динамического процесса преобразования положительного аргумента суммы (+Si+1)k условно «i+1» разряда в условно «k» «Зоне минимизации» выражения (475)
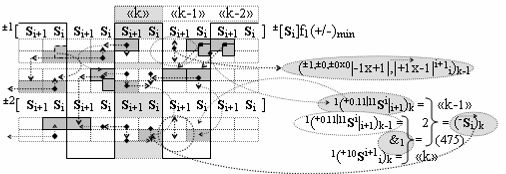
в объединенной структуре слагаемых ±[Si]f1(+/-)min в условно «k-1» «Зоне минимизации» «Комплексный аргумент» (±1,±0,±0х0|-1х+1|,|+1х-1|i+1 i)k-1 активен, поскольку не активны аргументы в условно «i+1» разряде и его активность приведет к активизации положительного аргумента этого разряда, что приводит к «Дефекту» в «k» «Зоне минимизации». Поэтому из структуры логических функций (463)
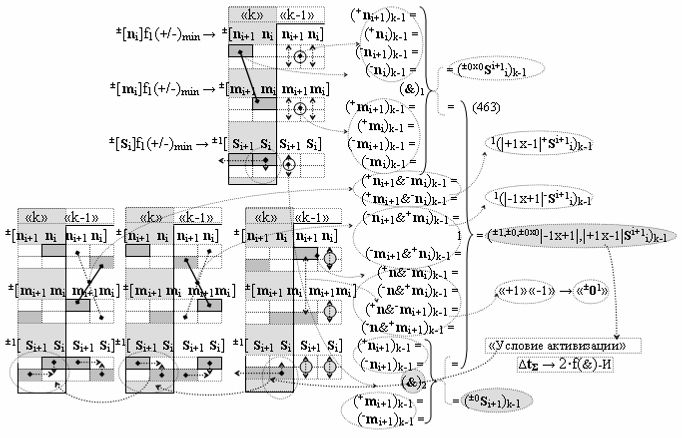
«k-1» «Зоны минимизации» необходимо исключить функциональную структуру с входной логической функцией f2(}&)-ИЛИ-НЕ, которая активизирует преобразованный аргумент (±0Si+1)k-1. В результате структуру логических функций математической модели сумматора ±f(ΣRU)min условно «k-1» «Зоны минимизации» запишем в виде структуры логических функций (482),
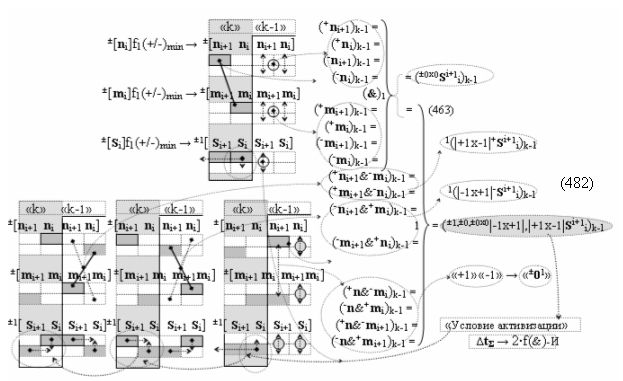
а структуру логических функций математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» запишем в виде структуры логических функций (483),
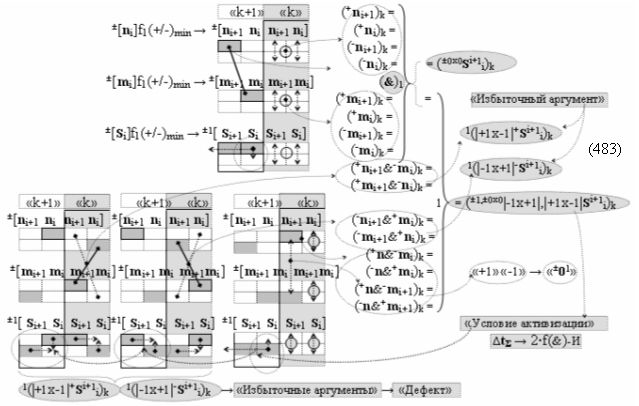
При этом следует отметить, что преобразованный аргумент (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k должен являться аргументом «Условия активизации» в условно «k» «Зоне минимизации», но совокупность аргументов 1(|+1х-1|+Si+1 i)k и 1(|-1х+1|-Si+1 i)k (484)
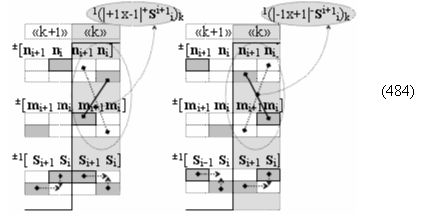
не являются «Условием активизации», поэтому они «Избыточные аргументы», формирующие «Дефект» при активизации аргумента результирующей суммы (+Si)k условно «i» разряда, и они должны быть исключены из системы логической функции f1(})-ИЛИ выражения (483), а функциональную структуру аргумента «Условия активизации» в условно «k» «Зоне минимизации» запишем в виде аналитического выражения (485)
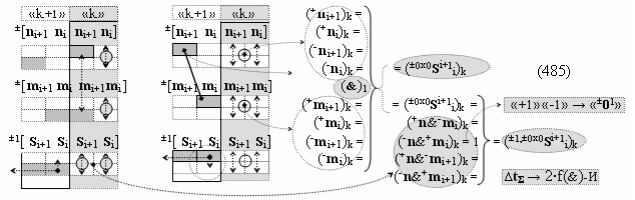
а структуры логических функций (463) запишем в виде аналитического выражения (486)
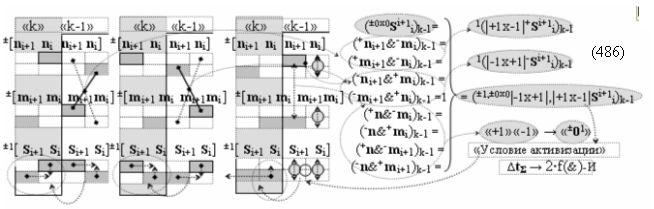
с входным преобразованным аргументом структуры логических функций (485). Поскольку если записать функциональную структуру (487),
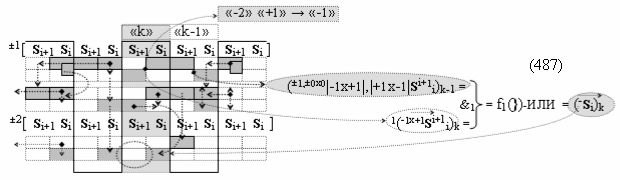
и функциональную структуру (488),
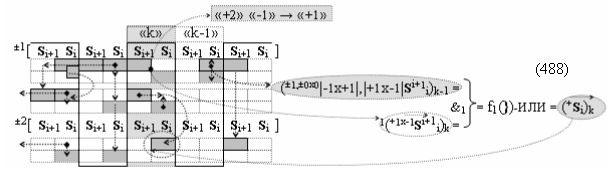
посредством которых реализуется преобразование аргументов в условно «k» «Зоне минимизации» с применением обратных арифметических аксиом «-2» «+1» → «-1» и «+2» «-1» → «+1», то они активизируют условно отрицательный аргумент результирующей суммы (-Si)k и положительный аргумент результирующей суммы (+Si)k условно «i» разряда. При этом если записать функциональную структуру (489),
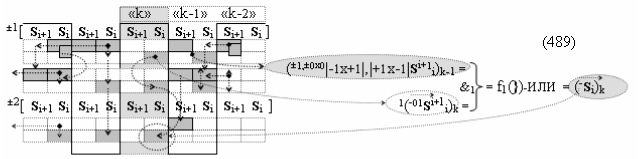
и функциональную структуру (490),
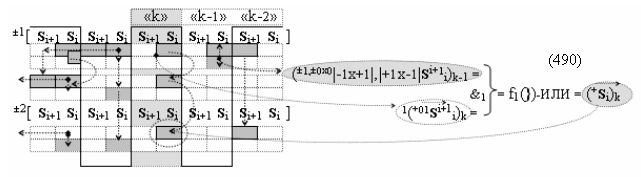
которые также активизируют результирующий аргумент суммы (-Si)k и (+Si)k, то они могут быть записаны совместно с функциональными структурами (487) и (488) в виде общего аналитического выражения (491).
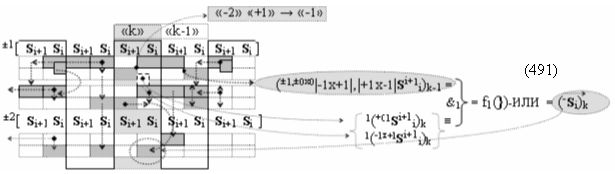
и в виде общего аналитического выражения (492).
Но если записать графоаналитическое выражение (493),
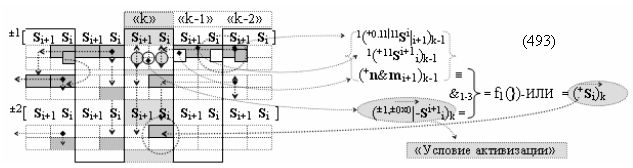
то активность аргумента (±1,±0х0Si+1 i)k в условно «k» «Зоне минимизации» позволяет активизировать посредством функциональной структуры f1-3(&)-И аргумент результирующей суммы (+Si)k условно «i» разряда в трех ситуациях. При этом следует отметить, что входные аргументы в фигурных скобках ({…}) могут быть объединены в системе логической функции f2(})-ИЛИ, но в этом случае технологический цикл ∆tΣ → 5∙f(&)-И такой структуры логических функций будет соответствовать пяти условным логическим функциям f(&)-И. Также имеет смысл отметить, что число возможных вариантов активизации аргумента результирующей суммы (+Si)k условно «i» разряда при активном аргументе (±1,±0х0Si+1 i)k может быть дополнено, если записать процедуру его активизации в выражении (494),
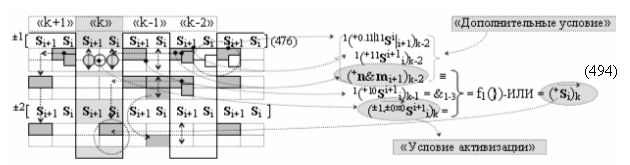
в структуре слагаемых Si]f1(+/-)min которого в условно «k-1» «Зоне минимизации» активен положительный аргумент 1(+10Si+1 i)k-1, а в условно «k-2» «Зоне минимизации» активент аргумент локального переноса, записанный в системе в виде входных аргументов (+n&mi+1)k-2, 1(+11Si+1 i)k-2 и 1(+0.11|11Si|i+1)k-2. При этом следует отметить, что число возможных вариантов активизации положительного аргумента результирующей суммы (+Si)k условно «i» разряда при активном аргументе (±1,±0х0Si+1 i)k может также быть дополнено, если проанализировать графоаналитическое выражение (495),
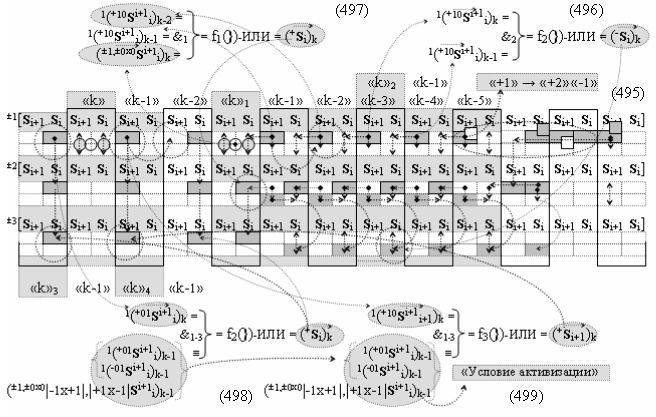
записав его логико-динамический процесс преобразования аргументов слагаемых Si]f1(+/-)min в предыдущих «k-1» - «k-5» «Зонах минимизации» относительно условно «k»1 «Зоны минимизации», в которых процедура преобразования положительных аргументов реализована с применением арифметической аксиомы «+1» → «+2»«-1», а результатом такого преобразования является условно отрицательный аргумент результирующей суммы (-Si)k условно «i» разряда в условно «k»2 «Зоне минимизации», и этот аргумент активизирует функциональная структура (496) с выходной логической функцией f2(&)-И. При этом из анализа всей последовательности положительных аргументов в предыдущих «k-1» - «k-5» «Зонах минимизации» следует, что для активизации условно отрицательного аргумента результирующей суммы (-Si)k условно «i» разряда в систему логической функции f2(&)-И достаточно включить только два входных аргумента 1(+10Si+1 i)k и 1(+10Si+1 i)k-1. А в условно «k»1 «Зоне минимизации» положительный аргумент результирующей суммы (+Si)k условно «i» разряда активизирует функциональная структура (498) с выходной логической функцией f1(&)-И, в систему которой помимо аргумента (±1,±0х0Si+1 i)k включены два последовательных аргумента 1(+10Si+1 i)k-1 и 1(+10Si+1 i)k-2. При этом из анализа логико-динамического процесса активизации аргументов результирующих сумм (496) следует, что функциональные структуры (498) и (499), которые активизируют условно отрицательный аргумент (-Si)k и (-Si+1)k условно «i» и «i+1» разряда, имеют общие «Условия активизации». В результате положительный аргумент 1(+10Si+1 i)k-2 условно «k-2» «Зоны минимизации» выражения (497) введем в совокупность аргументов «Дополнительного условия» выражения (494), которое является «Положительным каналом сумматора «i» разряда» и запишем его функциональную структуру (500),
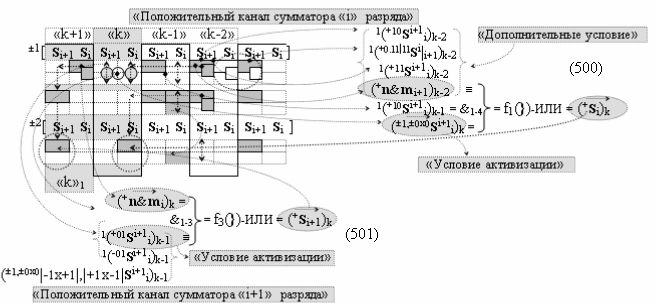
а также функциональную структуру (501) «Положительного канала сумматора «i+1» разряда» с выходной логической функцией f3(&)-И, в систему которой включены входные аргументы (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1, 1(+01Si+1 i)k и 1(-01Si+1 i)k «Условием активизации» положительного аргумента результирующей суммы (+Si+1)k условно «i+1» разряда.
Аналогичную функциональную структуру имеет и «Условно отрицательный канал сумматора «i» разряда» за исключением знака аргументов, которую запишем в виде аналитического выражения (502),
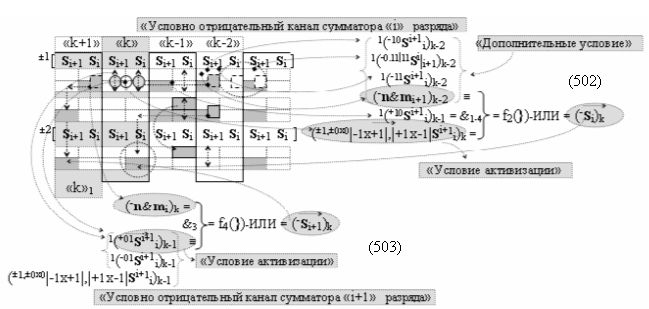
а также функциональную структуру (503) «Условно отрицательного канала сумматора «i+1» разряда» с выходной логической функцией f3(&)-И, в систему которой включены входные аргументы (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1, 1(+01Si+1 i)k и 1(-01Si+1 i)k «Условием активизации» положительного аргумента результирующей суммы (+Si+1)k условно «i+1» разряда. Поскольку если логико-динамический процесс преобразования положительных аргументов слагаемых +[Si]f1(+/-)min выражения (495) записать для аналогичной структуры условно отрицательных аргументов слагаемых -[Si]f1(+/-)min в виде графоаналитического выражения (504),
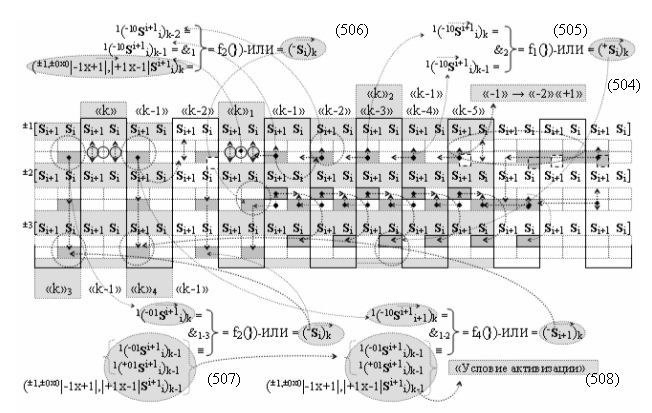
то логика формирования функциональных структур (506) - (508) и (496) - (499) эквивалентна, и они корректно активизируют результирующие аргументы суммы, также как и функциональные структуры (472), (475), (497) и (506). Поэтому перераспределим их между каналами сумматора и запишем «Положительный канал сумматора «i» разряда» в виде структуры логических функций (509),
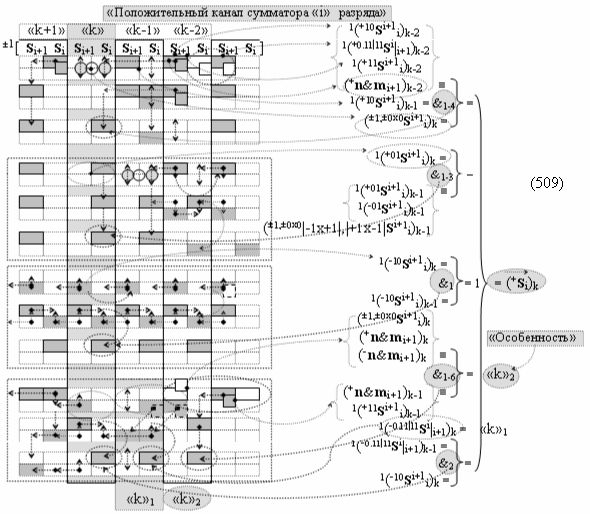
в которой «Особенностью» является функциональная входная структура с выходными логическими функциями f1-6(&)-И с двумя группами входных аргументов, при этом в первую группу включены аргументы (+n&mi+1)k, (-n&mi+1)k и (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k условно «k»2 «Зоны минимизации», а во вторую группу включены два аргумента (+n&mi+1)k-1 и 1(+11Si+1 i)k-1 условно «k-1»2 «Зоны минимизации», которые с технологическим циклом ∆tΣ → 4∙f(&)-И четыри условные логические функции f(&)-И формируют шесть функциональных структур, а если эти аргументы объединить в системе логических функций f2(&)-И и f3(&)-И и записать функциональную структуру (510),
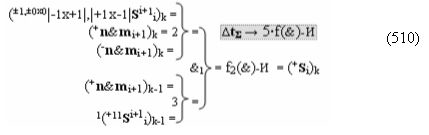
то технологический цикл ∆tΣ → 5∙f(&)-И будет соответствовать пяти условным логическим функциям f(&)-И.
Далее, «Положительный канал сумматора «i+1» разряда» запишем в виде структуры логических функций (511),
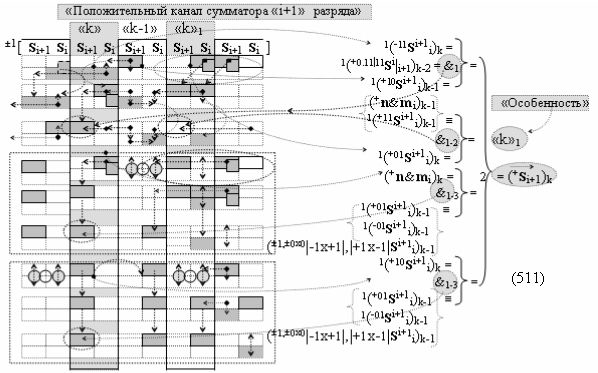
«Условно отрицательного канала сумматора «i» разряда» в виде структуры логических функций (512),
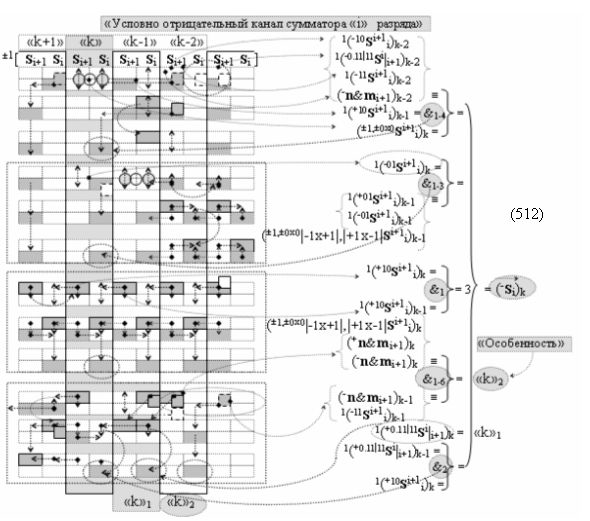
и «Условно отрицательного канала сумматора «i+1» разряда» в виде структуры логических функций (513),
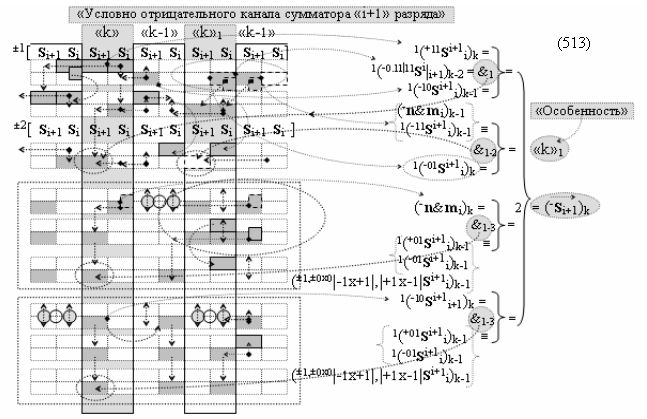
в которой, как и в структуре логических функций (511) «Положительного канала сумматора «i+1» разряда» «Особенностью» является функциональная входная структура с выходными логическими функциями f1-2(&)-И с группой входных аргументов (-n&mi)k-1 и 1(-11Si+1 i)k и общим входным аргументом 1(-01Si+1 i)k.
Далее, для формирования функционально законченной математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации» проанализируем возможные структуры аргументов слагаемых ±[Si]f1(+/-)min, которые активизируют результирующий аргумент суммы в условно «i» разряда. А для этого вернемся к анализу функциональной структуры (491) и (492), которые в условно «k» «Зоне минимизации» активизируют результирующий аргумент (-Si)k и (+Si)k с применением обратных арифметических аксиом «-2» «+1» → «-1» и «+2» «-1» → «+1» и которые запишем в виде аналитического выражения (514)
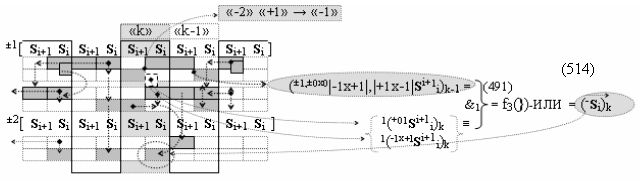
и в виде аналитического выражения (515).
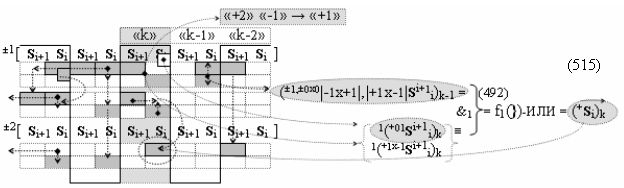
А учитывая то, что «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» эквивалентны по структуре логических функций, за исключением знаков аргументов, поэтому имеет смысл проанализировать возможные структуры аргументов слагаемых ±[Si]f1(+/-)min, которые активизируют результирующий положительный аргумент суммы (+Si)k в условно «i» разряда. Поэтому из анализа логико-динамического процесса преобразования аргументов (515) следует, что число возможных вариантов активизации положительного аргумента суммы (+Si)k в условно «i» разряде может быть существенно увеличено. Поскольку если записать функциональную структуру с выходной логической функцией f1-3(})-ИЛИ выражения (509), записав его в виде аналитического выражения (516),
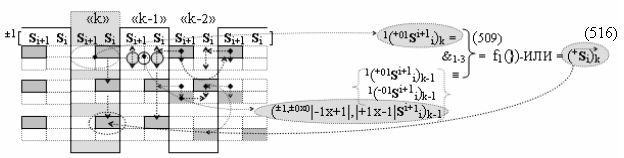
то из сопоставительного анализа входных аргументов выражения (515) и (516) следует, что их функциональные структуры могут быть объединены и записаны в виде аналитического выражения (517),
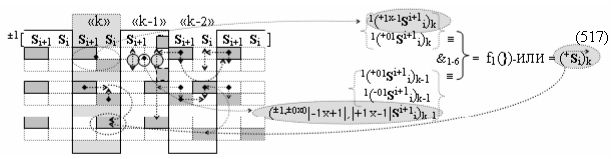
в котором включено шесть возможных комбинаций входных аргументов, активизирующих положительный аргумент суммы (+Si)k в условно «i» разряде. В результате в выражении (509) «Положительного канала сумматора «i» разряда» выполним замену входной функциональной структуры с выходной логической функцией f1-3(})-ИЛИ на функциональную структуру с выходной логической функцией f1-8(})-ИЛИ (517) и запишем его структуру логических функций в виде графоаналитического выражения (518)
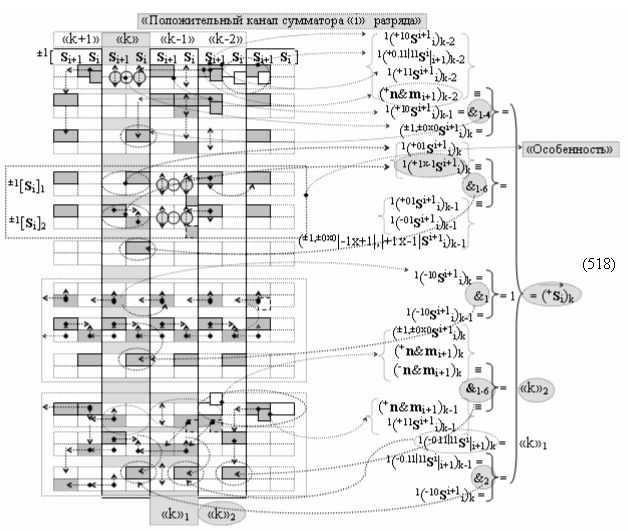
в котором «Особенностью» является запись двух исходных структур аргументов слагаемых ±1[Si]1 и ±1[Si]2.
Аналогичную скорректированную функциональную структуру, которая активизирует условно отрицательный аргумент суммы (-Si)k в условно «i» разряде запишем в виде аналитического выражения (519)
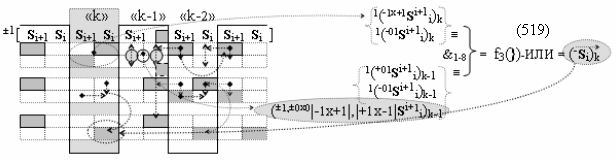
и введем в «Условно отрицательный канал сумматора «i» разряда» и запишем скорректированную структуру логических функций в виде аналитического выражения (520).
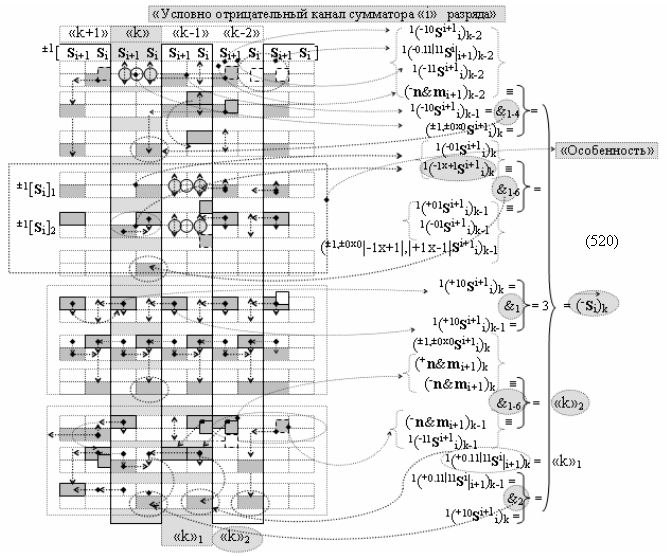
При этом следует отметить, что активные аргументы 1(+1х-1Si+1 i)k и 1(-1х+1Si+1 i)k могут быть активизированы и в условно «i+1» разряде, так посредством функциональной структуры (521)
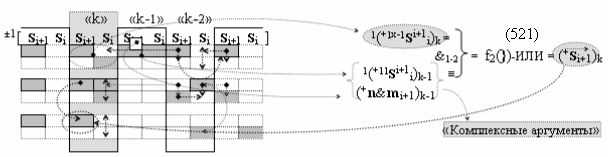
активизирован положительный аргумент (+Si+1)k, а посредством функциональной структуры (522)
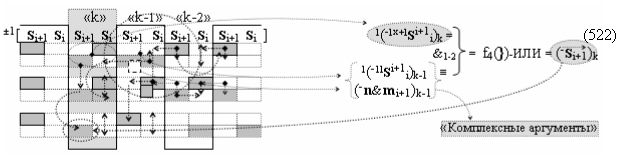
активизирован условно отрицательный аргумент (-Si+1)k. А если учесть, что объединенная структура аргументов слагаемых ±[Si]f1(+/-)min многовариантна и локальный сквозной перенос может быть сформирован в графоаналитическом выражении (523)
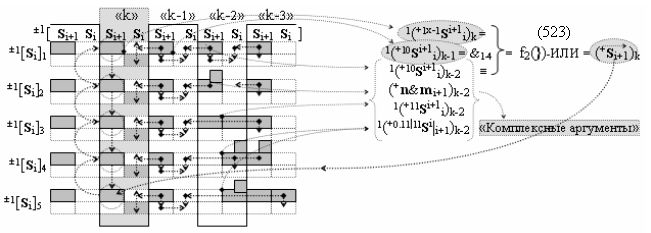
с активизацией положительного аргумента (-Si+1)k и в графоаналитической структуре (524)
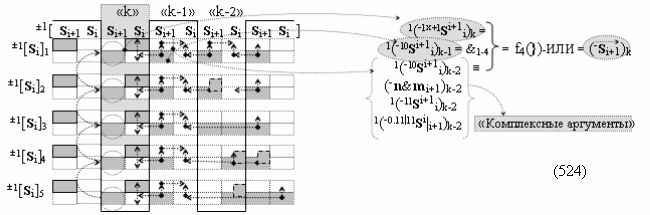
с активизацией условно отрицательного аргумента (-Si+1)k.
Аналогичная ситуация формируется и при преобразовании аргументов 1(-11Si+1 i)k и 1(+11Si+1 i)k в условно «k» «Зоне минимизации», когда активен аргумент локального переноса с противоположным знаком в условно «k-1» «Зоне минимизации», и логико-динамический процесс преобразования аргументов запишем в виде графоаналитических выражений.
Для условно отрицательного аргумента 1(-11Si+1 i)k и положительного аргумента локального переноса из условно «k-1» «Зоны минимизации» процедуру преобразования аргументов запишем в виде графоаналитического выражения (525).
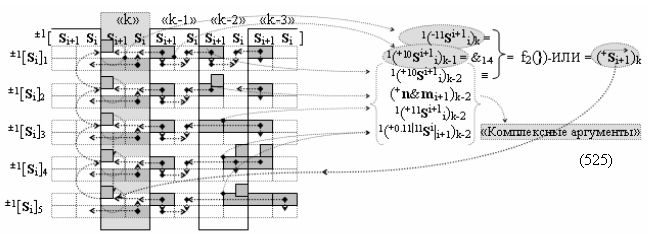
При этом если вернуться к анализу функциональной структуры с выходной логической функцией f1(&)-И «Положительного канала сумматора «i+1» разряда» выражения (511), записав ее в виде аналитического выражения (526),
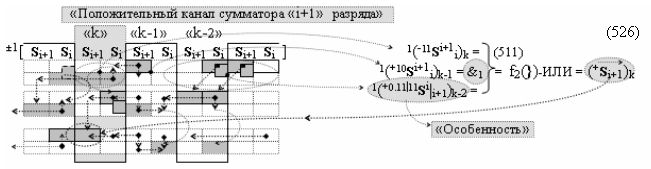
то «Особенностью» системы входных аргументов логической функции f1(&)-И (526) является входной аргумент 1(+0.11|11Si|i+1)k-2 условно «k-2» «Зоны минимизации» при двух входных аргументах 1(-11Si+1 i)k и 1(+10Si+1 i)k-1, один из которых также включен в систему логической функции f1(&)-И выражения (525). Поэтому функциональные структуры (525) и (526) могут быть объединены в одно аналитическое выражение (527),
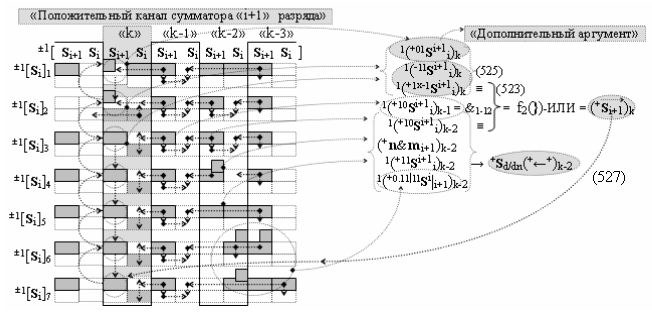
при этом в совокупность входных аргументов введен «Дополнительный аргумент» 1(+01Si+1 i)k, который также активизирует положительный аргумент суммы (+Si+1)k при активном входном аргументе 1(+10Si+1 i)k-1 условно «k-1» «Зоны минимизации» и активном положительном аргументе локального переноса +Sd/dn(+←+)k-2 из условно «k-2» «Зоны минимизации». В результате скорректированную структуру логических функций «Положительного канала сумматора «i+1» разряда» (511) запишем в виде графоаналитического выражения (528).
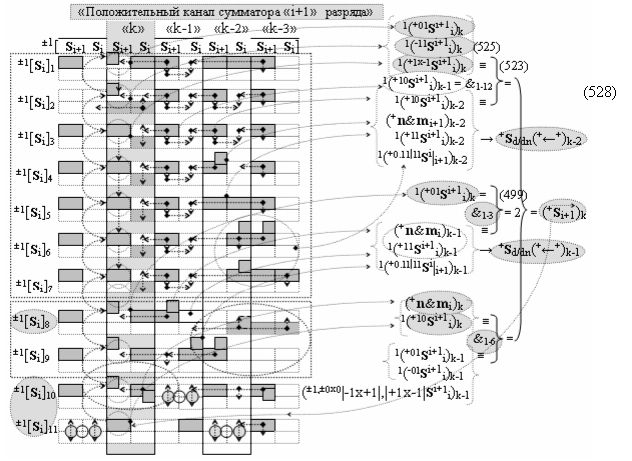
При этом следует отметить, что в скорректированном аналитическом выражении (528) в функциональную входную структуру с выходной логической функцией f1-3(&)-И, которая активизирует объединенную структуру аргументов слагаемых ±1[Si]7 в систему «Комплексных аргументов» (+n&mi)k-1 и 1(+11Si+1 i)k-1, введен дополнительный аргумент 1(+0.11|11Si|i+1)k-1 «Условия активизации» аргумента 1(+01Si+1 i)k в условно «k» «Зоне минимизации», но не введен аргумент 1(+10Si+1 i)k-1. Поскольку если записать графоаналитическое выражение (529),
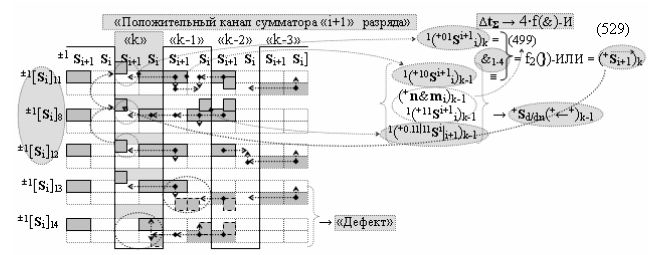
то возможны три структуры аргументов слагаемых ±1[Si]8, ±1[Si]11 и ±1[Si]12, которые корректно активизируют результирующий положительный аргумент суммы (+Si+1)k, но структуры аргументов слагаемых ±1[Si]13 и ±1[Si]14 активизируют «Дефект». При этом следует отметить, что число логических функций f1-3(&)-И в выражении (528) может быть минимизировано до одной логической функции f1(&)-И, если систему «Комплексных аргументов» ввести в систему логической функции f1(})-ИЛИ и записать аналитическое выражение (530)
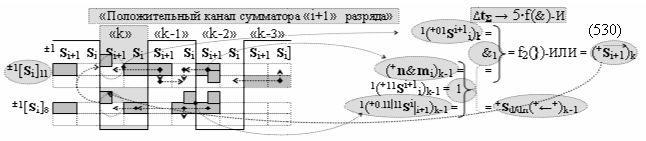
и в такой записи функциональной структуры с преобразованным аргументом локального сквозного переноса +Sd/dn(+←+)k-1 существенно будет минимизирована структура логических функций всего «Положительного канала сумматора «i+1» разряда». Поскольку с одной стороны функциональную структуру в выходной логической функцией f1-6(&)-И
запишем в виде структуры логических функций (532),
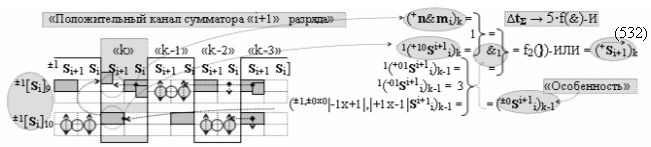
то технологический цикл ∆tΣ → 5∙f(&)-И преобразования аргументов будет соответствовать пяти условным логическим функциям f(&)-И. Поскольку формируется математическая модель сумматора ±f(ΣRU)min условно «k» «Зоне минимизации», то для минимизации аналитического выражения ее функциональной структуры различные «Комплексные аргументы» «Условия активизации» будем включать в систему общей их совокупности, под которой, в частности, подразумевается логическая функция f1(})-ИЛИ.
Возвращаясь к анализу функциональной структуры (531) с выходной логической функцией f1-6(&)-И, которая преобразует входные аргументы (+n&mi)k и 1(+10Si+1 i)k в условно «k» «Зоне минимизации» и в соответствии с дополнительными структурами аргументов слагаемых ±1[Si]9 - ±1[Si]9 скорректируем ее и запишем в виде аналитического выражения (533).
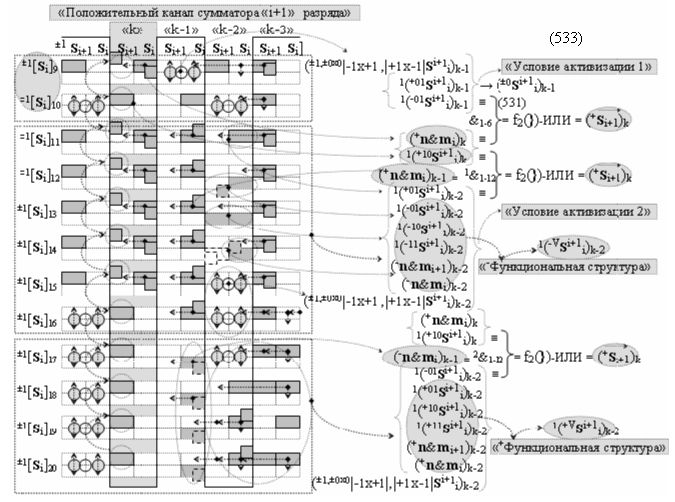
Из анализа аналитического выражения (533) следует, что дополнительные функциональные структуры с входной логической функцией f1-12(1&)-И и f1-12(2&)-И включающие совокупность входных аргументов одного знака могут быть минимизированы и записаны посредством общего преобразованного условно отрицательного аргумента 1(-VSi+1 i)k-2 «-Функциональной структуры» (534)
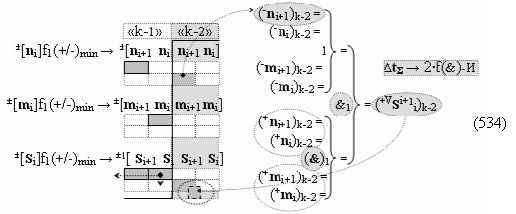
и общего преобразованного положительного аргумента 1(+Si+1 i)k-2 «+Функциональной структуры» (535),
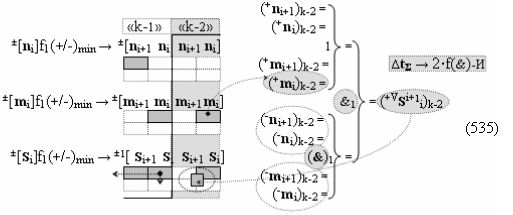
которые включают логическую функцию f1(})-ИЛИ с входными аргументами того знака, что и в преобразованном аргументе (-VSi+1 i)k-2 и (+VSi+1 i)k-2, а также включают логическую функцию f1(}&)-ИЛИ-НЕ с аргументами противоположного знака, при этом технологический цикл ∆tΣ → 2∙f(&)-И преобразования аргументов соответствует двум условным логическим функциям f(&)-И. При этом следует отметить, что преобразованные аргументы (-VSi+1 i)k-2 и (+VSi+1 i)k-2 также могут быть активизированы, когда в условно «k-1» «Зоне минимизации» активизирован условно отрицательный аргумент 1(-0.11|11Si|i+1)k-2 и положительный аргумент 1(+0.11|11Si|i+1)k-2. И если в структуре логических функций (533) выполнить замену условно отрицательной и положительной системы входных аргументов входной логической функции f1-12(1&)-И и f1-12(2&)-И, то минимизированную структуру логических функций запишем в виде аналитического выражения (536),
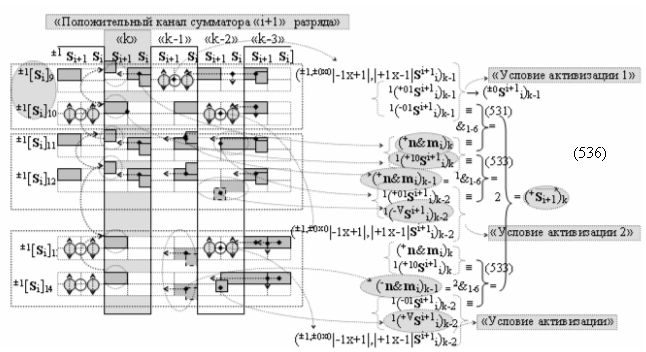
которое может быть введено в систему логической функции f2(})-ИЛИ выражения (528), но она функционально не закончена. Поскольку возможна структура аргументов слагаемых ±1[Si]1 - ±1[Si]3 (537),
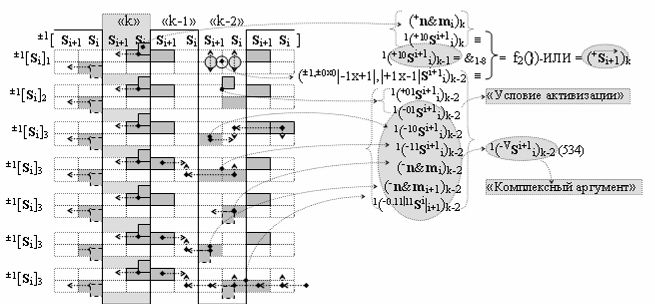
которые посредством функциональной структуры (537) с выходной логической функцией f1-8(&)-И также активизируют положительный аргумент (+Si+1)k условно «i+1» разряда. При этом следует отметить, что в «Условии активизации» совокупность входных условно отрицательных аргументов может быть заменена на «Комплексный аргумент» 1(-VSi+1 i)k-2 функциональной структуры (534), в результате математическую модель сумматора ±f(ΣRU)min «Положительный канал сумматора «i+1» разряда» условно «k» «Зоне минимизации» с учетом функциональных структур (536) и (537) запишем в виде аналитического выражения (538).
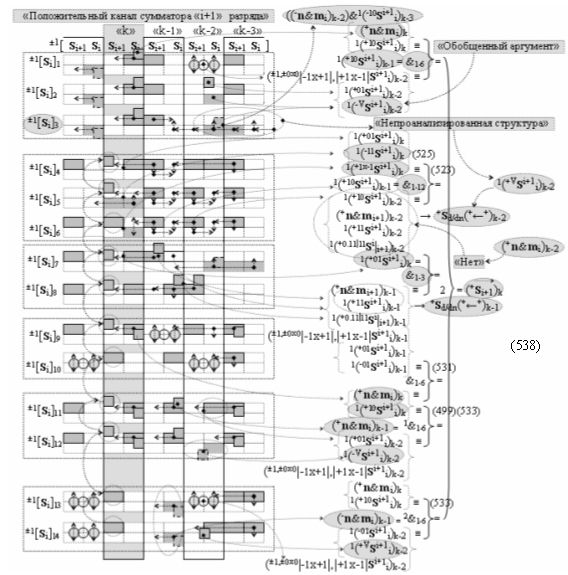
Из анализа графоаналитического выражения (538) следует, что совокупность объединенных структур слагаемых ±1[Si]1 - ±1[Si]14 включает «Непроанализированную структуру» ±1[Si]3, в которую включен условно отрицательный аргумент (-n&mi)k-2 условно «k-2» «Зоны минимизации» и условно отрицательный аргумент 1(-10Si+1 i)k-3 условно «k-3» «Зоны минимизации» и логика преобразования их «Комплексного аргумента» ((-n&mi)k-2)&1(-10Si+1 i)k-3 эквивалентна логике преобразования «Комплексного аргумента» 1(+0.11|11Si|i+1)k-2 при условии активности аргумента сквозного переноса +Sd/dn(+←+)k-3 из условно «k-3» «Зоны минимизации». Но анализируемая структура аргументов к активизации аргумента результирующей суммы (+Si+1)k не имеет отношения, поскольку в данной ситуации в функциональной входной структуре с выходной логической функцией f1-6(&)-И включен обобщенный условно отрицательный аргумент 1(-VSi+1 i)k-2, который корректно активизирует аргумент результирующей суммы (+Si+1)k и эту процедуру при технологическом цикле ∆tΣ → 4∙f(&)-И реализует шесть логических функций f1(&)-И. А если записать функциональную структуру с выходной логической функцией f1-12(&)-И в виде графоаналитического выражения (539),
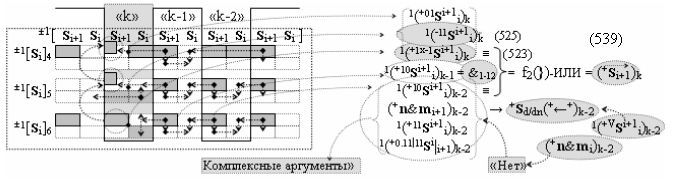
то для реализации процедуры преобразования аргументов с технологическим циклом ∆tΣ → 4∙f(&)-И необходимо двенадцать логических функций f1(&)-И. Но число их могло быть минимизировано, если в систему «Комплексных аргументов» локального переноса +Sd/dn(+←+)k-2 включить дополнительный аргумент (+n&mi)k-2 условно «i» разряда, который не относится к категории аргумента локального переноса +Sd/dn(+←+)k-2, а такое включение приведет к минимизации функциональной структуры (539) и ее можно записать в данной ситуации в виде аналитического выражения (540)
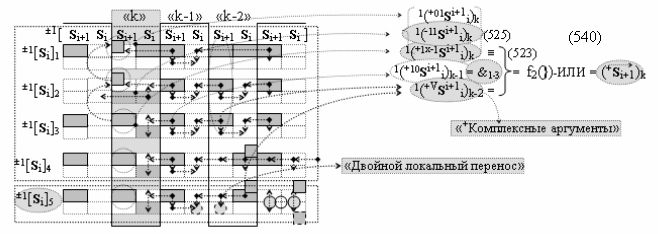
с одним «+Комплексным аргументом» 1(+VSi+1 i)k-2 при технологическом цикле ∆tΣ → 4∙f(&)-И и двумя логическими функциями f1(&)-И. При этом следует отметить, что результирующий положительный аргумент суммы (+Si+1)k в условно «k» «Зоне минимизации» корректно активизирован, но логика преобразования аргумента слагаемых ±1[Si]5 в условно «k-2» «Зоне минимизации» существенно изменена, поскольку в этой зоне положительный аргумент (+n&mi)k-2 условно «i» разряда в этом случае должен быть преобразован посредством «Двойного локального переноса» для корректной активизации условно отрицательного аргумента как в условно «k-1» «Зоне минимизации», где активизирован аргумент (-Si)k-1, так и в условно «k-2» «Зоне минимизации», где активизирован аргумент (-Si+1)k. Аналогичная ситуация и в графоаналитическом выражении (541),
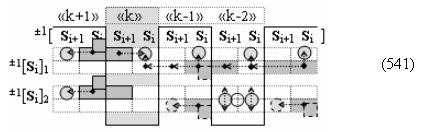
в котором активизирован положительный аргумент как в условно «k» «Зоне минимизации», где активен аргумент суммы (+Si)k, так и в условно «k-1» «Зоне минимизации», где активен аргумент суммы (+Si+1)k. Но прежде чем скорректировать логико-динамический процесс преобразования аргументов в «Положительном канале сумматора «i+1» разряда» выражения (538) вернемся к анализу процедуры преобразования аргументов в «Положительном канале сумматора «i» разряда» выражения (518), записав его в виде графоаналитического выражения (542).
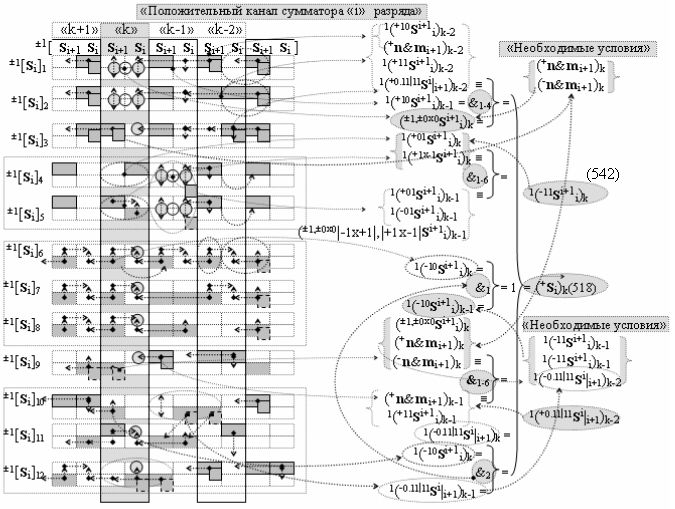
Из анализа объединенных структур аргументов слагаемых ±1[Si]1 - ±1[Si]12 (542) и входных аргументов структуры логических функций, посредством которой активизируют положительный аргумент суммы (+Si)k следует, что с одной стороны функциональные входные структуры с выходной логической функции f1(&)-И и f2(&)-И могут быть объединены, поскольку они имеют общий входной аргумент 1(-10Si+1 i)k, а входной условно отрицательный аргумент 1(-0.11|11Si|i+1)k-1 логической функции f2(&)-И включен в расширенную совокупность входных аргументов логической функцией f1(&)-И. С другой стороны, если скорректировать структуру логических функций (542) и записать ее в виде аналитического выражения (543),
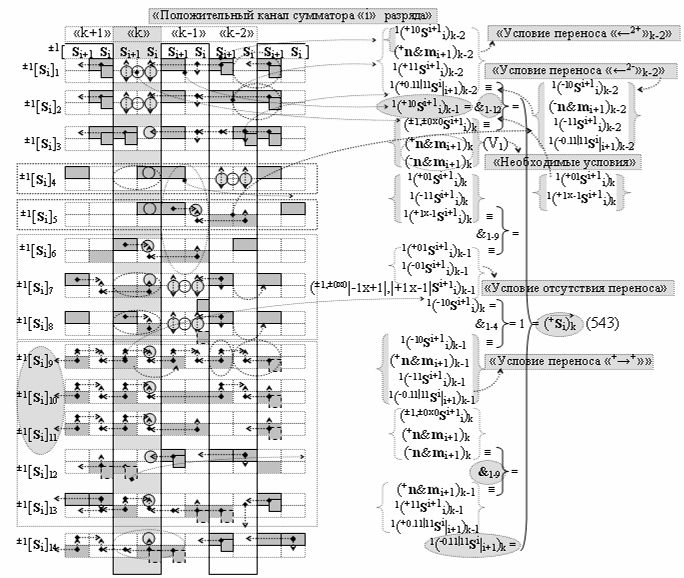
то функциональная входная структура с выходной логической функцией f1-12(&)-И с положительным входным аргументом 1(+10Si+1 i)k-1 условно «k-1» «Зоны минимизации» представляет собой многовариантную структуру, которая активизирует положительный результирующий аргумент суммы (+Si)k, поскольку в ее «Необходимые условия» включены два дополнительных аргумента (+n&mi+1)k и (-n&mi+1)k. Но если учесть, что аргументы «Необходимого условия» могут быть объединены посредством логической функции f1(})-ИЛИ → (V1), поскольку дополнительные аргументы (+n&mi+1)k и (-n&mi+1)k могут быть введены в систему функциональной структуры (485) с выходной логической функцией f1(})-ИЛИ и записаны в виде аналитического выражения (544).
При этом следует отметить, что результирующий аргумент вида
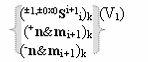
записан в структуре логических функций (544) в виде совокупности трех «Комплексных аргументов» для понимания его смыслового содержания в графоаналитических выражениях логико-динамического процесса преобразования аргументов слагаемых ±[ni]f1(+/-)min и ±[mi]f1(+/-)min → ±[Si]f1(+/-)min и технологический цикл ∆tΣ → 2∙f(&)-И его активизации соответствует двум условным логическим функциям f(&)-И.
Аналогичным образом может быть минимизировано «Условие переноса «←2+»k-2» в функциональной входной структуре (543) с выходной логической функцией f1-12(&)-И, поскольку в этом условии могут быть объединены аргументы (+n&mi+1)k-2 и 1(+0.11|11Si|i+1)k-2, и функциональную структуру такого объединения запишем в виде аналитического выражения (545),
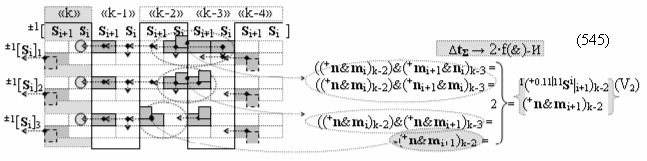
в которой также положительный результирующий аргумент
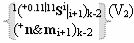
записан в виде совокупности двух «Комплексных аргументов». Функциональную аналогичную структуру за исключением знаков аргументов имеет результирующий условно отрицательный аргумент в виде совокупности двух «Комплексных аргументов»
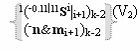
«Условия переноса «←2-»k-2», который активизирован посредством функциональной структуры (546).
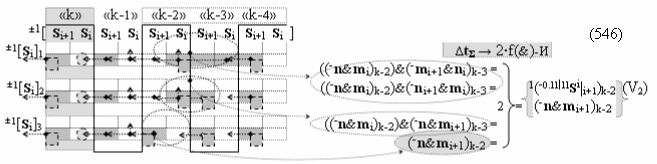
А если учесть то, что положительный результирующий аргумент суммы (+Si)k, а также результирующий условно отрицательный аргумент суммы (-Si)k, может быть активизирован при активном аргументе условно отрицательного слагаемого 1(-01Si+1 i)k и 1(-10Si+1 i)k-1 и положительного слагаемого 1(+01Si+1 i)k и 1(+10Si+1 i)k-1 соответственно в ситуациях, когда активна либо функциональная структура (547)
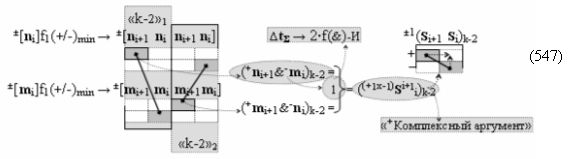
либо активна функциональная структура (548)
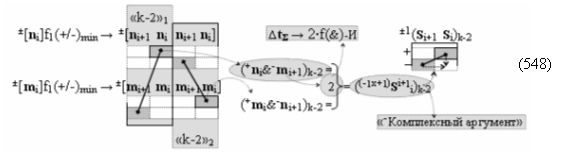
и учесть, что функциональные структуры (547) и (548) имеют выходную логическую функцию f1(})-ИЛИ, то для минимизации структуры логических функций математической модели сумматора ±f(ΣRU)min условно «k» «Зоны минимизации», то входные аргументы этих функциональных структур могут быть введены в систему одноименных выходных логических функций f1(})-ИЛИ и f2(})-ИЛИ выражений (545) и (546) и записаны в виде аналитического выражения (549)
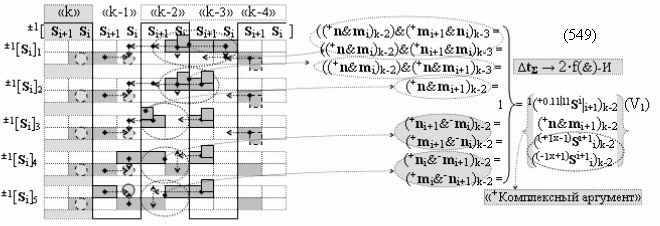
для активизации условно отрицательных аргументов слагаемых 1(-01Si+1 i)k и 1(-10Si+1 i)k-1 и аналитического выражения (550)
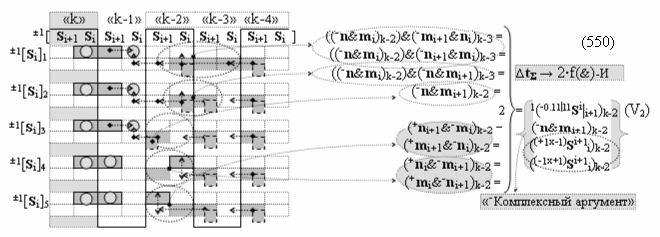
для положительных аргументов слагаемых 1(+01Si+1 i)k и 1(+10Si+1 i)k-1, а результирующие «+Комплексные аргументы» (549) в виде совокупности аргументов (551)
и «-Комплексные аргументы» (550) в виде совокупности аргументов (552)
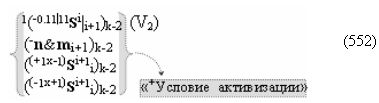
являются корректным «Условием активизации» положительного аргумента 1(+01Si+1 i)k и условно отрицательного аргумента 1(-01Si+1 i)k в условно «k» «Зоне минимизации» без их преобразования. Но совокупность аргументов (551) и (552) функционально незаконченная, поскольку к категории «Условий активизации» относятся и входные аргументы «Комплексного аргумента» (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k-2 неактивного логического нуля «±0i+1 i»k-2 и активного логического нуля «+1»«-1» → «±01» графоаналитического выражения (553).
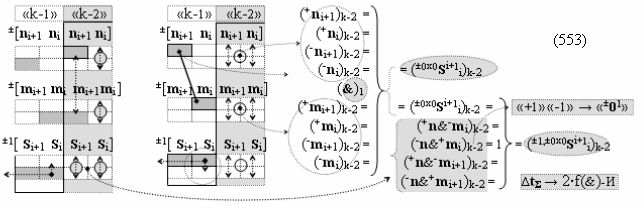
Поэтому аналитические выражения «+Комплексных аргументов» (549) запишем в виде функциональной структуры (554),
а аналитическое выражение «-Комплексных аргументов» (550) запишем в виде функциональной структуры (555).
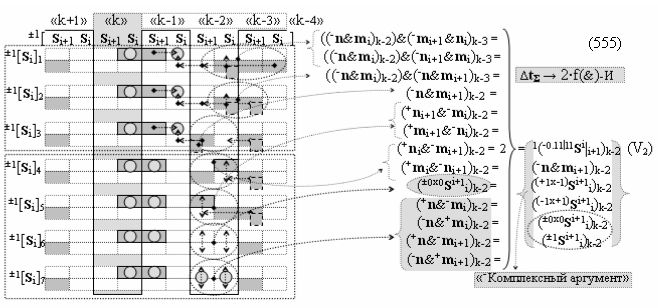
При этом следует отметить, что функциональные структуры (554) и (555) также функционально незаконченные, поскольку к категории «Условий активизации» относятся и входные аргументы «+Комплексного аргумента» (+11Si+1 i)k-2 аналитического выражения (556)
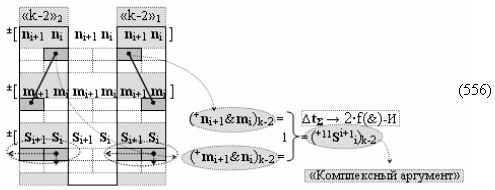
и входные аргументы «-Комплексного аргумента» (-11Si+1 i)k-2 аналитического выражения (557)
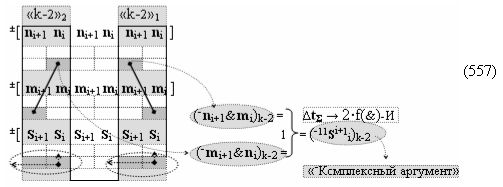
поэтому аналитические выражения совокупности «+Комплексных аргументов» (554) запишем в виде функциональной структуры (558),
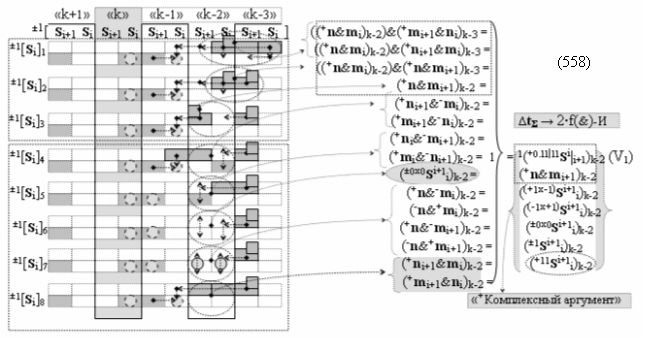
а аналитическое выражение совокупности «-Комплексных аргументов» (555) запишем в виде функциональной структуры (559).
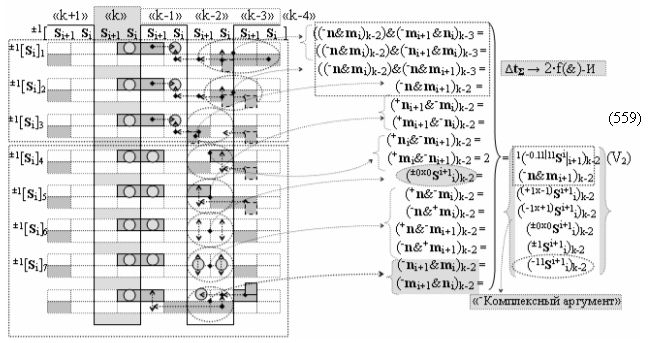
При этом следует отметить, что условно положительная совокупность «+Комплексных аргументов» (558), если их записать в виде графоаналитического выражения (560),
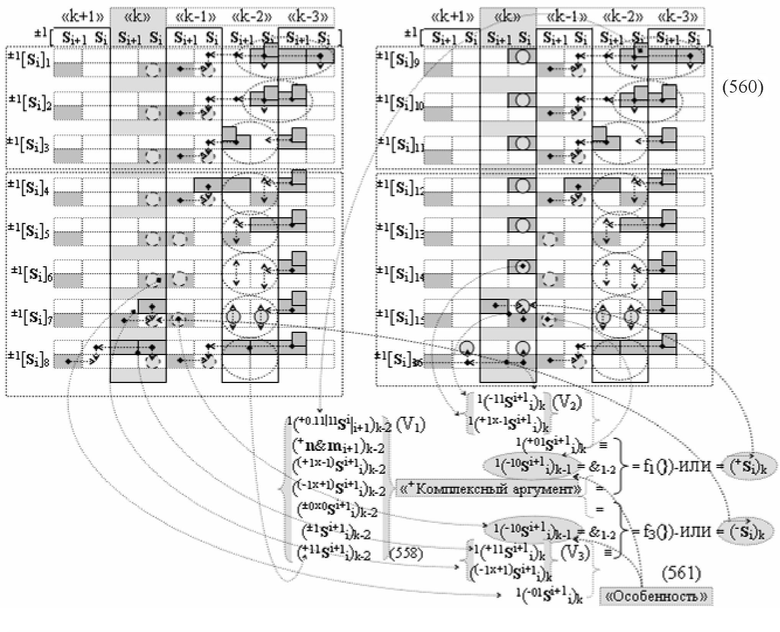
то функциональная структура (561) корректно активизирует не только положительный аргумент (+Si)k, но и условно отрицательный аргумент (-Si)k в чередующейся последовательности положительных и условно отрицательных аргументов слагаемых в условных «k-1» «k-2» «Зонах минимизации». Аналогичную фукциональную структуру запишем и для условно отрицательной совокупности «-Комплексных аргументов», которую запишем в виде графоаналитического выражения (562),
в которой также корректно активизирован не только положительный аргумент (+Si)k, но и условно отрицательный аргумент (-Si)k в чередующейся последовательности положительных и условно отрицательных аргументов слагаемых в условных «k-1» «k-2» «Зонах минимизации». При этом следует отметить, что «Особенностью» функциональных структур (561) и (562) является условно отрицательный аргумент 1(-10Si+1 i)k-1 и положительный аргумент 1(+10Si+1 i)k-1 условно «k-1» «Зоны минимизации», которые не изменяют свой знак при активизации как положительного аргумента суммы (+Si)k, так и условно отрицательного аргумента суммы (+Si)k, как это ранее предполагалось.
На основании полученных результатов следует, что с одной стороны в структуре логических функций (543) функциональная структура с выходной логической функцией f1-12(&)-И → f1-2(&)-И минимизирована до двух логических функций f1-2(&)-И, с другой стороны может быть сформирована дополнительная функциональная структура с двумя последовательно активными аргументами, один из которых активизирован в условно «k» «Зоне минимизации» 1(+01Si+1 i)k или 1(+1х-1Si+1 i)k или 1(-11Si+1 i)k, а второй аргумент 1(+10Si+1 i)k-1 активизирован в условно «k-1» «Зоне минимизации» и эти функциональные структуры запишем в виде аналитических выражений (556), (557) и (558).
При этом следует отметить, что аналитическая запись «Положительного канала сумматора «i» разряда» может быть минимизирована, поскольку с одной стороны структура логических функций (557) и (558) включает общие «Необходимые условия», поэтому эти структуры логических функций могут быть записаны в виде аналитического выражения с общими «Необходимыми условиями». С другой стороны, если ввести положительный «+Complex argument» ((+Comp)Si+1 i)k-2 и условно отрицательный «-Complex argument» ((+Comp)Si+1 i)k-2, то они, по существу, функционально относятся к «Положительному каналу сумматора «i» разряда» и «Условно отрицательному каналу сумматора «i» разряда», поэтому аналитические выражения (556), (557) и (558) «Положительного канала сумматора «i» разряда» в графоаналитическом выражении (559) запишем в виде трех аналитических выражений (560), (561) и (562).
А «Условно отрицательный канал сумматора «i» разряда» с учетом «Особенностей» функциональных структур и выражения (520) в скорректированном в графоаналитическом выражении (563) запишем в виде аналитических выражений (564), (565) и (566).
При этом следует отметить, что поскольку в графоаналитические выражения (559) и (563) включен положительный «+Complex argument» ((+Comp)Si+1 i)k-2 и условно отрицательный «-Complex argument» ((+Comp)Si+1 i)k-2 условно «k-2» «Зоны минимизации», а если учесть, что формируется математическая модель сумматора ±f(ΣRU)min условно «k» «Зоны минимизации». Поэтому в структуру логических функций «Положительных каналов сумматора «i+1» и «i» разряда» и «Условно отрицательных каналов сумматора «i+1» и «i» разряда» условно «k» «Зоны минимизации» должны быть включены такие функциональные структуры, которые активизируют «+Complex argument» ((+Comp)Si+1 i)k и условно отрицательный «-Complex argument» ((+Comp)Si+1 i)k. Поэтому «Положительный канал сумматора «i» разряда» (559) запишем в виде структуры логических функций (567), (568) и (569),
а «Условно отрицательный канал сумматора «i» разряда» (563) запишем в виде структуры логических функций (570), (571) и (572)
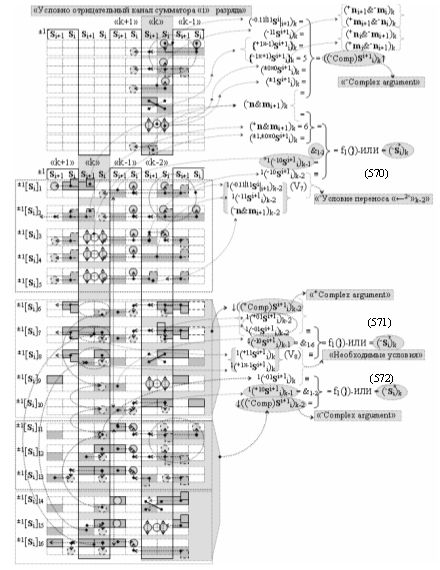
Далее, если вернуться к анализу структуры аргументов слагаемых ±1[Si]1 и ±1[Si]2 графоаналитического выражения (541), в котором активизирован условно отрицательный аргумент «-Условия переноса «←2-»k-2» из условно «i-2» разряда, записав его в виде выражения (573)
и процедуру активизации положительного аргумента «+Условия переноса «←2+»k-2» из условно «i-2» разряда, записав его в виде графоаналитического выражения (574),
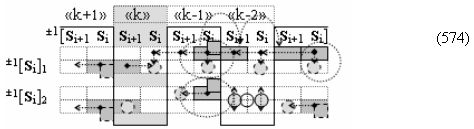
то последовательные структуры условно отрицательных аргументов (-n&mi)k-1 и 1(-10Si+1 i)k-2, а также последовательные структуры положительных аргументов (+n&mi)k-1 и 1(+10Si+1 i)k-2, которые позиционно расположены между «Зонами минимизации», имеют неоднозначную логику преобразования. Поскольку если процедуру преобразования объединенной структуры положительных аргументов слагаемых записать в виде логико-динамического процесса (575),
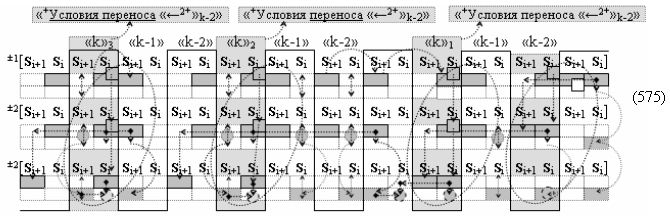
а процедуру преобразования объединенной структуры условно отрицательных аргументов слагаемых записать в виде логико-динамического процесса (576),
то в них представлены возможные три ситуации.
Ситуация 1. Структура положительных аргументов слагаемых (577)
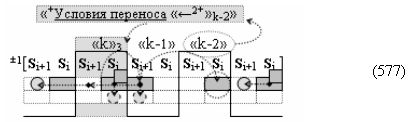
и структура условно отрицательных аргументов слагаемых (578),
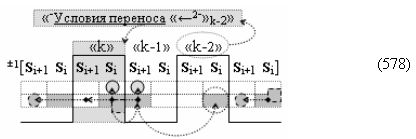
в которых «+Условия переноса «←2+»k-2» и «-Условия переноса «←2-»k-2» отсутствуют, и в этой ситуации могут быть активизирован условно отрицательный аргумент (-Si)k в соответствии с процедурой (577) и положительный аргумент (+Si)k в условно «k» «Зоне минимизации», преобразованы в соответствии с процедурой (578), и данная логика формирования результирующей суммы корректно актизирует структуру условно минимизированной суммы. Но если учесть, что объединенные структуры аргументов слагаемых многовариантны, то преобразование аргументов слагаемых 577) и (578) необходимо выполнить в соответствии с логико-динамическим процессом (579)
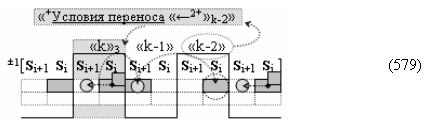
и в соответствии с логико-динамическим процессом (580),
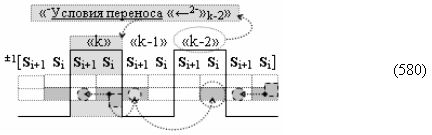
в которых в условно «k» «Зоне минимизации» преобразован только положительный аргумент (+n&mi)k и условно отрицательный аргумент (-n&mi)k, а положительный аргумент 1(+10Si+1 i)k-1 и условно отрицательный аргумент 1(-10Si+1 i)k-1 корректно не преобразованы. При этом оба результирующих аргумента выражения (579) функционально принадлежат «Положительному каналу сумматора «i+1» разряда» (538), а преобразование входных аргументов выполняют в соответствии с функциональной структурой (537), которую запишем с учетом скорректированной «графоаналитической информационной технологии» в виде графоаналитического выражения (581)
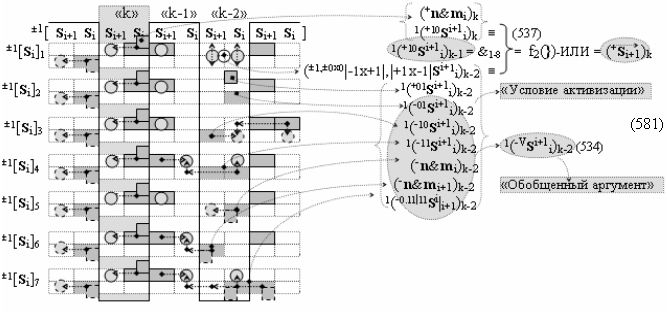
с совокупностью входных условно отрицательных аргументов 1(-VSi+1 i)k-2 условно «k-2» «Зоны минимизации». При этом особенностью «Обобщенного аргумента» 1(-VSi+1 i)k-2 является то, что он может быть сформирован посредством самостоятельной функциональной структуры (582),
которая включает входную логическую функцию f1(}&)-ИЛИ-НЕ с условно отрицательными аргументами и логическую функцию f2(}&)-ИЛИ-НЕ с положительными аргументами. В результате функциональную структуру (581) запишем в виде минимизированного аналитического выражения (583),
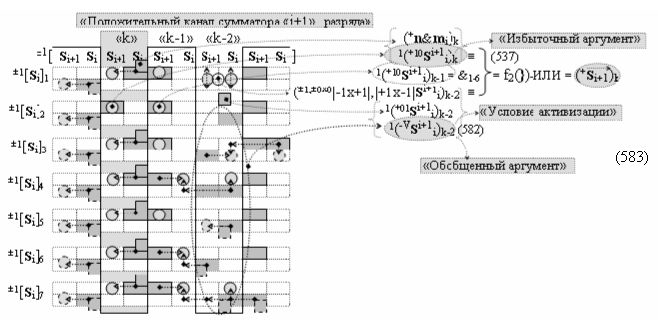
в котором в систему логической функции f1-6(&)-И включен «Избыточный аргумент» 1(+10Si+1 i)k. Аналогичный «Избыточный аргумент» включен и в функциональную структуру «Условно отрицательного канала сумматора «i+1» разряда», которую запишем в виде аналитического выражения (584),
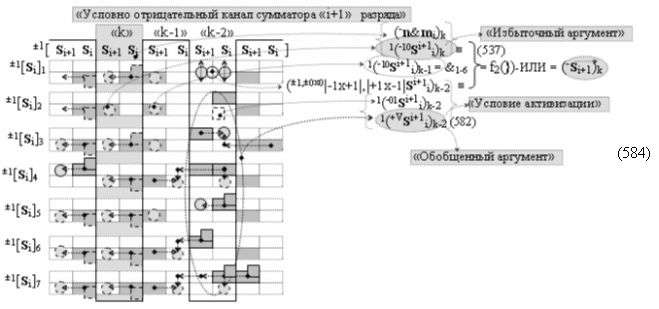
при этом положительный аргумент 1(+VSi+1 i)k-2 сформирован посредством самостоятельной функциональной структуры (585).
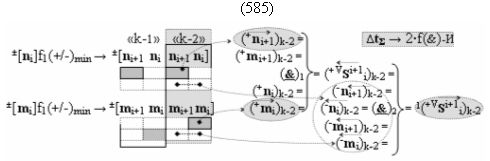
При этом следует отметить, что «Избыточность аргумента» 1(+10Si+1 i)k и 1(-10Si+1 i)k непосредственно связана с единой логикой преобразования аргументов слагаемых в «Положительном канале сумматора «i+1» разряда» и «Условно отрицательный канал сумматора «i+1» разряда», так и в «Положительном канале сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда». А если вернуться к предварительно сформированному «Положительному каналу сумматора «i» разряда» выражения (518), записав его без учета функциональных структур (567) - (569) в виде графоаналитического выражения (586)
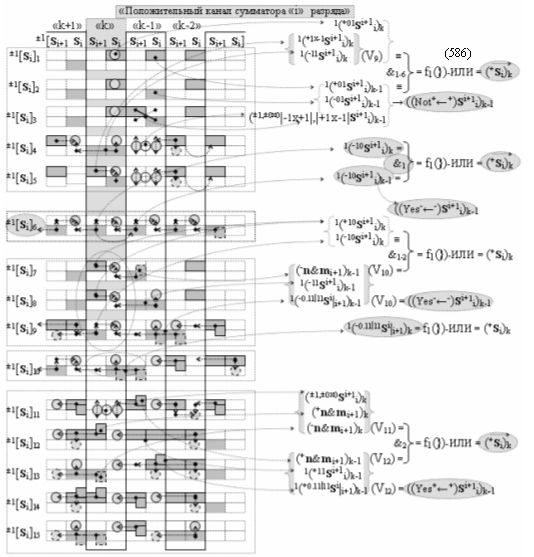
то преобразование аргументов слагаемых ±1[Si]6 выполняет функциональная структура с выходной логической функцией f1(&)-И, в систему которой включены два последовательных условно отрицательных аргумента 1(-10Si+1 i)k и 1(-10Si+1 i)k-1, и она реализует процедуру активизации результирующего положительного аргумента суммы (+Si)k условно «i» разряда. А функциональная структура (584) «Условно отрицательного канала сумматора «i+1» разряда» с двумя последовательными условно отрицательными аргументами 1(-10Si+1 i)k и 1(-10Si+1 i)k-1 реализует процедуру активизации результирующего условно отрицательного аргумента суммы (-Si+1)k условно «i+1» разряда, что недопустимо. Поэтому «Положительный канал сумматора «i+1» разряда» (538) запишем в виде графоаналитического выражения (587).
А если вернуться к предварительно сформированному «Условно отрицательному каналу сумматора «i» разряда» выражения (520), записав его без учета функциональных структур (570) - (572) в виде графоаналитического выражения (588)
то преобразование аргументов слагаемых ±1[Si]6 выполняет функциональная структура с выходной логической функцией f1(&)-И, в систему которой включены два последовательных положительных аргумента 1(+10Si+1 i)k и 1(+10Si+1 i)k-1, реализует процедуру активизации результирующего условно отрицательного аргумента суммы (-Si)k условно «i» разряда. А функциональная структура (583) «Положительного канала сумматора «i+1» разряда» с двумя последовательными положительными аргументами 1(+10Si+1 i)k и 1(+10Si+1 i)k-1 реализует процедуру активизации положительного результирующего аргумента суммы (+Si+1)k условно «i+1» разряда, что недопустимо. Поэтому «Условно отрицательный канал сумматора «i+1» разряда» запишем в виде графоаналитического выражения (589).
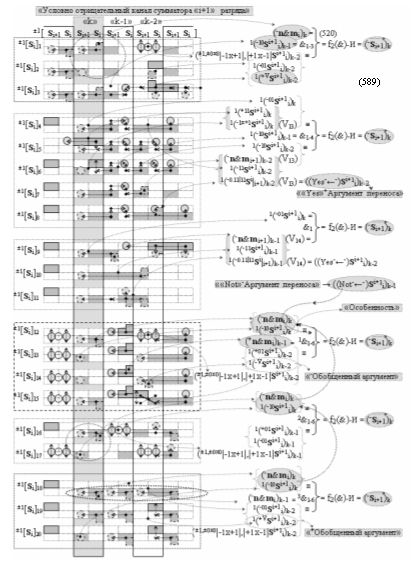
Из сопоставительного анализа логико-динамических процессов преобразования аргументов возможных структур слагаемых (586) - (589) следует, что, по существу, процедура активизации результирующего аргумента суммы в условно «k» «Зоне минимизации» может быть разделена на две категории, когда в условно «k-1» или «k-2» «Зоне минимизации» либо активизирован положительный аргумент локального переноса ««Yes»+Аргумент переноса» → ((Yes+←+)Si+1 i)k-1 или ((Yes+←+)Si+1 i)k-2, либо активен условно отрицательный аргумент локального переноса ««Not»-Аргумент переноса» → ((Not-←-)Si+1 i)k-1 или ((Yes-←-)Si+1 i)k-2. При этом в «Положительном канале сумматора «i+1» разряда» выражения (587) и «Условно отрицательном канале сумматора «i+1» разряда» выражения (589) есть «Особенность» и она заключается в трех вариантах преобразования положительных аргументов (+n&mi)k и 1(+10Si+1 i)k и условно отрицательных аргументов (-n&mi)k и 1(-10Si+1 i)k, которые активны в условно «k» «Зоне минимизации» и которые имеют эквивалентное «информационное содержание» и поэтому должны быть совместно включены во все функциональные структуры, а в качестве «Условия активизации» должны быть сформированы «Комплексные аргументы» (590).
При этом следует отметить, что ««Yes»+,-Аргумент переноса» и ««Not»+,-Аргумент переноса» должны иметь общую совокупность входных аргументов со взаимно противоположным информационным содержанием, поскольку если не активен ««Yes»+,-Аргумент переноса», то в этой ситуации активен ««Not»+,-Аргумент переноса». А поскольку ««Yes»+,-Аргумент переноса», по существу, представляет собой как активную последовательную структуру аргументов локального переноса, так и чередующую структуру активных и неактивных аргументов возможного переноса, и такие структуры аргументов слагаемых запишем в виде графоаналитического выражения (591).
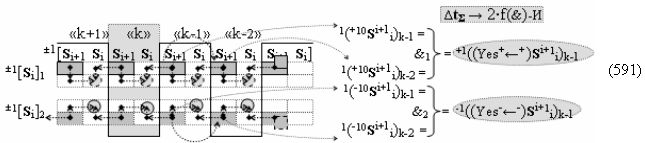
При этом функциональные структуры с выходной логической функцией f1(&)-И и f2(&)-И имеют технологический цикл ∆tΣ → 2∙f(&)-И, соответствующий двум условным логическим функциям f(&)-И. Поскольку входные положительные аргументы 1(+10Si+1 i)k-1 и 1(+10Si+1 i)k-2 сформированы посредством логической функции f1(&)-И и f2(&)-И, и общую их функциональную структуру запишем либо в виде аналитического выражения (593),
либо в виде минимизированного аналитического выражения (594).
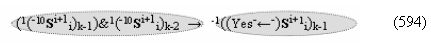
А объединенную функциональную структуру, которая активизирует условно отрицательный аргумент -101((Yes-←-)Si+1 i)k-1 запишем либо в виде аналитического выражения (595),
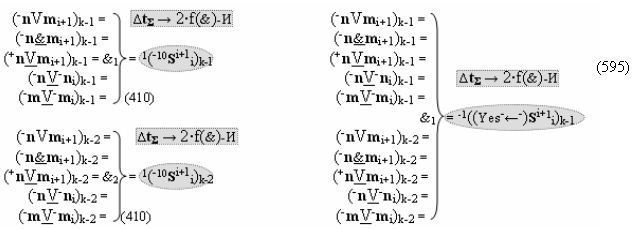
либо в виде минимизированного аналитического выражения (596).
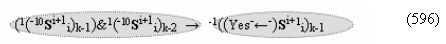
Но к потенциально возможному переносу могут быть отнесены и чередующие структуры активных и неактивных аргументов графоаналитического выражения (595)
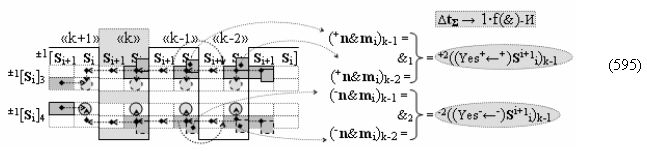
При этом функциональные структуры с выходной логической функцией f1(&)-И и f2(&)-И имеют технологический цикл ∆tΣ → 1∙f(&)-И, соответствующий одной условной логической функции f(&)-И. Поскольку положительные входные аргументы (+n&mi)k-1 и (+n&mi)k-2 сформированы также посредством логической функции f1(&)-И и f2(&)-И, и общую их функциональную структуру запишем либо в виде аналитического выражения (596),
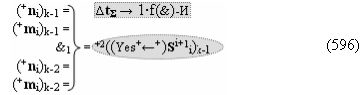
либо в виде минимизированного аналитического выражения (597).
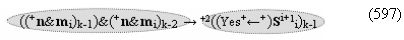
А объединенную функциональную структуру, которая активизирует условно отрицательный аргумент -2(Yes-←-)Si+1 i)k-1 запишем в виде аналитического выражения (598),
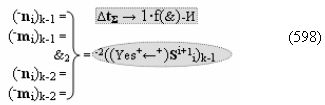
либо в виде минимизированного аналитического выражения (599).
А если учесть, что объединенная структура аргументов слагаемых ±[Si]f1(+/-)min многовариантна, то ««Yes»+,-Аргумент переноса» могут активизировать следующие функциональные структуры.
Функциональная структура 1. Последовательное чередование положительных «Комплексных аргументов» 1(+10Si+1 i)k-1 и (+n&mi)k-2 и условно отрицательных «Комплексных аргументов» 1(-10Si+1 i)k-1 и (-n&mi)k-2 в графоаналитическом выражении (600),
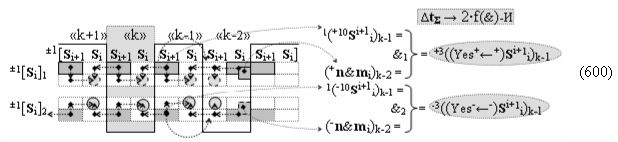
в котором функциональную структуру запишем либо в виде аналитического выражения (601),
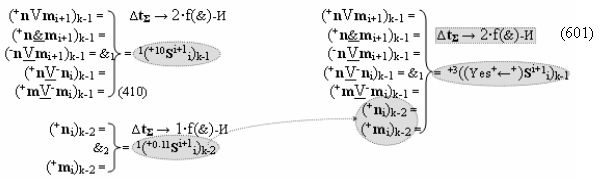
либо в виде минимизированного аналитического выражения (602).
А объединенную функциональную структуру, которая активизирует условно отрицательный аргумент -3((Yes-←-)Si+1 i)k-1 запишем в виде аналитического выражения (603),
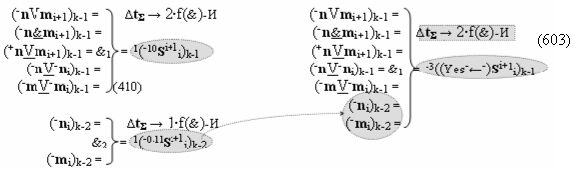
либо в виде минимизированного аналитического выражения (604).
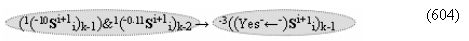
Функциональная структура 2. Последовательное чередование положительных «Комплексных аргументов» (+n&mi)k-1 и 1(+10Si+1 i)k-2 и условно отрицательных «Комплексных аргументов» (-n&mi)k-1 и 1(-10Si+1 i)k-2 в графоаналитическом выражении (605),
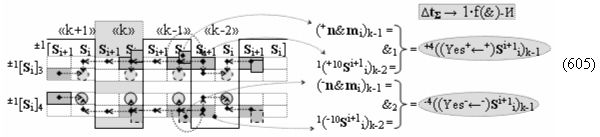
в котором функциональную структуру запишем либо в виде аналитического выражения (606),
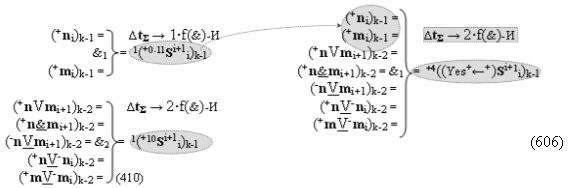
либо в виде минимизированного аналитического выражения (607).
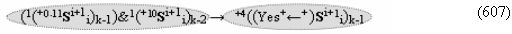
А объединенную функциональную структуру, которая активизирует условно отрицательный аргумент -4((Yes-←-)Si+1 i)k-1 запишем в виде аналитического выражения (608),
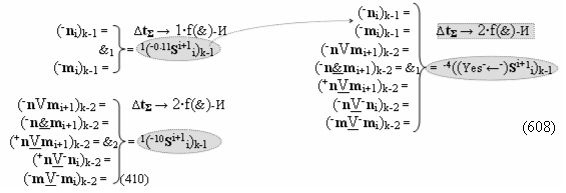
либо в виде минимизированного аналитического выражения (609).
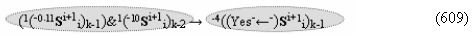
При этом если учесть, что ««Yes»+,-Аргумент переноса» также может быть активизирован в условно «k-1» «Зоне минимизации» посредством совокупности аргументов +0((Yes+←+)Si+1 i)k-1 и -0((Yes-←-)Si+1 i)k-1 в графоаналитическом выражении (610)
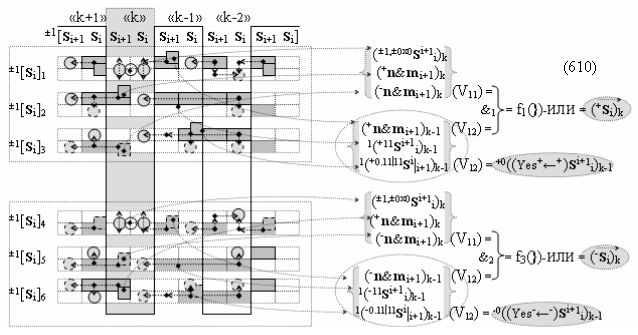
и эта же совокупность аргументов +5((Yes+←+)Si+1 i)k-1 и -5((Yes-←-)Si+1 i)k-1, позиционно расположенная в условно «k-2» «Зоне минимизации» может активизировать дополнительные ««Yes»+,-Аргумент переноса».
Функциональная структура 3. Последовательное чередование положительных «Комплексных аргументов» 1(+10Si+1 i)k-1 и 1(+11Si+1 i)k-2 и условно отрицательных «Комплексных аргументов» 1(-10Si+1 i)k-1 и 1(-11Si+1 i)k-2 в графоаналитическом выражении (611),
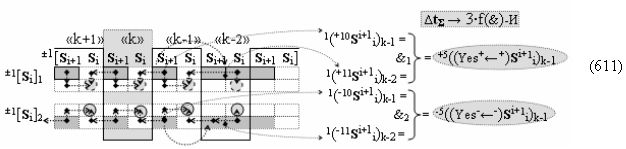
в котором функциональные структуры имеют технологический цикл ∆tΣ → 3∙f(&)-И, соответствующий трем условным логическим функциям f(&)-И. Поскольку если записать структуру логических функций «Комплексного аргумента» 1(+11Si+1 i)k-2 в виде аналитического выражения (612),
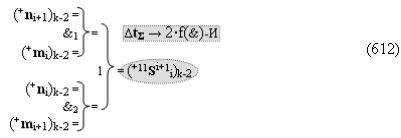
то только эта функциональная структура имеет технологический цикл ∆tΣ → 2∙f(&)-И, соответствующий двум условным логическим функциям f(&)-И. Но если выполнить преобразование структуры логических функций (612) в соответствии с векторной структурой (613),
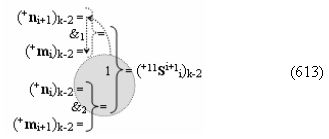
а также в соответствии с векторными структурами (614),
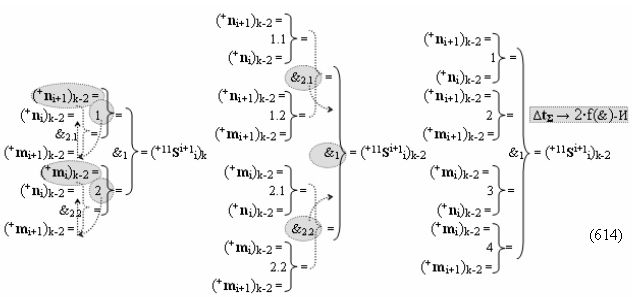
то результирующая структура логических функций, которую запишем в виде минимизированного аналитического выражения (615)
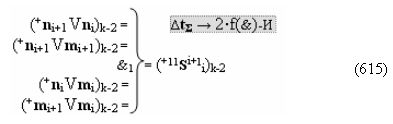
также имеет технологический цикл ∆tΣ → 2∙f(&)-И, соответствующий двум условным логическим функциям f(&)-И, но с выходной логической функцией f1(&)-И. В результате функциональную структуру (611), активизирующую положительный аргумент +5((Yes+←+)Si+1 i)k-1 запишем либо в виде аналитического выражения (616),
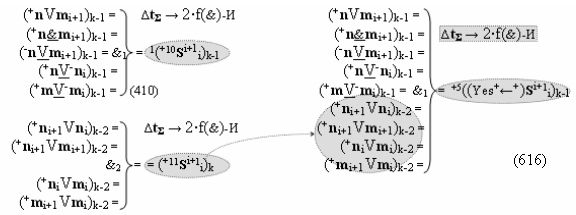
либо в виде минимизированного аналитического выражения (617).
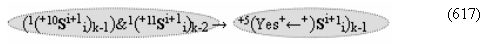
А объединенную функциональную структуру, которая активизирует условно отрицательный аргумент -5(Yes-←-)Si+1 i)k-1, запишем в виде аналитического выражения (618),
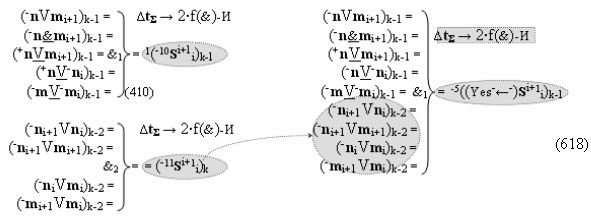
либо в виде минимизированного аналитического выражения (619).
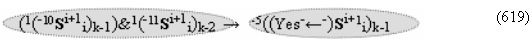
Функциональная структура 4. Последовательное чередование положительных «Комплексных аргументов» (+n&mi)k-1 и 1(+0.11|11Si|i+1)k-1 и условно отрицательных «Комплексных аргументов» (-n&mi)k-1 и 1(+0.11|11Si|i+1)k-2 в графоаналитическом выражении (620),
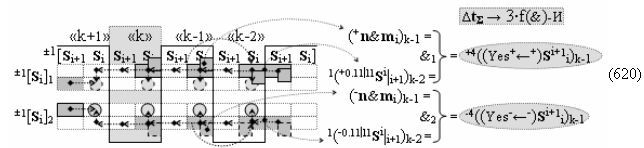
в котором функциональные структуры имеют технологический цикл ∆tΣ → 3∙f(&)-И, соответствующий трем условным логическим функциям f(&)-И. Поскольку если записать структуру логических функций положительного «Комплексного аргумента» 1(+0.11|11Si|i+1)k-2 в виде аналитического выражения (621),
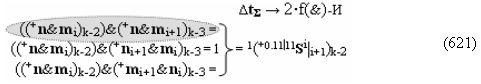
а структуру логических функций условно отрицательного «Комплексного аргумента» 1(-0.11|11Si|i+1)k-2 записать в виде аналитического выражения (622),
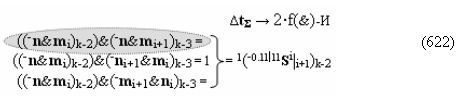
то только эти функциональные структуры имеют технологический цикл ∆tΣ → 2∙f(&)-И, соответствующий двум условным логическим функциям f(&)-И. Но если выполнить преобразование структуры логических функций ««Yes»+,-Аргумент переноса» (620) в соответствии с векторной структурой (623),
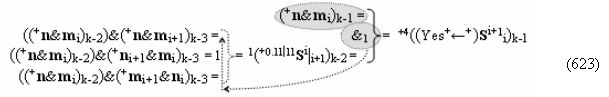
и в соответствии с векторной структурой (624),
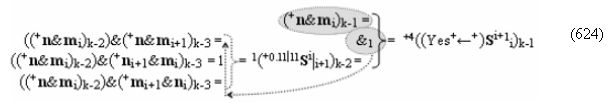
то запишем либо структуру логических функций (625)
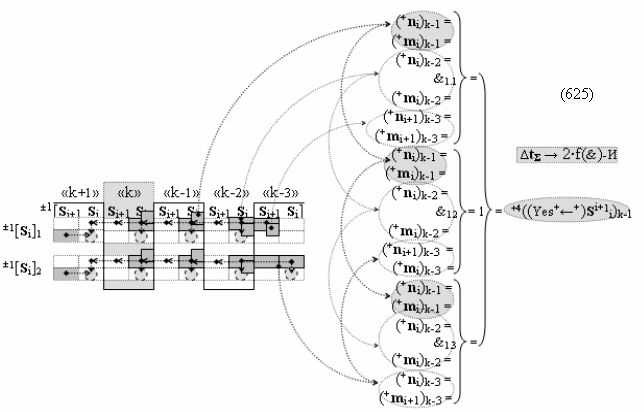
либо минимизированное аналитическое выражение (626)
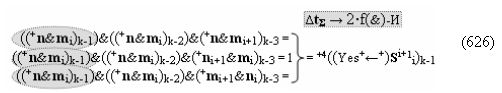
с технологическим циклом ∆tΣ → 2∙f(&)-И, который соответствует двум условным логическим функциям f(&)-И, а также для активизации условно отрицательного аргумента -4((Yes-←-)Si+1 i)k-1 запишем либо структуру логических функций (627)
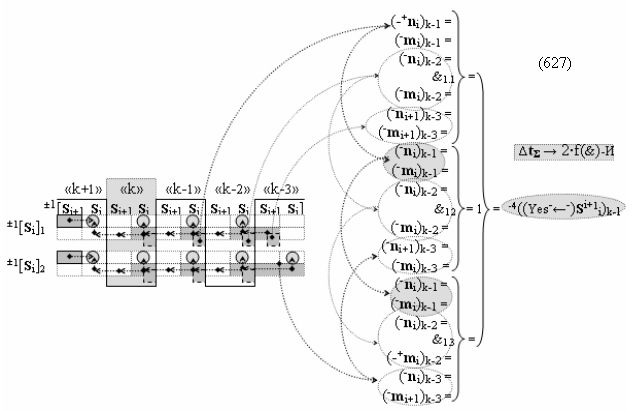
либо минимизированное аналитическое выражение (628).
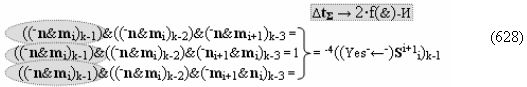
Функциональная структура 5. Последовательное чередование положительных «Комплексных аргументов» 1(+10Si+1 i)k-1 и 1(+0.11|11Si|i+1)k-2 и условно отрицательных «Комплексных аргументов» 1(-10Si+1 i)k-1 и 1(-0.11|11Si|i+1)k-2 в графоаналитическом выражении (629),
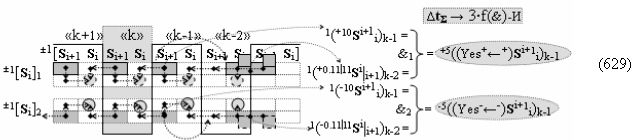
в котором функциональные структуры имеют технологический цикл ∆tΣ → 3∙f(&)-И, соответствующий трем условным логическим функциям f(&)-И. Но если выполнить преобразование структуры логических функций ««Yes»+,-Аргумент переноса» (629) для положительных аргументов 1(+10Si+1 i)k-1 и 1(+0.11|11Si|i+1)k-2 в соответствии с векторной структурой (630),
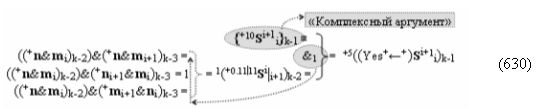
где под входным положительным «Комплексным аргументом» 1{+10Si+1 i}k-1 будем понимать совокупность входных аргументов (631),
поскольку они включены в систему входной логической функции f1(&)-И, а для условно отрицательных аргументов 1(-10Si+1 i)k-1 и 1(-0.11|11Si|i+1)k-2 в соответствии с векторной структурой (632),
где под входным условно отрицательным «Комплексным аргументом» {-10Si+1 i}k-1 будем понимать также совокупность входных аргументов (633),
то запишем для положительного Комплексного аргумента» {+10Si+1 i}k-1 либо минимизированное аналитическое выражение (634)
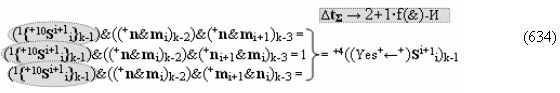
с технологическим циклом ∆tΣ → 2∙f(&)-И, который соответствует трем условным логическим функциям f(&)-И, либо запишем структуру логических функций (635).
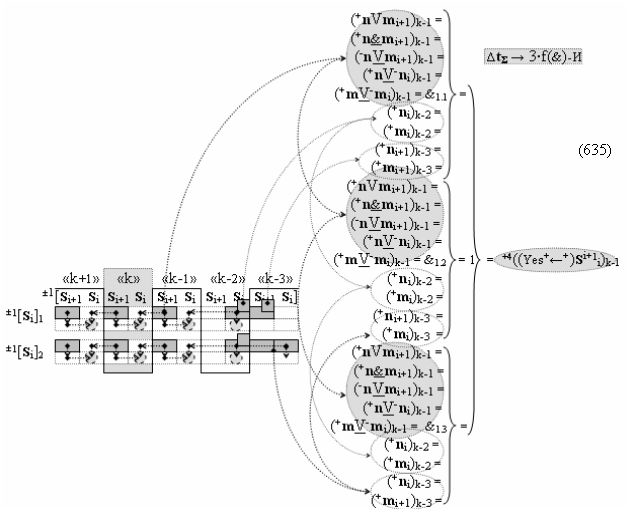
При этом следует отметить, что функциональная структура (635) также имеет технологический цикл ∆tΣ → 3∙f(&)-И, соответствующий трем условным логическим функциям f(&)-И, но этот технологический цикл не изменяется при активизации результирующего условно отрицательного аргумента суммы (-Si)k в условно «k» «Зоне минимизации», если преобразуемый положительный аргумент слагаемого 1(+10Si+1 i)k также запишем в виде «Комплексного аргумента» {+10Si+1 i}k (636).
В результате неминимизированную функциональную структуру, которая активизирует результирующий условно отрицательный аргумент суммы (-Si)k в условно «k» «Зоне минимизации», запишем в виде аналитического выражения (637),
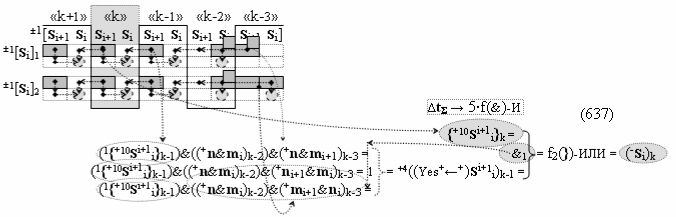
А после переноса функциональной структуры с выходной логической функцией f1(&)-И через систему логической функции f1(})-ИЛИ и после объединения логических функций запишем минимизированную функциональную структуру (638)
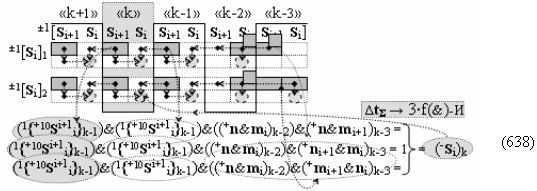
с технологическим циклом ∆tΣ → 3∙f(&)-И, который соответствует трем условным логическим функциям f(&)-И. Аналогичную функциональную структуру, которая активизирует результирующий положительный аргумент суммы (+Si)k в условно «k» «Зоне минимизации», запишем в виде аналитического выражения (638.1),
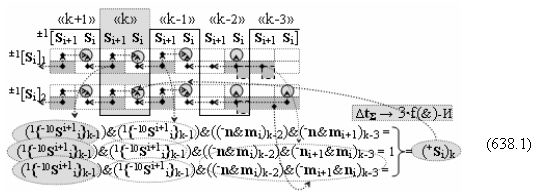
в котором также технологический цикл ∆tΣ → 3∙f(&)-И соответствует трем условным логическим функциям f(&)-И. При этом структуру логических функций, которая активизирует результирующий положительный аргумент суммы (+Si)k в условно «k» «Зоне минимизации», запишем в виде аналитического выражения (639).
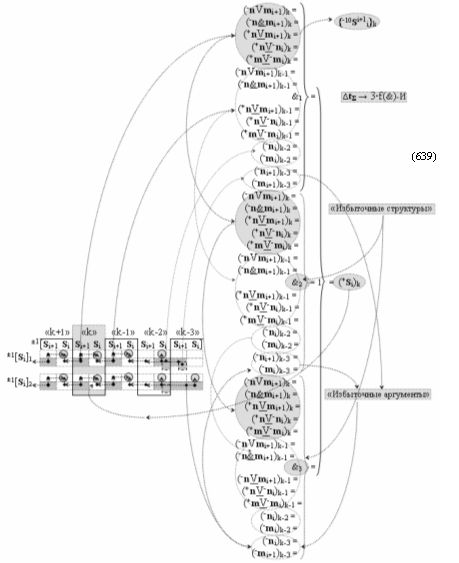
А структуру логических функций, которая активизирует результирующий условно отрицательный аргумент суммы (-Si)k в условно «k» «Зоне минимизации», запишем в виде аналитического выражения (640).
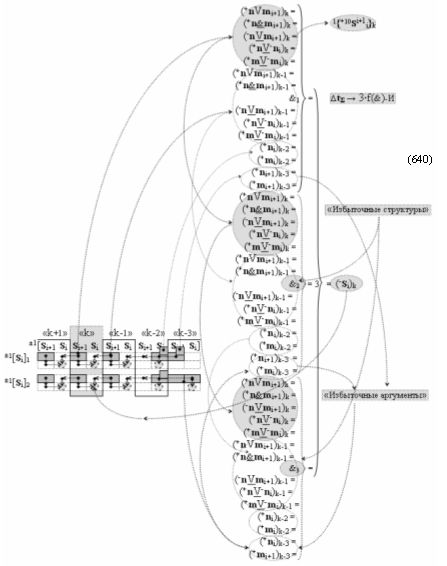
Из анализа графоаналитических выражений (639) и (640) следует, что в систему выходной логической функции f1(})-ИЛИ и f3(})-ИЛИ включены «Избыточные структуры» с выходной логической функцией f2(&)-И и f3(&)-И и включены «Избыточные аргументы» (+ni+1)k-3 и (+mi+1)k-3 условно «k-3» «Зоны минимизации», и функциональную структуру (639) запишем либо в виде аналитического выражения (641)
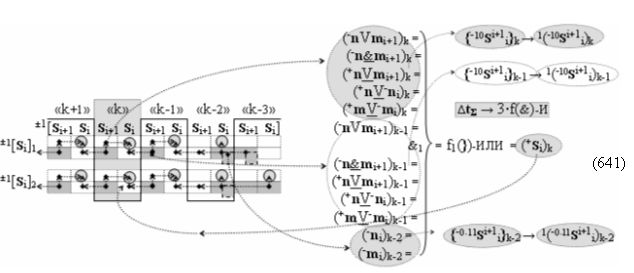
либо в виде минимизированного аналитического выражения (642)
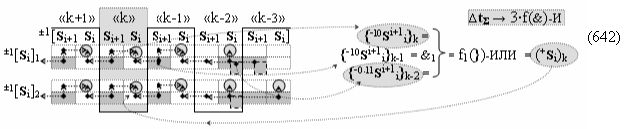
либо в виде неминимизированного аналитического выражения (643),
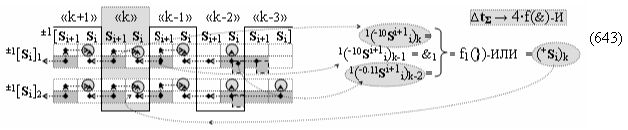
но с технологическим циклом ∆tΣ → 4∙f(&)-И, который соответствует четырем условным логическим функциям f(&)-И. А функциональную структуру (640), активизирующую условно отрицательный аргумент результирующей суммы (-Si)k, запишем либо в виде аналитического выражения (644),
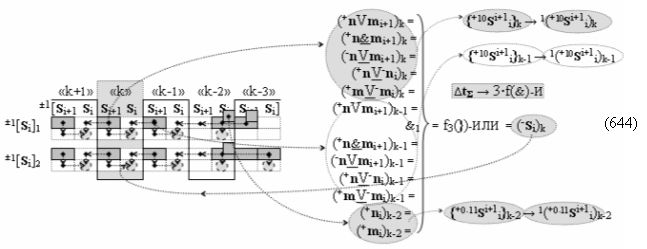
либо в виде минимизированного аналитического выражения (645)
либо в виде минимизированного аналитического выражения (646),
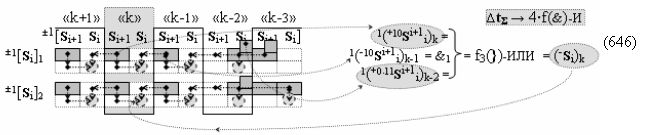
но с технологическим циклом ∆tΣ → 4∙f(&)-И, который соответствует четырем условным логическим функциям f(&)-И. И такая минимизация функциональных структур (639) и (640) возможна, поскольку если вернуться к анализу «Функциональной структуре 1» выражения (601) и (603), записав для аналогичной ситуации функциональную структуру (601) либо в виде графоаналитического выражения (647),
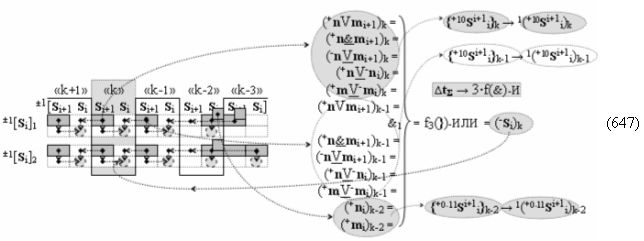
либо в виде минимизированного аналитического выражения (648)
где под системой входных аргументов {-10Si+1 i}k-1 и {-0.11Si+1 i}k-2 с символом -(Yes-←-)3
и функциональной связью (=), которая включена в систему логической функции f1(&)-И, будем понимать одновременную подачу записанных аргументов, активизирующих третий условно отрицательный аргумент -3((Yes-←-)Si+1 i)k-1 локального ««Yes»-Аргумент переноса» с технологическим циклом ∆tΣ → 3∙f(&)-И, соответствующий трем условным логическим функциям f(&)-И;
либо в виде неминимизированного аналитического выражения (649),
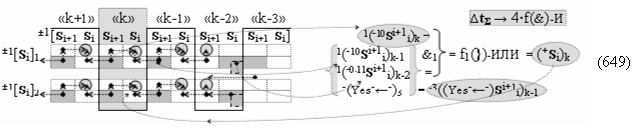
но с технологическим циклом ∆tΣ → 4∙f(&)-И, который соответствует четырем условным логическим функциям f(&)-И, а функциональную структуру (603), активизирующую условно отрицательный аргумент результирующей суммы (-Si)k, записав ее либо в виде графоаналитического выражения (650),
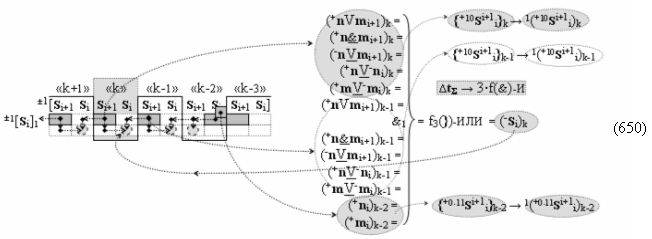
либо в виде минимизированного аналитического выражения (651)
либо в виде минимизированного аналитического выражения (652),
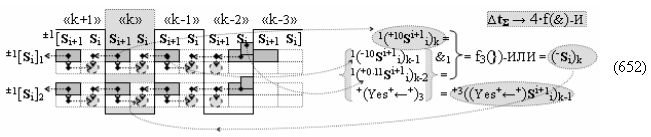
то из графоаналитических выражений (647) - (652) следует, что для корректного преобразования аргументов в условно «k» «Зоне минимизации» достаточно выполнить анализ активности аргументов в условно «k-2» «Зоне минимизации». Но если записать для положительной последовательности аргументов слагаемых (+n&mi)k, (+n&mi)k-1, … (+n&mi)k-g в виде графоаналитического выражения (653)
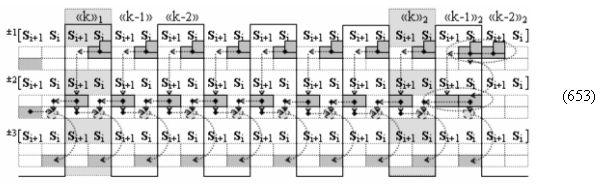
с активным аргументом локального переноса в условно «k-1»2 «Зоне минимизации» и графоаналитическое выражение (654)
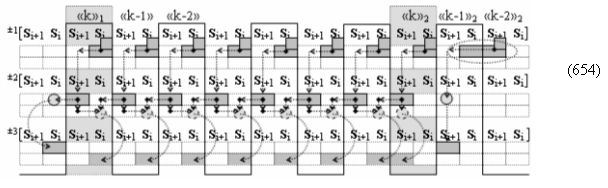
без активного аргумента локального переноса в условно «k-1»2 «Зоне минимизации», а также графоаналитическое выражение (655)
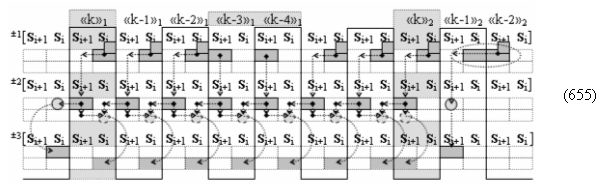
без активного аргумента локального переноса в условно «k-1»2 «Зоне минимизации», но с включенными последовательными положительными аргументами 1(+10Si+1 i)k-3 и 1(+10Si+1 i)k-4 и аналогичные процедуры преобразования условно отрицательных аргументов слагаемых (-n&mi)k, (-n&mi)k-1, … (-n&mi)k-g в виде графоаналитического выражения (656),
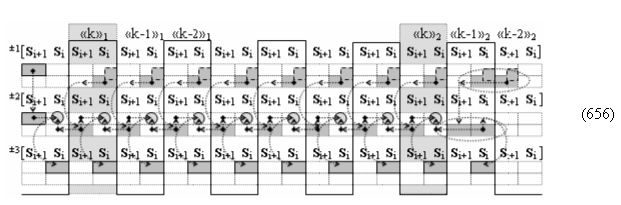
с активным аргументом локального переноса в условно «k-1»2 «Зоне минимизации» и графоаналитическое выражение (657)
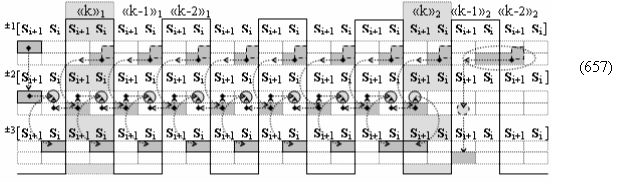
без активного аргумента локального переноса в условно «k-1»2 «Зоне минимизации», а также графоаналитическое выражение (658)
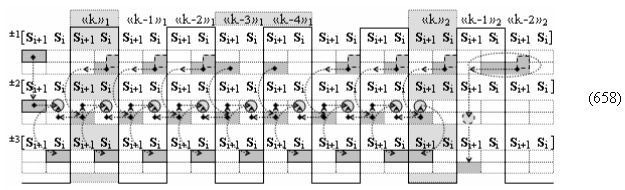
без активного аргумента локального переноса в условно «k-1»2 «Зоне минимизации», но с включенными последовательными условно отрицательными аргументами 1(-10Si+1 i)k-3 и 1(-10Si+1 i)k-4 и аналогичные процедуры преобразования условно отрицательных аргументов слагаемых (-n&mi)k, (-n&mi)k-1, … (-n&mi)k-g в виде графоаналитического выражения (658), то из анализа логико-динамического процесса преобразования аргументов объединенной структуры слагаемых ±[Si]f1(+/-)min и ±[Si]f2(+/-)min следует, что для корректного преобразования аргументов в условно «k» «Зоне минимизации» достаточно выполнить анализ активности аргументов в условно «k-1» «Зоне минимизации». При этом следует отметить, что в графоаналитических выражениях (653) - (658) были проанализированы объединенные структуры слагаемых ±[Si]f1(+/-)min и ±[Si]f2(+/-)min, в структуре которых последовательность аргументов записана одного знака либо положительных аргументов, либо условно отрицательных аргументов, но возможны последовательные объединенные структуры аргументов с чередующими знаками и логика преобразования таких последовательностей имеет «Особенность». И если записать логико-динамический процесс преобразования таких аргументов в виде графоаналитического выражения (659)
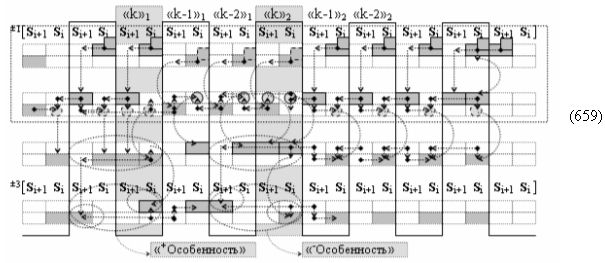
и в виде графоаналитического выражения (660)
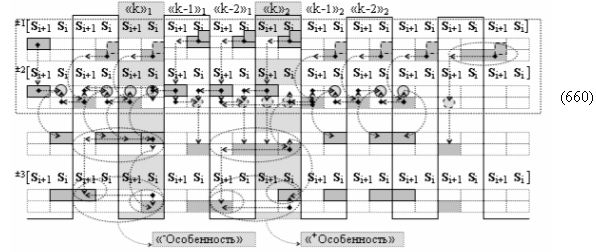
то из анализа векторной структуры логико-динамического процесса преобразования объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min следует, что для корректного преобразования аргументов в условно «k» «Зоне минимизации» не достаточно выполнить анализ активности аргументов в условно «k-1» «Зоне минимизации». А только анализ аргументов в условно «k-2» «Зоне минимизации» позволяет выполнить корректную активизацию аргумента результирующей условно минимизированной суммы ±[Si]f3(+/-)min, поскольку в процедуре преобразования аргументов есть «+Особенность» и «-Особенность». При этом следует отметить, что для корректного преобразования аргументов в условно «k» «Зоне минимизации» может быть два варианта.
Вариант 1. Конкретный аргумент +((Yes+←+)Si+1 i)k-2 и -((Yes-←-)Si+1 i)k-2 положительного локального переноса (661)
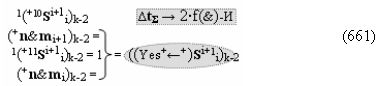
и конкретный аргумент -(Yes-←-)Si+1 i)k-2 условно отрицательного переноса (662)
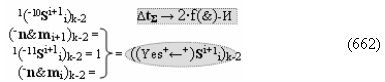
Вариант 2. Не конкретная структура аргументов в условно «k-2» «Зоне минимизации», посредством которой сформирован аргумент локального переноса, а ее знаковая составляющая, т.е. «+Обобщенный аргумент» 1(+VSi+1 i)k-2 выражения (585)
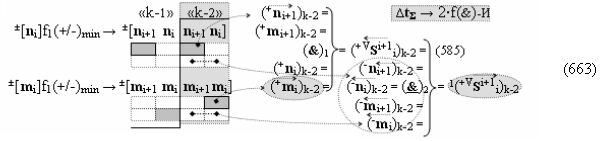
и «-Обобщенный аргумент» 1(-VSi+1 i)k-2 выражения (664).
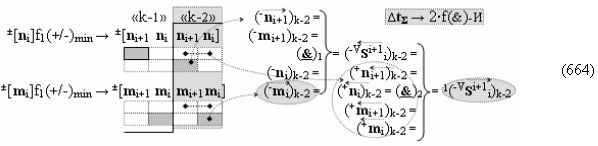
При этом следует отметить, что функциональные структуры (663) и (664) с выходной логической функцией f2(}&)-ИЛИ-НЕ имеют технологический цикл ∆tΣ → 2∙f(&)-И преобразования аргументов, соответствующий двум логическим функциям f(&)-И, но имеют особенность. Поскольку если записать аналитические выражения (663) и (664) в виде структуры логических функций (666),
то после переноса логических функций f2(&)-НЕ и f4(&)-НЕ через систему логических функций f3(})-ИЛИ и f6(})-ИЛИ они изменяют свои логические свойства в выражении (667)
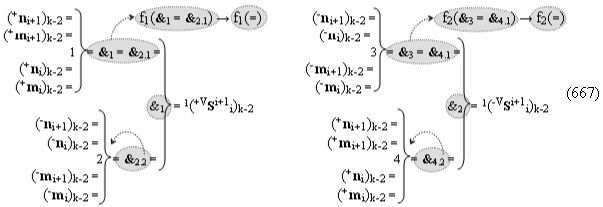
на свойства логических функций f1(&)-И и f2(&)-И, а после замены последовательных логических f1(&1 = &2.1) и f1(&2 = &4.1) на эквивалентные им функциональные связи f1(=) и f2(=) и объединения логических функций f2.2(&)-НЕ и f4.2(&)-НЕ с логическими функциями f2(})-ИЛИ и f4(})-ИЛИ, что приведет к формированию логических функций f1(}&)-ИЛИ-НЕ и f2(}&)-ИЛИ-НЕ в аналитических выражениях (668).
При этом следует отметить, что «Особенностью» аналитических выражений (668) являются выходные логические функции f1(&)-И и f2(&)-И, которые могут являться выходными логическими функциями при активизации результирующего аргумента суммы. А если учесть, что формируется математическая модель сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации», то в этой «Зоне минимизации» должны быть введены входные функциональные структуры выражения (668), которые запишем либо в виде аналитических выражений (669),
либо в виде системы «±Комплексных аргументов» (670).
с технологическим циклом ∆tΣ → 1∙f(&)-И. При этом следует отметить, что технологический цикл системы аргументов (670) меньше технологического цикла функциональных структур (661) и (662) на одну условную логическую функцию f(&)-И, что в конечном счете позволяет сформировать математическую модель сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации» с технологическим циклом ∆tΣ → 3∙f(&)-И, который соответствует трем условным логическим функциям f(&)-И. А при формировании функциональных структур, которые активизируют результирующий аргумент суммы, в качестве входного «±Обобщенного аргумента» будем записывать аргументы ↓1(+VSi+1 i)k-2 и ↓1(-VSi+1 i)k-2. И если вернуться к смысловому содержанию аналогичных аргументов 1(+VSi+1 i)k-2 и 1(-VSi+1 i)k-2, введенных в выражении (533), которые запишем в виде аналитических выражений (671),
то технологический цикл ∆tΣ → 2∙f(&)-И соответствует двум условным логическим функциям f(&)-И, а по своему смысловому содержанию эквивалентны «±Комплексным аргументам» (670). При этом особенностью информационного содержания «±Комплексным аргументам» ↓1(+VSi+1 i)k-2 и ↓1(-VSi+1 i)k-2, как выражения (670) и (671) является положительный аргумент и условно отрицательный аргумент 1(+01Si+1 i)k-2 и 1(-01Si+1 i)k-2, который существенно изменяет логику преобразования аргументов в условно «k» «Зоне минимизации». Поскольку если записать графоаналитическое выражение (672)
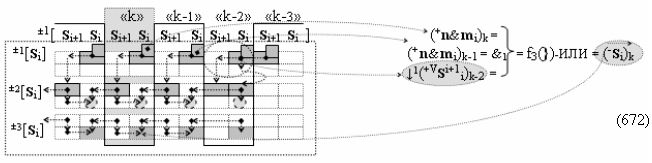
с активным аргументом локальных сквозных переносов и графоаналитическое выражение (673),
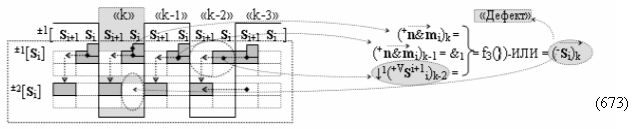
без активного аргумента локальных сквозных переносов, то возникает неопределенность в процедуре формирования аргумента результирующей суммы в последующих «Зонах минимизации». Но если объединенную структуру аргументов слагаемых (673) скорректировать и записать либо в виде графоаналитического выражения (674),
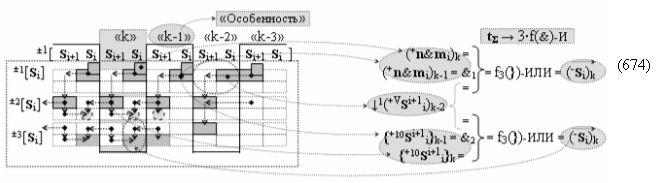
где {+10Si+1 i}k и {+10Si+1 i}k-1 - совокупность аргументов, которые активизируют результирующий аргумент 1(+10Si+1 i)k;
и в виде графоаналитического выражения (675)
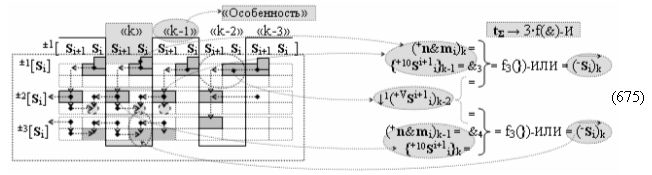
с технологическим циклом tΣ → 3∙f(&)-И, соответствующим трем условным логическим функциям f(&)-И, а в минимизированном аналитическом виде выражения (674) и (675) запишем в виде функциональной структуры (676)
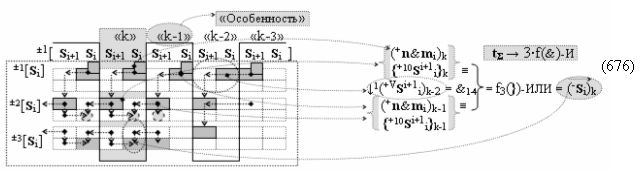
с четырьмя выходными логическими функциями f1-4(&)-И и с технологическим циклом tΣ → 3∙f(&)-И, соответствующим трем условным логическим функциям f(&)-И, либо в виде графоаналитического выражения (677)
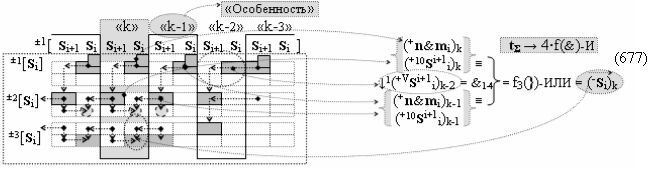
также с четырьмя выходными логическими функциями f1-4(&)-И, но с технологическим циклом tΣ → 4∙f(&)-И, соответствующим четырем условным логическим функциям f(&)-И. Но если записать все возможные активные и неактивные аргументы в условно «k-2» «Зоне минимизации» в виде графоаналитического выражения (678)
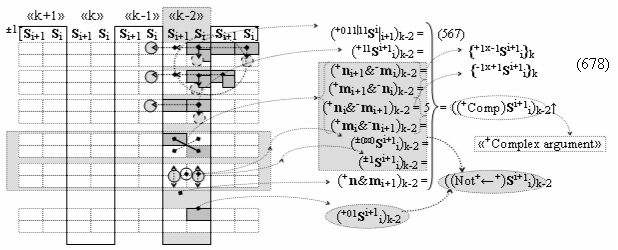
и в виде графоаналитического выражения (679),
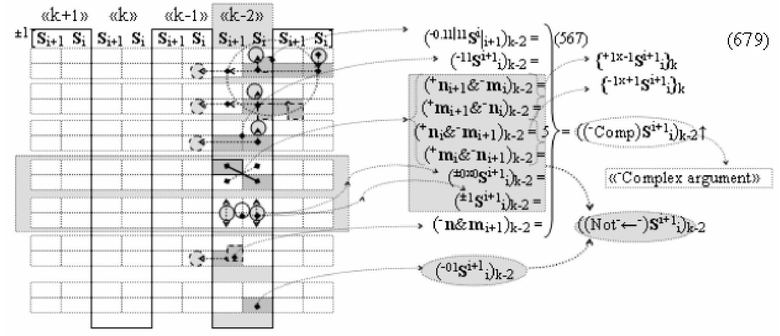
то корректная активизация условно отрицательного аргумента результирующей суммы (-Si)k в выражениях (676) и (677) возможна как при положительном аргументе локального переноса ((Not+←+)Si+1 i)k-2, так и при условно отрицательном аргументе локального переноса ((Not-←-)Si+1 i)k-2. Поскольку если вернуться к анализу процедуры преобразования объединенной структуры аргументов слагаемых (660), записаав его в виде графоаналитического выражения (680),
то преобразование положительных аргументов (+n&mi)kV(+10Si+1 i)k в условно «k» «Зоне минимизации» при активности положительных аргументов (+n&mi)k-1V(+10Si+1 i)k-1 с учетом аргументов локального переноса ((Not+←+)Si+1 i)k-2 и ((Not-←-)Si+1 i)k-2 выражений (678) и (679) не зависит от активности аргументов в условно «k-2» «Зоне минимизации». Поэтому входной аргумент ↓1(+VSi+1 i)k-2 в функциональных структурах (676) и (677) является «Избыточным аргументом», и эти функциональные структуры запишем в виде аналитического выражения (681)
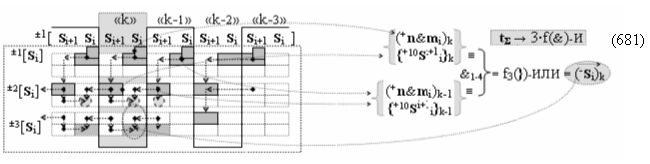
с четырьмя выходными логическими функциями f1-4(&)-И и с технологическим циклом tΣ → 3∙f(&)-И, либо в виде графоаналитического выражения (682)
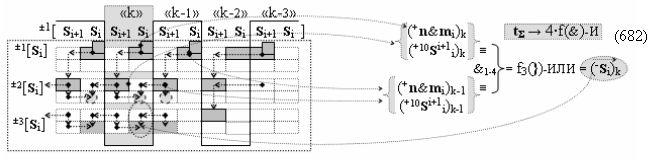
и с технологическим циклом tΣ → 4∙f(&)-И, которые активизируют условно отрицательный результирующий аргумент (-Si)k условно «i» разряда в условно «k» «Зоне минимизации».
Функциональные аналогичные структуры, которые активизируют положительный результирующий аргумент (+Si)k условно «i» разряда в условно «k» «Зоне минимизации» запишем в виде аналитического выражения (683)
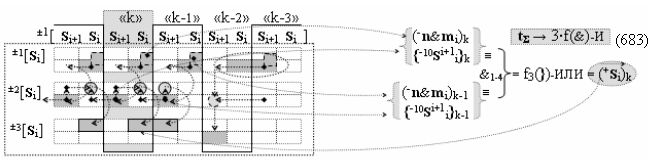
с четырьмя выходными логическими функциями f1-4(&)-И и с технологическим циклом tΣ → 3∙f(&)-И, либо в виде графоаналитического выражения (684)
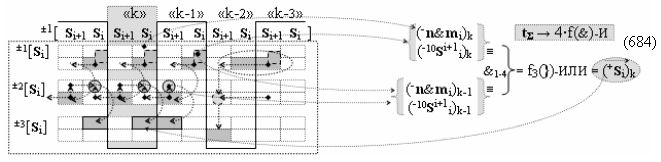
и с технологическим циклом tΣ → 4∙f(&)-И. И функциональные структуры (683) и (684) корректно активизируют положительный результирующий аргумент (+Si)k в условно «i» разряде, поскольку если вернуться к анализу процедуры преобразования объединенной структуры аргументов слагаемых (659), записав его в виде графоаналитическиго выражения (685),
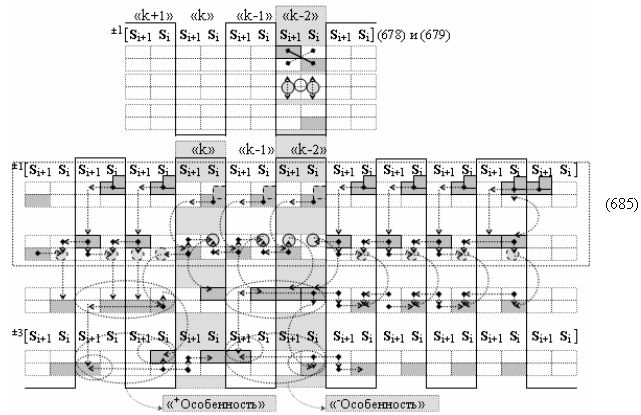
то преобразование условно отрицательных аргументов (-n&mi)kV(-10Si+1 i)k в условно «k» «Зоне минимизации» при активности условно отрицательных аргументов (-n&mi)k-1V(-10Si+1 i)k-1 с учетом аргументов локального переноса ((Not+←+)Si+1 i)k-2 и ((Not-←-)Si+1 i)k-2 выражений (678) и (679) не зависит от активности аргументов в условно «k-2» «Зоне минимизации».
Далее, если вернуться к анализу графоаналитического выражения «Положительного канала сумматора «i+1» разряда» (586) , то с одной стороны из него необходимо исключить выражение (686),
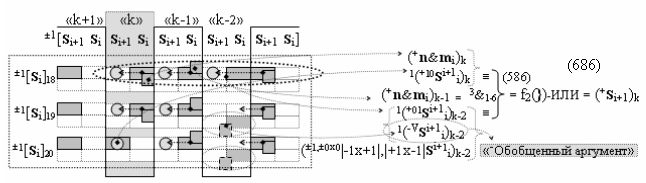
поскольку на основании полученных результатов преобразование положительных аргументов (-n&mi)kV(-10Si+1 i)k в условно «k» «Зоне минимизации» при активности положительных аргументов (-n&mi)k-1V(-10Si+1 i)k-1 активизирован должен быть условно отрицательный аргумент (-Si)k условно «i» разряда в условно «k» «Зоне минимизации». С другой стороны в «Положительный канал сумматора «i+1» разряда» (586) включена функциональная структура (687)
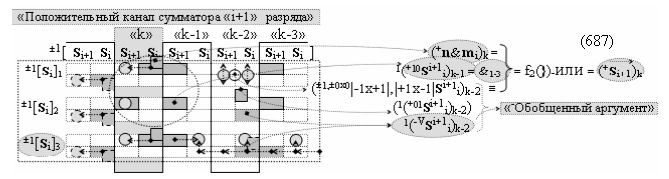
которая с учетом логико-динамического процесса преобразования аргументов (682), который запишем в виде графоаналитического выражения (688)
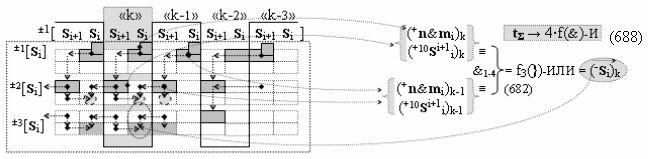
также должна быть исключена из этого канала, поскольку если скорректировать процедуру преобразования аргументов слагаемых (687) с учетом функциональной структуры (688), записав ее в виде графоаналитического выражения (689)
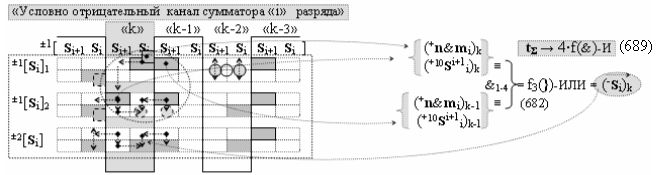
и в виде графоаналитического выражения (690),
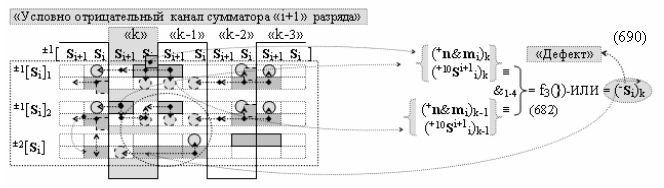
из анализа которых следует, что функциональная структура (690) имеет «Дефект», поскольку не учитывает возможный активный аргумент локального переноса из условно «k-2» «Зоны минимизации», что приводит к активизации двух последовательных аргументов в условно «k-1» «Зоне минимизации». Поэтому для корректного преобразования аргументов слагаемых в систему логических функций f1-4(&)-И функциональных структур (689) и (690) введем дополнительный ««Not»-Аргумент переноса» ((Not-←-)Si+1 i)k-1 и ««Yes»-Аргумент переноса» ((Yes-←-)Si+1 i)k-2 и запишем их в виде аналитического выражения (691)
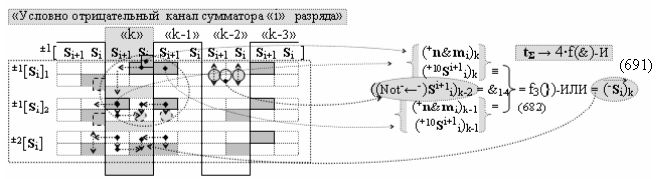
и в виде аналитического выражения (692).
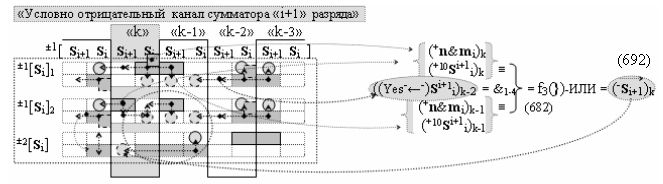
При этом ««Yes»-Аргумент переноса» ((Yes-←-)Si+1 i)k-2 может быть активизирован в следующих ситуациях, которые запишем в виде графоаналитического выражения (693),
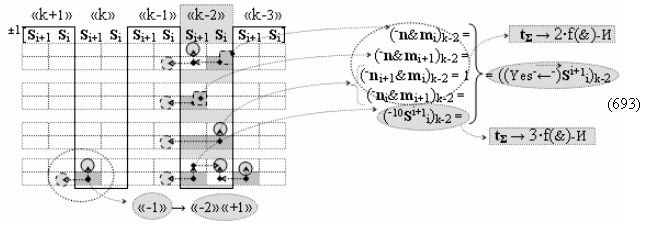
в котором в систему логической функции f1(})-ИЛИ введены все возможные «Комплексные аргументы» локального переноса ((Yes-←-)Si+1 i)k-2 и его активизация будет соответствовать трем условным логическим функциям f(&)-И, что приведет к увеличению технологического цикла tΣ → 5∙f(&)-И процедуры формирования результирующего аргумента условно отрицательной суммы (-Si+1)k выражения (692) до пяти условных логических функций f(&)-И. А для формирования «Комплексного аргумента» локального переноса ((Not-←-)Si+1 i)k-2 в функциональную структуру (693) введем выходную логическую функцию f1(&)-НЕ и запишем ее в виде аналитического выражения (694),
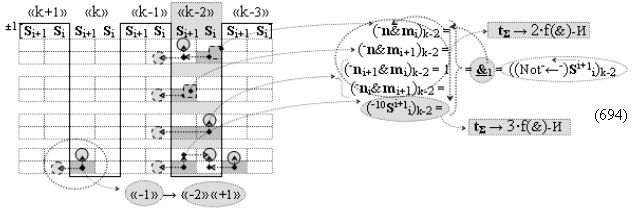
в котором выполним перенос введенной функции через систему логической функции f1(})-ИЛИ. В результате такого переноса изменяются логические свойства логической функции f1(})-ИЛИ на свойства логической функции f1(&)-И в аналитическом выражении (694.1),
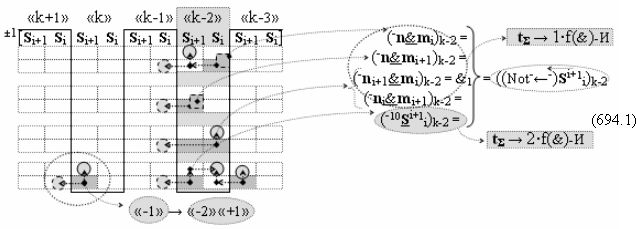
при этом после объединения перенесенной логической функции f1(&)-НЕ с входными «Комплексными аргументами» они также изменили свои логические свойства и символы их формирования записаны с измененным уровнем аналогового сигнала. А если учесть, что аргумент ((Not-←-)Si+1 i)k-2, сформированный посредством логической функции f1(&)-И, должен быть введен в выражении (691) в систему одноименной логической функции, поэтому технологический цикл tΣ → 1∙f(&)-И и tΣ → 2∙f(&)-И функциональной структуры (694) определяется технологическим циклом формирования ее входных аргументов. В результате если записать функциональную структуру (691) в виде аналитического выражения (695),
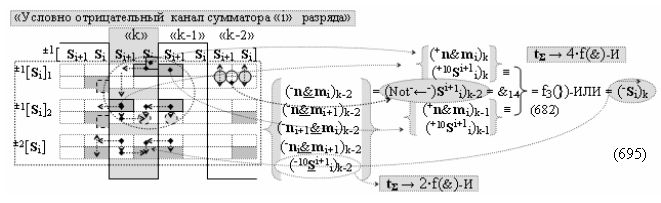
то максимальный технологический цикл tΣ → 4∙f(&)-И активизации результирующего условно отрицательного аргумента (-Si)k будет соответствовать четырем условным логическим функциям f(&)-И. При этом следует отметить, что технологический цикл tΣ → 4∙f(&)-И активизации результирующего условно отрицательного аргумента (-Si)k в функциональной структуре (695) непосредственно связан с положительными входными аргументами (+10Si+1 i)k и (+10Si+1 i)k-1 и условно отрицательным аргументом (-10Si+1 i)k-2 с измененным уровнем аналогового сигнала, технологический цикл tΣ → 2∙f(&)-И которых соответствует двум условным логическим функциям f(&)-И. Поэтому вернемся к дополнительному анализу функциональной структуры (407), записав ее в виде графоаналитического выражения (696)
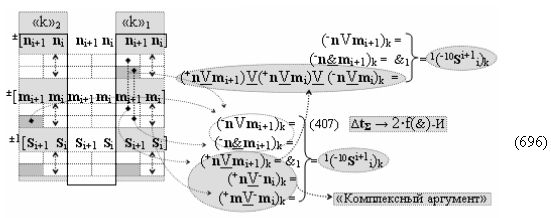
и функциональной структуры (410), записав ее в виде графоаналитического выражения (697)
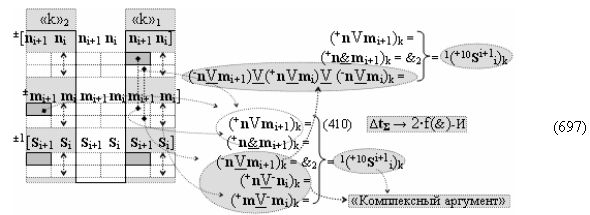
которые в минимизированном виде запишем в виде аналитических выражений (696) и (697) с входным «Комплексным аргументом» (+nVmi+1)V(+nVmi)V (-nVmi)k (698)
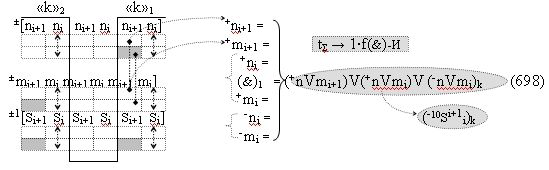
с выходной логической функцией f1(}&)-ИЛИ-НЕ и с входным «Комплексным аргументом» (-nVmi+1)V(+nVmi)V (-nVmi)k (699)
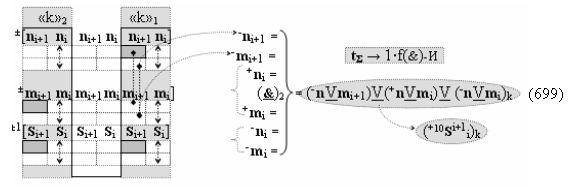
с выходной логической функцией f2(}&)-ИЛИ-НЕ.
Далее, если в функциональную структуру (696), которая активизирует без изменения уровня аналогового сигнала ввести выходную логическую функцию f1(&)-НЕ, то будет сформирована функциональная структура (700),
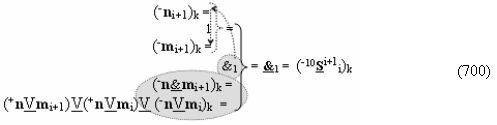
которая активизирует результирующий условно отрицательный аргумент (-10Si+1 i)k с измененным уровнем аналогового сигнала. А если выполнить перенос функциональной структуры с выходной логической функцией f1(&)-И через систему логической функции f1(})-ИЛИ и записать аналитическое выражение (701),
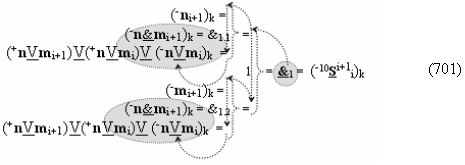
а также выполнить в соответствии с векторной структурой последовательный перенос функции f1(&)-НЕ через систему логической функции f1(})-ИЛИ, f1.1(&)-И и f1.2(&)-И, а затем объединить с входными «Комплексными аргументами», и запишем функциональную структуру (702),
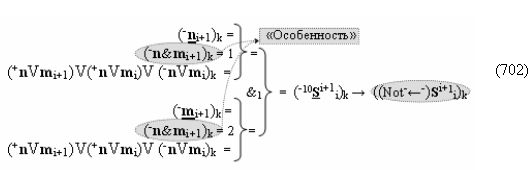
то в системе логических функций f1(})-ИЛИ и f2(})-ИЛИ входной условно отрицательный аргумент (-n&mi+1)k относится к категории «Особенности». Поскольку если функциональную структуру (702) записать для условно «k-2» «Зоны минимизации» в виде выражения (703)
и ввести ее в функциональную структуру (694), записав в виде структуры логических функций (704),
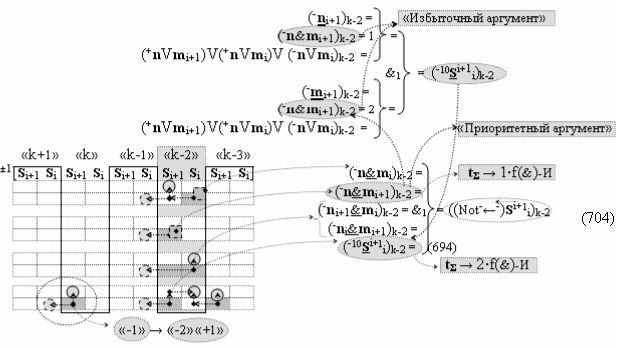
то в системе логических функций f1(})-ИЛИ и f2(})-ИЛИ входной условно отрицательный аргумент (-n&mi+1)k-2, сформированный посредством логической функции f(&)-И, является «Избыточным аргументом», если учесть, что в функциональную структуру (694) включен «Приоритетный аргумент» входной условно отрицательный аргумент (-n&mi+1)k-2, сформированный посредством логической функции f(&)-И-НЕ, и только его активность позволяет активизировать результирующий аргумент ((Not-←-)Si+1 i)k-2. Поэтому функциональную структуру (702) запишем в виде аналитического выражения (705),
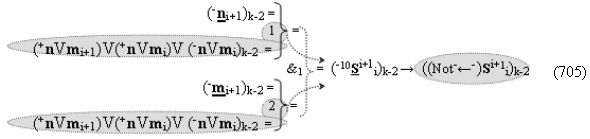
в которой выполним обратный перенос функциональной одноименной структуры с выходной логической функцией f1(})-ИЛИ и f2(})-ИЛИ через систему логической функции f1(&)-И и запишем минимизированное аналитическое выражение (706),
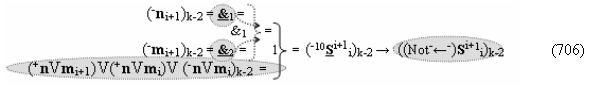
а после переноса логических функций f1(&)-НЕ и f2(&)-НЕ через систему логической функции f1(&)-И запишем либо в виде минимизированного аналитического выражения (707)
с входной логической функцией f1(}&)-ИЛИ-НЕ, либо в виде минимизированного аналитического выражения (708)
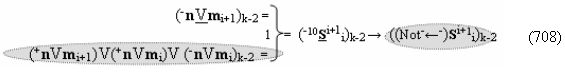
и введем в систему функциональной структуры (694), записав ее в виде графоаналитического выражения (709).
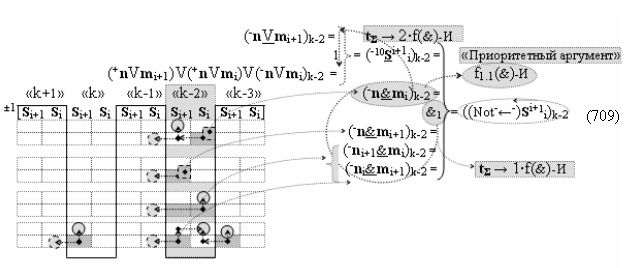
Из анализа входных аргументов функциональной структуры (709) следует, что в нее включены одноименные условно отрицательные аргументы, которые сформированы посредством трех логических функций f1}&)-ИЛИ-НЕ, f(})-ИЛИ и f(&)-И-НЕ, поэтому проведем дополнительный анализ на возможную избыточность условно отрицательных аргументов. А для этого выполним перенос функциональной структуры с выходной дополнительной логической функцией f1.1(&)-И с входным условно отрицательным аргументом (-n&mi)k-2 через систему логической функции f1(})-ИЛИ и запишем структуру логических функций (710),
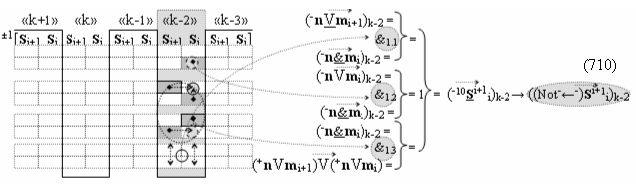
из анализа которой следует, что функциональные входные структуры с выходными логическими функциями f1.1(&)-И - f1.3(&)-И позволяют корректно активизировать результирующий аргумент ((Not-←-)Si+1 i)k-2 при отсутствии локального условно отрицательного аргумента переноса, поэтому функциональную структуру (709) запишем в виде аналитического выражения (711),
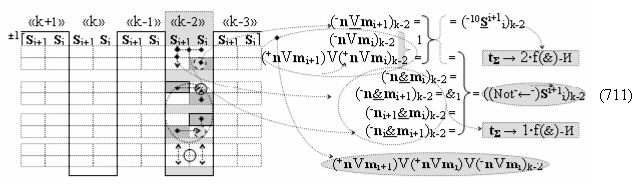
а функциональную структуру «Условно отрицательного канала сумматора «i» разряда» (691) запишем в виде не минимизированного аналитического выражения (712),
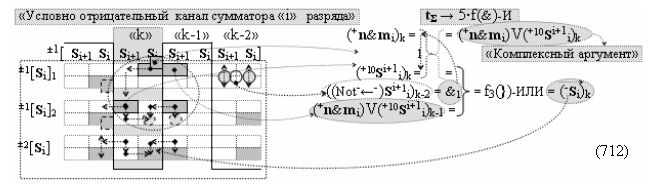
где (+n&mi)V(+10Si+1 i)k и +n&mi)V(+10Si+1 i)k-1 - «Комплексный аргумент» условно «k» и «k-1» «Зоны минимизации» с технологическим циклом tΣ → 5∙f(&)-И пять условных логических функций f(&)-И. Но функциональная структура (712) может быть скорректирована до технологического цикла tΣ → 4∙f(&)-И четыре условные логические функции f(&)-И, если выполнить перенос логической функции f1(&)-И через систему входной логической функции f1(})-ИЛИ, но целесообразно на первом этапе синтеза функционально законченной математической модели сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации» структуру логических функций (712) не минимизировать по технологическому циклу, а записать в виде минимизированного аналитического выражения (713).
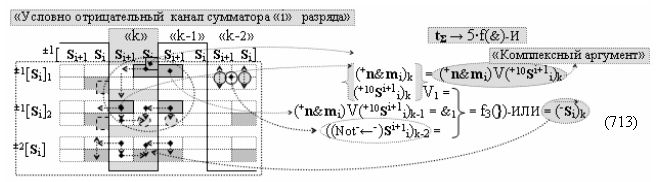
Поскольку на уровне технологического цикла tΣ → 5∙f(&)-И пять условных логических функций f(&)-И с одной стороны минимизировано число функциональных структур для возможных различных преобразований конкретного аргумента в условно «k» «Зоне минимизации», с другой стороны используемая аналитическая форма записи различных «Комплексных аргументов», совмещенная с графоаналитической структурой логико-динамического процесса преобразования аргументов слагаемых ±[Si]f1(+/-)min, имеет вполне простое смысловое содержание, которое позволит сформировать функционально законченную математическую модель сумматора ±f1(ΣRU)min условно «k-1» «Зоны минимизации». Так, в частности, аналитическая форма записи «Комплексного аргумента» (+n&mi)V(+10Si+1 i)k, который включает две позиционные структуры аргументов и логика их преобразования соответствует одной арифметической аксиоме «+1» → «+2»«-1», поскольку эти аргументы имеют эквивалентное «информационное содержание», а также введенный «Комплексный аргумент» ((Not-←-)Si+1 i)k-2 условно отрицательного локального переноса с минимизированным смысловым содержанием позволяет исключить достаточно большое число возможных вариантов такого переноса, которые включает функциональная структура (711),
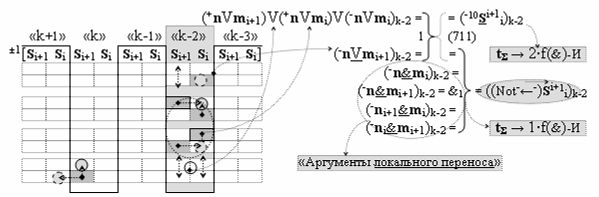
активизирующая результирующий условно отрицательный аргумент ((Not-←-)Si+1 i)k-2, аналогичное «информационное качество» имеет и условно отрицательный «Комплексный аргумент» ((Yes-←-)Si+1 i)k-2 в графоаналитическом выражении (693).
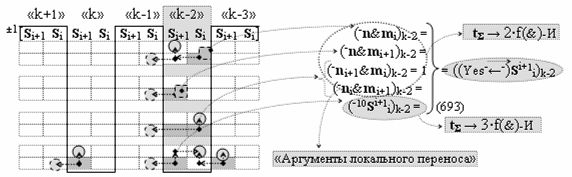
При этом аналогичное «информационное качество» имеет и положительный аргумент ((Not+←+)Si+1 i)k-2 в функциональной структуре (714),
который активен при неактивности положительного аргумента ((Yes+←+)Si+1 i)k-2 локального переноса функциональной структуры (715).
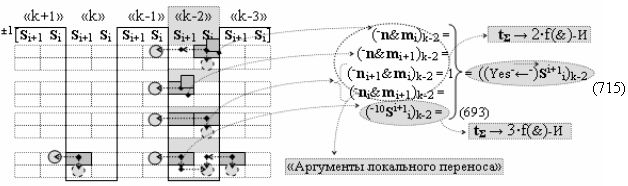
Далее, если вернуться к дополнительному анализу функциональной структуры (713), записав ее в виде графоаналитического выражения (716)
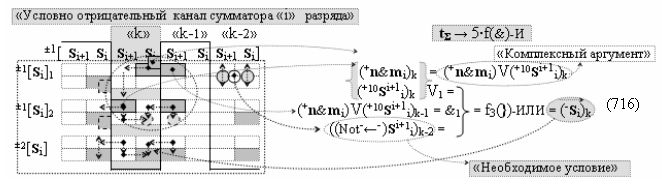
то при активности положительного «Комплексного аргумента» (+n&mi)V(+10Si+1 i)k и (+n&mi)V(+10Si+1 i)k-1 в систему логической функции f1(&)-И включен условно отрицательный аргумент ((Not-←-)Si+1 i)k-2 «Необходимого условия». Поскольку если записать логико-динамический процесс преобразования объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min с активным положительным аргументом (+n&mi)V(+10Si+1 i)k в условно «k» «Зоне минимизации» и активным условно отрицательным аргументом ((Yes-←-)Si+1 i)k-2 в условно «k-2» «Зоны минимизации» в виде графоаналитического выражения (717),
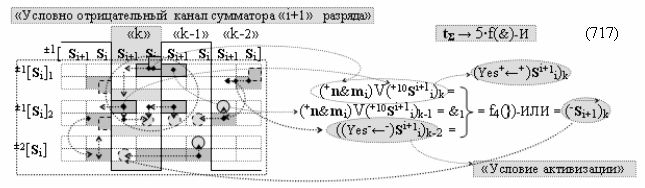
то в данной ситуации активизирован будет условно отрицательный аргумент результирующей суммы (-Si+1)k условно «i+1» разряда и он активизируется только при активном условно отрицательном аргументе ((Yes-←-)Si+1 i)k-2. Поскольку если записать логико-динамический процесс преобразования объединенной структуры аргументов слагаемых ±[Si]f1(+/-)min с активным аргументом (+n&mi)V(+10Si+1 i)k в условно «k» «Зоне минимизации» и с активным положительным «Комплексным аргументом» ((Yes+←+)Si+1 i)k-2 в условно «k-2» «Зоне минимизации» в виде графоаналитического выражения (718),
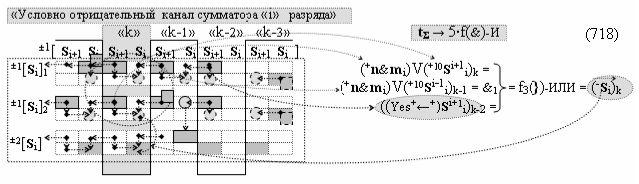
то в данной ситуации, также как и в графоаналитическом выражении (716)
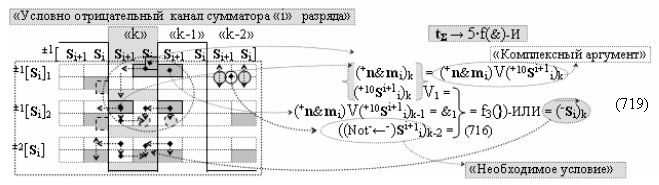
активизирован будет условно отрицательный аргумент результирующей суммы (-Si)k условно «i» разряда. Поэтому входные аргументы ((Yes+←+)Si+1 i)k-2 и ((Not-←-)Si+1 i)k-2 функциональных структур (718) и (719) должны быть объединены в системе логической функции f2(})-ИЛИ, функциональные структуры записаны в виде аналитического выражения (720),
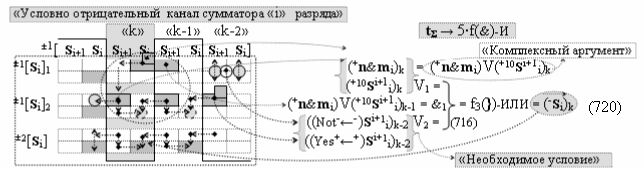
Функциональную аналогичную структуру имеет и «Положительный канал сумматора «i» разряда» и ее запишем в виде аналитического выражения (721)
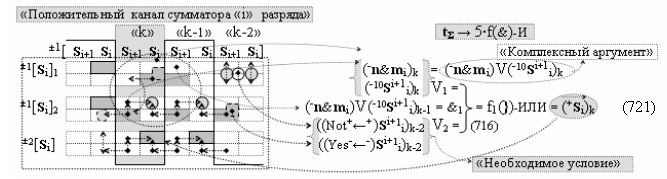
и аналогичную структуру имеет и «Положительный канал сумматора «i+1» разряда» и ее в соответствии с выражением (717)
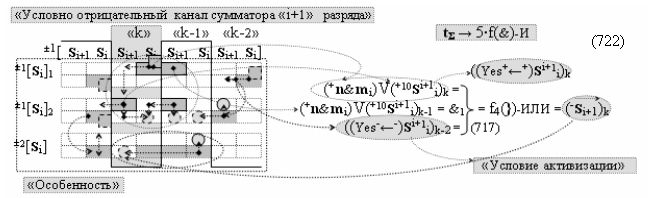
запишем в виде аналитического выражения (723)
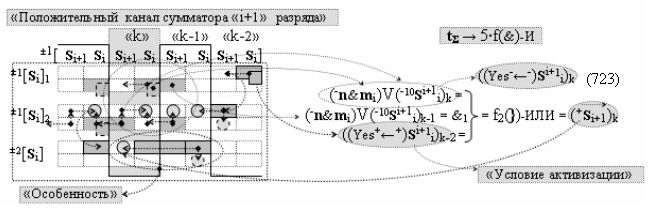
При этом следует отметить, что процедура преобразования аргументов слагаемых в выражении (722) и (723) с чередующимися аргументами ((Yes+←+)Si+1 i)k и ((Yes-←-)Si+1 i)k имеет «Особенность» активизации аргументов результирующей суммы в условно «k» «Зоне минимизации» и в условно «k-1» «Зоне минимизации», если записать процедуру преобразования аргументов (+n&mi)V(+10Si+1 i)k и ((Yes-←-)Si+1 i)k-1 в виде графоаналитического выражения (724),
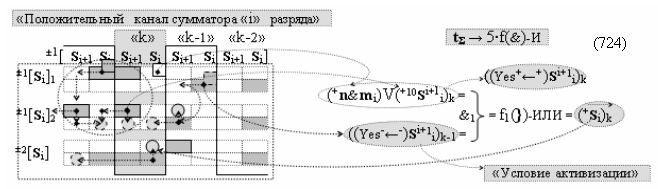
то в данной ситуации будет активизирован положительный аргумент результирующей суммы (+Si)k условно «i» разряда. А если записать процедуру преобразования аргументов (-n&mi)V(-10Si+1 i)k и ((Yes+←+)Si+1 i)k-1 в виде графоаналитического выражения (725),
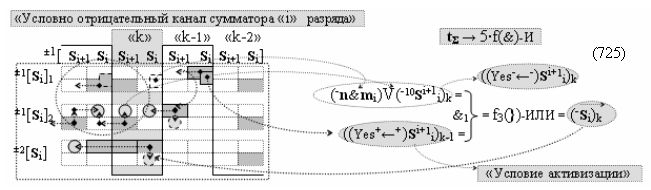
то в данной ситуации будет активизирован условно отрицательный аргумент результирующей суммы (-Si)k условно «i» разряда. При этом следует отметить, что входной «Комплексный аргумент» (+n&mi)V(+10Si+1 i)k и (-n&mi)V(-10Si+1 i)k непосредственно относится к категории аргумента ((Yes+←+)Si+1 i)k и ((Yes-←-)Si+1 i)k локального переноса, в который также включен и аргумент (+11Si+1 i)k и (-11Si+1 i)k с двумя последовательными активными аргументами и аргумент (+10Si+1 i)k и (-10Si+1 i)k, а также аргументы (+n&mi+1)k и (-n&mi+1)k. В результате аргумент ((Yes+←+)Si+1 i)k и ((Yes-←-)Si+1 i)k локального переноса может быть записан в виде выражения (726),
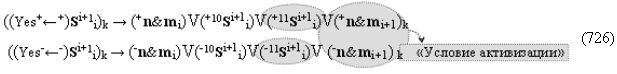
из анализа которого следует, что если в условно «k» «Зоне минимизации» активны аргументы (+11Si+1)k и (-11Si+1)k, то они относятся к «Условию активизации» аргумента локального переноса ((Yes+←+)Si+1 i)k-1 и ((Yes-←-)Si+1 i)k-1 из условно «k-1» «Зоны минимизации» и они включены в функциональную структуру (727)
в общую систему логической функции выражения (567) совместно с «Комплексным аргументом» (±1,±0х0Si+1 i)k. Что касается «Комплексного аргумента» (+11Si+1 i) и (-11Si+1 i), то логика их преобразования имеет свою «Особенность», которая в «Положительном канале сумматора «i» разряда» записана в виде функциональной структуры (688), которую запишем в виде графоаналитического выражения (728),
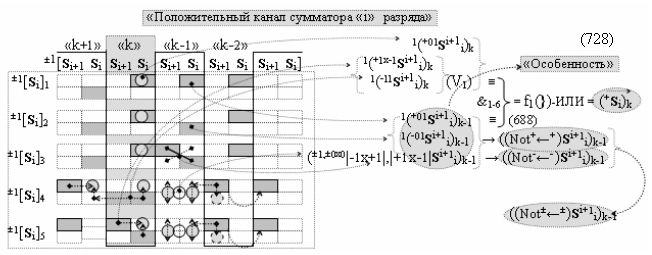
где система входных аргументов ((Not+←+)Si+1 i)k-1 и ((Not-←-)Si+1 i)k-1 и (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1 соответствует «Комплексному аргументу» ((Not+←+)Si+1 i)k-1 и ((Not-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации», а в «Условно отрицательный канал сумматора «i» разряда» записана в виде функциональной структуры (691), которую запишем в виде графоаналитического выражения (729),
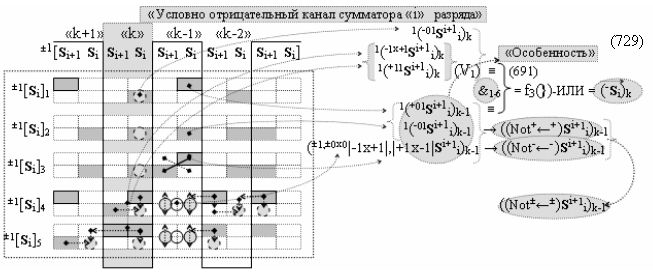
где также система входных аргументов 1(+01Si+1 i)k-1, 1(-01Si+1 i)k-1 и (±1,±0х0|-1х+1|,|+1х-1|Si+1 i)k-1 соответствует «Комплексному аргументу» ((Not+←+)Si+1 i)k-1 и ((Not-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации». А система «Комплексных аргументов» ((Not+←+)Si+1 i)k-1 и ((Not-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации», по существу, относится к категории аргумента ((Not±←±)Si+1 i)k-1, который включает смысловое содержание - «отсутствие любых переносов» из условно «k-1» «Зоны минимизации». При этом следует отметить, что «Комплексный аргумент» ((Not±←±)Si+1 i)k-1 условно «k-1» «Зоны минимизации» формируется в соответствии с функциональной структурой (730)
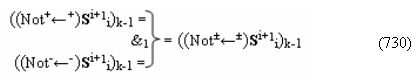
посредством логической функции f1(&)-И, а если записать функциональную структуру условно «k-1» «Зоны минимизации», активизирующую условно отрицательный аргумент ((Not-←-)Si+1 i)k-1 в виде графоаналитического выражения (731)
и функциональную структуру условно «k-1» «Зоны минимизации», активизирующую положительный аргумент ((Not+←+)Si+1 i)k-1 в виде графоаналитического выражения (732),
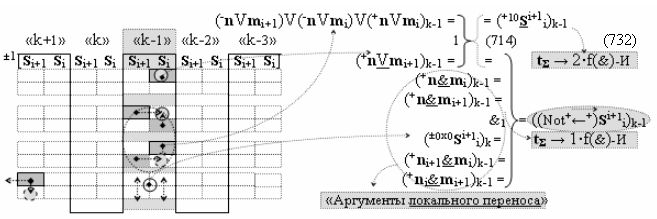
то «Комплексный аргумент» ((Not±←±)Si+1 i)k-1 «отсутствие любых переносов» в условно «k-1» «Зоне минимизации» запишем в виде аналитического выражения (733),
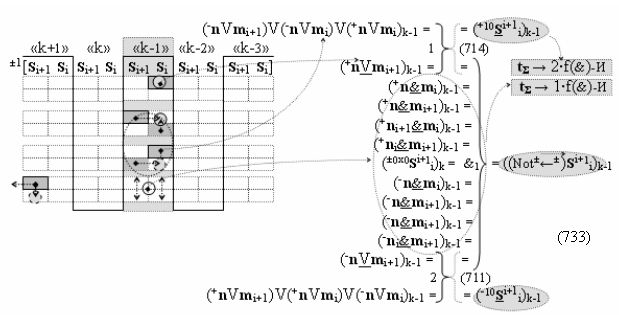
а если учесть, что «Комплексный аргумент» ((Not±←±)Si+1 i)k-1 «отсутствие любых переносов» в функциональной структуре «Положительного канала сумматора «i» разряда» (728) включен в систему логической функции f1-6(&)-И, то после объединения одноименных логических функций в выражении (734),
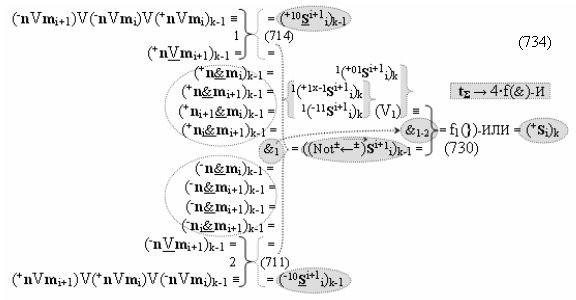
то с одной стороны число функциональных структур минимизировано в три раза, с другой стороны технологический цикл tΣ → 4∙f(&)-И активизации положительного аргумента (+Si)k условно «i» разряда будет соответствовать четырем условным логическим функциям f(&)-И. При этом функциональную структуру «Положительного канала сумматора «i» разряда» (728) с «Комплексным аргументом» ((Not±←±)Si+1 i)k-1 «отсутствие любых переносов» запишем в виде минимизированного аналитического выражения (735),
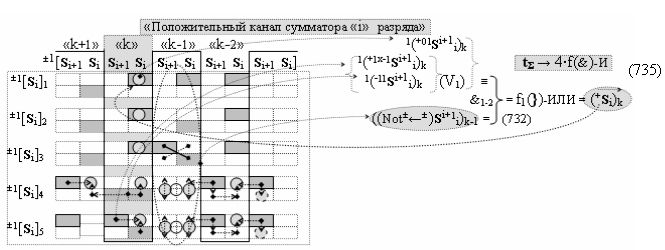
в котором «Комплексный аргумент» ((Not±←±)Si+1 i)k-1 запишем в виде системы входных преобразованных аргументов (736),
аналогично запишем и функциональную структуру «Условно отрицательного канала сумматора «i» разряда» (729) в виде минимизированного аналитического выражения (737).
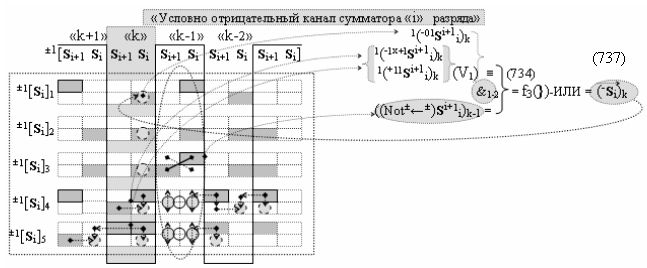
При этом следует отметить, что «Комплексный аргумент» ((Not±←±)Si+1 i)k-1 в виде системы входных преобразованных аргументов (736) функционально принадлежит условно «k-1» «Зоне минимизации», а поскольку формируется математическая модель сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации», то ее запишем либо в виде совокупности аргументов (738)
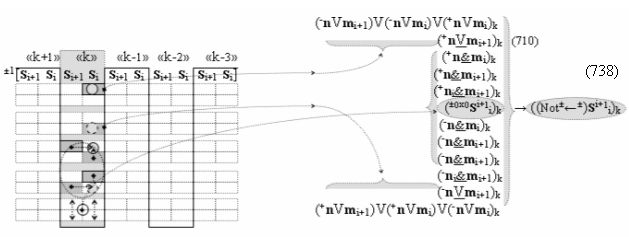
условно «k» «Зоны минимизации», либо в виде функциональной структуры (739).
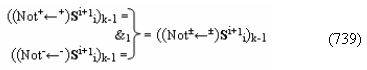
Поскольку логика преобразования аргументов в условно «k» «Зоны минимизации» существенно была изменена в связи с преобразованием «Комплексного аргумента» (+n&mi)V(+10Si+1 i)k и (-n&mi)V(-10Si+1 i)k, который включает две позиционные структуры аргументов и логика их преобразования соответствует арифметической аксиоме «+1» → «+2»«-1» и «-1» ← «-2»«+1», поскольку эти аргументы имеют эквивалентное «информационное содержание», поэтому запишем функциональные структуры для их корректного преобразования при активном аргументе ((Not±←±)Si+1 i)k-1 «отсутствие любых переносов». Для «Положительного канала сумматора «i+1» разряда» и «Условно отрицательного канала сумматора «i+1» разряда» запишем функциональную структуру (740),
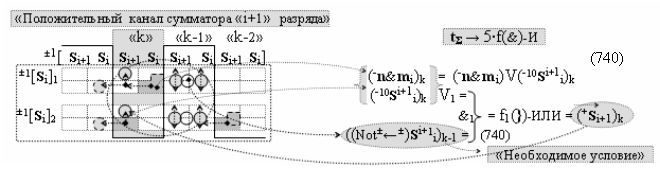
и функциональную структуру (741).
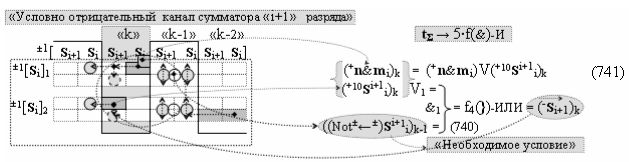
Далее, если вернуться к анализу функциональных структур (721) и (724), записав функциональную структуру (721) в виде аналитического выражения (742),
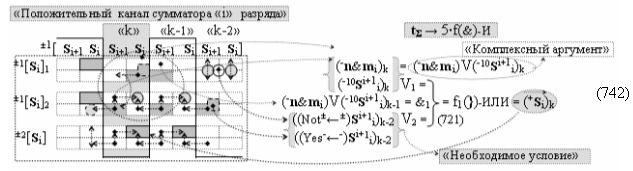
в котором входной аргумент ((Not+←+)Si+1 i)k-2 записан в виде аргумента ((Not±←±)Si+1 i)k-2, функциональную структуру (724) в виде аналитического выражения (743),
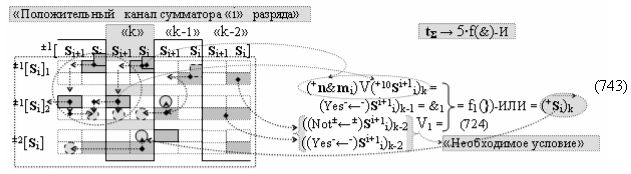
то функциональную структуру «Положительного канала сумматора «i» разряда» на данном этапе его синтеза запишем в виде графоаналитического выражения (744),
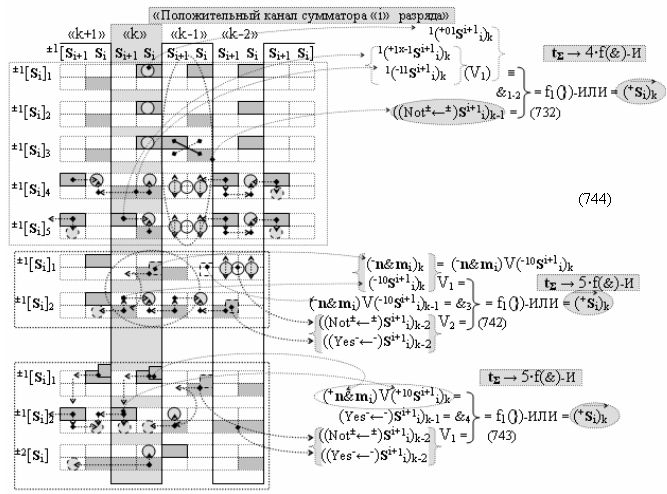
а «Положительный канал сумматора «i+1» разряда» с учетом функциональной структуры (723) и (740) запишем в виде графоаналитического выражения (745).
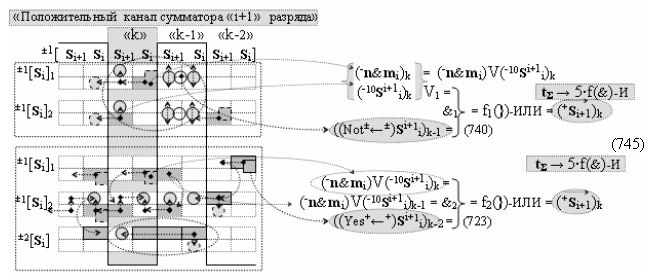
При этом «Условно отрицательный канал сумматора «i» разряда» с учетом функциональных структур (737) и (720), а также функциональной структуры
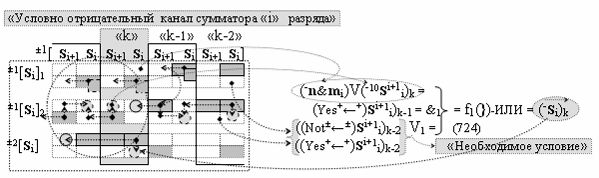
запишем в виде графоаналитического выражения (746),
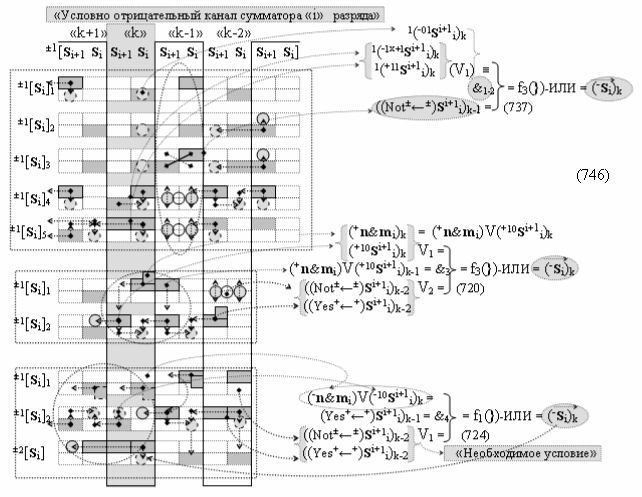
а «Условно отрицательный канал сумматора «i+1» разряда» с учетом функциональных структур (717) и (741) запишем в виде графоаналитического выражения (747).
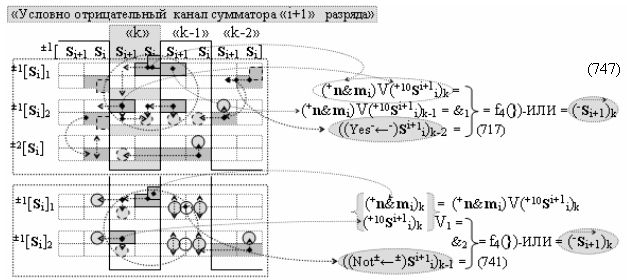
Далее, если вернуться к анализу предварительно сформированной функциональной структуры «Положительного канала сумматора «i» разряда» выражения (586) и функциональной структуры «Условно отрицательного канала сумматора «i» разряда» выражения (588), в которых в качестве отдельной процедуры преобразования объединенной структуры слагаемых ±[Si]f1(+/-)min записана функциональна структура 1(-0.11|11Si|i+1)k = f1(})-ИЛИ = (+Si)k(586), и функциональная структура 1(+0.11|11Si|i+1)k = f3(})-ИЛИ = (-Si)k(588), то учитывая скорректированную логику преобразования аргументов имеет смысл провести дополнительный анализ на корректность этих функциональных структур. А для этого запишем функциональную структуру 1(-0.11|11Si|i+1)k = f1(})-ИЛИ = (+Si)k(586) в виде графоаналитического выражения (748),
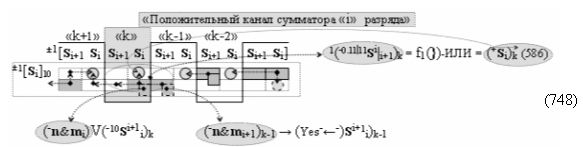
где ((Yes-←-)Si+1 i)k-1 - «аргумент переноса», сформированный посредством функциональной структуры (749);
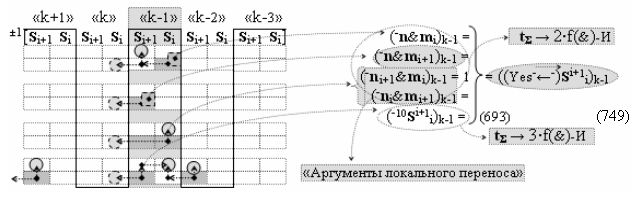
1(-0.11|11Si|i+1)k - «Комплексный аргумент», сформированный посредством функциональной структуры (750);
и запишем функциональную структуру «Положительного канала сумматора «i» разряда» выражения (742) в виде графоаналитического выражения (751),
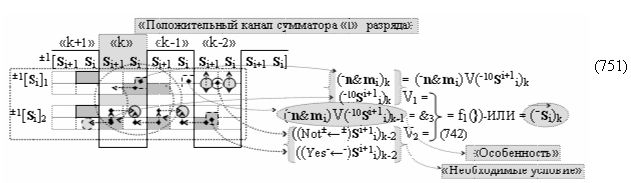
в которой «Особенностью» является входной условно отрицательный аргумент (-n&mi)V(-10Si+1 i)k-1 условно «k-1» «Зоны минимизации» в системе логической функции f3(&)-И и для активизации положительного результирующего аргумента суммы (+Si)k в систему этой функции включены «Необходимые условие» в виде двух аргументов ((Not±←±)Si+1 i)k-2 и ((Yes-←-)Si+1 i)k-2 условно «k-2» «Зоны минимизации». Поскольку если в условно «k-2» «Зоне минимизации» активизирован положительный аргумент ((Yes+←+)Si+1 i)k-1 - «аргумент переноса», то в соответствии с функциональной структурой «Положительного канала сумматора «i+1» разряда» выражения (745)
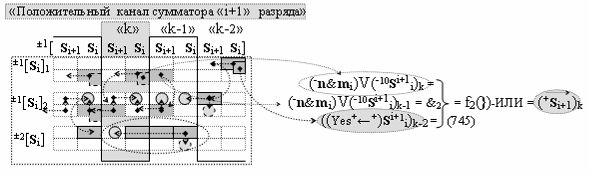
активизирован будет положительный аргумент (+Si+1)k условно «i+1» разряда. А если вернуться к анализу функциональной структуры (748) и с учетом функциональной структуры (750) записать графоаналитическое выражение (752)
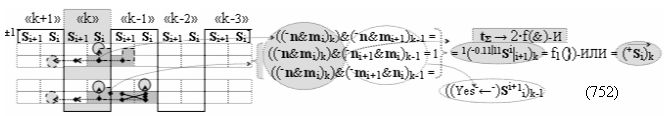
и выполнить перенос «Комплексных аргументов» через систему логической функции f1(})-ИЛИ, то запишем аналитическое выражение (753), (753)
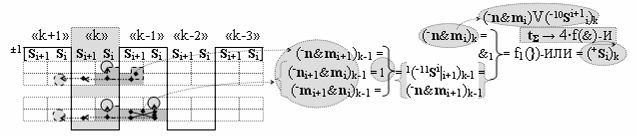
в котором выполним замену входного аргумента (-n&mi)k на «Комплексный аргумент» (-n&mi)V(-10Si+1 i)k и запишем скорректированное аналитическое выражение (754)
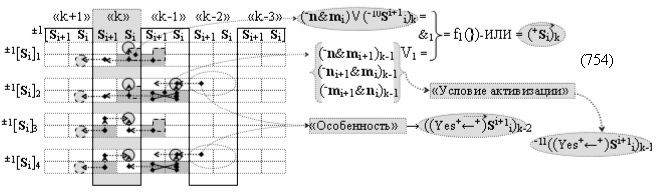
то «Особенностью» функциональной структуры (754) является корректная активизация положительного аргумента суммы (+Si)k при активном положительном «аргументе переноса» ((Yes+←+)Si+1 i)k-2. Поскольку совокупность активных аргументов «Условия активизации», а их в минимизированном виде запишем в виде «Комплексного аргумента» -11((Yes-←-)Si+1 i)k-1 → (-11Si+1 i)k, позволяет в условно «k-1» «Зоне минимизации» активизировать условно минимизированный положительный аргумент результирующей суммы (+Si+1)k-1, и такую активизацию запишем либо в виде графоаналитического выражения (755.1)
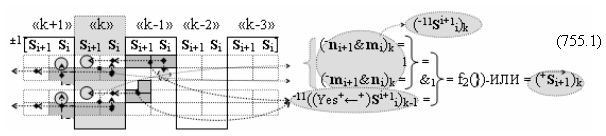
в котором условно отрицательный «Комплексный аргумент» (-11Si+1 i)k записан в виде совокупности аргументов (-ni+1&mi)k и (-mi+1&ni)k, либо в виде графоаналитического выражения (755)
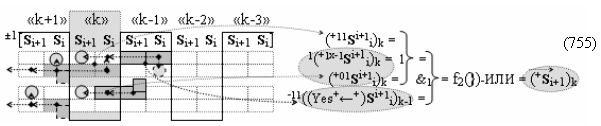
с положительным дополнительным входным аргументом (+01Si+1 i)k и 1(+1х-1Si+1 i)k, которые также активизирует положительный аргумент суммы (+Si+1)k. А если вернуться к анализу функциональной структуры «Положительного канала сумматора «i+1» разряда» выражения (586),
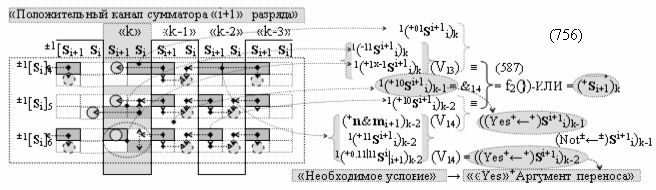
где также активизирован положительный аргумент суммы (+Si+1)k условно «i+1» разряда, то в системе логической функции f1-4(&)-И входной аргумент 1(+10Si+1 i)k-1 в связи с измененной логикой преобразования аргументов относится к категории «+Комплексного аргумента переноса» ((Yes+←+)Si+1 i)k-1, который активизирован в условно «k-1» «Зоне минимизации». При этом следует отметить, что в систему логической функции f1-4(&)-И введен также входной положительный «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k-2 условно «k-2» «Зоны минимизации» в качестве «Необходимого условия», поскольку если в этой «Зоне минимизации» будет активен условно отрицательный «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k-2, то положительный аргумент суммы (+Si+1)k условно «i+1» разряда в соответствии с графоаналитическим выражением (757),
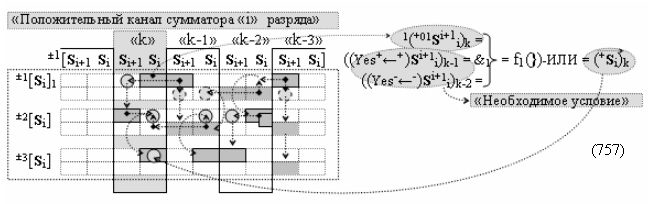
в соответствии с графоаналитическим выражением (757),
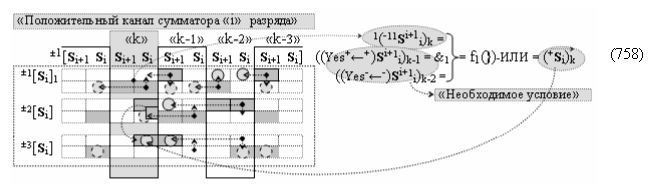
в соответствии с графоаналитическим выражением (758)
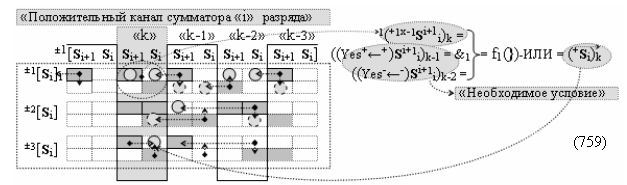
активизированным быть не может, а будет активизирован положительный аргумент суммы (+Si)k условно «i» разряда в соответствии с измененной логикой преобразования аргументов объединенной структуры слагаемых ±[Si]f1(+/-)min. И если выполнить объединение функциональных структур (757) - (759), то запишем минимизированное аналитическое выражение (760),
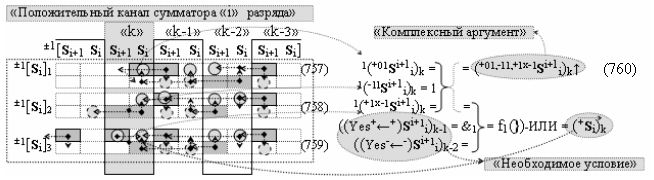
при этом функциональную структуру (756) с учетом комбинационного «Комплексного аргумента» (+01,-11,+1х-1Si+1 i)k выражения (760) запишем в виде аналитического выражения (761).
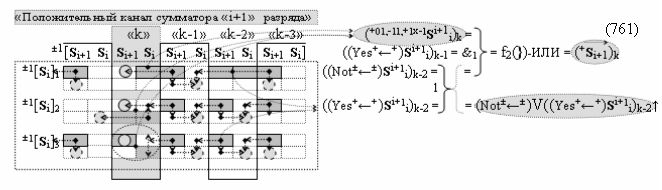
Поскольку сформированная функциональная структура (760) корректно активизирует результирующий аргумент суммы (+Si)k условно «i» разряда, поэтому введем ее в «Положительный канал сумматора «i» разряда» (744) и запишем совместное графоаналитическое выражение (762),
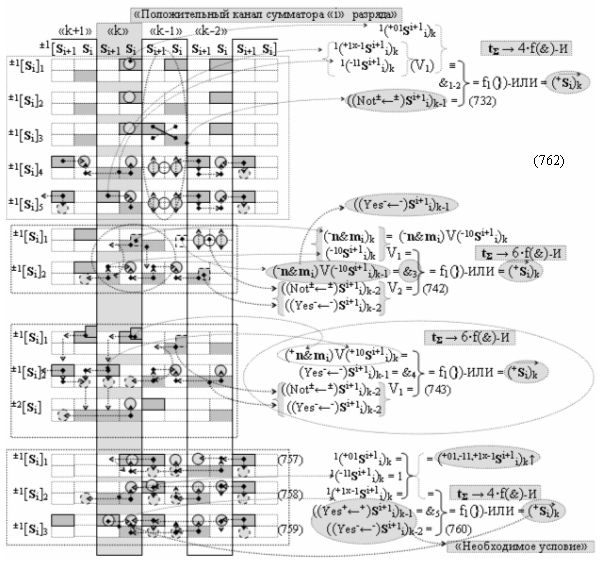
при этом следует отметить, что в функциональной структуре с выходной логической функцией f3(&)-И входной условно отрицательный аргумент (-n&mi)V(-10Si+1 i)k-1 может быть заменен на «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации» и в этом случае при активности входного аргумента 1(-11Si+1 i)k-1 в этой зоне также будет активизирован результирующий аргумент суммы (+Si)k условно «i» разряда. А «Положительный канал сумматора «i+1» разряда» с учетом функциональной структуры (755) и (761) запишем в виде графоаналитического выражения (763),
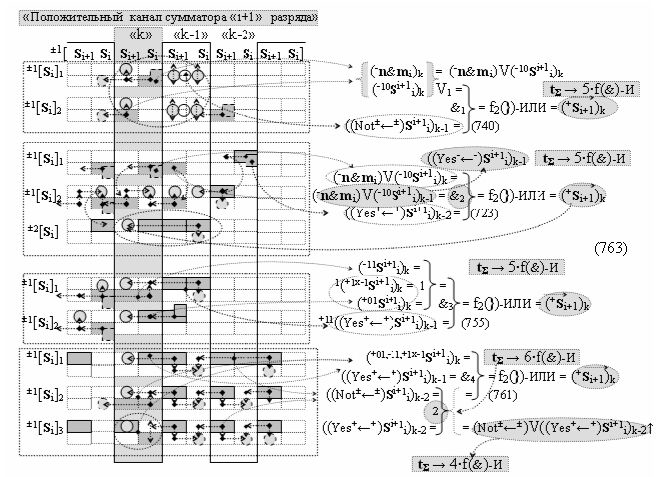
в котором также в функциональной структуре с выходной логической функцией f2(&)-И входной условно отрицательный аргумент (-n&mi)V(-10Si+1 i)k-1 может быть заменен на «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации» и в этом случае при активности входного аргумента 1(-11Si+1 i)k-1 в этой зоне также будет активизирован результирующий аргумент суммы (+Si+1)k условно «i+1» разряда. При этом следует отметить, что технологический цикл tΣ → 6∙f(&)-И процедуры активизации результирующего аргумента суммы (+Si+1)k условно «i+1» разряда будет соответствовать шести условным логическим функциям f(&)-И, поскольку активизация «Комплексного аргумента» (Not±←±)V((Yes+←+)Si+1 i)k-2 соответствует технологическому циклу tΣ → 4∙f(&)-И, который соответствует четырем условным логическим функциям f(&)-И. А для сокращения технологического цикла tΣ → 4∙f(&)-И процедуры активизации результирующего аргумента суммы (+Si+1)k условно «i+1» разряда до четырех условных логических функций f(&)-И необходимо функциональную структуру с выходной логической функцией f2(&)-И записать в виде аналитического выражения (764)
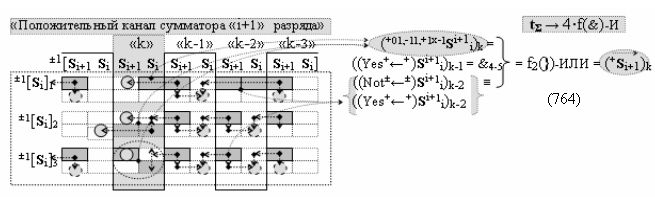
с двумя функциональными структурами и с входными аргументами ((Not±←±)Si+1 i)k-2 и ((Yes+←+)Si+1 i)k-2.
Функциональные аналогичные структуры должны быть введены в «Условно отрицательный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i+1» разряда», поскольку положительные и условно отрицательные объединенные структуры аргументов слагаемых ±[Si]f1(+/-)min равновероятны, поэтому структуру логических функций «Положительного канала сумматора «i» разряда» (760)
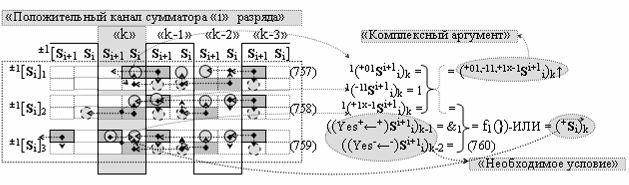
для «Условно отрицательного канала сумматора «i» разряда» запишем в виде аналитического выражения (765).
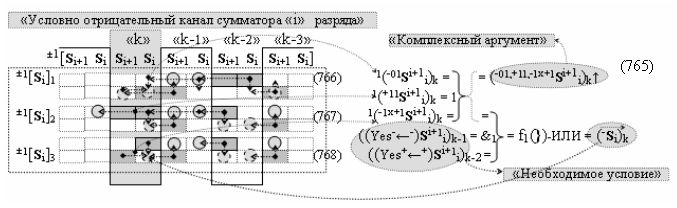
поскольку логико-динамический процесс преобразования входного условно отрицательного аргумента 1(-01Si+1 i)k может быть записан в виде графоаналитического выражения (766),
логико-динамический процесс преобразования входного положительного аргумента 1(+11Si+1 i)k может быть записан в виде графоаналитического выражения (767),
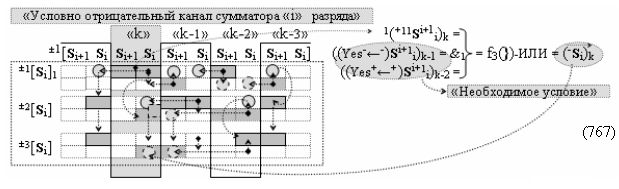
а логико-динамический процесс преобразования входного аргумента 1(-1х+1Si+1 i)k может быть записан в виде графоаналитического выражения (768),
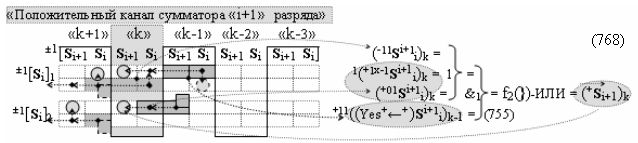
А структуру логических функций «Положительного канала сумматора «i+1» разряда» (755)
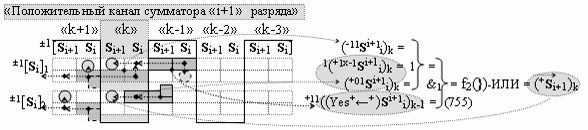
для «Условно отрицательного канала сумматора «i+1» разряда» запишем в виде аналитического выражения (769)
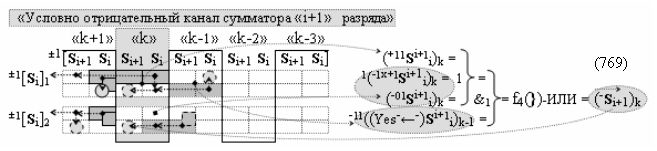
и структуру логических функций «Положительного канала сумматора «i+1» разряда» (761)
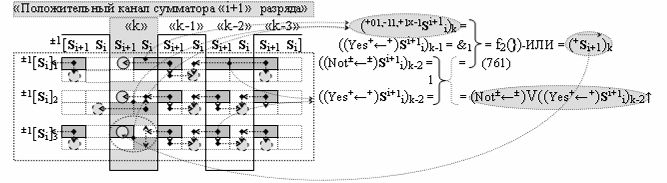
для «Условно отрицательного канала сумматора «i» разряда» запишем либо в виде аналитического выражения (770)
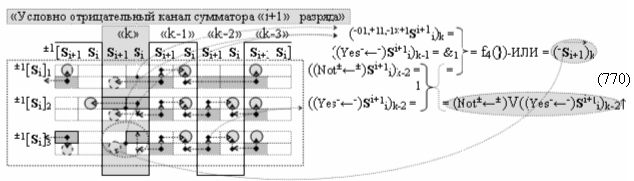
с технологическим циклом tΣ → 6∙f(&)-И преобразования аргументов слагаемых шесть условных логических функций f(&)-И, либо в виде минимизированного аналитического выражения (771)
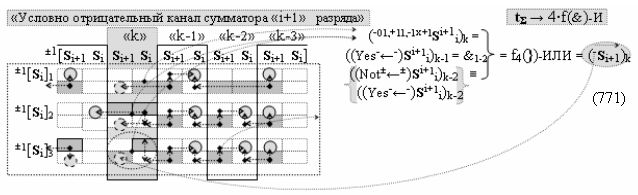
с технологическим циклом tΣ → 4∙f(&)-И преобразования аргументов слагаемых четыре условные логические функции f(&)-И. В результате «Условно отрицательный канал сумматора «i» разряда» выражения (746) с учетом функциональной структуры (765) запишем в виде графоаналитического выражения (772)
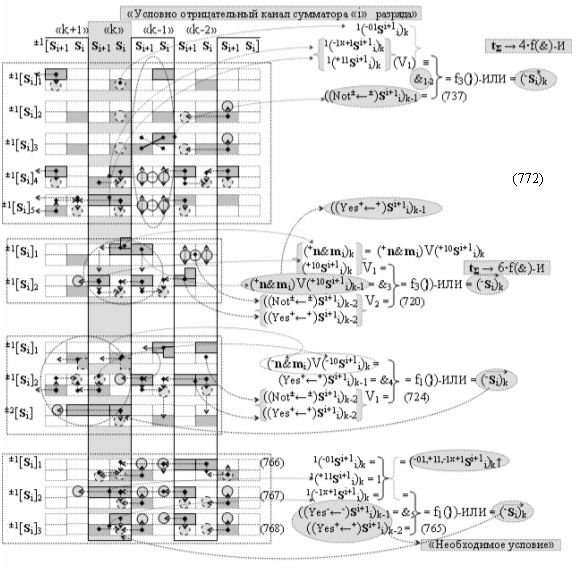
где также в функциональной структуре с выходной логической функцией f3(&)-И входной условно отрицательный аргумент (+n&mi)V(+10Si+1 i)k-1 может быть заменен на «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k-1 условно «k-1» «Зоны минимизации» и в этом случае при активности входного аргумента 1(+11Si+1 i)k-1 в этой зоне будет активизирован результирующий условно отрицательный аргумент суммы (-Si)k условно «i» разряда. При этом «Условно отрицательный канал сумматора «i+1» разряда» выражения (747) с учетом функциональных структур (769) и (771) запишем в виде графоаналитического выражения (773).
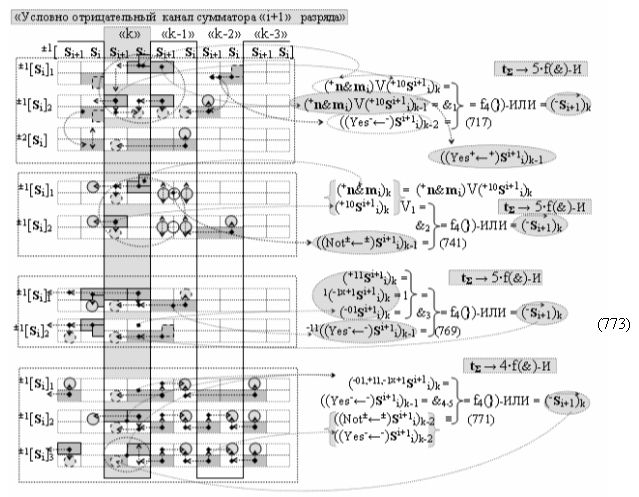
Далее, если вернуться к функциональной структуре «Положительного канала сумматора «i» разряда» (567), записав ее в виде графоаналитического выражения (774),
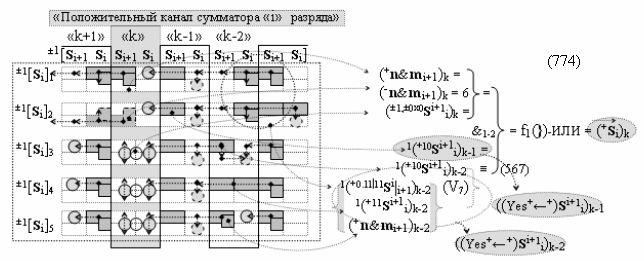
в котором с одной стороны выполнить указанные эквивалентные замены входных аргументов, с другой стороны скорректируем логико-динамический процесс преобразования объединенных структур аргументов слагаемых ±[Si]f1(+/-)min, то запишем скорректированное графоаналитическое выражение (775).
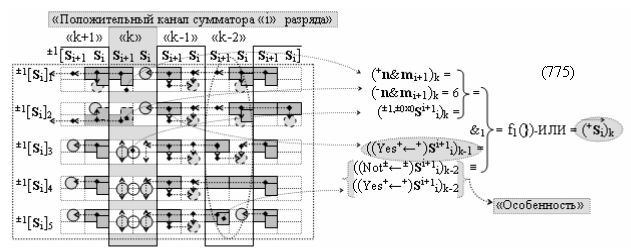
При этом следует отметить, что «Особенностью» функциональной структуры (775) является два входных «Комплексных аргумента» ((Not±←±)Si+1 i)k-2 и ((Yes+←+)Si+1 i)k-2 условно «k-2» «Зоны минимизации», при активности которых может быть активизирован положительный результирующий аргумент (+Si)k условно «i» разряда. Поскольку если записать графоаналитическое выражение (776),
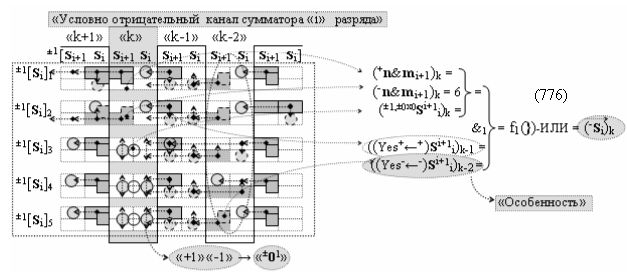
то в условно «i» разряде «k» «Зоны минимизации» одновременно активизирован как положительный аргумент (+Si)k, так и условно отрицательный аргумент (-Si)k, которые формируют активный логический ноль «+1»«-1» → «±01». Поэтому только неактивность «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k-2 в условно «k-2» «Зоне минимизации» может быть активизирован положительный результирующий аргумент суммы (+Si)k, а если вернуться к анализу входных аргументов функциональной структуры (775), то совокупность аргументов (777)
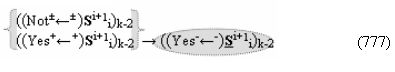
может быть записана посредством «-Комплексного аргумента переноса» ((Yes-←-)Si+1 i)k-2 с измененным уровнем аналогового сигнала, функциональную структуру которого запишем в виде графоаналитического выражения (778),
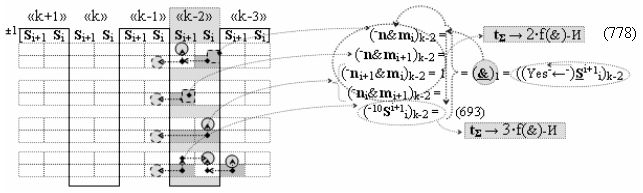
а после переноса логической функции f1(&)-НЕ через систему логической функции f1(})-ИЛИ и объединение перенесенной логической функции f1(&)-НЕ с функцией входных «Комплексных аргументов» запишем функциональную структуру (779)
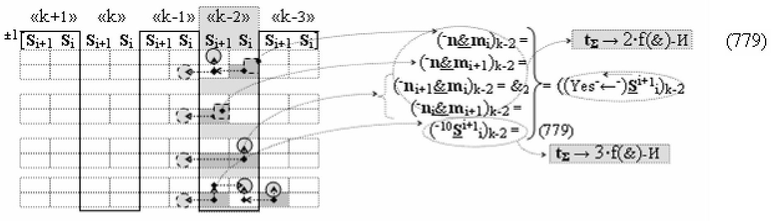
с выходной логической функцией f2(&)-И с входными «Комплексными аргументами» с измененными уровнями аналоговых сигналов. И если вернуться к аналитическому выражению «Положительного канала сумматора «i» разряда» (775) и ввести в систему логической функции f1(&)-И функциональную структуру (779), то после объединения одноименных логических функций f1(&)-И и f2(&)-И запишем скорректированное графоаналитическое выражение (780)
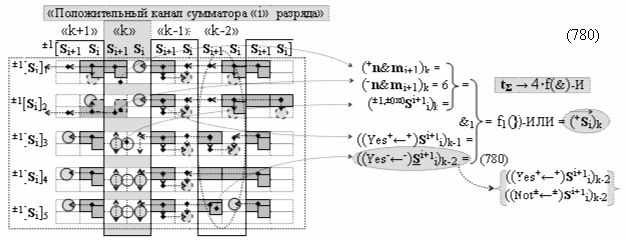
с технологическим циклом tΣ → 4∙f(&)-И, который соответствует четырем условным логическим функциям f(&)-И. И если записать «+Комплексного аргумента переноса» ((Yes+←+)Si+1 i)k-2 с измененным уровнем аналогового сигнала в виде аналитического выражения (781),
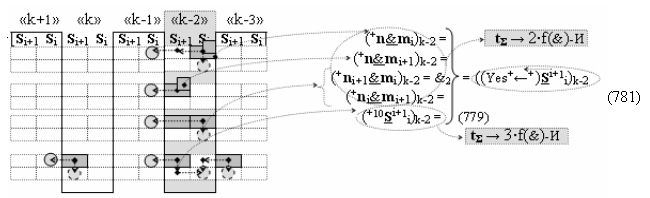
то функциональную аналогичную структуру имеет и «Условно отрицательный канал сумматора «i» разряда», которую запишем в виде графоаналитического выражения (782),
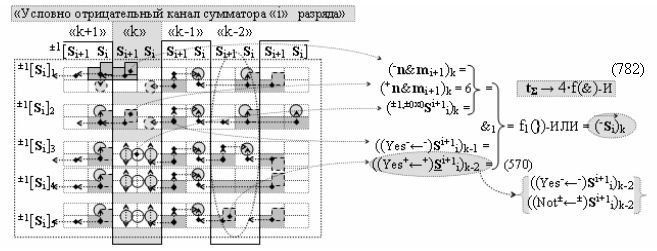
где также вместо совокупности аргументов (783)
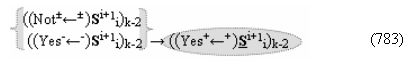
в систему логической функции f1(&)-И введен «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k-2 с измененным уровнем аналогового сигнала. При этом следует отметить, что «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k-2 с измененным уровнем аналогового сигнала может быть введен в функциональную структуру «Условно отрицательного канала сумматора «i» разряда» (772) и «Условно отрицательного канала сумматора «i+1» разряда» (773), а «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k-2 с измененным уровнем аналогового сигнала может быть введен в функциональную структуру «Положительного канала сумматора «i» разряда» (762) и «Положительного канала сумматора «i+1» разряда» (763), что позволит процедуру преобразования аргументов слагаемых выполнять с технологическим циклом tΣ → 4∙f(&)-И, который соответствует четырем условным логическим функциям f(&)-И. Поэтому «Положительный канал сумматора «i» разряда» (762) с учетом функциональной структуры (780) запишем в виде графоаналитического выражения (784),
а «Условно отрицательного канала сумматора «i» разряда» (772) с учетом функциональной структуры (782) запишем в виде графоаналитического выражения (784),
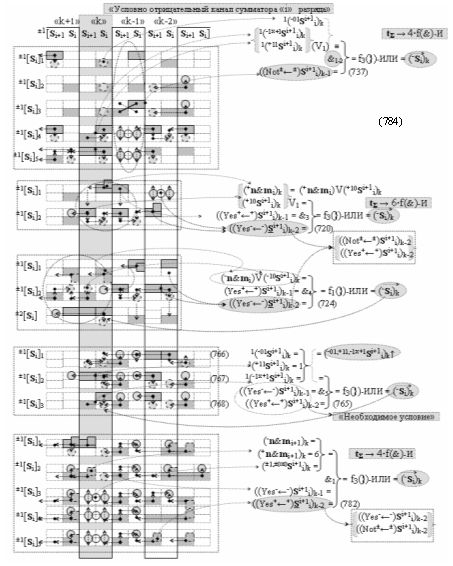
Аналогичную замену совокупностей входных аргументов выполним в «Положительном канале сумматора «i+1» разряда» (763) запишем его в виде графоаналитического выражения (785)
и в «Условно отрицательном канале сумматора «i+1» разряда» (773) и запишем его в виде графоаналитического выражения (786).
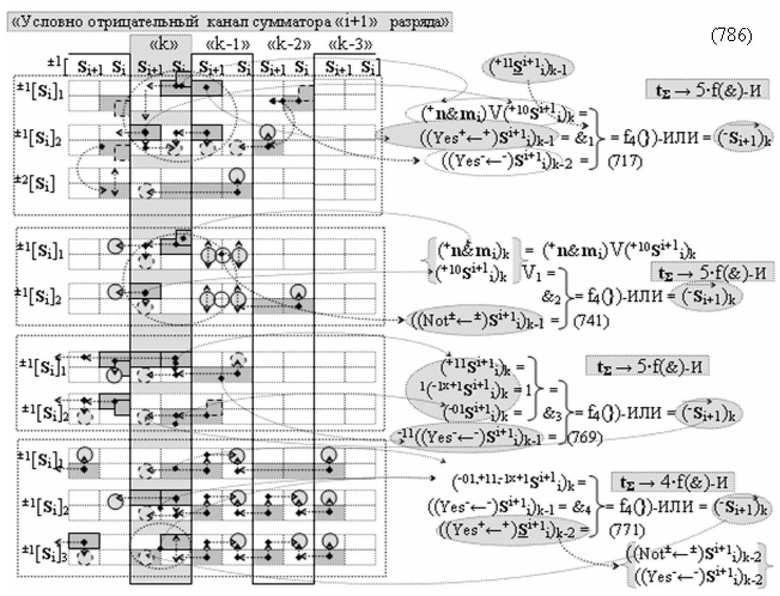
При этом из анализа функциональной структуры «Положительного канала сумматора «i+1» разряда» (785), которую запишем в виде графоаналитического выражения (787),
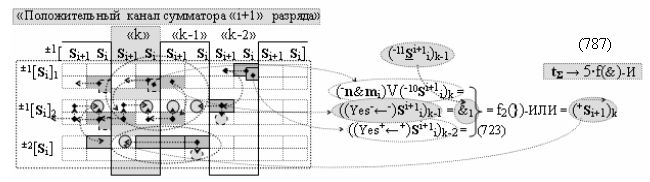
следует, что в систему логической функции должен быть введен «Комплексный аргумент» (-11Si+1 i)k-1 условно «k-1» «Зоны минимизации» с измененным уровнем аналогового сигнала. Поскольку если записать процедуру преобразования аргументов слагаемых с активным аргументом (-11Si+1 i)k-1 в условно «k-1» «Зоне минимизации» в виде выражения (788),
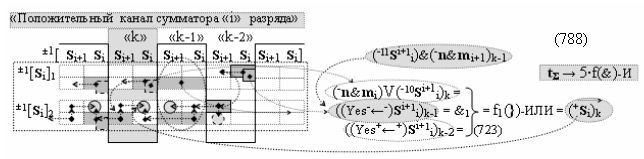
то корректно будет активизирован положительный аргумент суммы (+Si)k в условно «i» разряде, а функциональная структура (787) в этой ситуации будет формировать «Дефект». И если вернуться к анализу функциональной структуры «-Комплексного аргумента переноса» ((Yes-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации», записав ее в виде графоаналитического выражения (789),
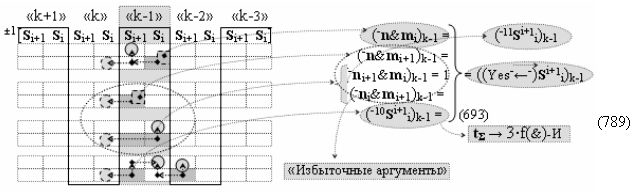
то из системы логической функции должны быть исключены «Избыточные аргументы», поскольку условно отрицательный аргумент (-11Si+1 i)k-1 и (-n&mi+1) условно «k-1» «Зоны минимизации» позволяет выполнить любые переносы аргумента из условно «k-2» «Зоны минимизации» и эти переносы позволяют формировать корректную условно минимизированную структуру аргументов результирующей суммы. Поэтому функциональную структуру «-Комплексного аргумента переноса» ((Yes-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации» запишем в виде двух аналитических выражений (790) и (791)
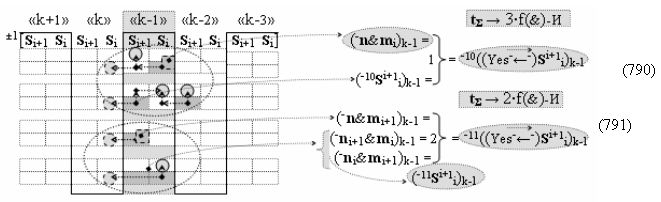
с выходной логической функцией f1(})-ИЛИ и f2(})-ИЛИ, которые активизируют «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k-1 с «Информационным содержанием» - в условно «k-1» «Зоне минимизации» активен только один условно отрицательный аргумент и «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k-1 с «Информационным содержанием» - в условно «k-1» «Зоне минимизации» активны два условно отрицательных аргумента. И эти «Комплексные аргументы» позволяют функциональную структуру (787) записать в виде аналитического выражения (792),
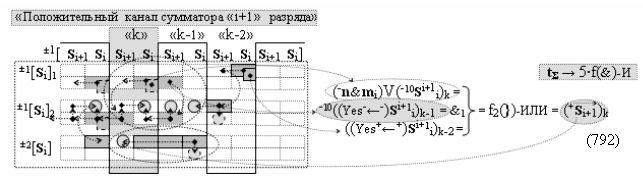
а функциональную структуру (788) запишем в виде аналитического выражения (793)
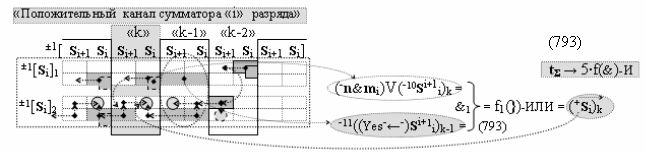
без входного «+Комплексного аргумента переноса» ((Yes+←+)Si+1 i)k-2 условно «k-2» «Зоны минимизации», поскольку «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k-1 в условно «k-1» «Зоне минимизации» с двумя условно отрицательными аргументами позволяет активизировать аргумент результирующей суммы в этой «Зоне минимизации». Поэтому «Положительный канал сумматора «i» разряда» (784) с учетом функциональной структуры (793) запишем в виде графоаналитического выражения (794),
а «Положительный канал сумматора «i» разряда» (785) с учетом функциональной структуры (792) запишем в виде графоаналитического выражения (795),
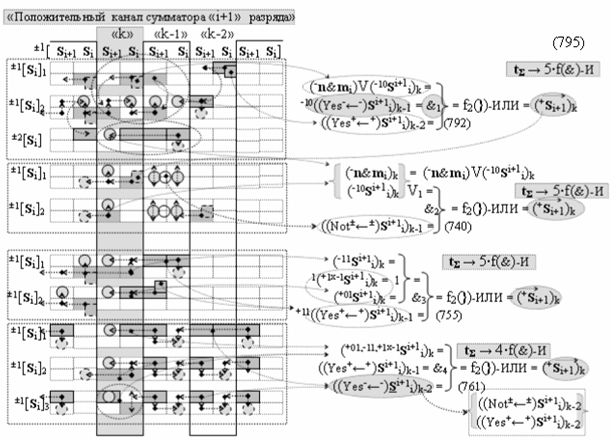
Аналогичную корректировку функциональной структуры выполним и в «Условно отрицательном канале сумматора «i+1» разряда» (786), которую запишем в виде графоаналитического выражения (796),
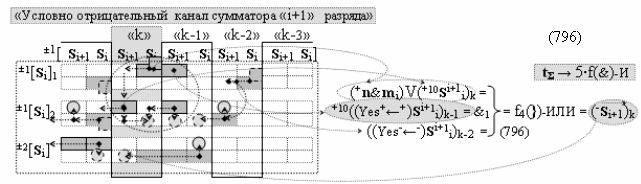
где «+Комплексного аргумента переноса» +10((Yes+←+)Si+1 i)k-1 условно «k-1» «Зоны минимизации» активизирует функциональная структура (797),
а аналогичную выражению (788) функциональную структуру, активизирующую условно отрицательный аргумент результирующей суммы (-Si)k запишем в виде аналитического выражения (799).
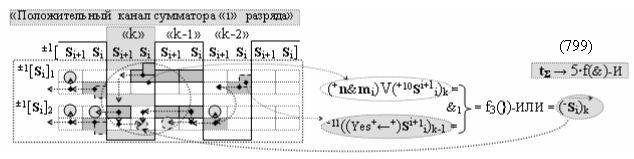
В результате «Условно отрицательный канал сумматора «i+1» разряда» (786) с учетом скорректированной функциональной структурой (796) запишем в виде графоаналитического выражения (800),
а «Условно отрицательный канал сумматора «i» разряда» (784) с учетом функциональной структуры (799) запишем в виде графоаналитического выражения (801),
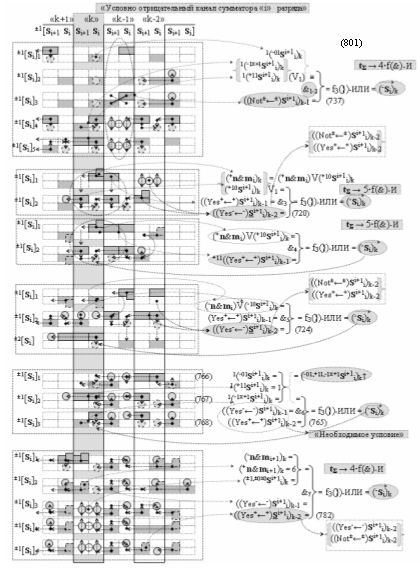
Поскольку все возможные структуры аргументов объединенной структуры слагаемых ±[Si]f1(+/-)min были проанализированы, а они функционально относятся к двум категориям, в одной из них преобразование аргументов в условно «k» «Зоне минимизации» выполняют с учетом того, что в условно «k-1» «Зоне минимизации» нет «+Комплексного аргумента переноса» ((Yes+←+)Si+1 i)k-1 и нет «-Комплексного аргумента переноса» ((Yes-←-)Si+1 i)k-1, а во второй объединенной структуре преобразование аргументов в условно «k» «Зоне минимизации» выполняют с учетом активности этих аргументов. Поэтому математическую модель «Положительного канала сумматора «i» разряда» условно «k» «Зоны минимизации» выражения (794) запишем либо в виде математической модели (802)
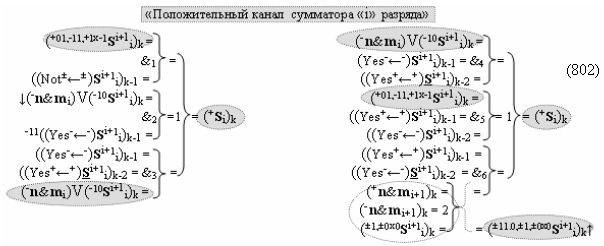
с функциональной входной структурой с выходной логической функцией f2(})-ИЛИ, либо в виде структуры логических функций (803),
в которой функциональная структура с выходной логической функцией f2(})-ИЛИ выражения (802) исключена из системы логической функции и записана в виде «Комплексного аргумента» (±11.0,±1,±0х0Si+1 i)k. Поскольку данная функциональная структура функционально принадлежит как «Положительному каналу сумматора «i» разряда» и «Условно отрицательному каналу сумматора «i» разряда» и ее запишем либо в виде отдельного аналитического выражения (804),
либо с учетом структуры логических функций (544) запишем в виде графоаналитического выражения (805)
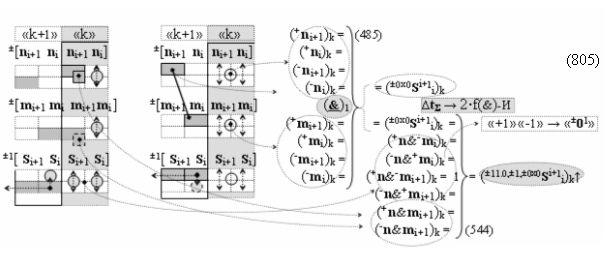
А математическую модель «Положительного канала сумматора «i+1» разряда» (795) также запишем в виде структуры логических функций (806),
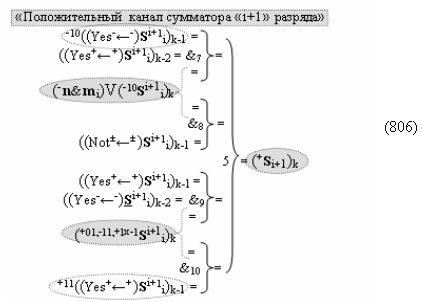
с входными «Комплексными аргументами» (-n&mi)V(-10Si+1 i)k и (+01,-11,+1х-1Si+1 i)k, которые также включены в функциональную структуру «Положительного канала сумматора «i» разряда», поэтому их функциональные структуры запишем для аргумента (+01,-11,+1х-1Si+1 i)kв виде аналитического выражения (807),
а для аргумента (-n&mi)V(-10Si+1 i)k в виде аналитического выражения (808),
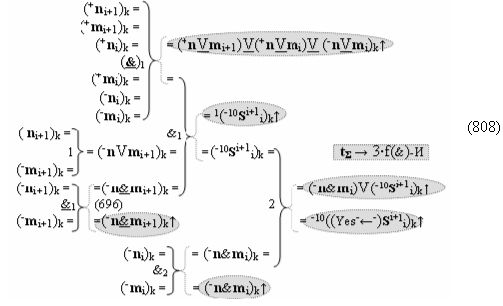
в котором выходные «Комплексные аргументы» (-n&mi)V(-10Si+1 i)k↑ и -10((Yes-←-)Si+1 i)k↑ имеют одинаковое «Информационное содержание». Поэтому «Положительный канал сумматора «i» разряда» выражения (803) запишем в виде структуры логических функций (809),
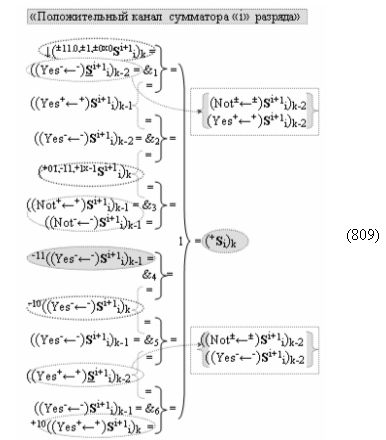
в которой «Комплексный аргумент» ((Not±←±)Si+1 i)k-1 условно «k-1» «Зоны минимизации» выражения (803) в системе логической функции f3(&)-И скорректированного выражения (809) записан в виде двух преобразованных аргументов ((Not+←+)Si+1 i)k-1 и ((Not-←-)Si+1 i)k-1. Поскольку если вернуться к анализу «Комплексного аргумента» ((Not±←±)Si+1 i)k-1 - «Отсутствие любых переносов» в условно «k-1» «Зоне минимизации» выражения (733), записав его в виде структуры логических функций (810),
то в системе логической функции f1(&)-И этого выражения включены две функциональные структуры, которые активизируют положительный «Комплексный аргумент» ((Not+←+)Si+1 i)k-1 и условно отрицательный «Комплексный аргумент» ((Not-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации». А если учесть, что эти две функциональные структуры в выражении (809) также включены в одноименную систему логической функции f3(&)-И, то функциональную структуру положительного «Комплексного аргумента» ((Not+←+)Si+1 i)k-1 условно «k-1» «Зоны минимизации» запишем в виде аналитического выражения (811),
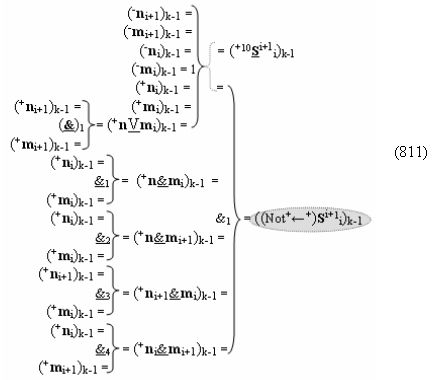
а функциональную структуру условно отрицательного «Комплексного аргумента» ((Not-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации» запишем в виде аналитического выражения (812).
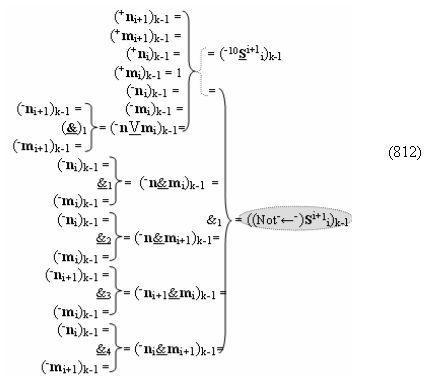
Но поскольку формируется математическая модель условно «k» «Зоны минимизации», поэтому функциональную структуру положительного «Комплексного аргумента» ((Not+←+)Si+1 i)k условно «k» «Зоны минимизации» запишем для этой зоны минимизации в виде аналитического выражения (813),
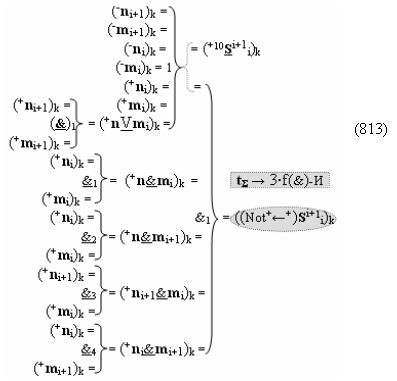
а функциональную структуру условно отрицательного «Комплексного аргумента» ((Not+←+)Si+1 i)k условно «k» «Зоны минимизации» для этой зоны минимизации запишем в виде аналитического выражения (814).
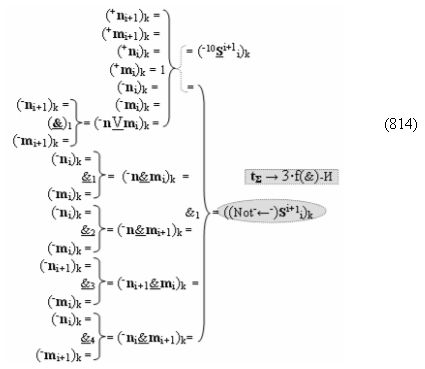
А математическую модель «Положительного канала сумматора «i+1» разряда» (806) с учетом корректировки входных аргументов и «Положительный канал сумматора «i» разряда» запишем в виде структуры логических функций (815),
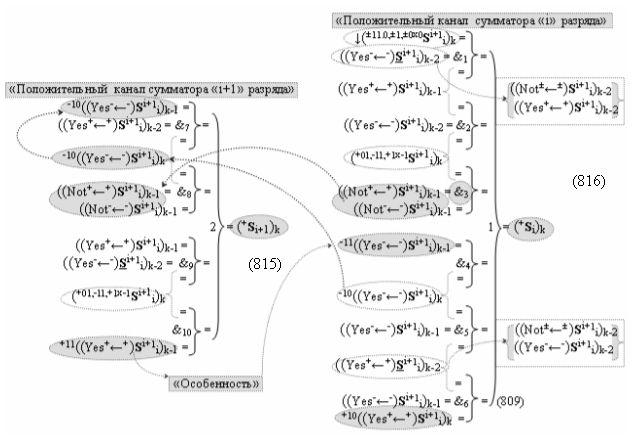
в которой также «Комплексный аргумент» ((Not±←±)Si+1 i)k-1 условно «k-1» «Зоны минимизации» выражения (806) в системе логической функции f8(&)-И скорректированного выражения (815) записан в виде двух преобразованных аргументов ((Not+←+)Si+1 i)k-1 и ((Not-←-)Si+1 i)k-1. При этом следует отметить, что в «Положительный канал сумматора «i+1» разряда» выражения (815) включены также «Комплексный аргумент» +11((Yes+←+)Si+1 i)k-1 условно «k-1» «Зоны минимизации», которые функционально относятся к данному каналу сумматора. Но поскольку формируется математическая модель условно «k» «Зоны минимизации» «Положительных каналов сумматора» (816) и «Условно отрицательных каналов сумматора» (817) и (818),
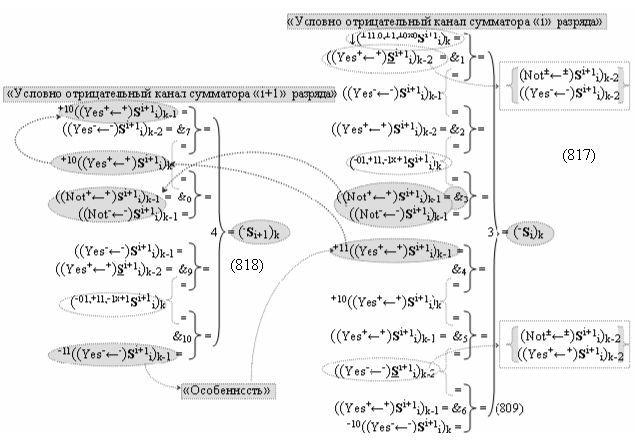
в которых структура логических функций эквивалентна структуре логических функций «Положительных каналов сумматора» (816) за исключением знаков входных аргументов. При этом следует отметить, что «Особенностью» «Положительного канала сумматора «i+1» разряда» (815) и «Условно отрицательного канала сумматора «i+1» разряда» (818) являются входной положительный «Комплексный аргумент» +11((Yes+←+)Si+1 i)k-1 и входной условно отрицательный аргумент -11((Yes-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации», который функционально принадлежит только этим каналам. Поэтому в аналитическое выражение (815) необходимо ввести функциональную структуру положительного «Комплексного аргумента» +11((Yes+←+)Si+1 i)k условно «k» «Зоны минимизации» и этот аргумент в соответствии с выражением (798), записав его в виде графоаналитического выражения (819)
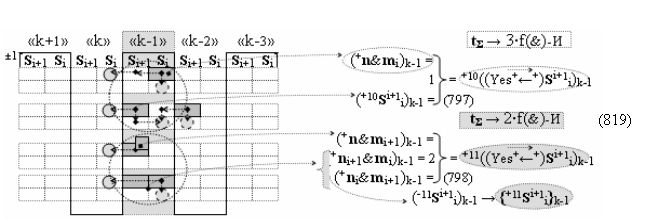
активизирует функциональная структура с выходной логической функцией f2(})-ИЛИ с входным преобразованным аргументом (+n&mi+1)k-1 и двумя входными аргументами (+ni+1&mi)k-1 и (+ni&mi+1)k-1, которые для минимизации аналитической записи будем записывать в виде совокупности преобразованных аргументов {+11Si+1 i}k в аналитическом выражении (820).
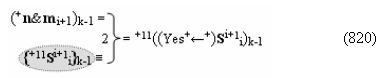
А в аналитическое выражение «Условно отрицательного канала сумматора «i+1» разряда» (818) необходимо ввести функциональную структуру «Комплексного аргумента» -11((Yes-←-)Si+1 i)k-1 условно «k-1» «Зоны минимизации» и этот аргумент в соответствии с выражением (791), записав его в виде графоаналитического выражения (821)
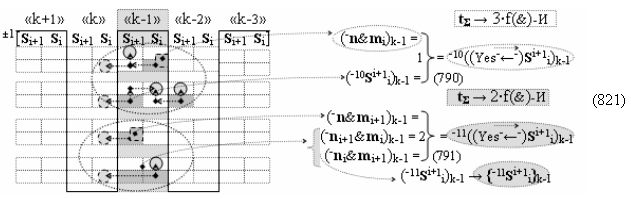
также запишем в виде аналитического выражения (822).
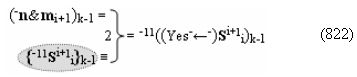
В результате структуру логических функций «Положительного канала сумматора «i+1» разряда» (815) запишем в виде графоаналитического выражения (823),
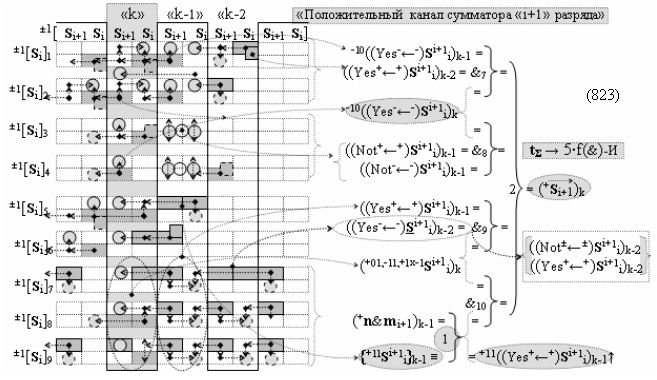
где {+11Si+1 i}k-1 - положительная совокупность преобразованных аргументов и ее активизирует совокупность функциональных структур, которую для «Комплексного аргумента» (-01,+11,-1х+1Si+1 i)k запишем в виде аналитического выражения (824)
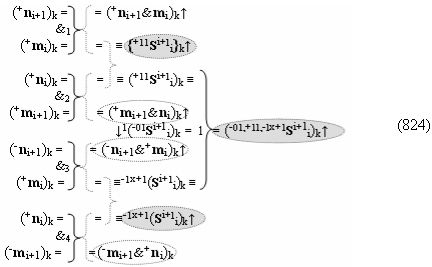
и из которой совокупность функциональных структур (825),
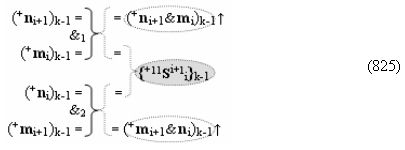
записанная для условно «k-1» «Зоны минимизации» активизирует положительная совокупность преобразованных аргументов {+11Si+1 i}k-1. А структуру логических функций «Условно отрицательного канала сумматора «i+1» разряда» (818) запишем в виде графоаналитического выражения (825),
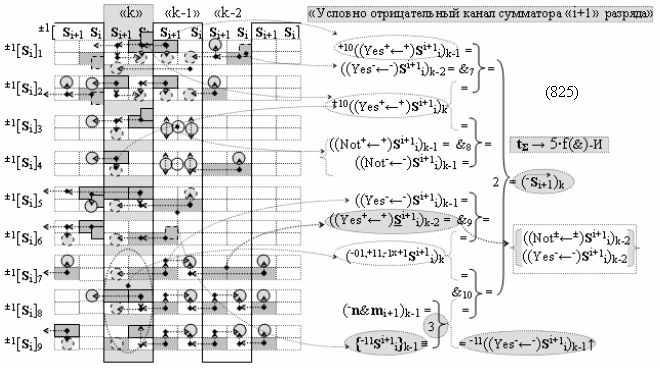
где {-11Si+1 i}k-1 - условно отрицательная совокупность преобразованных аргументов, которую активизирует совокупность функциональных структур выражения (807) и которую для условно «k-1» «Зоны минимизации» запишем в виде аналитического выражения (826).
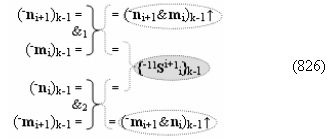
При этом следует отметить, что в «Положительном канале сумматора «i+1» разряда» (823) и в «Условно отрицательном канале сумматора «i+1» разряда» функциональные структуры с выходной логической функцией (825) записаны с преобразованным положительным аргументом +11((Yes+←+)Si+1 i)k-1↑ и преобразованным условно отрицательным аргументом -11((Yes-←-)Si+1 i)k-1↑. Поскольку условно отрицательный аргумент -11((Yes-←-)Si+1 i)k-1↑ включен в систему логической функции f4(&)-И «Положительного канала сумматора «i» разряда» (809), который запишем в виде графоаналитического выражения (827),
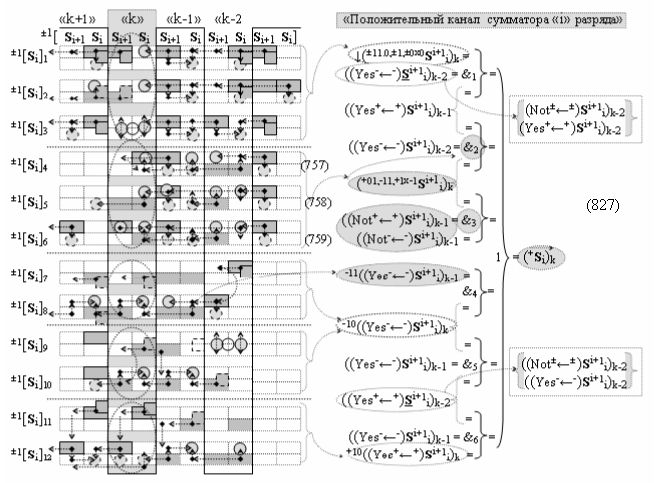
при этом процедуру активизации функциональной структуры с выходной логической функцией f3(&)-И и входными аргументами (+01,-11,+1х-1Si+1 i)k, ((Not+←+)Si+1 i)k-1 и ((Not-←-)Si+1 i)k-1 запишем в виде графоаналитического выражения (828).
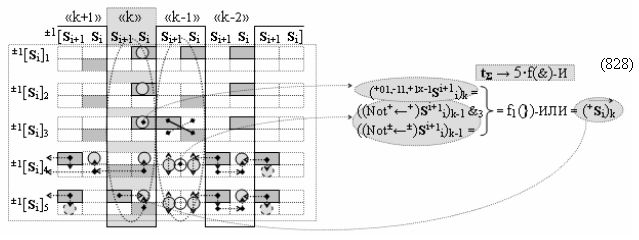
А преобразованный положительный аргумент +11((Yes+←+)Si+1 i)k-1↑ включен в систему логической функции f4(&)-И «Условно отрицательного канала сумматора «i» разряда» выражения (817) и запишем ее в виде графоаналитического выражения (829),
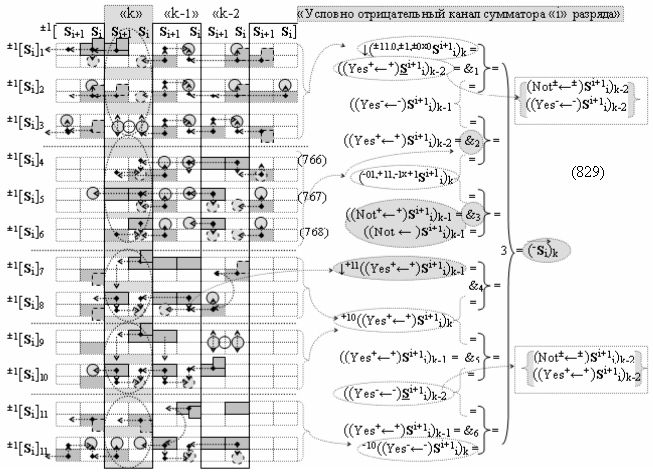
при этом процедуру активизации функциональной структуры с выходной логической функцией f3(&)-И и входными аргументами (-01,+11,-1х+1Si+1 i)k, ((Not+←+)Si+1 i)k-1 и ((Not-←-)Si+1 i)k-1 запишем в виде графоаналитического выражения (830).
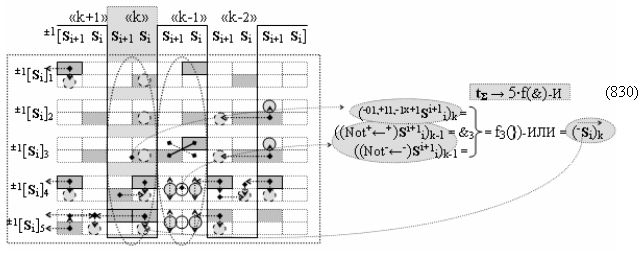
На основании полученных результатов математическую модель «Положительного канала сумматора «i+1» и «i» разряда» (816) условно «k» «Зоны минимизации» запишем в виде структуры логических функций (831)
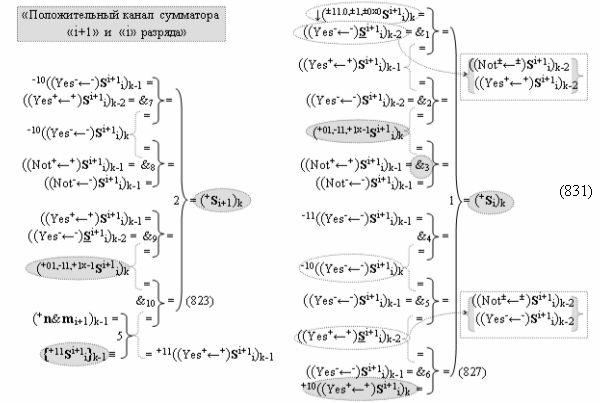
с общей функциональной структурой (807), посредством которой активизируют «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k↑ и {+11Si+1 i}k↑, которую запишем в виде графоаналитического выражения (832).
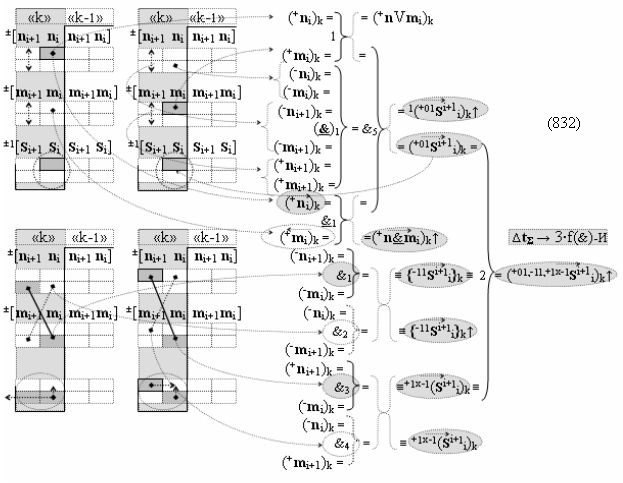
А математическую модель «Условно отрицательного канала сумматора «i+1» и «i» разряда» (817) условно «k» «Зоны минимизации» запишем в виде структуры логических функций (833),
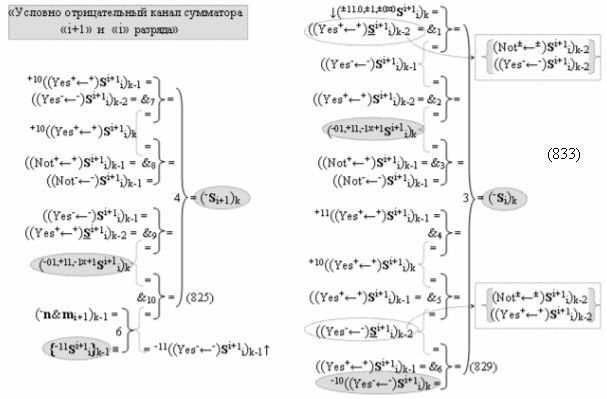
с общей функциональной структурой (824), посредством которой активизируют «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k↑ и {-11Si+1 i}k↑, которую запишем в виде графоаналитического выражения (834).
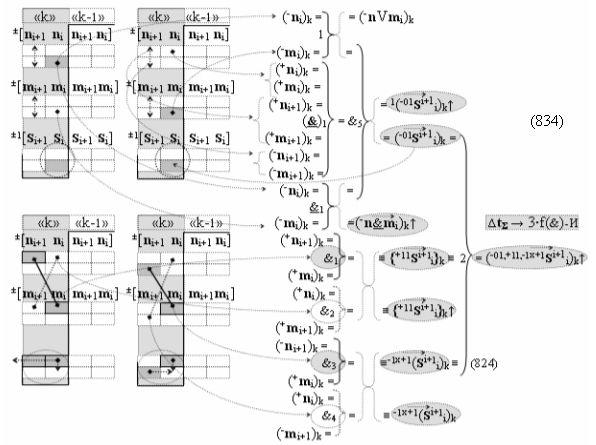
При этом общими функциональными структурами сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации» являются функциональные структуры, которые активизируют следующие «Комплексные аргументы»:
Функциональная структура 1. «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k (835).
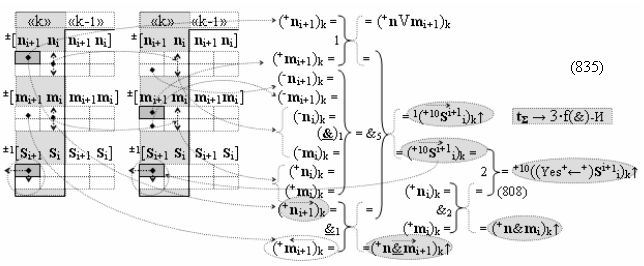
Функциональная структура 2. «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k (836).
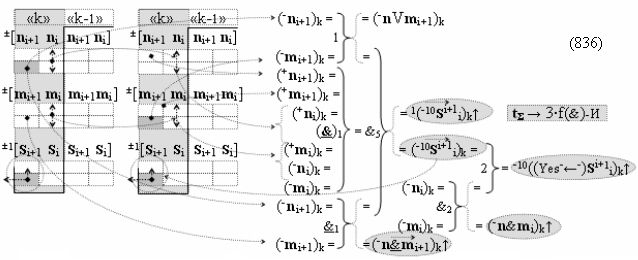
Функциональная структура 3. «Комплексный аргумент» ((Not+←+)Si+1 i)k, который с учетом преобразованного аргумента (+n&mi+1)k и с учетом функциональной структуры (837),
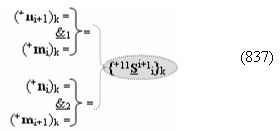
активизирующая совокупность аргументов {+11Si+1 i}k с измененным уровнем аналогового сигнала, а также с учетом преобразованного аргумента (±0х0Si+1 i)k функциональной структуры (838),
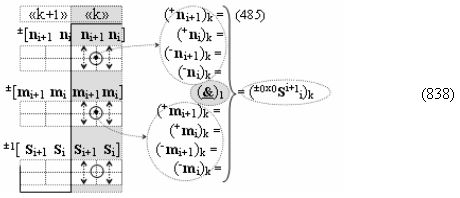
формирует структура логических функций (838).
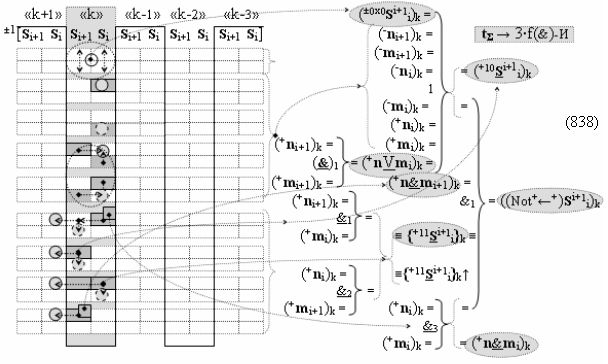
Функциональная структура 4. «Комплексный аргумент» ((Not-←-)Si+1 i)k, который с учетом преобразованных аргументов (-n&mi+1)k и с учетом функциональной структуры (839),
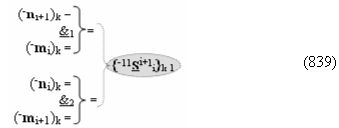
активизирующая совокупность аргументов {-11Si+1 i}k с измененным уровнем аналогового сигнала, а также с учетом преобразованного аргумента (±0х0Si+1 i)k функциональной структуры (838), формирует структура логических функций (840).
Функциональная структура 5. «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала, который активизирует структура логических функций (841).
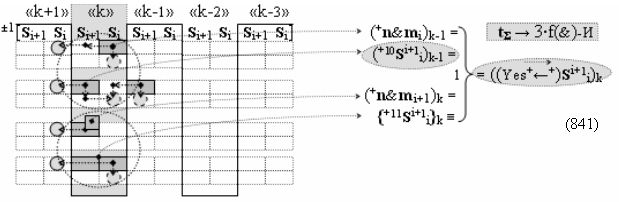
Функциональная структура 6. «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала, который активизирует структура логических функций (842).
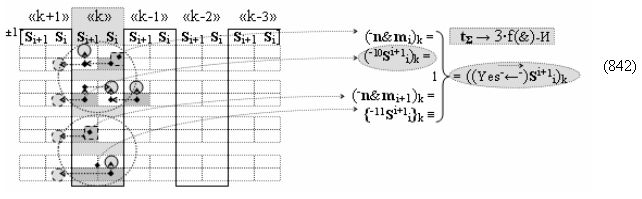
Функциональная структура 7. «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала активизирует функциональная структура (843).
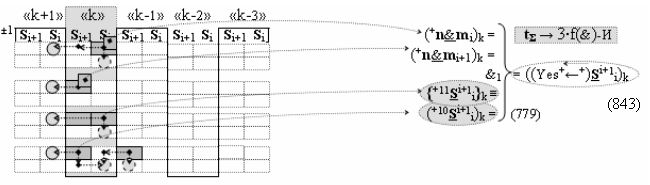
Функциональная структура 8. «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала активизирует функциональная структура (844).
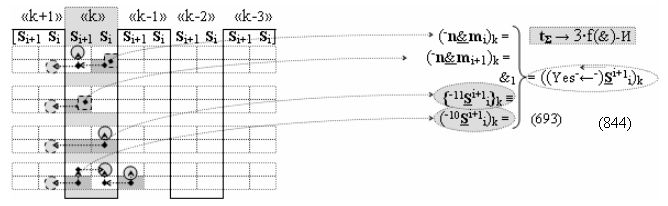
Функциональная структура 9. «Комплексный аргумент» (±11.0,±1,±0х0Si+1 i)k «Условия активизации» аргумента локального переноса в условно «k» «Зоне минимизации» активизирует функциональная структура (845).
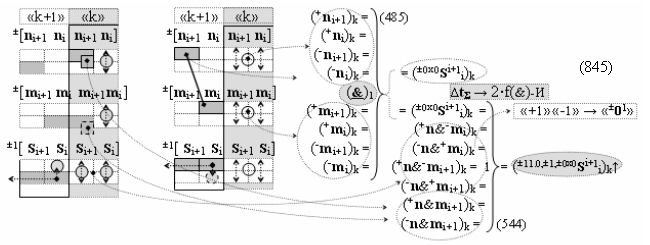
При этом следует отметить, что технологический цикл ∆tΣ → 3∙f(&)-И функциональных входных структур сумматора ±f1(ΣRU)min, которые выполняют процедуру преобразования условно минимизированных структур аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в условно «k» «Зоне минимизации» и активизируют «Комплексные аргументы», соответствует трем условным логическим функциям f(&)-И, а технологический цикл ∆tΣ → 2∙f(&)-И функциональных выходных структур сумматора ±f1(ΣRU)min, которые выполняют процедуру преобразования «Комплексных аргументов» и активизируют результирующие положительные аргументы суммы (+Si)k и (+Si+1)k и условно отрицательные аргументы суммы (-Si)k и (-Si+1)k, соответствует двум условным логическим функциям f(&)-И, в результате технологический цикл ∆tΣ → 3∙f(&)-И функциональных структур сумматора ±f1(ΣRU)min соответствует ∆tΣ → 5∙f(&)-И пяти условным логическим функциям f(&)-И.
Далее, синтезированные математические модели функциональных выходных структур «Положительного канала сумматора «i» и «i+1» разряда» (815) и (818), которые запишем в виде аналитических выражений (846)
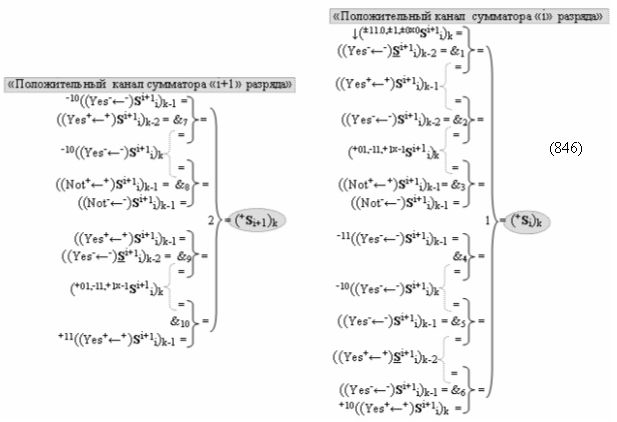
и синтезированные математические модели функциональных выходных структур «Условно отрицательного канала сумматора «i» и «i+1» разряда» (817) и (818), которые запишем в виде аналитических выражений (847)
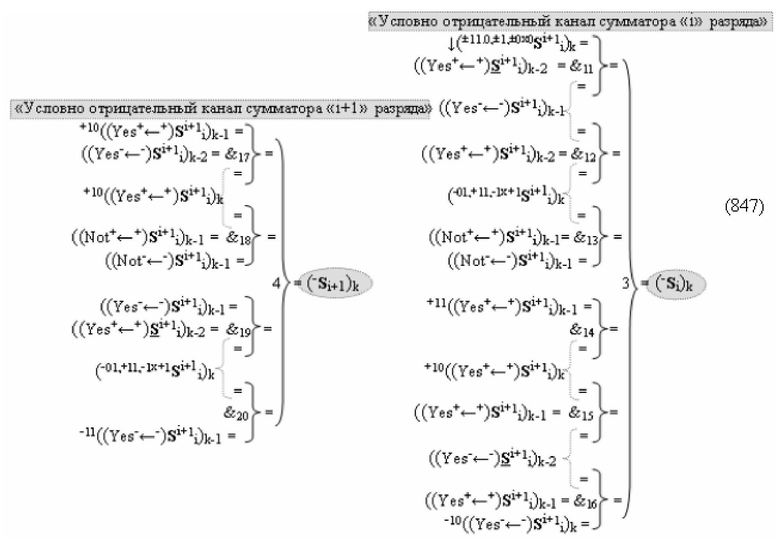
первого варианта могут быть записаны посредством других логических функций. При этом следует отметить, что поскольку структуры логических функций двух каналов эквивалентны, поэтому достаточно формализованные преобразования логических функций выполнить, например, в математической модели «Положительного канала сумматора «i» и «i+1» разряда» (846).
Вариант 2. Для синтеза математических моделей функциональных выходных структур «Положительного канала сумматора «i» и «i+1» разряда» (846) второго варианта выполним замену функциональных входных связей f(=) логической функции f1(})-ИЛИ и f2(})-ИЛИ на соответствующие им функции двойного изменения уровня аналогового сигнала f1(&1=&2) в соответствии с графоаналитической структурой (848).
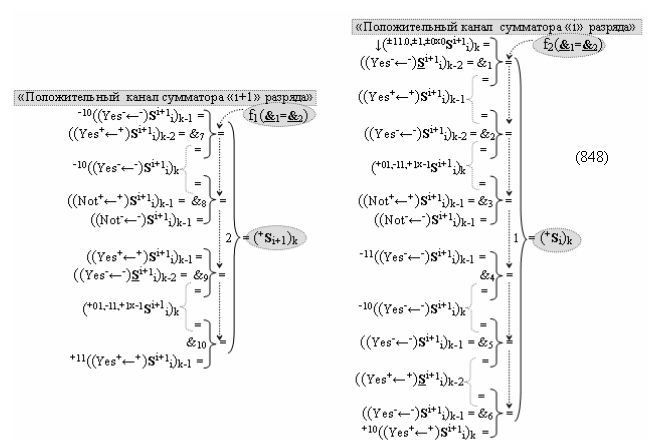
И запишем графоаналитическое выражение (849),
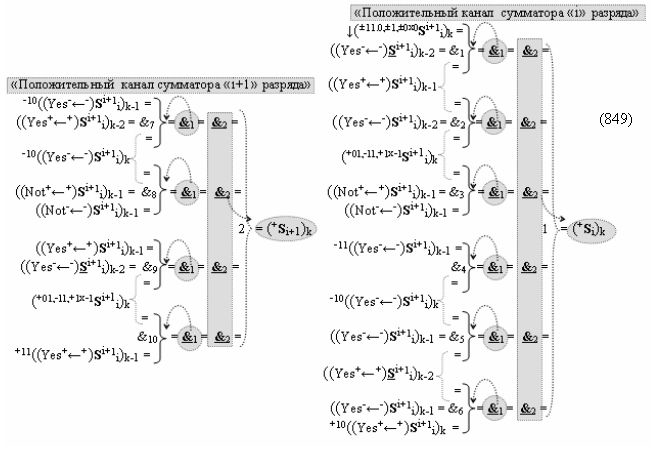
в котором выполним объединение входных логических функций f1(&)-И - f10(&)-И с логическими функциями f1(&)-И, которые преобразуются в выражении (850)
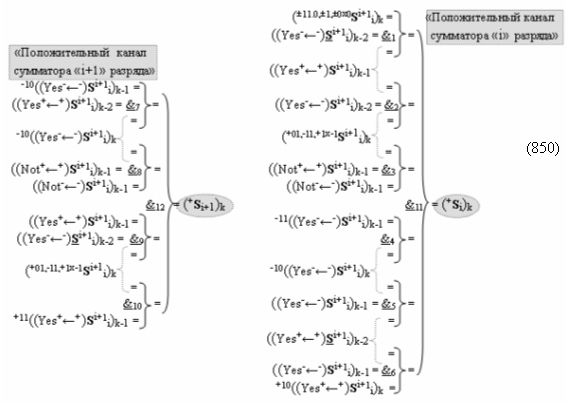
в логические функции f1(&)-И-НЕ - f10(&)-И-НЕ. А после переноса логических функций f2(&)-И в выражении (849) через выходную логическую функцию f1(})-ИЛИ и f2(})-ИЛИ они изменяют свои логические свойства на свойства логической функции f11(&)-И-НЕ и f12(&)-И-НЕ.
Аналогичную структуру логических функций имеет и функциональная структура «Условно отрицательного канала сумматора «i» и «i+1» разряда» (847), которую запишем в виде аналитических выражений (851).
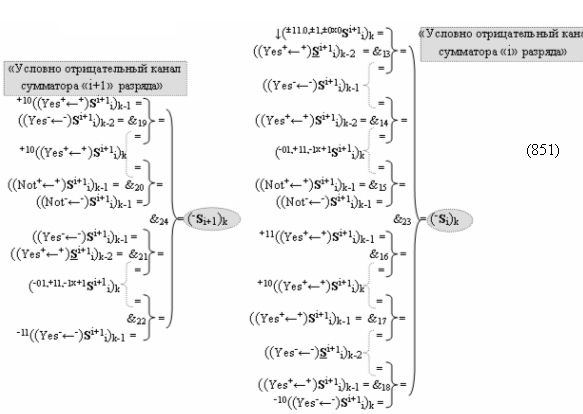
Поскольку были выполнены формализованные преобразования в аналитических выражениях (850) и (1851), поэтому для проверки корректности преобразования в них «Комплексный аргумент» сформируем векторные структуры активизации логических функций и запишем в виде графоаналитического выражения (852),
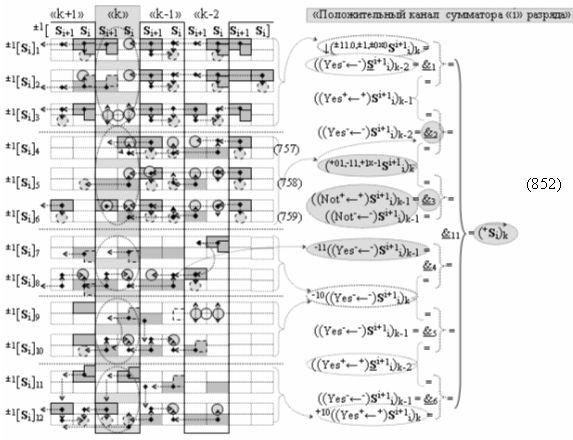
в виде графоаналитического выражения (853)
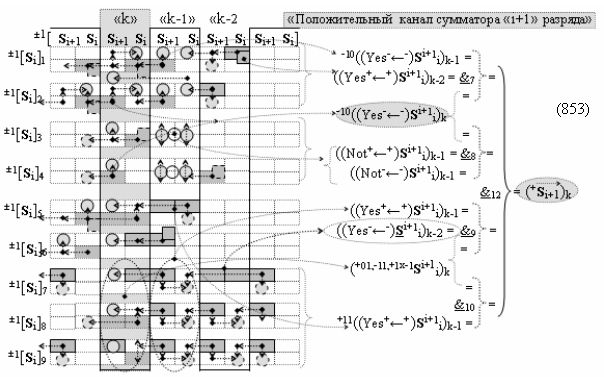
в виде графоаналитического выражения (854)
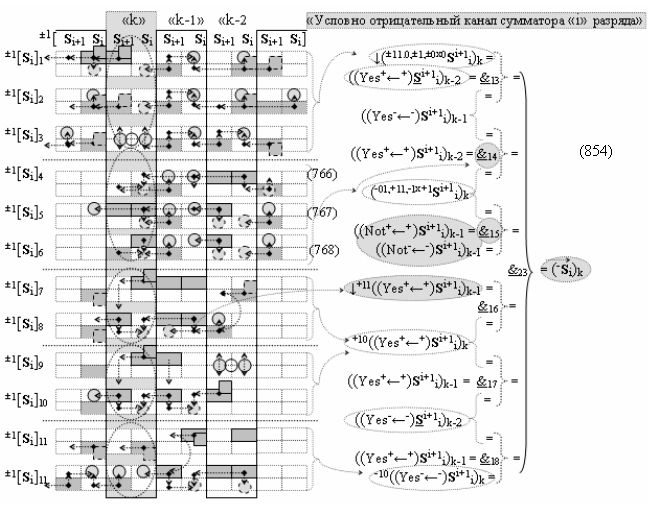
и в виде графоаналитического выражения (855),
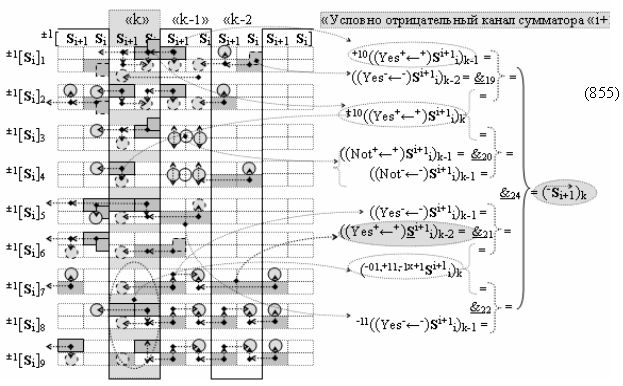
из анализа которых следует, что положительные результирующие аргументы суммы (+Si)k и (+Si+1)k и условно отрицательные аргументы суммы (-Si)k и (-Si+1)k для соответствующих входных структур «Комплексных аргументов» в условно «k» «Зоне минимизации» активизированы корректно, поскольку в системах выходных логических функций f11(&)-И-НЕ, f12(&)-И-НЕ и f23(&)-И-НЕ, f24(&)-И-НЕ не активны входные логические функции f1(&)-И-НЕ - f6(&)-И-НЕ, f7(&)-И-НЕ - f10(&)-И-НЕ, f13(&)-И-НЕ - f18(&)-И-НЕ и f19(&)-И-НЕ - f22(&)-И-НЕ, поэтому формализованные преобразования аналитических выражений (850) и (851) были выполнены корректно.
Вариант 3. Для синтеза математической модели функциональных выходных структур «Положительного канала сумматора «i» и «i+1» разряда» (846) третьего варианта скорректируем в выражении (849) перенос логической функции f1(&)-НЕ в соответствии с графоаналитическим выражением (856).
В результате переноса логических функций f2(&)-НЕ в выражении (856) через выходную логическую функцию f1(})-ИЛИ и f2(})-ИЛИ они изменяют свои логические свойства на свойства логической функции f1(&)-И-НЕ и f2(&)-И-НЕ. А в результате переноса логических функций f1(&)-НЕ через систему логических функций f1(&)-И - f10(&)-И они изменяют свои логические свойства на свойства логических функций f1(})-ИЛИ - f10(})-ИЛИ, а дальнейший перенос логических функций f1(&)-НЕ через входные «Комплексные аргументы» они изменяют свой уровень аналогового сигнала в аналитическом выражении (857),
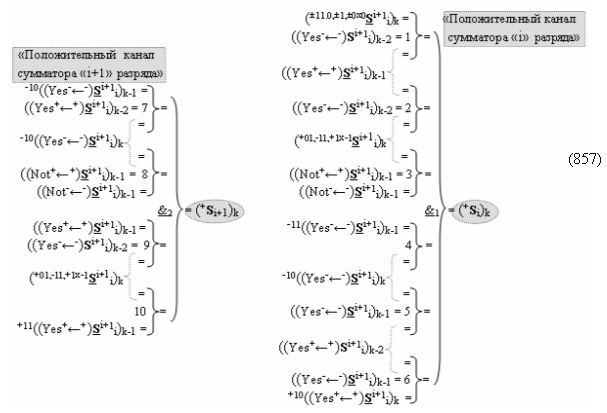
которое и является математической моделью выходной структуры сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации».
Аналогичную структуру логических функций имеет и функциональная структура «Условно отрицательного канала сумматора «i» и «i+1» разряда» (847), которую запишем в виде аналитических выражений (858).
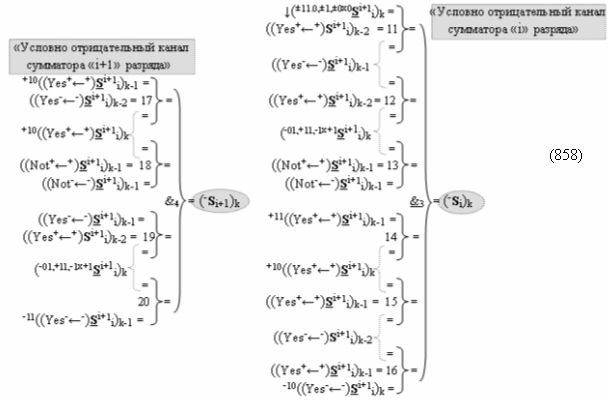
При этом следует отметить, что поскольку в аналитических выражениях (857) и (858) во входных «Комплексных аргументов» изменены уровни аналоговых сигналов, поэтому введем в соответствующие им функциональные структуры выходную логическую функцию f1(&)-НЕ, которая изменяет уровень их аналогового сигнала, и выполним формализованное объединение ее с выходной логической функцией соответствующей функциональной структуры «Комплексного аргумента» и запишем скорректированные функциональные структуры.
Функциональная структура 1. «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k с измененным уровнем аналогового сигнала аналитического выражения (832) с выходной логической функции f1(&)-НЕ запишем в виде структуры логических функций (859),
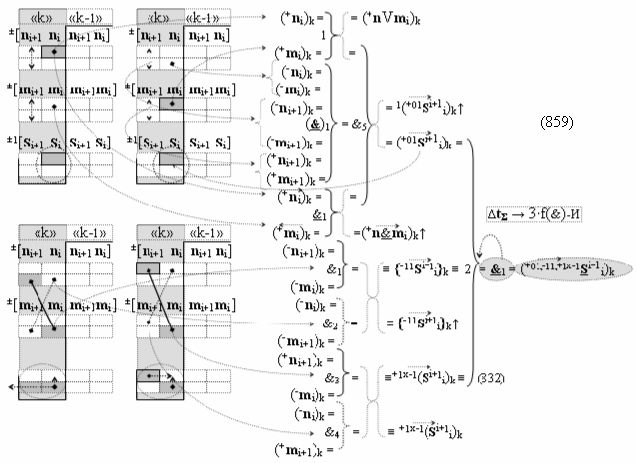
которую после объединения логической функции f1(&)-НЕ с выходной логической функцией f2(})-ИЛИ запишем в виде графоаналитического выражения (860) с выходной логической функцией f2(}&)-ИЛИ-НЕ. При этом следует отметить, что функциональная структура (860) функционально относится только к выходным структурам «Положительных каналов сумматора «i» и «i+1» разряда».
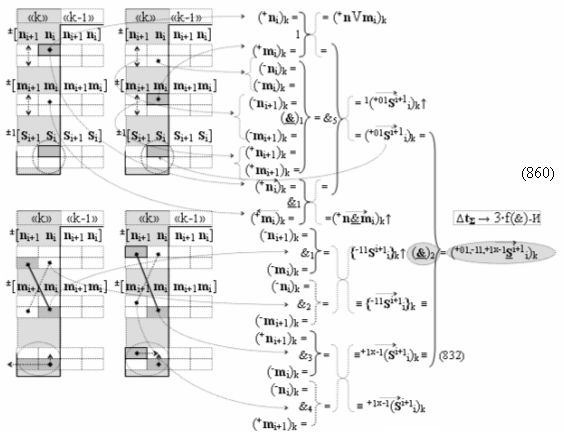
Функциональная структура 2. «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k с измененным уровнем аналогового сигнала аналитического выражения (834) с выходной логической функцией f1(&)-НЕ запишем в виде структуры логических функций (861),
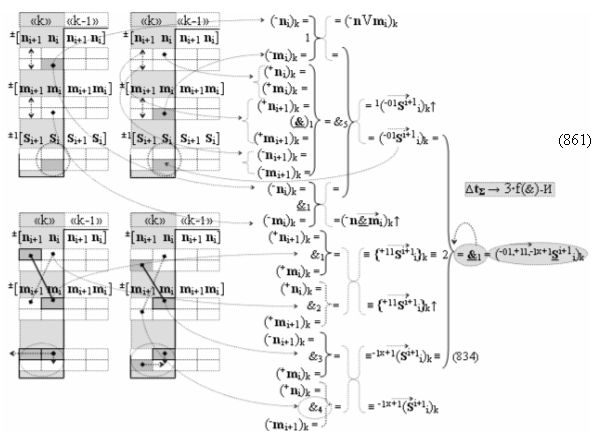
которую после объединения логической функции f1(&)-НЕ с выходной логической функцией f2(})-ИЛИ запишем в виде графоаналитического выражения (862)
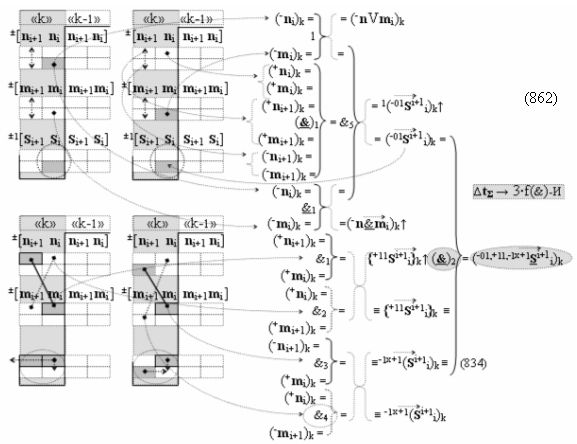
с выходной логической функцией f2(}&)-ИЛИ-НЕ. При этом следует отметить, что функциональная структура (860) функционально относится только к выходным структурам «Условно отрицательным каналам сумматора «i» и «i+1» разряда».
При этом общими функциональными структурами сумматора ±f1(ΣRU)min условно «k» «Зоны минимизации» являются функциональные структуры, которые активизируют следующие «Комплексные аргументы»:
Функциональная структура 3. «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k скорректированного выражения (835) запишем в виде графоаналитического выражения (863).
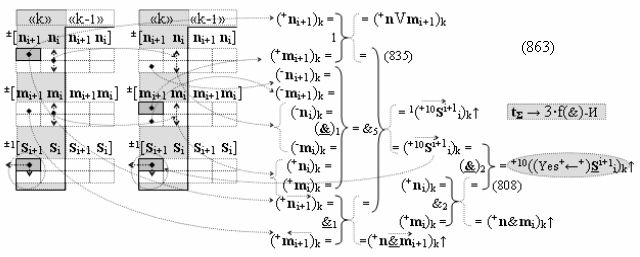
с выходной логической функцией f2(}&)-ИЛИ-НЕ.
Функциональная структура 4. «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала скорректированного выражения (836) запишем в виде графоаналитического выражения (864).
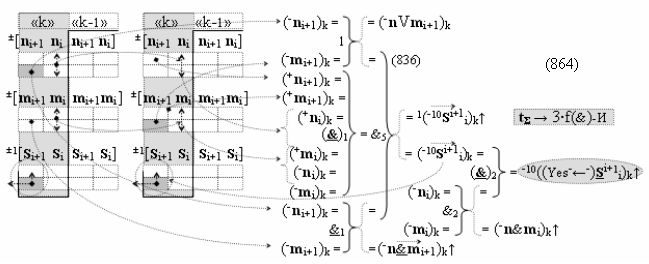
с выходной логической функцией f2(}&)-ИЛИ-НЕ.
Функциональная структура 5. «Комплексный аргумент» ((Not+←+)Si+1 i)k с измененным уровнем аналогового сигнала выражения (838), которое запишем в виде графоаналитического выражения (865)
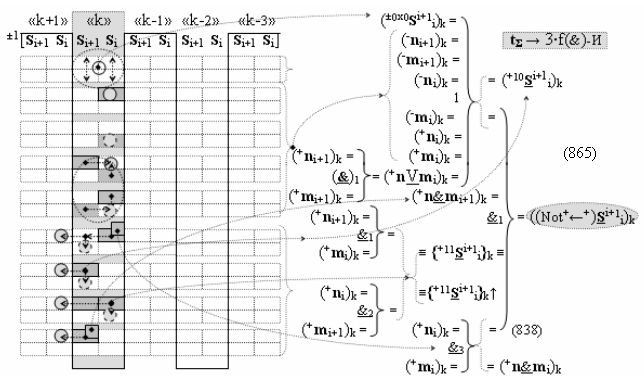
с выходной логической функцией f1(&)-И-НЕ.
Функциональная структура 6. «Комплексный аргумент» ((Not-←-)Si+1 i)k с измененным уровнем аналогового сигнала выражения (840) и его запишем в виде графоаналитического выражения (866)
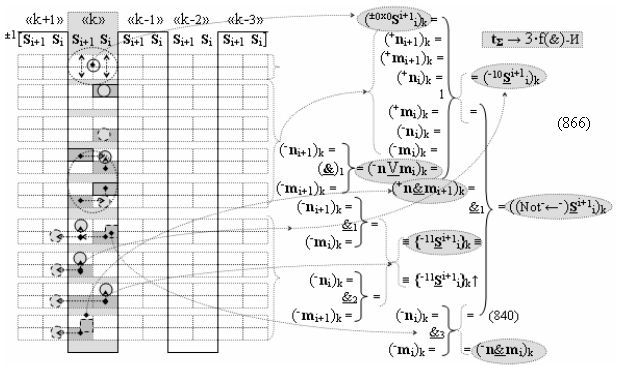
с выходной логической функцией f1(&)-И-НЕ.
Функциональная структура 7. «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала, который активизирует структура логических функций (841) и ее запишем в виде графоаналитического выражения (867)
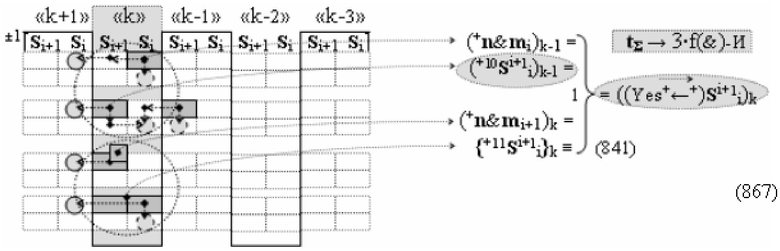
с выходной логической функцией f1(})-ИЛИ.
Функциональная структура 8. «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала, который активизирует структура логических функций (842), и запишем ее в виде графоаналитического выражения (868)
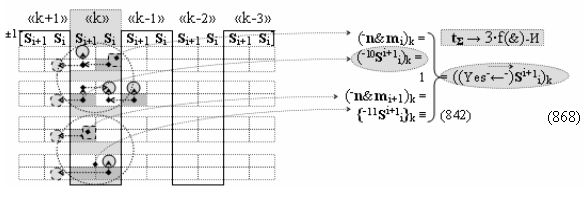
с выходной логической функцией f1(})-ИЛИ.
Функциональная структура 9. «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала (843), активизацию которого запишем в виде графоаналитического выражения (869)
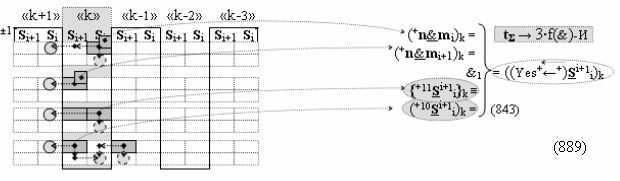
с выходной логической функцией f1(&)-И.
Функциональная структура 10. «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала (844), которую запишем в виде графоаналитического выражения (890)
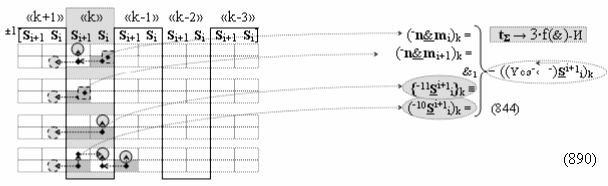
с выходной логической функцией f1(&)-И.
Функциональная структура 11. «Комплексный аргумент» (±11.0,±1,±0х0Si+1 i)k «Условия активизации» аргумента локального переноса в условно «k» «Зоне минимизации» с измененным уровнем аналогового сигнала скорректированного выражения (845) и его запишем в виде графоаналитического выражения (891)
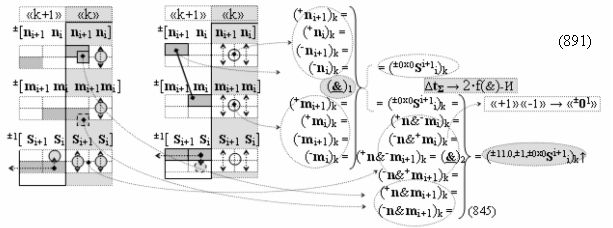
с выходной логической функцией f2(}&)-ИЛИ-НЕ.
При этом следует отметить, что технологический цикл ∆tΣ → 3∙f(&)-И функциональных входных структур сумматора ±f1(ΣRU)min, которые выполняют процедуру преобразования условно минимизированных структур аргументов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в условно «k» «Зоне минимизации» и активизируют «Комплексные аргументы», соответствует трем условным логическим функциям f(&)-И, а технологический цикл ∆tΣ → 2∙f(&)-И функциональных выходных структур сумматора ±f1(ΣRU)min, которые выполняют процедуру преобразования «Комплексных аргументов» и активизируют положительные результирующие аргументы суммы (+Si)k и (+Si+1)k и условно отрицательные аргументы суммы (-Si)k и (-Si+1)k, соответствует двум условным логическим функциям f(&)-И, в результате технологический цикл ∆tΣ → 3∙f(&)-И функциональных структур сумматора ±f1(ΣRU)min соответствует ∆tΣ → 5∙f(&)-И пяти условным логическим функциям f(&)-И.
Далее, поскольку были выполнены формализованные преобразования в аналитических выражениях (857) и (858), поэтому для проверки корректности преобразования в них «Комплексный аргумент» сформируем векторные структуры активизации логических функций и запишем в виде графоаналитического выражения (892),
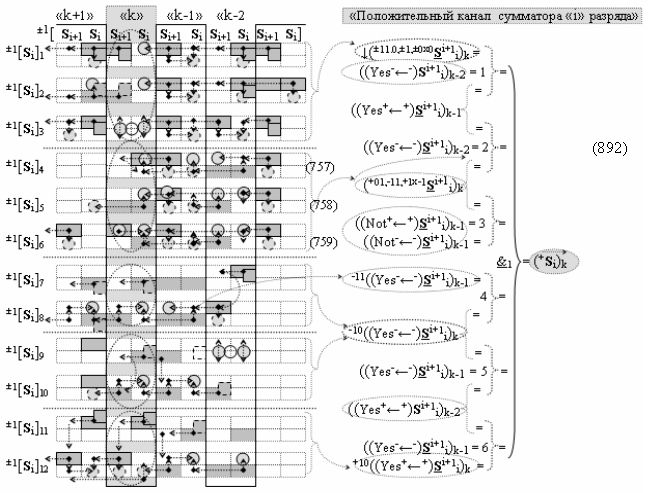
в виде графоаналитического выражения (893)
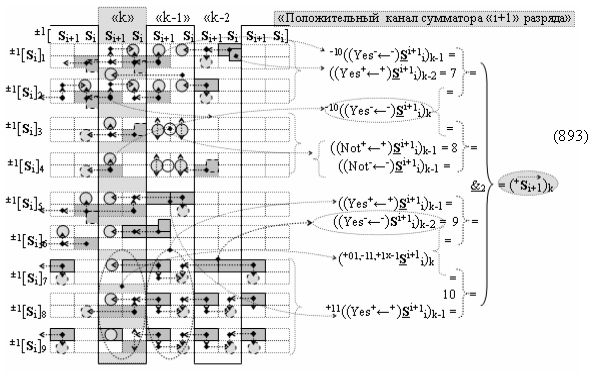
в виде графоаналитического выражения (894)
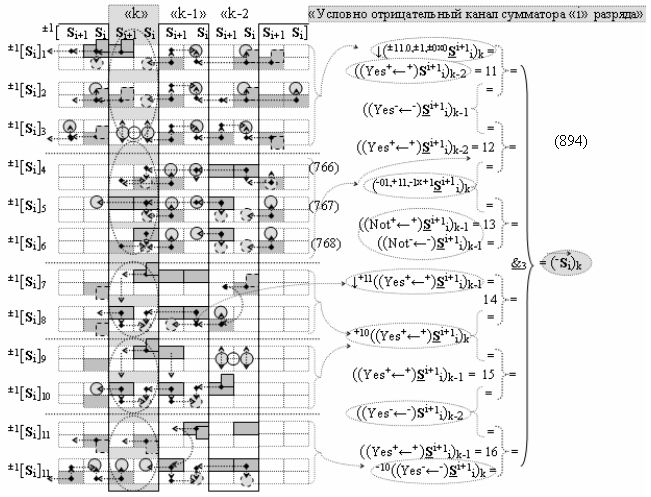
и в виде графоаналитического выражения (895),
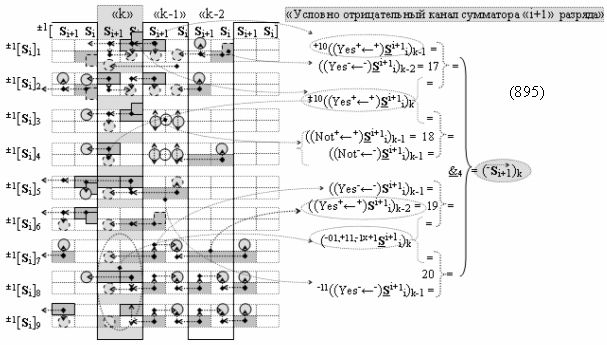
из анализа которых следует, что результирующие положительные аргументы суммы (+Si)k и (+Si+1)k и условно отрицательные аргументы суммы (-Si)k и (-Si+1)k для соответствующих входных структур «Комплексных аргументов» в условно «k» «Зоне минимизации» активизированы корректно, поскольку в системах выходных логических функций f1(&)-И-НЕ, f2(&)-И-НЕ и f3(&)-И-НЕ, f4(&)-И-НЕ не активны входные логические функции f1(})-ИЛИ - f6(})-ИЛИ, f7(})-ИЛИ - f10(})-ИЛИ, f11(})-ИЛИ - f16(})-ИЛИ и f17(})-ИЛИ - f20(})-ИЛИ, поэтому формализованные преобразования аналитических выражений (857) и (858) были выполнены корректно.
Вариант 4. Для синтеза математической модели функциональных выходных структур «Положительного канала сумматора «i» и «i+1» разряда» (846) четвертого варианта скорректируем в выражении (849) перенос логических функций f1(&)-НЕ и f2(&)-НЕ в соответствии с графоаналитическим выражением (896).
В результате переноса логических функций f1(&)-НЕ через систему входных логических функций f1(&)-И - f10(&)-И они изменяют свои логические свойства на свойства логических функций f1(})-ИЛИ - f10(})-ИЛИ, а дальнейший перенос логических функций f1(&)-НЕ через входные «Комплексные аргументы» они изменяют свой уровень аналогового сигнала в аналитическом выражении (857), а объединение скорректированных логических функций f1(})-ИЛИ - f10(})-ИЛИ с соответствующей логической функцией f2(&)-НЕ в выражении (896) они изменяют свои логические свойства на свойства логических функций f1(}&)-ИЛИ-НЕ - f10(}&)-ИЛИ-НЕ в аналитическом выражении (897).
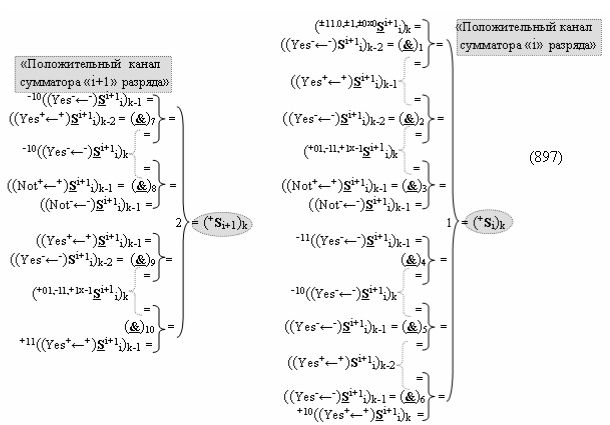
Аналогичную структуру логических функций имеет и функциональная структура «Условно отрицательного канала сумматора «i» и «i+1» разряда» (847), которую запишем в виде аналитических выражений (898).
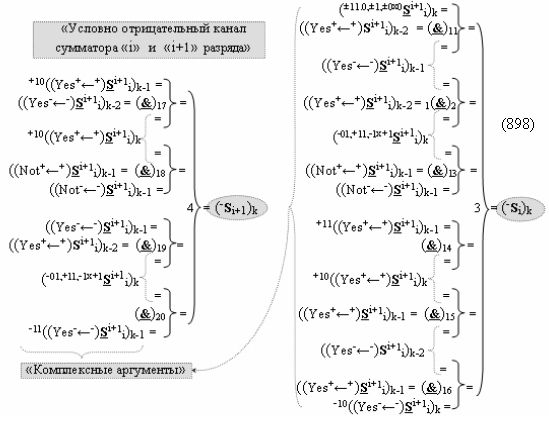
Поскольку были выполнены формализованные преобразования в аналитических выражениях (897) и (898), поэтому для проверки корректности преобразования в них «Комплексный аргумент» сформируем векторные структуры активизации логических функций и запишем в виде графоаналитического выражения (899),
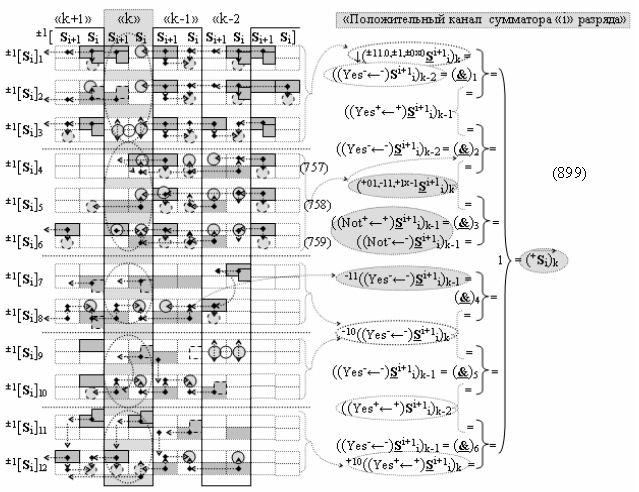
в виде графоаналитического выражения (900)
в виде графоаналитического выражения (901)
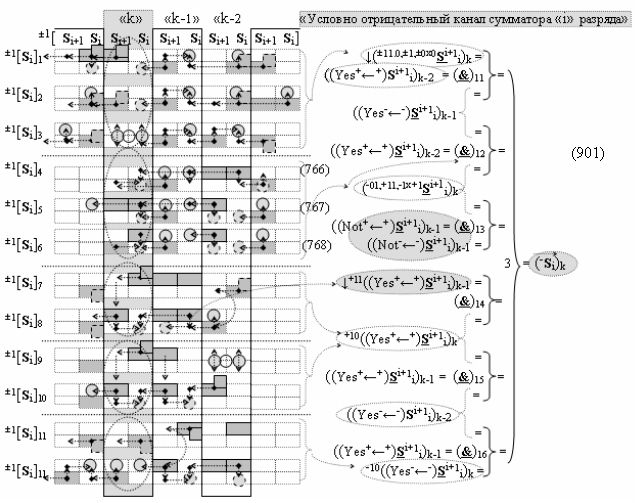
и в виде графоаналитического выражения (902),
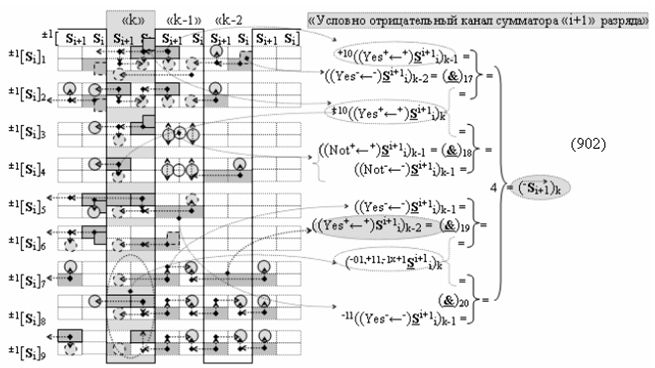
из анализа которых следует, что положительные результирующие аргументы суммы (+Si)k и (+Si+1)k и условно отрицательные аргументы суммы (-Si)k и (-Si+1)k для соответствующих входных структур «Комплексных аргументов» в условно «k» «Зоне минимизации» активизированы корректно, поскольку в системах выходных логических функций f1(})-ИЛИ, f2(})-ИЛИ и f3(})-ИЛИ и f4(})-ИЛИ активны входные логические функции f1(}&)-ИЛИ-НЕ - f6(}&)-ИЛИ-НЕ, f7(}&)-ИЛИ-НЕ - f10(}&)-ИЛИ-НЕ, f11(}&)-ИЛИ-НЕ - f16(}&)-ИЛИ-НЕ и f17(}&)-ИЛИ-НЕ - f20(}&)-ИЛИ-НЕ, поэтому формализованные преобразования аналитических выражений (897) и (898) были выполнены корректно.
Использование изобретения позволяет сформировать процесс преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) с процедурой одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1).
Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических процедур суммирования и умножения условно минимизированных аргументов аналоговых сигналов слагаемых. Техническим результатом является повышение быстродействия. В одном из вариантов функциональная структура реализована на логических элементах И, ИЛИ, ИЛИ-НЕ, И-НЕ. 5 н.п. ф-лы.
1. Способ формирования логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной
структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованный с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1) (Русская логика), в соответствии с которым в «Положительном канале сумматора «i» разряда» и «Условно отрицательном канале сумматора «i» разряда» условно «k» «Зоны минимизации» выполняют одновременный анализ аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min посредством функциональных структур
с выходными логическими функциями f5(})-ИЛИ и f6(})-ИЛИ, в систему которых включают положительные аргументы аналоговых сигналов (+ni)k и (+mi)k и условно отрицательные аргументы аналоговых сигналов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», активизирующие положительный «Комплексный аргумент» (+nVmi)k и условно отрицательный «Комплексный аргумент» (-nVmi)k и посредством функциональных структур с выходными логическими функциями f1(}&)-ИЛИ-НЕ, f3(}&)-ИЛИ-НЕ и f1(&)-И-НЕ вида
в «Положительном канале сумматора «i» разряда», в систему которых включают положительные аргументы аналоговых сигналов (+ni)k и (+mi)k и условно отрицательные аргументы аналоговых сигналов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» и активизируют обобщенный «Комплексный аргумент» (-Comp)Si+1 i)k и +(±Comp)Si+1 i)k и положительный «Комплексный аргумент» (+n&mi)k с измененным уровнем аналогового сигнала, а посредством функциональных структур с выходными логическими функциями f2(}&)-ИЛИ-НЕ , f4(}&)-ИЛИ-НЕ и f2(&)-И-НЕ вида
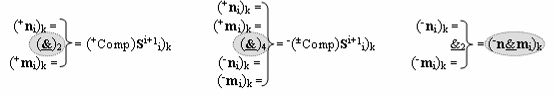
в «Условно отрицательном канале сумматора «i» разряда», в систему которых также включают положительные аргументы аналоговых сигналов (+ni)k и (+mi)k и условно отрицательные аргументы аналоговых сигналов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», активизируют обобщенный «Комплексный аргумент» (+Comp)Si+1 i)k и -(±Comp)Si+1 i)k, которые подают на соответствующие функциональные входные связи входных логических функций f1(&)-И - f6(&)-И в «Положительном канале сумматора «i» разряда» и подают на соответствующие функциональные входные связи входных логических функций f11(&)-И - f16(&)-И в «Условно отрицательном канале сумматора «i» разряда» условно «k» «Зоны минимизации», которые включают в систему выходных логических функций f1(})-ИЛИ и f3(})-ИЛИ в соответствии с аналитическим выражением вида
и посредством которых активизируют положительный аргумент результирующей суммы (+Si)k и условно отрицательный аргумент результирующей суммы (-Si)k, отличающийся тем, что для одновременного анализа аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в соответствии с графоаналитическим выражением вида
где 
и 
- положительный аргумент и условно отрицательный аргумент соответственно;
и 
- положительный двойной аргумент и условно отрицательный двойной аргумент в условно «i» и «i+1» разряда соответственно;
в каждой условно «k» «Зоне минимизации», в которую включают по два последовательных разряда - условно «i» разряд и условно «i+1» разряд и активизируют следующие «Комплексные аргументы»:
▶ «+Комплексный аргумент» (+01Si+1 i)k активизируют посредством функциональной структуры графоаналитического выражения вида
с входными логическими функциями f5(})-ИЛИ, f1(}&)-ИЛИ-НЕ и f1(&)-И-НЕ и выходной логической функцией f21(&)-И;
▶ «-Комплексный аргумент» (-01Si+1 i)k активизируют посредством функциональной структуры вида
с входными логическими функциями f6(})-ИЛИ, f2(}&)-ИЛИ-НЕ и f2(&)-И-НЕ и выходной логической функцией f22(&)-И;
▶ «+Комплексный аргумент» (+10Si+1 i)k активизируют посредством функциональной структуры графоаналитического выражения вида
с входными логическими функциями f7(})-ИЛИ, f3(}&)-ИЛИ-НЕ и f3(&)-И-НЕ и выходной логической функцией f23(&)-И;
где 
и 
- преобразованный положительный и условно отрицательный результирующий аргумент, которые активизированы посредством применения арифметических аксиом троичной системы счисления fRU(+1,0,-1);
▶ «-Комплексный аргумент» (-10Si+1 i)k активизируют посредством функциональной структуры графоаналитического выражения вида
с входными логическими функциями f8(})-ИЛИ, f4(}&)-ИЛИ-НЕ и f4(&)-И-НЕ и выходной логической функцией f24(&)-И;
▶ «+Комплексный аргумент» (+11Si+1 i)k без изменения уровня аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
с входными логическими функциями f25(&)-И и f26(&)-И;
▶ «+Комплексный аргумент» (+11Si+1 i)k с измененным уровнем аналогового сигнала активизируют посредством функциональных структур вида
с входными логическими функциями f5(&)-И-НЕ и f6(&)-И-НЕ;
▶ «-Комплексный аргумент» (-11Si+1 i)k → {-11Si+1 i}k без изменения уровня аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
с входными логическими функциями f27(&)-И и f28(&)-И;
▶ «-Комплексный аргумент» (-11Si+1 i)k → {-11Si+1 i}k с измененным уровнем аналогового сигнала активизируют посредством функциональных структур вида
с входными логическими функциями f7(&)-И-НЕ и f7(&)-И-НЕ;
▶ «+Комплексный аргумент» (+n&mi)k активизируют посредством функциональной структуры графоаналитического выражения вида
с выходной логической функцией f29(&)-И;
▶ «-Комплексный аргумент» (-n&mi)k активизируют посредством функциональной структуры графоаналитического выражения вида
с выходной логической функцией f30(&)-И;
▶ «+Комплексный аргумент» (+n&mi+1)k активизируют посредством функциональной структуры графоаналитического выражения вида
с выходной логической функцией f31(&)-И;
▶ «-Комплексный аргумент» (-n&mi+1)k активизируют посредством функциональной структуры графоаналитического выражения вида
с выходной логической функцией f32(&)-И;
▶ «±Комплексный аргумент» (+1х-1Si+1 i)k → {+1х-1Si+1 i}k активизируют посредством функциональных структур графоаналитического выражения вида
с входными логическими функциями f33(&)-И и f34(&)-И;
▶ «±Комплексный аргумент» (-1х+1Si+1 i)k → {-1х+1Si+1 i}k активизируют посредством функциональных структур графоаналитического выражения вида
с входными логическими функциями f35(&)-И f36(&)-И;
при этом «±0Комплексный аргумент» (±0x0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» активизируют посредством функциональной структуры графоаналитического выражения вида
с входной логической функцией f5(}&)-ИЛИ-НЕ;
и «±Комплексный аргумент» (±11.0,±1,±0x0Si+1 i)k одновременной активности положительных и условно отрицательных аргументов в условно «k» «Зоне минимизации», которые соответствуют арифметической аксиоме «+1»«-1» → «±01» и неактивности аргументов в условно «k» «Зоне минимизации» активизируют посредством функциональной структуры графоаналитического выражения вида
с входными логическими функциями f37(&)-И, f38(&)-И, f39(&)-И, f40(&)-И и выходной логической функцией f9(})-ИЛИ;
после чего выполняют одновременный анализ активных «Комплексных аргументов» аналоговых сигналов слагаемых в соответствующих условно «k» «Зонах минимизации» в соответствии с графоаналитическим выражением вида
и активизируют возможные дополнительные «Комплексные аргументы»:
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k активизируют посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f10(})-ИЛИ;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k активизируют посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f11(})-ИЛИ;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k активизируют посредством совокупности преобразованных положительных аргументов {+11Si+1 i}k графоаналитического выражения вида
с выходной логической функцией f12(})-ИЛИ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k активизируют посредством совокупности преобразованных условно отрицательных аргументов {-11Si+1 i}k графоаналитического выражения вида
с выходной логической функцией f13(})-ИЛИ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k активизируют посредством функциональных структур графоаналитического выражения вида
с входными логическими функциями f6(}&)-ИЛИ-НЕ, f14(})-ИЛИ и f9(&)-И-НЕ и с выходной логической функцией f41(&)-И;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k активизируют посредством функциональных структур графоаналитического выражения вида
с входными логическими функциями f7(}&)-ИЛИ-НЕ, f15(})-ИЛИ и f10(&)-И-НЕ и с выходной логической функцией f42(&)-И;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f16(})-ИЛИ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f17(})-ИЛИ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f43(&)-И;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала активизируют посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f44(&)-И;
▶ «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f18(})-ИЛИ и входными логическими функциями f5(})-ИЛИ, f1(}&)-ИЛИ-НЕ, f21(&)-И, f1(&)-И-НЕ, f27(&)-И, f28(&)-И, f33(&)-И и f34(&)-И;
▶ «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k посредством функциональных структур графоаналитического выражения вида
с выходной логической функцией f19(})-ИЛИ и входными логическими функциями f6(})-ИЛИ, f4(}&)-ИЛИ-НЕ, f24(&)-И, f2(&)-И-НЕ, f27(&)-И, f28(&)-И, f35(&)-И и f36(&)-И;
затем посредством выходной функциональной структуры «Положительного канала сумматора «i» разряда» вида
с общей выходной логической функцией f1(})-ИЛИ и в соответствии с графоаналитическим выражением вида
выполняют одновременный анализ активных «Комплексных аргументов» аналоговых сигналов слагаемых в соответствующих условно «k» «Зонах минимизации» и активизируют положительный результирующий аргумент суммы (+Si)k,
где ((Yes+←+)Si+1 i)k-1 и ((Yes-←-)Si+1 i)k-2 - «Комплексные аргументы» условно «k-1» «Зоны минимизации» и условно «k-1» «Зоны минимизации» соответственно;
а также посредством выходной функциональной структуры «Условно отрицательный канал сумматора «i» разряда» вида
с общей выходной логической функцией f3(})-ИЛИ и в соответствии с графоаналитическим выражением вида
выполняют одновременный анализ активных «Комплексных аргументов» аналоговых сигналов слагаемых в соответствующих условно «k» «Зонах минимизации» и активизируют результирующий условно отрицательный аргумент суммы (-Si)k, при этом посредством дополнительной выходной функциональной структуры с выходной логической функцией f2(})-ИЛИ «Положительного канала сумматора «i+1» разряда» в соответствии с графоаналитическим выражением вида
и дополнительной выходной функциональной структуры с выходной логической функцией f2(})-ИЛИ «Условно отрицательного канала сумматора «i+1» разряда» в соответствии с графоаналитическим выражением вида
выполняют одновременный анализ активных «Комплексных аргументов» аналоговых сигналов слагаемых в соответствующих условно «k» «Зонах минимизации» и активизируют положительный результирующий аргумент результирующей суммы (+Si+1)k и условно отрицательный аргумент результирующей суммы (-Si+1)k условно «i+1» разряда.
2. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной
структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), включающая «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации», которые включают выходную структуру логических функций, реализованную в соответствии с математической моделью вида
и с входными логическими функциями f1(&)-И - f6(&)-И и с входными логическими функциями f11(&)-И - f16(&)-И, функциональные выходные связи (=) которых являются функциональными входными связями выходной логической функции f1(})-ИЛИ и f3(})-ИЛИ для активизации положительного аргумента суммы (+Si)k условно «i» разряда и для активизации условно отрицательного аргумента (-Si)k условно «i» разряда, при этом «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации» также включает функциональную входную структуру, сформированную в соответствии с математической моделью вида
и с выходными логическими функциями f5(})-ИЛИ и f6(})-ИЛИ, функциональные входные связи которых являются функциональными входными связями для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», для активизации положительного «Комплексного аргумента» (+nVmi)k и условно отрицательного «Комплексного аргумента» (-nVmi)k, при этом «Положительный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
с выходными логическими функциями f1(}&)-ИЛИ-НЕ, f3(}&)-ИЛИ-НЕ и f1(&)-И-НЕ, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для активизации «Комплексных аргументов» (-Comp)Si+1 i)k, +(±Comp)Si+1 i)k и «Комплексного аргумента» (+n&mi)k с измененным уровнем аналогового сигнала, при этом «Положительный канал сумматора «i» разряда» также включает логическую функцию f21(&)-И, а «Условно отрицательный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
и с выходными логическими функциями f2(}&)-ИЛИ-НЕ, f4(}&)-ИЛИ-НЕ и f2(&)-И-НЕ, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для активизации «Комплексных аргументов» (+Comp)Si+1 i)k, -(±Comp)Si+1 i)k и «Комплексного аргумента» (-n&mi)k с измененным уровнем аналогового сигнала, при этом «Условно отрицательный канал сумматора «i» разряда» также включает логическую функцию f22(&)-И, отличающаяся тем, что в условно «k» «Зону минимизации» введены в соответствии с аналитическим выражением вида
дополнительная структура логических функций с входными логическими функциями f7(&)-И - f10(&)-И, функциональные выходные связи которых являются функциональными входными связями логической функции f2(})-ИЛИ, которая активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда в «Положительном канале сумматора «i+1» разряда», и дополнительная структура логических функций с входными логическими функциями f17(&)-И - f20(&)-И, функциональные выходные связи которых являются функциональными входными связями логической функции f4(})-ИЛИ, которая активизирует условно отрицательный результирующий аргумент (-Si+1)k условно «i+1» разряда в «Условно отрицательном канале сумматора «i+1» разряда», при этом в систему входных логических функций f1(&)-И - f10(&)-И «Положительного канал сумматора «i» разряда» и «Положительного канал сумматора «i+1» разряда», которые сформированы в соответствии с математической моделью вида
с входными «Комплексными аргументами», которые включены также и в «Условно отрицательный канал сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k функциональной входной структуры, которая сформирована в соответствии с математической моделью вида
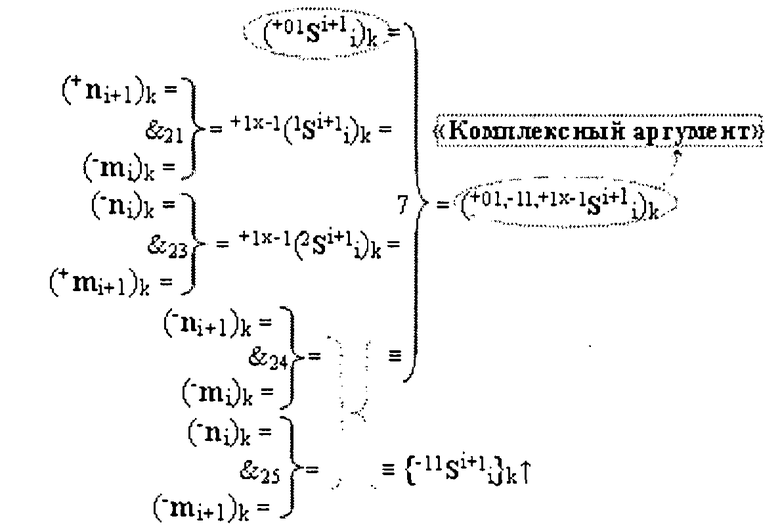
и с выходной логической функцией f18(})-ИЛИ и входными логическими функциями f45(&)-И, f46(&)-И, f47(&)-И и f48(&)-И, в которой «+Комплексный аргумент» (+01Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f5(})-ИЛИ, f1(}&)-ИЛИ-НЕ и f1(&)-И-НЕ и выходной логической функцией f21(&)-И;
а в систему входных логических функций f1(&)-И - f10(&)-И «Условно отрицательного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i+1» разряда», которые сформированы в соответствии с математической моделью вида
включены «Комплексные аргументы», которые являются общими аргументами с «Положительным каналом сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k функциональной входной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f8(})-ИЛИ и входными логическими функциями f22(&)-И, f27(&)-И, f28(&)-И и f29(&)-И, в которой «-Комплексный аргумент» (-01Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f6(})-ИЛИ, f2(}&)-ИЛИ-НЕ и f2(&)-И-НЕ и выходной логической функцией f30(&)-И;
при этом «Комплексные аргументы» в выходных функциональных структурах, которые реализованы в соответствии с математической модели «Положительного канала сумматора «i+1» и «i» разряда» и математической модели «Условно отрицательного канала сумматора «i+1» и «i» разряда» сформированы посредством следующих функциональных структур:
▶ «±Комплексный аргумент» (±11.0,±1,±0x0Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f31(&)-И, f32(&)-И, f33(&)-И, f34(&)-И и выходной логической функцией f9(})-ИЛИ, в которой «±0Комплексный аргумент» (±0x0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входной логической функцией f5(}&)-ИЛИ-НЕ, «+Комплексный аргумент» (+n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f35(&)-И, а «-Комплексный аргумент» (-n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
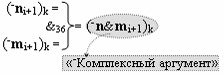
с выходной логической функцией f36(&)-И;
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
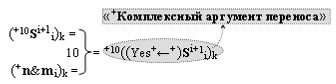
с выходной логической функцией f10(})-ИЛИ, в которой «+Комплексный аргумент» (+10Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f11(})-ИЛИ, f3(}&)-ИЛИ-НЕ и f3(&)-И-НЕ и выходной логической функцией f37(&)-И, а «+Комплексный аргумент» (+n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f38(&)-И;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
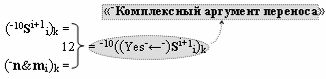
с выходной логической функцией f12(})-ИЛИ, в которой «-Комплексный аргумент» (-10Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f13(})-ИЛИ, f4(}&)-ИЛИ-НЕ и f4(&)-И-НЕ и выходной логической функцией f39(&)-И, а «-Комплексный аргумент» (-n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f40(&)-И;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f14(})-ИЛИ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
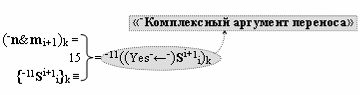
с выходной логической функцией f15(})-ИЛИ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f6(}&)-ИЛИ-НЕ, f16(})-ИЛИ и f1(&)-И-НЕ и с выходной логической функцией f41(&)-И, в которой «+Комплексный аргумент» {+11Si+1 i}k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f5(&)-И-НЕ и f6(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f7(}&)-ИЛИ-НЕ, f17(})-ИЛИ и f2(&)-И-НЕ и с выходной логической функцией f42(&)-И, в которой «-Комплексный аргумент» (-11Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f7(&)-И-НЕ и f8(&)-И-НЕ;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
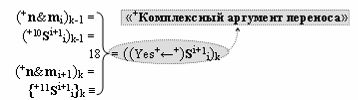
с выходной логической функцией f18(})-ИЛИ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f119(})-ИЛИ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
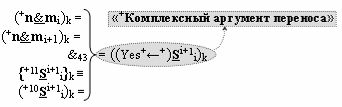
с выходной логической функцией f43(&)-И;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
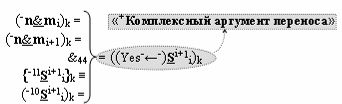
с выходной логической функцией f44(&)-И.
3. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной
структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), включающая «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации», которые включают выходную структуру логических функций, реализованную в соответствии с математической моделью вида
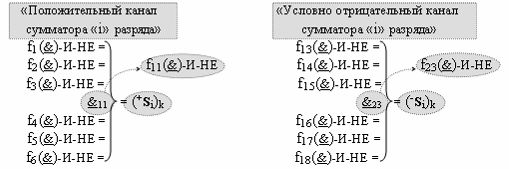
и с входными логическими функциями f1(&)-И-НЕ - f6(&)-И-НЕ и с входными логическими функциями f13(&)-И-НЕ - f18(&)-И-НЕ, функциональные выходные связи (=) которых являются функциональными входными связями выходной логической функции f11(&)-И-НЕ и f23(&)-И-НЕ для формирования положительного аргумента суммы (+Si)k условно «i» разряда и для активизации условно отрицательного аргумента (-Si)k условно «i» разряда, при этом «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации» также включает функциональную входную структуру, сформированную в соответствии с математической моделью вида
и с выходными логическими функциями f1(})-ИЛИ и f2(})-ИЛИ, функциональные входные связи которых являются функциональными входными связями для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», для активизации положительного «Комплексного аргумента» (+nVmi)k и условно отрицательного «Комплексного аргумента» (-nVmi)k, при этом «Положительный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
и с выходными логическими функциями f1(}&)-ИЛИ-НЕ, f3(}&)-ИЛИ-НЕ и f25(&)-И-НЕ, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для формирования обобщенного «Комплексного аргумента» (-Comp)Si+1 i)k и +(±Comp)Si+1 i)k и положительного «Комплексного аргумента» (+n&mi)k с измененным уровнем аналогового сигнала, при этом «Положительный канал сумматора «i» разряда» также включает логическую функцию f26(&)-И-НЕ и f5(}&)-ИЛИ-НЕ;
а «Условно отрицательный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
и с выходными логическими функциями f2(}&)-ИЛИ-НЕ, f4(}&)-ИЛИ-НЕ и f27(&)-И-НЕ, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для формирования обобщенного «Комплексного аргумента» (+Comp)Si+1 i)k и -(±Comp)Si+1 i)k и условно отрицательного «Комплексного аргумента» (-n&mi)k с измененным уровнем аналогового сигнала, при этом «Условно отрицательный канал сумматора «i» разряда» также включает логическую функцию f28(&)-И-НЕ и f6(}&)-ИЛИ-НЕ; отличающаяся тем, что в условно «k» «Зону минимизации» введены в соответствии с аналитическим выражением вида
дополнительная структура логических функций с входными логическими функциями f7(&)-И-НЕ - f10(&)-И-НЕ, функциональные выходные связи которых являются функциональными входными связями логической функции f12(&)-И-НЕ, которая активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда в «Положительном канале сумматора «i+1» разряда», и дополнительная структура логических функций с входными логическими функциями f19(&)-И-НЕ - f22(&)-И-НЕ, функциональные выходные связи которых являются функциональными входными связями логической функции f24(&)-И-НЕ, которая активизирует условно отрицательный результирующий аргумент (-Si+1)k условно «i+1» разряда в «Условно отрицательном канале сумматора «i+1» разряда», при этом в систему входных логических функций f1(&)-И-НЕ - f10(&)-И-НЕ «Положительного канал сумматора «i» разряда» и «Положительного канал сумматора «i+1» разряда», реализованные в соответствии с математической моделью вида
с входными «Комплексными аргументами», которые включены также и в «Условно отрицательный канал сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k функциональной входной структуры, которая сформирована в соответствии с математической моделью вида
и с выходной логической функцией f3(})-ИЛИ и входными логическими функциями f1(&)-И, f2(&)-И, f3(&)-И и f4(&)-И, в которой «+Комплексный аргумент» (+01Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f1(})-ИЛИ, f1(}&)-ИЛИ-НЕ и f25(&)-И-НЕ и выходной логической функцией f5(&)-И;
а в систему входных логических функций f11(&)-И-НЕ - f20(&)-И-НЕ «Условно отрицательного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i+1» разряда», сформированные в соответствии с математической моделью вида
с входными «Комплексными аргументами», которые являются общими аргументами с «Положительным каналом сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k функциональной входной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f4(})-ИЛИ и входными логическими функциями f6(&)-И, f7(&)-И, f8(&)-И и f9(&)-И, в которой «-Комплексный аргумент» (-01Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f2(})-ИЛИ, f2(}&)-ИЛИ-НЕ и f27(&)-И-НЕ и выходной логической функцией f10(&)-И;
при этом «Комплексные аргументы» в выходных функциональных структурах, которые реализованы в соответствии с математической модели «Положительного канала сумматора «i+1» и «i» разряда» и математической модели «Условно отрицательного канала сумматора «i+1» и «i» разряда», сформированы посредством следующих функциональных структур:
▶ «±Комплексный аргумент» (±11.0,±1,±0x0Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f11(&)-И, f12(&)-И, f13(&)-И, f14(&)-И и выходной логической функцией f5(})-ИЛИ, в которой «±0Комплексный аргумент» (±0x0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входной логической функцией f5(}&)-ИЛИ-НЕ, «+Комплексный аргумент» (+n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
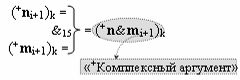
с выходной логической функцией f15(&)-И, а «-Комплексный аргумент» (-n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
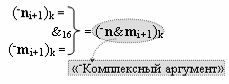
с выходной логической функцией f16(&)-И;
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f6(})-ИЛИ, в которой «+Комплексный аргумент» (+10Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f7(})-ИЛИ, f3(}&)-ИЛИ-НЕ и f26(&)-И-НЕ и выходной логической функцией f17(&)-И, а «+Комплексный аргумент» (+n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
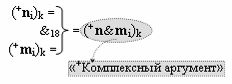
с выходной логической функцией f18(&)-И;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
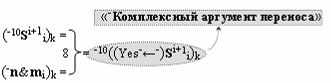
с выходной логической функцией f8(})-ИЛИ, в которой «-Комплексный аргумент» (-10Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f9(})-ИЛИ, f4(}&)-ИЛИ-НЕ и f28(&)-И-НЕ и выходной логической функцией f19(&)-И, а «-Комплексный аргумент» (-n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f20(&)-И;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
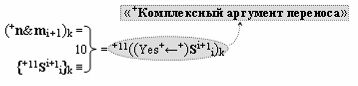
с выходной логической функцией f10(})-ИЛИ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
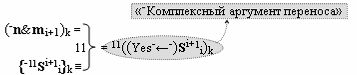
с выходной логической функцией f11(})-ИЛИ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f6(}&)-ИЛИ-НЕ, f12(})-ИЛИ и f29(&)-И-НЕ и с выходной логической функцией f21(&)-И, в которой «+Комплексный аргумент» {+11Si+1 i}k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f30(&)-И-НЕ и f31(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f7(}&)-ИЛИ-НЕ, f13(})-ИЛИ и f32(&)-И-НЕ и с выходной логической функцией f22(&)-И, в которой «-Комплексный аргумент» (-11Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f33(&)-И-НЕ и f34(&)-И-НЕ;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f14(})-ИЛИ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
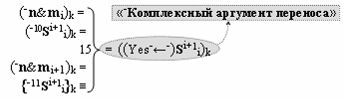
с выходной логической функцией f15(})-ИЛИ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
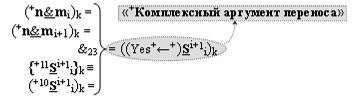
с выходной логической функцией f23(&)-И;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
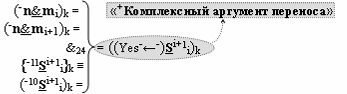
с выходной логической функцией f24(&)-И.
4. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной
структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), включающая «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации», которые включают выходную структуру логических функций, реализованную в соответствии с математической моделью вида
и с входными логическими функциями f1(})-ИЛИ - f6(})-ИЛИ и с входными логическими функциями f11(})-ИЛИ - f16(})-ИЛИ, функциональные выходные связи (=) которых являются функциональными входными связями выходной логической функции f1(&)-И-НЕ и f3(&)-И-НЕ для формирования положительного аргумента суммы (+Si)k условно «i» разряда и для активизации условно отрицательного аргумента (-Si)k условно «i» разряда, при этом «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации» также включает функциональную входную структуру, которая сформирована в соответствии с математической моделью вида
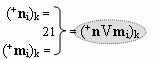
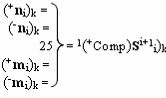
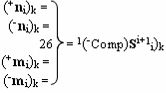
с выходной логической функцией f21(})-ИЛИ, f25(})-ИЛИ и f22(})-ИЛИ, f26(})-ИЛИ, в которых функциональные входные связи являются функциональными входными связями для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», для формирования положительного «Комплексного аргумента» (+nVmi)k и условно отрицательного «Комплексного аргумента» (-nVmi)k, при этом «Положительный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
с выходной логической функцией f1(}&)-ИЛИ-НЕ и f1(&)-И, функциональные входные связи которых являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k условно «i» разряда «k» «Зоны минимизации» для активизации обобщенного «Комплексного аргумента» (+Comp)Si+1 i)k и положительного «Комплексного аргумента» (+n&mi)k без изменения уровня аналогового сигнала, при этом «Положительный канал сумматора «i» разряда» также включает также логическую функцию f23(})-ИЛИ, а «Условно отрицательный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
с выходными логическими функциями f2(}&)-ИЛИ-НЕ и f2(&)-И, функциональные входные связи которых являются функциональными входными связями сумматора для приема условно отрицательных аргументов аналоговых сигналов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для формирования обобщенного «Комплексного аргумента» (-Comp)Si+1 i)k
и условно отрицательного «Комплексного аргумента» (-n&mi)k без изменения уровня аналогового сигнала, при этом «Условно отрицательный канал сумматора «i» разряда» включает также логическую функцию f24(})-ИЛИ, отличающаяся тем, что в условно «k» «Зону минимизации» введены в соответствии с аналитическим выражением вида
дополнительная структура логических функций с входными логическими функциями f7(})-ИЛИ - f10(})-ИЛИ, функциональные выходные связи которых являются функциональными входными связями логической функции f2(&)-И-НЕ, которая активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда в «Положительном канале сумматора «i+1» разряда», и дополнительная структура логических функций с входными логическими функциями f17(})-ИЛИ - f20(})-ИЛИ, функциональные выходные связи которых являются функциональными входными связями логической функции f4(&)-И-НЕ, которая формирует условно отрицательный результирующий аргумент (-Si+1)k условно «i+1» разряда в «Условно отрицательном канале сумматора «i+1» разряда», при этом в систему входных логических функций f1(})-ИЛИ - f10(})-ИЛИ «Положительного канал сумматора «i» разряда» и «Положительного канал сумматора «i+1» разряда», реализованные в соответствии с математической моделью вида
с входными «Комплексными аргументами», которые включены также и в «Условно отрицательный канал сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
и с выходной логической функцией f3(}&)-ИЛИ-НЕ и входными логическими функциями f3(&)-И, f4(&)-И, f5(&)-И и f6(&)-И, в которой «+Комплексный аргумент» (+01Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f21(})-ИЛИ, f4(}&)-ИЛИ-НЕ и f1(&)-И-НЕ и выходной логической функцией f7(&)-И;
а в систему входных логических функций f11(})-ИЛИ - f20(})-ИЛИ «Условно отрицательного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i+1» разряда», сформированные в соответствии с математической моделью вида
включены «Комплексные аргументы», которые являются общими аргументами с «Положительным каналом сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f5(}&)-ИЛИ-НЕ и входными логическими функциями f8(&)-И, f9(&)-И, f10(&)-И и f11(&)-И, в которой «-Комплексный аргумент» (-01Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f22(})-ИЛИ, f6(}&)-ИЛИ-НЕ и f2(&)-И-НЕ и выходной логической функцией f12(&)-И;
при этом «Комплексные аргументы» в выходных функциональных структурах, которые реализованы в соответствии с математической модели «Положительного канала сумматора «i+1» и «i» разряда» и математической модели «Условно отрицательного канала сумматора «i+1» и «i» разряда», сформированы посредством следующих функциональных структур:
▶ «±Комплексный аргумент» (±11.0,±1,±0x0Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f13(&)-И, f14(&)-И, f15(&)-И, f16(&)-И и выходной логической функцией f7(}&)-ИЛИ-НЕ, в которой «±0Комплексный аргумент» (±0x0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входной логической функцией f8(}&)-ИЛИ-НЕ, «+Комплексный аргумент» (+n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f17(&)-И, а «-Комплексный аргумент» (-n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
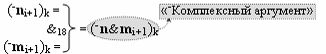
с выходной логической функцией f18(&)-И;
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
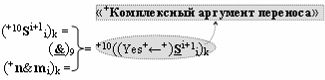
с выходной логической функцией f9(}&)-ИЛИ-НЕ, в которой «+Комплексный аргумент» (+10Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f23(})-ИЛИ, f1(}&)-ИЛИ-НЕ и f3(&)-И-НЕ и выходной логической функцией f19(&)-И, а «+Комплексный аргумент» (+n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f1(&)-И;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f10(}&)-ИЛИ, в которой «-Комплексный аргумент» (-10Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f24(})-ИЛИ, f2(}&)-ИЛИ-НЕ и f4(&)-И-НЕ и выходной логической функцией f20(&)-И, а «-Комплексный аргумент» (-n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
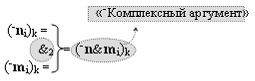
с выходной логической функцией f2(&)-И;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f11(}&)-ИЛИ-НЕ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f12(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f13(}&)-ИЛИ-НЕ, f25(})-ИЛИ и f6(&)-И-НЕ и с выходной логической функцией f5(&)-И-НЕ, в которой «+Комплексный аргумент» {+11Si+1 i}k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f7(&)-И-НЕ и f8(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f14(}&)-ИЛИ-НЕ, f26(})-ИЛИ и f10(&)-И-НЕ и с выходной логической функцией f9(&)-И-НЕ, в которой «-Комплексный аргумент» (-11Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f11(&)-И-НЕ и f12(&)-И-НЕ;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f15(}&)-ИЛИ-НЕ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f16(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f13(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
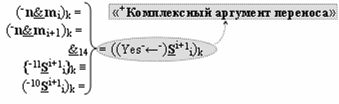
с выходной логической функцией f14(&)-И-НЕ.
5. Функциональная структура логико-динамического процесса преобразования условно минимизированных структур аргументов аналоговых сигналов слагаемых ±[ni]f(+/-)min и ±[mi]f(+/-)min в функциональной
структуре сумматора ±f1(ΣRU)min без сквозного переноса f1(±←←) и технологическим циклом ∆tΣ → 5∙f(&)-И пять условных логических функций f(&)-И, реализованная с применением процедуры одновременного преобразования аргументов слагаемых посредством арифметических аксиом троичной системы счисления fRU(+1,0,-1), включающая «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации», включающие выходную структуру логических функций, которая реализована в соответствии с математической моделью вида
и с входными логическими функциями f1(}&)-ИЛИ-НЕ - f6(}&)-ИЛИ-НЕ и с входными логическими функциями f11(}&)-ИЛИ-НЕ - f16(}&)-ИЛИ-НЕ, функциональные выходные связи (=) которых являются функциональными входными связями выходной логической функции f1(})-ИЛИ и f3(})-ИЛИ для активизации положительного аргумента суммы (+Si)k условно «i» разряда и для активизации условно отрицательного аргумента (-Si)k условно «i» разряда, при этом «Положительный канал сумматора «i» разряда» и «Условно отрицательный канал сумматора «i» разряда» условно «k» «Зоны минимизации» также включает функциональную входную структуру сформированной в соответствии с математической моделью вида
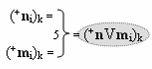
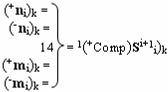
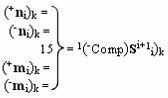
и с выходными логическими функциями f5(})-ИЛИ, f14(})-ИЛИ и f6(})-ИЛИ, f15(})-ИЛИ, в которых функциональные входные связи являются функциональными входными связями для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k и условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации», для активизации положительного «Комплексного аргумента» (+nVmi)k и условно отрицательного «Комплексного аргумента» (-nVmi)k, при этом «Положительный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
с выходными логическими функциями f21(}&)-ИЛИ-НЕ и f1(&)-И, в которых функциональные входные связи являются функциональными входными связями сумматора для приема положительных аналоговых сигналов аргументов (+ni)k и (+mi)k условно «i» разряда «k» «Зоны минимизации» для активизации обобщенного «Комплексного аргумента» (+Comp)Si+1 i)k «Комплексного аргумента» (+n&mi)k, при этом «Положительный канал сумматора «i» разряда» также включает логическую функцию f25(}&)-ИЛИ-НЕ, а «Условно отрицательный канал сумматора «i» разряда» также включает функциональные входные структуры, сформированные в соответствии с математической моделью вида
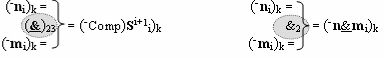
с выходными логическими функциями f4(}&)-ИЛИ-НЕ и f2(&)-И, функциональные входные связи которых являются функциональными входными связями сумматора для приема условно отрицательных аналоговых сигналов аргументов (-ni)k и (-mi)k условно «i» разряда «k» «Зоны минимизации» для активизации обобщенного «Комплексного аргументоа»
(-Comp)Si+1 i)k и «Комплексного аргумента» (-n&mi)k, при этом «Условно отрицательный канал сумматора «i» разряда» также включает логическую функцию f26(}&)-ИЛИ-НЕ, отличающаяся тем, что в условно «k» «Зону минимизации» введены в соответствии с аналитическим выражением вида
дополнительная структура логических функций с входными логическими функциями f7(}&)-ИЛИ-НЕ - f10(}&)-ИЛИ-НЕ, функциональные выходные связи которых являются функциональными входными связями логической функции f2(})-ИЛИ и которая активизирует положительный результирующий аргумент (+Si+1)k условно «i+1» разряда в «Положительном канале сумматора «i+1» разряда», и дополнительная структура логических функций с входными логическими функциями f17(}&)-ИЛИ-НЕ - f20(}&)-ИЛИ-НЕ, функциональные выходные связи которых являются функциональными входными связями логической функции f4(})-ИЛИ и которая активизирует условно отрицательный результирующий аргумент (-Si+1)k условно «i+1» разряда в «Условно отрицательном канале сумматора «i+1» разряда», при этом в систему входных логических функций f1(}&)-ИЛИ-НЕ - f10(}&)-ИЛИ-НЕ «Положительного канал сумматора «i» разряда» и «Положительного канал сумматора «i+1» разряда», которые реализованы в соответствии с математической моделью вида
включены «Комплексные аргументы», которые также включены и в «Условно отрицательный канал сумматора «i+1» и «i» разряда», а также включен «Комплексный аргумент» (+01,-11,+1х-1Si+1 i)k с измененным уровнем аналогового сигнала и он является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f22(}&)-ИЛИ-НЕ и входными логическими функциями f3(&)-И, f4(&)-И, f5(&)-И и f6(&)-И, в которой «+Комплексный аргумент» (+01Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f5(})-ИЛИ, f25(}&)-ИЛИ-НЕ и f1(&)-И-НЕ и выходной логической функцией f7(&)-И;
а в систему входных логических функций f1(})-ИЛИ - f10(})-ИЛИ «Условно отрицательного канала сумматора «i» разряда» и «Условно отрицательного канала сумматора «i+1» разряда», сформированные в соответствии с математической моделью вида
включены «Комплексные аргументы», которые являются общими аргументами с «Положительным каналом сумматора «i+1» и «i» разряда», а также «Комплексный аргумент» (-01,+11,-1х+1Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f24(}&)-ИЛИ-НЕ и входными логическими функциями f8(&)-И, f9(&)-И, f10(&)-И и f11(&)-И, в которой «-Комплексный аргумент» (-01Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f6(})-ИЛИ, f21(}&)-ИЛИ-НЕ и f2(&)-И-НЕ и выходной логической функцией f12(&)-И;
при этом «Комплексные аргументы» в выходных функциональных структурах, которые реализованы в соответствии с математической моделью «Положительного канала сумматора «i+1» и «i» разряда» и математической моделью «Условно отрицательного канала сумматора «i+1» и «i» разряда», сформированы посредством следующих функциональных структур:
▶ «±Комплексный аргумент» (±11.0,±1,±0x0Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f13(&)-И, f14(&)-И, f15(&)-И, f16(&)-И и выходной логической функцией f27(}&)-ИЛИ-НЕ, в которой «+Комплексный аргумент» (+n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
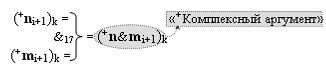
с выходной логической функцией f17(&)-И, «-Комплексный аргумент» (-n&mi+1)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
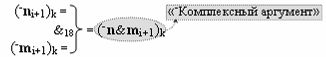
с выходной логической функцией f18(&)-И, а «±0Комплексный аргумент» (±0x0Si+1 i)k неактивности аргументов в условно «k» «Зоне минимизации» является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входной логической функцией f28(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент переноса» +10((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
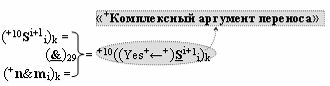
с выходной логической функцией f29(}&)-ИЛИ-НЕ, в которой «+Комплексный аргумент» (+10Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f7(})-ИЛИ, f21(}&)-ИЛИ-НЕ и f3(&)-И-НЕ и выходной логической функцией f19(&)-И, а «+Комплексный аргумент» (+n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f1(&)-И;
▶ «-Комплексный аргумент переноса» -10((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
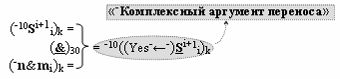
с выходной логической функцией f30(}&)-ИЛИ, в которой «-Комплексный аргумент» (-10Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f8(})-ИЛИ, f23(}&)-ИЛИ-НЕ и f4(&)-И-НЕ и выходной логической функцией f20(&)-И, а «-Комплексный аргумент» (-n&mi)k является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f2(&)-И;
▶ «+Комплексный аргумент переноса» +11((Yes+←+)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
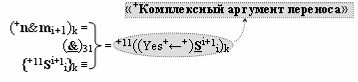
с выходной логической функцией f31(}&)-ИЛИ-НЕ;
▶ «-Комплексный аргумент переноса» -11((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
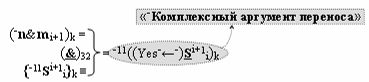
с выходной логической функцией f32(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент» ((Not+←+)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f33(}&)-ИЛИ-НЕ, f14(})-ИЛИ и f6(&)-И-НЕ и с выходной логической функцией f5(&)-И-НЕ в которой «+Комплексный аргумент» {+11Si+1 i}k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f7(&)-И-НЕ и f8(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Not-←-)Si+1 i)k с изменением уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f34(}&)-ИЛИ-НЕ, f15(})-ИЛИ и f10(&)-И-НЕ и с выходной логической функцией f9(&)-И-НЕ, в которой «-Комплексный аргумент» (-11Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с входными логическими функциями f11(&)-И-НЕ и f12(&)-И-НЕ;
▶ «+Комплексный аргумент переноса» ((Yes+←+)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
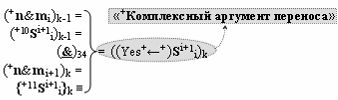
с выходной логической функцией f34(}&)-ИЛИ-НЕ;
▶ «-Комплексный аргумент переноса» ((Yes-←-)Si+1 i)k без изменения уровня аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
с выходной логической функцией f35(}&)-ИЛИ-НЕ;
▶ «+Комплексный аргумент» ((Yes+←+)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
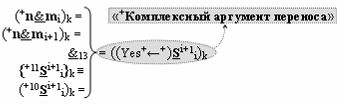
с выходной логической функцией f13(&)-И-НЕ;
▶ «-Комплексный аргумент» ((Yes-←-)Si+1 i)k с измененным уровнем аналогового сигнала является преобразованным аргументом функциональной структуры, которая сформирована в соответствии с математической моделью вида
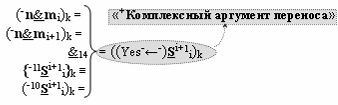
с выходной логической функцией f14(&)-И-НЕ.
| ФУНКЦИОНАЛЬНАЯ ВХОДНАЯ СТРУКТУРА СУММАТОРА С ИЗБИРАТЕЛЬНЫМ ЛОГИЧЕСКИМ ДИФФЕРЕНЦИРОВАНИЕМ d*/dn ПЕРВОЙ ПРОМЕЖУТОЧНОЙ СУММЫ ±[S ] МИНИМИЗИРОВАННЫХ СТРУКТУР АРГУМЕНТОВ СЛАГАЕМЫХ ±[n]f(+/-) и ±[m]f(+/-) (ВАРИАНТЫ) | 2009 |
|
RU2424548C1 |
| ФУНКЦИОНАЛЬНАЯ ВХОДНАЯ СТРУКТУРА СУММАТОРА С ПРОЦЕДУРОЙ ЛОГИЧЕСКОГО ДИФФЕРЕНЦИРОВАНИЯ d/dn ПЕРВОЙ ПРОМЕЖУТОЧНОЙ СУММЫ МИНИМИЗИРОВАННЫХ АРГУМЕНТОВ СЛАГАЕМЫХ ±[n]f(+/-) И ±[m]f(+/-) (ВАРИАНТЫ РУССКОЙ ЛОГИКИ) | 2009 |
|
RU2427028C2 |
| Последовательный сумматор в избыточной двоичной системе счисления | 1988 |
|
SU1619251A1 |
| JP 62221727 A, 29.09.1987 | |||
| JP 2002014804 A, 18.01.2002 | |||
| US 7274211 B1, 25.09.2007 | |||
