Изобретение относится к области поиска (определения координат) скрытых ферромагнитных объектов, от подводных лодок до неразорвавшихся боеприпасов (бомб, снарядов, донных мин) или зарытых в земле единиц стрелкового оружия (пулемет, карабин, автомат, пистолет) и т.д.
Многие сосредоточенные источники магнитного поля можно аппроксимировать (точечным) диполем с магнитным моментом М=Mm, где М - модуль магнитного момента, m - единичный вектор направления магнитного момента. Различают задачи обнаружения, пеленгации и локализации (неподвижного или движущегося) диполя по параметрам его магнитного поля в одной или нескольких точках наблюдения. При локализации определяют радиус-вектор Х=Хn, где Х - модуль расстояния, n - единичный вектор направления. Другими словами, при локализации определяют неизвестные координаты вектора Х в системе координат наблюдения. При пеленгации определяют неизвестные углы или косинусы углов единичного направления n в системе координат наблюдения. При обнаружении определяют параметры неоднородного магнитного поля на фоне поля Земли, по которым судят о том, что «где-то что-то есть». Некоторые специалисты под обнаружением понимают и пеленгацию, и локализацию. Однако мы для определенности будем различать эти задачи.
Задачу пеленгации магнитного диполя, по-видимому, впервые поставил О.П.Хвостов [Магнитный пеленгатор // Геофизическое приборостроение. Л.: Гостехиздат. 1963. С.3-11], который также предложил приближенное решение ее по градиенту модуля дипольной индукции.
Первое аналитическое (точное) решение задачи пеленгации диполя по градиенту вектора дипольной индукции получил C.Frahm [W.M.Wynn a.o. Advanced Superconducting Gradiometer/Magnetometer Arrays and a Novel Signal Processing Technique // IEEE Transactions on Magnetics, vol. MAG-11, no.2, March 1975 P.701-707]. Решение Frahm'a было неоднозначным. Оно включало 4 направления, одно из которых было истинным. Там же приводились результаты экспериментальных исследований локализации диполя с помощью пятикомпонентного градиентометра на сверхпроводниковых датчиках в комбинации с трехкомпонентным феррозондовым магнитометром.
Затем T.Kolbenhayer [Prispevok krieseniu obratenej magnetometrickey ulohy predipol // Banickey listy. 1976. #4 31-35 (Реферативный Журнал Геология. 1980. №12. С.20)] нашел аналитическое решение задачи локализации по заданным вектору и градиенту вектора дипольной индукции, опираясь на теорему Эйлера для однородных функций. Его решение было однозначным, но неустойчивым к ориентации искомого диполя.
Сообщение о работе Kolbenhayer'a появилось в СССР с задержкой на 4 года (См. выше соответствующую ссылку в Реферативном Журнале по Геологии). Получилось так, что работа В.Г. Семенова [Решение обратной задачи для источника физического поля дипольной или квадрупольной модели // Методы и средства точных магнитных измерений / Сб. научных трудов НПО «ВНИИМ им. Д.И.Менделеева». 1980. С.3-19] сначала независимо повторила, а затем и радикально усовершенствовала решение Kolbenhayer'a [1977] в части устойчивости. Факт устойчивости подтвердили А.Ю.Симонов и соавторы [Возмущение решения обратной задачи для магнитостатического диполя ошибками исходных данных // Известия вузов MB и ССО СССР. Физика. 1985. №6. С.17-22], которые сравнили оба решения (исходное и усовершенствованное), моделируя их на ЭВМ. Итак, метод Семенова [1980] (далее просто [1980]) представляет собой однозначное и устойчивое к ориентации искомого диполя решение задачи локализации в явном виде в реальном масштабе времени по результатам измерения магнитного поля в одной произвольно выбранной точке, а именно вектора магнитного поля искомого диполя (3 компоненты) и его градиента (5 независимых из 9 компонент).
Кроме того, там же [1980] получено решение в общем виде относительно магнитного момента в векторной и матричной (инвариантной) форме по заданной индукции магнитного поля диполя. Это ускоряет численное решение задачи локализации диполя по двум (и более) точкам измерения дипольной индукции, благодаря возможности исключения магнитного момента из числа искомых неизвестных, что также показано в статье [Ю.М.Иванов и В.Г.Семенов. Оценки погрешностей пеленгации и локализации источника магнитного поля дипольной модели // Измерительная техника №5. 2008. С.30-35 и №7. 2008. С.72].
Следует также отметить, что работе [1980] предшествовала другая работа [В.Г.Семенов и Г.Н.Дзария. Решение обратной задачи по определению дипольного магнитного момента // Метрология №12. 1977. С.29-35], которая представила дипольную индукцию и ее пространственные производные в развернутой матричной (инвариантной) форме и, по-видимому впервые, применила прием исключения магнитного момента из числа искомых неизвестных.
В последующей работе [В.Г.Семенов и В.Э.Сонина. Анализ методов измерения магнитных моментов // Метрология №8. 1992. С.3-46] получено решение в общем виде относительно магнитного момента в матричной (инвариантной) форме по заданному пространственному приращению магнитного поля диполя и определено условие устойчивости этого решения.
Наконец, известны следующие приемы повышения точности измерения пространственного приращения магнитной индукции, а также базы приращения:
- Патент РФ №2256930. Способ минимизации погрешностей в переносном дифференциальном магнитометре. Приоритет изобретения от 07.04.2003 г.;
- Патент РФ №2257593. Способ минимизации погрешностей в дифференциальном магнитометре. Приоритет изобретения от 07.04.2003 г.;
- Патент РФ №2290657. Способ определения местоположения и ориентации трехкомпонентного датчика магнитометра относительно меры магнитного момента. Приоритет изобретения от 09.08.2005 г.;
- Патент РФ №2313801. Способ измерения приращения индукции магнитного поля трехкомпонентным дифференциальным магнитометром. Приоритет изобретения от 04.05.2006 г.
В качестве прототипа выбран способ локализации источника магнитного поля дипольной модели [1980] по совокупности существенных признаков, наиболее близких к заявляемому способу.
Известный способ [1980] включает измерения пространственного приращения индукции магнитного поля между каждой из двух пар периферийных точек, выбранных вдоль двух ортогональных направлений симметрично относительно центра наблюдения, и коррекцию нулей средств измерения индукции магнитного поля в центре наблюдения в условиях отсутствия искомого источника магнитного поля дипольной модели, а также измерения расстояния между каждой парой периферийных точек, затем измерения перечисленных параметров магнитного поля в присутствии искомого источника, обработку результатов измерения для определения в явном виде неизвестных радиуса-вектора между центром наблюдения и искомым диполем и его вектора магнитного момента.
Причиной, препятствующей достижению указанного ниже технического результата для известного способа, является то, что известный способ использует две ортогональные измерительные штанги конечной длины для измерения пространственных производных индукции магнитного поля локализуемого источника или градиента индукции (совокупности девяти производных по координатам). На значительных удалениях производные могут быть аппроксимированы пространственными приращениями, но при малых удалениях возникает значительная методическая погрешность. Кроме того, коррекция нулей измерителя магнитного поля при локализации источника по известному способу возможна лишь в стационарных условиях при удаленном локализуемом источнике. Поэтому известный способ применяют стационарно, например для охраны водного района от проникновения ПЛ и подводных аппаратов противника.
Задача, на решение которой направлено заявляемое изобретение, состоит в повышении точности локализации за счет направленного приближения измерительного узла к искомому источнику.
Технический результат, получаемый при осуществлении изобретения, заключается в обеспечении возможности такого приближения благодаря способу локализации источника одной переносной магнитометрической штангой, основанному на измерении приращений индукции между центром и концами штанги.
Указанный технический результат достигается тем, что заявляемый способ локализации источника магнитного поля дипольной модели, включающий измерения пространственных приращений индукции магнитного поля и расстояниий между парами периферийных точек, выбранных симметрично относительно центра наблюдения, обработку результатов измерения для определения неизвестных радиуса-вектора Х между центром наблюдения и искомым диполем и его вектора магнитного момента М, отличается тем, что в центре 0 и на краях 1 и 2 переносной штанги устанавливают трехкомпонентные датчики магнитного поля для измерения приращений индукции В
10 между точками 1 и 0 и В
02 между точками 0 и 2, затем штангу приближают в район местоположения источника до появления удобочитаемых значений В
10 и В
02, после чего ее ориентируют приблизительно до максимума модуля приращения  и решают относительно Х и М следующую систему уравнений
и решают относительно Х и М следующую систему уравнений
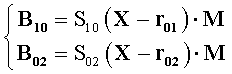
где В 10, В 02 - результаты измерения приращений индукции, соответствующие указанной ориентации штанги;
S10 и S02 - симметричные 3×3 матрицы, элементы которых нелинейные функции компонент векторов соответственно Х-r 01 и Х-r 02;
r 01, r 02 - заранее определенные радиусы-векторы, связывающие точки 0 и 1, 0 и 2;
при этом решение начинают с исключения из системы магнитного момента, затем результаты решения уточняют, для чего штангу направленно приближают к источнику, используя предварительные результаты, и вновь решают указанную выше систему уравнений.
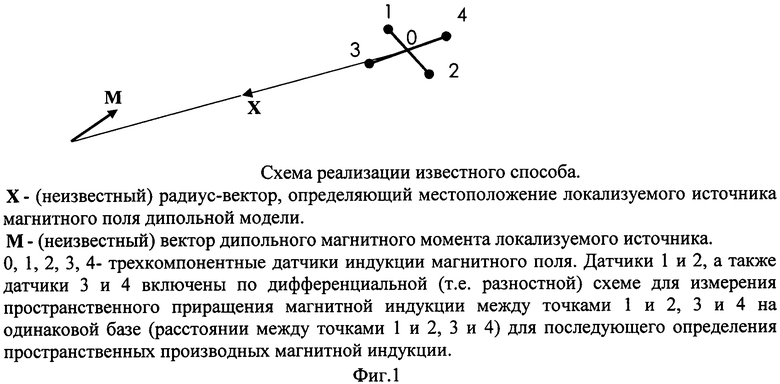
На Фиг.1 изображена схема реализации известного способа.
На Фиг.2 изображена схема реализации заявляемого способа.
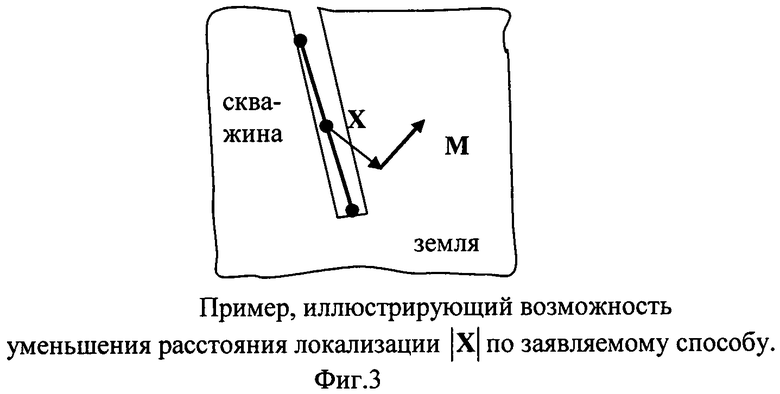
На Фиг.3 проиллюстрирована возможность использования заявляемого способа в скважине небольшого диаметра.
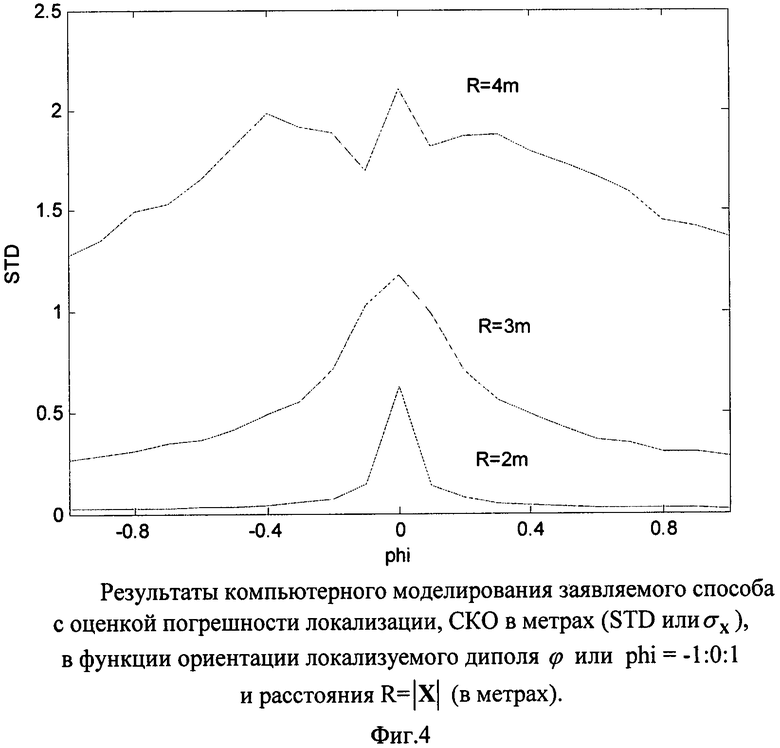
На Фиг.4 представлены результаты компьютерного моделирования заявляемого способа с оценкой погрешностей локализации в функции ориентации локализуемого диполя и расстояния до него.
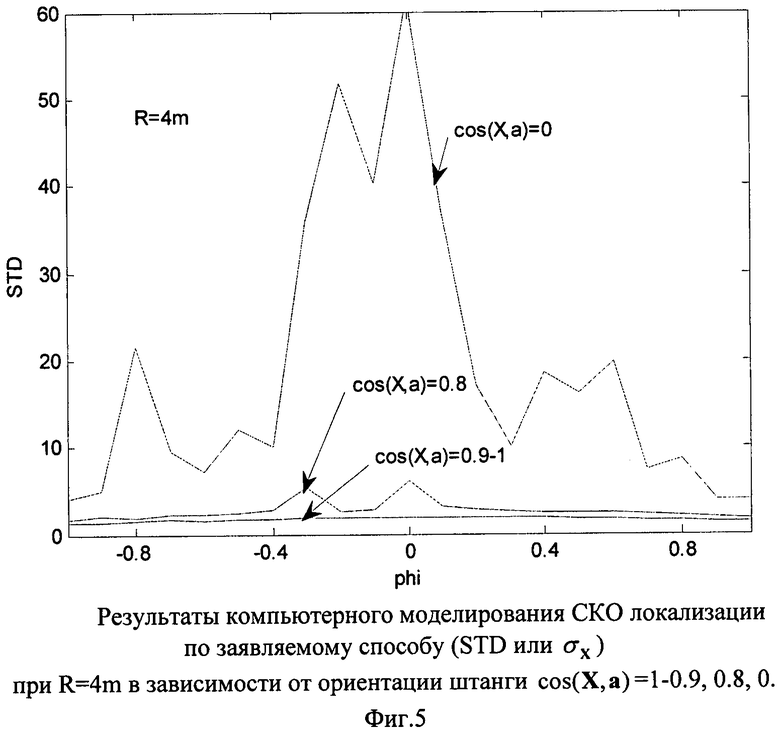
На Фиг.5 представлены результаты компьютерного моделирования СКО локализации по заявляемому способу в зависимости от ориентации штанги.
Схема, изображенная на Фиг.1, содержит трехкомпонентные датчики индукции магнитного поля 0, 1, 2, 3, 4, магниточувствительные оси которых ориентированы вдоль базовой ортогональной системы координат двух измерительных штанг 1-2 и 3-4. Датчики 1 и 2 (3 и 4) включены по дифференциальной (разностной) схеме. Соответствующий этим датчикам измерительный канал регистрирует результат измерения разности (пространственного приращения) между точками 1 и 2 В
12=В
1-В
2. Обратим внимание, что измерительный канал (для простоты он на чертеже не обозначен) измеряет только три компоненты вектора разности В
12=(В12x В12y B12z), но не сами величины векторов В
1 и В
2. Направление от точки 0 к точке 1 является направлением оси х базовой системы координат измерительного канала или направлением орта i. Одновременно другой измерительный канал измеряет разность В
34=(0 B34y B34z). Направление от точки 0 к точке 3 является направлением оси у или орта j. Соответственно направление оси z определится как k=i x j. Еще один канал измеряет индукцию в точке 0 В
0=(В0x В0y B0z). Обозначим расстояние от точки 0 до точек 1, 2, 3, 4 через а (величину а измеряют заранее при настройке всего измерительного узла). X=(Xх Хy Xz) обозначает искомый неизвестный радиус-вектор от точки 0 до локализуемого диполя (до локализуемого объекта или локализуемого источника магнитного поля дипольной модели). М=(Mx Мy Мz) обозначает неизвестный вектор магнитного момента диполя (дипольного магнитного момента). Очевидно, что если 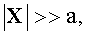 то
то
B12x/2a≈∂Bx/∂x=Bxx, B12y/2a≈∂Bx/∂y=Bxy, B12z/2a≈∂Bx/∂z=Bxz
B34y/2a≈∂By/∂y=Byy, B34z/2a≈∂By/∂z=Byz
Известно, что согласно следствиям из уравнений Максвелла rotB=(Byz-Bzy Bxz-Bzx Byx-Bxy)=0, т.е Вyz=Вzy, Bxz=Bzx, Вyx=Вxy и divB=Вxx+Вyy+Вzz=0, т.е. Вzz=-(Вxx+Вyy). Таким образом, пяти вышеперечисленных приращений (В12x В12y В12z В34y В34z) /2а достаточно, чтобы построить весь градиент или все 9 компонент пространственных производных вектора дипольной индукции
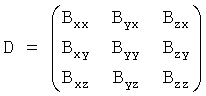
Для измерения дипольной индукции необходимо предварительно скорректировать нули измерителя индукции в точке 0 и скомпенсировать до нуля однородное поле Земли. Для измерения градиента необходимо скорректировать нули всех пяти компонент измерителей приращений. Нули корректируют при отсутствии локализуемого объекта. Итак, по известному способу [1980] измеряют вектор дипольной индукции В 0 и градиент вектора В 0-D, по которым определяют искомый радиус-вектор
Х=3(D+λ1 I)·В 0/λ2λ3
где λ1, λ2, λ3 - собственные числа матрицы D, I - единичная матрица.
Схема, изображенная на Фиг.2, содержит трехкомпонентные датчики индукции магнитного поля 0, 1, 2, магниточувствительные оси которых ориентированы вдоль базовой ортогональной системы координат измерительной штанги 1-2. Датчики 1 и 0, а также датчики 0 и 2 включены по дифференциальной (разностной) схеме. Итак, по заявляемому способу измеряют два приращения индукции магнитного поля искомого диполя В 10 и В 02. Для измерения корректируют нули всех компонент измерителей приращений. Кроме того, предварительно измеряют расстояния между точками 1-0 и 0-2.
Заявляемый способ основан на соотношениях, полученных в статье [1980]
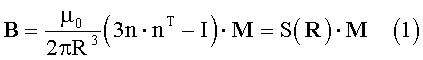
где В - вектор индукции магнитного поля диполя в точке;
µ0=4π×10-7 Гн/м - магнитная постоянная;
R - радиус-вектор, связывающий точку с диполем;
R - модуль радиуса-вектора R;
n=R/R - вектор-столбец единичного направления;
nT=(α β γ) - транспонированный n или вектор-строка единичного направления;
α, β, γ - направляющие косинусы единичного направления относительно осей соответственно x, y, z системы координат;
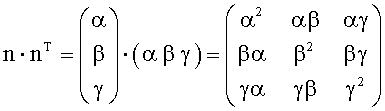 - диада в матричном виде, особая группа тензоров 2-го ранга.
- диада в матричном виде, особая группа тензоров 2-го ранга.
В статье [1980] уравнение (1) решено относительно магнитного момента в общем виде
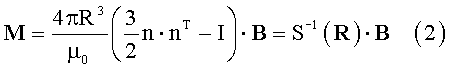
и показано, что решение (2) справедливо при всех ориентациях диполя m=М/М, т.е. при всех φ=nT·m, изменяющихся от -1 до +1.
В статье [Семенов и Сонина, 1992] для приращения дипольной индукции между точками 1 и 2
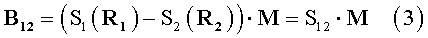
дано решение относительно магнитного момента (в общем виде)
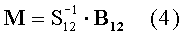
и показано, что обратная матрица 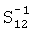 расходится, если точки 1 и 2 равноудалены от диполя (здесь общий вид матрицы
расходится, если точки 1 и 2 равноудалены от диполя (здесь общий вид матрицы 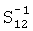 мы не приводим из-за ее громоздкости).
мы не приводим из-за ее громоздкости).
По заявляемому способу корректируют нули измерителей приращения индукции магнитного поля на штанге 12 вдали от локализуемого источника, т.е. в условиях однородного поля Земли. Затем штангу 12 переносят в район локализуемого источника и измеряют приращения индукции его магнитного поля. Результаты измерения выражают по аналогии с обозначениями уравнений (1)-(3)
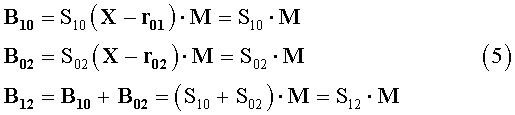
где В 10, В 02 - результаты измерений (6 чисел) приращений индукции между точками 1-0 и 0-2 в системе координат штанги 1-2;
Х - радиус-вектор от точки 0 до локализуемого диполя;
Х-r 01 - радиус-вектор от точки 1 до локализуемого диполя;
Х-r 02 - радиус-вектор от точки 2 до локализуемого диполя;
r 01 и r 02 - радиусы-векторы от точки 0 до точек 1 и 2.
Любые два уравнения из (5) представляют собой систему нелинейных уравнений относительно компонент искомого неизвестного Х и систему линейных уравнений относительно компонент М. Эти неизвестные находят в результате численного решения системы из (5). Численное решение системы из (5) оказывается примерно в 300 раз более долгим в сравнении с известным способом [1980], поскольку известный способ [1980] является решением в явном виде. Для повышения быстродействия заявляемого способа при нахождении неизвестного Х из (5) исключают неизвестный вектор М.
Ранее аналогичный прием исключения был использован в работе [Семенов и Дзария 1977]. По соотношениям (5) возможны 9 вариантов исключения М. Например,
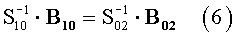
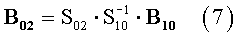
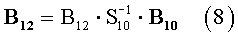
и т.д. Этот прием исключения М повышает быстродействие численного решения по сравнению с (5) примерно в 4 раза.
Для предварительной настройки датчиков на штанге 1-0-2 используют вспомогательную меру магнитного момента, с помощью которой по способу [Патент РФ №2313801] определяют необходимые для заявляемого способа векторы расстояния r 01 и r 02, а также угловую ориентацию магнитометров 1 и 2 в системе координат магнитометра точки 0. Для компенсации углового рассогласования и различий чувствительностей магнитометров точек 0, 1, 2 используют способ [Патент РФ №2256930], по которому сигнал, пропорциональный индукции в точке 0, используют для непрерывной следящей компенсации поперечных и продольных компонент индукции в точках 1 и 2. Благодаря этому устраняется влияние неидентичности измерительных каналов 1-0-2 при перемещении и вращении штанги 1-0-2. Однако к заявляемому способу эти мероприятия имеют косвенное (вспомогательное или подготовительное) отношение. Основное содержание заявляемого способа выражают уравнения (5)-(8).
Итак, штангу переносят в район, где расположен источник магнитного поля дипольной модели с магнитным моментом М, как показано на Фиг.2. Источник обнаруживают по наличию сигналов приращений индукции В
10 и В
02. Штангу вращают пока модуль суммы этих приращений не обратится приблизительно в максимум 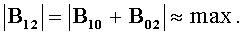 Тогда измеряют приращения В
10 и В
02 в системе координат датчиков штанги, соответствующие данной ориентации штанги, и, решая систему (5) с учетом (6)-(8), находят искомые векторы Х и М (см. Фиг.2) в той же системе координат. Эти результаты принимают за предварительные результаты, которые показывают, где приблизительно залегает искомый источник. Затем, учитывая предварительные результаты, штангу приближают к источнику, вновь ориентируют ее по максимуму приращения
Тогда измеряют приращения В
10 и В
02 в системе координат датчиков штанги, соответствующие данной ориентации штанги, и, решая систему (5) с учетом (6)-(8), находят искомые векторы Х и М (см. Фиг.2) в той же системе координат. Эти результаты принимают за предварительные результаты, которые показывают, где приблизительно залегает искомый источник. Затем, учитывая предварительные результаты, штангу приближают к источнику, вновь ориентируют ее по максимуму приращения 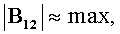 измеряют соответствующие B
10 и B
02, решают систему (5) с учетом (6)-(8) и находят уточненные искомые векторы Х и М. Как показывают исследования погрешностей заявляемого способа, при уменьшении расстояния до источника в два раза погрешность (СКО локализации) уменьшается в 64 раза. Другими словами, направленное приближение к источнику в заявляемом способе является мощнейшим рычагом повышения точности локализации малогабаритных ферромагнитных тел. Как показано схематически на Фиг.3, заявляемый способ позволяет осуществлять направленный поиск, помещая штангу даже в скважину небольшого размера.
измеряют соответствующие B
10 и B
02, решают систему (5) с учетом (6)-(8) и находят уточненные искомые векторы Х и М. Как показывают исследования погрешностей заявляемого способа, при уменьшении расстояния до источника в два раза погрешность (СКО локализации) уменьшается в 64 раза. Другими словами, направленное приближение к источнику в заявляемом способе является мощнейшим рычагом повышения точности локализации малогабаритных ферромагнитных тел. Как показано схематически на Фиг.3, заявляемый способ позволяет осуществлять направленный поиск, помещая штангу даже в скважину небольшого размера.
Проверка заявляемого способа произведена компьютерным моделированием. С помощью вычислительной системы МатЛаб рассчитывают приращения индукции магнитного поля диполя B
10=В
1-В
0 и В
02=В
0-В
2 для заданных магнитного момента М, расстояния Х и размеров штанги r
01 и r
02 и ее ориентации. Затем к рассчитанным компонентам индукции добавляют случайные погрешности с заданным средним квадратическим отклонением (СКО) σB, находят по заявляемому способу искомое расстояние 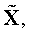 повторяют эту операцию несколько сотен раз, вычисляют СКО всей совокупности решений
повторяют эту операцию несколько сотен раз, вычисляют СКО всей совокупности решений 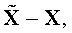 т.е. вычисляют σх в функции всех ориентации диполя φ, изменяющихся от -1 до +1 через 0.1 (относительно φ см. также пояснения к (2)). Результаты расчета σх представлены графически на Фиг.4 при
т.е. вычисляют σх в функции всех ориентации диполя φ, изменяющихся от -1 до +1 через 0.1 (относительно φ см. также пояснения к (2)). Результаты расчета σх представлены графически на Фиг.4 при 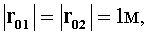
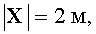 σB=0.1 нТл,
σB=0.1 нТл, 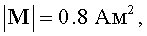 м, что соответствует магнитному моменту винтовки по данным книги Р.Б.Семевского и соавторов [Специальная магнитометрия. 2002. С.38].
м, что соответствует магнитному моменту винтовки по данным книги Р.Б.Семевского и соавторов [Специальная магнитометрия. 2002. С.38].
Как видно из графиков на Фиг.4, точность локализации заявляемым способом во всем диапазоне 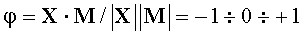 резко повышается с уменьшением расстояния до локализуемого источника менее 4 м. Что касается известного способа [1980], то он не позволяет менять расстояние, так как является стационарным способом локализации движущихся скрытых объектов. Коррекция нулей измерителя индукции в известном способе [1980] осуществляется при отсутствии локализуемого объекта, скорректированные нули сохраняются некоторое время при условии неподвижности датчиков. Кроме того, даже в стационарном варианте у известного способа возникают проблемы при уменьшении расстояния, так как способ [1980] основан на измерении пространственных производных через измерения пространственных приращений. При уменьшении расстояния или при увеличении базы приращения приращения перестают соответствовать производным. Заявляемый же способ основан непосредственно на измерении приращений независимо от базы приращения и расстояния до источника. В результате при средних и более расстояниях, например при R>4 м, известный способ [1980] лучше заявляемого по точности, а на малых расстояниях (R<4 м) заявляемый способ оказывается вне конкуренции по точности. Известный способ просто не предполагает использования на малых расстояниях, также как заявляемый способ - на больших расстояниях.
резко повышается с уменьшением расстояния до локализуемого источника менее 4 м. Что касается известного способа [1980], то он не позволяет менять расстояние, так как является стационарным способом локализации движущихся скрытых объектов. Коррекция нулей измерителя индукции в известном способе [1980] осуществляется при отсутствии локализуемого объекта, скорректированные нули сохраняются некоторое время при условии неподвижности датчиков. Кроме того, даже в стационарном варианте у известного способа возникают проблемы при уменьшении расстояния, так как способ [1980] основан на измерении пространственных производных через измерения пространственных приращений. При уменьшении расстояния или при увеличении базы приращения приращения перестают соответствовать производным. Заявляемый же способ основан непосредственно на измерении приращений независимо от базы приращения и расстояния до источника. В результате при средних и более расстояниях, например при R>4 м, известный способ [1980] лучше заявляемого по точности, а на малых расстояниях (R<4 м) заявляемый способ оказывается вне конкуренции по точности. Известный способ просто не предполагает использования на малых расстояниях, также как заявляемый способ - на больших расстояниях.
Одновременно с определением СКО локализации σx заявляемым способом определялось быстродействие заявляемого способа τ, поскольку МатЛаб предоставляет такую возможность. Для уравнения (5) τ=0.09 с, для (6)-(8) τ=0.024 с. Таким образом, процедура исключения магнитного момента в процессе решения примерно в 4 раза улучшает быстродействие заявляемого способа. Отметим попутно, что быстродействие известного способа [1980] τ=0.0003 с значительно выше, потому что он основан на явном (аналитическом) решении, в то время как заявляемый способ основан на численном решении.
На Фиг.5 представлены зависимости СКО локализации по заявляемому способу от начальной ориентации штанги а относительно искомого радиуса-вектора Х или относительно некоторого направления, соответствующего максимуму приращения индукции 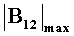 (это направление отличается от Х не более чем на 15°). График показывает, что локализация по заявляемому способу некритична к точности ориентации штанги по максимуму приращения
(это направление отличается от Х не более чем на 15°). График показывает, что локализация по заявляемому способу некритична к точности ориентации штанги по максимуму приращения 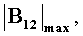 если cos(X,a)≥0.8, но очень важно избегать неблагоприятной исходной ориентации, когда штанга ортогональна вектору X, то есть когда cos(X,a)≈0. Кривые на графике показывают, что приближенная ориентация штанги по максимуму
если cos(X,a)≥0.8, но очень важно избегать неблагоприятной исходной ориентации, когда штанга ортогональна вектору X, то есть когда cos(X,a)≈0. Кривые на графике показывают, что приближенная ориентация штанги по максимуму 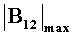 надежно защищает от неблагоприятной ситуации cos(X,a)≈0.
надежно защищает от неблагоприятной ситуации cos(X,a)≈0.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ЛОКАЛИЗАЦИИ МАГНИТНОГО ДИПОЛЯ | 2010 |
|
RU2456642C2 |
| СПОСОБ ЛОКАЛИЗАЦИИ ИСТОЧНИКА МАГНИТНОГО ПОЛЯ ДИПОЛЬНОЙ МОДЕЛИ | 2012 |
|
RU2521134C2 |
| СПОСОБ ПОВЕРКИ МАГНИТОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ | 2012 |
|
RU2503026C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИПОЛЬНОГО МАГНИТНОГО МОМЕНТА ОСТАТОЧНОЙ НАМАГНИЧЕННОСТИ И ТЕНЗОРА МАГНИТНОЙ ПОЛЯРИЗУЕМОСТИ ОБЪЕКТА И СТЕНД ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2020 |
|
RU2744817C1 |
| Способ определения напряженности магнитного поля дипольного источника | 1984 |
|
SU1267306A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И ОРИЕНТАЦИИ ТРЕХКОМПОНЕНТНОГО ДАТЧИКА МАГНИТОМЕТРА ОТНОСИТЕЛЬНО МЕРЫ МАГНИТНОГО МОМЕНТА | 2005 |
|
RU2290657C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ЛОКАЛЬНОЙ МАГНИТНОЙ АНОМАЛИИ | 2007 |
|
RU2411550C2 |
| Способ измерения приращения индукции магнитного поля дифференциальным магнитометром | 2021 |
|
RU2789143C2 |
| УСТРОЙСТВО ДЛЯ БЕСКОНТАКТНОЙ ДИАГНОСТИКИ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ С ВОЗМОЖНОСТЬЮ КАЛИБРОВКИ В ПОЛЕВЫХ УСЛОВИЯХ | 2016 |
|
RU2620326C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОМПОНЕНТ ГЕОМАГНИТНОГО ПОЛЯ | 1986 |
|
SU1426256A1 |
Изобретение относится к поиску скрытых ферромагнитных объектов с помощью переносной штанги с датчиками для измерения приращений индукции магнитного поля. Сущность изобретения заключается в том, что в центре и на концах штанги размещают датчики трехкомпонентных магнитометров и определяют расстояния между ними. При движении штанги измеряют приращения индукции, при обнаружении удобочитаемых сигналов штангу ориентируют по максимуму приращения индукции и решают относительно искомого радиуса-вектора систему нелинейных уравнений, из которой вначале исключают магнитный момент источника. Затем результаты уточняют, для чего штангу направленно приближают к источнику, и вновь решают упомянутую систему. Технический результат - повышение точности локализации. 5 ил.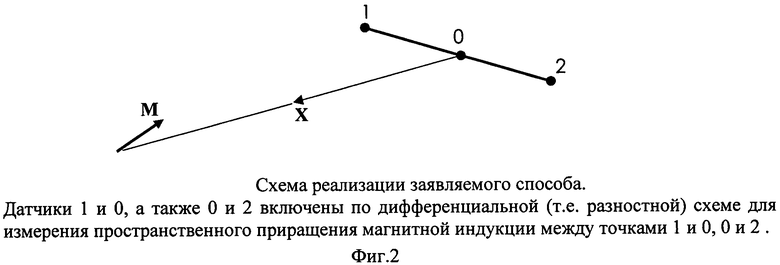
Способ локализации источника магнитного поля дипольной модели, включающий измерения пространственных приращений индукции магнитного поля и расстояний между парами периферийных точек, выбранных симметрично относительно центра наблюдения, обработку результатов измерения для определения неизвестных радиуса-вектора Х между центром наблюдения и искомым диполем и его вектора магнитного момента М, отличающийся тем, что в центре 0 и на краях 1 и 2 переносной штанги устанавливают трехкомпонентные датчики магнитного поля для измерения приращений индукции В10 между точками 1 и 0 и В02 между точками 0 и 2, затем штангу приближают в район местоположения источника до появления удобочитаемых значений В10 и В02, после чего ее ориентируют приблизительно до максимума модуля приращения |B12| и решают относительно Х и М следующую систему уравнений:
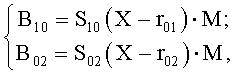
где В10, В02 - результаты измерения приращений индукции, соответствующие указанной ориентации штанги;
S10 и S02 - симметричные 3×3 матрицы, элементы которых - нелинейные функции компонент векторов соответственно X-r01 и Х-r02;
r01, r02 - заранее определенные радиусы-векторы, связывающие точки 0 и 1, 0 и 2;
при этом решение начинают с исключения из системы магнитного момента, затем результаты решения уточняют, для чего штангу направленно приближают к источнику, используя предварительные результаты, и вновь решают указанную выше систему уравнений.
| ИВАНОВ Ю.М., СЕМЕНОВ В.Г | |||
| ОЦЕНКИ ПОГРЕШНОСТЕЙ ПЕЛЕНГАЦИИ И ЛОКАЛИЗАЦИИ ИСТОЧНИКОВ МАГНИТНОГО ПОЛЯ ДИПОЛЬНОЙ МОДЕЛИ | |||
| // ИЗМЕРИТЕЛЬНАЯ ТЕХНИКА | |||
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОРРЕКТИРУЮЩЕЙ МАТРИЦЫ ТРЕХКОМПОНЕНТНОГО МАГНИТОМЕТРА | 2002 |
|
RU2229727C1 |
| Дифференциальный магнитометр | 1984 |
|
SU1267307A1 |
| US 5239474 A, 24.08.1993. | |||
Авторы
Даты
2011-11-10—Публикация
2010-08-25—Подача