Изобретение относится к области определения координат местоположения скрытых ферромагнитных объектов, от подводных лодок и неразорвавшихся боеприпасов (бомб, снарядов, донных мин), до зарытых в земле единиц стрелкового оружия (винтовка, автомат, пистолет) и т.д.
Многие сосредоточенные источники магнитного поля можно аппроксимировать (точечным) диполем с магнитным моментом М=Mm, где М - модуль магнитного момента, m - единичный вектор направления магнитного момента. Различают задачи обнаружения, пеленгации и локализации (неподвижного или движущегося) диполя по параметрам его магнитного поля, измеренным в одной или нескольких точках наблюдения. При локализации определяют радиус-вектор X=Xn, где X - модуль расстояния, n - единичный вектор направления. Другими словами, при локализации определяют неизвестные координаты вектора X в системе координат наблюдения. При пеленгации определяют единичный вектор направления n или направляющие косинусы углов его в системе координат наблюдения. При обнаружении определяют параметры неоднородного магнитного поля на фоне поля Земли, по которым судят о том, что «где-то что-то есть». Некоторые специалисты под обнаружением понимают и пеленгацию и локализацию. Однако мы для определенности будем различать эти задачи.
Задачу пеленгации магнитного диполя, по-видимому, впервые поставил О.П.Хвостов [Магнитный пеленгатор. // Геофизическое приборостроение. - Л.: Гостехиздат. 1963. С.3-11], который также предложил приближенное решение ее по градиенту модуля дипольной индукции.
Первое аналитическое (явное) решение задачи пеленгации диполя по градиенту вектора дипольной индукции получил C.Frahm [W.M.Wynn а.о. Advanced Superconducting Gradiometer. / Magnetometer Arrays and a Novel Signal Processing Technique. // IEEE Transactions on Magnetics, vol. MAG-11, no.2, March 1975 Р.701-707]. Решение Frahm′a было неоднозначным. Оно включало 4 направления, одно из которых было истинным, остальные три - ложными. Вместе с тем решение Frahm′a осталось нераскрытым, поскольку не было найдено удобной формы представления этого решения.
Затем T.Kolbenhayer [Prispevok krieseniu obratenej magnetometrickey ulohy predipol. // Banickey listy. 1976. #4 31-35 (Реферативный Журнал Геология. 1980. №12. C.20)] нашел явное решение задачи локализации по заданным вектору и градиенту вектора дипольной индукции, опираясь на теорему Эйлера для однородных функций. Однако решение Kolbenhayer′a оказалось неустойчивым к ориентации искомого диполя.
Позднее оба упомянутых решения были радикально усовершенствованы в работе [В.Г.Семенов. Решение обратной задачи для источника физического поля дипольной или квадрупольной модели. // Методы и средства точных магнитных измерений. / Сб. научных трудов НПО «ВНИИМ им. Д.И.Менделеева». 1980. С.3-19]. В результате задача локализации обрела устойчивость, а для задачи пеленгации было найдена простая и удачная форма выражения этого решения. В последующие годы работы Frahm′a [1975] и Семенова [1980] подверглись несправедливой критике в части неоднозначности решения в статье [В.В.Тихонов и Б.Н.Шалаев Особенности решения обратных задач при электромагнитном исследовании подводных сред. Известия ЛЭТИ им.Ульянова (Ленина). Выпуск 327 Л-д 1983 г. Стр.28] и монографии [под редакцией лауреата Гос. премии СССР Е.Г.Пащенко «Оптико-физические средства исследования океана». Л-д. Судостроение 1984. Стр.207]. Авторы этих публикаций предложили якобы однозначное решение задачи вместо решения [Семенов 1980]. Ответная статья [В.Г.Семенов и А.Я.Зайончковский. Сравнительный анализ градиентных методов локализации источников магнитного поля дипольной модели. Сб. научных трудов «Создание средств измерений для метрологического обеспечения прецизионных нанотесламетров». ВНИИМ им. Менделеева Л-д. 1988 г. С.56-67] показала несостоятельность претензий на однозначность решения Тихонова и Шалаева. Вместе с тем, Семенов и Зайончковский [1988] получили аналитическое выражение погрешности способа Frahm′a [1975]/Семенова [1980], выявившее некоторую неустойчивость этого способа, который ранее считался полностью устойчивым. Много лет спустя это аналитическое выражение было перепроверено компьютерным моделированием [Ю.М.Иванов и В.Г.Семенов. Оценки погрешностей пеленгации и локализации источника магнитного поля дипольной модели. // Измерительная техника №5. 2008. С.30-35 и №7. 2008. С.72]. Результаты компьютерного моделирования подтвердили существование наличие области неустойчивости.
Итак, известны два на сегодня лучших способа явного решения, а потому и высокого быстродействия:
а) способ локализации [Семенов, 1980]. Этот способ устойчив и однозначен, но он не позволяет осуществлять локализацию в движении носителя средств измерения;
б) способ пеленгации [Семенов и Зайончковский, 1988]. Этот способ позволяет выполнять измерения при движении средств измерения, но он неоднозначен, так как дает четыре решения (какое из них истинное неизвестно), к тому же в некоторой узкой области этот способ неустойчив. Но самое главное, это способ пеленгации, а не локализации.
Наконец, известны следующие приемы повышения точности измерения пространственного приращения магнитной индукции, а также базы приращения:
- Патент РФ №2256930 Способ минимизации погрешностей в переносном дифференциальном магнитометре. Приоритет изобретения от 07.04.2003 г.;
- Патент РФ №2257593 Способ минимизации погрешностей в дифференциальном магнитометре. Приоритет изобретения от 07.04.2003 г.;
- Патент РФ №2290657 Способ определения местоположения и ориентации трехкомпонентного датчика магнитометра относительно меры магнитного момента. Приоритет изобретения от 09.08.2005 г.;
- Патент РФ №2313801 Способ измерения приращения индукции магнитного поля трехкомпонентным дифференциальным магнитометром. Приоритет изобретения от 04.05.2006 г.
В качестве прототипа заявляемого способа выбран способ пеленгации источника магнитного поля дипольной модели [Семенов и Зайончковский, 1988] (далее, просто [1988]) по совокупности существенных признаков, наиболее близких к заявляемому способу.
Известный способ [1988] включает предварительные измерения расстояний между датчиками трехкомпонентных магнитометров, которыми измеряют градиент индукции магнитного поля источника, определение по градиенту его собственных чисел и векторов, через которые выражают единичный вектор направления радиус-вектора между точкой измерения градиента и искомым источником, а также единичное направление магнитного момента этого источника, причем оба направления определяют с точностью до одного из четырех возможных решений, лежащих в одной плоскости (одно из решений истинное, три другие - ложные), кроме того через найденные собственные числа определяют скалярную интенсивность градиента и косинус угла между найденными направлениями.
Причиной, препятствующей достижению указанного ниже технического результата для известного способа, является то, что известный способ не располагает достаточным объемом входной измеряемой информации для решения задачи локализации, а именно он использует пять измеряемых чисел, или пять независимых компонент градиента, которые после обработки определяют пять выходных параметров: четыре числа на два единичных направления и пятое число - скалярная интенсивность градиента.
Задача, на решение которой направлено заявляемое изобретение, заключается в доработке способа пеленгации до способа локализации, а также в устранении его неоднозначности и в снижении его неустойчивости.
Технический результат, получаемый при осуществлении изобретения, заключается в обеспечении возможности локализации источника магнитного поля в движении.
Указанный технический результат достигается тем, что заявляемый способ локализации магнитного диполя, включающий предварительные измерения расстояний между датчиками трехкомпонентных магнитометров, затем измерения с помощью этих датчиков градиента индукции магнитного поля, определение собственных чисел градиента λ2≥λ1≥λ3, которыми определяют скалярную интенсивность его 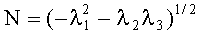 , а также определение соответствующих собственных векторов u1, u2, u3, по которым находят четыре единичных направления на диполь ni и направления его магнитного момента mi по формулам
, а также определение соответствующих собственных векторов u1, u2, u3, по которым находят четыре единичных направления на диполь ni и направления его магнитного момента mi по формулам
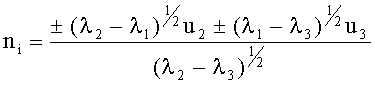
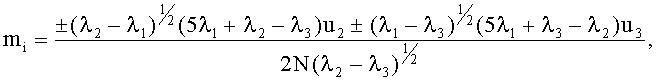
где i=1, 2, 3, 4 - индекс пары решений (одно истинное, три ложных), отличается тем, что с помощью датчиков трехкомпонентных магнитометров, размещенных у одного из концов переносной штанги на полуосях ее системы координат, соосно и на одинаковом удалении от ее центра, измеряют пространственные приращения индукции магнитного поля относительно опорного датчика на другом конце штанги, по которым вычисляют среднее приращение по всем полуосям, а также разности приращений для каждой одноименной пары полуосей, строят симметричную матрицу разностей, при этом из каждого диагонального элемента матрицы вычитают треть ее следа, а единичные направления находят по формулам, зависящим от размера числа φ=λ1/N:
при -0.95≤φ<0.95: 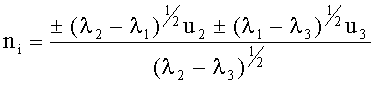
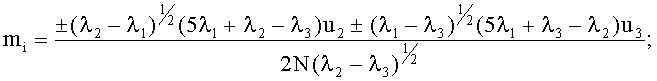
при -1≤φ<-0,95: 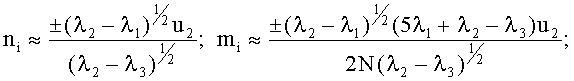
при 0,95<φ≤1: 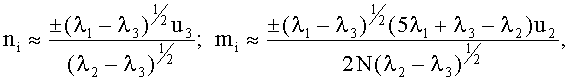
после чего, нормируя вектор среднего приращения, получают векторное уравнение с одним неизвестным k=a/r:
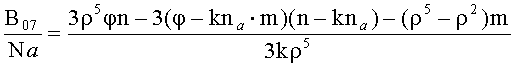
где В07 - вектор среднего приращения;
a - расстояние между центром опорного датчика и центром системы координат;
ρ=(1+k2-2kna·n)1/2;
na - единичный вектор направления штанги,
в свою очередь, векторное нормированное уравнение сводят к модульному |B07|/Na=f(k), решая которое для каждой из четырех пар найденных векторов ni и mi, получают соответствующее значение ki, затем каждую пару величин ni, mi, если ей соответствует физически приемлемое значение ki, подставляют в векторное нормированное уравнение, рассчитывают его и отбирают тройку истинных решений n, m и k по минимуму модуля разности рассчитанной и измеренной версий этого уравнения, после чего определяют искомое расстояние до источника r=a/k.
На Фиг.1 изображена схема реализации заявляемого способа.
Схема, изображенная на Фиг.1, содержит датчики трехкомпонентных магнитометров, установленные на переносной штанге. Датчики 1-6 расположены у одного конца штанги, опорный датчик 7 - у другого конца ее. Датчики 1-2 размещены на полуосях х+ и х- системы координат (СК) штанги, на одинаковом расстоянии от центра 0 СК, датчики 3-4 - на полуосях y+ и y-, датчики 5-6 - на полуосях z+ и z-. Все датчики 1-7 сориентированы своими осями вдоль осей СК штанги.
Заявляемый способ действует следующим образом. Датчики 1-6 включены по схеме измерения приращений магнитной индукции относительно опорного датчика 7. Это означает, что при измерении вектора приращения магнитной индукции, например, парой 1-7, регистрирующие устройства отсчитывают три проекции разности В17=В1-В7, но не сами векторы В1 и В7. Предварительно измеряют расстояния между датчиками, а также их взаимную ориентацию с помощью внешней трехкомпонентной меры магнитного момента (ММ). Для этого используют способ определения местоположения и ориентации трехкомпонентного датчика магнитометра относительно меры ММ [Патент РФ №2290657]. При работе оперируют следующими результатами измерения: приращениями магнитной индукции В17, В27, В37, В47, В57, В67 и заранее определенными расстояниями между соответствующими датчиками a 12, a 34, a 56, а также расстоянием между центрами СК 0 и датчика 7 - a.
Если штанга находится в магнитном поле Земли, которое можно считать однородным, то есть не зависящим от координаты, то показания магнитометров штанги будут нулевыми. Если на некотором расстоянии от штанги находится источник магнитного поля дипольной модели, то есть источник неоднородного поля, или зависящего от координаты, то показания магнитометров отличаются от нулей. Задача пеленгации заключается в том, чтобы по этим показаниям определить направление на диполь, а задача локализации - в том, чтобы определить и расстояние до него вдоль этого направления.
Сначала с помощью измеренных приращений строят матрицу 3×3:
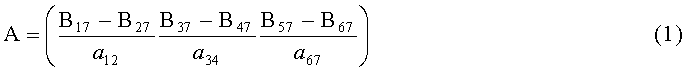
с помощью которой находят матрицу градиента
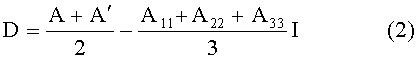
где А′ - транспонированная матрица А,
A11+A22+A33 - след матрицы А,
I - единичная матрица 3×3.
Операции (2) придают матрице градиента симметрию и обнуляют его след, поскольку известно, что градиент вектора магнитной индукции симметричен и бесследен. Затем стандартными приемами по матрице градиента находят его собственные числа λ2≥λ1≥λ3 и векторы u1, u2, u3, которыми определяют скалярную интенсивность градиента N, число φ, которое является скалярным произведением единичных векторов направлений на источник из центра СК n и магнитного момента m, а также сами направления n и m по формулам, зависящим от размера φ:
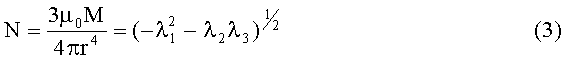
где µ0=4π×10-7 Гн/м - магнитная постоянная;
М - размер магнитного момента источника;
r - расстояние между источником и центром СК;
(Обратим внимание на то, что сами величины М и r по градиенту не определяются);

при -0.95≤φ<0.95: 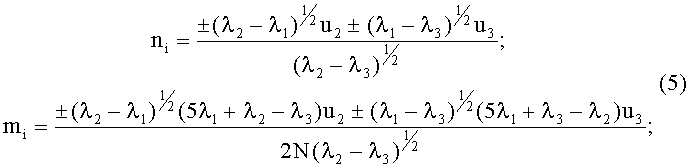
при -1≤φ<-0,95: 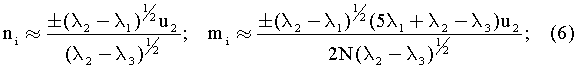
при 0.95<φ≤1: 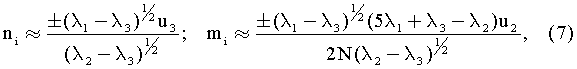
где i=1, 2, 3, 4.
Формулы (5)-(7) дают неоднозначное решение, т.к они определяют 4 пары решений, одна пара - истинное решение, три - ложные. Какая пара истинная, неизвестно, так как все решения удовлетворяют градиенту. Проявляется это в том, что собственные векторы определяются с точностью до знака.
Обратим внимание, что формулы (5)-(7) применяют в зависимости от размера φ. Анализ погрешностей показал, что первые две строчки (5), каждая из двух слагаемых, методически безупречны, но при наличии погрешностей одно слагаемое расходится при φ≈-1, а другое при φ≈+1. Поэтому выгодно, при |φ|≈1÷0,95 использовать одно из этих слагаемых, допуская незначительную методическую погрешность, но повышая устойчивость к погрешностям входных данных. Таким образом, разбивка (5) на подвыражения, зависящие от размера φ, устраняет неустойчивость, имеющую место в известном способе [1988].
Далее определяют вектор среднего приращения
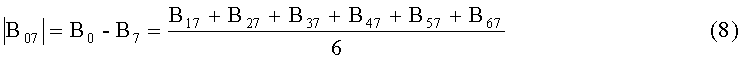
Равенство (8) основано на общеизвестной теореме Гаусса о среднем. Для источника дипольной модели вектор среднего приращения можно записать как
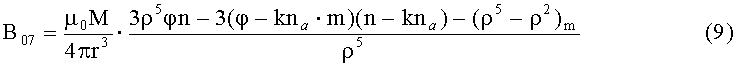
В правой части (9) помимо неизвестного k=a/r фигурирует еще два неизвестных: М и r. Для того чтобы избавиться от этих двух неизвестных, используют отношение
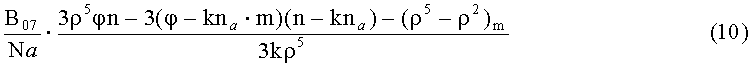
Выражение (10) представляет собой векторное нелинейное уравнение относительно только одного скалярного неизвестного k, учитывая, что величины φ, ni, mi известны из вышеприведенных решений, а вектор na известен как орт СК вдоль продольной оси штанги. Далее из (10) составляют модульное уравнение вида
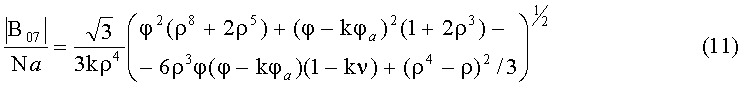
где φa=m·na,
решая которое для каждой пары ni, mi, получают соответствующее ki. Иногда полученное ki не является физически приемлемым решением, например слишком большим, (NaN - термин МатЛаб′а), такие решения отбрасывают. Каждую тройку решений ni, mi, ki, где ki физически приемлемое решение, подставляют в уравнение (10) и рассчитывают его. Истинную тройку решений определяют по наименьшему модулю разности Δi измеренной и рассчитанной версий уравнения (10).
Таким образом в заявляемом способе устраняется неоднозначность решений, присущая известному способу [1988].
Затем по найденному истинному k определяют искомое расстояние до источника r=a/k, что завершает переход от (устойчивой и однозначной) пеленгации к (устойчивой и однозначной) локализации источника.
Заявляемый способ проверен с помощью компьютерного моделирования в пакете МатЛаб. По МатЛаб′у рассчитывают компоненты градиента, к ним добавляют случайные погрешности с нулевым средним и заданным уровнем СКО компоненты 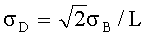 , и осуществляют пеленгацию по известному способу [1988] 500 раз для каждого из 21 значения φ=-1, -0.9, -0.8 …, 1. Всю совокупность обрабатывают для определения СКО пеленгации σn.
, и осуществляют пеленгацию по известному способу [1988] 500 раз для каждого из 21 значения φ=-1, -0.9, -0.8 …, 1. Всю совокупность обрабатывают для определения СКО пеленгации σn.
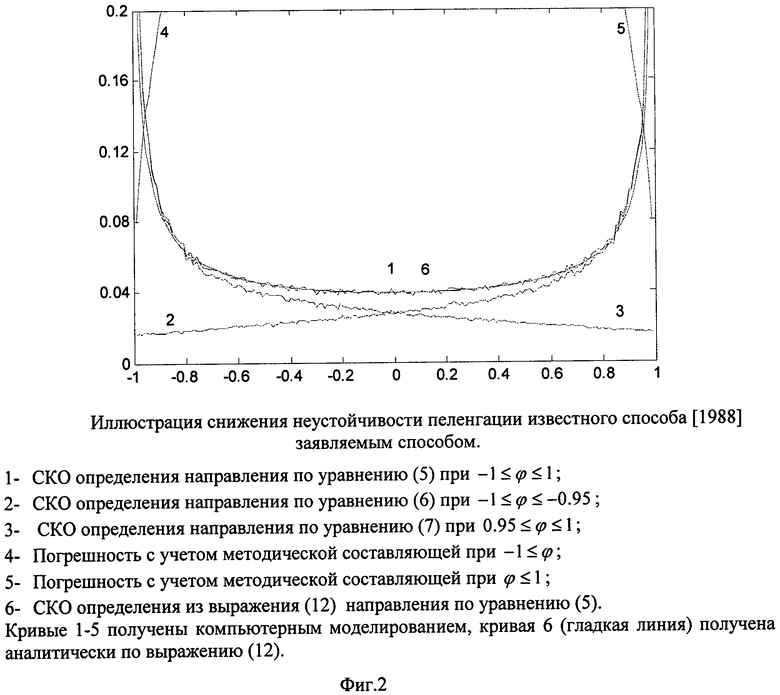
На Фиг.2 кривая 1 соответствует СКО пеленгации по уравнению (5), кривая 2 - по (6), 3 - по (7). Таким образом, при 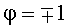 только одно из слагаемых (5) содержит почти всю полезную информацию, а другое слагаемое (5) - только «шумит», поэтому его отбрасывают. Отбрасывание второго слагаемого (5) создает методическую погрешность пеленгации, которая в диапазоне 0.95≤|φ|≤1 еще не велика и ею можно пренебречь в этой части диапазона. Кривая 2 представляет СКО первого члена (5), кривая 3 - СКО второго члена (5), кривая 4 - сумму методической погрешности плюс удвоенное СКО первого члена (5), кривая 5 - сумму методической погрешности плюс удвоенное СКО второго члена (5). Как показано на Фиг.2, при -1≤φ≤-0.95 пеленгация по методически неточному уравнению (6) выгоднее, чем по точному уравнению (5), а при 0.95≤φ≤1 по уравнению (7) выгоднее, чем по (5). Значение φ определяют в начале пеленгации по уравнению (4).
только одно из слагаемых (5) содержит почти всю полезную информацию, а другое слагаемое (5) - только «шумит», поэтому его отбрасывают. Отбрасывание второго слагаемого (5) создает методическую погрешность пеленгации, которая в диапазоне 0.95≤|φ|≤1 еще не велика и ею можно пренебречь в этой части диапазона. Кривая 2 представляет СКО первого члена (5), кривая 3 - СКО второго члена (5), кривая 4 - сумму методической погрешности плюс удвоенное СКО первого члена (5), кривая 5 - сумму методической погрешности плюс удвоенное СКО второго члена (5). Как показано на Фиг.2, при -1≤φ≤-0.95 пеленгация по методически неточному уравнению (6) выгоднее, чем по точному уравнению (5), а при 0.95≤φ≤1 по уравнению (7) выгоднее, чем по (5). Значение φ определяют в начале пеленгации по уравнению (4).
Пример, представленный на Фиг.2, соответствует погрешностям пеленгации диполя с магнитным моментом М=0.8 Ам2 на расстоянии r=2.5 м от центра 0 СК штанги при расстоянии между датчиками 1-6 1=0.75 м. Уровень СКО шумов компоненты датчика σB=10-10 Тл.
Аналитическое выражение СКО пеленгации (определения направления на искомый источник) по уравнению (5) имеет следующий вид:
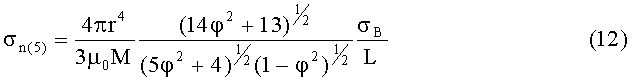
Как видно из кривой 6 (гладкая линия) на Фиг.2, аналитическое выражение (12) практически полностью совпадает с результатами компьютерного моделирования. Это совпадение доказывает, что выражение (12) выведено правильно, а также что моделирование проведено правильно.
Таким образом, разбивка по заявляемому способу уравнения (5) на два дополнительных (6) и (7) снижает неустойчивость пеленгации, присущую известному способу [1988] при 0.95≤|φ|≤1.
Далее в Таблице 1 представлены примеры устранения по заявляемому способу неоднозначности пеленгации, присущей известному способу [1988]. Эти примеры подготовлены также компьютерным моделированием пеленгации/локализации источника, удаленного на расстояние r=3.5 м от центра 0 СК штанги, у которой опорный датчик 7 расположен на расстоянии а=1.5 м от центра 0.
Как видно из каждой строки Таблицы 1, значение модуля разности Δ1 - наименьшее, поэтому тройку решений n1, m1, k1 в данном примере принимают за истинные направления n, m и истинное отношение k=a/r. Остальные тройки отбрасывают как ложные.
Таким образом, заявляемый способ устраняет неоднозначность решений, присущую известному способу [1988].
Наконец, по найденному и отобранному истинному значению отношения k=a/r определяют искомое расстояние до источника r=a/k.
Для примера в Таблице 1 r=1.5/0.4286=3.4998 м. Отклонение от расчетного расстояния 3.5 м произошло из-за округления числа 0.4285714286 до 0.4286.
Таким образом, заявляемый способ осуществляет не только однозначную (и устойчивую) пеленгацию, но однозначную (и устойчивую) локализацию источника, в то время как известный способ [1988] выполняет только (неоднозначную и неустойчивую) пеленгацию источника.
При этом, поскольку заявляемый способ основан на измерениях приращений магнитной индукции датчиками на переносной штанге, включенными по дифференциальной схеме, то заявляемый способ позволяет локализовать источник и в движении, так как само дифференциальное включение защищает от вредного влияния однородного поля Земли при перемещении штанги после коррекции нулей ее датчиков.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ЛОКАЛИЗАЦИИ ИСТОЧНИКА МАГНИТНОГО ПОЛЯ ДИПОЛЬНОЙ МОДЕЛИ | 2010 |
|
RU2433420C1 |
| СПОСОБ ЛОКАЛИЗАЦИИ ИСТОЧНИКА МАГНИТНОГО ПОЛЯ ДИПОЛЬНОЙ МОДЕЛИ | 2012 |
|
RU2521134C2 |
| СПОСОБ ПОВЕРКИ МАГНИТОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ | 2012 |
|
RU2503026C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИПОЛЬНОГО МАГНИТНОГО МОМЕНТА ОСТАТОЧНОЙ НАМАГНИЧЕННОСТИ И ТЕНЗОРА МАГНИТНОЙ ПОЛЯРИЗУЕМОСТИ ОБЪЕКТА И СТЕНД ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2020 |
|
RU2744817C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВНЕШНЕЙ ПОМЕХИ В ЦЕНТРЕ МЕРЫ МАГНИТНОЙ ИНДУКЦИИ | 2008 |
|
RU2394251C1 |
| СПОСОБ И УСТРОЙСТВО ДИАГНОСТИКИ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ПОДЗЕМНОГО ТРУБОПРОВОДА | 2012 |
|
RU2510500C1 |
| СПОСОБ МАГНИТНЫХ ИЗМЕРЕНИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2019859C1 |
| Способ измерения приращения индукции магнитного поля дифференциальным магнитометром | 2021 |
|
RU2789143C2 |
| УСТРОЙСТВО ДЛЯ БЕСКОНТАКТНОЙ ДИАГНОСТИКИ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ С ВОЗМОЖНОСТЬЮ КАЛИБРОВКИ В ПОЛЕВЫХ УСЛОВИЯХ | 2016 |
|
RU2620326C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И ОРИЕНТАЦИИ ТРЕХКОМПОНЕНТНОГО ДАТЧИКА МАГНИТОМЕТРА ОТНОСИТЕЛЬНО МЕРЫ МАГНИТНОГО МОМЕНТА | 2005 |
|
RU2290657C1 |
Изобретение относится к поиску скрытых ферромагнитных объектов с помощью переносной штанги с датчиками трехкомпонентных магнитометров. Согласно изобретению с помощью шести датчиков на одном конце штанги измеряют приращения индукции магнитного поля относительно опорного датчика на другом конце штанги. По этим приращениям определяют градиент вектора индукции в центре системы координат штанги и вектор приращения индукции между центром и опорным датчиком. По комбинации градиента и приращения осуществляют пеленгацию источника магнитного поля, а также находят расстояние до источника. Способ обеспечивает повышение устойчивости и надежности пеленгации, что позволяет осуществлять локализацию источника магнитного поля (представляемого дипольной моделью) в движении. 2 ил., 1 табл.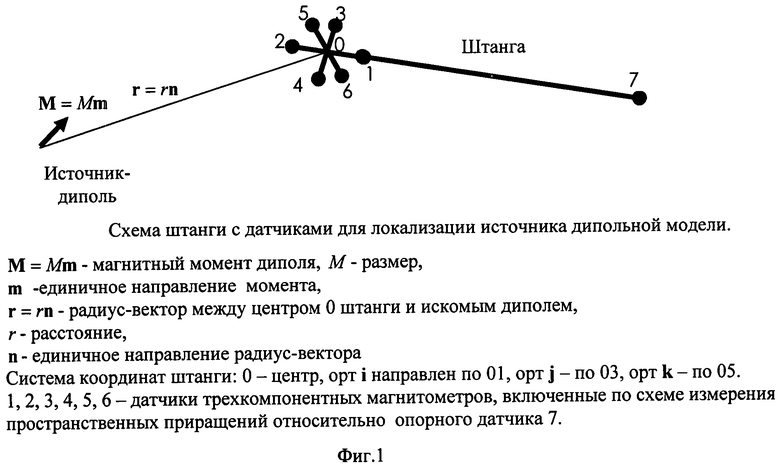
Способ локализации магнитного диполя, включающий предварительные измерения расстояний между датчиками трехкомпонентных магнитометров, затем измерения с помощью этих датчиков градиента индукции магнитного поля, определение собственных чисел градиента λ2≥λ1≥λ3, которыми определяют скалярную интенсивность его 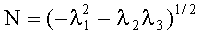 , а также определение соответствующих собственных векторов u1, u2, u3, по которым находят четыре единичных направления на диполь ni и направления его магнитного момента mi, где i=1, 2, 3, 4 - индекс пары решений (одно истинное, три ложных), отличающийся тем, что с помощью датчиков трехкомпонентных магнитометров, размещенных у одного из концов переносной штанги на полуосях ее системы координат, соосно и на одинаковом удалении от ее центра, измеряют пространственные приращения индукции магнитного поля относительно опорного датчика на другом конце штанги, по которым вычисляют среднее приращение по всем полуосям, а также разности приращений для каждой одноименной пары полуосей, строят симметричную матрицу разностей, при этом из каждого диагонального элемента матрицы вычитают треть ее следа, а единичные направления находят по формулам, зависящим от размера числа φ=λ1/N:
, а также определение соответствующих собственных векторов u1, u2, u3, по которым находят четыре единичных направления на диполь ni и направления его магнитного момента mi, где i=1, 2, 3, 4 - индекс пары решений (одно истинное, три ложных), отличающийся тем, что с помощью датчиков трехкомпонентных магнитометров, размещенных у одного из концов переносной штанги на полуосях ее системы координат, соосно и на одинаковом удалении от ее центра, измеряют пространственные приращения индукции магнитного поля относительно опорного датчика на другом конце штанги, по которым вычисляют среднее приращение по всем полуосям, а также разности приращений для каждой одноименной пары полуосей, строят симметричную матрицу разностей, при этом из каждого диагонального элемента матрицы вычитают треть ее следа, а единичные направления находят по формулам, зависящим от размера числа φ=λ1/N:
при -0,95≤φ<0,95: 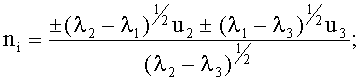
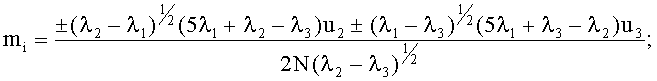
при -1≤φ<-0,95:
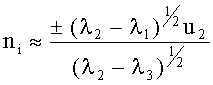
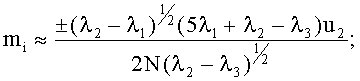
при 0,95<φ≤1:
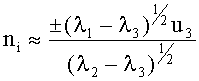
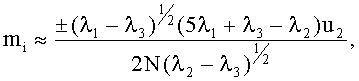
после чего, нормируя вектор среднего приращения, получают векторное уравнение с одним неизвестным k=а/r:
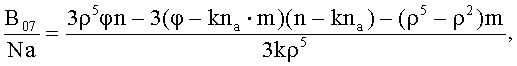
где В07 - вектор среднего приращения;
а - расстояние между центром опорного датчика и центром системы координат;
ρ=(1+k2-2kna·n)1/2;
na - единичный вектор направления штанги,
в свою очередь, векторное нормированное уравнение сводят к модульному |В07|/Na=f(k), решая которое для каждой из четырех пар найденных векторов ni и mi получают соответствующее значение ki, затем каждую пару величин ni, mi, если ей соответствует физически приемлемое значение ki, подставляют в векторное нормированное уравнение, рассчитывают его и отбирают тройку истинных решений n, m и k по минимуму модуля разности рассчитанной и измеренной версий этого уравнения, после чего определяют искомое расстояние до источника r=а/k.
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА МАГНИТНОГО ПОЛЯ С ПОДВИЖНОГО ОБЪЕКТА | 2002 |
|
RU2219497C1 |
| СПОСОБ ПРИВЕДЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ МАГНИТНОГО ПОЛЯ ЛИНЕЙНЫМ СТЕНДОМ К СИСТЕМЕ КООРДИНАТ ОБЪЕКТА | 1996 |
|
RU2142143C1 |
| Способ определения местоположения на плоскости объекта,обладающего магнитным моментом | 1986 |
|
SU1372261A1 |
| СИСТЕМА ДЛЯ ОБНАРУЖЕНИЯ МЕСТОПОЛОЖЕНИЯ ПОДЗЕМНОГО ОБЪЕКТА С ИСПОЛЬЗОВАНИЕМ МАГНИТНОГО МАРКЕРА | 2005 |
|
RU2315338C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И ОРИЕНТАЦИИ ТРЕХКОМПОНЕНТНОГО ДАТЧИКА МАГНИТОМЕТРА ОТНОСИТЕЛЬНО МЕРЫ МАГНИТНОГО МОМЕНТА | 2005 |
|
RU2290657C1 |
| МАГНИТОСКОП | 0 |
|
SU299813A1 |
| Магнитоскоп | 1972 |
|
SU437989A1 |
| КОМБИНИРОВАННОЕ МАГНИТНОЕ УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ РАССТОЯНИЯ | 2005 |
|
RU2354822C2 |
| МАГНИТОМЕТР (ВАРИАНТЫ) | 1993 |
|
RU2077733C1 |
| MX 2007002599 A, 14.11.2008 | |||
| Генератор случайных двоичных чисел | 1987 |
|
SU1481754A1 |
| JP 4152934 A, 26.05.1992 | |||
| JP 3277345 A, 09.12.1991. | |||
Авторы
Даты
2012-07-20—Публикация
2010-08-25—Подача