Изобретение относится к области определения координат местоположения скрытых ферромагнитных объектов, от подводных лодок и неразорвавшихся боеприпасов (бомб, снарядов, донных мин) до зарытых единиц стрелкового оружия (винтовка, автомат, пистолет) и т.д.
Многие сосредоточенные источники магнитного поля можно аппроксимировать (точечным) диполем с магнитным моментом М=Mm, где М - модуль магнитного момента, m - единичный вектор направления магнитного момента. Различают задачи обнаружения, пеленгации и локализации (неподвижного или движущегося) диполя по параметрам его магнитного поля, измеренным в одной или нескольких точках наблюдения. При локализации определяют радиус-вектор X=Rn, где R - модуль расстояния, n - единичный вектор направления или координаты вектора X в системе координат наблюдения. При пеленгации определяют единичный вектор направления n или направляющие косинусы углов его в системе координат наблюдения. При обнаружении определяют факт наличия неоднородного магнитного поля на фоне поля Земли.
Первое решение задачи пеленгации в явном виде по градиенту вектора дипольной индукции получил C.Frahm [W.M.Wynn а.о. Advanced Superconducting Gradiometer/Magnetometer Arrays and a Novel Signal Processing Technique // IEEE Transactions on Magnetics, vol. MAG-11, no.2, March 1975. P.701-707]. Решение было неоднозначным. Оно включало 4 направления, одно из которых было истинным, остальные три - ложными. Вместе с тем решение Frahm'a оставалось нераскрытым.
Первое решение задачи локализации в явном виде получил T.Kolbenhayer [Prispevok krieseniu obratenej magnetometrickey ulohy predipol // Banickey listy. 1976. #4 31-35 (Реферативный Журнал Геология. 1980. №12. C.20)] по заданным вектору и градиенту вектора дипольной индукции, опираясь на теорему Эйлера для однородных функций. Однако решение Kolben-hayer'a оказалось неустойчивым к ориентации искомого диполя.
Затем в работе [В.Г.Семенов. Решение обратной задачи для источника физического поля дипольной или квадрупольной модели // Методы и средства точных магнитных измерений / Сб. научных трудов НПО «ВНИИМ им. Д.И.Менделеева». 1980. С.3-19] в результате решения в общем виде характеристического уравнения для градиента решение Фрама было упрощено:
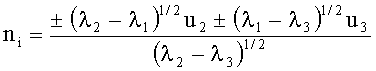
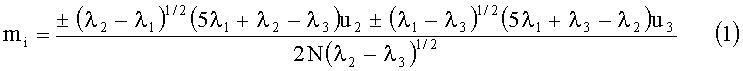
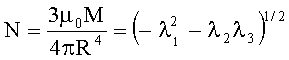
где ni, mi - единичные направления искомых радиус-вектора i=1, 2, 3, 4 - индекс пары решений;
λ1, λ2, λ3 и u2, u3 - собственные числа (λ2≥λ1≥λ3) и векторы матрицы (3×3) градиента индукции дипольного поля в точке наблюдения D;
N - скалярная интенсивность градиента D;
µ0 - магнитная постоянная;
М - значение магнитного момента искомого источника;
R - расстояние до искомого источника от точки наблюдения.
Таким образом, если в произвольной точке измерен градиент индукции D, то стандартными методами определяют его собственные числа и векторы, затем по (1) находят единичное направление на искомый диполь, направление его магнитного момента, а также отношение величин М к R4 (но не сами эти величины). Решение (1) неоднозначно (одно какое-то из 4 - истинное, остальные 3 - ложные).
Там же [1980] получено однозначное и устойчивое решение задачи локализации в виде
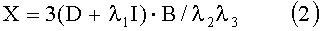
где В - вектор индукции дипольного поля в точке наблюдения.
Позднее для (1) и (2) были выведены выражения СКО погрешностей пеленгации σn и локализации σх [В.Г.Семенов и А.Я.Зайончковский. Сравнительный анализ градиентных методов локализации источников магнитного поля дипольной модели. Сб. научных трудов «Создание средств измерений для метрологического обеспечения прецизионных нанотесламетров». ВНИИМ им. Менделеева. Л-д. 1988 г. С.56-67].
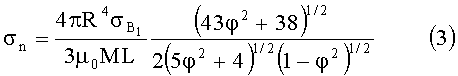
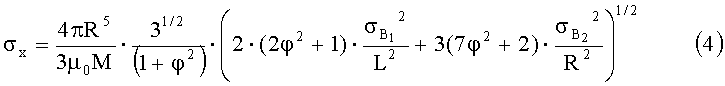
где φ=m·n; 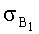
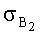
Выражения (3) и (4) были перепроверено компьютерным моделированием [Ю.М.Иванов и В.Г.Семенов. Оценки погрешностей пеленгации и локализации источника магнитного поля дипольной модели // Измерительная техника №5. 2008. С.30-35 и №7. 2008. С.72].
Из выражения (3) следует, что метод пеленгации (1) расходится в окрестности φ2≈1, это обстоятельство осталось незамеченным в работе [1980].
Выражение СКО (4) состоит из двух слагаемых, зависящих от 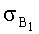
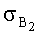
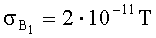
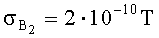
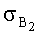
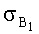
Способ [2012] выбран в качестве прототипа заявляемого способа по совокупности существенных признаков, наиболее близких к нему.
Известный способ локализации источника магнитного поля дипольной модели включает одновременные измерения приращений (разностей) индукции магнитного поля между удаленной опорной точкой и точкой на каждой полуоси системы координат, а также измерение расстояний между этими точками и определение по результатам измерений искомых радиуса-вектора до источника и его магнитного момента.
Причиной, препятствующей достижению указанного ниже технического результата для известного способа, является то, что известный способ основан на измерении градиента, что по определению предполагает ограничения размера баз приращений в зоне измерения градиента.
Задача, на решение которой направлено заявляемое изобретение, заключается в повышении точности и дальности локализации.
Технический результат, получаемый при осуществлении изобретения, заключается в возможности повышения базы каждого приращения до конструктивно удобного предела ради повышения точности и дальности локализации.
Указанный технический результат достигается тем, что заявляемый способ локализации источника магнитного поля дипольной модели, включающий одновременные измерения приращений индукции магнитного поля между опорной точкой и точкой на каждой полуоси системы координат, а также измерение расстояний между точками и определение по результатам измерений искомых радиус-вектора до источника и его магнитного момента, отличается тем, что опорную точку совмещают с центром системы координат, размер базы каждого приращения повышают до конструктивно удобного предела, при этом все искомые величины определяют численно без обращения к измерениям градиента.
На Фиг.1 изображена схема реализации заявляемого способа.
На Фиг.2 изображена схема реализации известного способа.
На Фиг.1 изображена система 7 жестко связанных трехкомпонентных или модульных датчиков магнитного поля В1,В2, В3, В4, В5, В6, В0, предназначенных для измерения 6 приращений индукции магнитного поля В10, В20, В30, В40, В50, В60 относительно центра системы координат 0, в которой размещен опорный датчик В0.
На Фиг.2 изображены 7 конструктивно жестко связанных трехкомпонентных датчиков магнитного поля, предназначенных для измерения 6 приращений индукции магнитного поля относительно опорного датчика, размещенного в удаленной точке 01. Разности пар 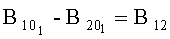
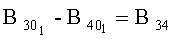
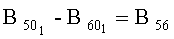
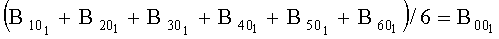
Заявляемый способ действует следующим образом. Измеряют расстояния между точками 1 и 0, 2 и 0, 3 и 0, 4 и 0, 5 и 0, 6 и 0 и выражают каждое из 6 приращений дипольной индукции через измеренное (известное) расстояние между соответствующими точками и неизвестный радиус-вектор X, и неизвестный магнитный момент М f1(X, M)…f6(X, M) измеряют (синхронно) все приращения В10…В60 и составляют систему нелинейных уравнений В10=f1(X, M)…B60=f6(Х, М), которую решают одним из численных методов, для которых в пакете МАТЛАБ составлены универсальные программы, например методом наименьших квадратов.
Таким образом, заявляемый способ основан на измерении приращения (разности) в строгом смысле этого слова и не содержит операций явного решения, связанных с измерением градиента, что характерно для известного способа. (Градиент - понятие точечное, приращение - двуточечное). В известном способе нельзя увеличивать базы 1 и 2…5 и 6, так как градиент по определению требует малую базу (в пределе стремящуюся к нулю), но базу 001 увеличивать необходимо для повышения размера приращения 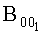
Поскольку заявляемый способ основан на измерениях приращений индукции в строгом смысле, он позволяет оптимизировать базы, выбирать их малыми, средними или большими, одинаковыми или разными, в зависимости от конструктивных особенностей носителя системы датчиков, либо оптимизировать базы из условия обеспечения максимальной точности при том или другом расстоянии локализации магнитного источника.
Заявляемый способ проверен (в сравнении с известным) с помощью компьютерного моделирования локализации с оценкой граничной (при доверительной вероятности 0.997) погрешности локализации (средней на компоненту)
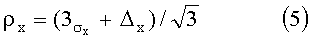
где σх - СКО локализации; Δх - оценка погрешности среднего.
Оценки (5) рассчитаны для заявляемого и известного метода при освоенном уровне СКО компонентных датчиков в режиме измерения приращений 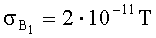
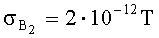
Отметим, что время счета одного цикла локализации по заявляемому способу лежит в пределах 0.1-2 с.
Как видно из таблиц, с повышением расстояния (за счет роста Х(2) или Х(3)) оценки погрешностей нарастают лавинообразно. Предельные расстояния Rпр определены как расстояния, при которых соответствующие оценки погрешности достигают половины соответствующего значения Х(2) или Х(3).
Приведенные в табл.1 и 2 данные позволяют сделать главный вывод: заявляемый способ лучше известного по точности и дальности локализации даже при меньшей базе, не говоря уже о равной или большей базах.
Особенность заявляемого способа, в отличие от известного, заключается в том, что его точность и дальность улучшается с повышением размера базы.
Сравним особенности локализации с помощью трехкомпонентных и модульных датчиков. Особенность модульных датчиков состоит в том, что они точнее, но менее информативны, чем трехкомпонентные, так как являются по сути однокомпонентными приборами. Поэтому локализация с помощью модульных датчиков зависит от измерительной ситуации, то есть от расположения локализуемого объекта и от ориентации его магнитного момента. Для них эта ситуация может оказаться благоприятной или неблагоприятной. Например, условия табл.1 оказались благоприятными и модульные датчики на расстояниях более 200 м дали лучшие результаты, чем трехкомпонентные, а условия табл.2 оказались неблагоприятными и модульные датчики уступили трехкомпонентным на всех расстояниях. Отметим также, что на 200 м (см. табл.1) модульные датчики даже при благоприятной ситуации проигрывают по точности локализации трехкомпонентным. (Трехкомпонентные датчики почти не зависят от измерительной ситуации).
В заключение добавим, что локализация также возможна, если использовать не 6 приращений (см. Фиг.2), а меньше 5…2 (любых трехкомпонентных) приращений, но тогда снижаются точность и дальность локализации и появляется заметная зависимость точности от измерительной ситуации.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОВЕРКИ МАГНИТОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ | 2012 |
|
RU2503026C1 |
| СПОСОБ ЛОКАЛИЗАЦИИ МАГНИТНОГО ДИПОЛЯ | 2010 |
|
RU2456642C2 |
| СПОСОБ ЛОКАЛИЗАЦИИ ИСТОЧНИКА МАГНИТНОГО ПОЛЯ ДИПОЛЬНОЙ МОДЕЛИ | 2010 |
|
RU2433420C1 |
| СПОСОБ МАГНИТНЫХ ИЗМЕРЕНИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2019859C1 |
| УСТРОЙСТВО ДЛЯ БЕСКОНТАКТНОЙ ДИАГНОСТИКИ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ С ВОЗМОЖНОСТЬЮ КАЛИБРОВКИ В ПОЛЕВЫХ УСЛОВИЯХ | 2016 |
|
RU2620326C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И ОРИЕНТАЦИИ ТРЕХКОМПОНЕНТНОГО ДАТЧИКА МАГНИТОМЕТРА ОТНОСИТЕЛЬНО МЕРЫ МАГНИТНОГО МОМЕНТА | 2005 |
|
RU2290657C1 |
| Устройство для измерения градиента магнитной индукции | 1991 |
|
SU1800411A1 |
| СПОСОБ ИЗМЕРЕНИЯ ПРИРАЩЕНИЯ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ТРЕХКОМПОНЕНТНЫМ ДИФФЕРЕНЦИАЛЬНЫМ МАГНИТОМЕТРОМ | 2006 |
|
RU2313801C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КАЛИБРОВОЧНОЙ МАТРИЦЫ ТРЕХКОМПОНЕНТНОГО МАГНИТОМЕТРА (ВАРИАНТЫ) | 2003 |
|
RU2262711C2 |
| Способ магнитных измерений и устройство для его осуществления | 1991 |
|
SU1824612A1 |

Предложен cпособ локализации источника магнитного поля дипольной модели. В способе одновременно измеряют приращения индукции магнитного поля между опорной точкой и точкой на каждой полуоси системы координат и измеряют расстояния между точками. Определяют по результатам измерений искомые радиус-вектор до источника и его магнитный момент. Опорную точку совмещают с центром системы координат, размер базы каждого приращения повышают до конструктивно удобного предела, при этом все искомые величины определяют численно без обращения к измерениям градиента. Техническим результатом является повышение точности и дальности локализации источника магнитного поля. 2 табл., 2 ил.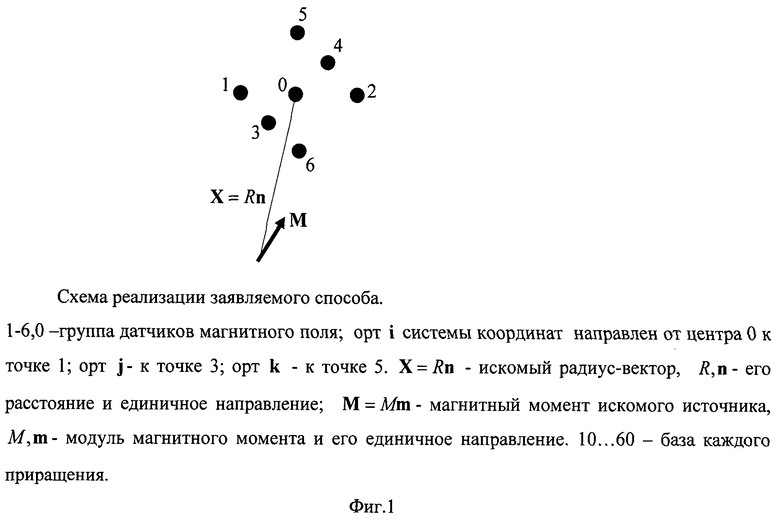
Способ локализации источника магнитного поля дипольной модели, включающий одновременные измерения приращений индукции магнитного поля между опорной точкой и точкой на каждой полуоси системы координат, а также измерение расстояний между точками и определение по результатам измерений искомых радиус-вектора до источника и его магнитного момента, отличающийся тем, что опорную точку совмещают с центром системы координат, размер базы каждого приращения повышают до конструктивно удобного предела, при этом все искомые величины определяют численно без обращения к измерениям градиента.
| СПОСОБ ЛОКАЛИЗАЦИИ МАГНИТНОГО ДИПОЛЯ | 2010 |
|
RU2456642C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВНЕШНЕЙ ПОМЕХИ В ЦЕНТРЕ МЕРЫ МАГНИТНОЙ ИНДУКЦИИ | 2008 |
|
RU2394251C1 |
| МАГНИТОМЕТР-ГРАДИЕНТОМЕТР НА ОСНОВЕ СКВИДОВ ПОСТОЯННОГО ТОКА ИЗ ВЫСОКОТЕМПЕРАТУРНЫХ СВЕРХПРОВОДНИКОВ | 2008 |
|
RU2384856C1 |
| US 8102260 B2, 24.01.2012 | |||
Авторы
Даты
2014-06-27—Публикация
2012-09-06—Подача