Изобретение относится к области гидроакустических навигационных систем и может быть использовано для навигационного обеспечения подводных аппаратов повышенной дальности действия, например, работающих в ледовых условиях, затрудняющих доступ к ним обеспечивающего судна, и также может быть использовано при проведении сейсмических и геологоразведочных работ на морском дне.
Известны способы и устройства, предназначенные для решения задач навигации и позиционирования посредством гидроакустических систем (RU 2032187 С1, 27.03.1995 [1], RU 2158431 С1, 27.10.2000 [2], RU 34020 U1, 20.11.2003 [3], RU 2289149 C2, 10.12.2006 [4], US 2008008045 A1, 10.01.2008 [5], US 4024491 A, 17.05.2007 [6]).
Известная гидроакустическая синхронная дальномерная навигационная система [1], содержит донную навигационную базу из М гидроакустических приемоответчиков с различными частотами ответа и размещенные на объекте навигации гидроакустический передатчик, генератор синхроимпульсов, М-канальный приемник, М измерителей времени распространения гидроакустических сигналов до приемоответчиков и обратно, M·N блоков преобразования временных интервалов в дистанции по N в каждом из каналов из М, М блоков выбора максимального значения дистанции из N значений и вычислитель координат объекта навигации, в котором каждый из М каналов введены по числу лучевых траекторий N-1 дополнительных измерителей времени распространения гидроакустических сигналов, N-1 мультивибраторов задержки, N-1 мультивибраторов строб-импульса, N-1 селекторов, причем первые входы N-1 измерителей распространения соединены с выходом генератора синхроимпульсов, вторые входы соединены с первыми выходами соответствующих селекторов, а выходы соединены с M·N входами блока преобразования временных интервалов в дистанции, первый вход каждого из селекторов соединен с выходом соответствующего мультивибратора строб-импульса, второй вход соединен с выходом соответствующего канала приемника, вход первого мультивибратора задержки соединен с выходом соответствующего канала приемника, а выход каждого последующего мультивибратора задержки соединен с вторым выходом соответствующего селектора, в каждый из М каналов введены N(N-1) дополнительных блоков преобразования временных интервалов в дистанции, N-1 дополнительных блоков выбора максимального значения дистанции и усреднитель дистанции, причем входы каждого из N-1 наборов по N блоков преобразования временных интервалов в дистанции соединены с соответствующими выходами N-1 дополнительных измерителей временных интервалов, а выходы соединены с входами N-1 дополнительных блоков выбора максимального значения, выходы всех блоков выбора максимального значения дистанции соединены с N входами усреднителя дистанций, а выход усреднителя дистанций соединен с входом вычислителя координат объекта навигации.
В данной системе реализован способ навигации подводного объекта, включающий размещение гидроакустических ответчиков на дне водоема, создание навигационной базы из М гидроакустических приемоответчиков с различными частотами ответа, калибровку с помощью внешних средств обеспечения навигационной базы, посредством гидроакустического передатчика, размещенного на подводном объекте, измеряют временные интервалы распространения сигналов с последующим их преобразованием в дистанции между подводным объектом и гидроакустическими приемоответчиками. Для получения достоверных результатов измерений измеренные дистанции усредняют.
Навигационная база таких систем, предварительно устанавливаемая на дне акватории, как правило, состоит из 12-16 маяков ответчиков и предварительно калибруется в относительных и в географических координатах (относительная и абсолютная калибровки) с помощью судна обеспечения, оснащенного бортовым комплексом спутниковой и гидроакустической системам навигации. После выработки своего энергетического ресурса маяки-ответчики заменяются, при этом производится новая калибровка донной навигационной базы. Данный способ позволяет обеспечить географическую привязку подводного аппарата в пределах площади до 100 квадратных километров и протяженностью до 50 километров.
Использование известного способа навигации подводных аппаратов требует значительных затрат судового времени, большого количества донных маяков-ответчиков с длительным сроком автономности, ограничивает радиус действия подводного аппарата дальностью связи с донной навигационной базой. С учетом того, что подводные станции подвержены влиянию гидрологических и литодинамических факторов, то для получения достоверных результатов навигации подводных объектов требуется калибровочные работы выполнять не только при установке и снятии подводных станций, но и в период их эксплуатации при изменении внешних факторов.
При проведении научно-исследовательских работ с применением автономных подводных обитаемых аппаратов, выполнении оперативно-тактических задач подводными аппаратами на морских полигонах протяженностью до тысяч километров и площадью десятки тысяч квадратных километров особое значение приобретает оперативное высоконадежное обеспечение этих работ без использования судна обеспечения.
Известен также способ навигации подводного объекта посредством гидроакустической навигационной системы, содержащей навигационную базу из М гидроакустических приемоответчиков с различными частотами ответа и размещенного на объекте навигации гидроакустического приемопередатчика, посредством которого измеряют временные интервалы распространения сигналов с последующим их преобразованием в дистанции между подводным объектом и гидроакустическими приемоответчиками.
Согласно данному способу гидроакустические приемоответчики размещают на дрейфующих станциях по водной поверхности, навигационные параметры подводного объекта относительно дрейфующей станции или базы из дрейфующих станций определяют в режиме с длинной и/или ультракороткой базой, и/или в комбинированном режиме (длинная + ультракороткая база), и/или в пеленгационной системе, при этом формируют из приемников две навигационные базы с общим центром базы, располагая их в плоскости, параллельной плоскости палубы подводного объекта, при этом ось одной базы Х направлена вдоль осевой линии подводного объекта, а ось другой базы Y направлена по траверзу вправо ([7] патент RU №2365939).
При реализации данного способа, в отличие от известных устройств [1-6], на поверхности моря размещается дрейфующая станция, снабженная соответствующей аппаратурой, и которая находясь в дрейфе, имеет возможность непрерывно принимать сигналы среднеорбитных спутниковых навигационных систем, обрабатывать их с определением высокоточных собственных координат в любой момент времени. В определенный момент времени (по сигналу запроса с подводного объекта или по программе работы дрейфующей станции) эта информация передается по гидроакустическому каналу в виде шумоподобного кодированного сигнала определенного формата на подводный объект. Определив свои координаты относительно дрейфующей станции и имея информацию о географических координатах последней, подводный объект выполняет собственное координирование в географической системе координат.
Общим недостатком известных устройств, представляющих собой гидроакустические навигационные системы [1-7], является существенная погрешность определения координат, связанная с изменчивостью скорости звука в морской воде. При этом погрешность определения дистанции и координат существенно возрастает при работе в мелком море, когда временные задержки между отдельными лучами уменьшаются, а сами лучи невозможно идентифицировать и выделить отдельно.
Для уменьшения погрешности измерений посредством вычислительных средств, как правило, используют методы на основе формульных зависимостей, что частично позволяет минимизировать погрешность оценки среднего арифметического значения гидроакустической характеристики по пространственно-временным массивам наблюдений.
В известных способах среднее арифметическое для любой задачи рассчитывают путем прямого суммирования всех измеренных значений, попадающих в рассматриваемый пространственно-временной объем, и делят на общее число измерений.
В действительности такой метод расчета среднего арифметического гидрологической характеристики не позволяет получить минимально возможную погрешность в оценке среднего. Причиной этого является то, что в принятом методе игнорируется распределение точек наблюдения по пространственно-временному объему. Более того, точность оценки среднего значения применяемого метода уменьшается с увеличением размерности пространства координат наблюдений.
В навигационной практике при определении обсервации по трем и более расстояниям или/и пеленгам точка места подводного объекта относится к центру треугольника погрешностей. Возникает вопрос о степени достоверности такого правила. Это вопрос важен, например, для обоснованности утверждения, что площадь треугольника погрешностей служит мерой точнее обсервации - чем больше площадь треугольника погрешностей, тем точнее обсервация. Это утверждение имеет смысл, только если известно, что точка обсервации лежит внутри сравниваемых треугольников погрешностей.
При этом, при обработке полученных данных посредством гидроакустической системы, на навигационную карту наносят дуги окружностей, центрами которых являются изображения ориентиров (донных маяков), а радиусы равны в масштабе карты измеренным расстояниям, а обсервованное место (координаты) подводного объекта определяют в точке пересечения дуг. При этом, если окружности в одной точке не пересекаются, то обсервованное место принимается в середине фигуры погрешностей. При этом, если погрешность велика (ее стороны на карте составляют более 5 мм), то проверяют правильность опознания ориентиров, измерений и прокладки (Справочник вахтенного офицера / Проничкин А.П., Чуприков М.К., Скворцов М.И. и др. - М.: Воениздат, 1975, с.205-206). При этом обработка результатов измерений отягощена существенной трудоемкостью, обусловленной многочисленными операциями по проверке правильности опознания ориентиров, измерений и прокладки, и в конечном итоге имеет место сравнительно не высокая достоверность определения координат.
В известных гидроакустических навигационных системах задача оценки места по известным расстояниям решается на основе линейного метода (Коломийчук Н.Д. Гидрография. Л.: Изд. ГУ ВМФ, 1975, - 470 с.). В основе этого метода лежит известная зависимость справедливая для геометрии на плоскости, что искомое место лежит на пересечении окружностей с центрами в опорных точках (ориентирах) и радиусами, соответствующими измеренному расстоянию до них. Эта зависимость, справедливая для малых расстояний, для больших расстояний требует введения специальных поправок, учитывающих положение опорных точек в трехмерном пространстве и скорость распространения звука в воде на разных горизонтах, что обуславливает трудоемкость известных способов. Кроме того, при линейной постановке решения этой задачи невозможно получить оценку точности получаемых координат, а также погрешности, обусловленные прокладкой линий положения на навигационной карте.
Относительные координаты в известных системах определяются азимутально-дальномерным способом (измеряемые параметры пеленг и дистанция), или посредством метода, заключающегося в том, что на подводном подвижном объекте одновременно фиксируются пеленг и момент прихода сигнала от маяков ответчиков. В основе измерения дистанции лежит измерение промежутка времени от момента излучения сигнала маяком ответчиком (информация об этом содержится в кодированном сигнале) до момента его получения на подводном подвижном объекте. Возможно также использования метода пеленгования, в котором производится только измерение пеленгов, или комбинированный метод, заключающийся в том, что измеряют дистанции и/или пеленга и учитывают пройденное за это время расстояние по штатному лагу подводного объекта (преимущественно абсолютному лагу, измеряющему скорость относительно грунта).
В первом варианте определение координат требует высокоточного знания скорости распространения звука в воде, который влияет на точность определения дистанции, а также наличие погрешности в измерение дистанции за счет рефракции. Для второго варианта также характерно внесение погрешностей в измерении дистанции за счет рефракции. Основным условием реализации третьего варианта, путем контроля пройденного расстояния по лагу, с точки зрения обеспечения требуемой точности, является достижение максимальной точности измерения вектора пройденного за время обсервации расстояния, что требует использования в период обсервации выполнения измерений пройденного расстояния по абсолютному гидроакустическому лагу, основная составляющая погрешности которого также обусловлена изменением скорости звука в водной среде.
При проведении научно-исследовательских работ с применением автономных подводных обитаемых аппаратов, выполнении оперативно-тактических задач подводными аппаратами на морских полигонах протяженностью до тысяч километров и площадью десятки тысяч квадратных километров особое значение приобретает оперативное высоконадежное обеспечение этих работ без использования судна обеспечения. Известная система, состоящая из размещенных донных маяков-ответчиков для обеспечения последующей географической привязки местонахождения подводного аппарата имеет существенные ограничения как по границам радиуса действия полигона, так и по трудоемкости выполнения калибровочных работ и работ, связанных с размещением и установкой донных станций при каждой замене источников питания, имеющих ограниченный срок работы.
При реализации каждого из известных способов определения координат по ориентирам необходимым условием для получения требуемой точности является, чтобы измеренные параметры, характеризующие линии положения при построении их на навигационной карте, пересекались в одной точке, что обеспечивается только в том случае, если наблюдения, вычисления и прокладка не содержали никаких ошибок. При этом на практике линии пеленгов образуют треугольник погрешностей, и если величина сторон треугольника погрешностей небольшая, то вероятное место судна принимают в центре треугольника. Нахождение этих прямых, а следовательно, и места судна является минимаксной оптимизационной задачей. Прямое непосредственное ее решение - сложная задача, поэтому при ее решении известными способами очень сложно получить необходимую точность определения координат подвижных морских объектов относительно ориентиров. Достижение приемлемой точности требует трудоемких расчетов даже при использовании автоматизированных средств. Это обусловлено тем, что существующие стандарты представления чисел в ЭВМ не поддерживают всех необходимых свойств обеспечения арифметических операций.
Например, при выполнении арифметических действий, в формате с плавающей точкой, не выполняются законы коммутативности, ассоциативности и дистрибутивности, обязательные в арифметике (Акритас А. Основы компьютерной алгебры с приложениями. - М.: Мир, 1994. - 544 с.). Это обстоятельство не позволяет найти прямые линии, пересекающиеся в одной точке, для которых сумма отклонений от пеленгов минимальна.
Построение треугольника погрешностей также не решает полностью задачу получения достоверных координат, так как при нахождении погрешностей используется интервальный анализ, который основан на окружении вещественных чисел, характеризующих координаты, интервалами, что приводит к необходимости решения проблемы разноточных числовых данных (противоречие между непрерывным и дискретным). Географические координаты абстрактно определяются в непрерывном пространстве и представляются в виде действительных цифр. Далее действительные числа представляются (аппроксимируются) рациональными числами - дискретным множеством. В свою очередь рациональные числа записываются чаще всего в десятичной форме, что еще больше искажает модель непрерывности географических координат. Это приводит к разноточности в оценке полученных координат, обусловленной как несоответствием между действительной точностью измерения и представлением этого измерения в цифровой форме, т.е. несоответствием между количеством обеспеченных точностью значащих цифр и количеством значащих цифр в представленном результате, так и несоответствием в точности двух и более сравниваемых значений координат.
Для получения достоверных данных результаты измерений представляются в цифровой форме с количеством значащих цифр, соответствующих погрешности измерений. Это приводит к избытку значащих цифр, что при представлении измеренной информации приводит к увеличению объемов обрабатываемой информации, увеличению требуемых объемов постоянной памяти для ее хранения и оперативной памяти при ее обработке и самого времени обработки. Источником возникновения разноточности измеренных данных является и процедура обмена информации между ЭВМ и инструментальными средствами измерения. В известных способах для представления значений географических координат используются числа в формате плавающей точки. Поэтому географические координаты, записанные первоначально в градусной мере (рациональными числами), при вводе в ЭВМ переводятся в десятичное представление. Для хранения измеренных географических координат используется формат с максимальной разрядностью, доступной для используемой ЭВМ, что приводит к числам с большим количеством десятичных разрядов, не обеспеченных точностью измерений. При представлении географических координат в ЭВМ в формате с плавающей точкой соответствующие числовые значения имеют неоправданно высокую точность, а действительная погрешность обычно не определена. Все измеренные значения географических координат представляются десятичными числами с одинаковым числом десятичных разрядов. Количество разрядов определяется не погрешностью измерений географических координат, а разрядностью процессора используемой ЭВМ. Одинаковая разрядность представления географических координат создает иллюзию правомерности выполнения картометрических задач с использованием наборов измеренных данных, имеющих различную точность географических координат.
Задачей настоящего технического предложения является повышение надежности при обеспечении навигации подводных объектов с одновременным снижением трудоемкости.
Поставленная задача решается за счет того, что в способе навигации подводного объекта посредством гидроакустической навигационной системы, включающем размещение навигационной базы из М гидроакустических приемоответчиков с различными частотами ответа и размещение на подводном объекте навигации гидроакустического приемопередатчика, посредством которого измеряют временные интервалы распространения сигналов с последующим их преобразованием в дистанции между подводным объектом навигации и гидроакустическими приемоответчиками, размещение гидроакустических приемоответчиков на дрейфующих станциях по водной поверхности и донных станциях на морском дне, определение навигационных параметров подводного объекта навигации относительно донных или/и дрейфующей станции или базы из дрейфующих станций, которые определяют в режиме с длинной и/или ультракороткой базой, и/или в комбинированном режиме (длинная + ультракороткая база), и/или в пеленгационной системе, при этом формируют из приемников две навигационные базы с общим центром базы, располагая их в плоскости, параллельной плоскости палубы подводного объекта навигации, при этом ось одной базы Х направлена вдоль осевой линии подводного объекта навигации, а ось другой базы Y направлена по траверзу вправо, обработку результатов измерений по пространственно-временным массивам наблюдений, определение координат подводного объекта навигации путем вычислений, согласно изобретению при вычислении координат выполняют минимизацию погрешности по распределению измеренных координат, при этом в вычислительное устройство вводят локальные декартовые координаты для рассматриваемой пространственно-временной области, в которой размещены дрейфующая станция, донные маяки-ответчики и подводный объект, при этом определяют временной ход гидроакустической характеристики для полученных временных рядов, экстремальные значения гидроакустической характеристики в каждом полученном ряду измерений методом статистики Герста, а оценку среднего арифметического значения гидроакустической характеристики по пространственно-временным массивам наблюдений выполняют путем вычислений по многомерным квадратурным формулам и функциям Хаара.
Определение временного хода гидроакустической характеристики для полученных временных рядов, путем определения экстремальных значений гидроакустической характеристики в каждом полученном ряду измерений методом статистики Герста, и выполнение оценки среднего арифметического значения гидроакустической характеристики по пространственно-временным массивам наблюдений путем вычислений по многомерным квадратурным формулам и функциям Хаара позволяет минимизировать погрешности в измерении координат подводного объекта..
Предлагаемый способ реализуется следующим образом.
В районе исследований формируют навигационную базу путем размещения на морском дне донных маяков-ответчиков, а на водной поверхности - дрейфующих станций, которые представляют собой устройство, состоящее из полиуретанового корпуса, на котором установлена мачта с размещенными на ней спутниковой антенной и при необходимости метеорологическими датчиками. Внутри корпуса установлена аппаратура измерения, обработки и хранения информации. Конструкция устройств для реализации предлагаемого способа и принцип их работы аналогичны устройствам прототипа.
При установке большой группы дрейфующих станций средства связи могут также включать ретранслятор, который осуществляет прием радиосигнала от дрейфующей станции в диапазоне ДМВ (401-403 МГц), объединение с сигналами других дрейфующих станций и донных маяков-ответчиков, находящихся в зоне действия дрейфующей станции, в общий групповой сигнал и одновременную передачу на наземные пункты приема в двух стволах диапазона СМВ (4/6, 7/8 ГГц), а при необходимости в состав средства связи может входить и береговая станция спутниковой связи, которая осуществляет прием излучаемого группового сигнала ретранслятора и содержит аппаратуру восстановления сообщений, включающую декодер и устройство обработки и восстановления сообщений, запоминающее устройство, устройство управления.
Обработка сообщений включает помехоустойчивое кодирование, разбивку каждого сообщения на пакеты с длительностью, зависящей от состояния взволнованной поверхности, передачу пакетов сообщения на ретранслятор по алгоритму, автоматически формируемому в зависимости от морского волнения, которое определяется посредством спутниковой навигационной системы в соответствии с известными алгоритмами (описание к патенту РФ №2254600).
Применение дрейфующих буйковых станций (дрифтеров), оснащенных GPS приемником и аппаратурой гидроакустического канала связи, в качестве навигационных маяков, расположенных на морской поверхности в сочетании с донными маяками-ответчиками, позволяет обеспечить высокоточную навигацию для подводных объектов.
Очевидно, что расположение навигационного маяка-дрифтера на морской поверхности не требует проведения относительной и абсолютной калибровок полигона, который необходим при использовании донных гидроакустических маяков-ответчиков, так как наличие у дрифтера GPS приемника позволяет ему «знать» свои географические координаты в реальном масштабе времени с высокой точностью (например, точность определения координат посредством спутникового навигационного измерительного модуля типа СНИМ разработки российской фирмы «Навис» не хуже 5 метров). Навигация подводного объекта относительно дрейфующей станции или базы из дрейфующих станций может осуществляется как в режиме с длинной, ультракороткой базой (ДБ и УКБ), так и в комбинированном режиме ДБ/УКБ.
Подводный объект оснащается соответствующими режиму работ гидроакустическими приемо-передающими антеннами, навигационным контроллером и навигационным программно-математическим обеспечением. Маяк-дрифтер работает в режиме «запрос-ответ» и в режиме «пингер» (маяк). В режиме с длинной базой для определения координат подводного объекта используются сигналы минимум от 3-4 маяков-дрифтеров (аналогично как в спутниковой GPS) и решается триангуляционная задача. При этом площадь или протяженность зоны действия системы зависит от энергетической дальности действия гидроакустической связи, количества дрифтеров, глубины расположения подводного объекта, гидрологии, шумов подводного объекта и морской поверхности. При этом, в отличие от навигации с использованием только донной навигационной базы, навигация с помощью маяков-дрифтеров, которая не требует калибровок, существенно расширяет функциональные возможности подводного объекта, дает возможность оперативно оборудовать рабочий полигон любой площади и протяженности необходимым количеством дрифтеров, позволяет подводному объекту определять свои координаты в реальном времени, оперативно менять свои тактические задачи без потери навигационной информации, получать данные по своим координатам в любое необходимое время или постоянно в автоматическом режиме.
При навигации подводного объекта при ее работе на глубинах более одного километра целесообразно работать на частотах в диапазоне от 8 до 15 кГц, при этом энергетическая дальность связи с маяком-дрифтером будет достигать 10-14 км, а погрешность определения координат аппарата составит 7-10 метров в режиме ДБ и 0,3% от дальности в режиме УКБ и 0,5 град по углу пеленгации. При рабочей глубине менее одного километра целесообразно использовать рабочие частоты в диапазоне 25-35 кГц и работать в режиме УКБ. При этом максимальная дальность связи будет достигать порядка 3 км.
Особое назначение имеет возможность подводного объекта определять свои координаты с помощью маяков-дрифтеров в пассивном режиме. В этом случае маяки-дрифтеры переводятся в режим автоматического периодического излучения гидроакустических сигналов (режим «пингер») с высокой точностью синхронизации, а подводный объект, принимая эти сигналы и используя при этом специальный алгоритм и программно-математическое обеспечение обработки, определяет свои географические координаты относительно координат маяка-дрифтера или навигационной базы из маяков-дрифтеров. Необходимо отметить при этом, что каждый сигнал маяка-дрифтера имеет специальный формат и кодировку и несет в себе информацию о географических координатах маяка-дрифтера, его индивидуальном номере, направлении и скорости его перемещения на поверхности.
Алгоритм работы навигационной системы с применением дрифтеров имеет гибкую структуру и может быть легко адаптирован как под заранее прокладываемый маршрут подводного объекта на полигоне, так и под определение координат подводного объекта в любое конкретное время ее работы на полигоне в различных гидрологических условиях, условиях шума. Дополнительные возможности по обеспечению оперативной навигации подводного объекта дает установка (запуск) маяка-дрифтера непосредственно с подводного объекта в необходимый момент времени.
При этом в процессе всплытия на поверхность маяк-дрифтер может измерять профиль скорости звука и гидрологические параметры, что необходимо при расчете точных координат подводного объекта. После подъема дрифтера на поверхность он переходит в режим приема спутниковых сигналов системы GPS и передачи гидроакустических сигналов на подводный объект в режиме «запрос-ответ» или режиме «пингер». Подводный объект фиксирует дистанцию и пеленг до маяка-дрифтера (режим УКБ) и вычисляет свои точные географические координаты, используя информацию, принятую от маяка-дрифтера по гидроакустическому каналу связи. Скорость передачи по гидроакустическому каналу связи может составлять 9600-12400 бод. Наиболее оптимальная дальность связи в режиме УКБ при глубине подводного объекта до 500 метров - 1 км. Точность определения координат до 5 метров.
Наличие гидроакустического канала связи между дрифтером и подводным объектом позволяет также обеспечивать передачу служебной информации из наземного центра на подводный объект по спутниковому телеметрическому связному каналу через дрейфующую станцию, находящуюся в зоне гидроакустической связи с подводным объектом.
В предлагаемом способе применена комбинированная система гидроакустической навигации с длинной и ультракороткой базой, которая позволяет использовать пеленгационную систему решения задачи выхода подводного объекта в точку установки дрейфующей станции. При этом гидроакустическая антенна подводного объекта представляет две имеющие общий центр базы из приемников. При этом, если две приемные базы расположены в плоскости, параллельной плоскости палубы, и ортогональны, ось одной базы направлена вдоль осевой линии подводного объекта, а ось другой базы направлена по траверзу вправо.
Две имеющие общий центр базы из приемников позволяют определить направление на источник сигнала как линию пересечения двух конических поверхностей с совпадающими вершинами.
Так как плоскость палубы практически никогда не совпадает с плоскостью горизонта, то учитывается также влияние углов крена и дифферента.
Информация о координатах дрейфующей станции относительно подводного объекта позволяет решить задачу выхода подводного объекта в реперную точку, так как она легко преобразуется в значения курсового угла и дистанции. Решение обратной задачи дает возможность определить координаты подводного объекта на карте или планшете, на который предварительно наносится реперная точка. В том случае, когда определяется также наклонное расстояние до дрейфующей станции, третьей поверхностью положения является сфера с радиусом, равным наклонному расстоянию.
Составные части подводного объекта включают приемную гидроакустическую антенну, состоящую из четырех гидрофонов. Секция антенны состоит из двух одноканальных и одного двухканального модуля, располагающихся на линейном несущем кронштейне. Расстояние между приемными гидрофонами двухканального модуля составляет 50 мм. Максимальное разнесение крайних приемников на кронштейне составляет 1000 мм. Кронштейн перфорирован, что позволяет располагать приемники в непосредственной близости друг от друга для проведения фазовой калибровки и с произвольным разнесением для проведения измерений направления прихода акустического сигнала. В качестве приемников-гидрофонов использованы пьезокерамические сферы диаметром 30 мм, внутри которых размещены предварительные усилители с коэффициентом усиления 30 дБ. Сферы размещаются на стальной пластине размером 145×145×10 мм, снабженной элементами крепления и акустической заглушкой с тыльной стороны. Коэффициент подавления звукового сигнала с тыльной стороны составляет не менее 30 дБ.
Антенный комплекс состоит из 8-канальной 2-секционной приемной гидроакустической антенны и гидроакустической излучающей антенны.
Каждая секция приемной антенны представляет собой 4-элементный неэквидистантный гидрофонный модуль, предназначенный для измерения проекции вектора прихода акустического сигнала на одну из горизонтальных осей в режиме ультракороткой базы, в пеленгационном режиме, либо для приема сигналов в режиме длинной базы на 4 рабочих частотах. Секции приемной антенны расположены в горизонтальной плоскости перпендикулярно друг к другу.
Таким образом, когда все гидрофоны производят прием на одной и той же рабочей частоте, реализуется режим определения задержки и направления прихода отклика от фиксированной дрейфующей станции в режиме ультракороткой базы, а когда каждый из гидрофонов настроен на свою рабочую частоту, осуществляется режим измерения задержек от дрейфующих станций в режиме длинной базы. Аналогичное устройство имеют и донные маяки-ответчики.
Система передачи информации по гидроакустическому каналу на подводном объекте реализуется с использованием штатных средств гидроакустической связи. При этом в качестве устройств формирования и обработки сигналов могут быть применены как имеющаяся в составе гидроакустическая аппаратура, обеспечивающая режим гидроакустической связи, так и дополнительные устройства в виде приставок, подключаемых к их передающему и приемному трактам.
В качестве сигналов местоположения использованы тональные сигналы с частотой 3 кГц, излучаемые как в автоматическом режиме по специальной программе, так и в режиме запроса.
Спутниковый связной модуль предназначен для формирования пакетов и алгоритмов управления передаваемой информации.
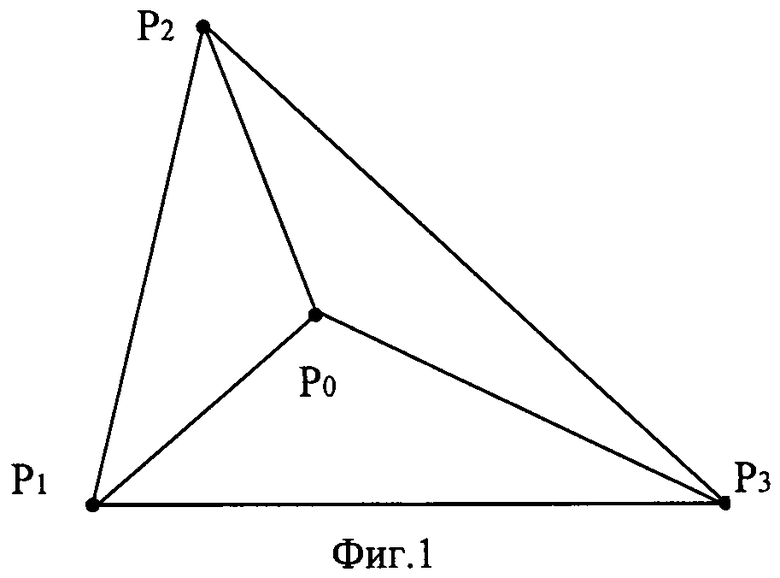
В результате пеленгования получают массив данных (расстояний и/или пеленгов). Наносят на навигационную карту положения ориентиров (фиг.1) p1, p2, р3 и измеренных пеленгов d1, d2, d3. Для определения координат подвижного морского объекта выполняют построения на двойственной плоскости (фиг.2), где точки ориентиров p1, p2, р3 будут соответствовать двойственным прямым p1, p2, р3, координаты которых определяются по формуле d:у=ax+b→d(a,-b). Прямые пеленгов d1, d2, d3 будут соответствовать двойственным точкам d1, d2, d3, координаты которых определяются по формуле р(а,b)→р:ax-b. Если на основной плоскости пеленги не пересекаются в одной точке, то на двойственной плоскости точки d1, d2, d3 не лежат на одной прямой. Методом наименьших квадратов находят прямую линию ро, наименее уклоняющуюся от точек d1, d2, d3. Этой прямой на двойственной плоскости соответствует искомая точка ро места морского подвижного объекта на основной плоскости (О - точка на фиг.1). Прямая линия ро на двойственной плоскости пересекает все три прямые p1, p2, р3. На фиг.2 точки пересечения обозначены кружками (О). Эти точки пересечения соответствуют таким пеленгам на основной плоскости (пунктирные прямые на фиг.1), которые пересекаются в одной точке ро.
Далее числовые значения полученных координат представляются в виде символов, количество которых соответствует представлению числа с заданной точностью, что практически равно числу разрядов в двоичном представлении этого числа с той же точностью. При этом запись числа в символьной системе содержит информацию не только об измеренном значении, но и содержит информацию о погрешности представления числа. Эта операция осуществляется посредством ЭВМ, составляющей наряду со средствами измерения расстояний и пеленгов и графопостроителем автоматизированную систему определения места подвижного морского объекта. При этом символьное представление чисел, характеризующих измеренные значения координат, осуществляется путем построения бинарного дерева Штерна-Брока (Грэхем Р., Кнут Д., Паташник О. Конкретная математика. - М.: БИНОМ. Лаборатория знаний, 2006. - 703 с.).
Последовательность символов в представлении числа, характеризующего координаты, определяют все соответствующие узлы в дереве Штерна-Броко. Для наинизшего узла находятся его соседи как по вертикали, так и по горизонтали, что позволяет оценить точность представления числа и при необходимости перейти к представлению этого числа с другой (требуемой) точностью.
В задачах учета влияния гидрологических явлений на скорость распространения звука в водной среде большое значение имеет выбор функции распределения гидрологических характеристик для оценки экстремальных значений, определяющих степень влияния гидрологических условий на скорость распространения звука на разных горизонтах водной среды.
Ввиду того, что экстремальные значения гидрологических и гидроакустических характеристик распределены не по экспоненциальному закону, как это свойственно нормально распределенным случайным величинам, а по степенному закону, то это приводит к тому, что ущерб от экстремальных значений значительно выше, чем это обычно оценивается при использовании нормального закона распределения. Обоснованием этому может служить классическая теория экстремумов (Лидбеттер М., Ротсен X., Линдгрен Г. Экстремумы случайных последовательностей и процессов. - М.: Мир, 1989. - 392 с.), в которой рассматривается распределение максимума:
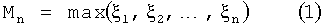
где n независимых и одинаково распределенных случайных величин ξ с функцией распределения F(x) при больших значениях n.
Основной результат этой теории утверждает, что если для некоторых последовательностей нормирующих констант an>0, bn случайная величина an(Mn-bn) имеет невырожденную предельную функцию распределения G(x), то эта функция G(x) должна иметь одну из трех возможных форм
Тип 1: G(x)=ехр(-е-x), -∞<х<∞,
Тип 2: 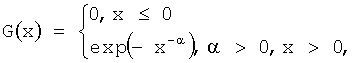
Тип 3: 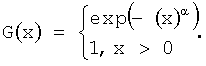
В частности доказывается, что "хвосты" всех функций распределения F(x) имеют только два типа:
- экспоненциальный (е-x) для типа 1 (например, для нормального закона распределения);
- степенной (х-α, α>0) для типов 2 и 3.
Покажем, что экстремальные значения гидроакустических характеристик распределены по степенному закону. Логика доказательства следующая.
Прямыми статистическими оценками рядов наблюдений нельзя оценить поведение "хвоста" распределения в силу редкости экстремальных событий. Воспользуемся косвенным приемом, а именно тем, что поведение "хвостов" распределений разбивает все множество невырожденных распределений случайных величин на два класса эквивалентности - степенной и экспоненциальный. Причем линейные статистики не нарушают этого разбиения. Выберем такую статистику L(an,bn) для временного хода гидрологической характеристики ξ(n), которая приводит к случайной величине η(n), распределенной по некоторому закону F*(y), для которой известен из классической теории экстремумов тип распределения ее "хвоста". Тогда такой же тип распределения "хвоста" будет у значений экстремумов гидроакустической характеристики.
В качестве линейной статистики воспользуемся статистикой Герста, которая имеет вид (Федер Е. Фракталы. - М.: Мир, 1991. - 260 с.):
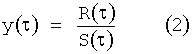
где
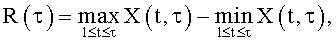
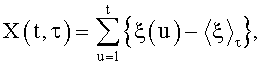
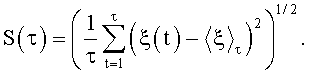
Оценим функцию распределения F*(y) случайной величины η, полученную с помощью этого преобразования.
Обработка временных рядов гидрологических характеристик приводит к следующей степенной зависимости
F*(y)~τH,
где 1/2<H<1.
Следовательно, статистика Герста определяет случайную функцию, распределенную по степенному закону, который, как доказывается в теории экстремумов, имеет степенное распределение "хвоста". Значит и "хвосты" гидроакустических характеристик имеют степенное распределение.
Ущерб от экстремального значения гидроакустической характеристики, очевидно, является некоторой степенной функцией от величины экстремума
Q~xn, n<1.
Если в качестве количественной оценки влияния экстремальных значений гидроакустических характеристик при проектировании использовать математическое ожидание ущерба
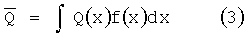
где f(x) - функция плотности распределения "хвоста" гидроакустической характеристики, то очевидно получаем:
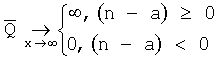
Для нормального закона распределения 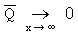 при любом n. Для наблюдаемых гидроакустических процессов α~1, и вероятнее всего большое влияние "хвоста" распределения на величину ущерба от возникновения экстремального значения гидроакустической характеристики.
при любом n. Для наблюдаемых гидроакустических процессов α~1, и вероятнее всего большое влияние "хвоста" распределения на величину ущерба от возникновения экстремального значения гидроакустической характеристики.
Оценку погрешности определения координат по пеленгам выполняют в следующей последовательности.
Оценка погрешности определения координат по пеленгам поясняется чертежами.
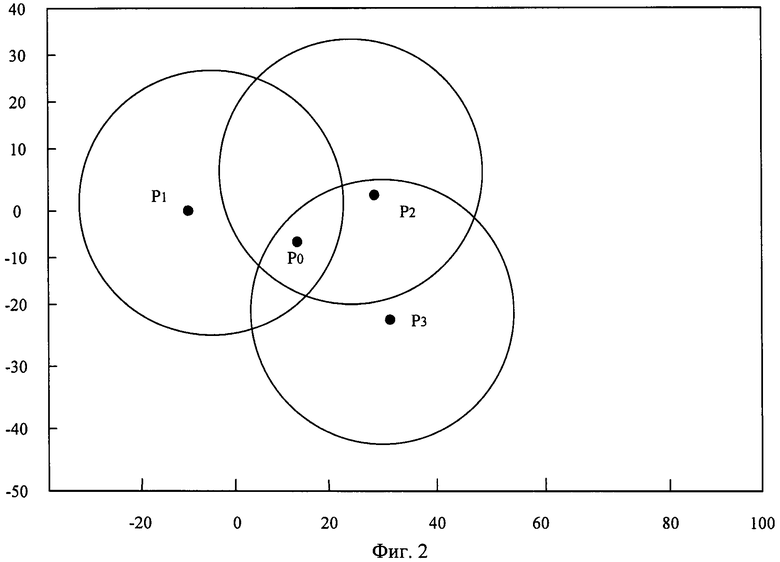
Фиг.3. Расположение пеленгов относительно истинного пеленга. Точка ориентира 1, истинная точка обсервации 2, истинный пеленг 3, левый измеренный пеленг 4, правый измеренный пеленг 5.
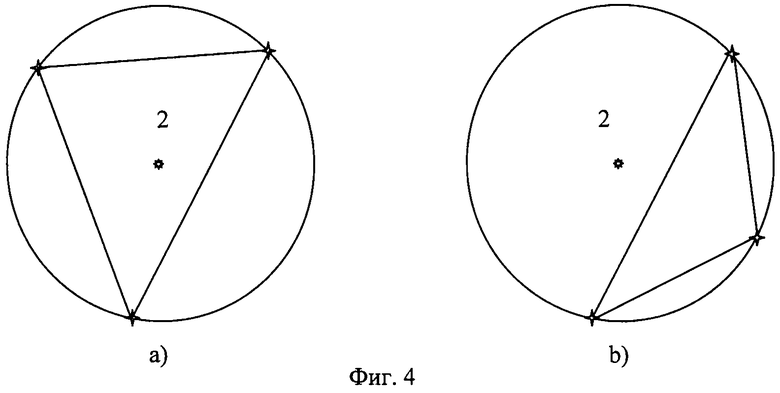
Фиг.4. Классы геометрических конфигураций трех ориентиров и точки обсервации. Ориентиры 1, истинная точка обсервации 2, фиг.4а - точка обсервации 2 находится в треугольнике с вершинами в точках ориентиров 1, фиг.4б - точка обсервации 2 находится вне треугольника с вершинами в точках ориентиров 1.
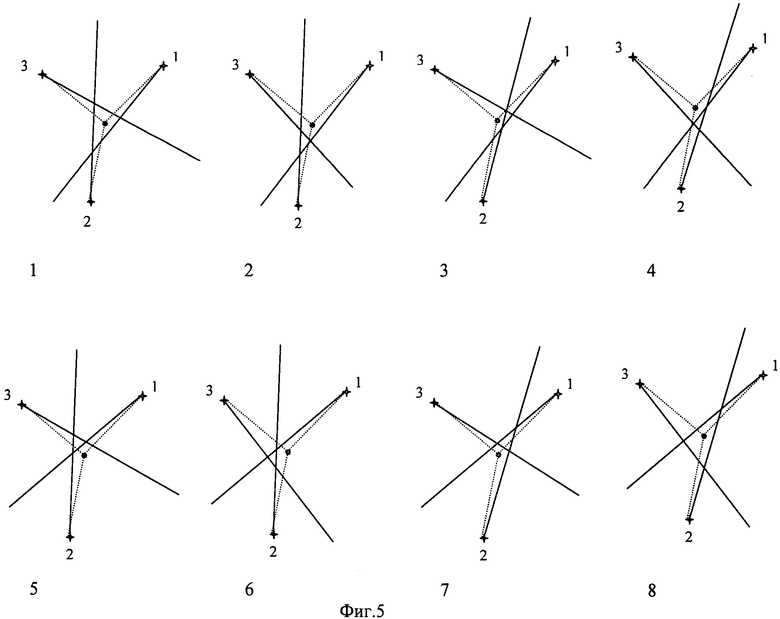
Фиг.5. Классы конфигураций. Сплошные прямые - измеренные пеленги, пунктирные - истинные пеленги.
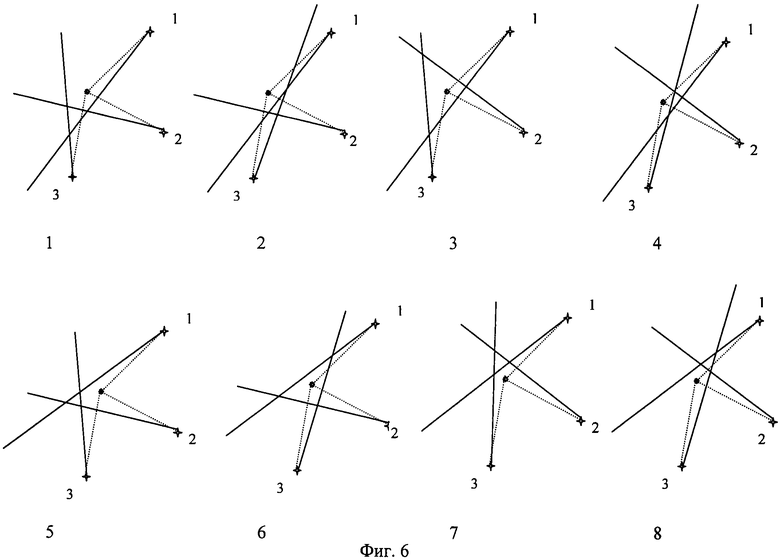
Фиг.6а. Класс конфигураций, при которых точка обсервации 2 находится внутри треугольника с вершинами в точках ориентиров.
Фиг.6b. Класс конфигураций, при которых точка обсервации 2 находится вне вершины треугольника с вершинами в точках ориентиров 1.
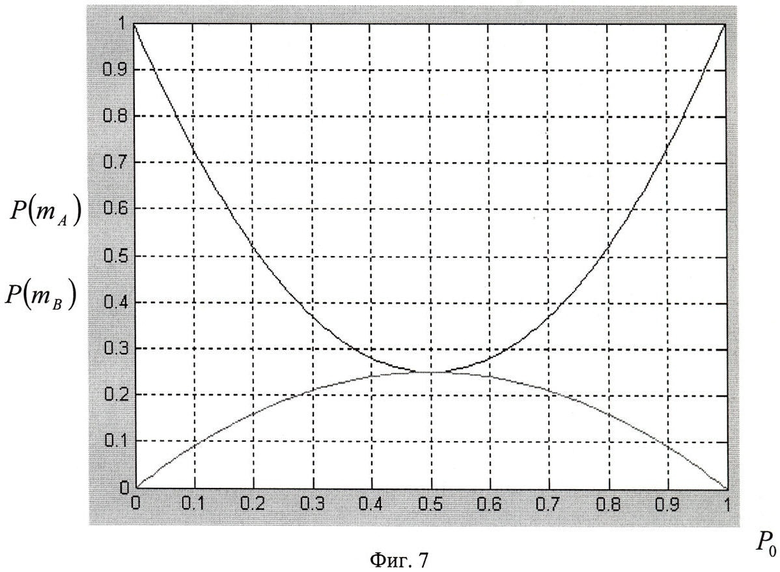
Фиг.7. Графики вероятности расположения точки обсервации 2 внутри треугольника погрешностей.
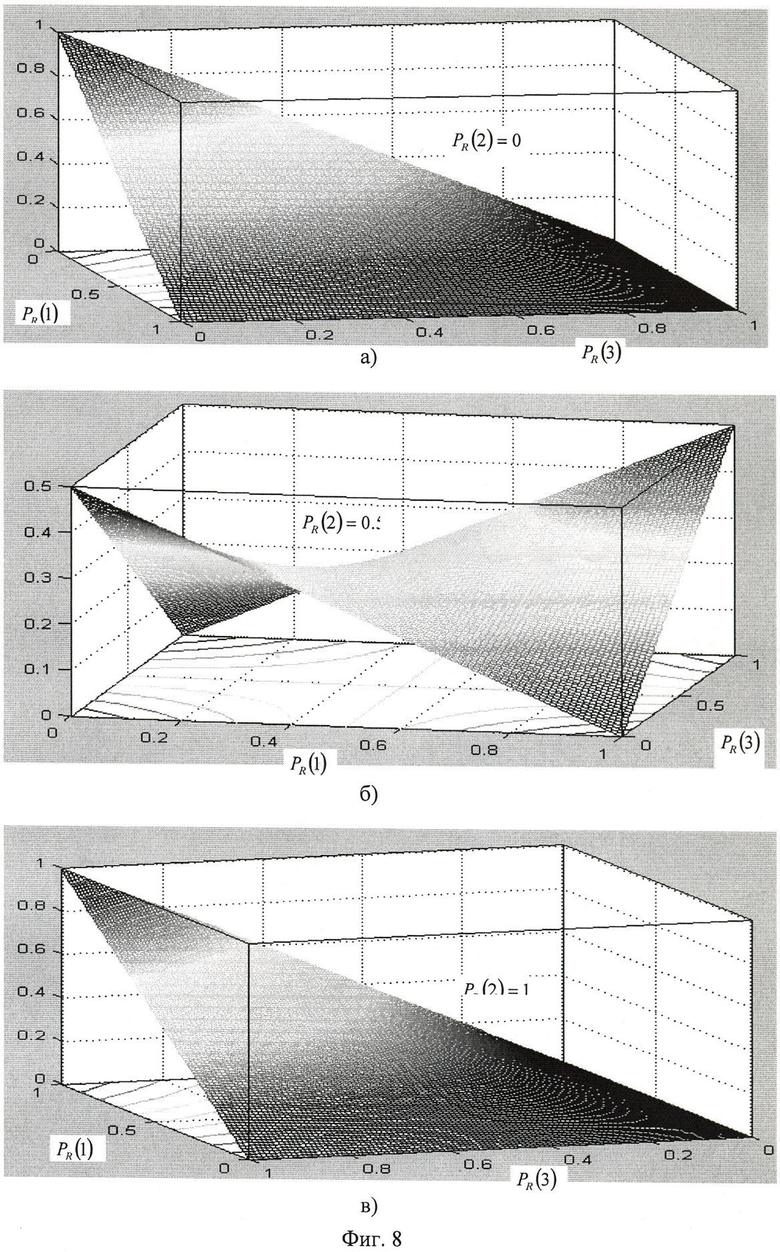
Фиг.8а, б, в. Примеры графиков суммарной вероятности нахождения точки обсервации в треугольнике погрешностей.
Теоретически определение погрешности основывается на количественной оценке этой степени достоверности в виде вероятности нахождения точки обсервации внутри треугольника погрешностей. Решения поставленной задачи лежат в области комбинаторной вероятности с некоторыми естественными предположениями относительно вероятностных свойств геометрических объектов. Предварительно приведем несколько технических уточнений для однозначности дальнейшего изложения.
Будем считать, что измеренный пеленг на ориентир всегда имеет случайную погрешность относительно истинного пеленга. Измеренный пеленг может лежать слева или справа относительно истинного пеленга (фиг.3). Если измеренный пеленг лежит справа от истинного, то это событие будем обозначать символом R, а если слева, то - L.
Сделаем следующие предположения относительно вероятностных свойств отклонения измеренного пеленга относительно истинного.
1. Функция плотности распределения отклонения измеренного пеленга относительно истинного существует, но неизвестна. Пусть в соответствии с этой функцией плотности распределения вероятность нахождения измеренного пеленга слева относительно истинного будет равна PL, тогда вероятность нахождения измеренного пеленга справа относительно истинного будет равна PR=1-PL.
2. При обсервации по трем пеленгам множество погрешностей являются попарно независимыми случайными событиями со своими функциями плотности распределения и, следовательно, со своими PL(n) и PR(n), n∈(1, 2, 3).
Таким образом, при измерении одного пеленга имеется только два несовместимых события: R и L. Эта пара событий образует в рассматриваемой задаче полную группу событий измерения одного пеленга Ω1={R1,L1}. При измерении трех пеленгов будем иметь ΩN={R1,L1,R2,L2,R3,L3}.
С учетом вышеизложенного, решение поставленной задачи сводится к следующим этапам:
1. Выявить все возможные комбинации нахождения измеренных пеленгов слева или справа относительно истинных М={ε1, ε2, ε3}, где ε={R, L}.
2. Определить среди списка комбинаций М подмножество m комбинаций, для которых точка обсервации будет лежать в треугольнике погрешностей.
3. Вычислить суммарную вероятность Р(m) появления подмножества комбинаций, для которых точка обсервации будет лежать в треугольнике погрешностей.
Для упрощения изложения положим, что PL(n)=PR(n)=0.5 (требование равно вероятности) для всех n=1, 2, 3 (в дальнейшем это ограничение будет снято).
Ориентиры занумеруем по часовой стрелке относительно точки обсервации. Выбор первого ориентира - произволен. Номера ориентиров никак не связаны с порядком измерения пеленгов.
Выполнение первого этапа решения. Число возможных комбинаций (элементов множества М) равно 23. В таблице 1 перечислены все возможные комбинации.
На втором этапа решения поставленной задачи все геометрические конфигурации имеет два класса геометрических конфигураций трех ориентиров и точки обсервации, обладающих различными типами комбинаций m, для которых точка обсервации будет лежать в треугольнике погрешностей. Это определяется тем, что расстояния от точки обсервации до ориентиров не имеют значения (поэтому будем изображать положения ориентиров на окружности единичного радиуса с центром в точке обсервации с учетом пеленга).
Один класс, обозначим его класс-А, состоит из конфигураций, при которых точка обсервации лежит в треугольнике с вершинами в точках ориентиров (фиг.4а), а другой класс, обозначим его класс-В, состоит из конфигураций, в которых точка обсервации лежит вне треугольника с вершинами в точках ориентиров (фиг.4b).
Типичные ситуации нахождения измеренных пеленгов слева или справа относительно истинных для всех комбинаций таблицы 1 представлены для конфигураций класса А на фиг.5а, для класса В на фиг.5b.
Из этих рисунков следует, что для конфигураций класс-А для которых точка обсервации будет лежать в треугольнике погрешностей состоит из комбинаций, соответствующих номерам 1 и 8 таблицы 1 (mA={{R,R,R},{L,L,L}}), а для конфигураций класса-В состоит из комбинаций, соответствующих номерам 3 и 6 (mB={{R,L,R},{L,R,L}}).
Таким образом, результат второго этапа состоит в доказательстве того, что при обсервации по трем пеленгам точка обсервации лежит в треугольнике погрешностей только при двух комбинациях в каждом из двух классов конфигураций.
Третий этап включает вычисления суммарной вероятности Р(m) нахождения точки обсервации в треугольнике погрешностей. Сделанные ранее предположения о вероятностных свойствах погрешностей измерения пеленга позволяют воспользоваться теорией комбинаторной вероятности. Получим:
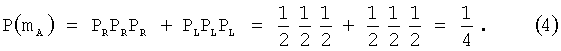
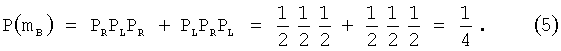
Таким образом, при условии равновероятности (0.5) получения измеренного значения пеленга слева или справа относительно истинного значения вероятность того, что точка обсервации будет лежать в треугольнике погрешностей равна 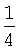 в каждом из двух классов конфигураций. Ясно, что всякая конкретная обсервация относится только к одному из двух классов конфигураций.
в каждом из двух классов конфигураций. Ясно, что всякая конкретная обсервация относится только к одному из двух классов конфигураций.
Ослабим требование равно вероятности. Положим, что PR(n)=Р0 принимает некоторое значение в интервале нуль - единица, причем одно и то же для всех n=1, 2, 3. n.
Тогда (4) и (5) запишутся в виде
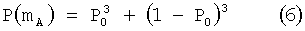
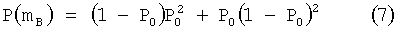
Значения функции (3) при стремлении Р0 к нулю или к единице стремятся к единице. Действительно, если Р0 стремится к нулю, то первое слагаемое в (6) стремится к нулю, а второе к единице, а если Р0 стремится к единице, то первое слагаемое в (6) стремится к единице, а второе к нулю. Так как (6) непрерывная не постоянная функция, имеющая максимальное значение, равное единице, то (6) должна иметь минимум. Он равен 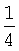 и достигается в точке Р0=1/2.
и достигается в точке Р0=1/2.
Значения функции (7) при стремлении Р0 к нулю или к единице стремятся к нулю. Действительно, если Р0 стремится к нулю или единице, то первое и второе слагаемые в (4) стремятся к нулю. Так как (7) непрерывная не постоянная функция, имеющая минимальное значение равное нулю, то (6) должна иметь максимум. Он равен 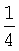 и достигается в точке Р0=1/2.
и достигается в точке Р0=1/2.
Графики для выражений (6) и (7) представлены на фиг.6.
Таким образом, в случае PR(n)=Р0 вероятность того, что точка обсервации лежит внутри треугольника погрешностей существенно зависит от класса конфигурации. Увеличение несимметричности в нахождении измеренного пеленга слева или справа относительно истинного для класса-А увеличивает вероятность нахождения точки обсервации в треугольнике погрешностей, а для класса-В - наоборот - уменьшает. При P0=1/2, вероятность нахождения точки обсервации в треугольнике погрешностей равна 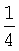 и для класса-А и для класса-В. Однако при этом для класса-А это точка минимума, а для класса-В - точка максимума (фиг.6).
и для класса-А и для класса-В. Однако при этом для класса-А это точка минимума, а для класса-В - точка максимума (фиг.6).
Положим, что PR(n) имеет любое значение в интервале нуль - единица, причем свое для каждого n=1, 2, 3. Тогда (6) и (7) примут вид
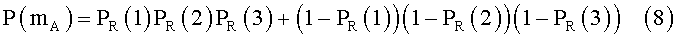
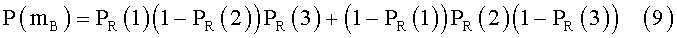
Значение функции (8) будет максимально (единица), если все PR(n) (n=1, 2, 3) будут равны единице или нулю одновременно. Значение функции (8) будет минимально (нуль), если одно из PR(n) равно единице, а любое другое равно нулю. Отсюда, так как функция (8) непрерывная, то значения (8) лежат в интервале нуль - единица.
Значение функции (9) будет максимально (единица), если PR(1) и PR(3) равны единице, а PR(2) равна нулю, или если PR(1) и PR(3) равны нулю, а PR(2) равна единице. Значение функции (9) будет минимально (нуль), если PR(1) или PR(3) равна нулю и PR(2) равна нулю, или если PR(1) или PR(3) равны единице и PR(2) равна единице. Отсюда, так как функция (9) непрерывная, то значения (9) лежат в интервале нуль - единица.
Некоторые примеры графиков для (8) представлены на фиг.7.
Таким образом, в случае, когда PR(п) имеет любое значение в интервале нуль - единица, причем свое для каждого n=1, 2, 3, вероятность того, что точка обсервации лежит внутри треугольника погрешностей также существенно зависит от класса конфигурации. Для класса-А увеличение несимметричности в нахождении каждого измеренного пеленга в одну строну (влево или вправо) относительно истинного увеличивает вероятность нахождения точки обсервации в треугольнике погрешностей. Для класса-В вероятность нахождения точки обсервации в треугольнике погрешностей достигается при увеличении больших (малых) значений PR(1) и PR(3) и одновременно малых (больших) значений PR(2).
В результате теоретического анализа установлено, что:
1. Вероятность нахождения точки обсервации внутри треугольника погрешностей зависит от двух классов взаимного расположения (конфигурации) точки обсервации и ориентиров, а именно класса (класс-А), когда точка обсервации находится внутри треугольника с вершинами в точках ориентиров, и класса (класс-В), когда точка лежит вне треугольника с вершинами в точках ориентиров.
2. В предположении, что в процессе одной обсервации вероятность того, что каждый измеренный пеленг находится с фиксированной стороны от истинного пеленга, равна одному фиксированному для этой обсервации значению Р0∈[0,1], вероятность того, что точка обсервации лежит внутри треугольника погрешностей равна:
- для класса-А не меньше чем 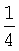 ;
;
- для класса-В не больше чем 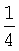 .
.
3. При более слабом предположении, если PR(n) имеет любое значение в интервале нуль - единица, причем свое для каждого n=1, 2, 3, вероятность того, что точка обсервации лежит внутри треугольника погрешностей может иметь любое значение в интервале нуль - единица. Причем искусственно вводя «систематическую» погрешность в измеренные значения пеленгов, можно получить треугольник погрешностей, который с вероятностью, близкой к единице, содержит точку обсервации.
Практическая реализация метода заключается в следующем.
Измеряют компасные пеленги видимых и нанесенных на навигационную карту ориентиров, начиная от ориентиров, лежащих ближе к диаметральной плоскости подводного объекта.
Исправляют компасные пеленги поправкой компаса. Прокладывают на навигационной карте от соответствующих ориентиров линии вычисленных пеленгов, точка пересечения которых является местом подводного объекта. При этом, если при определении по трем ориентирам линии пеленгов в одной точке не пересекаются, образуя треугольник погрешностей, выполняют построение треугольника погрешностей, включающего точку обсервации в следующей последовательности.
Полученные значения трех измеренных пеленгов {φ1, φ2, φ3} пронумеровывают по порядку.
Задают значение угла α, по величине сравнимого с предполагаемым значением абсолютной ошибки при измерении пеленгов, соответствующей величине поправки компаса.
Определяют класс конфигураций, образуемый точкой обсервации и ориентирами.
Рассчитывают значения пеленгов {ϕ1, ϕ2, ϕ3} с учетом величины поправки компаса при этом:
- для ситуации класса-А: складывают (или вычитают) значения {φ1, φ2, φ3} и α;
- для ситуации класса-В: складывают (или вычитают) значения {φ1, φ3}и α и вычитают (или складывают) значения {φ2} и α;
- строят треугольник погрешностей по значениям пеленгов {ϕ1, ϕ2, ϕ3}.
Величину погрешности устанавливают по значениям точек обсервации, находящихся внутри треугольника.
В практике обработки гидроакустических наблюдений существует задача оценки среднего значения гидроакустической характеристики в некотором пространственно-временном объеме по дискретным наблюдениям. Каждое дискретное наблюдение фиксируется четырьмя координатами: временем, широтой, долготой и глубиной (высотой). Другими словами, значение гидроакустической характеристики в общем случае является функцией, заданной в четырехмерном координатном пространстве. В частных случаях эта размерность может принимать и меньшие значения. Размерность определяется числом координат точек наблюдений, значения которых меняются в массиве наблюдений. Например, для типичных задач по расчету среднего значения гидроакустической характеристики по дискретным наблюдениям:
1) по дискретным во времени измерениям в географической точке с фиксированными координатами на фиксированной глубине;
2) по одновременным наблюдениям в некоторой пространственной области на фиксированной глубине;
3) по наблюдениям в некотором районе в разные моменты времени и в разных точках на фиксированной глубине;
4) по наблюдениям в некотором фиксированном районе за некоторый интервал времени в некотором интервале глубин.
Нумерация задач соответствует размерности пространства задания гидроакустической характеристики.
В известных способах среднее арифметическое для любой задачи рассчитывают путем прямого суммирования всех измеренных значений, попадающих в рассматриваемый пространственно-временной объем, и делят на общее число измерений.
В действительности такой метод расчета среднего арифметического гидроакустической характеристики не позволяет получить минимально возможную погрешность в оценке среднего. Причиной этого является то, что в принятом методе игнорируется распределение точек наблюдения по пространственно-временному объему. Более того, точность оценки среднего значения применяемого метода уменьшается с увеличением размерности пространства координат наблюдений.
В заявляемом способе применен адекватный метод расчета среднего арифметического значения гидроакустической характеристики, минимизирующий погрешность.
Задача определения среднего значения гидроакустической характеристики по значениям характеристики в дискретных пространственно-временных точках с математической точки зрения является задачей оценки среднего арифметического значения непрерывной функции в пространственно-временном объеме по ее значениям в дискретных точках. Погрешность в оценке среднего арифметического, при условии изотропности изменчивости функции, определяется структурой «неравномерности» расположения точек измерения в пространственно-временном объеме. Наименьшую погрешность дают точки, равномерно распределенные по рассматриваемому объему. Точки называются равномерно распределенными в n-мерном единичном кубе, если в любом гиперкубе число точек пропорционально объему гиперкуба (Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М.: Наука, 1969. - 288 с.).
Формально это определяется следующим образом. Обозначим через Kn единичный куб в n-мерном пространстве: Kn состоит из всех точек Р с декартовыми координатами Р=(x1, …, xn), которые удовлетворяют неравенствам 0≤xj≤1 (j=1, 2, …, n). Рассмотрим последовательность точек P0, P1, …, Pi,…, принадлежащих кубу Kn размерности n, и обозначим через SN (G) количество точек Pi с номерами 0<i<N-1, принадлежащими множеству G. Последовательность точек Р0, Р1, …, Pi,… называется равномерно распределенной в Kn (сокращенно p.p.), если для любого n-го параллелепипеда π с ребрами, параллельными координатным осям,
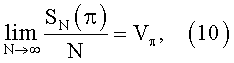
где Vπ - объем параллелепипеда π. Можно доказать, что если G произвольная область, расположенная в Kn и имеющая объем VG, то из (10) вытекает, что
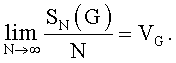
Таким, образом, при больших N количество точек p.p.последовательности, принадлежащих любой области G, пропорционально объему G.
По теореме Вейля (Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М.: Наука, 1969. - 288 с.) для того, чтобы {Pi} была p.p., необходимо и достаточно, чтобы для любой интегрируемой, по Риману, функции f(P) выполнялось соотношение
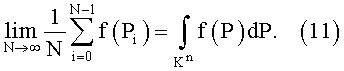
Выражение (11) является оценкой среднего арифметического. Оценка погрешности (11) определяется выражением
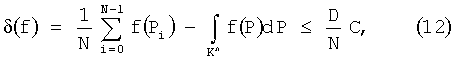
где С - константа, разная для функций с различной изменчивостью, D - отклонение распределения точек от p.p.
Отклонение D определяется следующим образом. Рассмотрим в Kn сетку, состоящую из N произвольных точек Р0, Р1, …, PN-1. Каждой точке Р из Kn поставим в соответствие параллелепипед πP с диагональю ОР (О - начало координат). Объем VP этого параллелепипеда равен произведению x1…xn координат точки Р. Отклонением сетки P0, P1, …, PN-1 называется число
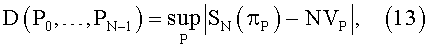
где верхняя грань берется по всем Р∈Kn.
Для того, чтобы последовательность точек была p.p., необходимо и достаточно, чтобы при N→∞
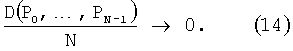
Характеристика D(P0, …, PN-1) является весьма сложной функцией от структуры расположения точек. Верхняя граница D≤N, нижняя граница ее до сих пор не известна (за исключением случая n=1, когда inf D=1/2). Существует предположение, что наилучшая возможная оценка D для n-мерной сетки, состоящей из N точек, равна
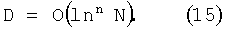
Необходимо отметить, что в гидрометеорологии исследователи ошибочно полагают, что кубические сетки (их называют «регулярные», «равномерные» и т.п.) всегда очень «хорошие» и целью сбора информации является получение измерений на такой сетке.
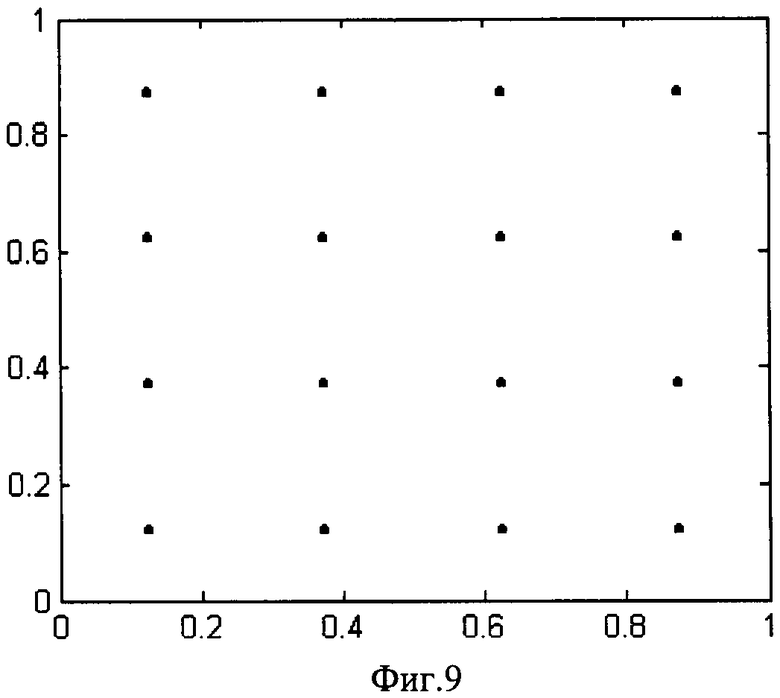
Кубическая сетка для N=M2 точек задается координатами
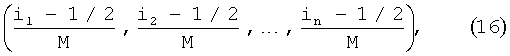
где i1, i2,…, in - независимо пробегают значения 1, 2, …, M. На фиг.9 изображена кубическая сетка при n=2, М=4.
Нетрудно проверить, что для таких сеток значение 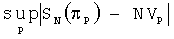 будет максимальным, например, в точке P'=(1/2M,1,1,…,1), когда SN(πp')=0, NVP'=N/2M=Mn -1/2. Следовательно,
будет максимальным, например, в точке P'=(1/2M,1,1,…,1), когда SN(πp')=0, NVP'=N/2M=Mn -1/2. Следовательно,
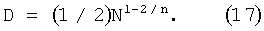
Из формулы (17) следует, что при n=1 кубические сетки оптимальны. Однако с увеличением n равномерность сеток (16) ухудшается и порядки в формуле (17) приближаются к наихудшим, равным N. Уже при n=2 порядок (17) оказывается равным 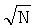 - такой же порядок соответствует случайным сеткам, состоящим из N независимых случайных точек, равномерно распределенных в Kn. Значит при n≥3 сетки (16) асимптотически хуже случайных.
- такой же порядок соответствует случайным сеткам, состоящим из N независимых случайных точек, равномерно распределенных в Kn. Значит при n≥3 сетки (16) асимптотически хуже случайных.
Пусть в Kn задано множество точек наблюдений за гидроакустической характеристикой Р0, Р1, …, PN-1. Этот набор точек далек от p.p. Необходимо определить такое подмножество точек 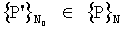 , которое образует сетку с наибольшей степенью равномерного распределения. Решение этой задачи будем искать следующим образом. Определим подходящую опорную сеть точек, имеющую p.p. Сравнивая координаты точек наблюдений с координатами точек опорной p.p. сетки, найдем искомое подмножество
, которое образует сетку с наибольшей степенью равномерного распределения. Решение этой задачи будем искать следующим образом. Определим подходящую опорную сеть точек, имеющую p.p. Сравнивая координаты точек наблюдений с координатами точек опорной p.p. сетки, найдем искомое подмножество 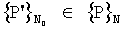 , которое будет давать минимальную ошибку в оценке среднего арифметического, в соответствии с (12).
, которое будет давать минимальную ошибку в оценке среднего арифметического, в соответствии с (12).
В вычислительной математике построено много вариантов сеток близких к p.p. Для нашей задачи целесообразно выбрать такую сетку с последовательностью точек Q0, Q1, …, Qi, …, которая удовлетворяет трем требованиям:
1) равномерность распределения сетки должна быть асимптотически оптимальной;
2) равномерность расположения точек должна наблюдаться не только при N→∞, но уже при малых N;
3) алгоритм расчета точек Qi должен быть достаточно простым.
Этим требованиям удовлетворяют, например, так называемые LPτ - последовательности (Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М.: Наука, 1969. - 288 с.).
Не излагая теоретического обоснования p.p. свойств этих последовательностей, приведем простой алгоритм расчета.
В этом алгоритме координаты (qi1, …, qin) точки Qi из LPT - последовательности вычисляется по формуле
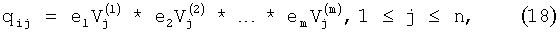
где i=em…e2e1 - представление i в двоичной системе, 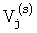 - двоично-рациональные числа вида
- двоично-рациональные числа вида 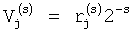 , числители которых табулированы.
, числители которых табулированы.
В таблице 2 представлены 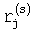 для 1≤s≤20 и 1≤j≤4, что позволяет легко вычислять точки Qi размерности n≤4 в количестве N≤220.
для 1≤s≤20 и 1≤j≤4, что позволяет легко вычислять точки Qi размерности n≤4 в количестве N≤220.
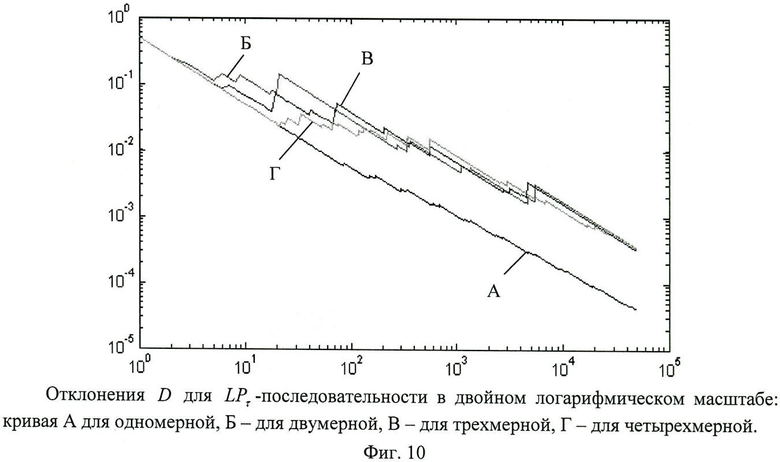
Отклонения D для LPτ-последовательности в двойном логарифмическом масштабе, соответственно для одномерной (А), двумерной (Б), трехмерной (В) и четырехмерной (Г) LPτ-последовательности представлены на фиг.10.
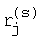
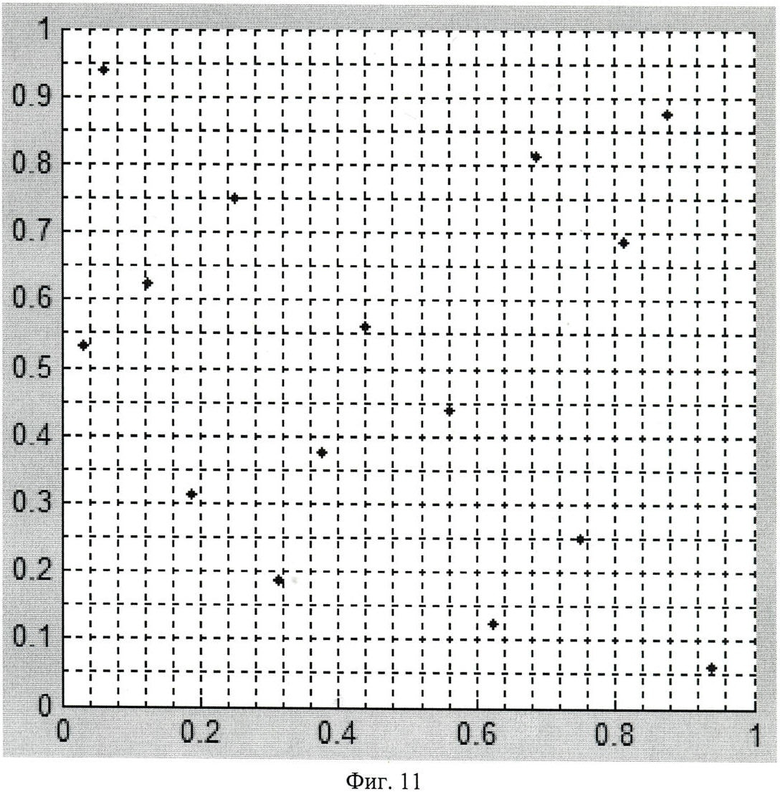
Для примера на фиг.11 представлено для двумерной единичной области положение LPτ-последовательности для первых 16 точек. Положение точек свидетельствует, что оно значительно отличается от «регулярного расположения», представленного на фиг.10. Алгоритм выбора репрезентативных точек можно представить в следующем виде:
Задано: множество из N точек наблюдений P0, Р1, …, РN-1 в n-мерном кубе Kn, n=1, 2, 3, 4. Каждая точка наблюдений представлена нормированными координатами P=(х1, …, xn), 0≤хj≤1, j=1, 2, …, n.
Требуется: определить подмножество точек 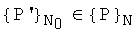 , которые дают наименьшую ошибку в оценке среднего арифметического функции, измеренной в этих точках (т.е наиболее репрезентативный набор точек измерений для оценки среднего или, что тождественно, образуют сетку с наибольшей степенью равномерного распределения).
, которые дают наименьшую ошибку в оценке среднего арифметического функции, измеренной в этих точках (т.е наиболее репрезентативный набор точек измерений для оценки среднего или, что тождественно, образуют сетку с наибольшей степенью равномерного распределения).
Инициация: Tk=T0=⌀ - набор точек-кандидатов на k шаге.
Последовательность операций решения:
1. Вычислить N точек Qk (k=i, …N) LPτ-последовательности по формуле (18).
2. Последовательно для каждого k от 1 до N:
2.1. Для каждой точки Qk найти ближайшую в евклидовой метрике точку 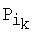 среди множества точек {Р1, …, РN}\Тk-1,
среди множества точек {Р1, …, РN}\Тk-1, 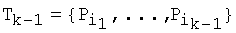 , и добавить ее в набор точек-кандидатов на k, образуя
, и добавить ее в набор точек-кандидатов на k, образуя 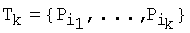 .
.
Вычислить отклонение Dk=D(Tk) для точки Рi по формуле (7).
5. Последовательно для каждого k от 1 до N найти D0k=max(D1, …, Dk).
6. Найти k0, для которого существует минимальное значение D0k.
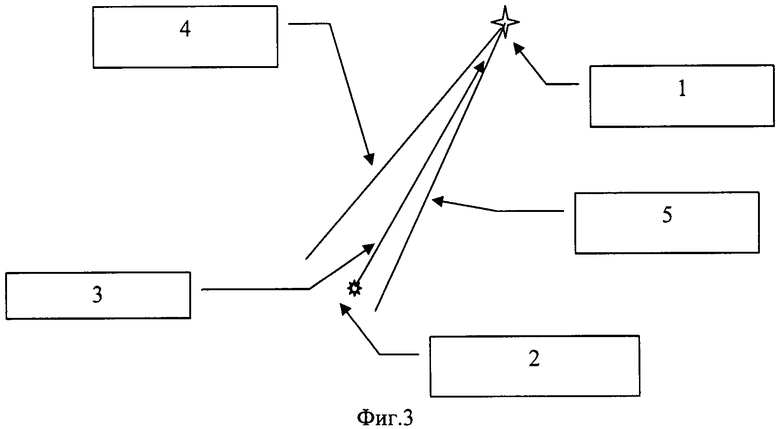
Результат: набор точек 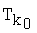 является искомым множеством точек наблюдений, дающим минимальную ошибку в оценке среднего арифметического.
является искомым множеством точек наблюдений, дающим минимальную ошибку в оценке среднего арифметического.
Таким образом, при расчете среднего арифметического значения гидроакустической характеристики по дискретным наблюдениям в некотором пространственно-временном объеме для минимизации погрешности необходимо учитывать распределение координат измерений. Для корректности вычислений в вычислительное устройство вводят локальные декартовы координаты для рассматриваемой пространственно-временной области, в которой размещены дрейфующая станция, донные маяки-ответчики и подводный объект.
Способ навигации подводного объекта посредством гидроакустической навигационной системы реализуется посредством навигационной базы из М гидроакустических приемоответчиков с различными частотами ответа и размещенного на объекте навигации гидроакустического приемопередатчика, посредством которого измеряют временные интервалы распространения сигналов с последующим их преобразованием в дистанции между подводным объектом и гидроакустическими приемоответчиками.
Гидроакустические приемоответчики размещают на дрейфующих станциях по водной поверхности и донных станциях на морском дне, навигационные параметры подводного объекта относительно донных или/и дрейфующей станции или базы из дрейфующих станций определяют в режиме с длинной и/или ультракороткой базой, и/или в комбинированном режиме (длинная + ультракороткая база), и/или в пеленгационной системе, при этом формируют из приемников две навигационные базы с общим центром базы, располагая их в плоскости, параллельной плоскости палубы подводного объекта, при этом ось одной базы Х направлена вдоль осевой линии подводного объекта, а ось другой базы Y направлена по траверзу вправо.
При обработке результатов измерений выполняют оценку среднего арифметического значения гидроакустической характеристики по пространственно-временным массивам наблюдений путем вычислений.
При вычислении координат выполняют минимизацию погрешности по распределению измеренных координат, при этом в вычислительное устройство вводят локальные декартовые координаты для рассматриваемой пространственно-временной области, в которой размещены дрейфующая станция, донные маяки-ответчики и подводный объект, при этом определяют временной ход гидроакустической характеристики для полученных временных рядов, при этом определяют экстремальные значения гидроакустической характеристики в каждом полученном ряду измерений методом статистики Герста, а оценку среднего арифметического значения гидроакустической характеристики по пространственно-временным массивам наблюдений выполняют путем вычислений по многомерным квадратурным формулам и функциям Хаара.
Использование предлагаемого способа позволяет эффективно осуществлять требуемые операции сравнения координат за счет исключения из обработки разно точных данных при определении координат подвижного морского объекта.
Промышленная реализация способа технической сложности не представляет, так как для его реализации используются штатные судовые средства пеленгации.
Источники информации
1. Патент RU №2032187 C1, 27.03.1995.
2. Патент RU №2158431 C1, 27.10.2000.
3. Патент RU №34020 U1, 20.11.2003.
4. Патент RU №2289149 C2, 10.12.2006.
5. Заявка US №2008008045 A1, 10.01.2008.
6. Патент US №4024491 A, 17.05.2007.
7. Патент RU №2365936 C1, 03.06.2008.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НАВИГАЦИИ ПОДВОДНОГО ОБЪЕКТА ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2011 |
|
RU2456634C1 |
| ГИДРОАКУСТИЧЕСКАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2011 |
|
RU2463624C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2010 |
|
RU2431156C1 |
| СПОСОБ НАВИГАЦИИ ПОДВОДНОГО ОБЪЕКТА | 2008 |
|
RU2365939C1 |
| ГИДРОАКУСТИЧЕСКАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2008 |
|
RU2371738C1 |
| ГИДРОАКУСТИЧЕСКАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2010 |
|
RU2451300C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДРЕЙФА МОРСКИХ ЛЬДОВ И СИСТЕМА ДЛЯ ОПРЕДЕЛЕНИЯ ДРЕЙФА МОРСКИХ ЛЬДОВ | 2010 |
|
RU2453865C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДРЕЙФА МОРСКИХ ЛЬДОВ | 2010 |
|
RU2416070C1 |
| ГИДРОАКУСТИЧЕСКИЙ ЛОКАЦИОННЫЙ КОМПЛЕКС | 2010 |
|
RU2426149C1 |
| ГИДРОАКУСТИЧЕСКАЯ СИНХРОННАЯ ДАЛЬНОМЕРНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ПОЗИЦИОНИРОВАНИЯ ПОДВОДНЫХ ОБЪЕКТОВ В НАВИГАЦИОННОМ ПОЛЕ ПРОИЗВОЛЬНО РАССТАВЛЕННЫХ ГИДРОАКУСТИЧЕСКИХ МАЯКОВ-ОТВЕТЧИКОВ | 2011 |
|
RU2483326C2 |
Изобретение относится к области гидроакустических навигационных систем и может быть использовано для навигационного обеспечения подводных аппаратов. Способ навигации подводного объекта осуществляется посредством гидроакустической навигационной системы, содержащей навигационную базу из М гидроакустических приемоответчиков с различными частотами ответа и размещенного на объекте навигации гидроакустического приемопередатчика. Гидроакустические приемоответчики размещают на дрейфующих станциях по водной поверхности и донных станциях на морском дне. Обработку результатов измерений выполняют по пространственно-временным массивам наблюдений. При вычислении координат выполняют минимизацию погрешности по распределению измеренных координат, при этом в вычислительное устройство вводят локальные декартовые координаты для рассматриваемой пространственно-временной области, в которой размещены дрейфующая станция, донные маяки ответчики и подводный объект. Технический результат: повышение надежности при обеспечении навигации подводных объектов. 11 ил., 2 табл.
Способ навигации подводного объекта посредством гидроакустической навигационной системы, включающий размещение навигационной базы из М гидроакустических приемоответчиков с различными частотами ответа и размещенного на подводном объекте навигации гидроакустического приемопередатчика, посредством которого измеряют временные интервалы распространения сигналов с последующим их преобразованием в дистанции между подводным объектом навигации и гидроакустическими приемоответчиками, размещение гидроакустических приемоответчиков на дрейфующих станциях по водной поверхности и донных станциях на морском дне, определение навигационных параметров подводного объекта навигации относительно донных или/и дрейфующей станции или базы из дрейфующих станций, которые определяют в режиме с длинной и/или ультракороткой базой, и/или в комбинированном режиме (длинная + ультракороткая база), и/или в пеленгационной системе, при этом формируют из приемников две навигационные базы с общим центром базы, располагая их в плоскости, параллельной плоскости палубы подводного объекта, при этом ось одной базы Х направлена вдоль осевой линии подводного объекта, а ось другой базы Y направлена по траверзу вправо, обработку результатов измерений по пространственно-временным массивам наблюдений, определение координат подводного объекта навигации путем вычислений, отличающийся тем, что при вычислении координат выполняют минимизацию погрешности по распределению измеренных координат, при этом в вычислительное устройство вводят локальные декартовые координаты для рассматриваемой пространственно-временной области, в которой размещены дрейфующая станция, донные маяки ответчики и подводный объект, при этом определяют временной ход гидроакустической характеристики для полученных временных рядов, при этом определяют экстремальные значения гидроакустической характеристики в каждом полученном ряду измерений методом статистики Герста, а оценку среднего арифметического значения гидроакустической характеристики по пространственно-временным массивам наблюдений выполняют путем вычислений по многомерным квадратурным формулам и функциям Хаара.
| СПОСОБ НАВИГАЦИИ ПОДВОДНОГО ОБЪЕКТА | 2008 |
|
RU2365939C1 |
| ГИДРОАКУСТИЧЕСКАЯ СИНХРОННАЯ ДАЛЬНОМЕРНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 1992 |
|
RU2032187C1 |
| ГИДРОАКУСТИЧЕСКАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2008 |
|
RU2371738C1 |
| Станок для обточки деревянных бочек | 1952 |
|
SU97539A1 |
| US 7483337 B2, 27.01.2009 | |||
| US 4024491 A, 17.05.1977. | |||
Авторы
Даты
2012-03-10—Публикация
2010-09-21—Подача