Текст описания приведен в факсимильном виде.
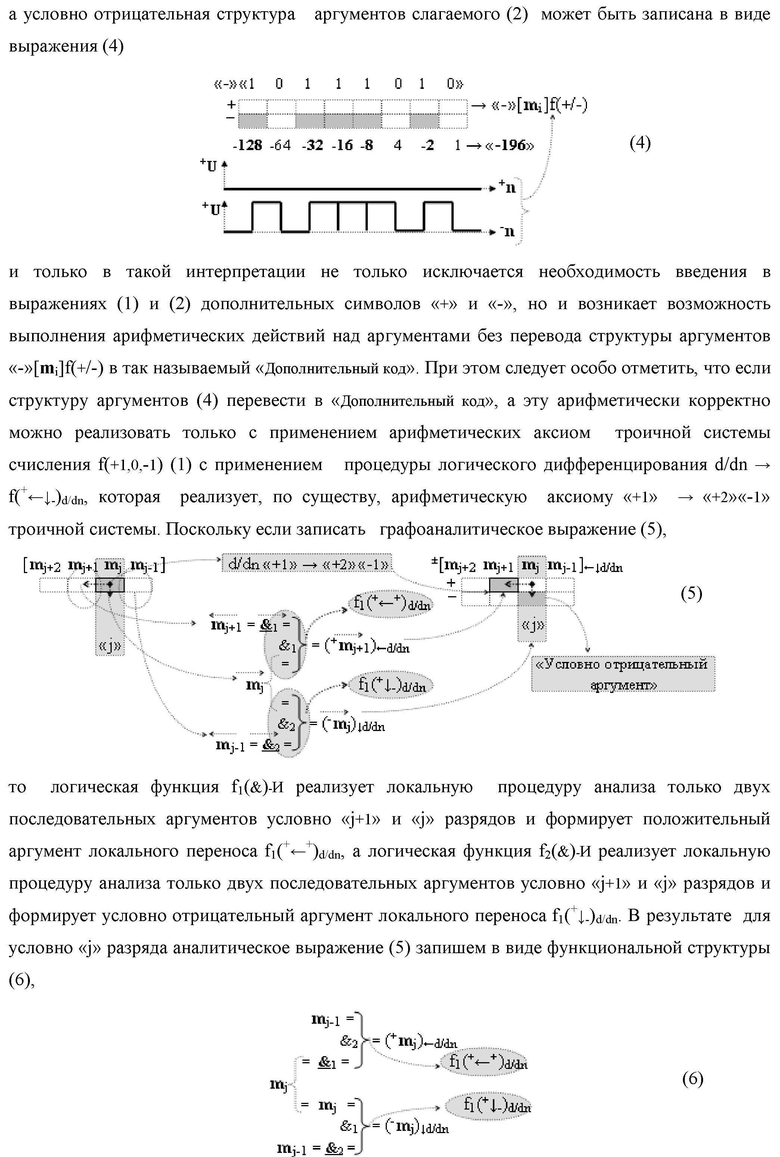
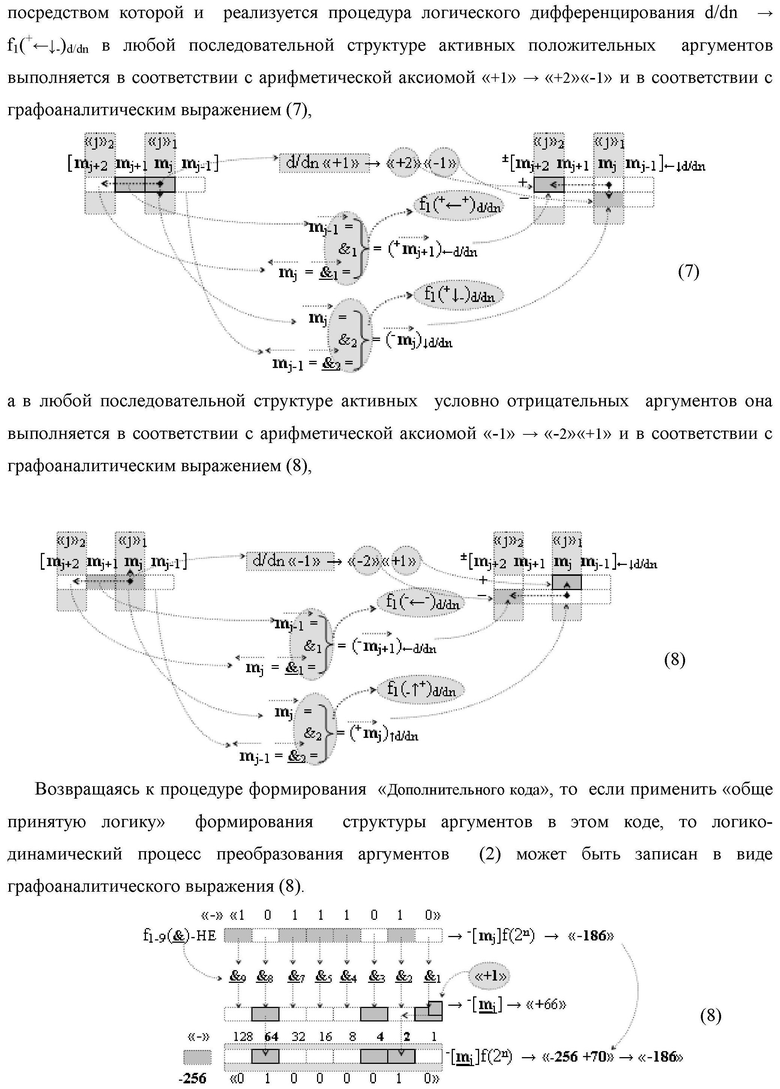
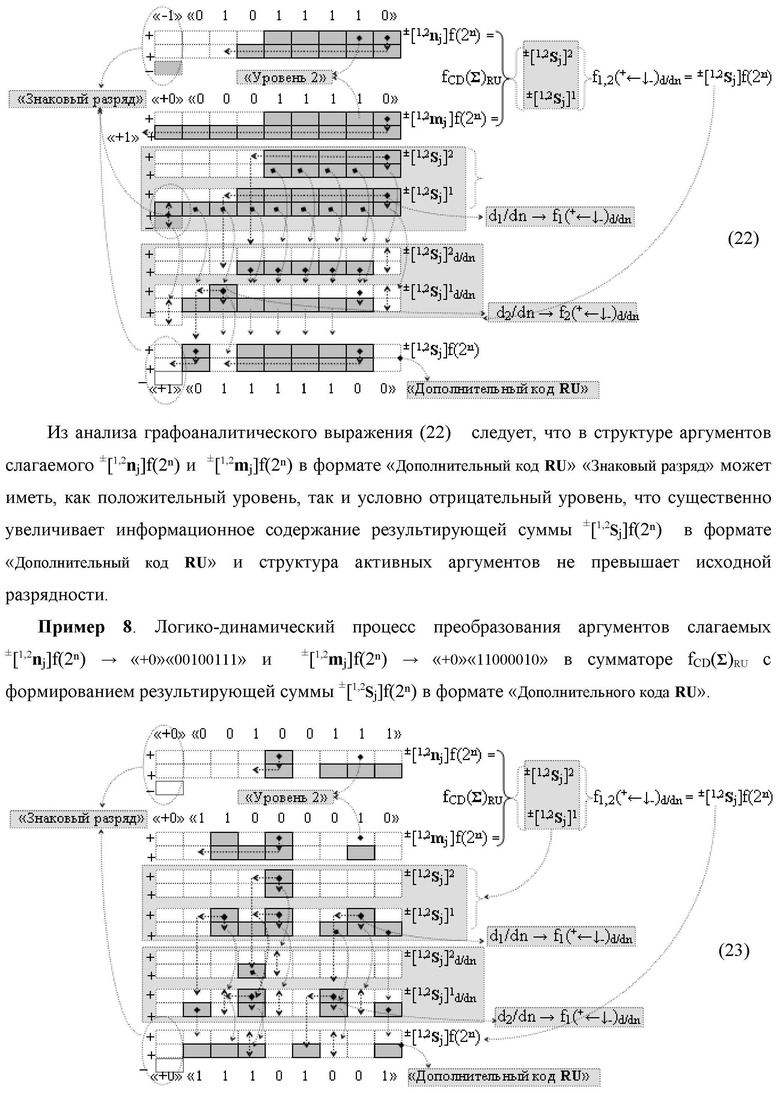
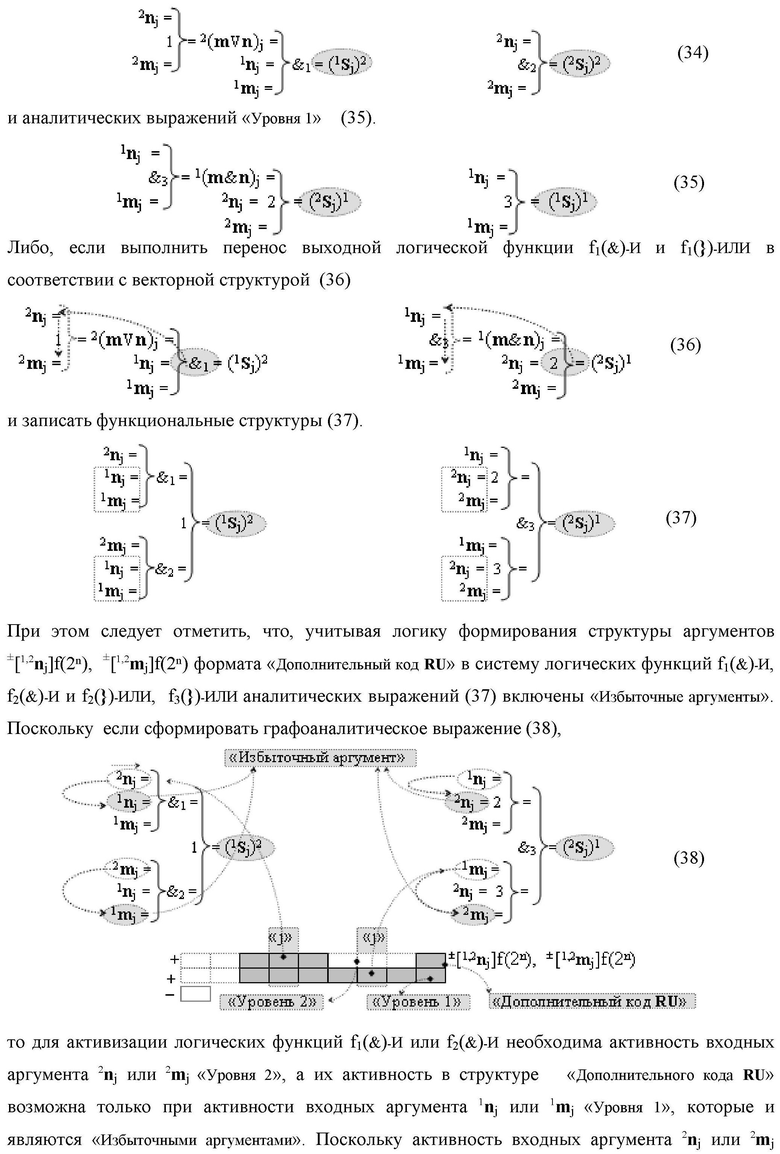
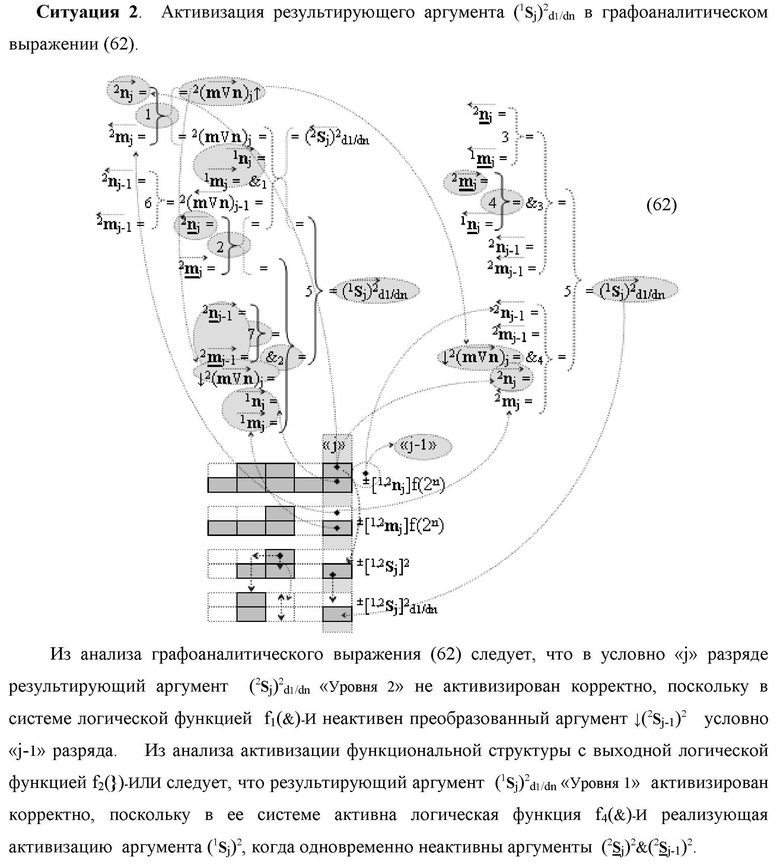
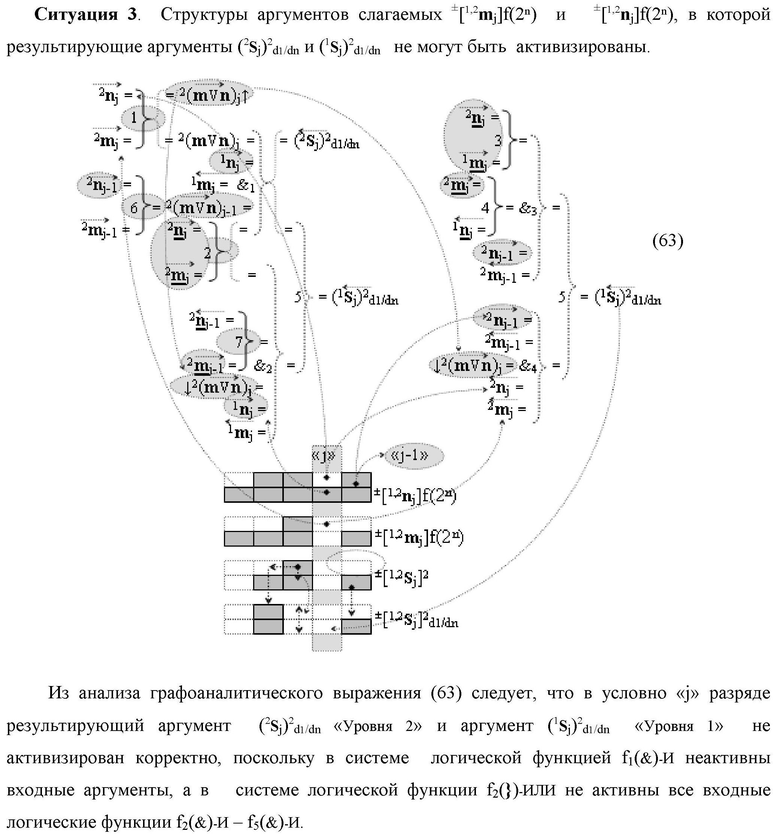
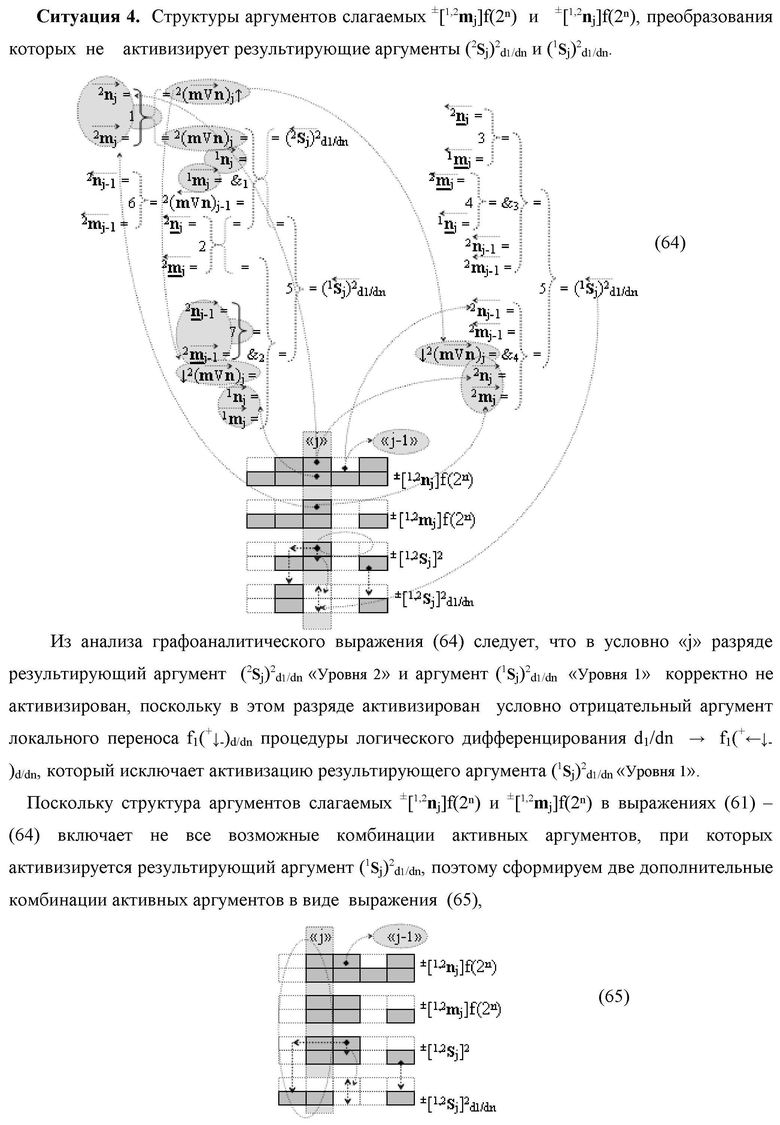
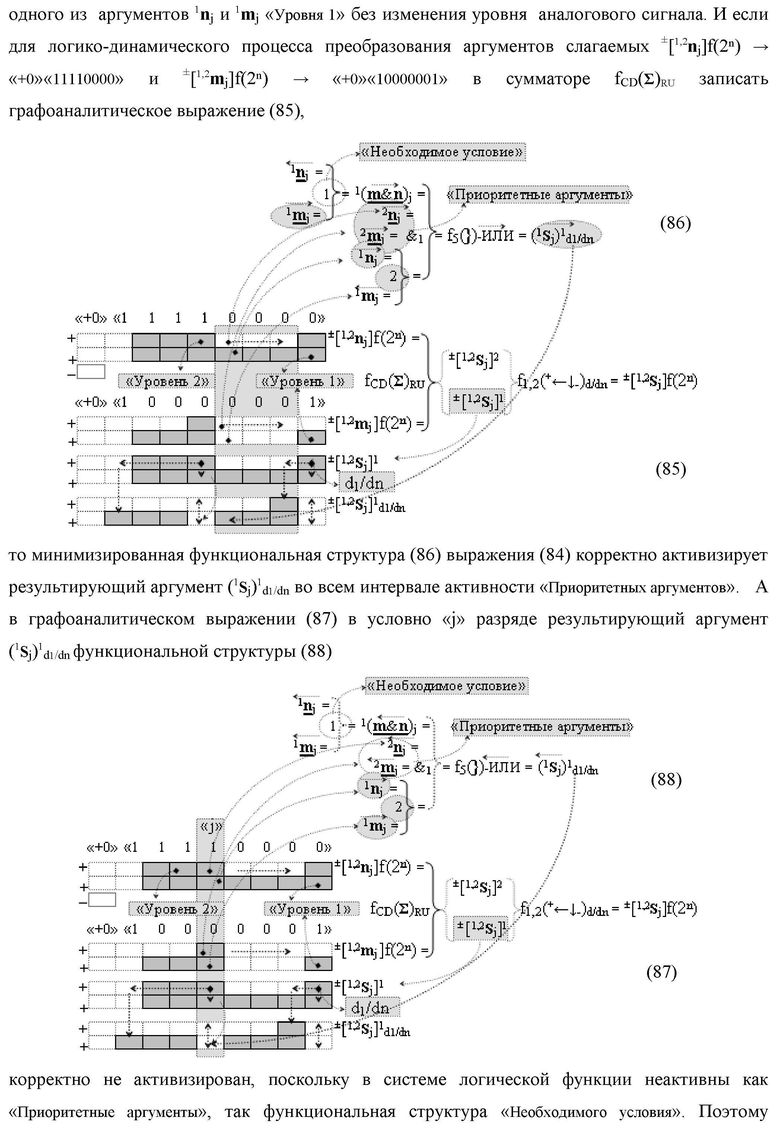
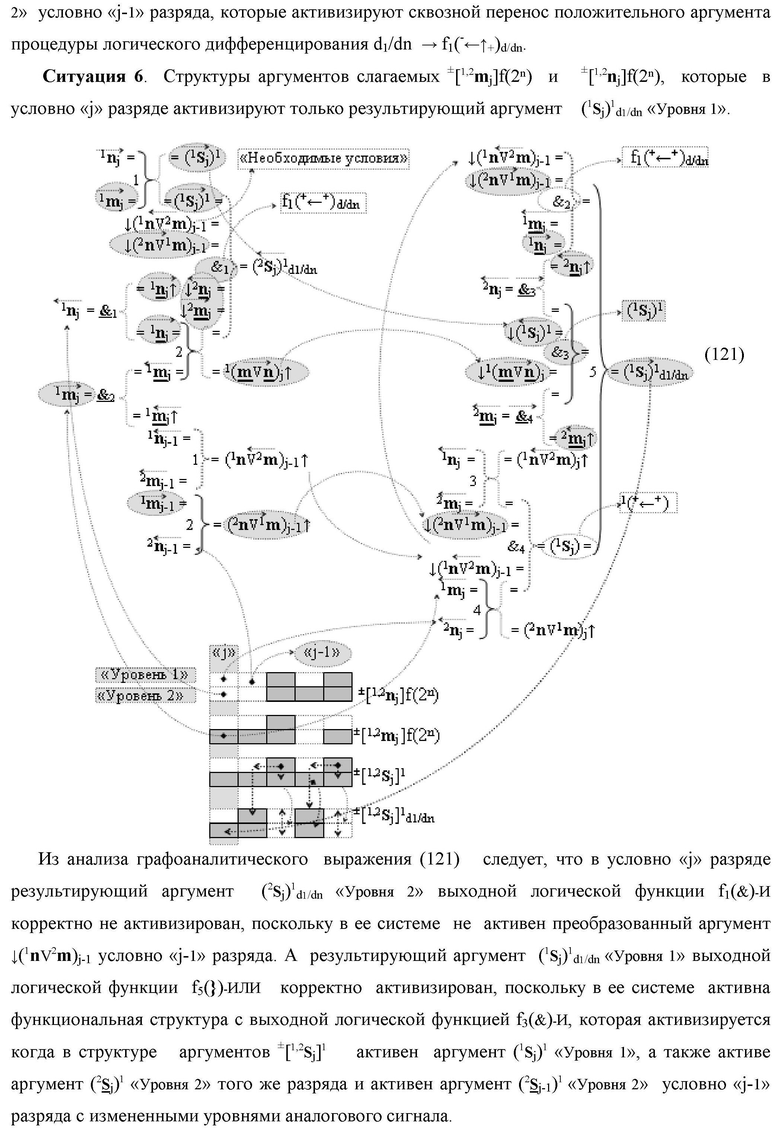
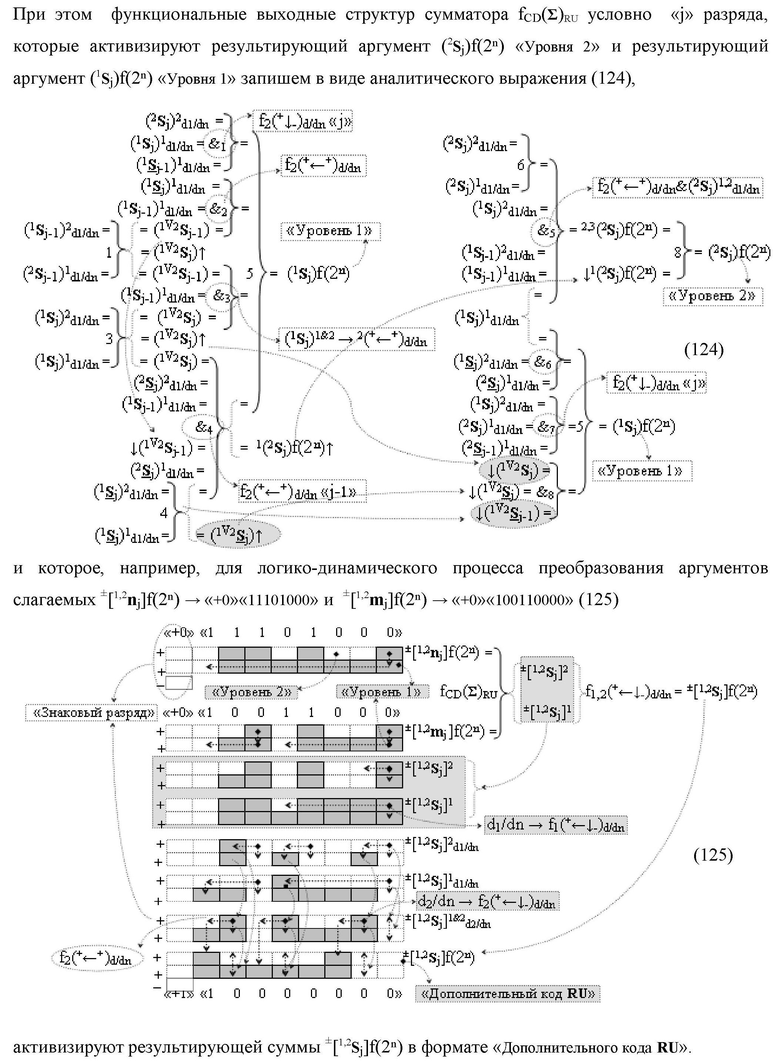
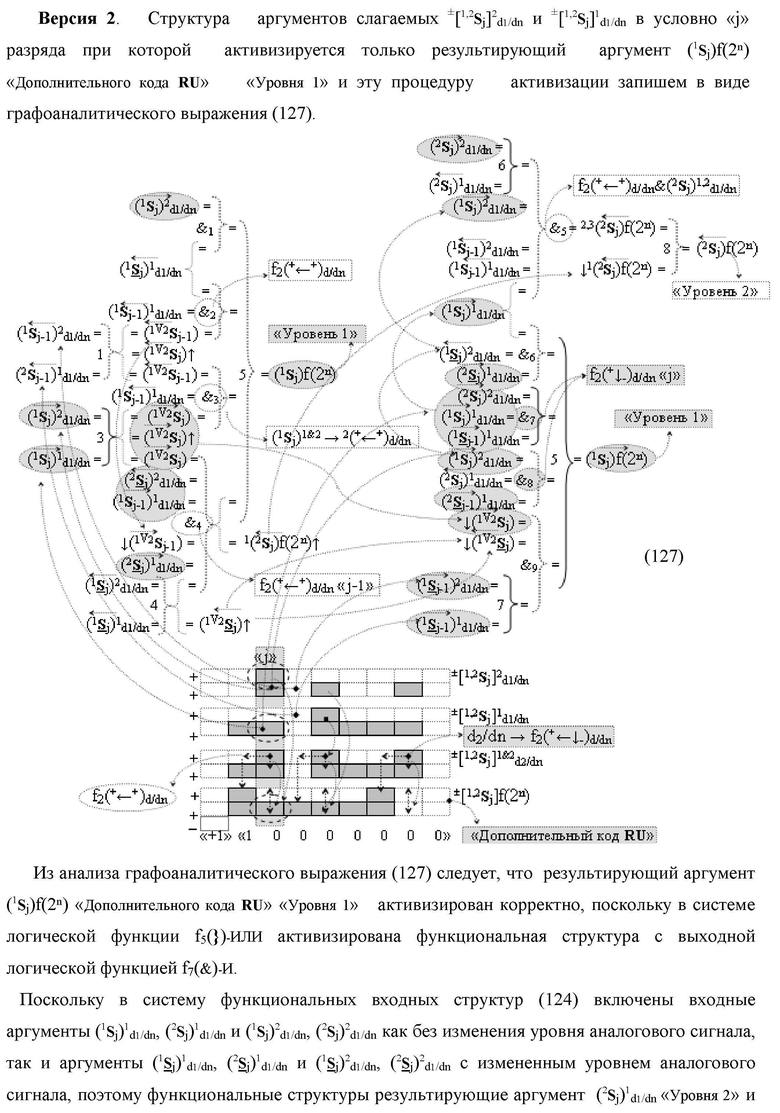
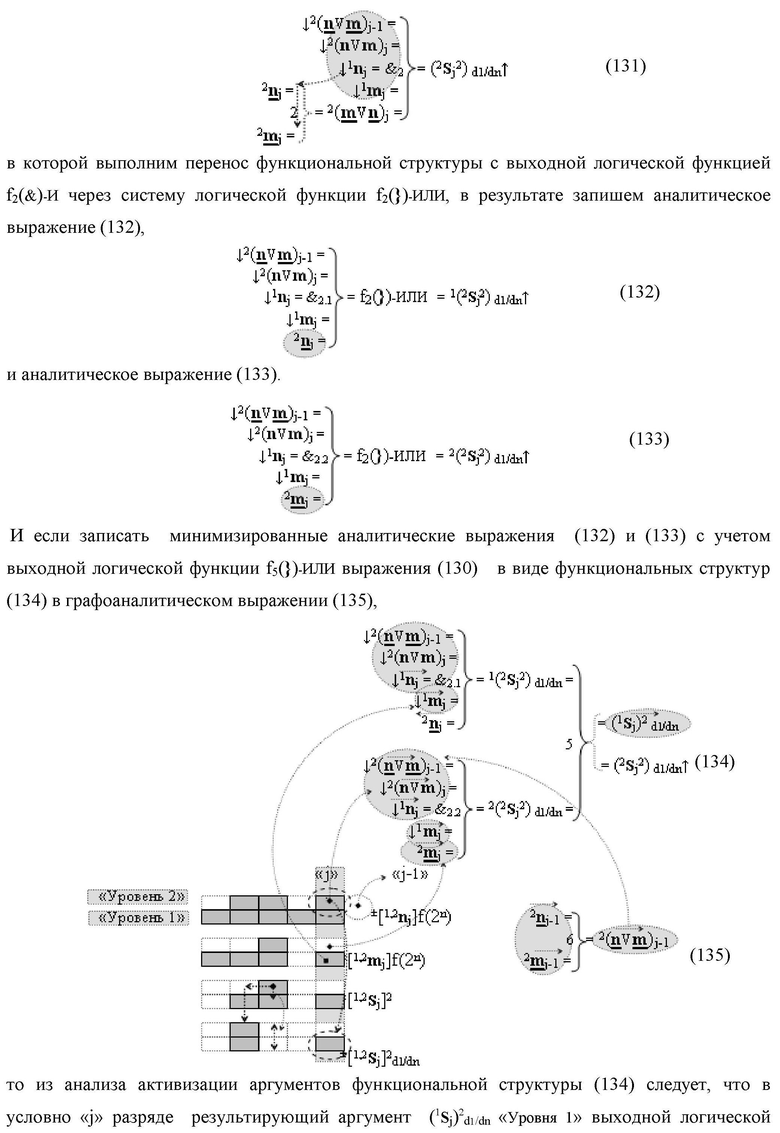
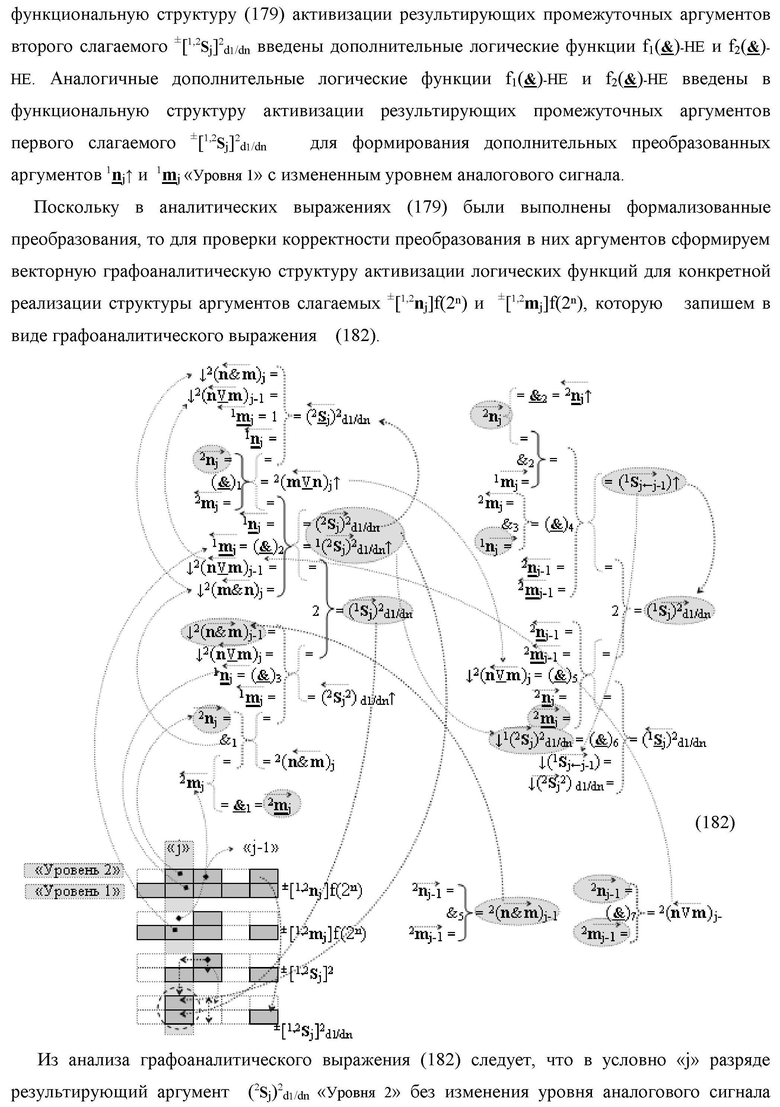
Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств и выполнении арифметических процедур суммирования позиционных аргументов слагаемых. Техническим результатом является повышение быстродействия процесса преобразования аргументов во входной структуре сумматора. В одном из вариантов изобретения условно «j»-й разряд входной функциональной структуры сумматора реализован с использованием логических элементов И-НЕ, ИЛИ-НЕ, И, ИЛИ, НЕ. 9 н.п. ф-лы, 1 прилож.
1. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате выполнена в виде двух структур логических функций, которые включают логические функции f1(&)-И-НЕ, f1(}&
)-ИЛИ-НЕ, f2(&)-И, f4(&)-И, f2(})-ИЛИ, f3(})-ИЛИ и f4(})-ИЛИ, а также логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, в которых функциональные выходные связи являются функциональной входной связью логической функции f2(})-ИЛИ и f3(})-ИЛИ, при этом функциональные входные связи логической функции f3(&)-И являются функциональными выходными связями логических функций f3(})-ИЛИ и f4(})-ИЛИ соответственно, а функциональные входные связи логической функции f1(&)-И-НЕ являются первой и второй функциональной входной связью структуры для приема аргумента слагаемых 1
n
j и 1
m
j «Уровня 1», при этом функциональные выходные связи логических функций f3(})-ИЛИ и f4(})-ИЛИ являются функциональными входными связями логической функции f3(&)-И, отличающаяся тем, что в структуру условно «j» разряда
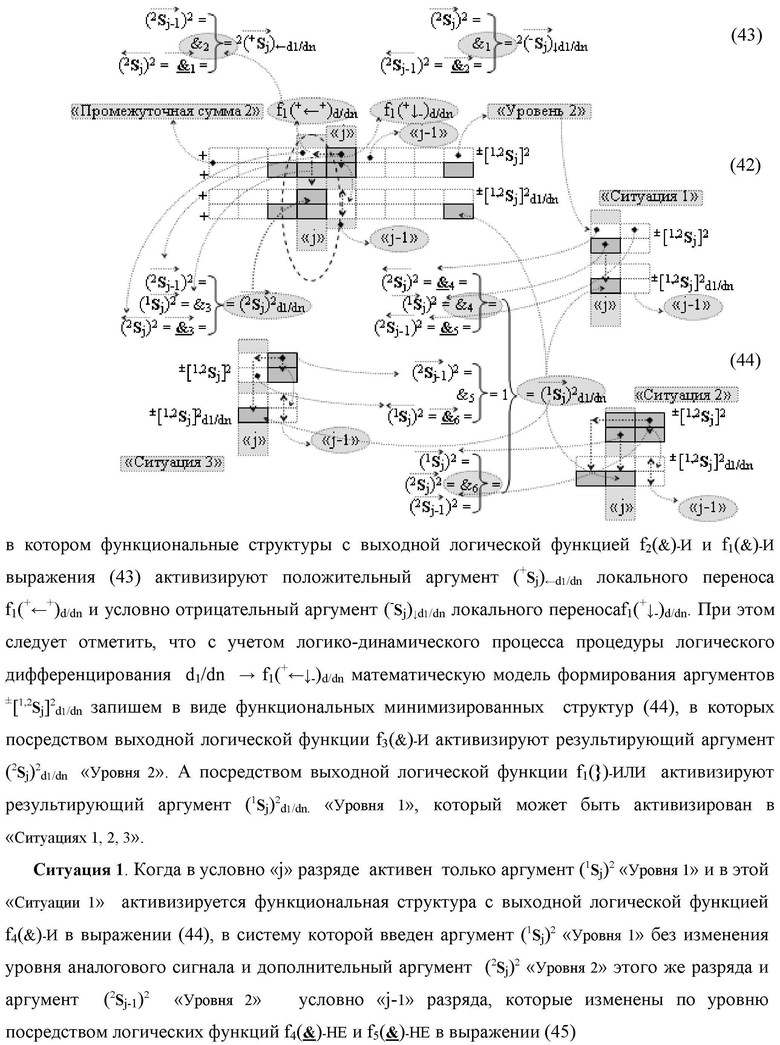
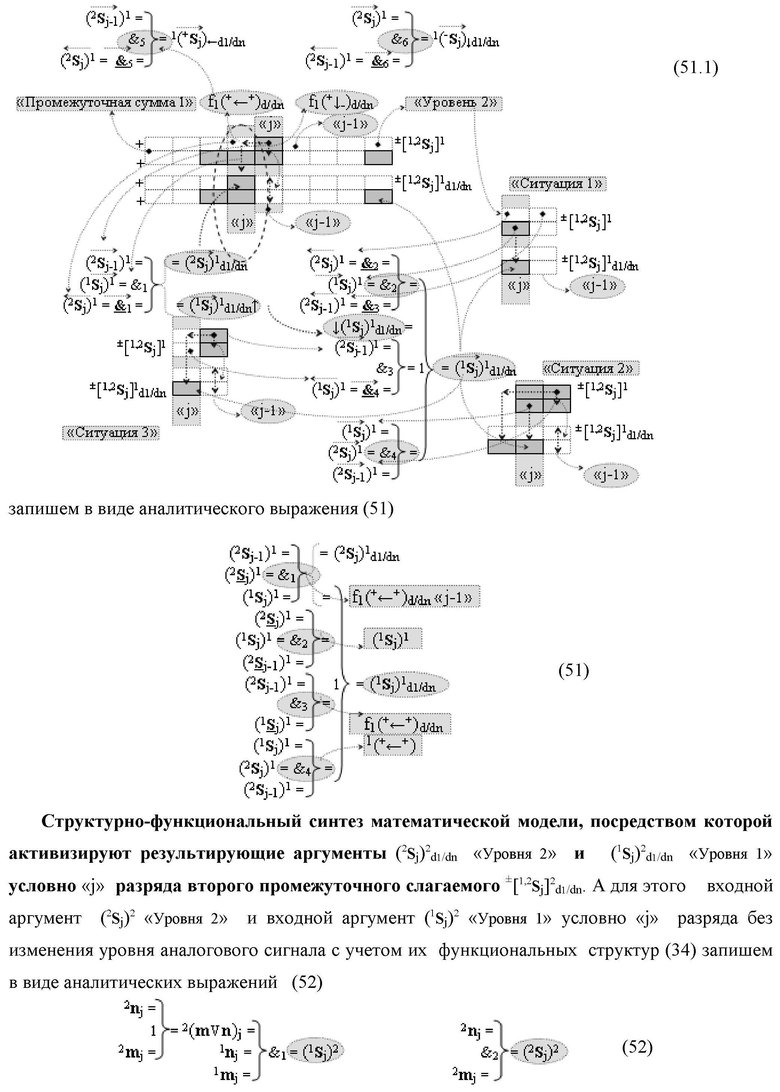
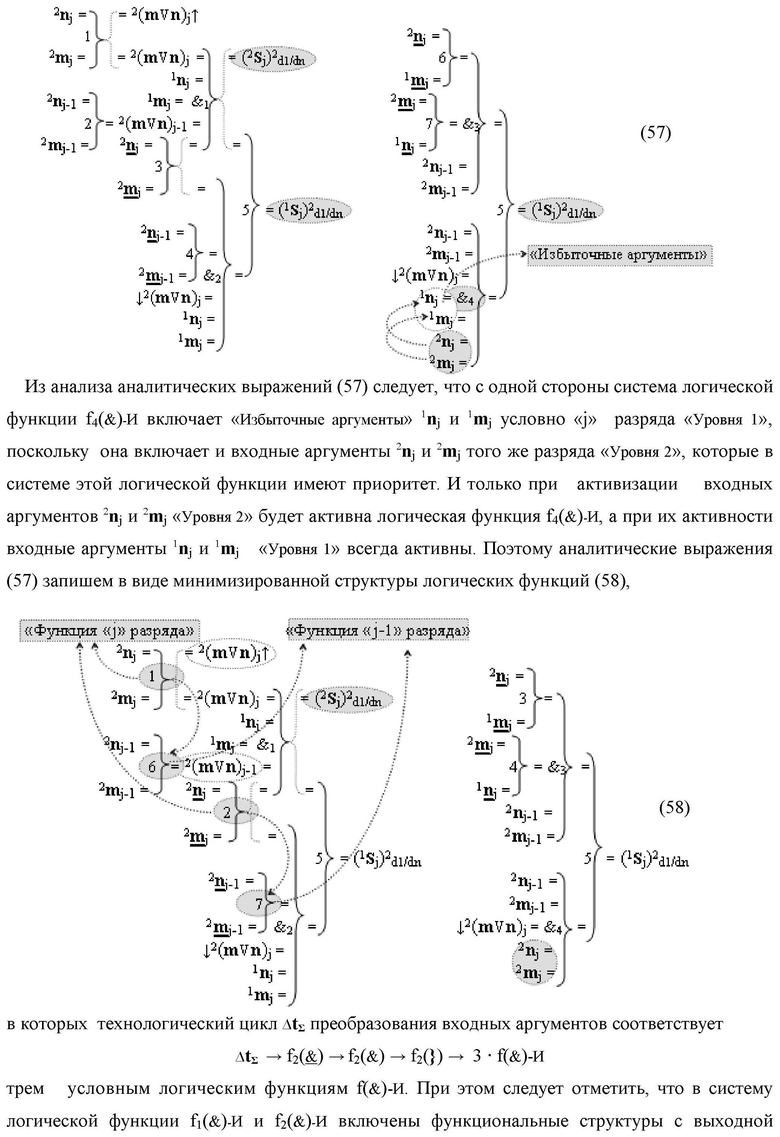
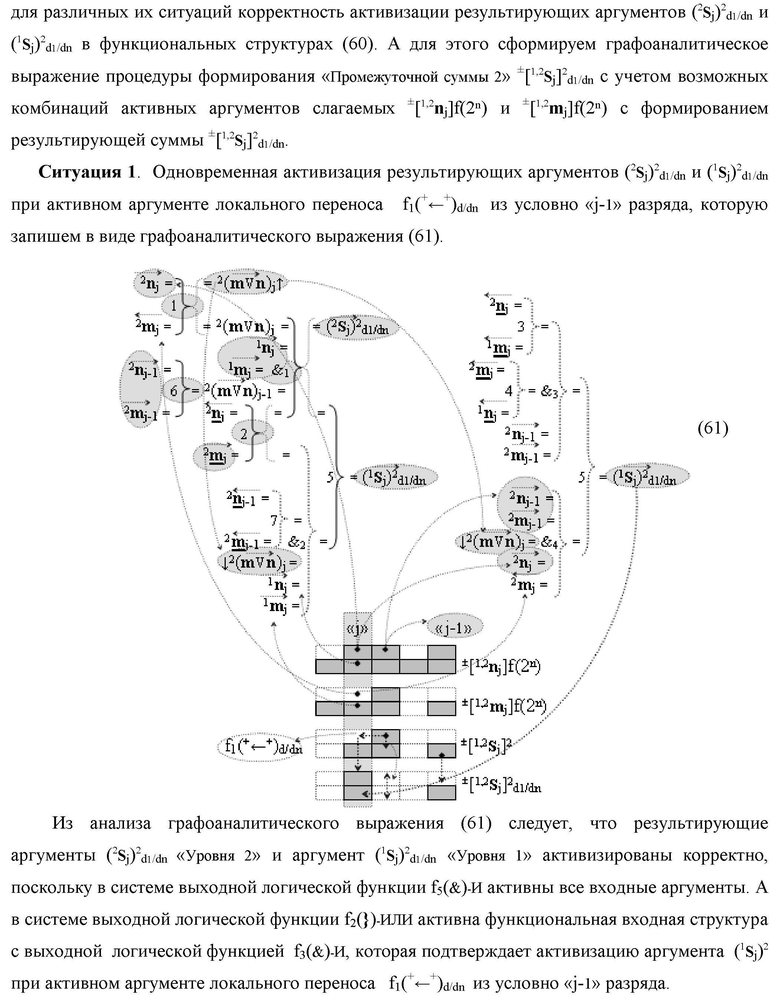
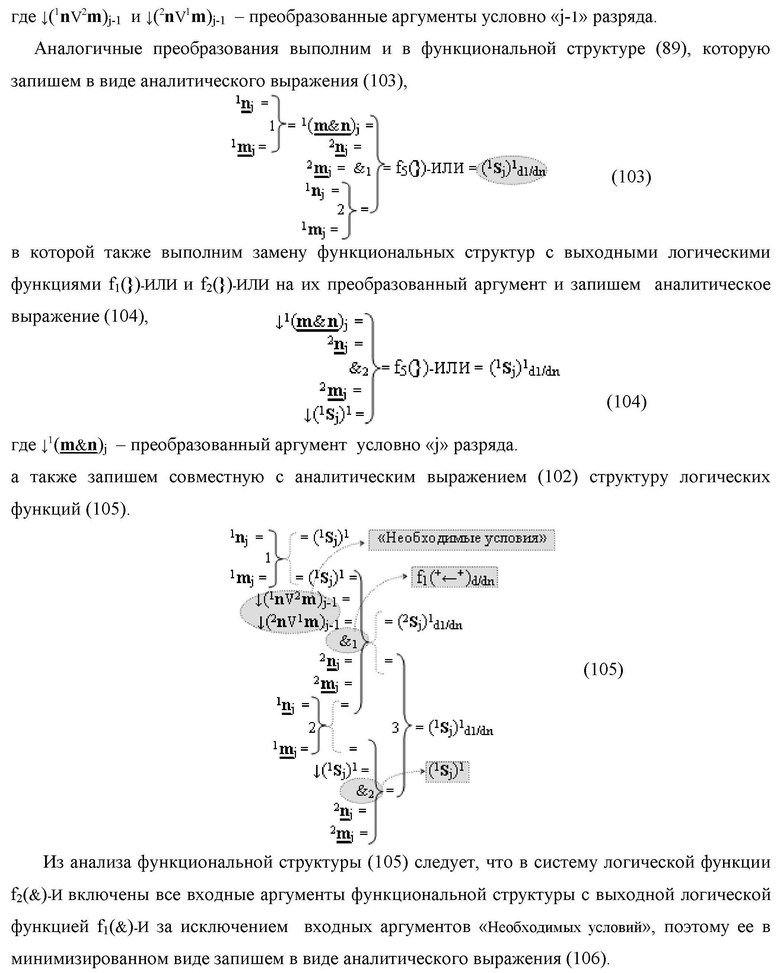
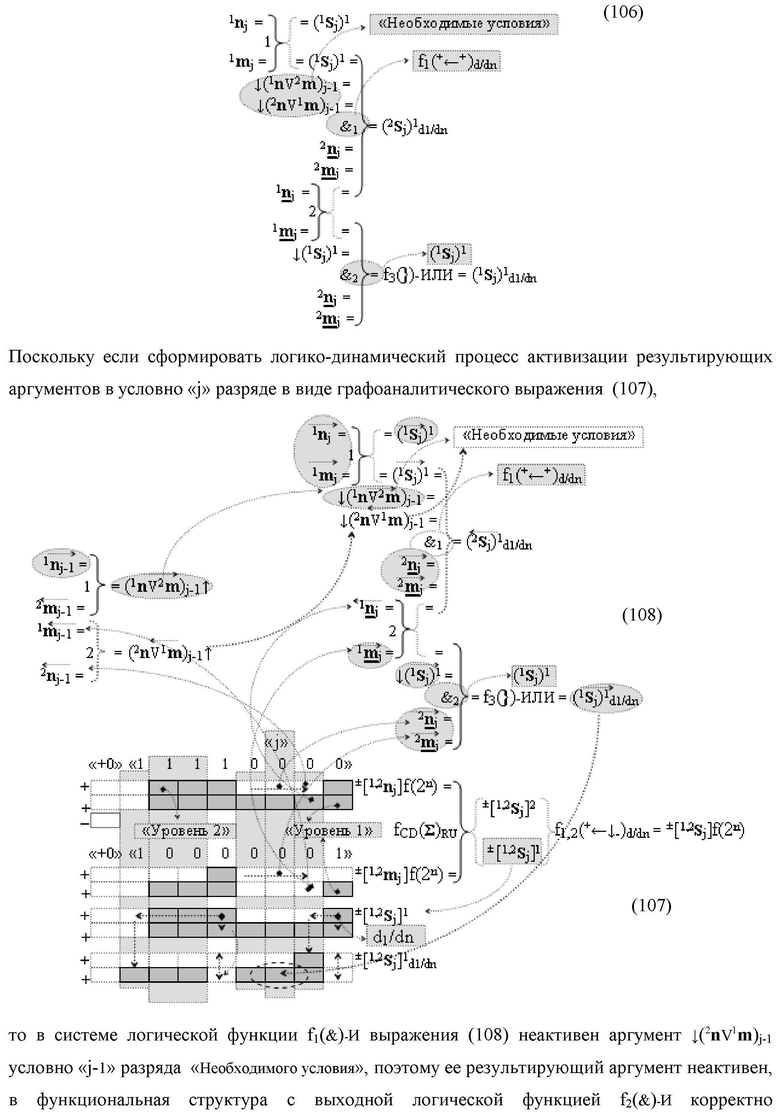
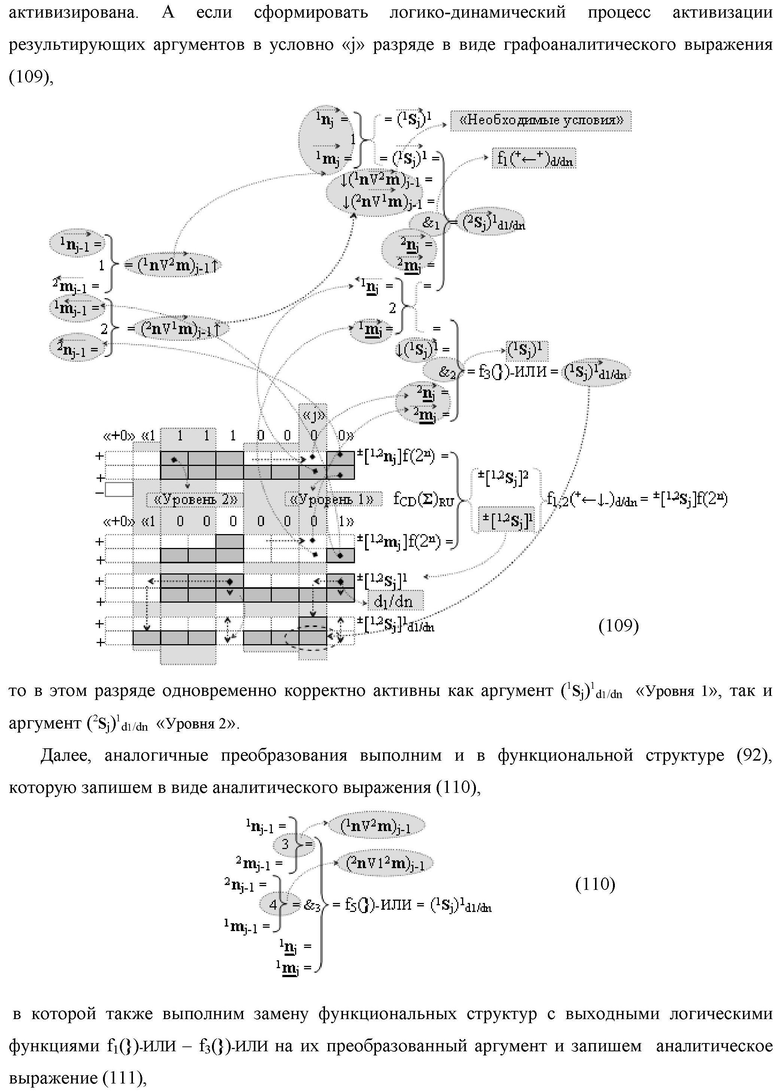
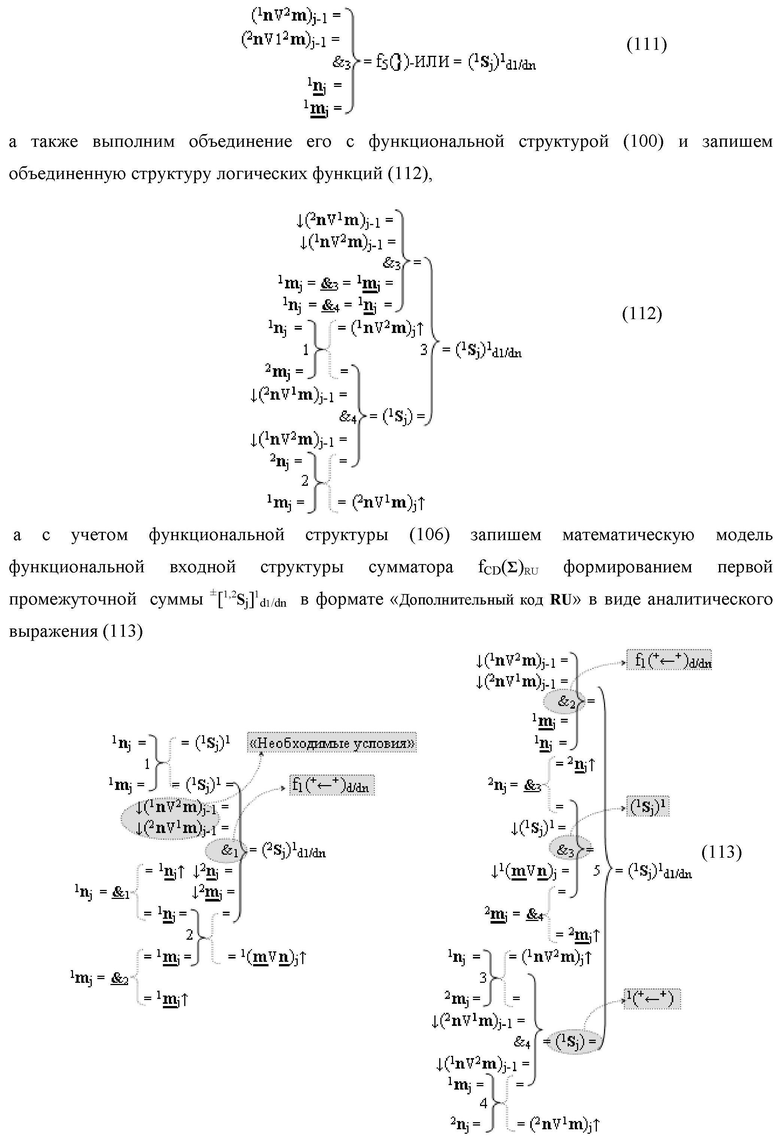
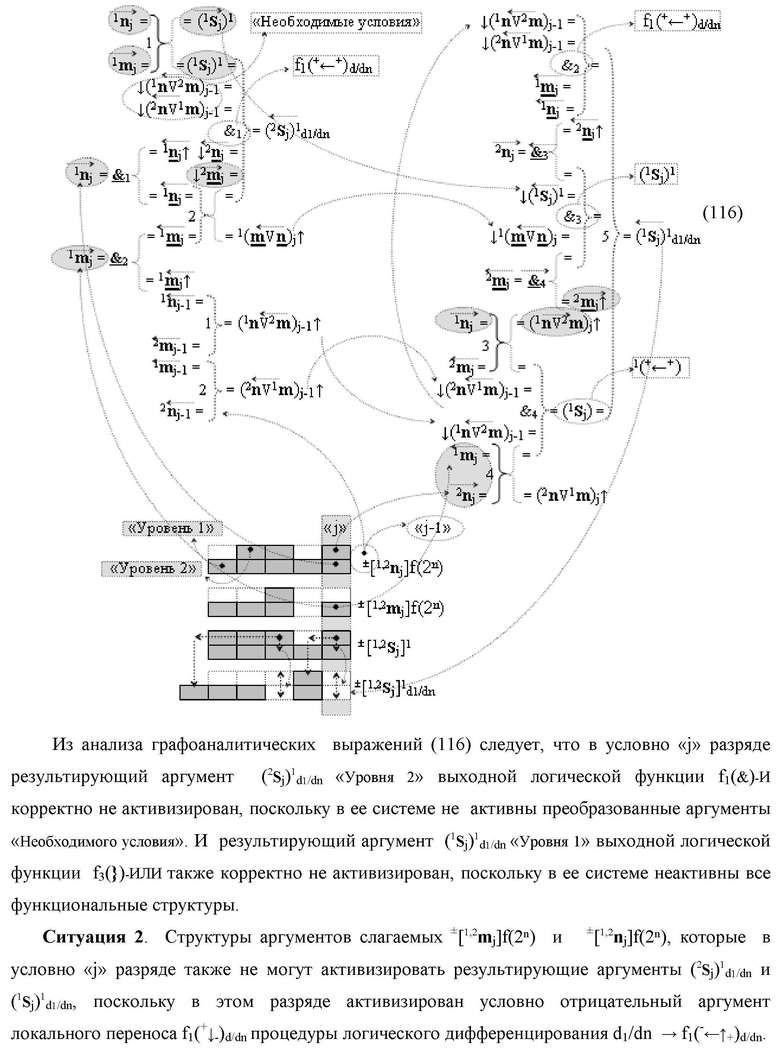
введены дополнительные логические функции f1(})-ИЛИ, f5(})-ИЛИ, f1(&)-И и f4(&)-И, при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
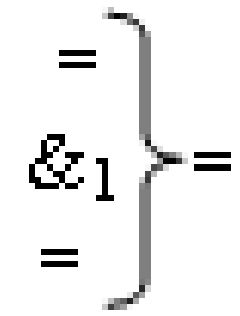- логическая функция f1(&)-И; 
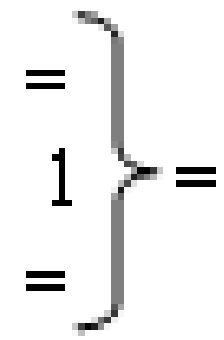- логическая функция f1(})-ИЛИ;
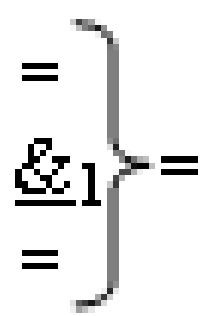- логическая функция f1(&)-И-НЕ; 
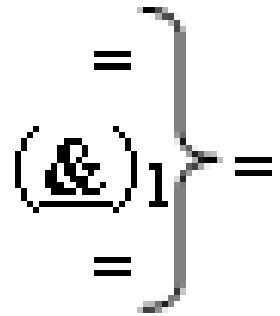- логическая функция f1(}&
)-ИЛИ-НЕ;
«=
&
1=» - логическая функция f1(
&
)-НЕ изменения уровня аналогового сигнала входного аргумента.
2. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате выполнена в виде двух структур логических функций, которые включают логические функции f1(}&
)-ИЛИ-НЕ, f1(&)-И, f2(&)-И, f1(})-ИЛИ, f2(})-ИЛИ, f3(})-ИЛИ, f1(
&
)-НЕ и f2(
&
)-НЕ, а также логическую функцию f1(&)-И-НЕ, в которой функциональные входные связи являются первой и второй функциональной входной связью структуры для приема аргумента слагаемых 1
n
j и 1
m
j «Уровня 1», при этом функциональная входная связь логической функции f1(&)-И являются функциональной выходной связью логической функции f2(})-ИЛИ, а функциональная входная связь логической функции f2(&)-И является функциональной выходной связью логической функции f1(
&
)-НЕ, отличающаяся тем, что в структуру условно «j» разряда
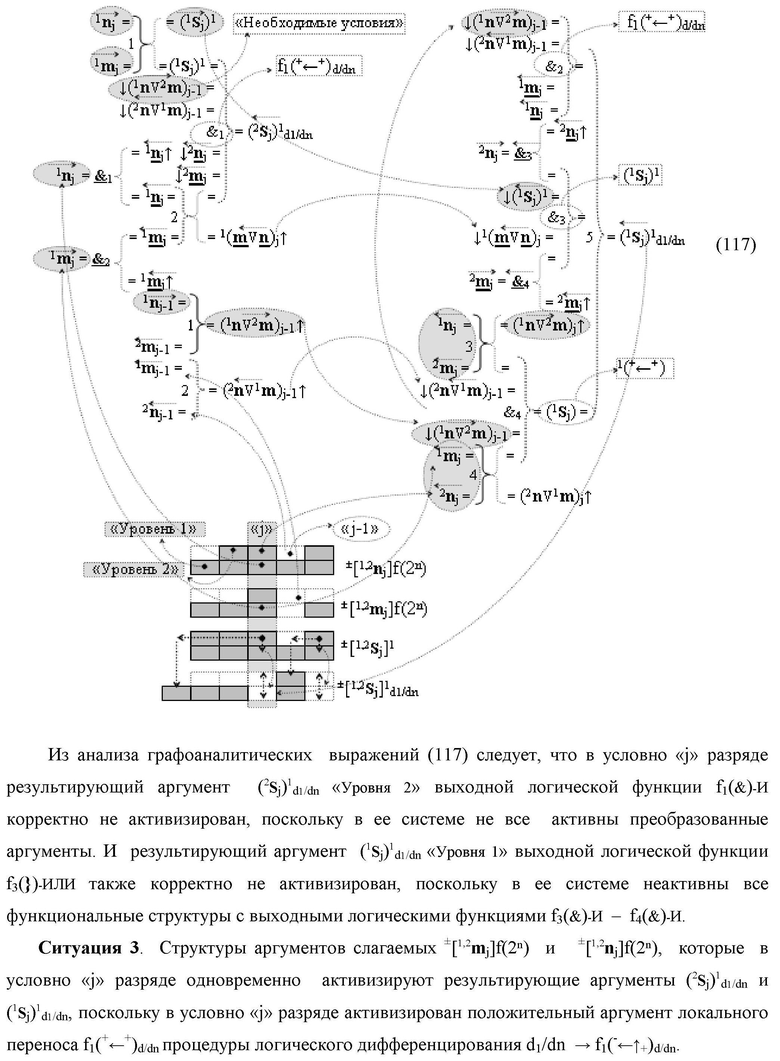
введены дополнительные логические функции f3(&)-И, f4(&)-И и f5(&)-И, а входные преобразованные аргументы ↓(1
n
V2
m
)j и ↓(2
n
V1
m
)j сформированы посредством функциональных структур вида
при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
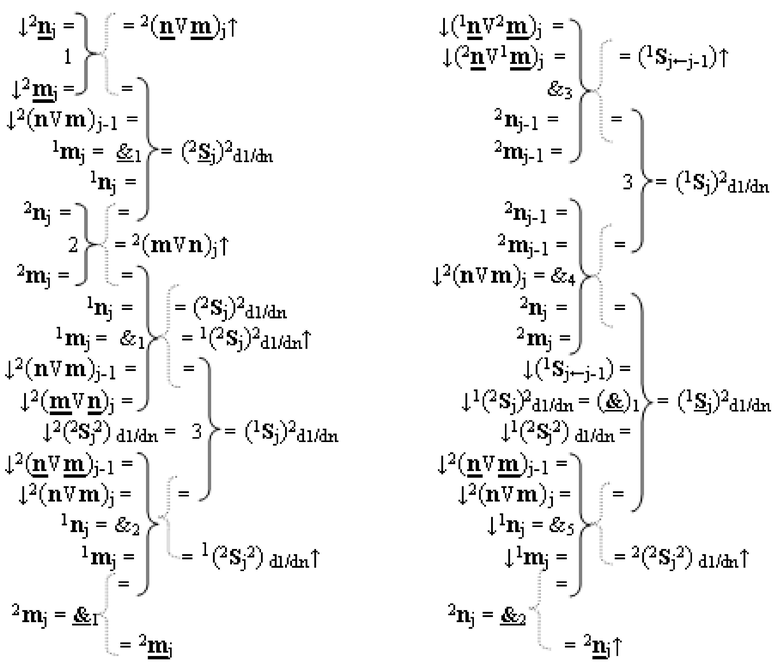
3. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате выполнена в виде двух структур логических функций, которые включают логические функции f1(&)-И, f2(&)-И, f1(})-ИЛИ, f2(})-ИЛИ, f3(})-ИЛИ, f1(
&
)-НЕ и f2(
&
)-НЕ, а также логическую функцию f1(&)-И-НЕ, в которой функциональные входные связи являются первой и второй функциональной входной связью структуры для приема аргумента слагаемых 1
n
j и 1
m
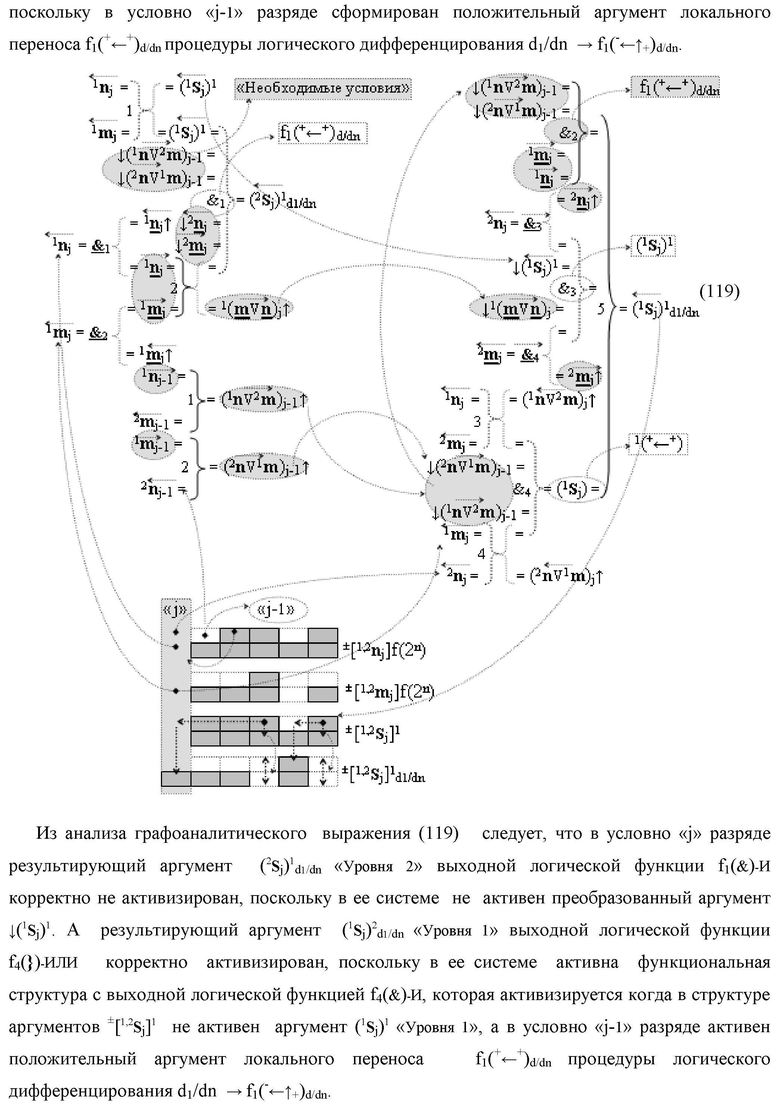
j «Уровня 1», при этом функциональные входные связи логической функции f1(&)-И являются функциональными выходными связями логических функций f1(})-ИЛИ и f2(})-ИЛИ, отличающаяся тем, что в структуру условно «j» разряда
введены дополнительные логические функции f1(&)-И-НЕ, f1(&)-И-НЕ, f1(&)-И-НЕ, f1(&)-И-НЕ, f1(&)-И-НЕ и f1(&)-И-НЕ, при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
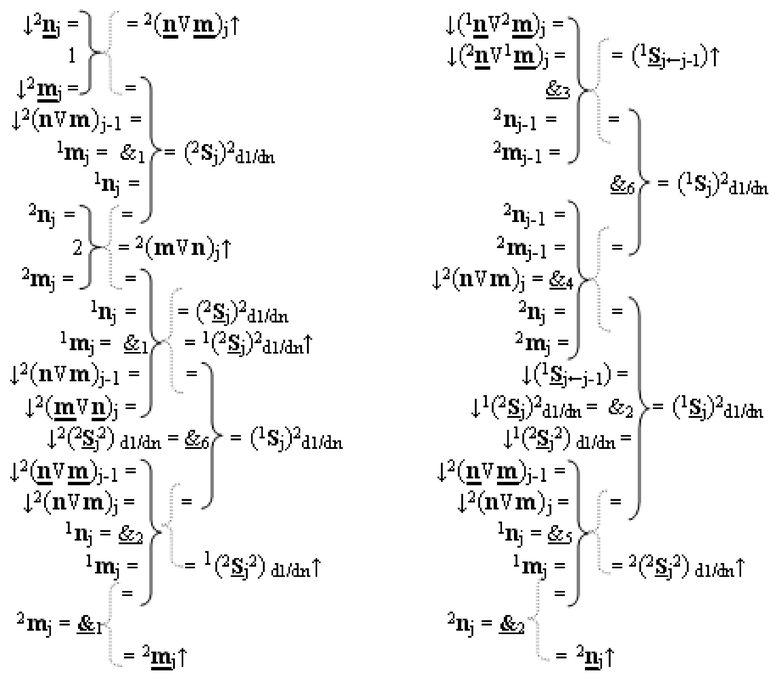
4. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате выполнена в виде двух структур логических функций, которые включают логические функции f1(})-ИЛИ, f2(})-ИЛИ, f1(
&
)-НЕ и f2(
&
)-НЕ, а также логическую функцию f2(}&
)-ИЛИ-НЕ, в которой функциональные входные связи являются первой и второй функциональной входной связью структуры для приема аргумента слагаемых 2
n
j и 2
m
j «Уровня 2», отличающаяся тем, что в структуру условно «j» разряда
введены дополнительные логические функции f1(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ, f4(}&
)-ИЛИ-НЕ, f5(}&
)-ИЛИ-НЕ, f6(}&
)-ИЛИ-НЕ, f7(}&
)-ИЛИ-НЕ и f8(}&
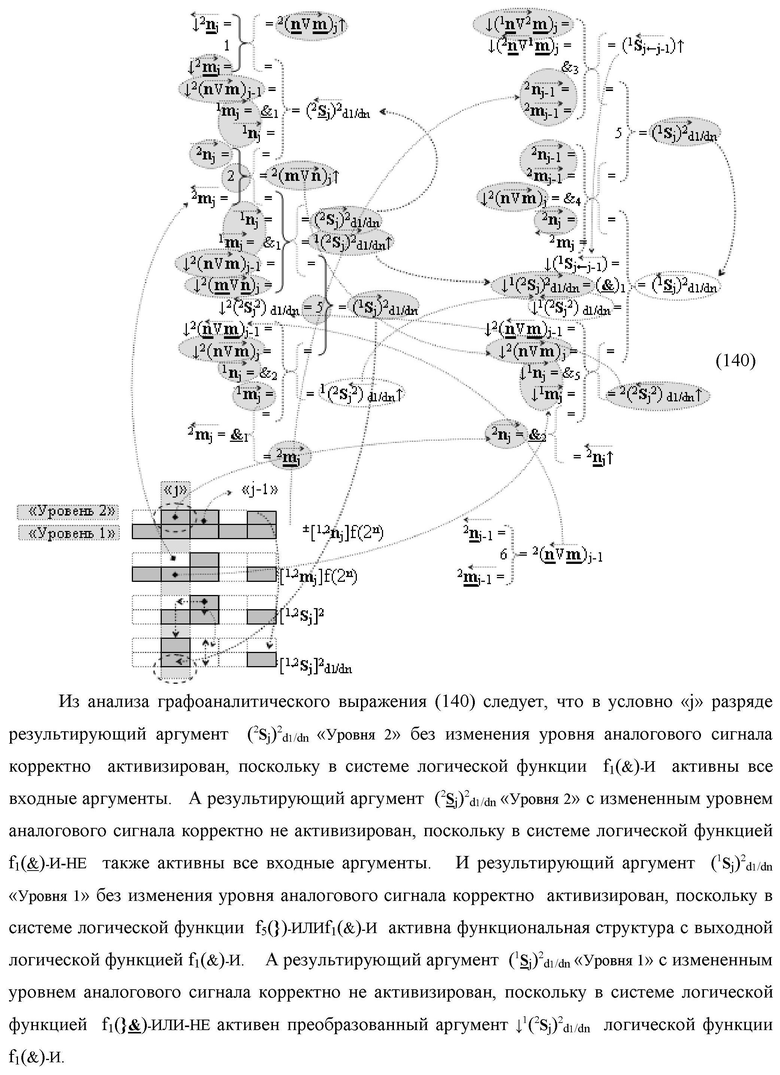
)-ИЛИ-НЕ, при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
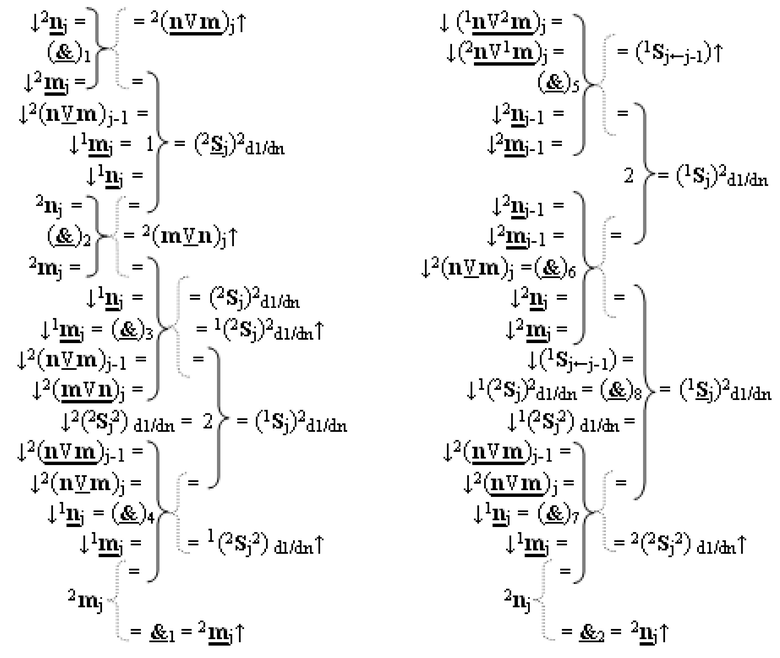
5. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате выполнена в виде двух структур логических функций, которые включают логические функции f1(}&
)-ИЛИ-НЕ, f1(&)-И, f2(&)-И, f1(})-ИЛИ, f2(})-ИЛИ, f1(
&
)-НЕ и f2(
&
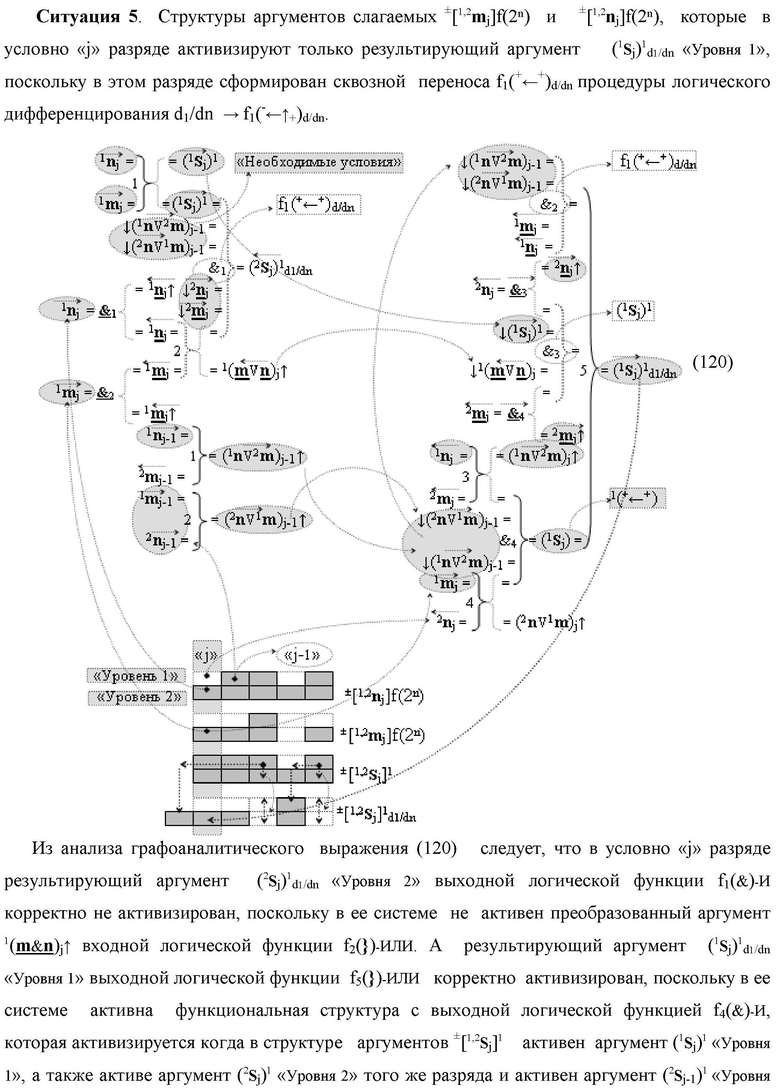
)-НЕ, отличающаяся тем, что в структуру условно «j» разряда
введены дополнительные логические функции f2(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ, f4(}&
)-ИЛИ-НЕ, f5(}&
)-ИЛИ-НЕ и f6(}&
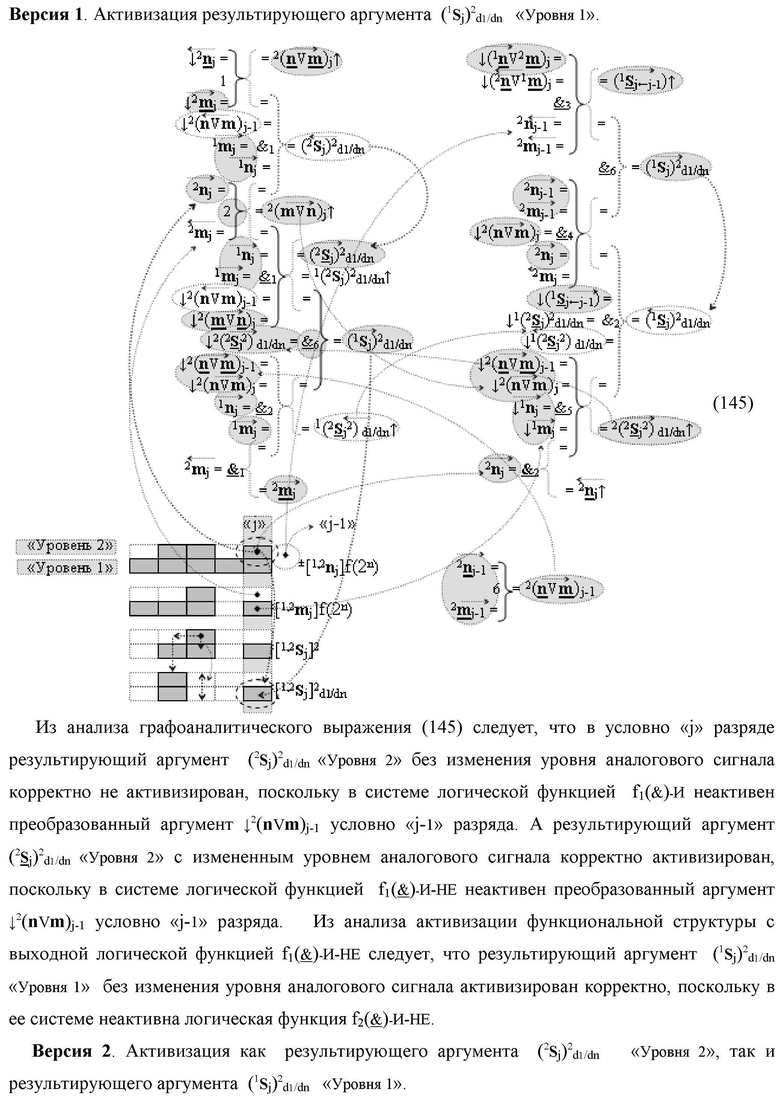
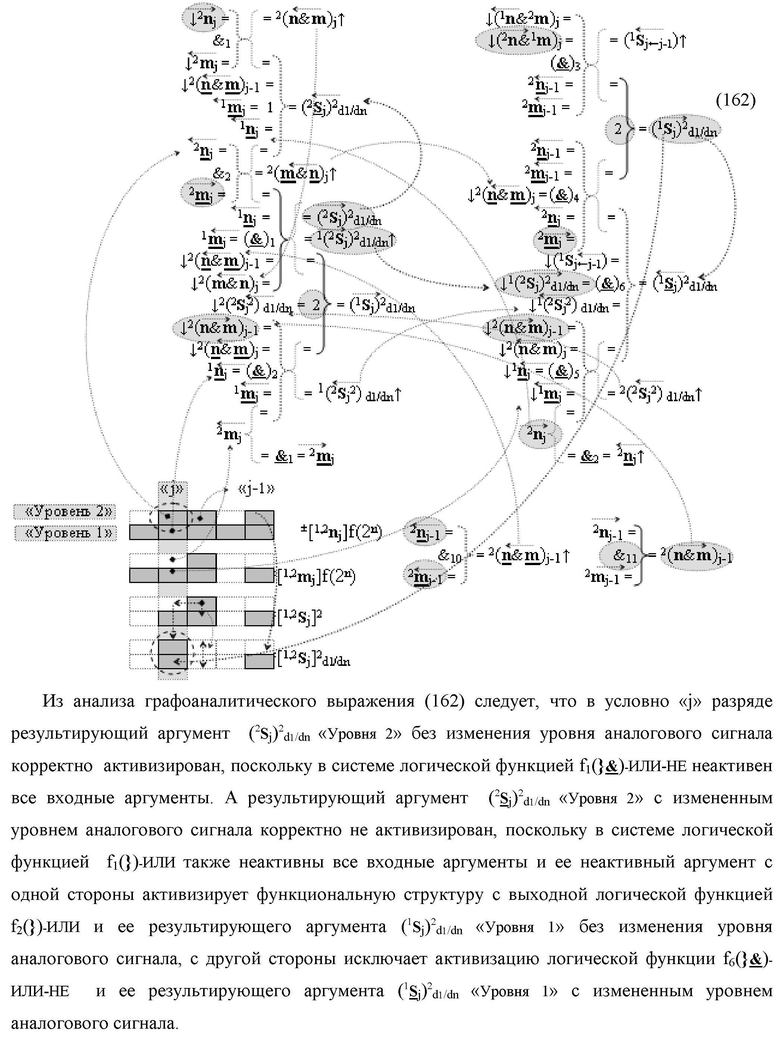
)-ИЛИ-НЕ, при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
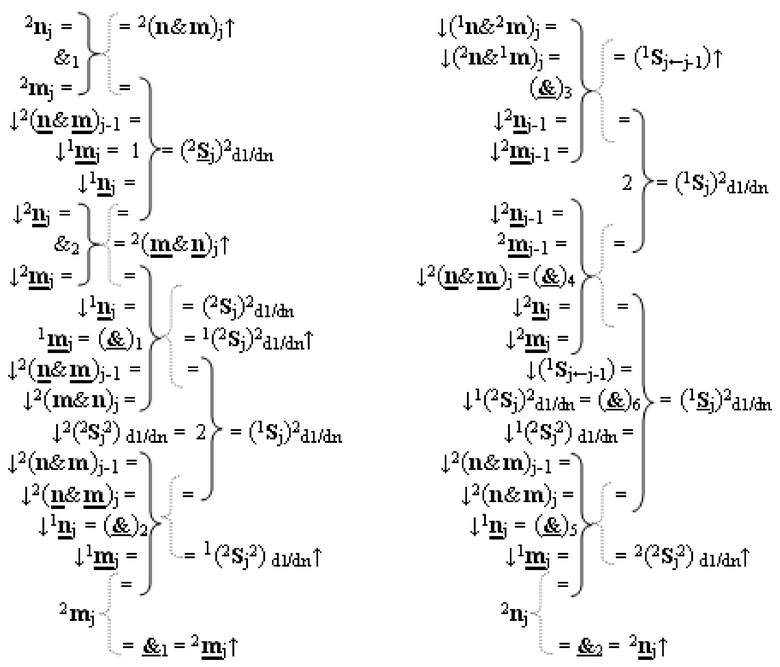
6. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате выполнена в виде двух структур логических функций, которые включают логические функции f1(&)-И-НЕ, f1(}&
)-ИЛИ-НЕ, f2(&)-И, f3(&)-И, f2(})-ИЛИ, f4(})-ИЛИ и f5(})-ИЛИ, а также логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, в которых функциональные выходные связи являются функциональной входной связью логической функции f2(})-ИЛИ и f5(})-ИЛИ, при этом функциональные входные связи логической функции f3(&)-И являются функциональными выходными связями логических функций f4(})-ИЛИ и f5(})-ИЛИ, отличающаяся тем, что в структуру условно «j» разряда
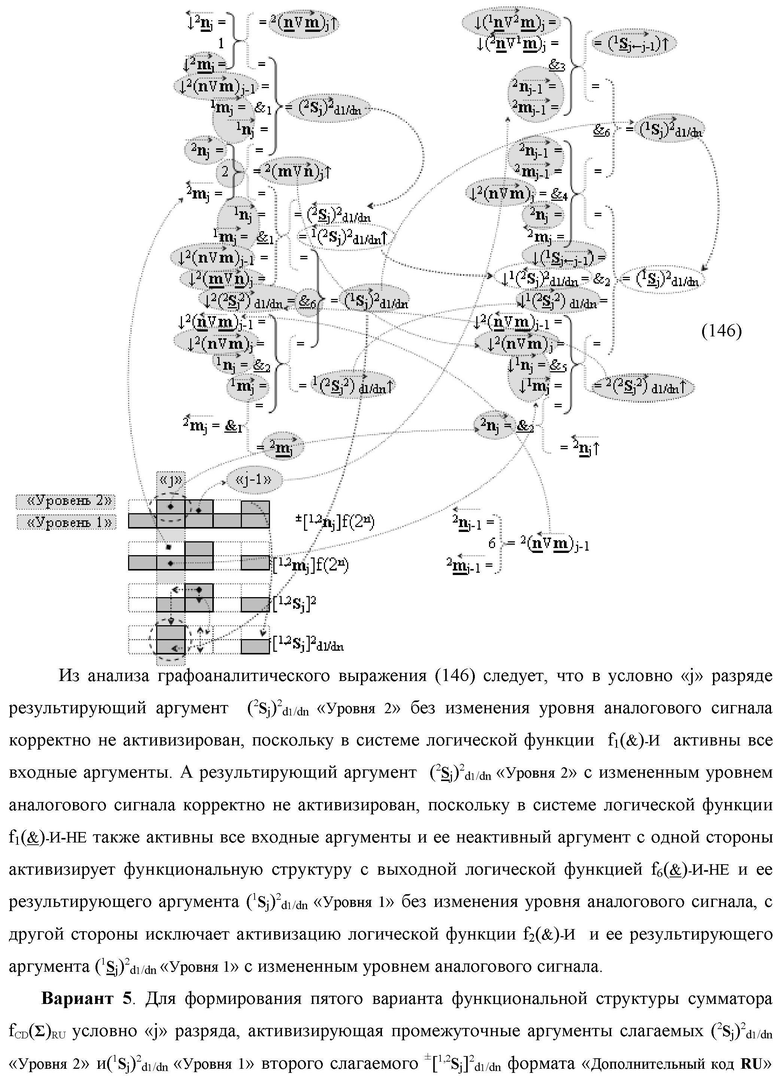
введены дополнительные логические функции f1(&)-И, f1(})-ИЛИ и f3(})-ИЛИ, при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
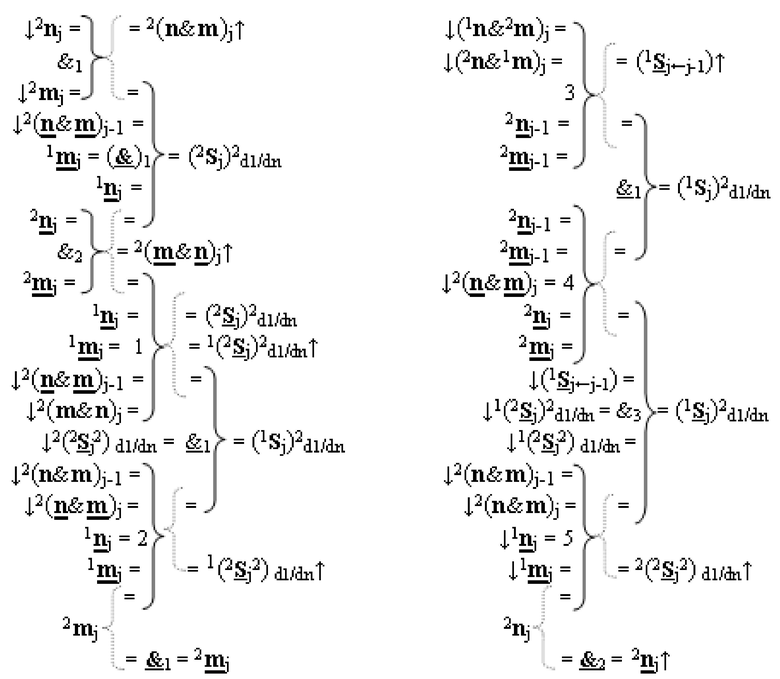
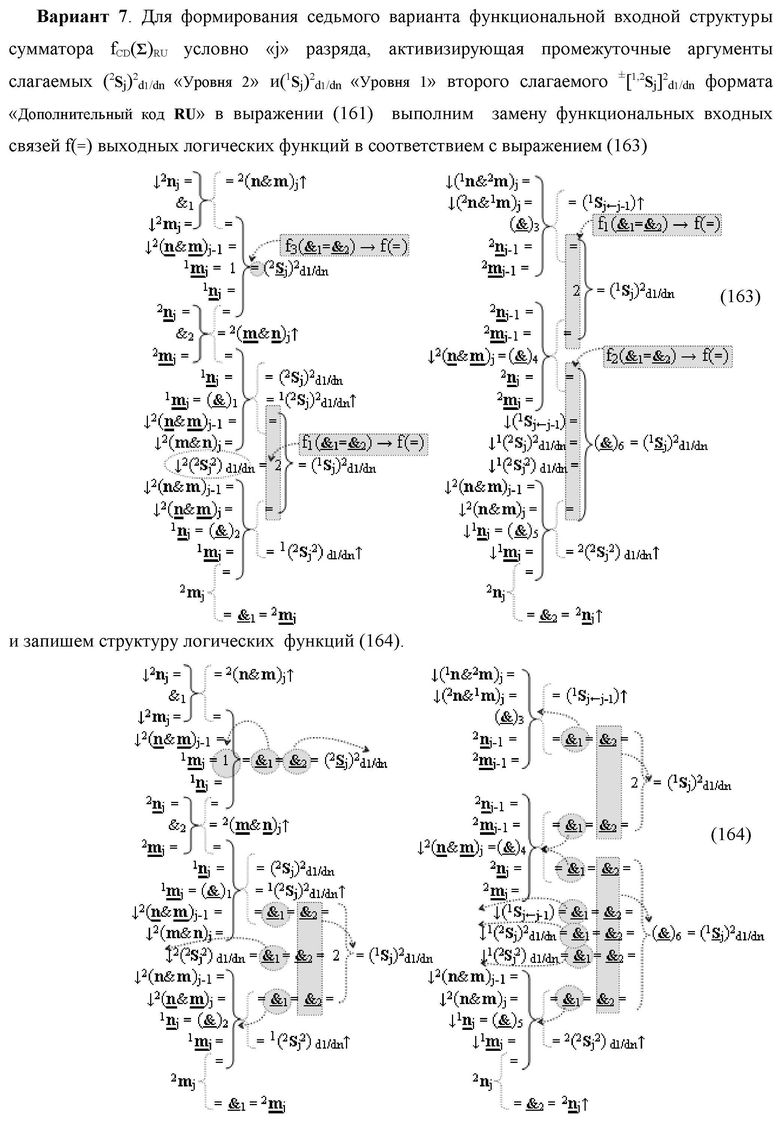
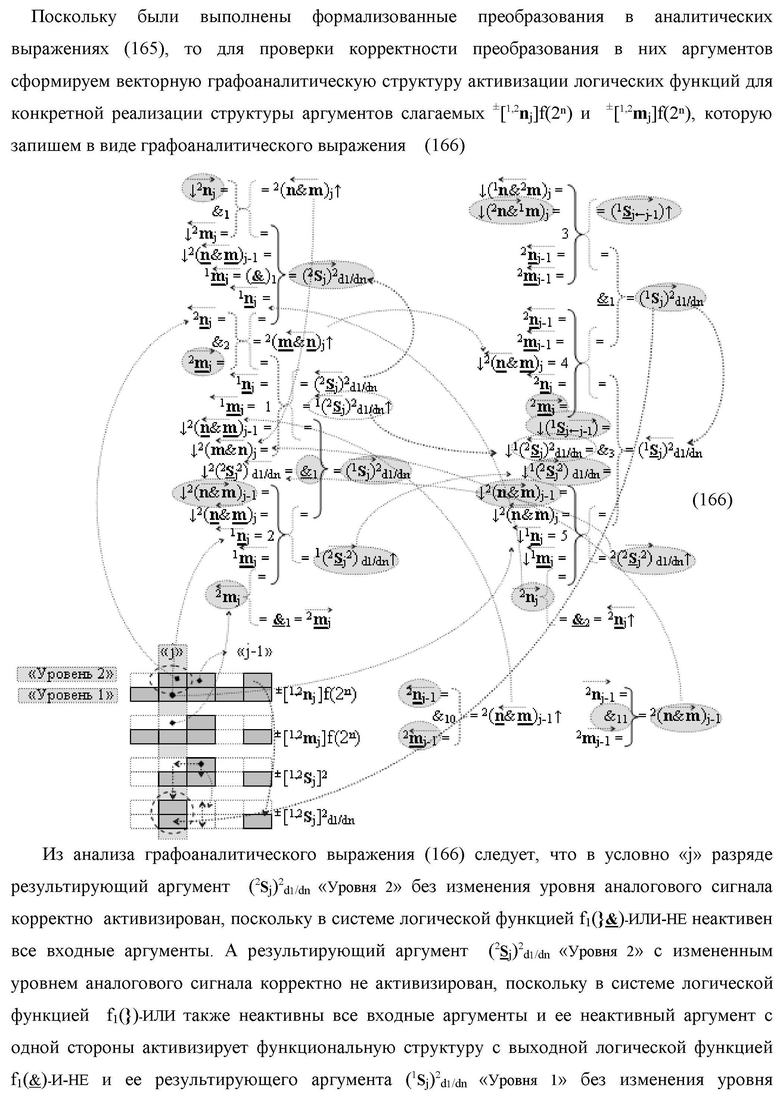
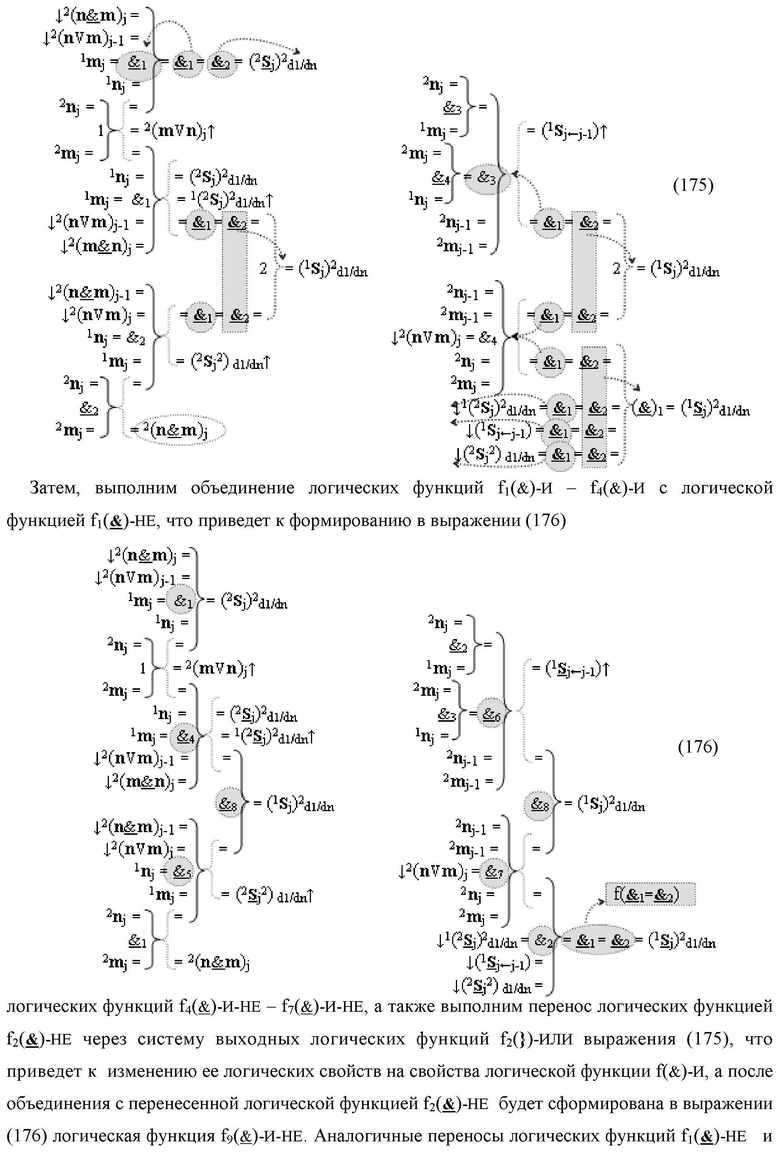
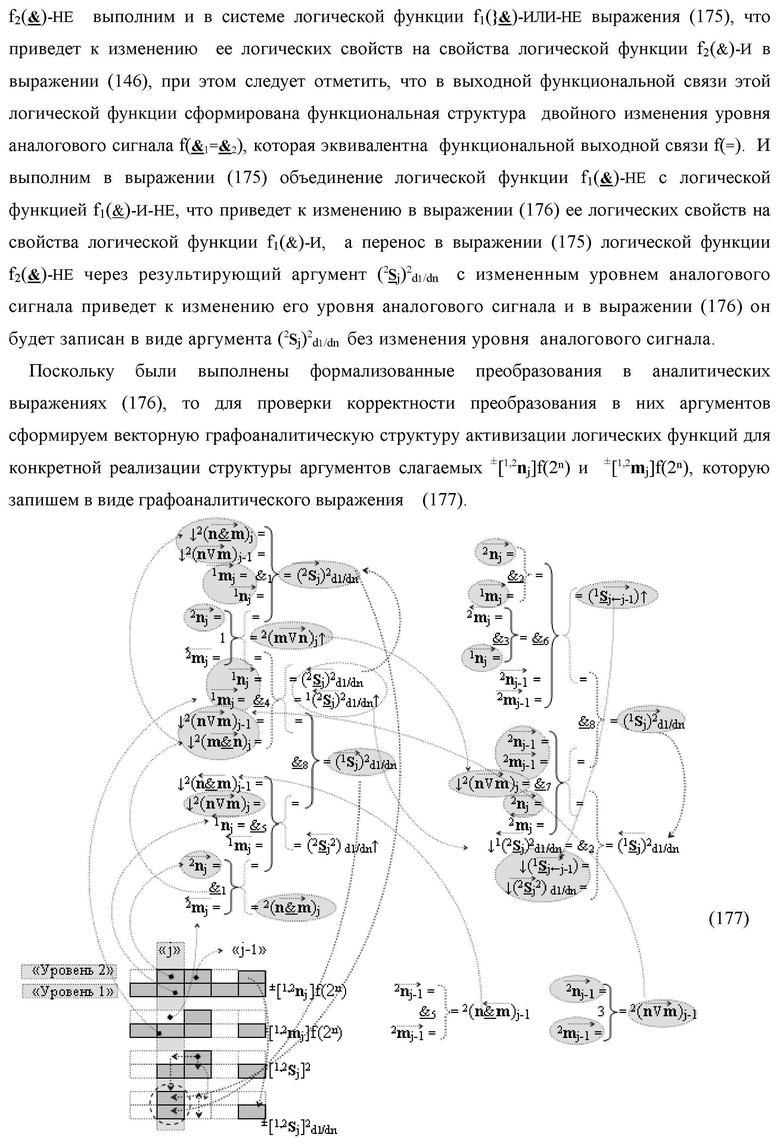
7. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате выполнена в виде двух структур логических функций, которые включают логические функции f1(}&
)-ИЛИ-НЕ, f1(&)-И, f2(&)-И, f1(})-ИЛИ и f2(})-ИЛИ, а также логическую функцию f1(&)-И-НЕ, в которой функциональные входные связи являются первой и второй функциональной входной связью структуры для приема аргумента слагаемых 1
n
j и 1
m
j «Уровня 1», при этом функциональная входная связь логической функции f1(&)-И является функциональной выходной связью логической функции f1(})-ИЛИ, отличающаяся тем, что в структуру условно «j» разряда
введены дополнительные логические функции f3(&)-И, f4(&)-И, f2(&)-И-НЕ, f3(&)-И-НЕ и f4(&)-И-НЕ, при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
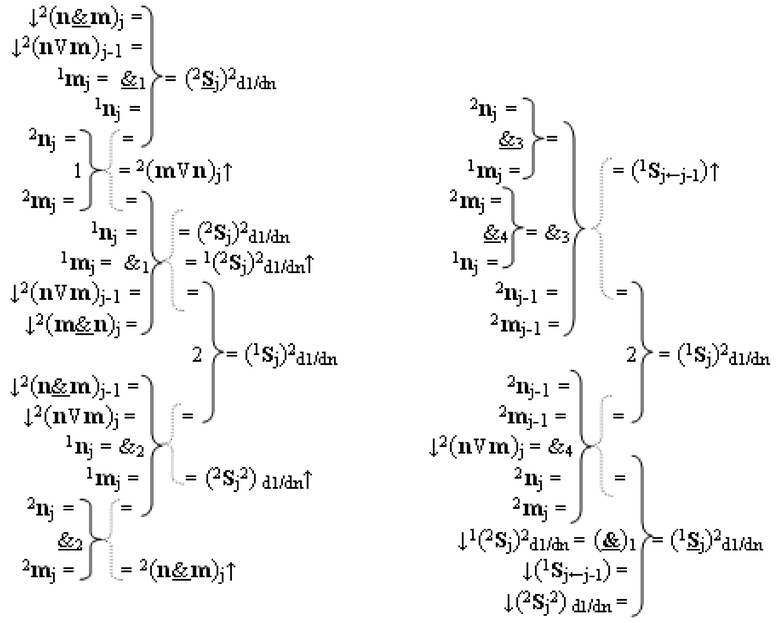
8. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате выполнена в виде двух структур логических функций, которые включают логические функции f1(&)-И, f2(&)-И, и f2(})-ИЛИ, а также логическую функцию f1(&)-И-НЕ, в которой функциональные входные связи являются первой и второй функциональной входной связью структуры для приема аргумента слагаемых 2
n
j и 2
m
j «Уровня 2», при этом функциональная входная связь логической функции f1(&)-И является функциональной выходной связью логической функции f1(})-ИЛИ, отличающаяся тем, что в структуру условно «j» разряда
введены дополнительные логические функции f2(&)-И-НЕ, f3(&)-И-НЕ, f4(&)-И-НЕ, f5(&)-И-НЕ, f6(&)-И-НЕ, f7(&)-И-НЕ и f8(&)-И-НЕ, при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
9. Функциональная вторая входная структура условно «j» разряда
сумматора
fCD(Σ)RU с максимально минимизированным технологическим циклом
∆t
Σ для аргументов слагаемых
±[1,2
n
j]f(2n) и
±[1,2
m
j]f(2n) формата
«Дополнительный код RU» с формированием промежуточной суммы (2
S
j)2 d1/dn «Уровня 2» и
(1
S
j)2 d1/dn «Уровня 1» второго слагаемого в том же формате, выполнена в виде двух структур логических функций, которые включают логические функции f1(&)-И, f2(&)-И, f1(})-ИЛИ, f2(})-ИЛИ, f1(
&
)-НЕ и f2(
&
)-НЕ, а также логическую функцию f2(}&
)-ИЛИ-НЕ, в которой функциональные входные связи являются первой и второй функциональной входной связью структуры для приема аргумента слагаемых 2
n
j и 2
m
j «Уровня 2», отличающаяся тем, что в структуру условно «j» разряда
введены дополнительные логические функции f3(&)-И, f2(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ, f4(}&
)-ИЛИ-НЕ, f5(}&
)-ИЛИ-НЕ и f6(}&
)-ИЛИ-НЕ, при этом функциональные связи логических функций во входной структуре сумматора выполнены в соответствии с математической моделью вида
| Дж.Уэйклер | |||
| Проектирование цифровых устройств | |||
| - М.: ПОСТМАРКЕТ, 2002, с.508 | |||
| ВХОДНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО СУММАТОРА В ПОЗИЦИОННО-ЗНАКОВЫХ КОДАХ f(+/-) (ВАРИАНТЫ) | 2007 |
|
RU2378682C2 |
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА СУММАТОРА f(Σ) УСЛОВНО "i" РАЗРЯДА ЛОГИКО-ДИНАМИЧЕСКОГО ПРОЦЕССА СУММИРОВАНИЯ ПОЗИЦИОННЫХ АРГУМЕНТОВ СЛАГАЕМЫХ [n]f(2) и [m]f(2) С ПРИМЕНЕНИЕМ АРИФМЕТИЧЕСКИХ АКСИОМ ТРОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+1,0,-1) (ВАРИАНТЫ РУССКОЙ ЛОГИКИ) | 2010 |
|
RU2429522C1 |
| US 7274211 B1, 25.09.2007 | |||
| JP 2002014804 A, 18.01.2002. | |||
