Изобретение относится к вычислительной технике и может быть использовано в системах контроля и управления в совокупности с арифметическими устройствами, которые реализуют различные арифметические процедуры над аргументами аналоговых сигналов ± m&[1,2 m i]f(2n) формата «Дополнительный код RU» и формируют посредством функциональной структуры цифроаналогового преобразователя f1(ЦАП) аналоговый сигнал управления ± U kf([1,2 m i]).
Известна функциональная структура преобразования позиционно-знаковой структуры аргументов аналоговых сигналов ±[m i]f(-1/+1,0,…+1) формата «Дополнительный код» в аналоговый сигнал управления ± U kf([m i]) (см. У. Титце, К. Шенк. Полупроводниковая схемотехника. М. «Мир», 1982 г. С. 451, рис. 24.14), в которой если ввести аналитическую запись функциональных структур:

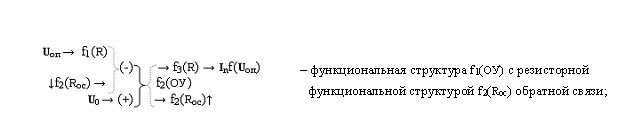
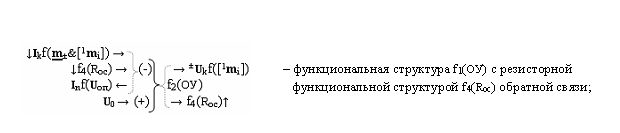
где (=) - функциональная цифровая связь позиционных аргументов; (→) - функциональная аналоговая связь аналоговых аргументов напряжения и энергетического тока; (↑) и (↓) - функциональная прерванная связь;
то математическую модель логико-динамического процесса преобразования позиционно-знаковой структуры аргументов аналоговых сигналов ±[m i]f(-1/+1,0,…+1) «дополнительный код» в аналоговый сигнал управления ± U kf([m i]) можно записать в виде аналитического выражения вида
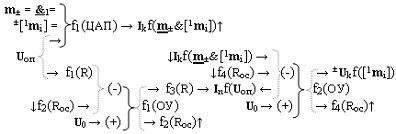
При этом логико-динамический процесс преобразование позиционно-знаковой структуры аргументов аналоговых сигналов ±[m i]f(-1/+1,0,…+1) «дополнительный код» в аналоговый сигнал управления ± U kf([m i]) может быть записан в виде графоаналитического выражения вида
И результирующий аргумент «аналогового» сигнала ± U kf([m i]) формирует функциональная структура f2(ОУ) из векторной суммы входного аргумента ↓I kf( m ±&[1 m i]) функциональной структуры f1(ЦАП) и входного аргумента I nf(U оп) функциональной структуры f1(ОУ) операционного усилителя. При этом величина входного аргумента I nf(U оп) функциональной структуры f1(ОУ) должна быть эквивалентна информационному содержанию знакового аргумента m ±, который в системе функциональной структуры f1(ЦАП) для условно отрицательных аргументов [m i] не активный, а для положительных аргументов [m i] активизирует логическая функция f1( & )-НЕ, что и приводит к компенсации величины входного аргумента I nf(U оп) функциональной структуры f1(ОУ). В результате динамический диапазон изменения аргумента результирующего «аналогового» сигнала ± U kf([m i]) функциональной структуры f2(ОУ) существенно ограничен на величину старшего разряда функциональной структуры f1(ЦАП) (прототип).
Известный прототип имеет технические возможности, которые заключаются в том, что реализуют процедуру преобразования позиционно-знаковой структуры аргументов ±[m i]f(-1/+1,0,…+1) «Дополнительный код» в аналоговый сигнал управления ± U kf([m i]).
Недостатком известного технического решения является ограничение функциональных возможностей, поскольку не может быть преобразована структура аргументов аналоговых сигналов ±[1,2 m i]f(2n) формата «Дополнительный код RU» в аналоговый сигнал управления ± U kf([1,2 m i]). При этом следует отметить, что структура аргументов аналоговых сигналов ±[1,2 m i]f(2n) формата «Дополнительный код RU» позволяет все арифметические преобразования выполнять без выполнения сквозных переносов, что приводит к существенному сокращению технологического цикла ∆t S их выполнения.
Техническим результатом предложенного изобретения является расширение функциональных возможностей функциональной структуры цифроаналогового преобразователя f1(ЦАП).
Указанный технический результат достигается следующей функциональной структурой.
Функциональная структура цифроаналогового преобразования позиционно-знаковых структур аргументов аналоговых сигналов ±[1,2 m i]f(2n) формата «Дополнительный код RU» в аналоговый сигнал управления ± U kf(±[1,2 m i, включающая функциональную структуру цифроаналогового преобразователя f1(ЦАП)
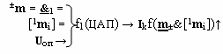
где ± m - аргумент знакового разряда; [1 m i] - входная информационная структура аргументов «Дополнительного кода RU» «Уровня 1»; & 1 - логическая функция f1( & )-НЕ; I kf( m ±&[1 m i])↑ - результирующих аргумент тока;
функциональную структуру операционного усилителя f1(ОУ)
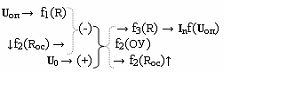
где f1(Rос) - резисторная функция обратной связи; U 0 - аргумент условно нулевого напряжения; U оп - аргумент опорного напряжения, f1(Rос) - функциональная структура резисторной функции обратной связи; f2(R) - функциональная структура резисторной функции выходной функциональной связи;
и функциональную структуру операционного усилителя f2(ОУ)
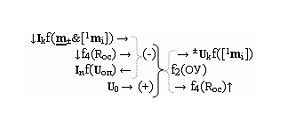
где f2(Rос) - функциональная структура резисторной функции обратной связи;
при этом функциональные связи выполнены в соответствии с математической моделью вида
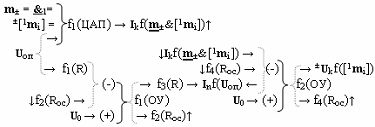
при этом введена функциональная дополнительная структура f2(ЦАП)
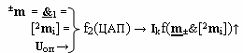
[2 m i] - входная информационная структура аргументов «Дополнительного кода RU» «Уровня 2»,
а функциональные связи выполнены в соответствии с математической моделью вида

Принципы формирования математических моделей с «аналоговой» формой информации, в основе которых лежит функциональная структура f(ОУ) операционного усилителя. Разработанные схемные технические решения функциональных структур для преобразования аргументов с «аналоговой» формой информации не относятся к категории аналитической формы записи конкретных логико-динамических процессов. А на их основе также могут быть выполнены не только различные «арифметические» преобразования, такие как сложение и умножение аргументов, но и процедуры контроля и управления различными технологическими процессами, которые реализованы не только на техническом уровне, но и на уровне функциональных химических структур. И если для «цифровых» структур аргументов была сформирована аналитическая форма записи различных логических функций и сформированы правила преобразования их функциональных структур, то и для «аналоговых» аргументов также необходимо сформировать аналитическую форму записи функциональных различных структур, в которых основным элементом является функциональная структура операционного усилителя f(ОУ).
Из анализа условного графического обозначения операционного усилителя (ОУ) и его реального содержания следует, что если применить только аналитические символы, то его можно записать в виде аналитического выражения (1)
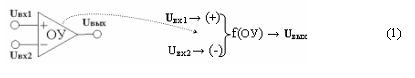
в котором графическое обозначение записано в виде символа системы (}) с входными и выходной функциональными связями f(→). При этом функциональные входные связи конкретизированы дополнительными символами «+» и «-» и они имеют однозначное смысловое содержание, которое принято при записи в графическом изображении (ОУ). Аналогичный результат может быть получен и для других функциональных структур, а для этого приведем несколько конкретных примеров.
Пример 1. Функциональная структура f(ОУ) с отрицательной обратной связью, которую запишем в виде графоаналитического выражения (2)
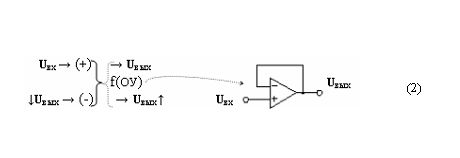
Из сопоставительного анализа аналитического выражения функциональной структуры f(ОУ) с отрицательной обратной связью и графической ее записи следует, что они эквивалентны в смысловом их содержании, поскольку в качестве обратной связи в аналитическом выражении записан результирующий аргумент U вых↑ с прерванной функциональной связью и тот же аргумент ↓U вых на условно отрицательной функциональной связи системы функциональной структуры f(ОУ).
Пример 2. Функциональная структура f(ОУ) неинвертирующего сумматора может быть записана в виде графоаналитического выражения (3)
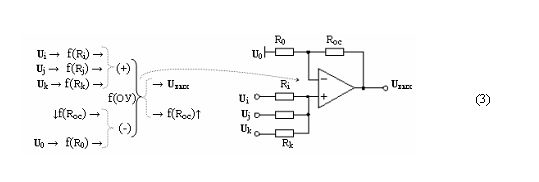
особенностью которой являются дополнительные входные системы положительной (+) и условно отрицательной (-) входной системы функциональной структуры f(ОУ). И эти дополнительные системы функциональной структуры f(ОУ) соответствуют объединению токов резисторных функций.
Пример 3. Функциональная структура f(ОУ) инвертирующего сумматора может быть записана в виде графоаналитического выражения (4)
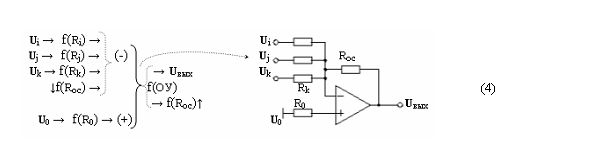
в котором логика формирования математической модели существенно не отличается от логики формирования математической модели (3)
Пример 4. Первый вариант с последовательными функциональными структурами f(ОУ), который запишем в виде графоаналитического выражения (5)
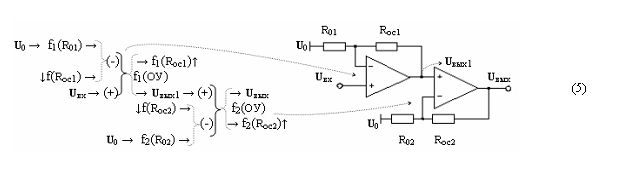
Пример 5. Второй вариант с последовательными функциональными структурами f(ОУ), который запишем в виде графоаналитического выражения (6)
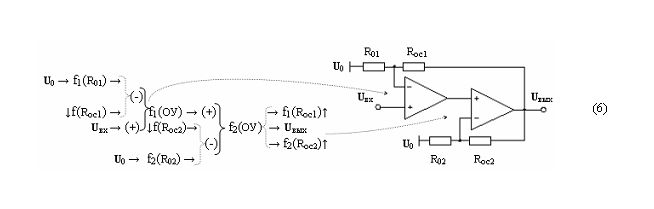
Пример 6. Первый вариант функциональной структуры f(ОУ) с коммутируемой отрицательной обратной связью, который запишем в виде графоаналитического выражения (7)
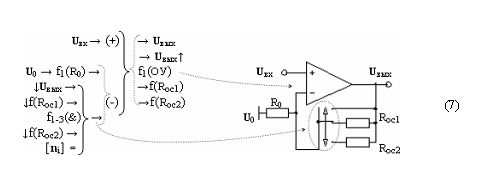
Пример 7. Второй вариант функциональной структуры f(ОУ) с коммутируемой отрицательной обратной связью, который запишем в виде графоаналитического выражения (8)
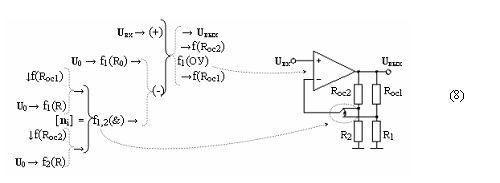
Пример 8. Парный вариант функциональной структуры f(ОУ) с регулируемой отрицательной обратной связью, которую запишем в виде графоаналитического выражения (9)
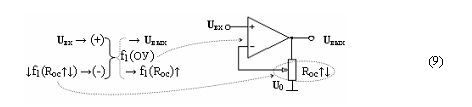
Пример 9. Второй вариант функциональной структуры f(ОУ) с регулируемой отрицательной обратной связью, которую запишем в виде графоаналитического выражения (10)
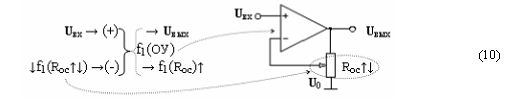
Пример 10. Третий вариант функциональной структуры f(ОУ) с регулируемой отрицательной обратной связью, которую запишем в виде графоаналитического выражения (11)
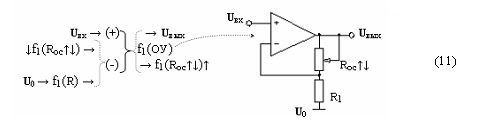
Пример 11. Четвертый вариант функциональной структуры f(ОУ) с регулируемой отрицательной обратной связью, которую запишем в виде аналитического выражения (12)
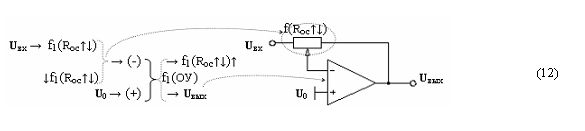
Из анализа аналитических выражений (2)-(12) следует, что, с одной стороны, они полностью соответствуют их графическим аналогам, с другой стороны, могут быть использованы для записи математических моделей различных технологических процессов преобразования с различной «формой информации» аргументов. И в качестве такого примера синтезируем математическую модель цифроаналогового преобразователя, посредством которого может быть реализован процесс преобразования структуры аргументов аналоговых сигналов ±[1,2 m i]f(2n) формата «Дополнительный код RU» в аналоговый сигнал управления ± U kf([1,2 m i]). При этом следует отметить, что структура аргументов аналоговых сигналов ±[1,2 n i]f(2n) формата «Дополнительный код RU» позволяет все арифметические преобразования аргументов реализовывать без выполнения сквозных переносов fΣ(+← ←+), что приводит к существенному сокращению технологического цикла ∆t S их выполнения.
Если записать структуру аргументов ±[m j]f(2n) - «Дополнительный код» в виде выражения (13)
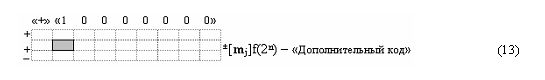
то она может быть отнесена к одному из вариантов структур аргументов троичной системы счисления f(+1,0,-1), которые в аналитической форме могут быть записаны в виде выражения (14)
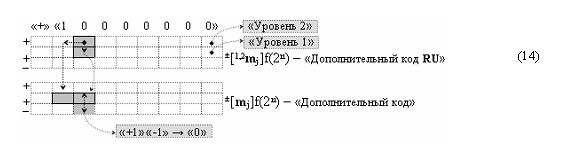
где (1,2) - индекс, соответствующий тому, что каждый условно «j» разряд в структуре аргументов ±[1,2 m j]f(2n) формата «Дополнительный код RU» включает аргумент «Уровня 1» и может включать аргумент «Уровня 2». Для формирования смыслового содержания структуры аргументов ±[1,2 m j]f(2n) - «Дополнительный код RU» приведем несколько примеров структур аргументов «Дополнительный код RU» и логико-динамический процесс перехода к структуре аргументов «Дополнительный код».
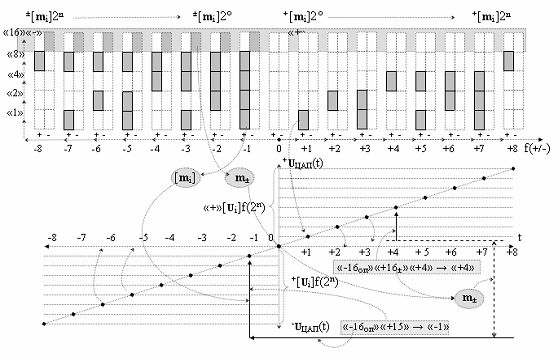
Пример 1. Логико-динамический процесс перехода от структуры положительных аргументов ±[1,2 m j]f(2n) → «0111111(1,21)» - «Дополнительный код RU» к структуре аргументов ±[m j]f(2n) → «10000000» - «Дополнительный код»
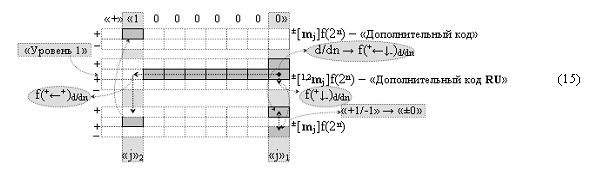
Из анализа графоаналитического выражения (15) следует, что данная конкретная реализация структуры аргументов ±[1,2 m j]f(2n) - «Дополнительный код RU» может быть преобразована в структуру аргументов ±[m j]f(2n) - «Дополнительный код» посредством процедуры логического дифференцирования d/dn «Уровня 1». А в результате такого преобразования структуры аргументов ±[1,2 m j]f(2n) формируется условно отрицательный аргумент локального переноса f(+↓-)d/dn процедуры логического дифференцирования d/dn → f1(+←↓-)d/dn, который в условно «j»1 разряде с положительным аргументом второго уровня формирует активный логический ноль «+1/-1» → «±0», а в в условно «j»2 разряде положительный аргумент локального переноса f(+←+)d/dn формирует результирующий аргумент, соответствующий аргументу в структуре ±[m j]f(2n) - «Дополнительный код». При этом следует отметить, что функциональные структуры процедуры логического дифференцирования d/dn → f(+←↓-)d/dn реализуют с применением арифметической аксиомы «+1» → «+2»«-1» троичной системы счисления f(+1,0,-1), а в ней они минимизированы до трех возможных вариантов прямых и обратных аксиом, которые запишем в виде выражения (16).
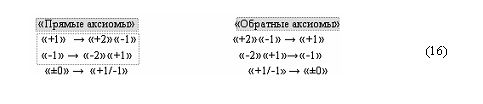
И если выполнить преобразование аргумента в соответствии с арифметической аксиомой «+1» → «+2»«-1», то может быть записано графоаналитическое выражение (17)
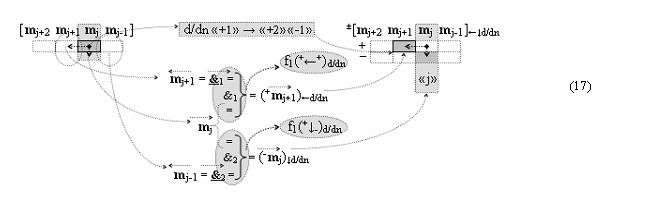
 - логическая функция f1(&)-И; =
&
1
= - логическая функция f1(&)-НЕ;
- логическая функция f1(&)-И; =
&
1
= - логическая функция f1(&)-НЕ;
в котором логические функции f1(&)-И и f2(&)-И реализуют локальную процедуру анализа только двух последовательных аргументов. В результате для условно «j» разряда аналитическое выражение (17) запишем в виде функциональной структуры (18)
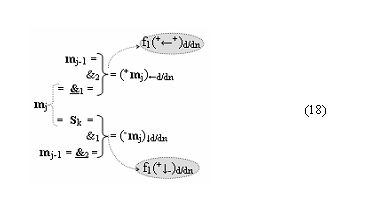
посредством которой и реализуется процедура логического дифференцирования d/dn → f1(+←↓-)d/dn аргументов в соответствии с графоаналитическим выражением (19)
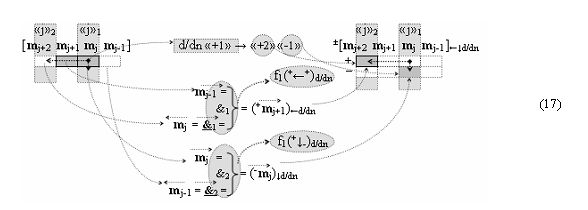
Возвращаясь к анализу структуры аргументов ±[1,2 m j]f(2n) - «Дополнительный код RU», следует отметить, что ее структура аргументов многовариантна конкретного информационного содержания, поскольку если сформировать графоаналитические выражения (18)-(20)
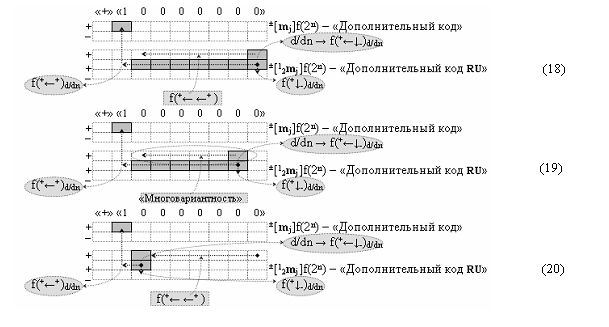
то «Многовариантность» формирует сквозной нереализованный перенос f(+← ←+).
Пример 2. Логико-динамический процесс перехода от структуры положительных аргументов ±[1,2 m j]f(2n) → «01111(1 21)11» - «Дополнительный код RU» к структуре аргументов ±[m j]f(2n) → «10000011» - «Дополнительный код»
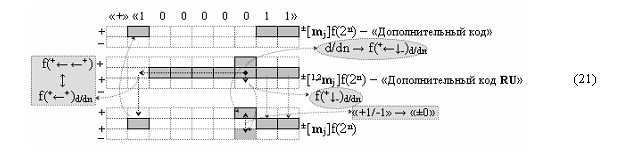
Из анализа графоаналитического выражения (21) следует, что если учесть, что процедура логического дифференцирования d/dn → f(+←↓-)d/dn является арифметически корректной процедурой сквозного переноса f(+← ←+), поскольку f(+←+)d/dn ↔ f(+← ←+), то переход структуры аргументов ±[1,2 m j]f(2n) - «Дополнительный код RU» к структуре аргументов ±[m j]f(2n) - «Дополнительный код» выполняется путем реализации сквозного переноса. А его реализация при формировании результирующей суммы в сумматоре f1(Σ) и умножителе fΣ(Σ) не целесообразна, поскольку быстродействие их при формировании результирующей суммы в «Дополнительном коде» определяется технологическим циклом ∆t S сквозного переноса fΣ(+← ←+). Поэтому все арифметические преобразования целесообразно выполнять с применением неминимизированных структур аргументов ±[1,2 m j]f(2n) - «Дополнительный код RU», которая также является структурой аргументов троичной системы счисления f(+1,0,-1).
Пример 3. Логико-динамический процесс преобразования аргументов слагаемых ±[1,2 m i] → «+»«10000000» и ±[1,2 m j] → «+»«11100000» в сумматоре fCD(Σ) с формированием результирующей суммы ±[1,2 S k] в формате «Дополнительного кода RU»
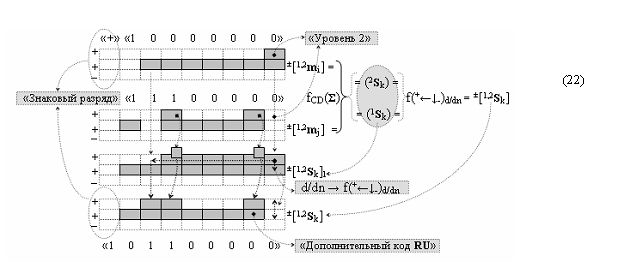
Пример 4. Логико-динамический процесс преобразования аргументов слагаемых ±[1,2 m i] → «+1»«01000000» и ±[1,2 m j] → «+»«11100000» в сумматоре fCD(Σ) с формированием результирующей суммы ±[1,2 S k] в формате «Дополнительного кода RU»
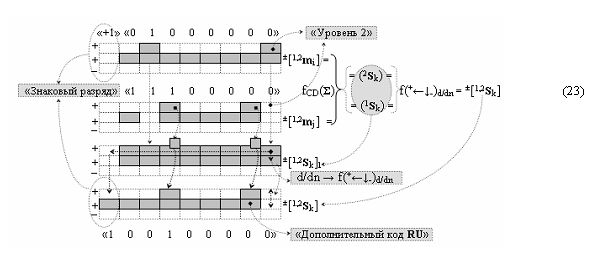
Из анализа графоаналитических выражений (22) и (23) следует, что структура аргументов слагаемых ±[1,2 m i] и ±[1,2 m j] «Уровня 2» может включать любую последовательность активных аргументов и эта последовательность аргументов в результате реализации процедуры логического дифференцирования d/dn → f(+←↓-)d/dn может быть минимизирована до структуры аргументов результирующей суммы ±[1,2 S k] формата «Дополнительный код RU».
Пример 5. Логико-динамический процесс преобразования аргументов слагаемых ±[1,2 m i] → «+1»«01111110» и ±[1,2 m j] → «+1»«00111110» в сумматоре fCD(Σ) с формированием результирующей суммы ±[1,2 S k] в формате «Дополнительного кода RU»
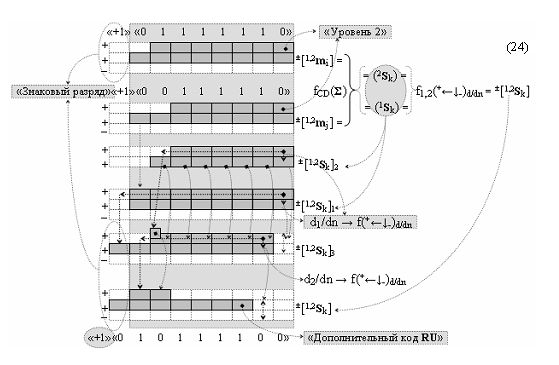
Из анализа графоаналитического выражения (24) следует, что результирующая сумма ±[1,2 S k] сформирована в результате двух последовательных процедур логического дифференцирования d1/dn → f(+←↓-)d/dn и d2/dn → f(+←↓-)d/dn. При этом первая процедура логического дифференцирования d1/dn → f(+←↓-)d/dn выполняется только в «Уровне 2» структур аргументов ±[1,2 S k]1 и ±[1,2 S k]2, которые сформированы в результате объединения аргументов слагаемых ±[1 m i] и ±[1 m j] «Уровня 1» и аргументов слагаемых ±[2 m i] и ±[2 m j] «Уровня 2». А вторая процедура логического дифференцирования d2/dn → f(+←↓-)d/dn выполняется после объединения скорректированных структур аргументов ±[1,2 S k]1 и ±[1,2 S k]2, в результате результирующая сумма ±[1,2 S k] может быть сформирована в формате «Дополнительный код RU». А если учесть, что процедуры логического дифференцирования d1/dn → f(+←↓-)d/dn и d2/dn → f(+←↓-)d/dn, по существу, реализуют сквозной перенос f1,2(+←+)d/dn и он реализуется в результате локального анализа активных аргументов в «Уровне 2», то технологический цикл ∆t S при формировании результирующей суммы ±[1,2 S k] в формате «Дополнительного кода RU» является максимально минимизированной процедурой. При этом следует отметить, что двойная процедура логического дифференцирования d1/dn → f(+←↓-)d/dn и d2/dn → f(+←↓-)d/dn позволяет сформировать функциональную структуру сумматора fCD(Σ) неограниченной разрядностью с минимальным технологическим циклом ∆t S.
Поскольку любая результирующая структура аргументов может быть использована в системах управления, где информационное содержание позиционно-знаковых структур аргументов аналоговых сигналов ±[1,2 m i]f(2n) формата «Дополнительный код RU» преобразуют в аналоговый сигнал управления ± U kf(±[1,2 m i]) с тем же информационным содержанием, поэтому сформируем графоаналитическое выражение (25)
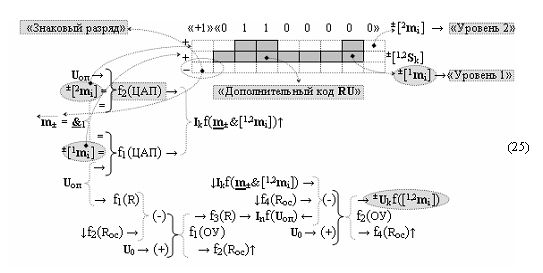
в котором функциональная структура f1(ЦАП) осуществляет преобразование позиционно-знаковой структуры аргументов ±[1 m i] «Уровня 1», а введенная функциональная дополнительная структура f2(ЦАП) осуществляет преобразование позиционно-знаковой структуры аргументов ±[2 m i] «Уровня 2» в энергетический аргумент тока I kf( m ±&[1,2 m i])↑, который поступает на инвертирующую функциональную связь (-) функциональной структуры операционного усилителя f2(ОУ), в котором активизируется аналоговый сигнал управления ± U kf(±[1,2 m i]) с информационным содержанием позиционно-знаковой структуры аргументов аналоговых сигналов ±[1,2 m i]f(2n) формата «Дополнительный код RU».
Использование предложенного технического решения позволяет реализовать процедуру преобразования структуры аргументов аналоговых сигналов ±[1,2 m i]f(2n) формата «Дополнительный код RU» в аналоговый сигнал управления ± U kf(±[1,2 m i]).
Изобретение относится к вычислительной технике и может быть использовано в системах контроля и управления в совокупности с арифметическими устройствами, которые реализуют арифметические процедуры над аргументами, имеющими позиционно-знаковую структуру аргументов аналоговых сигналов. Техническим результатом является реализация преобразования структуры аргументов аналоговых сигналов в аналоговый сигнал управления. Функциональная структура реализована на операционных усилителях и цифроаналоговых преобразователях.
Функциональная структура цифроаналогового преобразования позиционно-знаковых структур аргументов аналоговых сигналов ±[1,2
m
i]f(2n) формата
«Дополнительный код RU» в аналоговый сигнал управления ±
U
kf(±[1,2
m
i]), включающая функциональную структуру цифроаналогового преобразователя f1(ЦАП)
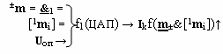
где ±
m
- аргумент знакового разряда; [1
m
i] - входная информационная структура аргументов «Дополнительного кода RU» «Уровня 1»;
&
1 - логическая функция f1(
&
)-НЕ; I
kf(m
±&[1
m
i])↑ - результирующий аргумент тока;
функциональную структуру операционного усилителя f1(ОУ)
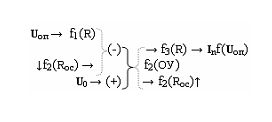
где f1(Rос) - резисторная функция обратной связи; U
0 - аргумент условно нулевого напряжения; U
оп - аргумент опорного напряжения, f1(Rос) - функциональная структура резисторной функции обратной связи; f2(R) - функциональная структура резисторной функции выходной функциональной связи; и
функциональную структуру операционного усилителя f2(ОУ)
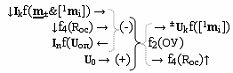
где f2(Rос) - функциональная структура резисторной функции обратной связи;
при этом функциональные связи выполнены в соответствии с математической моделью вида
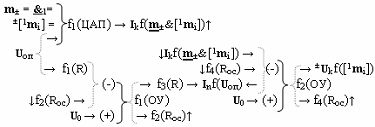
отличающаяся тем, что введена функциональная дополнительная структура f2(ЦАП)
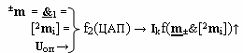
где [2
m
i] - входная информационная структура аргументов «Дополнительного кода RU» «Уровня 2»,
а функциональные связи выполнены в соответствии с математической моделью вида

| ТИТЦЕ У., ШЕНК К | |||
| Полупроводниковая схемотехника | |||
| - М.: Мир, 1982, с.451, рис.24.14 | |||
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПРЕОБРАЗОВАТЕЛЯ ПОЗИЦИОННО-ЗНАКОВЫХ СТРУКТУР АРГУМЕНТОВ АНАЛОГОВЫХ СИГНАЛОВ «±»[n]f(-1\+1,0,…+1) "ДОПОЛНИТЕЛЬНЫЙ КОД" В ПОЗИЦИОННУЮ СТРУКТУРУ УСЛОВНО ОТРИЦАТЕЛЬНЫХ АРГУМЕНТОВ АНАЛОГОВЫХ СИГНАЛОВ «-»[n]f(2) С ПРИМЕНЕНИЕМ АРИФМЕТИЧЕСКИХ АКСИОМ ТРОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+1,0,-1) (ВАРИАНТЫ) | 2010 |
|
RU2443052C1 |
| JP 4081129 А, 13.03.1992 | |||
| JP 57116419 А, 20.07.1982. | |||
Авторы
Даты
2013-04-27—Публикация
2012-02-28—Подача