Настоящее изобретение относится к области спутниковой навигации и геодезии.
Глобальные навигационные спутниковые системы (ГНСС) позволяют определять координаты (x, y, z) объекта (фазового центра расположенной на объекте антенны навигационного приемника) по измеренным значениям псевдодальностей до спутников и их эфемеридам (пространственным координатам спутников, заданным на строго определенные моменты времени).
Геометрическое расстояние между объектом и j-ым спутником равно:
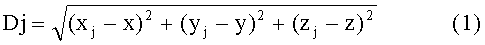
где {х, y, z} - искомые координаты объекта в момент приема сигнала,
{xj, yj, zj] - координаты j-го спутника в момент излучения сигнала.
Приемник на объекте измеряет время прохождения сигнала с момента его излучения до момента приема, которое, умноженное на скорость света c, равняется так называемой «псевдодальности» ρj. Ввиду того, что сигнал распространяется в атмосфере, а не в вакууме, то измеряемое время включает в себя атмосферные задержки, погрешности, связанные с переотражением сигнала, и др. Кроме того, метка времени, транслируемая спутником в излучаемом сигнале, оказывается смещенной относительно системного времени ГНСС из-за нестабильности частоты бортового генератора. Еще большее отличие псевдодальности ρj от величины Dj связано с уходом часов навигационного приемника относительно системного времени орбитальной группировки.
Обозначим момент излучения (emission) сигнала j-тым спутником 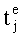
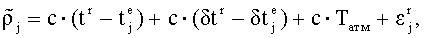
или с учетом (1),
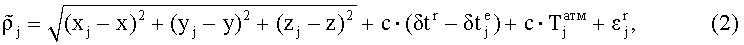
где δtr - отклонение временной шкалы приемника от шкалы системного времени ГНСС в момент приема сигнала приемником,
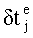
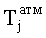
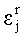
Используя эфемеридную информацию и соответствующие математические модели, можно частично скомпенсировать и учесть в выражении (2) отклонение 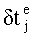
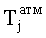
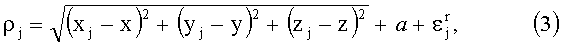
где 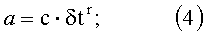
a - временной параметр, характеризующий расхождение временной шкалы приемника и системной шкалы времени спутниковой группировки.
Выражение (3) называется навигационным уравнением. В нем имеется четыре неизвестных (x, y, z, δtr).
При этом погрешность 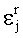
Таким образом, для определения местоположения объекта необходимо, как минимум, четыре уравнения, т.е. четыре одновременно видимых спутника. Для повышения надежности и точности определения координат объекта современные навигационные приемники делаются двух системными, т.е. одновременно принимающими сигналы двух (ГЛОНАСС и GPS) орбитальных группировок.
Обычно данную систему линеаризуют, раскладывая в ряд Тейлора, в окрестности первого приближения (x0, y0, z0, 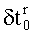
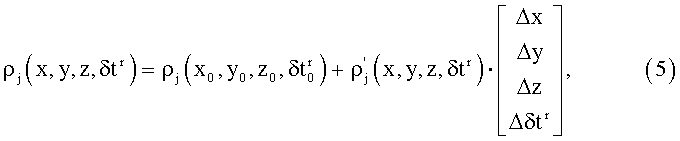
где 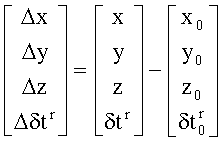
Известны различные аналитические (безитерационные) способы вычисления координат объекта при использовании 4 спутников: способы, предложенные Краузе [1] в 1987 г, Клеусбергом [2] в 1994 г., Графаредом и Шаном [3] в 1996 г. Недостатками данных способов является невозможность использования в них избыточного количества спутников.
Наиболее близким к заявленному способу является способ, предложенный в 1985 г Банкрофтом [4]. Он предназначен для решения избыточной системы навигационных уравнений в случае одной орбитальной группировки, но не применим при одновременном использовании сигналов от двух группировок. Это связано с тем, что уход часов приемника от системного времени орбитальных группировок ГЛОНАСС и GPS различен. Кроме того, в навигационных приемниках пользователя обычно частоты гетеродинов в каналах ГЛОНАСС и GPS имеют независимые уходы частоты. Поэтому неизвестными становятся пять величин: координаты объекта x, y, z и времена δt1 и δt2 ухода часов приемника (или a 1, a 2 определяемых по формуле 4) в каналах ГЛОНАСС и GPS.
Актуальной является задача определения местонахождения объекта, когда часть навигационных спутников принадлежит орбитальной группировке ГЛОНАСС, а другая - GPS (например, имеется три спутника ГЛОНАСС и два GPS).
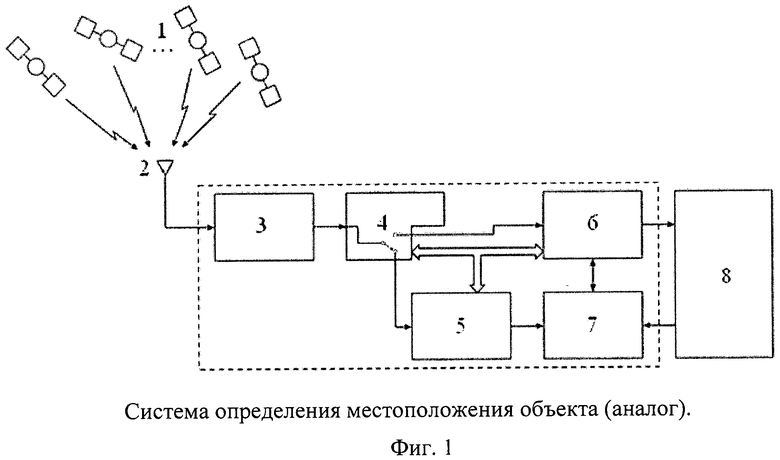
Типовая реализация системы определения местоположения объекта, наиболее распространенная в настоящее время, описана в патенте US 4672382 «Система определения местоположения» от 04.12.1985, выбранная в качестве аналога. Блок-схема системы приведена на фиг.1, где:
1. Орбитальная группировка навигационных спутников;
2. Приемная антенна навигационных сигналов;
3. Блок формирования измерений;
4. Блок условия;
5. Блок грубой начальной оценки;
6. Блок итерационных вычислений координат;
7. Блок оценки хранения координат в памяти;
8. Блок управления маршрутом.
В блоке формирования измерений происходят измерение (оценка) псевдодальностей и выделение эфемерид всех спутников. В блоке итерационного вычисления координат производится селекция навигационных спутников, присвоение весов каждой из оценок псевдодальности, расчет координат спутников на момент измерения псевдодальностей, далее методом последовательных приближений решается линеаризованная система навигационных уравнений (5) с последующим сглаживанием и выдачей рассчитанных координат на средство, использующее эту информацию, например, в блок управления маршрутом.
Система навигационных уравнений (3), связывающая координаты объекта x, y, z и величину δt с текущими значениями координат спутников, является нелинейной. Она решается итерационным методом с помощью линеаризации уравнений в окрестности априорно известных координат объекта. Если количество спутников более четырех, число уравнений в системе становится избыточным. Применением метода наименьших квадратов оно сводится к четырем. Как правило, критерием сходимости итерационного алгоритма решения навигационных уравнений является минимизация некоего функционала.
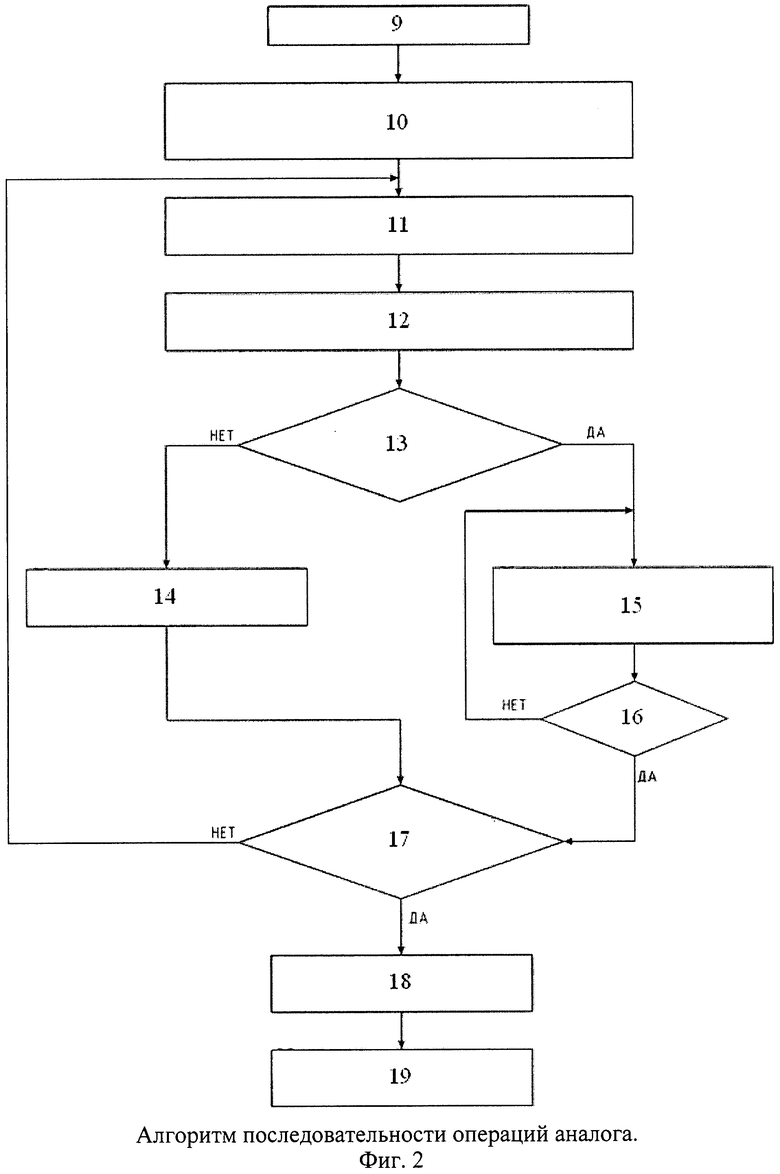
Последовательность операций для аналога (фиг.1) показана на фиг.2, где:
9. Прием навигационного сигнала;
10. Первичная цифровая обработка навигационных сигналов (с выделением эфемерид и служебной информации) и формирование псевдодальностей;
11. Присвоение весов псевдодальностям, селекция спутников, коррекция псевдодальностей;
12. Прогноз координат спутников по актуальным эфемеридам на моменты времени излучения сигналов;
13. Условия существования первого приближения x, y, z, δtr;
14. Вычисление первого приближения x, y, z, δtr;
15. Решение линеаризованной системы навигационных уравнений, итерация вычисления очередных x, y, z, δtr;
16. Условие выполнимости Δδtr<ε, где ε - допустимая величина невязки по времени между шкалой приемника и системного времени ГНСС;
17. Норма невязки исходной системы должна быть меньше заданной величины;
18. Сглаживание результатов фильтром Калмана;
19. Запись вычислений и вывод x, y, z, δtr для пользователя.
Недостатками итерационных способов решения системы навигационных уравнений являются:
- необходимость задания начального приближения;
- вероятность несходимости вычислений для заданной точности;
- время расчета (объем вычислений) зависит не только от количества спутников, но и от условий наблюдения.
Задача, на решение которой направлено заявляемое изобретение, заключается в создании способа и системы определения местоположения объекта при использовании двух орбитальных группировок навигационных спутников с аналитической оценкой навигационных параметров.
Техническим результатом, заявляемого изобретения является безитерационное получение оптимального результата определения местонахождения объекта по методу наименьших квадратов (МНК) для избыточного количества спутников двух орбитальных группировок за фиксированное время.
Технический результат достигается тем, что способ определения местоположения объекта при использовании глобальных навигационных спутниковых систем заключающийся в том, что:
- принимают сигналы от первой GPS и второй ГЛОНАСС орбитальных группировок навигационных спутников;
- производят первичную цифровую обработку навигационных сигналов с выделением эфемерид и псевдодальностей;
- рассчитывают скорректированные псевдодальности;
- прогнозируют координаты спутников по актуальным эфемеридам на моменты времени излучения навигационных сигналов;
- определяют координаты x, y, z, временной параметр a 1, соответствующий расхождению часов навигационного приемника от системного времени первой орбитальной группировки и временной параметр a 2, соответствующий расхождению часов навигационного приемника от системного времени второй орбитальной группировки методом наименьших квадратов, используя информацию от всех спутников с одинаковым весом первой и второй орбитальных группировок, путем аналитического решения системы нелинейных уравнений с минимизацией невязок;
- проверяют выполнимость условия a 1<ε, где ε - допустимая величина невязки по времени между шкалой навигационного приемника и системного времени глобальной навигационной спутниковой системы (ГНСС);
- подводят часы навигационного приемника до системного времени ГНСС;
- сглаживают результаты определения фильтром Калмана;
- записывают результаты определения x, y, z, a 1, a 2 и выводят их для пользователя.
Система определения местоположения объекта при использовании глобальных навигационных спутниковых систем включающая:
- первую орбитальную группировку навигационных спутников GPS;
- вторую орбитальную группировку ГЛОНАСС;
- приемную антенну навигационных спутниковых сигналов от первой орбитальную группировки навигационных спутников GPS и второй орбитальной группировки ГЛОНАСС;
- блок формирования измерений;
- блок вычислений координат и временных параметров;
- блок записи и вывода результатов вычислений на пользователя;
причем выход приемной антенны навигационных спутниковых сигналов соединен с входом блока формирования измерений, вход блока вычислений координат и временных параметров соединен с выходом блока формирования измерений, вход блока вывода результатов вычислений соединен с выходом блока вычислений координат и временных параметров, выход блока записи и передачи результатов вычислений является выходом системы.
Блок вычислений координат и временных параметров содержит арифметико-логическое устройство с возможностью операций сложения, умножения и вычитания, первый вход которого соединен с выходом блока формирования измерений, блок расчета комплексно-сопряженной матрицы, вход которого соединен с выходом блока формирования измерений, блок расчета скалярных построчных произведений вектора с матрицей и матрицы с матрицей, вход которого соединен с выходом блока формирования измерений, второй и третий входы арифметико-логического устройства соединены с выходами комплексно-сопряженной матрицы и блока расчета скалярных построчных произведений вектора с матрицей и матрицы с матрицей соответственно, блок расчета корней полинома, вход которого соединен с выходом арифметико-логического устройства с возможностью операций сложения, умножения и вычитания, блок вычисления вектора состояний {x, y, z, a 1, a 2}, вход которого соединен с выходом блока расчета корней полинома, выход блока вычисления вектора состояний {x, y, z, a 1, a 2} является выходом блока вычислений координат и временных параметров.
Обобщенная блок-схема заявляемой системы определения местоположения объекта при использовании глобальных навигационных спутниковых систем приведена на фиг.3., где:
20. Первая орбитальная группировка навигационных спутников GPS;
21. Вторая орбитальная группировка навигационных спутников ГЛОНАСС;
22. Приемная антенна навигационных сигналов;
23. Блок формирования измерений;
24. Блок вычислений координат и временных параметров;
25. Блок записи и вывода результатов вычислений на пользователя.
Блок-схема последовательности определения координат для заявленной системы, работающей по двум ГНСС, показана на фиг.4., где:
26. Прием навигационного сигнала;
27. Первичная цифровая обработка навигационных сигналов (с выделением эфемерид и служебной информации) и формирование псевдодальностей. Выполнение коррекции псевдодальностей;
28. Прогноз координат спутников по актуальным эфемеридам на моменты времени излучения сигналов;
29. Определение x, y, z, a 1, a 2 путем аналитического решения системы нелинейных уравнений с минимизацией невязок;
30. Условие выполнимости a 1<ε, где ε - допустимая величина невязки по времени между шкалой приемника и системного времени ГНСС;
31. Подвод часов приемника до системного времени ГНСС;
32. Сглаживание результатов фильтром Калмана;
33. Завершение вычисления и вывод x, y, z, a 1, a 2.
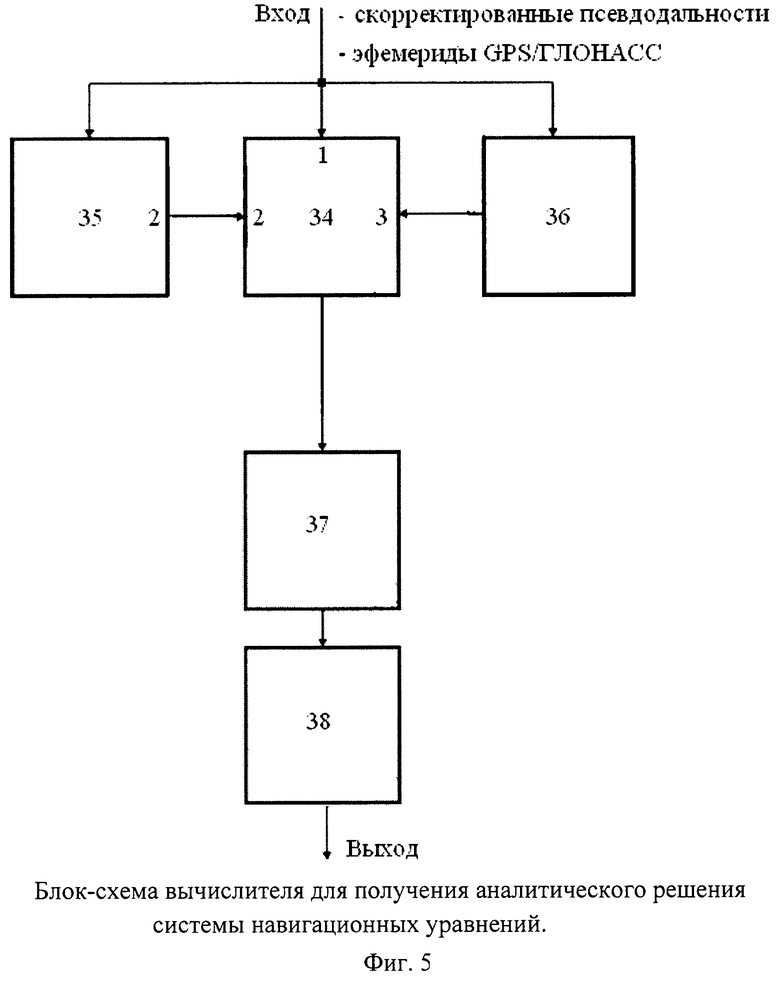
На фигуре 5 представлена блок-схема блока вычислений координат и временных параметров для получения аналитического решения системы навигационных уравнений, где:
34. Арифметико-логическое устройство (сложение, умножение, вычитание);
35. Блок расчета комплексно-сопряженной матрицы;
36. Блок расчета скалярного произведения для пар векторов, вектор-матрица (построчно), матрица-матрица (построчно);
37. Блок расчета корней полинома;
38. Блок вычисления вектора состояний {x, y, z, a 1, a 2}.
В соответствии с предлагаемой последовательностью (фиг.4), на первых двух шагах происходит прием навигационной спутниковой антенной 22 и первичная цифровая обработка навигационных сигналов (с выделением эфемерид и служебной информации) и формирование псевдодальностей блоком формирования измерений 23. В блоке 23 так же проводится коррекция измеренной псевдодальности ρj на величину атмосферной задержки по общепринятым моделям, учет ухода часов спутников о системного времени. Окончательным этапом обработки данных в блоке 23 является прогноз координат спутников по актуальным эфемеридам на моменты времени излучения сигналов.
На следующем шаге выполняется определение {x, y, z, a 1, a 2} путем аналитического решения в блоке вычислений координат и временных параметров 24.
Для минимизации количества вычислений в приемнике его временную шкалу необходимо привязать к системному времени одной из ГНСС. На фиг.4 показан пример с привязкой к шкале времени первой ГНСС. После вычисления решения системы навигационных уравнений, если уход времени приемника больше допустимого, необходимо подвести часы приемника к шкале выбранной ГНСС и пересчитать однократно решение с учетом скорректированного положения спутников.
На последних этапах обработки при необходимости происходит сглаживание информации фильтром Калмана и вывод полученных значений {x, y, z, a 1, a 2}в блок записи и передачи результатов вычислений, выполненного с возможностью записи данных и передачи их пользователю.
Ниже описан алгоритм обработки данных в вычислителе.
Для понимания последовательности обработки данных необходимо составить систему навигационных уравнений определенного вида, с учетом пяти неизвестных.
Для орбитальной группировки под номером 21 (фиг.3.) (ГЛОНАСС), уравнение для j-го спутника в соответствии с (3) имеет вид:
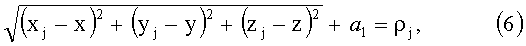
где [x, y, z] - искомые координаты приемника,
[xj, yj, zj) - координаты j-го спутника,
ρj - скорректированная псевдодальность до j-го спутника,
a 1 - временной параметр, характеризующий расхождение временной шкалы приемника от системного времени первой орбитальной группировки, умноженное на скорость света.
Для орбитальной группировки под номером 20 (фиг.2) (GPS), уравнение для g-го спутника в соответствии с (6) имеет вид:
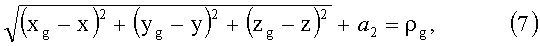
где {xg, yg, zg}- координаты g-го спутника,
ρj - скорректированная псевдодальность до g-го спутника,
a 2 - временной параметр, характеризующий расхождение временной шкалы приемника от системного времени второй орбитальной группировки, умноженное на скорость света.
После переноса временного параметра в правую часть уравнений (6), (7) и возведения в квадрат получим:
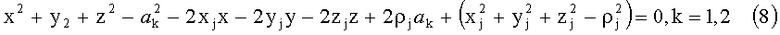
Далее необходимо учесть, что из каждой ОГ может наблюдаться разное кол-во спутников, пусть в ОГ ГЛОНАСС наблюдается количество спутников =n1, а в GPS - n2, общее кол-во спутников n=n1+n2. Отклонение шкалы приемника от ГЛОНАСС и GPS будут a 1 и а 2 соответственно. В результате получим систему из n уравнений вида (8).
Для решения данной системы необходимо перейти в пятимерное линейное пространство векторов L(R), такое, что для двух векторов 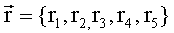
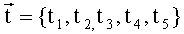
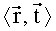
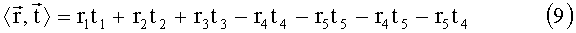
Определим следующий искомый 5-мерный вектор:
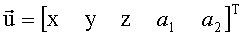
Решение системы уравнений вида (8).
Определим следующие 5-мерные векторы:
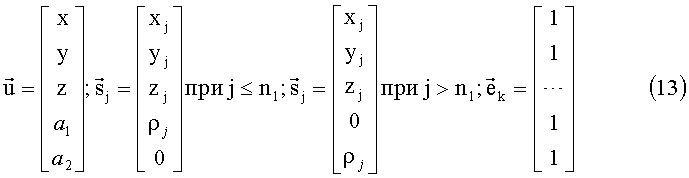
Где индекс k обозначает размерность единичного вектора 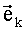
Тогда система будет решаться относительно искомого вектора 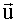
Для выбранных векторов, в соответствии с (8) имеем:
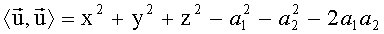
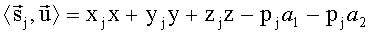 при любом j
при любом j
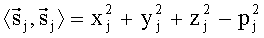
В этом случае систему навигационных уравнений для ГЛОНАСС и GPS можно записать в следующем виде:
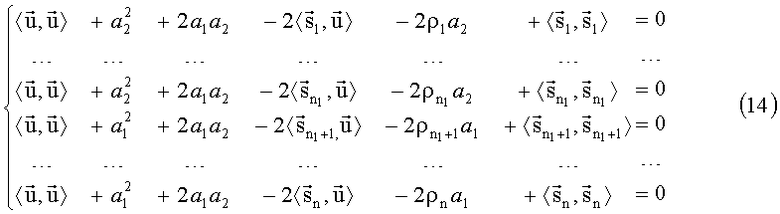
Систему уравнений (14) можно переписать в матричном виде. Для этого необходимо перейти к операциям линейной алгебры, заменив скалярное произведение и арифметические операции с векторами в каждом отдельном уравнении системы на матрично-векторные операции.
Введем обозначения:
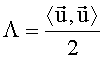
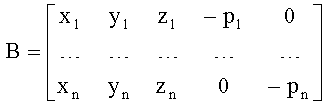
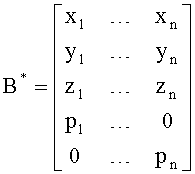
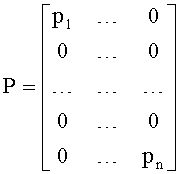
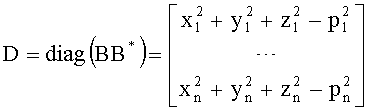
Λ - скалярная величина,
B и B* - матрица системы и комплексно сопряженная ей матрица,
D - вектор, составленный из значащих элементов диагональной матрицы, с элементами главной диагонали произведения BB*.
P - диагональная матрица, с элементами pj на главной диагонали.
Введем также обозначение составного вектора, следующего вида:
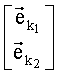
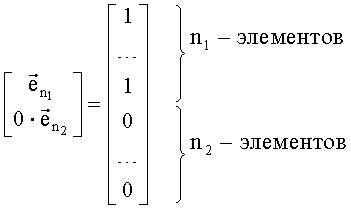
Используя введенные обозначения, получим следующий вид системы навигационных уравнений (14):
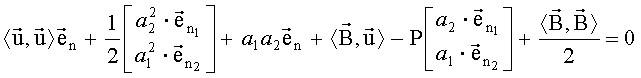 ,
,
после выражения обобщенного произведения Лоренца матричными операциями получим:
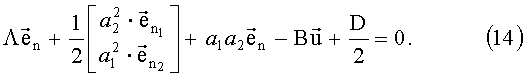
Данная система уравнений решается однозначно относительно неизвестного вектора 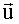
Решение системы будет иметь следующий вид:
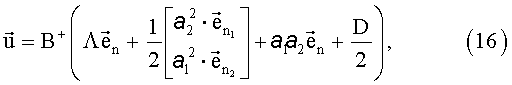
где B+=(BTB)-1BT
a
1; a
2 - параметры при поиске решения, а Λ найдем исходя из его определения 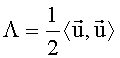
Произведение В+ на любое слагаемое в скобках дает вектор размерности 5. Таким образом (16) является системой из пяти уравнений с шестью неизвестными 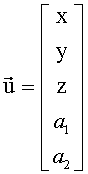
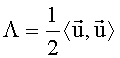
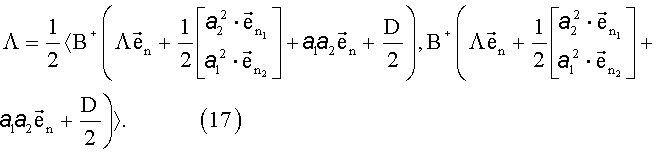
Используя свойство линейности выбранного скалярного произведения векторов, в результате преобразований получим:
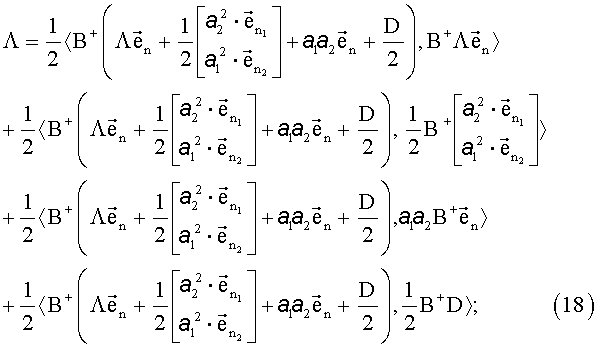
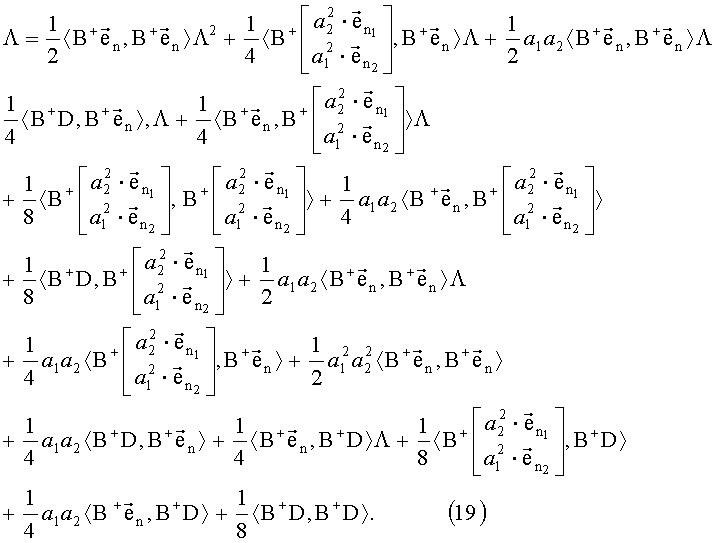
Путем алгебраических преобразований получим выражение вида:
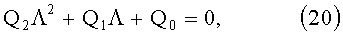
где Q2, Q1, Q0 имеют следующий вид:
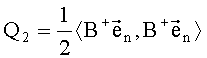
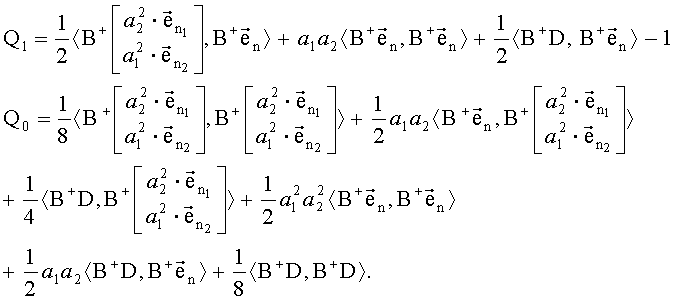
Решения квадратного уравнения с параметрами (20) имеют следующий вид:
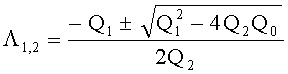
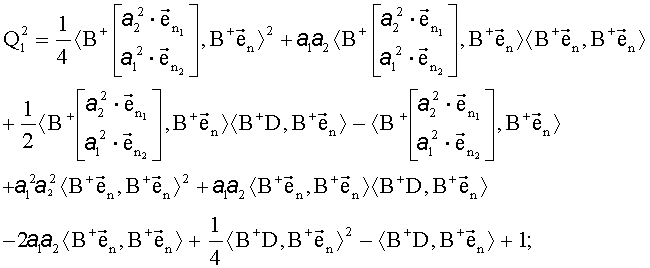
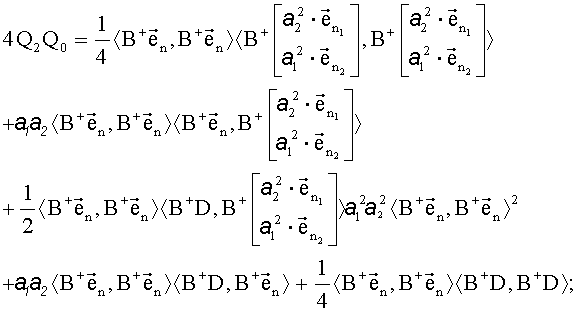
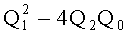
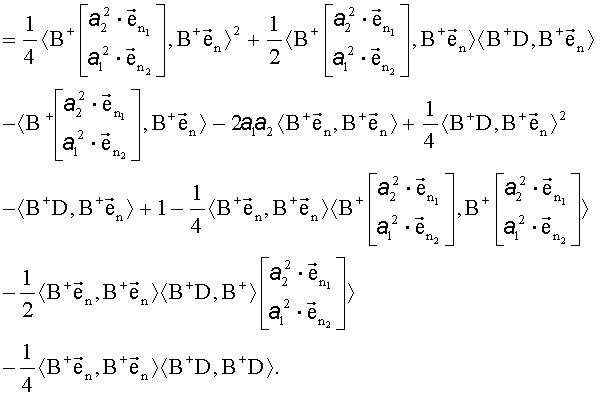
Полученные результаты подставляются в (16):
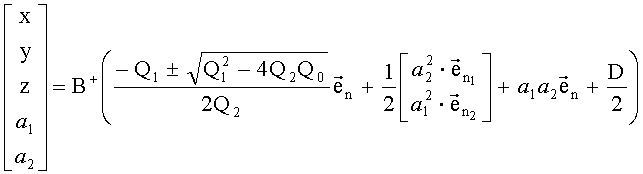 .
.
Вообще говоря, необходимо решать только последние два уравнения, так как первые три (x, y, z) уже выражены через параметры (a 1, a 2).
Последних двух уравнений необходимо подставить в буквенном выражении Q0, Q1, Q2, перенести иррациональность в левую часть, а параметры в правую и возвести обе части в квадрат. После всех преобразований должна получиться подсистема с двумя неизвестными и двумя уравнениями, решив которую значения параметров можно будет поставить в первые три уравнения.
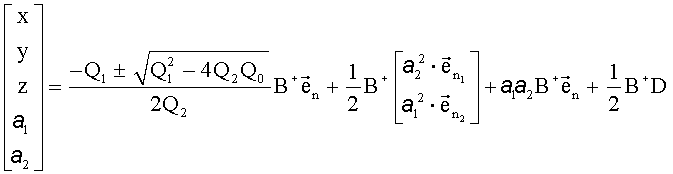
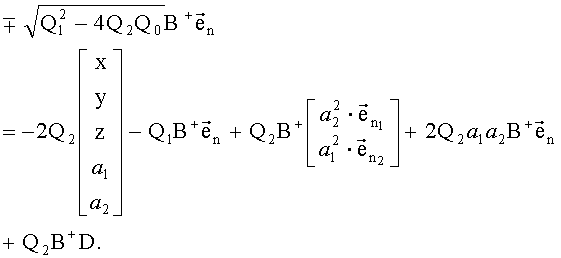
При общем количестве спутников n размерность матрицы В+ будет 5×n. Для выполнения дальнейших выкладок введем следующее обозначение:
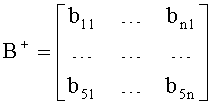
Последние два последних уравнения системы (16) в этом случае имеют вид:
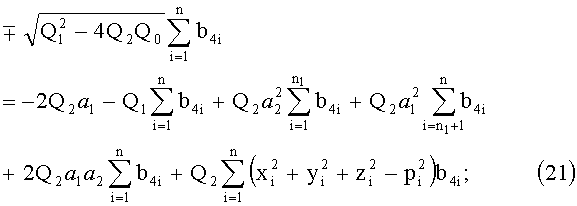
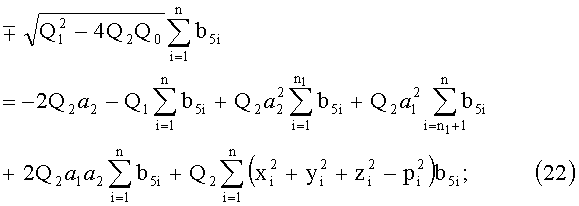
Обозначим 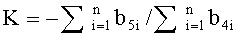
После подстановки получим уравнение:
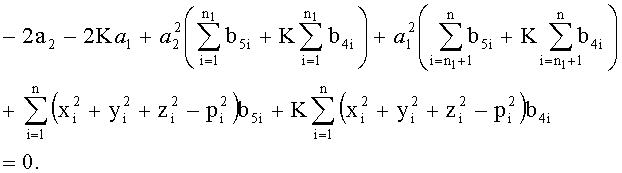
Получаем квадратное уравнение, из которого найдем a 1 как функцию от а 2. Введем следующие обозначения
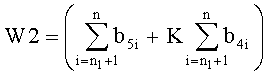
W1=-2K
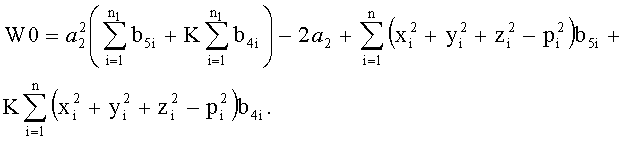
Решение имеет следующий вид:
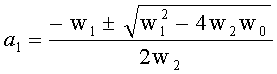
Найденное значение подставляем в выражение (22):
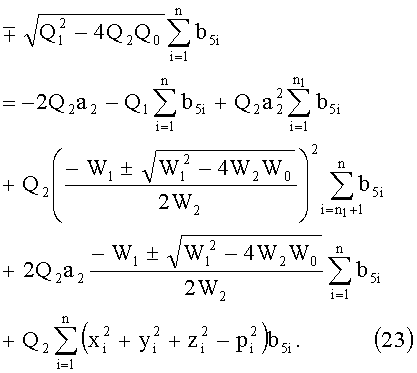
Подставляя в (23) в символьном виде значения Q2 и 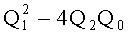
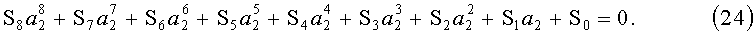
Коэффициенты полинома (24) не содержат неизвестных и вычисляются с использованием входных данных. В общем виде коэффициенты вычисляемы, но ввиду их громоздкости не приводятся. Используя среды мат. моделирования MATLAB/Maple коэффициенты последнего уравнения можно получить в символьном виде с целью дальнейшей реализации алгоритма на языках низкого уровня (C/C++).
Для нахождения корней полинома восьмой степени целесообразно использовать метод сопровождающей матрицы(companion matrix) [5].
Далее, используя полученные действительные значения а 2 вычислить a 1. А используя полученные параметры, получить решение x, y, z.
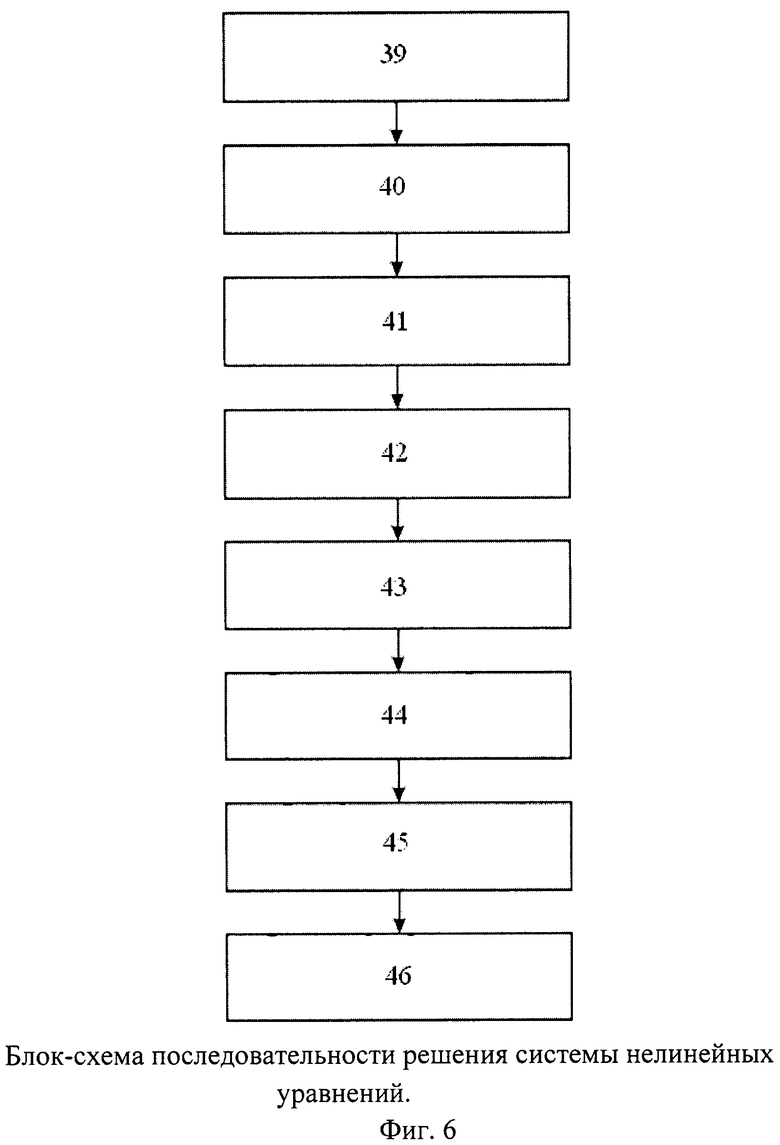
Таким образом, блок-схему последовательности решения системы нелинейных уравнений для двух орбитальных группировок с учетом избыточности можно представить в виде, показанном на фиг.6., где:
39. Формирование матрицы B и B+ для двух ОГ;
40. Расчет вспомогательных коэффициентов;
41. Расчет коэффициентов восьмого порядка;
42. Решение уравнения методом сопровождающей матрицы, отсев корней а 2 высокого порядка;
43. Вычисление времени a 1, а так же Q0, Q1, Q2;
44. Вычисление координат приемника x, y, z зная a 1, а 2, Q0, Q1, Q2;
45. Отсев лишних групп решений {x, y, z, a 1, а 2}исходя из физического смысла;
46. Оперативный контроль качества решения по невязкам исходной системы.
Блок вычисления координат и временных параметров, показанный на фиг.4 может иметь две различные реализации:
- частичная аппаратная реализация, где используется блок с оптимизированными векторными вычислениями (например, графический процессор) и стандартное арифметико-логическое устройство;
- полностью программная модель устройства.
Для анализа качества работы предлагаемого способа, в части определения навигационных параметров, имеет смысл сравнивать его с методом Банкрофта, так как классический итерационный подход в случае одной группировки даст при хорошем начальном приближении и определенном количестве итерации аналогичный результат.
Рассмотрим качество работы описанного выше способа и сравним с методом Банкрофта в двух случаях:
1) кол-во спутников равно количеству неизвестных (пять);
2) избыточное созвездие.
В качестве предварительного этапа подготовки исходных данных необходимо привести координатные сетки и временные шкалы в одно координатно-временное пространство, выбрав, к примеру, за основу шкалу времени GPS и координаты WGS-84. Рассчитать на текущий момент времени (момент измерения псевдодальностей) координаты спутников GPS и ГЛОНАСС в WGS-84. Большой проблемой в данном случае является матрица перехода из ПЗ-90 в WGS-84, так как нет единого стандарта. Но для метода решения системы нелинейных уравнений данная особенность значения не имеет. Так как с математической точки зрения система решается и решение должно обращать исходную систему в тождество при пяти спутниках и иметь минимум ошибки по МНК в случае избыточности. Далее необходимо составить матрицу В по спутникам GPS и ГЛОНАСС и отдельно по каждой группировке. Возьмем «тяжелый» случай, смешанную систему, в которой имеется всего 3 спутника GPS и 2 спутника ГЛОНАСС. Классический метод Банкрофта в этом случае не сможет дать результат отдельно по каждой из группировок, поэтому будут получены решения на созвездии из 4 спутников GPS (включающем указанные 3) и на созвездии из 4 спутников ГЛОНАСС (включающем указанные 2), далее составлено решение с осредненными координатами x, y, z по системам GPS и ГЛОНАСС, а так же добавлены временные поправки a 1 по системе GPS и a 2 по системе ГЛОНАСС. Невязки при подстановке указанного вектора-решения будут сравниваться с невязками, полученными по обобщенному методу для двух орбитальных группировок.
Исходные матрицы для решения классическим методом Банкрофта имеют следующий вид (x, y, z и скорректированная псевдодальность до спутника):

Строки матрицы BGPS соответствуют системным номерам спутников GPS 20, 23, 30 и 31 соответственно.

Строки матрицы BGL0NASS соответствуют системным номерам спутников ГЛОНАСС 3, 13, 15 и 20 соответственно.
Полученные решения (см. табл.1, все единицы в метрах)
Таким образом, можно взять за основу решение, полученное методом Банкрофта вида:

Вектор решения по обобщенному методу для двух ОГ, имеющих в составе 3 GPS(23, 30, 31)+2 ГЛОНАСС (15, 20):

Видно, что решения близкие, а в a 1, а 2 во втором случае вошли ошибки преобразования координат, вектора невязок и их нормы для смешанной исходной системы имеют следующие величины (см. табл.2):
Очевидно, что в случае метода Банкрофта невязки, близкие к нулю, получаются только на первых трех уравнениях (GPS), так как координаты и время соответствуют решению только по GPS, а от решения ГЛОНАСС взята только временная поправка.
В случае с обобщенным методом получены близкие к нулю невязки, но не нулевые, так как это обусловлено точностью разрядной сетки. Норма вектора невязки для типовых случаев расположения спутников, как правило, не превышает 10-6 м, при вычислениях с плавающей запятой двойной точности. Данная точность является достаточной для высокоточных приложений. Однако, исходя из значений поправок характеризующих время в векторе решения, следует серьезно проработать значения матриц перехода в единое координатно-временное пространство, так как это будет источником ошибок, уводящим временные поправки от истинных значений.
В случае избыточности ситуация с методом Банкрофта еще сложнее:
Полученные решения (см. табл.3, все единицы в метрах)
Таким образом, можно взять за основу решение, полученное методом Банкрофта вида:

Вектор решения по обобщенному методу для двух ОГ, имеющих в составе избыточную группировку GPS/ГЛОНАСС:
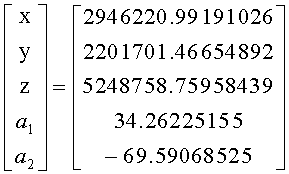
Нормы векторов невязок для смешанной исходной системы имеют следующие величины (см. табл.4):
Как видно, обобщенный метод эффективно работает и может быть рекомендован для вычисления координат точек с минимизацией вектора ошибки по МНК сразу по всей смешанной орбитальной группировке ГЛОНАСС/GPS, чего нельзя добиться используя классический метод Банкрофта.
Список используемой литературы
1. Krause, L.O. (1987): A Direct Solution to GPS-Type Navigation Equations. IEEE Transactions on Aerospace and Electronic Systems, Vol. AES-23, No. 2, pp.225-232
2. Kleusberg, A. (1994): Die direkte Lösung des räumlichen Hyperbelschnitts. Zeitschrift fur Vermessungswesen, Vol. 119, No. 4, pp.188-192
3. Grafarend, E.W. and Chan, J. (1996): A Closed-form Solution of the Nonlinear Pseudo-Ranging Equations (GPS), ARTIFICIAL SATELLITES Planetary Geodesy, No. 28, pp.133-147
4. Bancroft, S. (1985): An Algebraic Solution of the GPS Equations. IEEE Transactions on Aerospace and Electronic Systems, Vol. AES-21, No. 6, pp.56-59
5. Метод сопровождающей матрицы: http://en.wikipedia.org/wiki/Companion_matrix
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ВЗАИМНОГО ПОЛОЖЕНИЯ ОБЪЕКТОВ ПО СИГНАЛАМ ГЛОБАЛЬНЫХ НАВИГАЦИОННЫХ СПУТНИКОВЫХ СИСТЕМ | 2015 |
|
RU2592077C1 |
| Способ определения взаимного положения объектов по сигналам глобальных навигационных спутниковых систем | 2016 |
|
RU2624268C1 |
| СПОСОБ И СИСТЕМА ДЛЯ ОПРЕДЕЛЕНИЯ КОРРЕКЦИЙ ЧАСОВ | 2012 |
|
RU2574333C2 |
| УСТРОЙСТВО ОПРЕДЕЛЕНИЯ ВЫСОКОТОЧНОГО ОТНОСИТЕЛЬНОГО МЕСТОПОЛОЖЕНИЯ ДВИЖУЩЕГОСЯ ОБЪЕКТА ПО СИГНАЛАМ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 1998 |
|
RU2143123C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СКОРОСТИ РАСПРОСТРАНЕНИЯ И НАПРАВЛЕНИЯ ПРИХОДА ИОНОСФЕРНОГО ВОЗМУЩЕНИЯ | 2013 |
|
RU2560094C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ОБЪЕКТОВ-ПОТРЕБИТЕЛЕЙ НАВИГАЦИОННОЙ ИНФОРМАЦИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2009 |
|
RU2402786C1 |
| СПУТНИКОВАЯ РАДИОНАВИГАЦИОННАЯ СИСТЕМА ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ОБЪЕКТА | 1999 |
|
RU2152050C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВОГО ПОЛОЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА ПО ДАННЫМ ПРИЕМНИКОВ СПУТНИКОВОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2008 |
|
RU2388008C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ НАВИГАЦИОННЫХ СПУТНИКОВ С КОМПЕНСАЦИЕЙ ПОГРЕШНОСТЕЙ НАВИГАЦИОННОГО ПРИЕМНИКА | 2015 |
|
RU2638411C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ НАВИГАЦИОННЫХ СПУТНИКОВ | 2015 |
|
RU2587666C1 |
Изобретение относится к области авиационно-космического приборостроения и может найти применение в системах спутниковой навигации и геодезии. Технический результат - расширение функциональных возможностей. Для этого предложена соответствующая система (фиг.3) и последовательность операций для работы по двум орбитальным группировкам (фиг.4). Кроме того, введен специализированный вычислитель, в котором в системе навигационных уравнений учитывается пятый временной параметр, отвечающий за расхождения часов навигационного приемника от системного времени второй орбитальной группировки. При этом выполняется переход к определенному линейному векторному пространству, в котором определяется решение системы навигационных уравнений в параметрическом виде относительно двух неизвестных, с последующим определением данных неизвестных путем вычисления корней полиномиального уравнения. 2 н. и 1 з.п. ф-лы, 6 ил., 4 табл.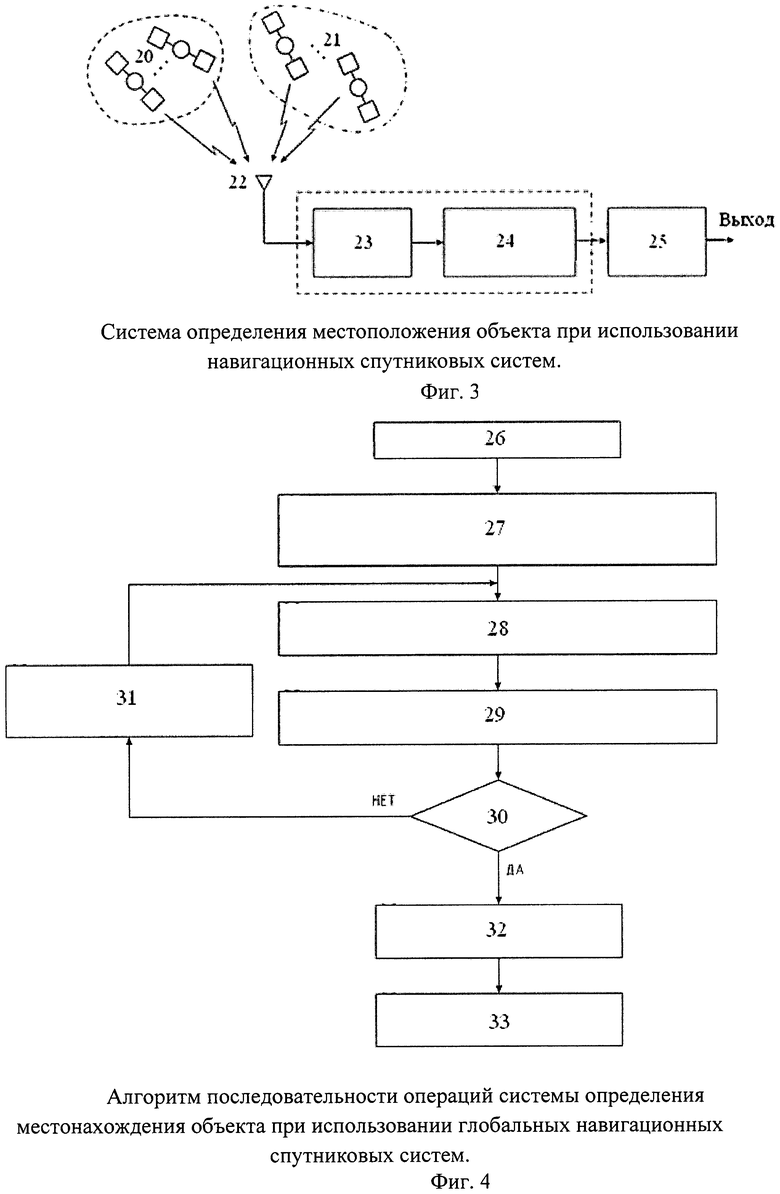
1. Способ определения местоположения объекта при использовании глобальных навигационных спутниковых систем, заключающийся в том, что:
принимают сигналы от первой GPS и второй ГЛОНАСС орбитальных группировок навигационных спутников;
производят первичную цифровую обработку навигационных сигналов с выделением эфемерид и псевдодальностей;
рассчитывают скорректированные псевдодальности;
прогнозируют координаты спутников по актуальным эфемеридам на моменты времени излучения навигационных сигналов;
определяют координаты x, y, z, временной параметр а1, соответствующий расхождению часов навигационного приемника от системного времени первой орбитальной группировки, и временной параметр а2, соответствующий расхождению часов навигационного приемника от системного времени второй орбитальной группировки методом наименьших квадратов, используя информацию от всех спутников с одинаковым весом первой и второй орбитальных группировок, путем аналитического решения системы нелинейных уравнений с минимизацией невязок;
проверяют выполнимость условия a1<ε, где ε - допустимая величина невязки по времени между шкалой навигационного приемника и системного времени глобальной навигационной спутниковой системы (ГНСС);
подводят часы навигационного приемника до системного времени ГНСС;
сглаживают результаты определения фильтром Калмана;
записывают результаты определения x, y, z, а1, а2 и выводят их для пользователя.
2. Система определения местоположения объекта при использовании глобальных навигационных спутниковых систем, включающая:
первую орбитальную группировку навигационных спутников GPS;
вторую орбитальную группировку ГЛОНАСС;
приемную антенну навигационных спутниковых сигналов от первой орбитальной группировки навигационных спутников GPS и второй орбитальной группировки ГЛОНАСС;
блок формирования измерений;
блок вычислений координат и временных параметров;
блок записи и вывода результатов вычислений на пользователя;
причем выход приемной антенны навигационных спутниковых сигналов соединен с входом блока формирования измерений, вход блока вычислений координат и временных параметров соединен с выходом блока формирования измерений, вход блока записи и вывода результатов вычислений соединен с выходом блока вычислений координат и временных параметров, выход блока записи и вывода результатов вычислений является выходом системы.
3. Система по п.2, отличающаяся тем, что блок вычислений координат и временных параметров содержит арифметико-логическое устройство с возможностью операций сложения, умножения и вычитания, первый вход которого соединен с выходом блока формирования измерений, блок расчета комплексно-сопряженной матрицы, вход которого соединен с выходом блока формирования измерений, блок расчета скалярных построчных произведений вектора с матрицей и матрицы с матрицей, вход которого соединен с выходом блока формирования измерений, второй и третий входы арифметико-логического устройства соединены с выходами комплексно-сопряженной матрицы и блока расчета скалярных построчных произведений вектора с матрицей и матрицы с матрицей соответственно, блок расчета корней полинома, вход которого соединен с выходом арифметико-логического устройства с возможностью операций сложения, умножения и вычитания, блок вычисления вектора состояний {x, y, z, а1, а2}, вход которого соединен с выходом блока расчета корней полинома, выход блока вычисления вектора состояний {x, y, z, а1, а2} является выходом блока вычислений координат и временных параметров.
| СПОСОБ ФОРМИРОВАНИЯ НАВИГАЦИОННЫХ РАДИОСИГНАЛОВ НАВИГАЦИОННЫХ КОСМИЧЕСКИХ АППАРАТОВ (НКА) НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ (ГСО) И/ИЛИ НАВИГАЦИОННЫХ КОСМИЧЕСКИХ АППАРАТОВ (НКА) НА ГЕОСИНХРОННОЙ НАКЛОННОЙ ОРБИТЕ (ГСНО) С ПОМОЩЬЮ ЗЕМНЫХ СТАНЦИЙ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2474845C1 |
| ИНТЕГРИРОВАННАЯ ИНЕРЦИАЛЬНО-СПУТНИКОВАЯ СИСТЕМА ОРИЕНТАЦИИ И НАВИГАЦИИ ДЛЯ ОБЪЕКТОВ, ДВИЖУЩИХСЯ ПО БАЛЛИСТИЧЕСКОЙ ТРАЕКТОРИИ С ВРАЩЕНИЕМ ВОКРУГ ПРОДОЛЬНОЙ ОСИ | 2008 |
|
RU2375680C1 |
| ИНТЕГРИРОВАННАЯ ИНЕРЦИАЛЬНО-СПУТНИКОВАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2004 |
|
RU2277696C2 |
| АФЕНКО К.А | |||
| и др | |||
| Применение двухступенчатого субоптимального фильтра при решении задачи позиционирования / В кн.: Навигация и управление летательными аппаратами / Труды МИЭА, под | |||
| ред | |||
| А.Г | |||
| КУЗНЕЦОВА, вып | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| СТЕПАНОВ О.А., КОШАЕВ Д.А. | |||
Авторы
Даты
2013-09-10—Публикация
2012-03-01—Подача