1. Область техники, к которой относится изобретение
Изобретение относится к области гироскопических систем ориентации и навигации подвижных объектов, конкретно - к бесплатформенным инерциальным навигационным системам (БИНС) и бесплатформенным инерциальным системам ориентации (БИСО) на трехосных волоконно-оптических гироскопах с одним общим источником излучения.
2. Уровень техники



Известны трехосные ВОГ (ТВОГ) двух типов:
I тип - ТВОГ на трех автономных одноосных ВОГ,
II тип - ТВОГ с одним общим источником излучения (ОИИ) (патенты США: №4,815,853, МПК4 G01B 9/02, 28.03.1989; №4,828,389, МПК4 G01B 9/02, 09.05.1989; №5,184,195, МПК5 G01C 19/72, 02.02.1993; №5,818,589, МПК6 G01C 19/64, 06.10.1998; №5,854,678, МПК6 G01C 19/72, 29.12.1998).
Известны многоосные (более трех осей чувствительности) ВОГ, например, четырехосные ВОГ с ОИИ (патент США №7,746,476 В2, МПК G01C 19/72 (2006.01), 29.06.2010).
Принципиальное различие ТВОГ (и многоосных ВОГ) I и II типа состоит в следующем. В ТВОГ I типа шумы в трех измерительных каналах (ИК) ТВОГ независимы. В ТВОГ II типа шумы в трех ИК ТВОГ зависимы, что обусловлено наличием одного и того же шума ОИИ одновременно в трех ИК ТВОГ ("синхронная помеха"). В результате в корреляционной матрице шумов (КМШ) ТВОГ I типа отличны от нуля только три диагональных элемента КМШ, а в КМШ ТВОГ II типа отличны от нуля все девять элементов КМШ ТВОГ.
Оси чувствительности (ОЧ) ТВОГ номинально взаимно ортогональны. Три орта 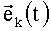 (k=1, 2, 3), направленных по ОЧ ТВОГ ("измерительный базис"), образуют
(k=1, 2, 3), направленных по ОЧ ТВОГ ("измерительный базис"), образуют 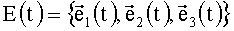 , жестко связанный с управляемым объектом (УО).
, жестко связанный с управляемым объектом (УО).
Задача БИСО состоит в определении ориентации (углового положения) связанного базиса E(t) относительно его начального положения - инерциального базиса I
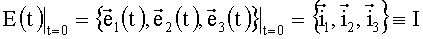
на основании интегрирования кинематических уравнений (КУ) в терминах тех или иных кинематических параметров (КП) и формализмов [1].

Предпосылки создания изобретения:
Заявленный способ повышения точности БИСО на основе ТВОГ с ОИИ не следует из уровня техники, - возможность повышения точности БИСО на основе ТВОГ с ОИИ можно было заметить систематически исследуя влияние погрешностей и шумов ТВОГ на точность БИСО [2-6].
Вектору абсолютной угловой скорости (ВАУС) ставятся в соответствие матрицы-столбцы (I - представление 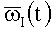 и E-представление
и E-представление 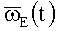 ВАУС):
ВАУС):
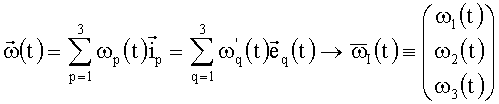 ;
; 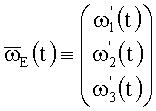 ,
,
которые связаны матрицами направляющих косинусов (МНК) [1]:
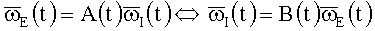 ;
;
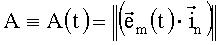 ;
; 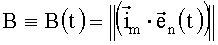 ;
;
B(t)=AT(t)=A-1(t)⇔A(t)=BT(t)=B-1(t); detA(t)=detB(t)=+1.
E-представление ВАУС измеряется гироскопами с погрешностями. В результате в БИСО используется возмущенная информация ("T" - символ транспонирования матрицы):
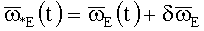 ;
; 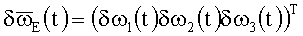 ,
,
где
δωi(t) (i=1, 2, 3) - ошибки гироскопов.
Известна теорема о погрешности БИСО.
Теорема. [7, 8]. Погрешность определения ориентации посредством БИСО представляет собой вращение вычисленного алгоритмом БИСО (на основании интегрирования КУ в терминах тех или иных КП и формализмов) образа инерциалъного базиса 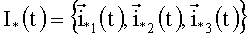
I - представление ВАУС базиса I*(t) имеет вид: 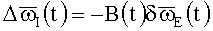 .
.
Здесь:
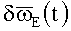 - погрешность измерения Е-представления ВАУС;
- погрешность измерения Е-представления ВАУС;
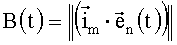 - МНК, характеризирующая вращение объекта.
- МНК, характеризирующая вращение объекта.
На основании этой теоремы в качестве строгих КУ ошибок (КУО) БИСО можно использовать любые КУ (в терминах любых КП и формализмов). Например, в терминах МНК ΔA и ΔB 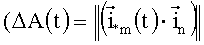 ; ΔB=ΔA-1=ΔAT) строгие КУО БИСО принимают вид:
; ΔB=ΔA-1=ΔAT) строгие КУО БИСО принимают вид:
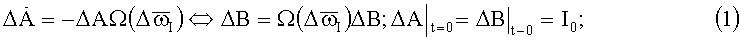
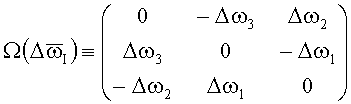 ;
; 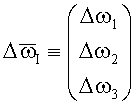 ;
; 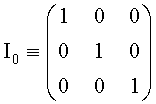 .
.
Решения КУО (1) представляются рядом последовательных приближений (РПП) в форме ряда Пикара, который сходится равномерно и абсолютно:
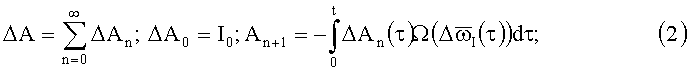
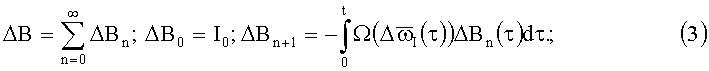
МНК АА и АВ параметризируются вектором эйлерова поворота (ВЭП)
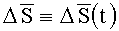 ,
,
характеризующим вращение базиса I*(t) относительно базиса I:
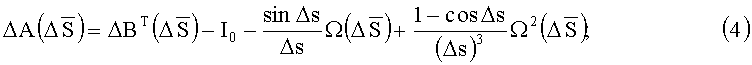
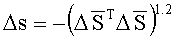 .
.
ВЭП 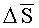 называется "вектор погрешности ориентации" (ВПО) БИСО. Критерий точности БИСО - угол эйлерова поворота (УЭП) Δs(t) базиса I*(t) относительно базиса I - "угол погрешности ориентации" (УПО). С учетом (2)-(4) имеем:
называется "вектор погрешности ориентации" (ВПО) БИСО. Критерий точности БИСО - угол эйлерова поворота (УЭП) Δs(t) базиса I*(t) относительно базиса I - "угол погрешности ориентации" (УПО). С учетом (2)-(4) имеем:
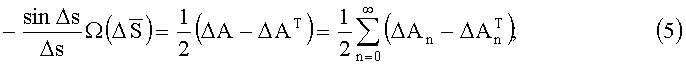
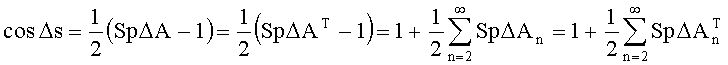
Здесь:
SpX - след (сумма диагональных элементов) матрицы X.
Сходимость рядов (2), (3) гарантирует сходимость рядов (5).
На основании (5) ВПО и УПО можно представить в виде РПП:
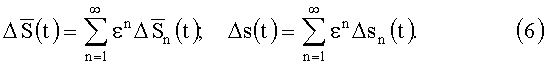
Для построения РПП введен "малый" параметр 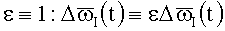 .
.
В используемых на практике БИСО ошибки малы: Δs(t)<<1, с учетом sinΔs(t)/Δs(t)≈1 Два первых приближения теории возмущений имеют вид:

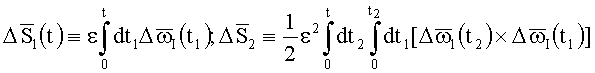 .
.
Двух первых приближений (~ε и ~ε2) (7), как правило, достаточно (за редкими исключениями [4]) для корректного анализа точности БИСО в зависимости от шумов гироскопов и вида вращения УО.
Дисперсия ошибки БИСО определяется следующим образом:
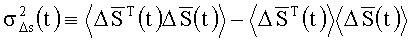 ,
,
где
〈.〉 - символ статистического усреднения по ансамблю.
В первом ("корреляционном") приближении теории возмущений дисперсия ошибки БИСО вычисляется квадратурой [3]:
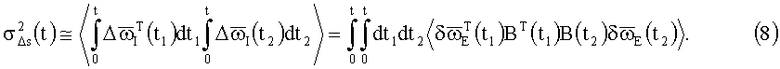
Модель ошибок (МО) ТВОГ содержит три структурные составляющие: аддитивную (не зависящую от ВАУС), мультипликативную (линейную по ВАУС) и нелинейную:
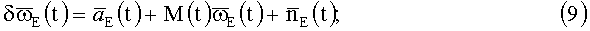
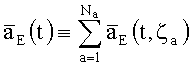
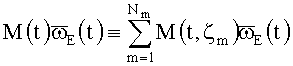 ;
; 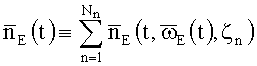
Индексы a, m, n, по которым проводится суммирование, нумеруют процессы ζa, ζm, ζn, влияющие на соответствующие составляющие МО.
МО ТВОГ (9) содержит только случайные составляющие (предполагается что систематические составляющие МО калибруются, паспортизируются и алгоритмически корректируются в БИСО известными способами):
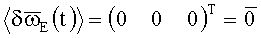 .
.
В КМШ ТВОГ I типа (ТВОГ на трех одноосных автономных ВОГ) отличны от нуля только три диагональных элемента
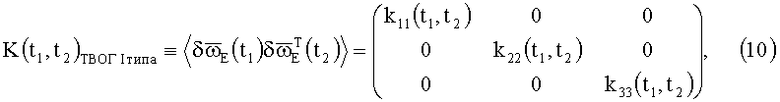
а в КМШ ТВОГ II типа (ТВОГ с ОИИ) - все девять элементов ненулевые:
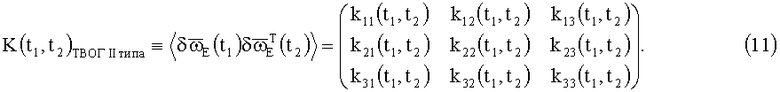
Отношение дисперсии ошибки БИСО на ТВОГ II типа к дисперсии ошибки БИСО на ТВОГ I типа (в корреляционном приближении (Δs(t))=0) имеет вид [3]:
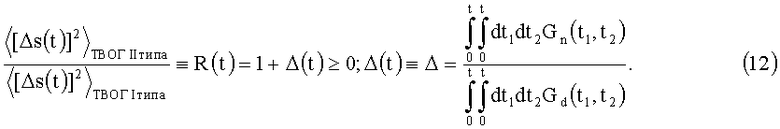
Функция зависит только от диагональных элементов КМШ, а функция
Gn - только от недиагональных элементов КМШ.
На основании (8)-(11) различие ошибок БИСО на ТВОГ I и II типа можно анализировать для произвольных вращений B(f) и произвольных КМШ (11).
Рассмотрим модель КМШ ТВОГ, соответствующую "синхронной помехе", обусловленной использованием в ТВОГ ОИИ (в предположении марковского процесса с коэффициентом корреляциии k(τ)=ехр(-τ/τ0)) [3]
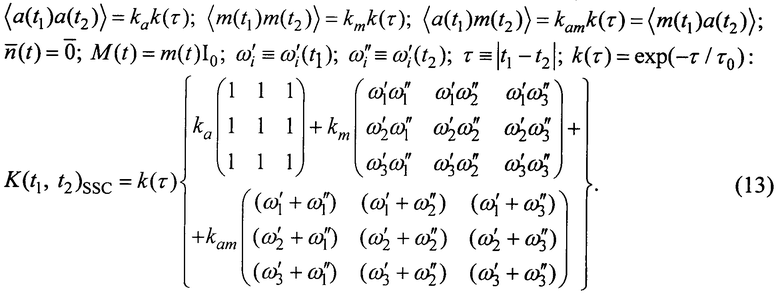
Рассмотрим вращение объекта с постоянной угловой скоростью, например, соответствующее движению искусственного спутника Земли (ИСЗ) 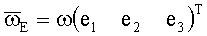 ;
; 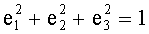 ;
; 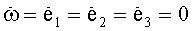 . Отношение дисперсий ошибок БИСО (12) принимает вид:
. Отношение дисперсий ошибок БИСО (12) принимает вид:
R=1+Δ; 
где
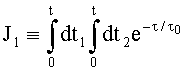 ;
; 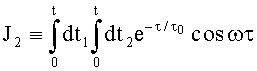 ;
;
c1=3ka+2kamω(e1+e2+e3)+kmω2;
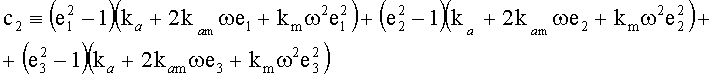
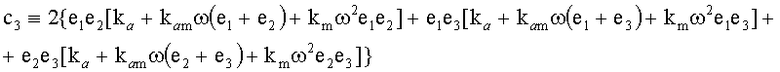 .
.
Для "быстрых" (естественных) флуктуации (τ0=τ0e) различие точности БИСО на ТВОГ I и II типа пренебрежимо мало, так как ωτ0<<1. Для "медленных" (технических) флуктуации (τ0=τ0T) параметр ωτ0 не является малым, так как времена корреляции технических флуктуаций τ0T>>τ0е имеют порядок минут и часов.
Вычисляя (14), при t>>τ0 получаем:
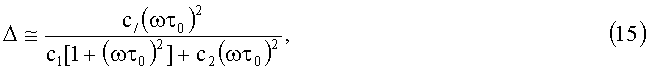
так как
J1≅2τ0t; J2≅2τ0t[1+ωτ0)2]-1; 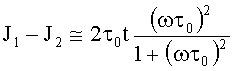 .
.
Скалярная функция Δ (15) при t>>τ0 не зависит от времени и является анизотропной функцией векторного аргумента - зависит от направления ВАУС относительно базиса E.
Возможны три ситуации:
1) Δ=0. Точности БИСО на ТВОГ I и II типа совпадают.
2) Δ>0. Точность БИСО на ТВОГ I типа превосходит точность БИСО на ТВОГ II типа.
3) Δ<0. Точность БИСО на ТВОГ II типа превосходит точность БИСО на ТВОГ II типа.
Рассмотрим вклады корреляционных функций ka и km (13) при t/τ0>>1:
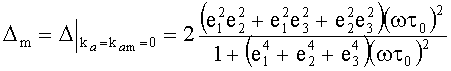 ;
;
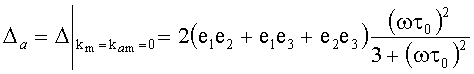 .
.
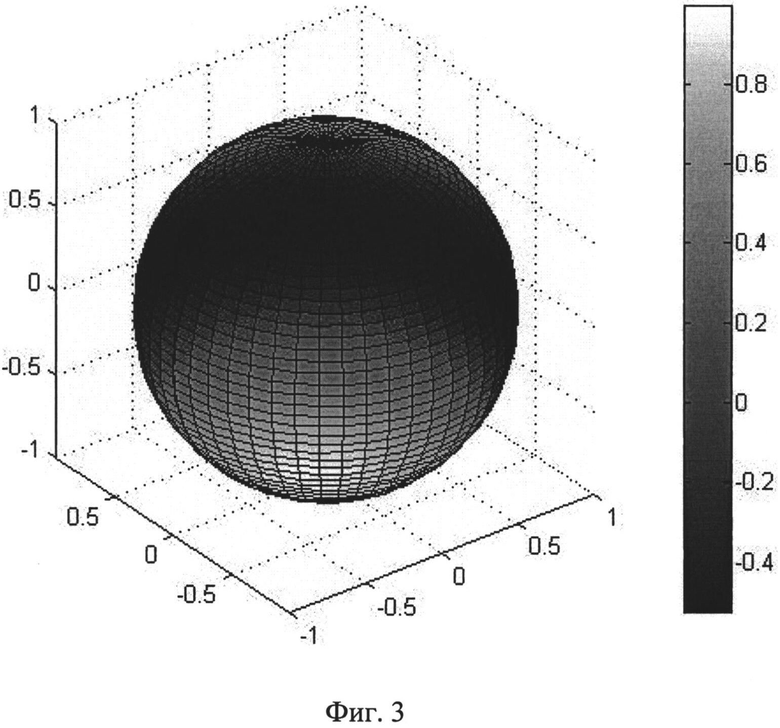
Графики анизотропных функций Δm/2 и Δa/2 (при ωτ0>>1) представлены на Рис.2 и Рис.3.
При вращениях с "большими" угловыми скоростями, когда
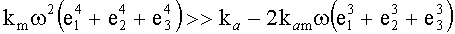 ,
,
точность БИСО на ТВОГ II типа ни при каких дополнительных условиях не превосходит точность БИСО на ТВОГ I типа, так как
Δ=Δm∈[0, 2]⇔R∈[1, 3].
При вращениях с "малыми" угловыми скоростями, когда
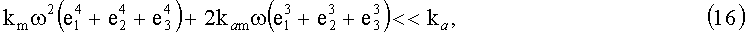
точность БИСО на ТВОГ II типа может превосходить (причем превосходить
существенно - на порядки) точность БИСО на ТВОГ I типа, так как


Условие (18) означает, что в первом приближении (~ε) ошибка БИСО на ТВОГ II типа не возрастает во времени - строго равна нулю. Для расчета возрастающей во времени ошибки БИСО необходимо учитывать второе приближение (~ε2) (7). Но ошибки БИСО, учитываемые во втором приближении теории возмущений (6), (7), имеют второй порядок малости. Результат (18) означает, что в первом порядке теории возмущений решения строгих КУО БИСО - в корреляционном приближении (8) - при малых постоянных угловых скоростях УО при определенных ориентациях ВАУС УО относительно связанного базиса УО в БИСО может реализовываться полная (то есть 100-процентная) автокомпенсация "синхронной помехи" -коррелированных шумов ТВОГ, обусловленных шумом ОИИ.
3. Сущность изобретения
Целью заявляемого изобретения является способ повышения точности БИСО на основе ТВОГ с ОИИ. Поставленная цель достигается с учетом новой (впервые обнаруженной автором) анизотропной зависимости точности БИСО - дисперсии ошибки БИСО - от направления ВАУС УО относительно связанного базиса - измерительного базиса, образованного ортами 04 ТВОГ, за счет использования следующих существенных признаков изобретения:
1) Использование нового установленного свойства зависимости погрешности БИСО от недиагональных элементов КМШ трехосных гироскопов;
2) Использование информации о структуре КМШ трехосного гироскопа, в том числе о диагональных и недиагональных элементах КМШ;
3) Использование информации о синхронной помехе в ТВОГ с ОИИ. Известны способы ослабления влияния шумов трехосных гироскопов на точность определения пространственной ориентации (углового положения) в различных гироскопических и инерциальных навигационных устройствах в результате автокомпенсации вращением систематических и медленно изменяющихся погрешностей ВОГ и ТВОГ, например, [9, 10] (аналоги). Очевидным недостатком таких способов является существенное техническое усложнение, связанное с использованием дополнительных устройств для принудительного вращения гироскопов и/или инерциальных измерительных блоков.
Известен способ фильтрации шумов гироскопов в составе БИСО и БИНС [11, 12] (прототип). Недостатком такого способа является только частичное ослабление влияния шумов гироскопов на точность определения ориентации. Заявляемое изобретение представляет собой способ повышения точности БИСО на основе ТВОГ с ОИИ без повышения точности ТВОГ, без алгоритмической коррекции, без фильтрации и без каких-либо технических усложнений ТВОГ и БИСО. В предложенном изобретении осуществляется стопроцентная (в корреляционном приближении) автокомпенсация в БИСО синхронной помехи ТВОГ, обусловленной шумами ОИИ и существенное повышение точности БИСО.
Погрешность БИСО (6) - это функционал двух функций [4]: погрешностей ТВОГ ТГ 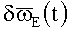 и вращения УО B{t). В частности, в первом приближении теории возмущений решений строгих КУО БИСО - в корреляционном приближении, в котором для оценок точности БИСО достаточна информация только о КМШ ТВОГ (информация о статистических моментах выше второго порядка и о типе статистики шумов не требуется):
и вращения УО B{t). В частности, в первом приближении теории возмущений решений строгих КУО БИСО - в корреляционном приближении, в котором для оценок точности БИСО достаточна информация только о КМШ ТВОГ (информация о статистических моментах выше второго порядка и о типе статистики шумов не требуется):
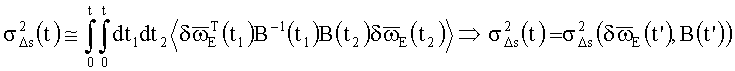 ;
;
t'∈[0, t].
Исследование этого функционала показывает, что при фиксированной КМШ, как в общем случае нестационарных шумов, когда КМШ ТВОГ имеет вид
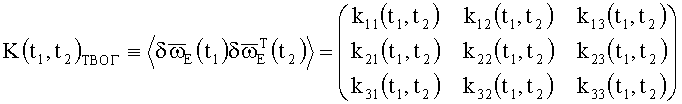 ,
,
так и в частном случае стационарных шумов, когда КМШ ТВОГ имеет вид
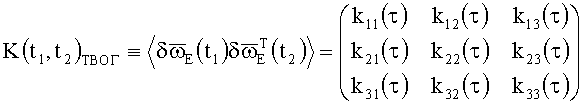 ,
,
4. Краткое описание чертежей
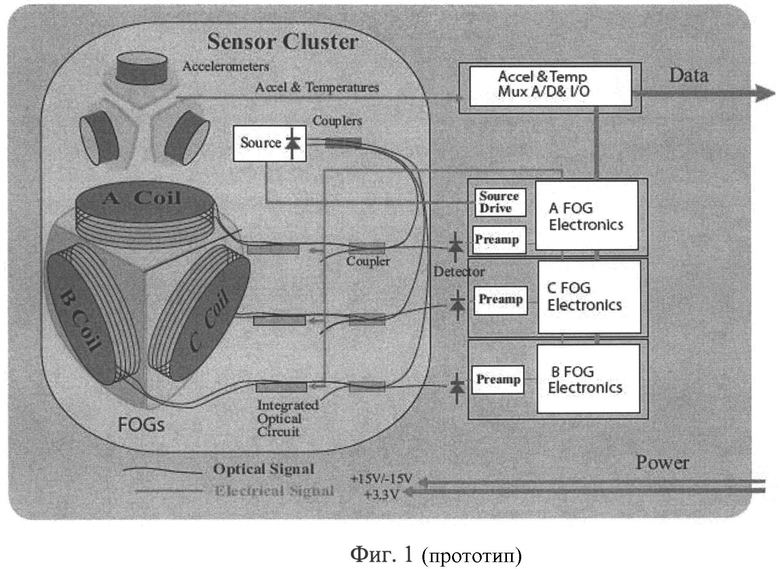
На Фиг.1. в качестве иллюстрации представлен ТВОГ с ОИИ в составе бесплатформенного измерительного блока фирмы Northrop Grumman [13]. На Фиг.2. представлен трехмерный график анизотропной функции Δm/2
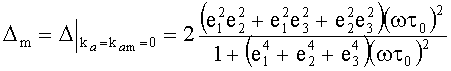 .
.
При вращениях с большими угловыми скоростями, когда
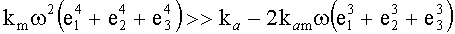 ,
,
автокомпенсация шумов ТВОГ с ОИИ в БИСО не происходит так как для произвольного вращения УО с большими угловыми скоростями
Δ=Δm∈[0, 2]⇔R∈[1, 3].
На Фиг.3. представлен трехмерный график анизотропной функции Δa/2
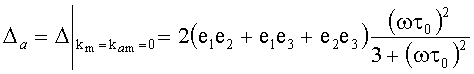 .
.
При вращениях УО с малыми угловыми скоростями, когда
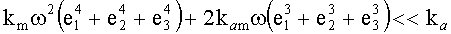
точность БИСО на ТВОГ с ОИИ может превосходить (причем превосходить существенно - на порядки, если вклад шумов ОИИ в результирующую погрешность БИСО превосходит вклад независимых в ИК шумов ТВОГ в погрешность БИСО) точность БИСО на основе ТВОГ на трех автономных одноосных ВОГ
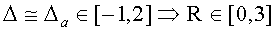 ;
;
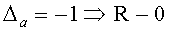
5. Осуществление изобретения
Для УО, вращающихся в инерциальном пространстве с малыми постоянными угловыми скоростями, например, для ИСЗ, в МО ТВОГ (9) можно учитывать только аддитивные составляющие (составляющие дрейфа нуля ВОГ [14]), которые вносят основной вклад в погрешность БИСО (при вращении УО с малыми угловыми скоростями).
На ИСЗ и других УО, вращающихся в инерциальном пространстве с малыми постоянными угловыми скоростями, когда основной вклад в ошибку БИСО вносят дрейфы нулей ТВОГ (16), использование ТВОГ с ОИИ позволяет повысить точность БИСО (17) за счет специальной ориентации 04 ТВОГ относительно ВАУС спутника.
Выбором ориентации связанного базиса E относительно ВАУС УО можно обеспечить выполнение условия: R→0 (в пределе: R=0) (17). Критерий выбора ориентации связанного базиса Е относительно ВАУС УО в типичном случае коэффициента корреляции синхронной помехи в виде, соответствующем марковскому случайному процессу: k(τ)=ехр(-τ/τ0) (13 имеет вид: 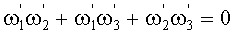 .
.
Реально в ТВОГ с ООИИ шумы в трех ИК преддставляют собой суммы двух слагаемых - синхронной помехи (шум ОИИ ζ(t) общий для всех трех ИК ТВОГ) и некоррелированных в трех ИК ТВОГ слагаемых ζ2(t) (i=1, 2, 3), обусловленных всеми остальными (за исключением ОИИ) источниками шумов ТВОГ
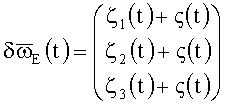
Здесь:
ζi(t) (i=1, 2, 3) - некоррелированные в трех ИК ТВОГ шумы;
ς(t) - тождественный в трех ИК ТВОГ шум, обусловленный шумом ОИИ (синхронная помеха);
〈ς=(t)〉=〈ζ1(t)〉=〈ζ2(t)〉=〈ζ3(t)〉=0;
〈ς(t1)ζ1(t2)〉=〈ς(t1)ζ2(t2)〉=〈ς(t1)ζ3(t2)〉=0;
〈ζ1(t1)ζ2(t2)〉=〈ζ1(t1)ζ3(t2)〉=〈ζ2(t1)ζ2(t3)〉=0.
В общем случае КМШ ТВОГ с ОИИ имеет вид
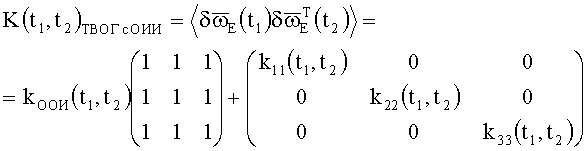
Здесь:
〈ς(t1)ς(t2)〉=kООИ(t1, t2);
〈ζ1(t1)ζ1(t2)〉=k11(t1, t2);
〈ζ2(t1)ζ2(t2)〉=k22(t1, t2);
〈ζ3(t1)ζ3(t2)〉=k33(t1, t2).
Для применений ТВОГ в составе БИСО ИСЗ и других УО с длительным функционированием и временем предстартовой подготовки, превышающим времена переходных процессов в информационных сигналах ТВОГ после включения, - шумы ТВОГ можно считать стационарными
kООИ(t1, t2)=kООИ(τ);
k11(t1, t2)=k11(τ);
k22(t1, t2)=k22(τ);
k33(t1, t2)=k33(τ);
τ≡|t1-t2|.
При достаточной отработке ВОГ в производстве точностные характеристики трех ИК ТВОГ идентичны, в частности
k11(τ)=k22(τ)=k33(τ)=k(τ).
В результате КМШ ТВОГ с ОИИ принимает вид
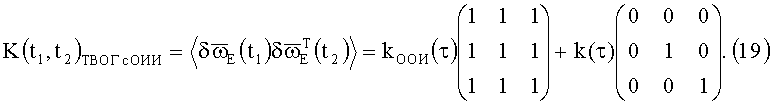
Полезность изобретения
Точность современных ВОГ от 10 град/час до 0,0001 град/час [3].
В случае, если шум ОИИ существенно превосходит некоррелированные шумы в ИК ТВОГ, т.е. когда

в КМШ ТВОГ (19) для оценок точности БИСО можно учитывать только первое слагаемое.
В этом случае, при точности БИСО на ТВОГ на основе трех автономных ВОГ (в КМШ (19) учитывается только второе слагаемое) порядка (0,05÷0,0005) град (за время функционирования БИСО) точность БИСО на ТВОГ на основе ОИИ при использовании заявленного изобретения может превосходить точность БИСО на ТВОГ на основе трех автономных ВОГ на 2-6 порядков (в 102÷106 раз). Иными словами, используя специальный выбор ориентации 04 ТВОГ относительно ВАУС УО, предложенный в заявленном изобретении, точность БИСО на ТВОГ с ОИИ можно повысить в 102÷106, раз (если шум ОИИ существенно превосходит некоррелированные шумы в ИК ТВОГ).
В настоящее время, на современном этапе отработки ВОГ в РФ, отношение недиагональных элементов КМШ ТВОГ с ОИИ к диагональным элементам КМШ ТВОГ с ОИИ (отношение интенсивности шума ОИИ к интенсивности некоррелированных шумов ИК ТВОГ с ОИИ) составляет (40-80)% [15]
kООИ(τ)/k(τ)~(0,4÷0,%),
что позволяет повысить точность БИСО на основе ТВОГ с ОИИ, в соответствии со способом заявленного изобретения, в (2,5÷5) раз. В процессе последующей отработки ВОГ в производстве отношение недиагональных элементов КМШ ТВОГ с ОИИ к диагональным элементам КМШ ТВОГ с ОИИ (отношение интенсивности шума ОИИ к интенсивности некоррелированных шумов ИК ТВОГ с ОИИ) будет повышаться (шумы источника излучения ВОГ - один из основных принципиально неустранимых источников шумов ВОГ), что приведет к дальнейшему увеличению повышения точности БИСО на основе ТВОГ с ОИИ в соответствии со способом заявленного изобретения.
Список использованных источников
1. Бранец В.Н. Применение кватернионов в задачах ориентации твердого тела / В.Н. Бранец, И.П. Шмыглевский. - М.: Наука, 1973. - 320 с.
2. Кробка Н.И. Особенности бесплатформенных инерциальных систем ориентации на основе трехосных волоконно-оптических гироскопов с одним общим источником излучения // Юбилейная XV Санкт-Петербургская международная конференция по интегрированным навигационным системам (26-28 мая 2008 г., Санкт-Петербург, Россия). Сборник материалов. - Санкт-Петербург: ГНЦ РФ - ЦНИИ «Электроприбор». - 2008. - С.87-89.
3. Кробка Н.И. Новый некоммутативный кинематический эффект и его проявления в бесплатформенных инерциальных системах ориентации на основе волоконно-оптических гироскопов // Гироскопия и навигация. - 2009. - №1. - С.36-51.
4. Кробка Н.И. Некоммутативные кинематические эффекты и закономерности накопления шумов волоконно-оптических гироскопов в бесплатформенных инерциальных системах ориентации // XVI Санкт-Петербургская международная конференция по интегрированным навигационным системам. Сборник материалов. (25-27 мая 2009 г., Санкт-Петербург, Россия). - СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 2009. - С.69-72.
5. Кробка Н.И. Дифференциальные методы идентификации структуры шумов гироскопов // Гироскопия и навигация. - 2011. - №1 (72). - С.59-77.
6. Кробка Н.И. Некоммутативные кинематические эффекты вращения твердого тела вокруг точки и их проявления в особенностях построения бесплатформенных систем ориентации на лазерных и волоконно-оптических гироскопах // Вестник Нижегородского университета им. Н.И.Лобачевского. - 2011. - №4 (2) - С.181-183.
7. Krobka N.I. Accurate error equations of the strapdown inertial navigation systems // The Second Soviet-Chinese Symposium of Inertial Technology (Saint Petersburg, October 9-15, 1991). - Saint Petersburg: The Scientific Council on Problems of Motion Control and Navigation of the Academy of Sciences (Section of Autonomous Navigation and Sensors). Chinese Society of Inertial Technology. CSRI "Electropribor", 1992. - P.43-50.
8. Кробка H.И. Концепция строгих уравнений ошибок и оценки квантовых пределов точности бесплатформенных инерциальных навигационных систем на лазерных гироскопах, волоконно-оптических гироскопах и атомных интерферометрах на волнах де Бройля // XVII Санкт-Петербургская международная конференция по интегрированным навигационным системам (31 мая - 02 июня 2010 г., Санкт-Петербург, Россия). Сборник материалов. - СПб: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2010. - С.91-108.
9. Пешехонов В.Г., Несенюк Л.П., Старосельцев Л.П., Блажнов Б.А., Буравлев А.С. Гирогоризонткомпас на волоконно-оптических гироскопах с вращением блока чувствительных элементов // Гироскопия и навигация. - 2002. - №1. - С.57-63.
10. Мешковский И.К., Стригалев В.Е., Дейнека Г.Б., Пешехонов В.Г., Волынский Д.В., Унтилов А.А. Трехосный волоконно-оптический гироскоп. Результаты разработки // XVIII Санкт-Петербургская международная конференция по интегрированным навигационным системам. Сборник материалов. (30 мая - 01 июня 2011 г., Санкт-Петербург, Россия) / Гл. ред. акад. РАН В.Г. Пешехонов. - Санкт-Петербург: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2011. - С.8-14.
11. Степанов О. А. Применение теории нелинейной фильтрации в задачах обработки навигационной информации. - СПб.: ГНЦ РФ ЦНИИ "Электроприбор", 1998. - 370 с.
12. Степанов О.А. Основы теории оценивания с приложениями к задачам обработки навигационной информации. Ч. I. Введение в теорию оценивания. - СПб.: ГНЦ РФ ЦНИИ "Электроприбор", 2008. - 500 с.
13. FOG 2500. - www.northropgrumman.com.
14. IEEE Std 952-1997. IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Interferometric Fiber Optic Gyros.
15. Кробка H.И., Баландин А.И., Кеда С.В., Терешкин А.И., Щербицкий Д.С. Исследование корреляционных матриц шумов многоосных волоконно-оптических гироскопов с одним общим источником излучения // XVIII Санкт-Петербургская международная конференция по интегрированным навигационным системам. Сборник материалов. (30 мая - 01 июня 2011 г. Санкт-Петербург, Россия) / Гл. ред. акад. РАН В.Г. Пешехонов. - Санкт-Петербург: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2011. - С.56-60.
Изобретение относится к области навигационного приборостения и может найти применение в бесплатформенных инерциальных навигационных системах (БИНС) и бесплатформенных инерциальных системах ориентации (БИСО) на трехосных волоконно-оптических гироскопах (ТВОГ) с одним общим источником излучения (ОИИ). Технический результат - повышение точности. Для этого измеряют корреляционную матрицу шумов (КМШ) ТВОГ с ОИИ в условиях, максимально приближенных к условиям использования БИСО на управляемом объекте (УО); вычисляют оптимальную ориентацию (оптимальные ориентации) связанного базиса относительно корпуса УО, при которой (которых) проекции вектора измеряемой абсолютной угловой скорости (ВАУС) УО на оси связанного базиса таковы, что по определенному критерию обеспечивается минимум дисперсии ошибки БИСО; устанавливают БИСО на основе ТВОГ с ОИИ на УО и ориентируют оси чувствительности ТВОГ относительно измеряемого ВАУС УО по определенному критерию так, чтобы обеспечить минимум дисперсии ошибки БИСО. 1 з.п. ф-лы, 3 ил.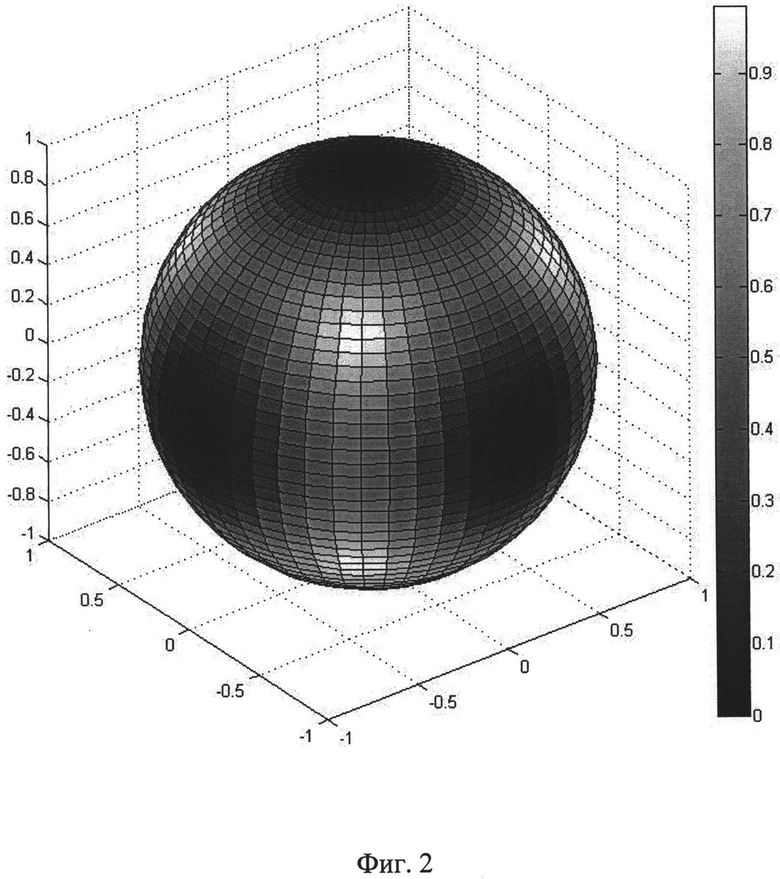
1. Способ повышения точности бесплатформенной инерциальной системы ориентации на основе трехосного волоконно-оптического гироскопа с одним общим источником излучения, основанный на ослаблении влияния шумов гироскопов на точность определения ориентации, отличающийся тем, что, с целью уменьшения дисперсии 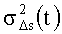
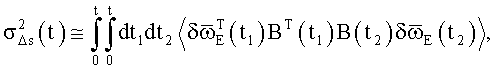
где 〈.〉 - символ статистического усреднения (усреднения по ансамблю);
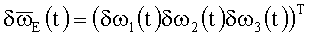
δωi(t) - ошибки измерения проекций вектора абсолютной угловой скорости 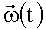
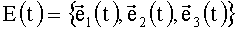
(.)T - символ транспонирования матрицы;
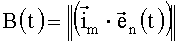
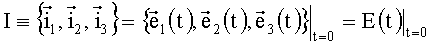
1) измеряют (калибруют и/или паспортизируют) корреляционную матрицу шумов трехосного волоконно-оптического гироскопа
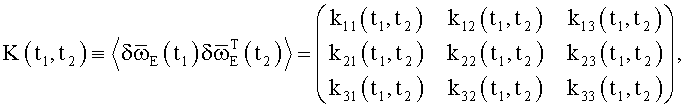
в частности, в приближении стационарных шумов
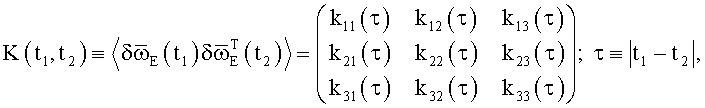
в условиях, максимально приближенным к условиям использования бесплатформенной инерциальной системы ориентации на объекте;
2) вычисляют оптимальную ориентацию (оптимальные ориентации) связанного базиса 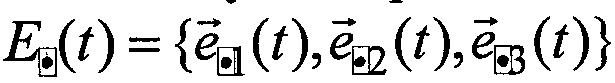 относительно корпуса объекта, при которой (которых) проекции вектора измеряемой абсолютной угловой скорости
относительно корпуса объекта, при которой (которых) проекции вектора измеряемой абсолютной угловой скорости 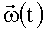
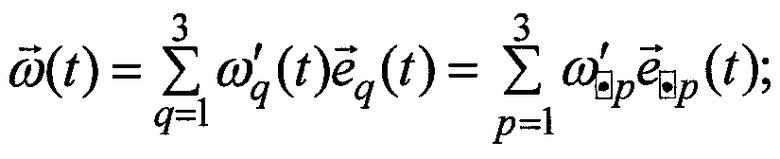
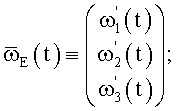
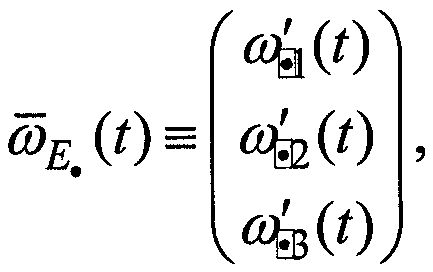
таковы 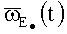
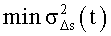
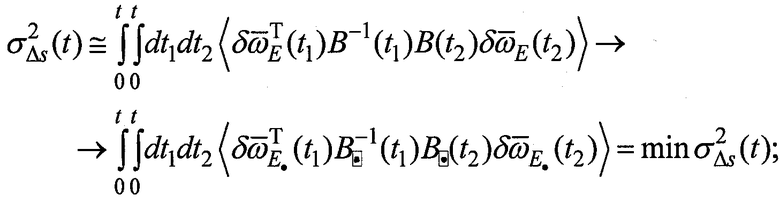
3) устанавливают корпус бесплатформенной инерциальной системы ориентации на корпусе управляемого объекта так, чтобы ориентация связанного базиса относительно корпуса управляемого объекта совпадала с одной из возможных оптимальных ориентации связанного базиса, при которой обеспечивается минимум 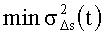
2. Способ по п.1, отличающийся тем, что при стационарных шумах общего источника излучения, когда корреляционная матрица шумов трехосного волоконно-оптического гироскопа имеет вид
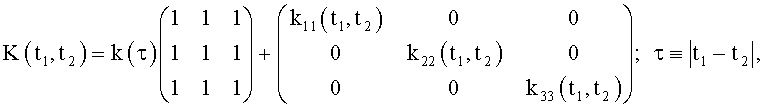
шум источника излучения является марковским процессом с корреляционной функцией k(τ)=kаехр(-τ/τ0), где kа и τ0 - постоянные величины, а управляемый объект вращается с постоянной малой угловой скоростью, критерий выбора оптимальной ориентации корпуса бесплатформенной инерциальной системы ориентации относительно корпуса объекта имеет вид:
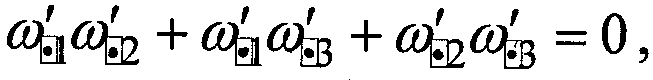
что обеспечивает стопроцентную автокомпенсацию шумов источником излучения и достижение локального минимума дисперсии ошибки ориентации бесплатформенной инерциальной системой ориентации.
| Гирогоризонткомпас на волоконно-оптических гироскопах с вращением блока чувствительных элементов / ПЕШЕХОНОВ В.Г., НЕСЕНЮК Л.П., СТАРОСЕЛЫДЕВ Л.П | |||
| и др | |||
| / Гироскопия и навигация | |||
| Топчак-трактор для канатной вспашки | 1923 |
|
SU2002A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Способ получения на волокне оливково-зеленой окраски путем образования никелевого лака азокрасителя | 1920 |
|
SU57A1 |
| СТЕПАНОВ О.А | |||
| Основы теории оценивания с приложениями к задачам обработки навигационной информации | |||
| Ч.I | |||
| Введение в теорию оценивания | |||
| - СПб.: ГНЦ | |||
Авторы
Даты
2013-12-20—Публикация
2011-11-25—Подача