Изобретение относится к навигационной технике, а именно определению положения наземных и надводных подвижных объектов на основе принципа счисления координат.
Известен способ выработки навигационных параметров (патент РФ на изобретение №2346240 2015 г.), включающий измерение составляющих кажущегося ускорения при помощи акселерометров, оси чувствительности которых связаны с гироплатформой, формирование сигналов управления гироплатформой, отработку сформированных сигналов при помощи гироскопа или датчиков абсолютной угловой скорости, или включающий измерение составляющих кажущегося ускорения при помощи акселерометров, измерение сигналов гироскопов или датчиков абсолютной угловой скорости, оси чувствительности которых направлены по осям приборного трехгранника, аналитическое решение задачи ориентации путем моделирования работы инерциальной системы, выработку навигационных параметров, отличающийся тем, что сравнивают одноименные сигналы, вырабатываемые инерциальной системой с линейной коррекцией с двумя идентичными гироплатформами или сравнивают одноименные сигналы, вырабатываемые инерциальной системой с линейной коррекцией и другой инерциальной системой, например, инерциальной системой с интегральной коррекцией, на основании указанных сравнений автономно определяют обобщенные координаты системы, используя которые находят оценки погрешностей выходных параметров, в частности курса объекта.
Известен способ определения истинного курса подвижного объекта (патент РФ на изобретение №2671937 2017 г.), заключающийся в том, что на объекте устанавливают три акселерометра и три датчика угловой скорости, так чтобы их оси и связанные оси объекта, определяющие углы его курса, тангажа и крена в выбранной системе координат, были параллельны, измеряют указанными акселерометрами и датчиками угловой скорости проекции векторов ускорения и угловой скорости объекта на соответствующие оси, по проекциям вектора ускорения, считая известным ускорение силы тяжести, определяют режим движения объекта по скорости: равномерный или ускоренный, при этом в равномерном режиме по данным акселерометров определяют углы тангажа и крена объекта, в ускоренном режиме по данным датчиков угловой скорости выбирают интервалы, в течение которых проекции вектора угловой скорости объекта могут считаться постоянными, на каждом интервале корректируют значения направляющих косинусов связанных осей объекта относительно осей выбранной системы координат, отличающийся тем, что по текущим значениям истинного курса объекта определяют его режим движения по курсу: прямолинейный или непрямолинейный, при прямолинейном равномерном движении истинный курс определяют по значениям углов тангажа и крена и данным датчиков угловой скорости о проекциях вектора угловой скорости вращения Земли, при непрямолинейном равномерном или ускоренном движении истинный курс определяют по корректируемым значениям направляющих косинусов продольной связанной оси объекта относительно направлений на географические север и восток и местной вертикали, при переходе объекта в режим непрямолинейного равномерного или ускоренного движения в качестве начального условия коррекции указанных направляющих косинусов используют их значения, вычисленные по углам истинного курса и тангажа на момент начала движения неподвижного объекта или окончания его прямолинейного равномерного движения.
Общим недостатком указанных способов является снижение точности определения параметров ориентации объекта по одной из осей приборного трехгранника вследствие ориентации осей измерителей по взаимно-ортогональным направлениям.
В способе бесплатформенной инерциальной навигации на микромеханических чувствительных элементах (патент РФ №2577567 2015 г.) на борту подвижного объекта устанавливают микромеханические гироскопы и акселерометры, ориентируют их оси чувствительности относительно трех ортогональных его осей, затем гироскопами измеряют проекции вектора угловых скоростей, акселерометрами - проекции вектора действующего ускорения на оси координат объекта, полученные выходные сигналы фильтруют и вычисляют навигационные параметры и параметры ориентации, отличающийся тем, что на борту подвижного объекта устанавливают n тетрад микромеханических гироскопов и n тетрад микромеханических акселерометров, которые располагают осями чувствительности вдоль диагоналей куба одной механической базы, грани которой ориентируют параллельно ортогональным осям объекта, а измеренные выходные сигналы тетрад преобразуют в проекции сигналов, действующих на ортогональную систему координат объекта.
Недостатками данного способа являются: то, что число измерителей параметров углового движения больше минимально необходимого их числа, равного трем, и то, что ориентация входных осей этих измерителей не обеспечивает определение параметров ориентации объекта с минимально возможной погрешностью, поскольку точность определения параметров ориентации по осям заданной системы координат зависит как от числа измерителей, так и ориентации их входных осей.
В способе повышения точности бесплатформенной инерциальной системы ориентации на основе трехосных волоконно-оптических гироскопов с одним общим источником излучения (патент РФ №2502048 2011 г.) измеряют корреляционную матрицу шумов трехосного волоконно-оптического гироскопа в частности, в приближении стационарных шумов в условиях, максимально приближенным к условиям использования бесплатформенной инерциальной системы ориентации на объекте; вычисляют оптимальную ориентацию связанного базиса относительно корпуса объекта, при которой проекции вектора измеряемой абсолютной угловой скорости управляемого объекта таковы, что обеспечивается минимум дисперсии ошибки бесплатформенной инерциальной системы ориентации; устанавливают корпус бесплатформенной инерциальной системы ориентации на корпусе управляемого объекта так, чтобы ориентация связанного базиса относительно корпуса управляемого объекта совпадала с одной из возможных оптимальных ориентации связанного базиса, при которой обеспечивается минимум дисперсии ошибки бесплатформенной инерциальной системы ориентации.
Недостатком этого способа является низкая точность определения ориентации объекта по отношению к достижимому уровню точности, поскольку, связанный базис ориентируется как единое целое и взаимная ориентация трех входных осей не меняется. Следовательно, вычисляемые оптимальные углы ориентации входных осей обеспечивают минимум дисперсии ошибки ориентации объекта при ограничениях на углы взаимной ориентации трех входных осей, при этом углы между тремя осями составляют 90 градусов с точностью до малой инструментальной погрешности. Эти ограничения и являются причиной снижения точности выработки параметров ориентации объекта по отношению к возможному уровню точности.
Наиболее близким к заявляемому техническому решению по технической сущности и количеству общих признаков является способ определения двух горизонтальных координат бесплатформенной навигационной системой (Основы построения бесплатформенных инерциальных навигационных систем / В.В. Матвеев, В.Я. Распопов / Под общ. ред. д.т.н. В.Я. Распопова. - СПб.: ГНЦ РФ ОАО "Концерн "ЦНИИ Электроприбир", 2009. - 280 с. ISBN 978-5-900180-73-3, С. 127-128), в котором измеряют проекции вектора кажущегося ускорения объекта на ребра связанного трехгранника с помощью трех акселерометров, жестко связанных с объектом, измеряют первую, вторую и третью проекции вектора абсолютной угловой скорости объекта на первое, второе и третье ребра связанного трехгранника с помощью первого, второго и третьего датчиков угловой скорости, соответственно, по измеренным сигналам проекций вырабатываются приращения двух горизонтальных координат местоположения объекта, двух горизонтальных проекций скорости объекта, углы рыскания, тангажа и крена объекта.
Недостатком прототипа является невысокая точность определения горизонтальных координат объекта вследствие ортогональной ориентации входных осей датчиков угловой скорости по ребрам связного трехгранника.
Задачей предполагаемого способа является повышение точности определения координат объекта, определяющих его положение на земной поверхности.
Техническим результатом заявляемого способа является уменьшение погрешности определения горизонтального местоположения объекта путем ориентация входных осей измерителей параметров ориентации.
Для решения поставленной задачи в способе определения двух горизонтальных координат бесплатформенной навигационной системой, заключающемся в том, что измеряют проекции вектора кажущегося ускорения объекта на ребра связанного трехгранника с помощью трех акселерометров, жестко связанных с объектом, измеряют первую, вторую и третью проекции вектора абсолютной угловой скорости объекта на первое, второе и третье ребра связанного трехгранника с помощью первого, второго и третьего датчиков угловой скорости, соответственно, по измеренным сигналам проекций вырабатывают приращения двух горизонтальных координат местоположения объекта, двух горизонтальных проекций скорости объекта, углы рыскания, тангажа и крена объекта, вычисляют по два угла ориентации входной оси каждого измерителя параметров углового движения в связном трехграннике путем нахождения минимума погрешности горизонтального местоположения объекта, ориентируют входные оси измерителей параметров углового движения в связном трехграннике согласно вычисленным углам путем поворота каждого измерителя относительно основания, на котором он установлен, измеряют проекции вектора абсолютной угловой скорости объекта на входные оси каждого измерителя параметров углового движения, преобразуют измеренные проекции вектора абсолютной угловой скорости объекта в проекции вектора абсолютной угловой скорости объекта на ребра связанного трехгранника.
Примером реализации предполагаемого способа и достигаемого эффекта является имитационное моделирование процесса функционирования системы навигации наземного объекта с неортогональной в общем случае ориентацией входных осей датчиков угловой скорости.
Измерение проекций вектора кажущегося ускорения объекта на ребра связанного трехгранника с помощью трех акселерометров моделируют суммой соответствующих значений истинных проекций ускорения объекта и погрешностей акселерометров. Истинные проекции рассчитывают, исходя из условий движения объекта: из точки на широте 60 градусов, с постоянной линейной скоростью 8 м/с, в течение 7200 секунд, по земной поверхности при дирекционном угле 45 градусов, угле продольного наклона объекта 10 градусов и нулевом угле крена. Погрешности акселерометров моделируют с помощью псевдослучайных чисел так, что среднеквадратичная погрешность измерения продольной линейной скорости объекта составляет 0,1 м/с и период корреляции 300 секунд.
Измерение проекций вектора абсолютной угловой скорости объекта на ребра связанного трехгранника моделируют суммой соответствующих значений истинных проекций и погрешностей датчиков угловой скорости. Истинные проекции моделируют при тех же условиях, что и проекции ускорения объекта. Погрешности датчиков угловой скорости моделируют с помощью псевдослучайных чисел так, что среднеквадратичная погрешность измерения угловой скорости составляет 0,1 градуса за час и период корреляции 300 секунд.
По смоделированным измеренным сигналам проекций рассчитывают две координаты местоположения объекта на земной поверхности, две горизонтальные проекции скорости объекта, углы рыскания, тангажа и крена объекта согласно известным формулам (Основы построения бесплатформенных инерциальных навигационных систем / В.В. Матвеев, B.Я. Распопов / Под общ. ред. д.т.н. В.Я. Распопова. - СПб.: ГНЦ РФ ОАО "Концерн "ЦНИИ Электроприбир", 2009. - 280 с. ISBN 978-5-900180-73-3, C. 112-128), при этом период дискретности выработки указанных параметров составляет 1 секунду. В начальный момент времени моделирования с помощью псевдослучайных чисел моделируют начальные значения погрешностей: двух координат объекта на земной поверхности, азимута движения, угла продольного наклона объекта - таким образом, что среднеквадратичные погрешности составляют 10 метров, 60 угловых секунд, соответственно.
Углы ориентации входных осей датчиков угловой скорости моделируют следующим образом: в прототипе эти углы таковы, что входные оси трех датчиков угловой скорости взаимно ортогональны и направлены, соответственно, на север, на восток и вертикально от центра Земли. В предполагаемом способе входная ось первого датчика угловой скорости отклонена на север от вертикали на заданный угол, входная ось второго датчика угловой скорости направлена как в прототипе, входная ось третьего датчика угловой скорости отклонена на юг от вертикали на заданный угол. Величина заданного угла для первого и третьего датчиков угловой скорости одинакова, принимает дискретные значения: в диапазоне от 1 до 50 градусов с шагом 1 градус, а также значение угла оптимальной ориентации входных осей датчиков угловой скорости. Последнее значение угла находят известным методом градиентного спуска (Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. Пер. с англ. / Под общ. ред. И.Г. Арамановича. - М.: Наука. Гл. ред. физ.-мат. лит., 1968. - 720 с., с. 652) как значение, которому соответствует минимальная радиальная среднеквадратичная погрешность координат в конечный момент времени моделирования. Последовательным заданием значений указанных углов и моделируют ориентирование входных осей измерителей параметров углового движения в связном трехграннике путем поворота каждого измерителя относительно основания, на котором он установлен.
Таким образом, при каждом дискретном значении заданного угла ориентации первого и третьего датчиков угловой скорости рассчитывают две горизонтальные координаты местоположения объекта в конечный момент моделирования. Этот расчет проводится 1000 раз, причем каждый раз используются псевдослучайные числа для моделирования всех описанных выше параметров. По указанным координатам вычисляют радиальные среднеквадратичные погрешности горизонтальных координат местоположения объекта в конечный момент времени, соответствующие каждому дискретному значению угла ориентации входных осей датчиков угловой скорости. Их сравнение между собой доказывает эффект от использования изобретения: минимальная радиальная среднеквадратичная погрешность координат имеет место при оптимальном значении угла ориентации первого и третьего датчиков угловой скорости. Всем другим значениям этого угла, отличающимся от оптимального значения, соответствуют погрешности больше минимальной.
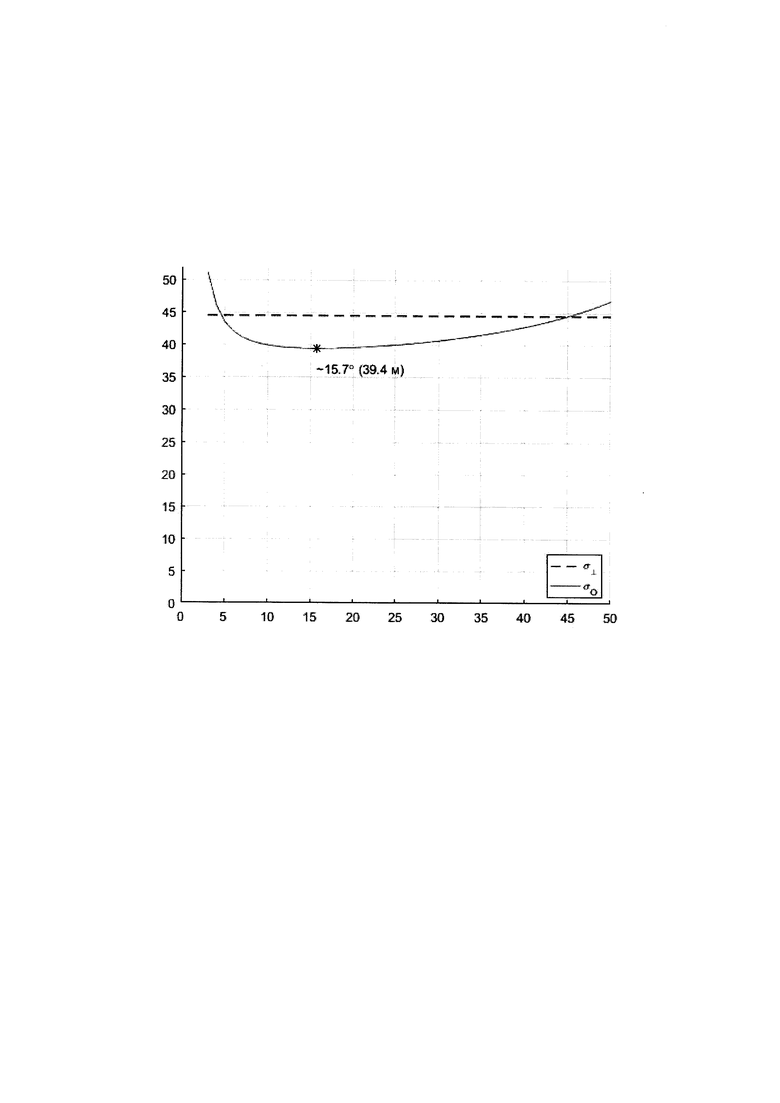
Результат моделирования процесса функционирования системы навигации наземного объекта приведен в виде графиков на чертеже. По оси абсцисс в градусной мере указаны значения углов ориентации первого и третьего датчиков угловой скорости, по оси ординат - радиальная среднеквадратичная погрешность горизонтальных координат местоположения объекта в метрах. Сплошной линией и символами «сто» показан график зависимости радиальной среднеквадратичной погрешности горизонтальных координат местоположения объекта от угла ориентации первого и третьего датчиков угловой скорости. Прерывистой прямой линией и символами «σ⊥» показан уровень этой же погрешности при взаимно ортогональной ориентации всех входных осей датчиков угловых скоростей. Наименьшая радиальная среднеквадратичная погрешность горизонтальных координат местоположения объекта 39,4 м имеет место при оптимальной ориентации входных осей датчиков угловой скорости под углом 15,7 градуса, что на чертеже показано символом «*». Это доказывает возможность осуществления предполагаемого способа с положительным эффектом в точности координат местоположения объекта.
Радиальная среднеквадратичная погрешность горизонтальных координат местоположения объекта 44,5 м в точке пересечения сплошной и прерывистой линий, соответствующая углу ориентации входных осей датчиков угловой скорости 45 градусов, одинакова в прототипе и предполагаемом способе. Это подтверждает правильность выполненного моделирования, поскольку в данном случае угол между входными осями первого и третьего датчиков угловой скорости равен 90 градусам и эти оси перпендикулярны входной оси второго датчика.
Эффект физически объясняется особенностью наземной навигационной системы, заключающейся в том, что наибольший вклад в погрешности координат на поверхности Земли вносит погрешность угла азимутальной ориентации продольной оси наземного подвижного объекта. Существенно меньшим является вклад погрешности угла продольного наклона этого объекта, а погрешность угла крена практически не сказывается на точности координат. Следовательно, повышение точности определения координат наземных подвижных объектов возможно путем уменьшения погрешности азимутальной ориентации за счет некоторого снижения точности измерения двух других углов. Это реализуемо при ориентации оптимальным образом входных осей измерителей параметров углового движения, входящих в приборный состав наземной навигационной системы.
При реализации предполагаемого способа в системах навигации входная ось каждого измерителя параметров углового движения может ориентироваться путем поворота измерителя на два оптимальных угла с помощью специальных механизмов относительно корпуса объекта. Поворот каждого измерителя параметров углового движения объекта относительно основания, на котором он установлен, может быть осуществлен на следующих этапах:
- размещение измерителей параметров углового движения на основании или на объекте посредством жесткой связи; здесь углы ориентации входных осей являются конструктивными параметрами устройства, реализующего заявляемый способ, и не подлежат изменению в течение жизненного цикла этого устройства;
- начальная настройка устройства, реализующего заявляемый способ, в исходной точке траектории движения объекта; здесь и на следующем этапе поворот каждого измерителя на два угла его ориентации может быть осуществлен относительно двух соответствующих осей с помощью специальных устройств;
- процесс выработки навигационных параметров во время движения объекта (горизонтальных координат объекта, углов ориентации объекта, других востребованных потребителем навигационных параметров) реализующим заявляемый способ устройством.
Пара оптимальных углов ориентации входной оси каждого измерителя параметров углового движения может быть получена с помощью вычислителя системы навигации путем нахождения минимума погрешности горизонтального местоположения объекта одним из известных методов, например, градиентным спуском (Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. Пер. с англ. / Под общ. ред. И.Г. Арамановича. - М.: Наука. Гл. ред. физ.-мат. лит., 1968. - 720 с., с. 652). При этом погрешность горизонтального местоположения объекта, выступающая в качестве минимизируемой функции искомых углов, определяется как сумма дисперсий погрешностей горизонтальных координат объекта. Возможны и другие варианты минимизируемой функции, в которых используются другие меры точности определения местоположения объекта (например, предельная погрешность), дополнительно учитываться вертикальная координата, скорости объекта по осям заданной системы координат, азимутальная ориентация в начальной и конечной точках маршрута объекта. В этих случаях дисперсии погрешностей горизонтальных координат или других навигационных параметров объекта определяются известными методами (Степанов О.А. Основы теории оценивания с приложениями к задачам обработки навигационной информации. Ч. 1. Введение в теорию оценивания. СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 2009. 480 с., ISBN 978-5-900780-86-3, с. 340) и с учетом условий функционирования объекта, таких как: начальные параметры движения, траектория объекта, линейная продольная скорость объекта, привлекаемая информация для формирования или коррекции координат и других.
| название | год | авторы | номер документа |
|---|---|---|---|
| НАВИГАЦИОННЫЙ КОМПЛЕКС ЛЕТАТЕЛЬНОГО АППАРАТА | 2005 |
|
RU2293950C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2634071C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2005 |
|
RU2313067C2 |
| Способ определения ориентации объекта в бесплатформенной инерциальной навигационной системе | 2022 |
|
RU2794283C1 |
| СПОСОБ КАЛИБРОВКИ ПАРАМЕТРОВ БЕСПЛАТФОРМЕННОГО ИНЕРЦИАЛЬНОГО ИЗМЕРИТЕЛЬНОГО МОДУЛЯ | 2004 |
|
RU2269813C2 |
| ИНТЕГРИРОВАННАЯ ИНЕРЦИАЛЬНО-СПУТНИКОВАЯ СИСТЕМА ОРИЕНТАЦИИ И НАВИГАЦИИ ДЛЯ ОБЪЕКТОВ, ДВИЖУЩИХСЯ ПО БАЛЛИСТИЧЕСКОЙ ТРАЕКТОРИИ С ВРАЩЕНИЕМ ВОКРУГ ПРОДОЛЬНОЙ ОСИ | 2008 |
|
RU2375680C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ ОБЪЕКТА И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 2017 |
|
RU2661446C1 |
| Способ автономной ориентации подвижного объекта с помощью инерциального измерительного модуля | 2019 |
|
RU2738342C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОРРЕКТИРУЮЩИХ ПОПРАВОК В БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЕ | 2017 |
|
RU2654964C1 |
| СПОСОБ ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ ИНФОРМАЦИИ И ЕЁ КОРРЕКЦИИ ПО ИЗМЕРЕНИЯМ ДОПЛЕРОВСКОГО ИЗМЕРИТЕЛЯ СКОРОСТИ | 2015 |
|
RU2614192C1 |
Изобретение относится к навигационной технике, а именно определению положения наземных и надводных подвижных объектов на основе принципа счисления координат. Способ счисления координат при неортогональной ориентации входных осей измерителей параметров углового движения заключается в том, что измеряют проекции вектора кажущегося ускорения объекта на ребра связанного трехгранника с помощью трех акселерометров, жестко связанных с объектом, измеряют первую, вторую и третью проекции вектора абсолютной угловой скорости объекта на первое, второе и третье ребра связанного трехгранника с помощью первого, второго и третьего датчиков угловых скоростей, соответственно, по измеренным сигналам проекций вырабатывают приращения двух горизонтальных координат местоположения объекта, двух горизонтальных проекций скорости объекта, углы рыскания, тангажа и крена объекта. При этом вычисляют по два угла ориентации входной оси каждого измерителя параметров углового движения в связном трехграннике путем нахождения минимума погрешности горизонтального местоположения объекта, ориентируют входные оси измерителей параметров углового движения в связном трехграннике согласно вычисленным углам путем поворота каждого измерителя относительно основания, на котором он установлен, измеряют проекции вектора абсолютной угловой скорости объекта на входные оси каждого измерителя параметров углового движения, преобразуют измеренные проекции вектора абсолютной угловой скорости объекта в проекции вектора абсолютной угловой скорости объекта на ребра связанного трехгранника. Технический результат – повышение точности определения местоположения объекта на земной поверхности. 1 ил.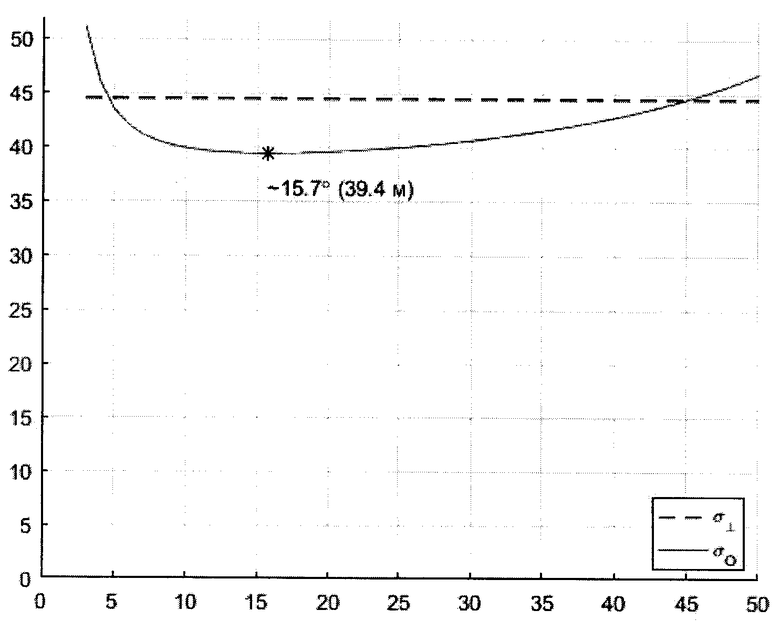
Способ счисления координат при неортогональной ориентации входных осей измерителей параметров углового движения, в котором измеряют проекции вектора кажущегося ускорения объекта на ребра связанного трехгранника с помощью трех акселерометров, жестко связанных с объектом, измеряют первую, вторую и третью проекции вектора абсолютной угловой скорости объекта на первое, второе и третье ребра связанного трехгранника с помощью первого, второго и третьего датчиков угловых скоростей, соответственно, по измеренным сигналам проекций вырабатывают приращения двух горизонтальных координат местоположения объекта, двух горизонтальных проекций скорости объекта, углы рыскания, тангажа и крена объекта, отличающийся тем, что вычисляют по два угла ориентации входной оси каждого измерителя параметров углового движения в связном трехграннике путем нахождения минимума погрешности горизонтального местоположения объекта, ориентируют входные оси измерителей параметров углового движения в связном трехграннике согласно вычисленным углам путем поворота каждого измерителя относительно основания, на котором он установлен, измеряют проекции вектора абсолютной угловой скорости объекта на входные оси каждого измерителя параметров углового движения, преобразуют измеренные проекции вектора абсолютной угловой скорости объекта в проекции вектора абсолютной угловой скорости объекта на ребра связанного трехгранника.
Авторы
Даты
2022-12-15—Публикация
2020-07-20—Подача