СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ КАЛИБРОВКИ ТРЕХОСНЫХ ЛАЗЕРНЫХ ГИРОСКОПОВ С ОДНИМ ОБЩИМ ВИБРАТОРОМ Российский патент 2013 года по МПК G01C25/00 

1. Область техники, к которой относится изобретение

Изобретение относится к области бесплатформенных инерциальных систем ориентации (БИСО) и бесплатформенных инерциальных навигационных систем (БИНС) на основе лазерных гироскопов (ЛГ), конкретно БИСО и БИНС на основе трехосных ЛГ (ТЛГ) с одним общим вибратором (ОВ).

2. Уровень техники

Известны различные способы линеаризации передаточной характеристики ЛГ - так называемые “частотные подставки” (ЧП), ослабляющие влияние эффекта “захвата” на точность ЛГ, на основе различных оптических фазово-невзаимных эффектов (эффекты Фарадея, Керра, Зеемана и другие), а также на основе вращения или колебания ЛГ относительно основания вокруг оси чувствительности (ОЧ) - так называемые “механические ЧП” (МЧП).

Известны ТЛГ двух принципиально различных типов:

I тип - ТЛГ, в котором МЧП реализуется однонаправленным или реверсивным вращением, либо колебаниями ТЛГ как целого. Типичные примеры - ТЛГ с ОВ и ТЛГ на реверсивно-вращающемся основании (РВО) [1]. Как правило, в ТЛГ I типа ось колебаний (или ось вращения) ТЛГ направлена по биссектрисе трехгранного угла, образованного ОЧ ТЛГ.

II тип - ТЛГ на основе трех автономных одноосных ЛГ с МЧП, например, ТЛГ на трех одноосных ЛГ на отдельных вибраторах, и ТЛГ на основе ЛГ с ЧП на основе различных оптических ЧП.

Принципиальное различие ТЛГ I и ТЛГ II типа состоит в следующем.

В ТЛГ II типа ОЧ неподвижны относительно основания ТЛГ (корпуса БИСО или БИНС). В ТЛГ I типа ОЧ подвижны (в соответствии с типом МЧП) относительно основания. Это обстоятельство приводит к особенностям калибровки ТЛГ на ОВ (и ТЛГ на РВО).

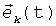
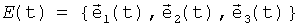
Три ОЧ ТВОГ на ОВ номинально ортогональны - три орта $${\overrightarrow{e}}_k(t)$$ (k=1, 2, 3), направленных по ОЧ ТВОГ, образуют измерительный ортонормированный базис $$E(t)=\{{\overrightarrow{e}}_1(t),{\overrightarrow{e}}_2(t),{\overrightarrow{e}}_3(t)\}$$ , жестко связанный с ТЛГ.

Предпосылки создания изобретения

Заявленный способ повышения точности калибровки ТЛГ с ОВ не следует из уровня техники, особенности калибровки ТЛГ с ОВ не следуют из уровня техники и были замечены автором на инженерной практике [1].

Особенности ТЛГ с ОВ состоят в следующем.

Кинематическая схема БИСО обычного типа (на основе гироскопов любого типа с неподвижными ОЧ относительно основания - корпуса БИСО) имеет вид:

$$I\underset{{\overline{\omega }}_E(t)}{\overset{\overline{S}(t)}{\to }}E(t).(1)$$

Здесь:

E(t) - связанный базис вращается относительно инерциального базиса I;

$${\overline{\omega }}_E(t)$$ - вектор абсолютной угловой скорости (ВАУС), представленный проекциями в связанном базисе E≡E(t);

$$\overrightarrow{\omega }(t)={\displaystyle \sum _{q=1}^3{\omega }_q^{\text{'}}(t){\overrightarrow{e}}_q(t)\to {\overline{\omega }}_E}(t)\equiv \left(\begin{array}{c}{\omega }_1^{\text{'}}(t)\\ {\omega }_2^{\text{'}}(t)\\ {\omega }_3^{\text{'}}(t)\end{array}\right):$$

$$\overline{S}(t)$$ - вектор эйлерова поворота (ВЭП), параметризирующий матрицу направляющих косинусов (МНК)

$$A(t)\equiv \Vert ({\overrightarrow{e}}_m(t)\cdot {\overline{i}}_n\Vert$$ ; $$A{\left|{}_{t=0}=I_0\iff \overline{S}\right|}_{t=0}=\overline{0}$$ ; $$I_0\equiv \left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

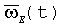
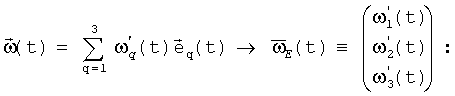
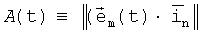
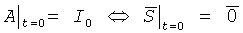
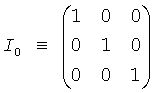
известным образом

$$A(t)=A[\overline{S}(t)]=\exp \{-\Omega [\overline{S}(t)]\}=I_0-\frac{\sin s(t)}{s(t)}\Omega [\overline{S}(t)]+\frac{1-\cos s(t)}{s^2(t)}{\Omega }^2[\overline{S}(t)];$$

$$\Omega [\overline{S}(t)]=\left(\begin{array}{ccc}0& -S_3(t)& S_2(t)\\ S_3(t)& 0& -S_1(t)\\ -S_2(t)& S_1(t)& 0\end{array}\right)$$ ; $$s(t)={[{\overline{S}}^T(t)\overline{S}(t)]}^{1/2}$$ .

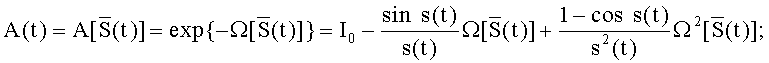
Задача БИСО состоит в определении ориентации (углового положения) связанного базиса E(t) относительно его начального положения - инерциального базиса

$$E(t){\left|{}_{t=0}=\{{\overrightarrow{e}}_1(t),{\overrightarrow{e}}_2(t),{\overrightarrow{e}}_3(t)\}\right|}_{t=0}=\{{\overrightarrow{i}}_1,{\overrightarrow{i}}_2,{\overrightarrow{i}}_3\}\equiv I$$

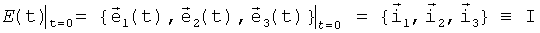
по измеряемым ТЛГ приращениям

$$\nabla {\overline{\Theta }}_E(t_n)\equiv {\overline{\Theta }}_E(t_n)-{\overline{\Theta }}_E(t_{n-1})$$

так называемого “вектора кажущегося поворота” (ВКП)

$${\overline{\Theta }}_E(t)\equiv {\displaystyle {\int }_0^t{\overline{\omega }}_E(\tau )}d\tau$$

на основании интегрирования кинематических уравнений (КУ) в терминах тех или иных кинематических параметров и формализмов [2].

Связанный базис (СБ), неизменно ориентированный относительно корпуса БИСО, совпадает с измерительным базисом (ИБ), орты которого направлены по ОЧ гироскопов (1).

Кинематическая схема БИСО на основе ТЛГ с ОВ принципиально отличается от обычной схемы БИСО (1) и имеет вид

$$I\underset{{\overline{\omega }}_E(t)}{\overset{\overline{S}(t)}{\to }}E(t)\underset{{\overline{\omega }}_{E_{•}}(t)}{\overset{{\overline{S}}_{•}(t)}{\to }}{E}_{•}(t).(2)$$

Здесь:

$$E_{•}(t)=\{{\overrightarrow{e}}_{•1}(t),{\overrightarrow{e}}_{•2}(t),{\overrightarrow{e}}_{•3}(t)\}\equiv E_{•}$$ - ИБ (ТЛГ в целом) вращается относительно СБ для создания МЧП;

$${\overline{S}}_{•}(t)$$ - ВЭП ИБ относительно СБ;

$${\overline{\omega }}_{E_{•}}(t)$$ - ВУС вращения ИБ относительного СБ, заданный проекциями в ИБ;

$$A_{•}(t)\equiv \Vert ({\overrightarrow{e}}_{•m}(t)\cdot {\overrightarrow{e}}_n(t))\Vert$$ ; $$A_{•}|{}_{t=0}=I_0$$ ;

$${\overline{\Theta }}_{E_{•}}(t)\equiv {\displaystyle {\int }_0^t[{\overline{\omega }}_{E_{•}}(\tau )+A_{•}(\tau ){\overline{\omega }}_E(\tau )]d\tau }$$ ;

$$\nabla {\overline{\Theta }}_{E_{•}}(t_n)\equiv {\overline{\Theta }}_{E_{•}}(t_n)-{\overline{\Theta }}_{E_{•}}(t_{n-1})$$ .

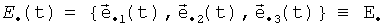
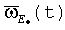
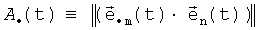
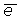
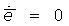
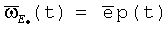
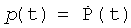
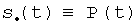
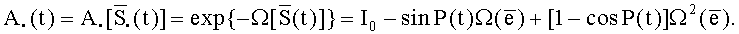
Номинально ТЛГ на ОВ совершает плоские колебания (орт $$\overline{e}$$ оси колебаний ОВ направлен по биссектрисе трехгранного угла, образованного ОЧ ТЛГ)

$${\overline{S}}_{•}(t)=\overline{e}{s}_{•}(t)$$ ; $$({\overline{e}}^T\overline{e})=1$$ ; $$\dot{\overline{e}}=0$$ ; $$s_{•}(t)={[{\overline{S}}_{•}^T(t){\overline{S}}_{•}(t)]}^{1/2};$$

$${\overline{\omega }}_{E_{•}}(t)=\overline{e}p(t)$$ ; $$p(t)=\dot{P}(t)$$ ; $$s_{•}(t)\equiv P(t)$$ ;

$$A_{•}(t)=A_{•}[{\overline{S}}_{•}(t)]=\exp \{-\Omega [\overline{S}(t)]\}=I_0-\sin P(t)\Omega (\overline{e})+[1-\cos P(t)]{\Omega }^2(\overline{e}).$$

Для целей представленного ниже анализа МЧП ТЛГ можно считать гармонической (на практике используются и более сложные формы ЧП):

P(t)=αsinνt.

Амплитуда α колебаний ОВ составляет несколько угловых минут, частота колебаний ν/2π - несколько сотен герц.

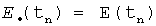
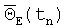
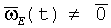
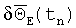
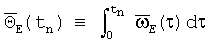
При съеме информации с ТЛГ на частоте ОВ ν/2π в моменты времени t_n:P(t_n)=0 ориентация ИБ и СБ совпадает: $$E_{•}(t_n)=E(t_n)$$ , но в измеряемом ВКП $${\overline{\Theta }}_{E_{•}}(t_n)$$ кроме информации о вращении основания ТЛГ в инерциальном пространстве $${\overline{\Theta }}_E(t_n)$$ содержится (при $${\overline{\omega }}_E(t)\ne \overline{0}$$ ) дополнительная составляющая $$\delta {\overline{\Theta }}_E(t_n)$$

$$\begin{array}{l}{\overline{\Theta }}_{E_{•}}(t_n)={\displaystyle {\int }_0^{t_n}[{\overline{\omega }}_{E_{•}}(\tau )+A_{•}(\tau ){\overline{\omega }}_E(\tau )]d\tau ={\displaystyle {\int }_0^{t_n}{A}_{•}(\tau ){\overline{\omega }}_E(\tau )d\tau =}}\\ ={\displaystyle {\int }_0^{t_n}\{I_0-\sin P(\tau )\Omega (\overline{e})+[1-\cos P(\tau )]{\Omega }^2(\overline{e})\}{\overline{\omega }}_E(\tau )d\tau ={\overline{\Theta }}_E(t_n)+\delta {\overline{\Theta }}_E(t_n)};\end{array}$$

$${\overline{\Theta }}_E(t_n)\equiv {\displaystyle {\int }_0^{t_n}{\overline{\omega }}_E(\tau )d\tau }$$ ;

$$\delta {\overline{\Theta }}_E(t_n)\equiv {\displaystyle {\int }_0^{t_n}\{-\sin P(\tau )\Omega (\overline{e})+[1-\cos P(\tau )]{\Omega }^2(\overline{e})\}{\overline{\omega }}_E(\tau )d\tau }.$$

Поэтому при использовании ТЛГ на ОВ в БИСО КУ вынужденно интегрируют на частотах, превосходящих частоту колебаний ОВ (в 8-64 раза), для устранения методической погрешности $$\delta {\overline{\Theta }}_E(t_n)$$ . Ориентацию СБ в инерциальном пространстве определяют, как правило, в дискретные моменты времени, используя датчик углового положения (ДУП), в моменты t_n:

$$A_{•}(t_n)=I_0\iff E_{•}(t_n)=E(t_n)\iff A(t_n)=\Vert ({\overrightarrow{e}}_m(t_n)\cdot {\overrightarrow{i}}_n)\Vert =\Vert ({\overrightarrow{e}}_{•m}(t_n)\cdot {\overrightarrow{i}}_n)\Vert$$ .

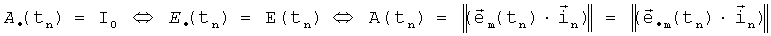
Вторая особенность ТЛГ на ОВ состоит в следующем.

Функционирование ТЛГ вызывает вынужденные колебания основания ТЛГ на частоте колебаний ОВ.

Кинематическая диаграмма БИСО на ТЛГ с ОВ принимает вид

$$I\underset{{\overline{\omega }}_E(t)}{\overset{\overline{S}(t)}{\to }}E(t)\underset{{\overline{\omega }}_{E\text{'}}^{\text{'}}(t)}{\overset{\overline{S}\text{'}(t)}{\to }}E\text{'}(t)\underset{{\overline{\omega }}_{E_{•}}}{\overset{{\overline{S}}_{•}(t)}{\to }}{E}_{•}(t).(3)$$

Здесь:

$$E\text{'}(t)=\{{\overrightarrow{e}}_1^{\text{'}}(t),{\overrightarrow{e}}_2^{\text{'}}(t),{\overrightarrow{e}}_3^{\text{'}}(t)\}$$ ;

$$A\text{'}(t)\equiv \Vert {\overrightarrow{e}}_m^{\text{'}}(t)\cdot {\overrightarrow{e}}_n(t)\Vert =\exp \{-\Omega [\overline{S}\text{'}(t)]\};$$

$$\overline{S}\text{'}(t)={\overline{c}}_1\epsilon \sin (\nu t+{\epsilon }_0)+{\overline{c}}_2\epsilon \cos (\nu t+{\epsilon }_0)$$ ;

$${\overline{c}}_1{}^T{\overline{c}}_1={\overline{c}}_2{}^T{c}_2=1$$ ; $${\overline{c}}_1{}^T{\overline{c}}_2=0$$ ; $$\dot{\epsilon }=0$$ ; $${[\overline{S}{\text{'}}^T(t)\overline{S}\text{'}(t)]}^{1/2}=\epsilon .(4)$$

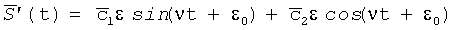
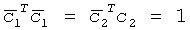
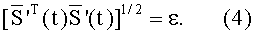
Возмущение основания ТЛГ на ОВ (или корпуса БИСО), соответствующее дополнительному относительному вращению E(t)→E'(t) на диаграмме (3), приводит к тому, что в ВКП:

$$\begin{array}{l}{\overline{\Theta }}^{\text{'}}{}_{E_{•}}(t_n)={\displaystyle {\int }_0^{t_n}[{\overline{\omega }}_{E_{•}}(\tau )+A_{•}(\tau ){\overline{\omega }}_{E\text{'}}(\tau )+A_{•}(\tau )A\text{'}(\tau ){\overline{\omega }}_E(\tau )]d\tau =}\\ ={\overline{\Theta }}_E(t_n)+\delta {\overline{\Theta }}^{\text{'}}{}_E(t_n)+\delta {\overline{\Theta }}^{"}{}_E(t_n)\end{array}$$

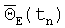
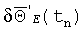
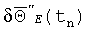
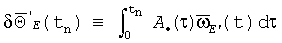
помимо ВКП основания ТЛГ $${\overline{\Theta }}_E(t_n)$$ содержатся две дополнительные составляющие $$\delta {\overline{\Theta }}^{\text{'}}{}_E(t_n)$$ и $$\delta {\overline{\Theta }}^{"}{}_E(t_n)$$ :

$${\overline{\Theta }}_E(t_n)\equiv {\displaystyle {\int }_0^{t_n}{\overline{\omega }}_E(\tau )d\tau }$$ ;

$$\delta {\overline{\Theta }}^{\text{'}}{}_E(t_n)\equiv {\displaystyle {\int }_0^{t_n}{A}_{•}(\tau ){\overline{\omega }}_{E\text{'}}(t)d\tau }$$ ;

$$\delta {\overline{\Theta }}^{"}{}_E(t_n)\equiv {\displaystyle {\int }_0^{t_n}[A_{•}(\tau )A^{\text{'}}(\tau )-I_0]{\overline{\omega }}_E(\tau )d\tau }$$ ;

$${\displaystyle {\int }_0^{t_n}{\overline{\omega }}_{E_{•}}}(\tau )d\tau =\overline{0}$$ .

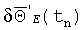
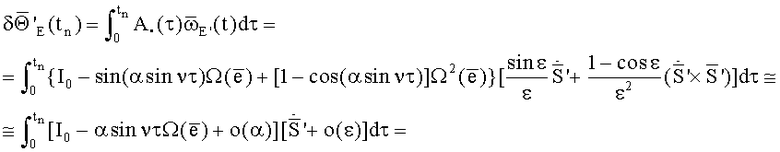
Составляющая $$\delta {\overline{\Theta }}^{\text{'}}{}_E(t_n)$$ не зависит от измеряемого ВАУС основания ТЛГ (корпуса БИСО) и содержит постоянные компоненты - фиктивные “смещения нулей” ТЛГ

$$\begin{array}{l}\delta \overline{\Theta }{\text{'}}_E(t_n)={\displaystyle {\int }_0^{t_n}{A}_{•}(\tau ){\overline{\omega }}_{E\text{'}}(t)d\tau =}\\ ={\displaystyle {\int }_0^{t_n}\{I_0-\sin (\alpha \sin \nu \tau )\Omega (\overline{e})+[1-\cos (\alpha \sin \nu \tau )]{\Omega }^2(\overline{e})\}[\frac{\sin \epsilon }{\epsilon }\dot{\overline{S}}\text{'}+\frac{1-\cos \epsilon }{{\epsilon }^2}(\dot{\overline{S}}\text{'}\times \overline{S}\text{'})]d\tau \cong }\\ \cong {\displaystyle {\int }_0^{t_n}[I_0-\alpha \sin \nu \tau \Omega (\overline{e})+o(\alpha )][\dot{\overline{S}}\text{'}+o(\epsilon )]d\tau }=\end{array}$$

$$={\displaystyle {\int }_0^{t_n}[I_0-\alpha sin\nu \tau \Omega (\overline{e})]}[{\overline{c}}_1\epsilon \nu cos(\nu t+{\epsilon }_0)-{\overline{c}}_2\epsilon \nu sin(\nu t+{\epsilon }_0)]d\tau +o(\alpha ,\epsilon )$$ ;

В частном случае симметричных возмущений основания ( $${\overline{c}}_1{}^T\overline{e}={\overline{c}}_2{}^T\overline{e}=0$$ для кругового конического движения (4) на частоте ОВ) модуль вектора фиктивных смещений нулей (5) не зависит от фазы ε₀

$$\delta {\Theta }_0^{\text{'}}(t_n)/t_n\equiv {[\delta {\overline{\Theta }}^{\text{'}}{}_E^T(t_n)\delta {\overline{\Theta }}^{\text{'}}{}_E(t_n)]}^{1/2}/t_n=\frac{1}{2}\epsilon \alpha \nu .(6)$$

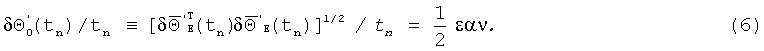
Эффект (5), (6) значителен по величине, так как является линейным по амплитуде ε углового возмущения основания (4). Для типичных значений параметров: частота колебаний ОВ ν/2π=200 Гц, амплитуда колебаний ОВ α=5', амплитуда возмущения основания ε=(1"-10") “фиктивные смещения нулей ТЛГ на ОВ” (5), (6) составляют (1-10) град/час.

Таким образом, основная особенность ТЛГ на ОВ состоит в том, что функционирующий ТЛГ создает вынужденные колебания (на частоте ОВ) основания (корпуса) и, одновременно, синхронно детектирует эти колебания - своеобразный кинематический “пространственный синхронный детектор”. Колебания основания ТЛГ на ОВ приводят к тому, что в ИК ТЛГ содержатся постоянные составляющие - фиктивные смещения нулей (5).

Эффект вынужденного возмущением основания ТЛГ на ОВ не создают проблем его использования в БИСО, так как ошибка ориентации из-за этого эффекта не возрастает во времени - ограничена углом 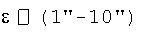конического возмущения основания. Проблема состоит в ином - этот эффект препятствует использованию традиционной методики калибровки ТЛГ по измеряемому ВКП без интегрирования КУ.

Модель ошибок (МО) ЛГ содержит три структурные составляющие: аддитивную (не зависящую от ВАУС), мультипликативную (линейную по ВАУС) и нелинейную [3]:

δω(t)=a(t)+m(t)ω(t)+n(t);

$$a(t)\equiv {\displaystyle \sum _{a=1}^{N_a}a(t,{\zeta }_a)}$$ ; $$m(t)\omega (t)\equiv {\displaystyle \sum _{m=1}^{N_m}m(t,{\zeta }_m)\omega (t)}$$ ; $$n(t)\equiv {\displaystyle \sum _{n=1}^{N_n}n(t,\omega (t),{\zeta }_n)}$$ .

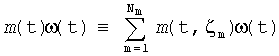
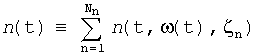
Индексы а, m, n, по которым проводится суммирование, нумеруют процессы ζ_a, ζ_m, ζ_n, влияющие на соответствующие составляющие МО ЛГ [3].

Известны способы калибровки смещения нуля и масштабного коэффициента одноосных ЛГ (аналоги) [3].

δω(t)=δω₀+mω(t).

Модель ошибок ТЛГ содержит также три структурные составляющие: аддитивную (не зависящую от ВАУС), мультипликативную (линейную по ВАУС) и нелинейную:

$$\delta {\overline{\omega }}_E(t)={\overline{a}}_E(t)+M(t){\overline{\omega }}_E(t)+{\overline{n}}_E(t)$$ ;

$${\overline{a}}_E(t)\equiv {\displaystyle \sum _{a=1}^{N_a}{\overline{a}}_E(t,{\zeta }_a)}$$ ; $$M(t){\overline{\omega }}_E(t)\equiv {\displaystyle \sum _{m=1}^{N_m}M(t,{\zeta }_m){\overline{\omega }}_E(t)}$$ ; $${\overline{n}}_E(t)\equiv {\displaystyle \sum _{n=1}^{N_n}{\overline{n}}_E(t,{\overline{\omega }}_E(t),{\zeta }_n).(7)}$$

Индексы а, m, n, по которым проводится суммирование, нумеруют процессы ζ_a, ζ_m, ζ_n, влияющие на соответствующие составляющие МО ЛГ [3].

Калибровке подлежат постоянные компоненты аддитивной $$\delta {\overline{\omega }}_0$$ (физические смещения нулей ТЛГ) и мультипликативной составляющей М МО ТЛГ (7)

$$\delta {\overline{\omega }}_E(t)=\left(\begin{array}{c}\delta {\omega }_{01}\\ \delta {\omega }_{02}\\ \delta {\omega }_{03}\end{array}\right)+\left(\begin{array}{ccc}{m}_{11}& m_{12}& m_{13}\\ m_{21}& m_{22}& m_{23}\\ m_{31}& m_{32}& m_{33}\end{array}\right){\overline{\omega }}_E(t)\equiv \delta {\overline{\omega }}_0+M{\overline{\omega }}_E(t).(8)$$

В случае ТЛГ II типа проблем с калибровкой параметров МО (8) не возникает. Для калибровки параметров МО (8) ТЛГ II типа, как и трехосного гироскопа (ТГ) на основе трех автономных гироскопов на других физических принципах, можно использовать “традиционный” трехпозиционный способ калибровки с использованием поворотно-наклонного стенда (ПНС) [4] (прототип). В соответствии с этим способом калибровки ТЛГ (например, в составе БИСО или БИНС) устанавливают на ПНС с известной начальной выставкой (ориентацией корпуса БИСО или БИНС относительно плоскости местного горизонта и направления на Север) последовательно в трех несовпадающих ориентациях (например, номинально ортогональных), поворачивают ПНС при каждой из трех ориентаций на заданные углы (например, кратные 2π радиан) в двух противоположных направлениях, по измеряемым ВКП и с учетом известных проекций ВАУС Земли на ОЧ ТЛГ на основании полученных 18 чисел вычисляют 12 калибруемых параметров МО (8).

Традиционный способ калибровки можно использовать для калибровки мультипликативных составляющих МО ТЛГ I типа (ТЛГ с ОВ) с достаточно высокой точностью, но при традиционном способе калибровки смещения нулей МО ТЛГ (8) калибруются принципиально ошибочно с недопустимо большой ошибкой (см. замечания [1] к работе [5]), поскольку в измеренном усредненном за время интегрирования векторе угловой скорости (5) кроме смещений нулей ТЛГ $$\delta {\overline{\omega }}_0$$ , подлежащих определению (калибровке), из-за вынужденных колебаний основания ТЛГ на частоте колебаний ОВ (3) и “пространственного синхронного детектирования” содержится дополнительное постоянное слагаемое (5).

Для того чтобы откалибровать смешения нулей ТЛГ с ОВ традиционным способом (по непосредственным показаниям ТЛГ - приращениям ВКП) с погрешностью, например, не более 0,01 град/час, необходимо тем или иным способом уменьшить амплитуду $${[\overline{S}{\text{'}}^T(t)\overline{S}\text{'}(t)]}^{1/2}$$ углового возмущения основания (3) (для типичных значений параметров: частота колебаний ОВ ν/2π=200 Гц, амплитуда колебаний OB α=5') до величины не более 0,01 угловой секунды, что невыполнимо на настоящем уровне развития техники.

3. Сущность изобретения

Задачей, на решение которой направлено это изобретение, является способ повышения точности калибровки смещения нулей ТЛГ на OB $$\delta {\overline{\omega }}_0$$ . При всех известных способах калибровки ТГ (и ТЛГ), основанных на измерении ВКП, в измеренном ТЛГ с ОВ и усредненном за время интегрирования ВАУС содержится сумма двух постоянных физически неразличимых слагаемых , где

$$\delta {\overline{\omega }}_0$$ - реальные постоянные смещения нулей ТЛГ, подлежащие калибровке; $$\epsilon \alpha \nu [(\overline{e}x{\overline{c}}_1)sin{\epsilon }_0+(\overline{e}x{\overline{c}}_2)cos{\epsilon }_0]/2$$ - дополнительное слагаемое - следствие синхронного детектирования вынужденных колебаний оснований ТЛГ с ОВ. В результате, при использовании любого известного способа калибровки ТГ (и ТЛГ), основанного на измерении ВКП, смещения нулей ТЛГ с ОВ калибруются с ошибкой, равной $$\epsilon \alpha \nu [(\overline{e}x{\overline{c}}_1)sin{\epsilon }_0+(\overline{e}x{\overline{c}}_2)cos{\epsilon }_0]/2$$ .

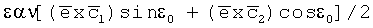
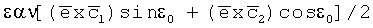
Цель этого изобретения достигается за счет использования нетрадиционного способа калибровки ТЛГ с ОВ. За основу можно взять любой известный способ калибровки ТГ на трех одноосных гироскопах, в т.ч. ТЛГ II типа.

Существенным отличием является то, что для повышения точности калибровки систематических составляющих смещения нулей ТЛГ с ОВ и, как следствие, повышения точности БИСО и БИНС на основе ТЛГ с ОВ калибровку смещений нулей ТЛГ с ОВ производят не по непосредственным показаниям ТЛГ - приращениям ВКП (интегралов проекций ВАУС на ОЧ ТЛГ), а по результирующей погрешности определения пространственной ориентации посредством БИСО на основе ТЛГ с ОВ с использованием строгих КУ ошибок БИСО [6].

4. Осуществление изобретения

Существует много вариантов заявленного способа калибровки ТЛГ с ОВ. Простейший (однопозиционный) вариант состоит в следующем:

1) ТЛГ с ОВ (в составе БИСО или БИНС) устанавливают на известным образом ориентированном неподвижном основании; 2) интегрируют КУ по алгоритму БИСО; 3) используя строгие КУ ошибок БИСО [6], вычисляют вектор погрешности ориентации (ВПО) БИСО $$\Delta \overline{S}(t_n)$$ [6]; 4) выделяют в $$\Delta \overline{S}(t_n)$$ гармонические составляющие на частоте ОВ (составляющие (…) ВПО не зависят от смещений нулей ТЛГ, не являются гармоническими на частоте ОВ и пренебрежимо малы в сравнении с калибруемыми смещениями нулей ТЛГ с ОВ):

$$\Delta \dot{\overline{S}}(t_n)=\alpha \sin \nu t_n\left(\begin{array}{ccc}1& -1/\sqrt{3}& 1/\sqrt{3}\\ 1/\sqrt{3}& 1& -1/\sqrt{3}\\ -1/\sqrt{3}& 1/\sqrt{3}& 1\end{array}\right)\left(\begin{array}{c}\delta {\omega }_{01}\\ \delta {\omega }_{02}\\ \delta {\omega }_{03}\end{array}\right)+(\dots );$$

5) вычисляют и калибруют смещения нулей ТЛГ с ОВ по формуле:

$$\left(\begin{array}{c}\delta {\omega }_{01}\\ \delta {\omega }_{02}\\ \delta {\omega }_{03}\end{array}\right)={\left(\begin{array}{ccc}1& -1/\sqrt{3}& 1/\sqrt{3}\\ 1/\sqrt{3}& 1& -1/\sqrt{3}\\ -1/\sqrt{3}& 1/\sqrt{3}& 1\end{array}\right)}^{-1}\frac{\Delta \dot{\overline{S}}(t_n)}{\alpha \sin \nu t_n}.$$

Список использованных источников

1. Кробка Н.И. Особенности калибровки трехосных лазерных гироскопов на одном общем вибраторе и на реверсивно вращающемся основании (30 и 20 лет спустя) // XVII Санкт-Петербургская международная конференция по интегрированным навигационным системам (31 мая - 02 июня 2010 г., Санкт-Петербург, Россия). Сборник материалов. - СПб: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2010. - С.60-63.

2. Бранец В.Н. Применение кватернионов в задачах ориентации твердого тела / В.Н.Бранец, И.П.Шмыглевский. - М.: Наука, 1973. - 320 с.

3. IEEE Std 647-1995. IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros.

4. Кробка Н.И. Методика калибровки многоосных лазерных гироскопов с избыточным числом информационных каналов / Доклад на совместном заседании Секций навигационных систем и их чувствительных элементов и Ленинградской секции автономной навигации и чувствительных элементов Научного совета АН СССР по проблемам управления движением и навигации по теме «Особенности построения инерциальных систем на лазерных гироскопах» (Москва, ИПМ АН СССР, 29 июня 1988 г.).

5. Федоров А.Е., Рекунов Д.А. Компенсация инструментальных погрешностей трехкомпонентного лазерного гироскопа моноблочной конструкции // XVI Санкт-Петербургская международная конференция по интегрированным навигационным системам (Санкт-Петербург, 25-27 мая 2009 г.). Сборник материалов / Гл. ред. акад. РАН В.Г.Пешехонов. - СПб: ГНЦ РФ ЦНИИ «Электроприбор», 2009. - С.42-47.

6. Кробка Н.И. Концепция строгих уравнений ошибок и оценки квантовых пределов точности бесплатформенных инерциальных навигационных систем на лазерных гироскопах, волоконно-оптических гироскопах и атомных интерферометрах на волнах де Бройля // XVII Санкт-Петербургская международная конференция по интегрированным навигационным системам (31 мая - 02июня 2010 г., Санкт-Петербург, Россия). Сборник материалов. - СПб: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2010. - С.91-108.

Изобретение относится к области приборостроения бесплатформенных инерциальных навигационных систем (БИНС) и бесплатформенных инерциальных систем ориентации (БИСО) на основе лазерных гироскопов (ЛГ), в частности на основе трехосных ЛГ (ТЛГ) с одним общим вибратором (ОВ). Технический результат - повышение точности калибровки. Для достижения данного результата калибровку смещений нулей ТЛГ с ОВ производят не непосредственно по показаниям ТЛГ - приращениям интегралов проекций вектора абсолютной угловой скорости на оси чувствительности ТЛГ, а по результирующей погрешности определения пространственной ориентации посредством бесплатформенной инерциальной системы ориентации на основе трехосных лазерных гироскопов с одним общим вибратором. 1 з.п. ф-лы.

1. Способ повышения точности калибровки трехосных лазерных гироскопов с одним общим вибратором, состоящий в калибровке систематических значений параметров модели ошибок трехосного лазерного гироскопа, в том числе систематических составляющих смещения нулей, отличающийся тем, что для повышения точности калибровки систематических составляющих смещения нулей трехосного лазерного гироскопа с одним общим вибратором и, как следствие, повышения точности бесплатформенных инерциальных систем ориентации и бесплатформенных инерциальных навигационных систем на основе трехосных лазерных гироскопов с одним общим вибратором, калибровку смещений нулей трехосных лазерных гироскопов с одним общим вибратором производят не по непосредственным показаниям трехосных лазерных гироскопов - приращениям интегралов проекций вектора абсолютной угловой скорости на оси чувствительности, а по результирующей погрешности определения пространственной ориентации посредством бесплатформенной инерциальной системы ориентации на основе трехосных лазерных гироскопов с одним общим вибратором.

2. Способ по п.1, отличающийся тем, что для уменьшения времени и упрощения калибровки используют однопозиционный вариант калибровки, при котором трехосный лазерный гироскоп в составе бесплатформенной инерциальной системы ориентации устанавливают на известным образом ориентированном основании, интегрируют кинематические уравнения по алгоритму бесплатформенной инерциальной системы ориентации, используя строгие кинематические уравнения ошибок бесплатформенной инерциальной системы ориентации, учитывая вращение Земли, вычисляют вектор погрешности ориентации 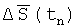$$\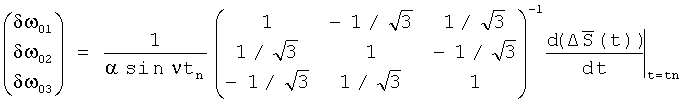Delta \overline{S}(t_n)$$ бесплатформенной инерциальной системы ориентации и калибруют смещения нулей по формуле (sinνt_n≠0)
$$\left(\begin{array}{c}\delta {\omega }_{01}\\ \delta {\omega }_{02}\\ \delta {\omega }_{03}\end{array}\right)=\frac{1}{\alpha \sin \nu t_n}{\left(\begin{array}{ccc}1& -1/\sqrt{3}& 1/\sqrt{3}\\ 1/\sqrt{3}& 1& -1/\sqrt{3}\\ -1/\sqrt{3}& 1/\sqrt{3}& 1\end{array}\right)}^{-1}{\frac{d(\Delta \overline{S}(t))}{dt}|}_{t=tn}$$ ,
где δω_0i, (i=1, 2, 3) - смещения нулей трехосного лазерного гироскопа с одним общим вибратором;
α - амплитуда угловых колебаний вибратора;
ν - круговая частота колебаний вибратора;
t_n - моменты времени.