Изобретение относится к области гидроакустики, а более конкретно к способам измерения глубин с последующей пространственной интерполяцией восстановления рельефа морского дна при дискретных измерениях глубин посредством гидроакустических средств, и может быть использовано при измерении параметров водной среды при решении прикладных задач, включая анализ ветровых полей, анализ радиологического и химического загрязнения, топографические исследования и т.д.
Известен способ определения глубин в стороне от судна посредством гидролокатора бокового обзора (интерферометра) путем измерения дальностей и направлений на элементы отражения донного рельефа на основе использования явления интерференции сигналов донной реверберации, принимаемых на две антенны, разнесенные по вертикали на величину нескольких длин волн упругих колебаний, возбуждаемых одной из антенн интерферометра. В результате выделения и фиксации времени задержки прихода на обе приемные антенны ряда синфазных сигналов, например, на самописце, формируется семейство интерференционных полос, содержащих информацию о направлениях прихода ряда синфазных сигналов и соответствующих им наклонных дальностей до дна (О некоторых особенностях обработки интерференционных эхограмм//Записки по гидрографии. Л.: ГУНиО МО СССР, №203, 1979, с.11-16, [1]. Тарасюк Ю.Ф. Дистанционный промер глубин//Судостроение за рубежом, 1975, №1, с.104-105, [2]. Наумов Е.А. Использование явления интерференции звуковых волн для определения угла наклона дна//Судовождение. Сборник научных трудов ЛВИМУ им. С.О.Макарова, 1974, вып.14, с.252-255, [3]).
Глубины Zn и соответствующие им горизонтальные отстояния Yn от антенн интерферометра вычисляются по формулам [1]:
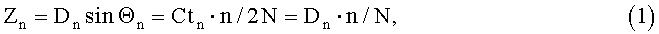
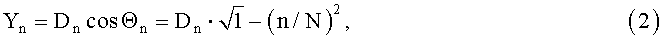
где Θn - углы от горизонта до направления прихода синфазных сигналов;
Dn - наклонные дальности до дна в направлении прихода ряда синфазных сигналов;
С - скорость распространения звука в воде;
n - порядковый номер интерференционной полосы;
N=b/λ - максимальное число ряда регистрируемых интерференционных полос;
λ - длина волны акустических колебаний;
b - величина базового разноса антенн по вертикали;
tn - время задержки прихода ряда синфазных сигналов.
Из формул (1) и (2) следует, что величины углов Θn функционально связаны с номерами интерференционных полос, которые непосредственно не определяются, что обуславливает возможность только качественной оценки характера изменения глубины в стороне от судна, а не количественное определение значений глубин.
Известен также способ определения номеров интерференционных полос, основанный на визуальном дешифровании предвычисленных совпадений полос с заданными номерами из двух семейств интерференционных полос, полученных, например, при использовании двух разных, но близких по величине антенных баз (О некоторых особенностях обработки интерференционных эхограмм//Записки по гидрографии. Л.: ГУНиО МО СССР, №203, 1979, с.11-16, [1]).
Основным недостатком способа является невозможность определения глубин непосредственно во время измерений, а также высокая вероятность ошибки на единицу в оцифровке ряда интерференционных полос при визуальном дешифровании совпадающих полос на зашумленной эхограмме при камеральной обработке. Ошибка в оцифровке полос на единицу приводит к недопустимым погрешностям в определении Zn и Yn. Кроме того, очевидна низкая производительность способа в силу необходимости получения двух семейств интерференционных полос и большой трудоемкости камеральной обработки и, как следствие этого, невысокая достоверность восстановления рельефа дна по измеренным глубинам посредством гидролокатора бокового обзора.
Задачей предлагаемого технического решения является повышение достоверности определения глубин посредством гидролокатора бокового обзора и последующего восстановления рельефа дна по измеренным глубинам посредством гидролокатора бокового обзора.
Поставленная задача решается за счет того, что в способе определения глубин в реальном масштабе времени при обследовании рельефа дна гидролокатором бокового обзора с последующим его восстановлением, включающим измерения времени задержки синфазных сигналов донной реверберации, принимаемых двумя антеннами, разнесенными по вертикали на несколько длин волн упругих колебаний, и разрешение неоднозначности измерений, вычисление глубин, в котором в отличие от прототипа при каждом совпадении фаз интерферирующих сигналов регистрируют мгновенное значение частоты сигнала в нижнем канале, измеряют время запаздывания появления сигнала в верхнем канале с тем же значением мгновенной частоты, измеренное значение времени запаздывания умножают на значение рабочей частоты интерферометра, определяют порядковую нумерацию ряда измерений задержки прихода синфазных сигналов в период каждого зондирования в реальном масштабе времени, глубины вычисляют, соответствующие каждой интерференционной полосе, а при последующем восстановлении рельефа дна по измеренным глубинам выполняют оценку репрезентативности (значимости) критических точек рельефа путем представления гладкой непрерывной поверхности рельефа дна деревом Кронрода-Риба.
Новые отличительные признаки, заключающиеся в том, что при каждом совпадении фаз интерферирующих сигналов регистрируют мгновенное значение частоты сигнала в нижнем канале, измеряют время запаздывания появления сигнала в верхнем канале с тем же значением мгновенной частоты, измеренное значение времени запаздывания умножают на значение рабочей частоты интерферометра, определяют порядковую нумерацию ряда измерений задержки прихода синфазных сигналов в период каждого зондирования в реальном масштабе времени, глубины вычисляют, соответствующие каждой интерференционной полосе, а при последующем восстановлении рельефа дна по измеренным глубинам выполняют оценку репрезентативности (значимости) критических точек рельефа путем представления гладкой непрерывной поверхности рельефа дна деревом Кронрода-Риба, позволяют достичь поставленного технического результата путем выполнения дополнительных измерений времени относительного запаздывания прихода сигналов с одинаковыми мгновенными частотами на разнесенные антенны (Δtn), при этом относительное запаздывание сигналов всегда будет наблюдаться в канале верхней антенны.
Для повышения достоверности измерений величины Δtn в условиях помех они производятся в пределах строба длительностью τ=b/с, а результаты измерений по каждой интерференционной полосе накапливаются за несколько циклов зондирования и осредняются. Повышение точности измерений величины Δtn обеспечивается тем, что в момент выделения синфазных сигналов фиксируется мгновенная частота сигнала на нижней антенне в момент формирования n-й полосы и относительное запаздывание определяется по времени запаздывания прихода сигнала той же частоты на верхнюю антенну.
Измерение времени запаздывания осуществляется по каждой полосе. Основанием к этому служит известное теоретическое положение о том, что сигнал донной реверберации на входе антенны представляет собой узкополосный гауссовский шум с нормальным законом распределения мгновенной частоты в пределах спектра сигнала. Ширина спектра сигнала донной реверберации примерно равна ширине спектра излученного импульса. Плотность вероятности мгновенных значений частоты такого сигнала на выходе предварительного усилителя приемника с высокой степенью точности соответствует также нормальному закону распределения (Ольшевский В.В. Статистические методы в гидролокации. Л.: Судостроение, 1983, с.100-130).
При этом ширина спектра у сигналов донной реверберации, принимаемых интерферометром, зависит от длительности излучаемых импульсов и лежит в пределах 1500÷500 Гц. Мгновенная частота сигнала принимает значение fT±(0÷750)·10-3 кГц, распределенное по нормальному закону. Дисперсия процесса определяется соотношением сигнал/шум.
При условии, что расстояние между антеннами значительно меньше интервала корреляции сигналов (обычно b<50λ), можно утверждать, что разность хода синфазных сигналов пропорциональна времени запаздывания появления в верхнем канале сигнала с мгновенной частотой, фиксированной в нижнем канале на момент стробирования. Очевидно, что 
Подставим в (3) значение sin Θn из формулы (1), получим 
Отсюда 
где F0 - рабочая частота интерферометра.
В случае получения дробных значений n из-за погрешности измерений полученные числа округляются до ближайшего целого.
Критерием достоверности оцифровки является регулярность полученных порядковых номеров. Отдельные выбросы могут быть сразу исправлены без повторных измерений.
Сущность предлагаемого технического решения поясняется чертежами.
Фиг.1. Блок-схема гидролокатора бокового обзора. Гидролокатор бокового обзора включает генератор 1 зондирующих импульсов, приемо-передающую верхнюю антенну 2, схему 3 измерения времени tn, приемо-передающую нижнюю антенну 4, интерферометр 5, схему 6 измерения времени Δtn, селектор 7, частотный детектор 8, опорный генератор 9, запоминающее устройство 10, схему 11 сравнения амплитуд, частотный детектор 12, вычислитель 13, антенный коммутатор 14, устройство 15 отображения и документирования.
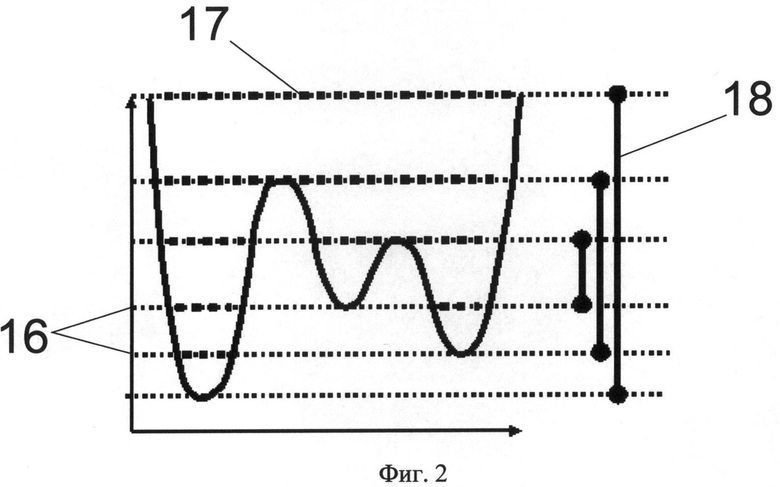
Фиг.2. Пример получения интервалов устойчивости (persistence intervals) для одномерной кривой. 16 - уровни сечения, 17 - отрезки сечения, 18 - интервалы устойчивости.
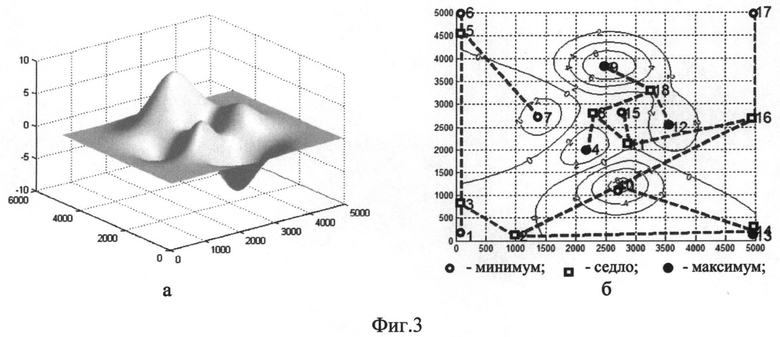
Фиг.3. График поверхности: а) - соответствующие изолинии высот и дерева Кронрода-Риба; б) - 18 критических точек.
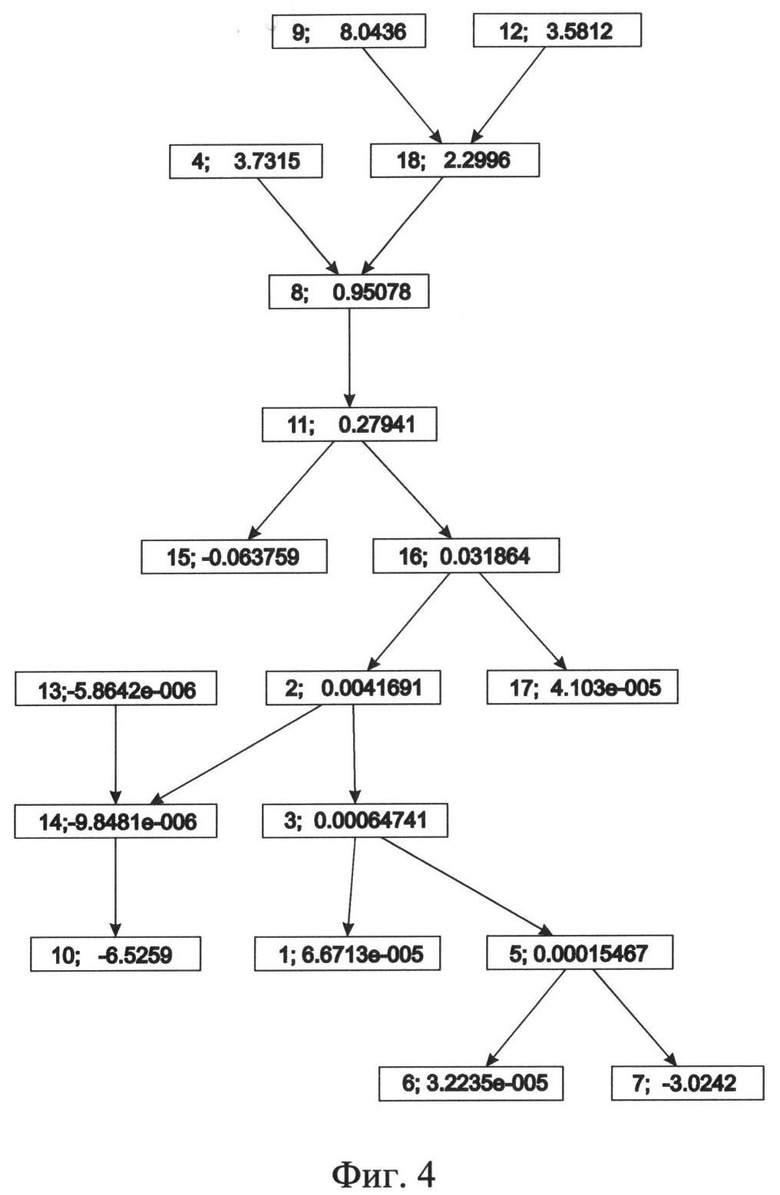
Фиг.4. Вертикальное представление для поверхности дерева Кронрода-Риба фиг.2а. Первая цифра в прямоугольнике - номер критической точки на фиг.26, вторая - высота критической точки.
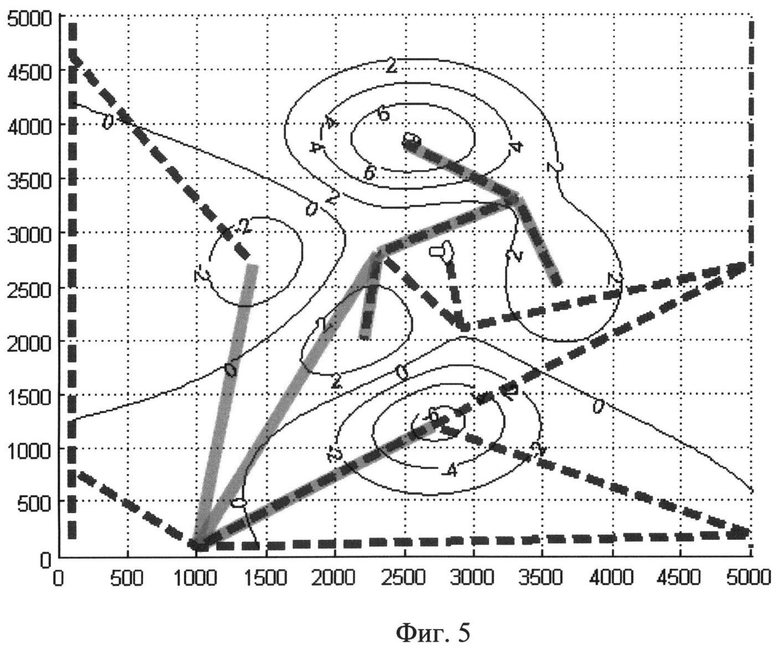
Фиг.5. Дерево Кронрода-Риба для репрезентативных точек поверхности, изображенной на фиг.2а.
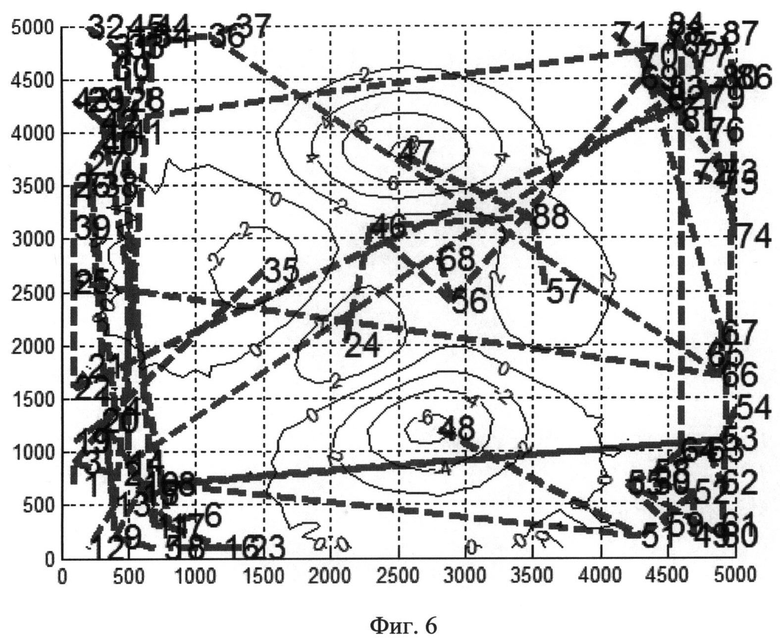
Фиг.6. Дерево Кронрода-Риба для зашумленной поверхности, изображенной на фиг.2а. (88 критических точек).
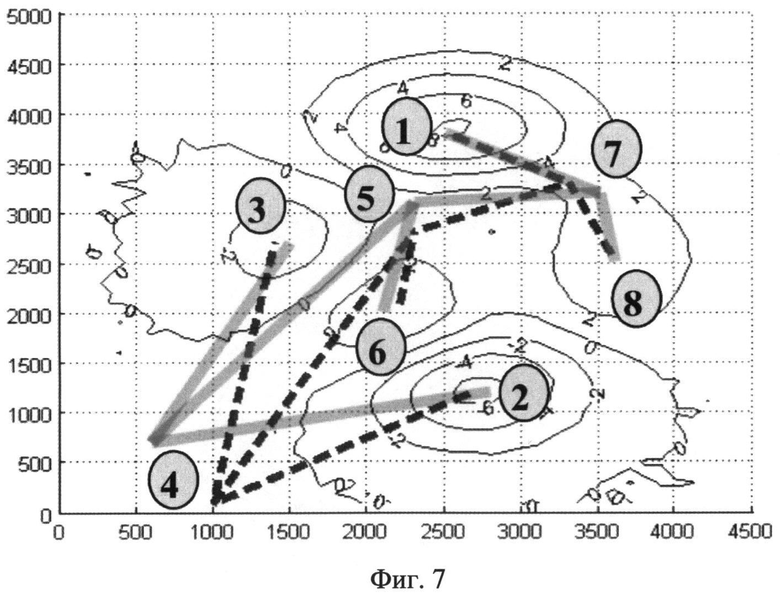
Фиг.7. Дерево Кронрода-Риба для поверхности, изображенной на фиг.2а, и дерево Кронрода-Риба для зашумленной поверхности.
Предлагаемый способ реализуется посредством гидролокатора бокового обзора (фиг.1). С генератора 1 зондирующих импульсов в момент времени t0 импульс с несущей частотой F0 через антенный коммутатор 14 поступает на приемо-передающую антенну 2. Одновременно передним фронтом этого импульса запускается схема 3 измерения времени tn. За период приема сигналов донной реверберации антеннами 2 и 4, в моменты совпадения фаз сигналов на этих антеннах с выхода интерферометра 5 на схему 3 поступает импульс для снятия очередного отсчета времени tn, на запуск схемы 6 измерения времени Δtn и на селектор 7. В селекторе 7 в момент tn производится выборка значения напряжения сигнала, поступающего с частотного детектора 8, при этом значение выборки пропорционально уходу мгновенной частоты сигнала от частоты опорного генератора 9. Значение выборки напряжения сигнала мгновенной частоты фиксируется в запоминающем устройстве 10 в своей ячейке памяти для каждой интерференционной полосы и подается на схему 11 сравнения амплитуд. В момент появления на втором входе схемы 11 сравнения амплитуд такого же значения напряжения сигнала, вырабатываемого частотным детектором 12, с выхода схемы 11 сравнения амплитуд на схему 6 поступает импульс для снятия отсчета времени Δtn.
Измеренные значения tn и соответствующие им значения Δtn подаются на вычислитель 13, реализованный на базе микроЭВМ, где последовательно вычисляется заданный ряд величин Dn и n и соответствующие им значения Zn и Yn. Значения Zn и Yn, увязанные со временем, поступают на устройство отображения и документирования 15.
По результатам измерений посредством устройства отображения и документирования строят рельеф морского дна, который на карте описывается гладкой поверхностью. Форма этой поверхности существенно связана с наличием особых точек поверхности: точек локальных экстремумов (минимумов, максимумов) и седловых точек. Совокупность таких точек, их местоположение и высота являются важными характеристиками в отображении формы поверхности рельефа, так как они играют роль дискретной структуры, репрезентативно представляющей непрерывную поверхность.
Построение поверхности рельефа на ЭВМ устройства отображения и документирования 15 по данным измерений всегда связано с наличием в исходных данных вычислительных и измерительных погрешностей, приводящих к искажениям в форме поверхности. Погрешности приводят как к искажению местоположения репрезентативных присутствующих в реальной поверхности рельефа критических точек, так и появлению нерепрезентативных ложных критических точек. Поэтому актуальна задача выявления репрезентативных критических точек в вычисленной поверхности. Решение этой задачи является необходимым условием для проведения фильтрации шумов и сглаживания вычисленной поверхности.
Решение этой задачи должно опираться на некоторую количественную характеристику, определяющую значимость критической точки для конкретной рассматриваемой поверхности. Пусть задан некоторый допустимый уровень значимости, а критические точки упорядочены в порядке убывания их величин значимости. Тогда репрезентативными будут те критические точки, которые имеют большую значимость, чем допустимый уровень. Алгоритм количественной оценки значимости критических точек основан на следующих определениях.
Так как величины абсолютной высоты (глубины) критических точек не позволяют судить, какие из них более репрезентативные, а какие нет, за исключением только точек с наибольшим значением минимума и максимума. Для определения понятия значимости критической точки поверхности в качестве подходящей основы воспользуемся широко используемым в зарубежной картографии понятием "топографической значимости" (topographic prominence) (Christopherson G.L. Using ARC/GRID to Calculate Topographic Prominence in an Archaeological Landscape. // Arc/INFO User Conference, 2003. - 15 pp. Podobnikar T. Method for Determination of the Mountain Peaks // 12th AGILE International Conference on Geographic Information Science, Leibniz Universitat Hannover, Germany, 2009, p.1-8).
Топографическая значимость - это перепад высот между вершиной и самой высокой седловой точкой, которая отделяет эту вершину от любой более высокой вершины. Однако прямое использование этого понятия в наших целях невозможно. Дело в том, что, во-первых, оно рассматривает только точки локальных максимумов и седловые точки, но не включает в рассмотрение точки локальных минимумов рельефа, и, во-вторых, оно не опирается на математические понятия, что не гарантирует отсутствие логических и алгоритмических ошибок. Последнее проявляется, например, в том, что определение топографической значимости не позволяет сделать однозначный выбор седловой точки, относительно которой отсчитывается высота вершины.
Вместе с тем, в отечественной географии существует схожее по смыслу понятие - "относительная высота", однако оно не совпадает с понятием "топографическая значимость". Относительная высота - это топографическое превышение какой-либо точки земной поверхности относительно другой точки, отсчитываемое по вертикали, равное разности абсолютных высот этих точек (например, высота горной вершины над уровнем дна ближайшей долины); расстояние по вертикали от указанного исходного уровня до уровня, точки или объекта, принятого за точку. Следовательно, понятие относительная высота имеет разный смысл в зависимости от контекста, что не позволяет им воспользоваться. Эта проблема может быть решена, если обобщить понятие топографической значимости путем включения в него локальных минимумов рельефа путем построения однозначного метода выявления для каждой седловой точки соответствующей ей точки минимума или максимума. Главная проблема на этом пути состоит в определении алгоритма выявления соответствия между седловыми точками и точками экстремумов. Эффективный метод оценки значимости можно получить, если использовать инструменты описания гладких функций, к которым относится картографическое представление поверхности рельефа (Жуков Ю.Н Математические инструменты описания картографического отображения рельефа Земли // Навигация и океанография. 2011, №32, стр.60-69).
Картографическое представление рельефа есть аналог математического объекта - невырожденной функции Морса. Такая функция имеет только простые критические точки:
седла, минимумы и максимумы, ее топологические свойства описаны, например, в работе (Милнор Дж. Теория Морса. - М.: Издательство ЛКИ, 2011. - 184 с.). Для функций этого типа разработаны методы выявления и упорядочивания критических точек поверхности с использованием топологических характеристик. В вычислительной топологии этот метод носит название топологической значимости (topological persistence) (Bauer U. Persistence in discrete Morse theory. Dissertation zur Eriangung des mathematisch-naturwissenschaftlichen Doktorgrades Doctor rerum naturalium der Georg-August-Universitat GOttingen, 2011. - 109 p.).
Естественно воспользоваться аналогом этого метода для решения нашей задачи нахождения соответствия между седловыми точками и точками экстремумов поверхности.
Не загружая текст математическими подробностями и деталями, приведем неформальное описание метода, адаптированное к нашей задаче, на примере получения интервалов устойчивости (persistence intervals) для одномерной кривой (фиг.2). Пусть дана гладкая одномерная кривая. Возьмем горизонтальную прямую, секущую данную кривую. На некотором уровне сечение кривой представляет собой набор несвязных горизонтальных интервалов (отрезков). Грубо говоря, целое число интервалов определяет топологический тип сечения на данном уровне. Рассмотрим, как изменяется топологический тип сечений кривой на каждом уровне при перемещении секущей прямой от минимального уровня кривой до наибольшего. При увеличении уровня сечения число интервалов меняется только в момент прохождении секущей через точку, соответствующую либо максимуму, либо минимуму. В диапазоне уровней между двумя последовательными экстремумами число интервалов сечения не меняется. Поэтому динамика числа интервалов сечения в процессе увеличения уровня сечения изменяется в соответствии со следующим простым правилом: если встречается минимум, то число интервалов увеличивается на единицу, если встречается максимум, то число интервалов уменьшается на единицу. В этом процессе всегда есть минимум, который создает интервал, и существует некоторый максимум, который этот интервал уничтожает. Более конкретно: текущий максимум является парой последнему предыдущему встреченному минимуму. Последовательные максимум и минимум являются сопряженной парой экстремумов. Сопряжение пары критических точек обусловлено собственно топологическими свойствами рассматриваемой кривой.
Указанная процедура позволяет однозначно получить множество пар минимумов-максимумов, определяемых топологией кривой. Величина абсолютной разности высот критических точек Δ=|hmin-hmax|, составляющих сопряженную пару, определяет количественную оценку интервала устойчивости и соответствующих сопряженных точек. Полученные указанным методом интервалы устойчивости являются искомыми объектами для одномерного случая.
Приведенный пример для одномерного случая дает основание ввести понятие "значимость" критической точки поверхности рельефа как меры топологической устойчивости той сопряженной пары критических точек, в которую она входит. Количественный критерий значимости ε определим следующим образом. Множеству пар критических точек П сопоставим множество разностей высот критических точек П={Δi} (i=1,…,N, N - число пар). Значимость конкретной пары критических точек в данном множестве пар П определим как отношение εi=Δi/Δmax - максимальное значение среди {Δi}. Таким образом, каждая точка в паре имеет одну и ту же величину значимости. Величина ε всегда нормирована и лежит в диапазоне 0÷1.
Реализация аналогичной процедуры для двумерной поверхности значительно сложнее. Среди критических точек двумерной поверхности появляются седловые точки, которых нет в одномерном случае. Эти точки существенно осложняют дело, так как в седловых точках тоже происходит смена топологического типа горизонтального сечения поверхности, так же как и в точках экстремумов. Кроме того, седловые точки на вертикальной оси всегда лежат между наибольшими максимумом и минимумом. При подъеме плоскости сечения точки седел могут встречаться в любой последовательности по отношению друг к другу и неосновным экстремумам.
В двумерном случае пара критических точек, образующих интервал устойчивости, всегда состоит либо из седла и минимума, либо из седла и максимума. Каждой такой паре критических точек сопоставим величину абсолютной разности высот критических точек Δ=|hs-he|, составляющих пару. Здесь hs - высота седловой точки, he - высота точки экстремума, минимума или максимума.
Для вычисления множества пар критических точек для двумерных гладких поверхностей обычно применяют вспомогательный математический аппарат - дерево Кронрода-Риба (дКР). Картографическое описание рельефа можно представить математическим объектом - функцией Морса, для которой дКР является дискретным аналогом, однозначно описывающим положение, высоту точек седел и локальных экстремумов, и главное, дКР описывает связь между ними, которая определяется топологией рассматриваемой поверхности. Каждой поверхности однозначно соответствует некоторое дКР. К настоящему времени разработаны алгоритмы вычисления дКР для всех типов представления поверхности в ЭВМ (Doraiswamy H., Natarajan V. Efficient Algorithms for Computing Reeb Graphs // Computational Geometry: Theory and Applications, Volume 42, Issue 6-7, August, 2009, p.606-616. Kunii Т.L. Constructing a reeb graph automatically from cross sections. // IEEE Comput. Graph. Appl. 11,6 (1991), 44-51. Pascucci V. Loops in Reeb graphs of 2-manifolds. // Discrete and Computational Geometry 32, 2 (2004), 231-244), и поэтому на процедуре вычисления дКР останавливаться не будем. Отметим важное практическое обстоятельство: вершины дКР естественным образом оснащаются координатами местоположения и высотой соответствующих критических точек.
Пример поверхности и соответствующая ей дКР представлены на фиг.3 и 4. В таблице 1 представлены интервалы устойчивости и величины значимости, вычисленные по дКР. Отметим, что в процессе вычисления дКР его вершины оснащаются пространственными и высотными координатами соответствующих критических точек, что дает возможность отображать дКР в плоскости изучаемой функции и в высотном изображении (фиг.4).
Алгоритм вычисления пар критических точек по дКР очевиден, но достаточно громоздок, чтобы его приводить полностью. В алгоритме используется представление, что точки дКР, соответствующие седлам, являются точками тройного ветвления, а точки, соответствующие минимумам и максимумам, являются точками с одним примыкающим ребром. Приведем только основную схему алгоритма. Ключ алгоритма состоит в использовании динамически меняющегося дКР в соответствии с последовательностью выявляемых пар критических точек. Последовательно просматривается снизу вверх список упорядоченных по высоте критических точек, начиная со второй снизу. Если точка является минимумом или максимумом, то ищется ближайшее к ней в дКР седло. Они образуют пару седло-экстремум. Вершины экстремумов, седел и связывающее их ребро удаляются из дКР, а нарушенные удалением связи восстанавливаются в соответствии с порядком вершин до удаления. Если вершина является седлом и имеет двух нижележащих потомков, то выбирается ближайший по высоте минимум, и они образуют пару критических точек. Соответствующие вершины и ребра удаляются из дКР с последующим восстановлением связей. В результате такого процесса окончательное дКР будет иметь только две вершины, соответствующие наибольшим минимуму и максимуму, и одно соединяющее их ребро. Эта пара критических точек образует наиболее значимую пару с Δmax.
Заметим, что приведенный метод оценки значимости форм рельефа включает понятие топографической значимости, но в отличие от последнего дает однозначный алгоритм получения пар точек седло-экстремум.
Для поверхности, представленной на фиг.3, в соответствии с ее дКР вычислены пары критических точек и их значимость. Результаты представлены в таблице 1.
Таблица 1
Таблица значимости критических точек для поверхности, изображенной на фиг.3.
Номер точки соответствует номеру критических точек на фиг.3б.
Продемонстрируем применение введенного понятия значимости на простейшем примере влияния шума в исходных данных на вычисленную форму поверхности.
Например, из таблицы 1 следует, что для некоторых критических точек их значимость чрезвычайно мала, составляет менее процента. Это признак того, что соответствующие критические точки являются результатом вычислительного шума при расчете поверхности. Эти нерепрезентативные критические точки можно удалить из дКР, оставив только значимые. На фиг.5 показан дКР после удаления.
Введем случайный равномерный на интервале [-0.5 0.5] шум в высотные координаты функции, изображенной на фиг.3а. Результаты построения изолиний такой поверхности и вычисленное для нее дКР представлены на фиг.6.
Из последнего примера следует, что предложенный метод чувствителен к шумовой составляющей. Поэтому он может быть эффективным инструментом в алгоритме предварительного сглаживания поверхности рельефа дна, полученной по измеренным глубинам. Кроме того, приведенные примеры показывают, что подобие двух поверхностей одного участка рельефа можно в первом приближении установить, используя значимые критические точки. Если значимость и пространственные координаты имеют достаточно близкие (с точки зрения решаемой задачи) значения, то соответствующие поверхности подобны. Другие, более тонкие, методы сравнения следует применять после проверки этого соответствия. Для иллюстрации этого утверждения на фиг.6 отображены два дКР для репрезентативных критических точек поверхностей, изображенных на фиг.3 и фиг.6, а в таблице 2 представлены величины значимости для репрезентативных точек этих поверхностей. Последние незначительно меняются под действием шума (таблица 2).
ческой точки
ческой точки
Определение репрезентативных критических точек представляет практическую ценность с точки зрения выявления шумовых возмущений в поверхности и сравнения двух поверхностей между собой. Дерево Кронрода-Риба является основным инструментом и структурой представления топологических и геометрических особенностей репрезентативных критических точек поверхности рельефа. Проблема выявления репрезентативности (значимости) критических точек рельефа с помощью ЭВМ решается путем использования представления гладкой непрерывной поверхности рельефа дна деревом Кронрода-Риба. Такая параметризация поверхности позволяет выявить значимые критические точки поверхности с учетом ее топологической структуры. Данный метод позволяет выявить шумовые возмущения в данных о поверхности и осуществить сравнение топологических свойств двух или нескольких поверхностей, полученных по результатам гидроакустических измерений. Совокупность общих с прототипом и отличительных признаков обеспечивает появление новых свойств у предлагаемого способа, а именно:
- повышение достоверности определения порядковой нумерации ряда наклонных расстояний, соответствующих интерференционным максимумам;
- упрощен процесс разрешения неоднозначности измерений;
- обеспечивается автоматизация определения глубин и их относительных координат в реальном масштабе времени без визуализации интерференционных полос и использования вспомогательной антенной базы;
- определение репрезентативных критических точек рельефа позволяет выявить шумовые возмущения в данных о поверхности и осуществить сравнение топологических свойств двух или нескольких поверхностей, полученных по результатам гидроакустических измерений. Техническая реализация способа осуществляется посредством гидролокатора бокового обзора, имеющего промышленную применимость и на отработанном программном математическом обеспечении. Источники информации.
1. О некоторых особенностях обработки интерференционных эхограмм//Записки по гидрографии. Л.: ГУНиО МО СССР, №203,1979, с.11-16.
2. Тарасюк Ю.Ф. Дистанционный промер глубин//Судостроение за рубежом, 1975, №1, с.104-105.
3. Наумов Е.А. Использование явления интерференции звуковых волн для определения угла наклона дна//Судовождение. Сборник научных трудов ЛВИМУ им. С.О.Макарова, 1974, вып.14, с.252-255.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБНАРУЖЕНИЯ ПОДВОДНЫХ ЗАЛЕЖЕЙ ГАЗОВЫХ ГИДРАТОВ | 2012 |
|
RU2490676C1 |
| СПОСОБ ВИЗУАЛИЗАЦИИ ТЕКУЩЕГО СОСТОЯНИЯ РЕЛЬЕФА ДНА ПРИ РАБОТЕ ЗЕМСНАРЯДА | 2020 |
|
RU2740297C1 |
| СПОСОБ НАВИГАЦИИ АВТОНОМНОГО НЕОБИТАЕМОГО ПОДВОДНОГО АППАРАТА | 2013 |
|
RU2563332C2 |
| СПОСОБ СТЕРЕОСЪЕМКИ РЕЛЬЕФА ДНА АКВАТОРИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2011 |
|
RU2487368C1 |
| СПОСОБ КАРТОГРАФИЧЕСКОГО ОТОБРАЖЕНИЯ ДВУХМЕРНЫХ РАСПРЕДЕЛЕНИЙ, ЗАДАННЫХ В ЦИФРОВОЙ ФОРМЕ | 2011 |
|
RU2484427C1 |
| СПОСОБ КАРТОГРАФИРОВАНИЯ ЛЕДНИКОВОЙ ГЕОМОРФОЛОГИИ | 2014 |
|
RU2570334C1 |
| СПОСОБ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ РЕЛЬЕФА И ОСАДКИ ПОДВОДНОЙ ЧАСТИ АЙСБЕРГА | 2016 |
|
RU2623830C1 |
| Способ измерения глубин в полосе бокового обзора фазового гидролокатора | 1991 |
|
SU1795395A1 |
| СПОСОБ ОБНАРУЖЕНИЯ ПОДВОДНЫХ ФЕРРОМАГНИТНЫХ ОБЪЕКТОВ И СИСТЕМА ДЛЯ ОБНАРУЖЕНИЯ ПОДВОДНЫХ ФЕРРОМАГНИТНЫХ ОБЪЕКТОВ | 2015 |
|
RU2615050C2 |
| СПОСОБ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ ОСАДКИ, ТОЛЩИНЫ И ВЫСОТЫ ЛЬДА | 2012 |
|
RU2500985C1 |
Изобретение относится к области гидроакустики. Сущность: способ определения глубин в реальном масштабе времени при обследовании рельефа дна гидролокатором бокового обзора с последующим его восстановлением, включающий измерения времени задержки синфазных сигналов донной реверберации, принимаемых двумя антеннами, разнесенными по вертикали на несколько длин волн упругих колебаний, и разрешение неоднозначности измерений, вычисление глубин, в котором для достижения технического результата при каждом совпадении фаз интерферирующих сигналов регистрируют мгновенное значение частоты сигнала в нижнем канале, измеряют время запаздывания появления сигнала в верхнем канале с тем же значением мгновенной частоты, измеренное значение времени запаздывания умножают на значение рабочей частоты интерферометра, определяют порядковую нумерацию ряда измерений задержки прихода синфазных сигналов в период каждого зондирования в реальном масштабе времени, глубины вычисляют, соответствующие каждой интерференционной полосе, а при последующем восстановлении рельефа дна по измеренным глубинам выполняют оценку репрезентативности (значимости) критических точек рельефа путем представления гладкой непрерывной поверхности рельефа дна деревом Кронрода-Риба. Гидролокатор бокового обзора включает генератор 1 зондирующих импульсов, приемо-передающую верхнюю антенну 2, схему 3 измерения времени tn, приемо-передающую нижнюю антенну 4, интерферометр 5, схему 6 измерения времени Δtn, селектор 7, частотный детектор 8, опорный генератор 9, запоминающее устройство 10, схему 11 сравнения амплитуд, частотный детектор 12, вычислитель 13, антенный коммутатор 14, устройство 15 отображения и документирования. Технический результат: повышение достоверности определения глубин посредством гидролокатора бокового обзора и последующего восстановления рельефа дна по измеренным глубинам посредством гидролокатора бокового обзора. 7 ил., 2 табл.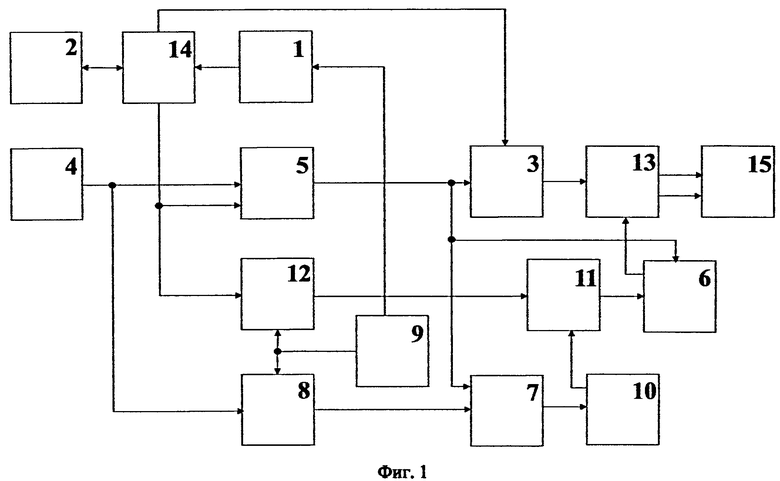
Способ определения глубин в реальном масштабе времени при обследовании рельефа дна гидролокатором бокового обзора с последующим его восстановлением, включающий измерения времени задержки синфазных сигналов донной реверберации, принимаемых двумя антеннами, разнесенными по вертикали на несколько длин волн упругих колебаний, и разрешение неоднозначности измерений, вычисление глубин, отличающийся тем, что при каждом совпадении фаз интерферирующих сигналов регистрируют мгновенное значение частоты сигнала в нижнем канале, измеряют время запаздывания появления сигнала в верхнем канале с тем же значением мгновенной частоты, измеренное значение времени запаздывания умножают на значение рабочей частоты интерферометра, определяют порядковую нумерацию ряда измерений задержки прихода синфазных сигналов в период каждого зондирования в реальном масштабе времени, глубины вычисляют, соответствующие каждой интерференционной полосе, а при последующем восстановлении рельефа дна по измеренным глубинам выполняют оценку репрезентативности (значимости) критических точек рельефа путем представления гладкой непрерывной поверхности рельефа дна деревом Кронрода-Риба.
| СПОСОБ ВОССТАНОВЛЕНИЯ ФОРМЫ РЕЛЬЕФА МОРСКОГО ДНА ПРИ ДИСКРЕТНЫХ ИЗМЕРЕНИЯХ ГЛУБИН ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКИХ СРЕДСТВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2326408C1 |
| ГИДРОАКУСТИЧЕСКАЯ СИСТЕМА ДЛЯ ВИЗУАЛИЗАЦИИ ПОДВОДНОГО ПРОСТРАНСТВА | 2011 |
|
RU2461845C1 |
| СПОСОБ СЪЕМКИ РЕЛЬЕФА ДНА АКВАТОРИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2434246C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ РЕЛЬЕФА МОРСКОГО ДНА ПРИ ИЗМЕРЕНИЯХ ГЛУБИН ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКИХ СРЕДСТВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2429507C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЛУБИН АКВАТОРИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2272303C1 |
| JP60143795 A, 30.07.1985 | |||
Авторы
Даты
2014-06-27—Публикация
2012-10-22—Подача