СПОСОБ УПРАВЛЕНИЯ ИНЕРЦИОННЫМ ПРИВОДОМ АНТЕННЫ, ОБЕСПЕЧИВАЮЩИЙ УСТОЙЧИВОЕ СОПРОВОЖДЕНИЕ ИНТЕНСИВНО МАНЕВРИРУЮЩИХ И ВЫСОКОСКОРОСТНЫХ ВОЗДУШНЫХ ОБЪЕКТОВ Российский патент 2015 года по МПК H01Q25/00 G01S13/66 

Изобретение относится к радиоэлектронным системам сопровождения, в частности к следящим системам по направлению, и может быть использовано для эффективного управления инерционными приводами антенн следящих угломеров в режиме сопровождения различных воздушных объектов, в том числе и интенсивно маневрирующие.

Необходимо подчеркнуть, что использование следящих угломеров с электромеханическим приводом по-прежнему остается актуальным, особенно в летательных системах одноразового применения.

Существующие системы радиолокационного сопровождения с электромеханическим приводом базируются на использовании следящих систем с астатизмом второго (редко - третьего) порядка. Применение в них типовых алгоритмов автоматического сопровождения приводит к существенному несоответствию динамических свойств интенсивно маневрирующих объектов (ИМО) и бортовых систем сопровождения. Это обусловливает отсутствие устойчивого сопровождения объектов при появлении в законах изменения сопровождаемых координат (дальности, углов) производных третьего и более высоких порядков.

Из известных технических решений наиболее близким является способ управления приводом антенны в угломере, приведенный в [2]. В данном алгоритме сигнал управления учитывает ошибки сопровождения по углу и угловой скорости в соответствии с формулой:

где: u_a - сигнал управления приводом антенны; K_φ - постоянный коэффициент усиления, определяющий вес ошибки управления по углу $$\Delta \varphi =\left({\stackrel{\wedge }{\varphi }}_{ц}-{\stackrel{\wedge }{\varphi }}_{а}\right)$$ ; $${\stackrel{\wedge }{\varphi }}_{ц}$$ - оценка пеленга цели; $${\stackrel{\wedge }{\varphi }}_{а}$$ - оценка угла поворота антенны;

K_ω - постоянный коэффициент усиления, определяющий вес сигнала $$\Delta \omega =\left(\stackrel{\wedge }{\omega }{}_{ц}-{\stackrel{\wedge }{\omega }}_{а}\right)$$ ошибки сопровождения по угловой скорости; $$\stackrel{\wedge }{\omega }{}_{ц}$$ - оцененная угловая скорость цели; $$\stackrel{\wedge }{\omega }{}_{а}$$ - оцененная угловая скорость привода антенны.

Недостатками прототипа являются:

1. При используемом в угломере способе управления приводом антенны недостаточно учитывается несоответствие динамических свойств цели и угломера.

2. Низкая устойчивость сопровождения при появлении в законах изменения сопровождаемых координат производных третьего и более высоких порядков.

Эти недостатки обусловлены тем, что в данном алгоритме не учитывается угловая скорость линии визирования. Их можно уменьшить, если управлять динамичностью РЛС с целью приближения ее к динамичности ЛА. Для этого необходимо использовать закон управления РЛС, на стадии синтеза которого будут скомпенсированы инерционные свойства следящей системы. Этого можно достичь учетом угловой скорости линии визирования и ее производных в сигнале управления приводом антенны.

Таким образом, задачей изобретения является разработка способа формирования сигнала управления приводом антенны, обеспечивающего высокоточное, устойчивое сопровождение интенсивно маневрирующих целей по направлению, без изменения конструкции привода.

Поставленная задача достигается тем, что сигнал управления, формируемый взвешенной суммой ошибок сопровождения по углу и угловой скорости, дополняется слагаемыми, учитывающими угловую скорость линии визирования и ее производные, вес которых зависит от соотношения коэффициентов усиления привода и его постоянной времени.

Технический результат, который может быть получен от использования предлагаемого изобретения, заключается в обеспечении высокой точности и устойчивости сопровождения по направлению ИМО.

Сущность предлагаемого изобретения заключается в разработке формирователя сигнала управления приводом антенны, обеспечивающего бессрывное высокоточное сопровождение ИМО. Для решения поставленной задачи воспользуемся математическим аппаратом СТОУ. Это позволяет [1] для системы

предназначенной для отработки процесса

сформировать сигнал управления

оптимальный по минимуму локального функционала качества

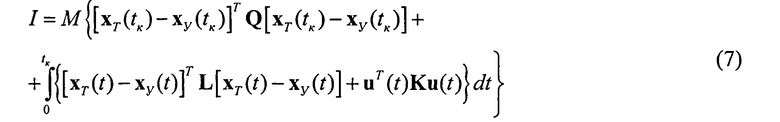
B(2)-(7):

t - текущее время,

x_T, и x_Y - n-мерные векторы состояния цели и следящей системы,

F_T и F_Y - динамические матрицы внутренних связей соответствующих векторов состояния,

u - r-мерный (r≤n) вектор сигналов управления,

B_Y - матрица эффективности r-мерного 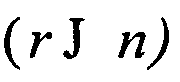вектора управления u,

ξ_У и ξ_Т - векторы шумов состояния,

Q - неотрицательно определенная матрица штрафов за ошибки в момент времени t_K окончания управления,

L - матрица штрафов за ошибки в текущий момент времени t,

K - положительно определенная матрица штрафов за величину сигналов вектора управления u,

P_Y - матрица весовых коэффициентов текущего состояния x_Y,

$$\stackrel{\wedge }{\rho }$$ - оценка вектора, учитывающего внешние воздействия x_T,

$$\stackrel{\wedge }{x}{}_T$$ и $$\stackrel{\wedge }{x}{}_Y$$ - оптимальные оценки векторов x_T и x_Y.

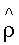
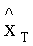
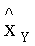
M - знак условного математического ожидания.

В дальнейшем для упрощения записей зависимость векторов и матриц от времени будет опущена.

Использование (4)-(6) не позволяет учесть в законе управления несоответствие динамических свойств цели и угломера. В связи с этим необходимо преобразовать исходное выражение к виду, в котором это несоответствие будет учтено. В общем случае несоответствие динамических свойств РЛС и цели можно выразить вектором ошибок:

изменение которого во времени можно найти посредством решения векторного уравнения:

Учитывая в (9) выражения (2) и (3) получим:

Решение этого неоднородного уравнения состоит из решения однородной части, определяемого первым слагаемым F_YΔx, и частного решения неоднородного уравнения, определяемого вторым и третьим слагаемыми - B_Yu+(F_T-F_Y)x_T.

Отсюда следует, что выбором сигнала управления можно скомпенсировать несоответствие динамических свойств РЛС и цели. Если динамические свойства (2) РЛС соответствуют требуемым значениям (F_Y=F_T), то ошибка будет убывать вплоть до нуля, со скоростью, определяемой динамическими свойствами РЛС (F_Y). В такой ситуации убывание можно ускорить за счет сигнала управления. Иначе, в случае несоответствия динамических свойств (F_Y≠F_T), в решении (10) появляется вынужденная составляющая, и коррекция не всегда будет давать в пределе нулевую ошибку.

Найдем управляющий сигнал, который будет минимизировать ошибку сопровождения при F_Y≠F_T. При использовании общих соотношений (4)-(6) для (10), полагая, что Δx=y получим:

где ξ_yu=(F_T-F_Y)x_T. Тогда сигнал управления:

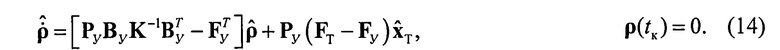
Далее без ограничения общности будем полагать, что наведение осуществляется в горизонтальной плоскости. Воспользовавшись теоремой статистической эквивалентности [1], будем считать, что ξ_Т(t)=0 и ξ_У(t)=0, при этом будем полагать, что используются высокоточные алгоритмы оптимальной фильтрации, при которых $$\stackrel{\wedge }{x}{}_T=x_{Т}$$ , $$\stackrel{\wedge }{x}{}_Y=x_Y$$ .

В качестве модели состояния системы сопровождения воспользуемся типовым уравнением привода антенны [2]:

а в качестве модели движения цели используем кинематические уравнения [2]:

где φ_а и ω_а - угол поворота антенны относительно продольной оси носителя и угловая скорость ее перемещения, T - постоянная времени привода угломера, b - коэффициент его усиления, φ_ц и ω_ц - пеленг цели и угловая скорость линии визирования, ψ - курс носителя, Д и $$\dot{Д}$$ - дальность до цели и ее производная, j_ц и j_н - поперечные ускорения цели и носителя, ξ_а и ξ_ц - шумы состояния привода и цели. Взаимное геометрическое расположение цели и носителя РЛС показано на фигуре 1, на котором точками O_oy и O_ц показано расположение объекта управления (ОУ) и цели. Тогда, исходя из (8), (15) и (16) можно определить ошибки сопровождения по углу и скорости:

Сопоставляя (15)-(17) и (2), (3), запишем в явном виде векторы состояния и динамические матрицы связей системы:

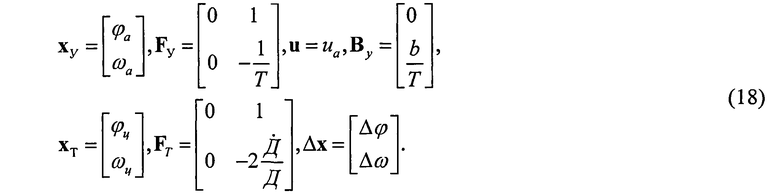
В свою очередь несоответствие динамических свойств РЛС и цели определяется матрицей:

Из (19) следует, что для соответствия динамических свойств цели и следящей системы необходимо выполнение условия $$T=-2Д/\dot{Д}$$ . Однако, при T=const обеспечить это условие невозможно, поскольку Д и $$\dot{Д}$$ меняются в процессе сопровождения. В связи с этим, целесообразно для решения этой задачи использовать расчет сигнала управления по правилу (12)-(14), при условии, что матрицы P_Y, Q, L и вектор ρ введены в общем виде:

Тогда используя (19) и (20) в формулах (12)-(14), получим:

Можно заметить, что система уравнений (22), не решаемая в общем случае в аналитическом виде, должна решаться численно в обратном времени. Следовательно, сигнал управления (21) не может быть получен в режиме реального времени. Однако может быть найдено стационарное решение системы (22) при условии $${\dot{p}}_{11}=0$$ , $${\dot{p}}_{12}=0$$ , $${\dot{p}}_{22}=0$$ , которое имеет место при t<<t_к.

Поскольку момент окончания управления неизвестен, то будет достаточно выбрать конечное время работы системы заведомо больше максимально возможного времени работы следящей системы.

В таком случае можно считать, что требуемое условие будет выполняться на всем участке работы следящей системы

Графики зависимостей p₁₂ и p₂₂, используемых в (21), для некоторых соотношений коэффициентов штрафов показаны на фигурах 2а, б. При этом номера 1, 2, 3, 4 кривых соответствуют парам соотношений 1) (m₁, n₁); 2) (m₂, n₁); 3) (m₁, n₂); 4) (m₂, n₂), где m_i=l₁₁/k, n_i=l₂₂/k, i=1, 2, m₂=100m₁, n₂=2n₁. Установившийся характер этих зависимостей на большей части временного диапазона показывает справедливость сделанных нами допущений (23).

Анализ переходных процессов, имеющих место при вычислении p₁₂, p₂₂, при различных соотношениях коэффициентов штрафов свидетельствуют о том, что время регулирования не превышает двух секунд (фигуры 2а, б). Принимая во внимание условие (23) можно утверждать, что в течение всего времени работы t_РЛС, значения p₁₂, p₂₂ будут постоянными. Это дает возможность при вычислении (21) использовать их установившееся значение. Тогда:

где были учтены выводы теоремы статистической эквивалентности о замене координат состояния их оценками [2].

Анализ закона управления (24) позволяет сделать следующие заключения.

1. Полученный закон отличается от прототипа (1) тем, что в нем учтена угловая скорость линии визирования и ее производные.

2. Варьируя значениями коэффициентов b, p₁₂, p₂₂, k, T можно получить широкий спектр законов управления, обеспечивающих сопровождение ИМО, адаптированных под конкретный тип привода антенны.

3. Для реализации полученного закона сопровождения в угломере требуется оценивать пеленг цели, угол поворота антенны, угловую скорость линии визирования, ее первую и вторую производные, что позволяет скомпенсировать его инерционность.

4. Предложенный алгоритм управления инерционным приводом угломера не накладывает принципиальных ограничений на возможность его реализации.

На основе результатов проведенного анализа следует отметить, что описанный способ управления приводом следящего угломера, в котором дополнительно учитываются угловая скорость и ее производные, является принципиально новым, устраняя недостатки и негативные последствия применения классических методов управления в существующих системах сопровождения по направлению, обеспечивая устойчивое высокоточное сопровождение ИМО. Также следует отметить, что информационное обеспечение алгоритма управления (24) может быть осуществлено в существующих угломерах с учетом реальных ограничений, что свидетельствует о возможности практической реализации метода.

Технический результат, который может быть получен от использования предлагаемого изобретения, заключается в обеспечении высокой точности и устойчивости сопровождения по направлению ИМО. При этом сигнал управления является функцией не только ошибок сопровождения, но и угловой скорости линии визирования, ее первой и второй производных, что собственно и позволяет учесть и скомпенсировать инерционность привода угломера. В этом случае инерционный угломер способен сопровождать цель, двигающуюся по сложному закону.

Проверка работоспособности предложенного способа управления приводом антенны осуществлялась в процессе имитационного моделирования маневра цели и движения антенны в соответствии с моделью (15). Для управления приводом антенны использовались предложенный алгоритм (24) и прототип (1).

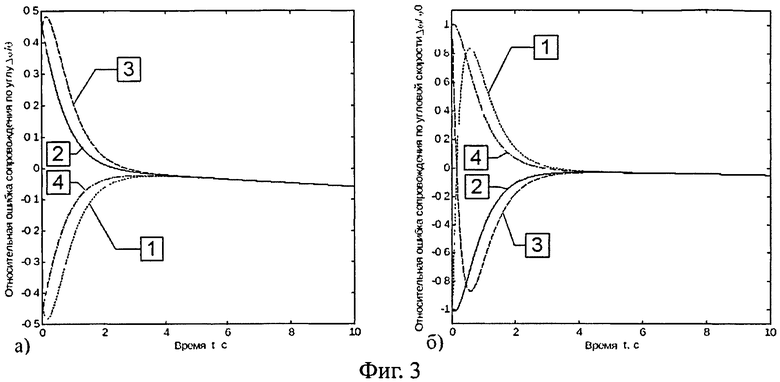
1. Алгоритм способен отрабатывать начальные ошибки сопровождения любого знака и в любом сочетании, что иллюстрируется графиками зависимостей относительных ошибок сопровождения цели по пеленгу и угловой скорости приведенными на фигуре 3, где различными линиями (сплошная, пунктирная, штриховая, штрихпунктирная) изображены зависимости для различных знаков ошибок захвата: 1) Δφ(0)<0, Δω(0)<0; 2) Δφ(0)>0, Δω(0)<0; 3) Δφ(0)>0, Δω(0)>0; 4) Δφ(0)<0, Δω(0)>0.

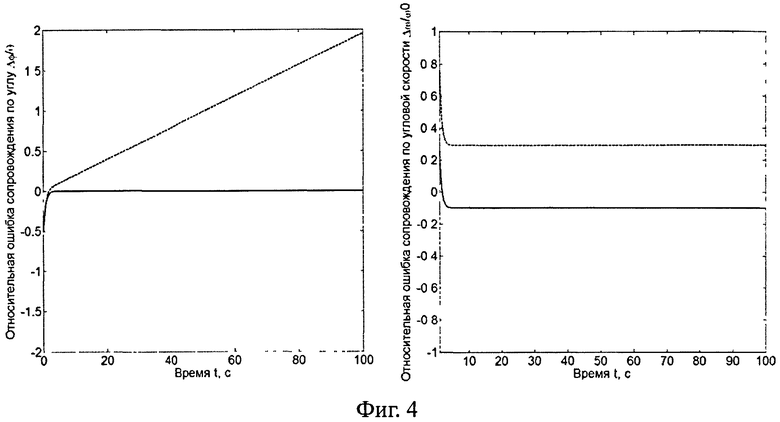
2. На фигуре 4 показано, что предложенный алгоритм способен сопровождать цели, двигающиеся по сложному закону, содержащему производные углов и угловых скоростей высоких порядков:

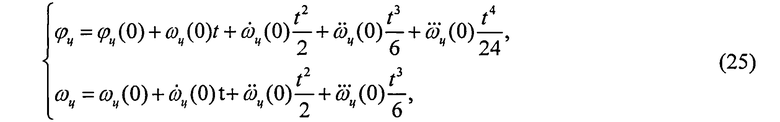
что иллюстрируется графиками зависимостей ошибок сопровождения цели по углу и по угловой скорости при использовании прототипа (пунктирная линия) и предложенного алгоритма (сплошная линия).

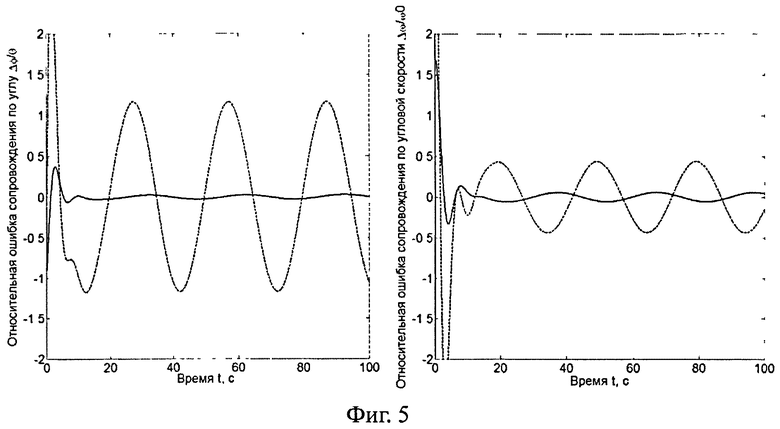
3. Сигнал управления способен обеспечить сопровождение цели, двигающейся по синусоидальному закону, характерному для гиперзвуковых летательных аппаратов:

что иллюстрируется графиками зависимостей ошибок сопровождения цели по углу и по угловой скорости при использовании прототипа (пунктирная линия) и предложенного алгоритма (сплошная линия) приведены на фигуре 5, где пеленг цели изменяется по синусоидальному закону.

Таким образом, на основании проведенных исследований можно сделать вывод, что алгоритм способен сопровождать цели, двигающиеся по любым законам.

В более общем виде алгоритм (24) можно представить в виде

,

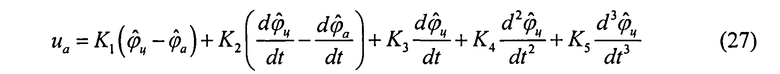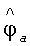
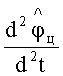
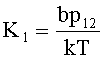
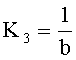
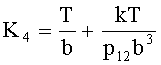
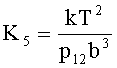
где $${\stackrel{\wedge }{\varphi }}_{а}$$ , $$\frac{d{\stackrel{\wedge }{\varphi }}_{а}}{dt}$$ - оценка угла поворота антенны и его производная; $${\stackrel{\wedge }{\varphi }}_{ц}$$ , $$\frac{d{\stackrel{\wedge }{\varphi }}_{ц}}{dt}$$ , $$\frac{d^2{\stackrel{\wedge }{\varphi }}_{ц}}{d^{2}t}$$ , $$\frac{d^3{\stackrel{\wedge }{\varphi }}_{ц}}{d^{3}t}$$ - оценка пеленга цели и его производные; $$K_1=\frac{b{p}_{12}}{kT}$$ , $$K_2=\frac{b{p}_{22}}{kT}$$ , $$K_3=\frac{1}{b}$$ , $$K_4=\frac{T}{b}+\frac{kT}{p_{12}{b}^3}$$ , $$K_5=\frac{k{T}^2}{p_{12}{b}^3}$$ - постоянные коэффициенты, зависящие от параметров привода антенны, определяющие вес измеряемых сигналов в сигнале управления приводом антенны.

Пример структурной схемы угломера, в котором использован закон управления (24), приведен на фигуре 6, где:

1 - датчик положения антенны

2 - привод угломера

3 - фильтр датчика положения антенны

4 - пеленгатор

5, 6 - вычитающие устройства

7 - фильтр угломера

8, 9, 10, 11, 12 - усилители

13 - сумматор

Примечание: двойная пунктирная линия обозначает механическую связь.

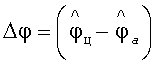
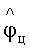
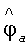
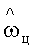
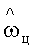
Функциональное назначение представленной на фигуре 6 структурной схемы системы управления приводом угломера заключается в формировании сигнала ошибки сопровождения по углу $$\Delta \varphi =\left({\stackrel{\wedge }{\varphi }}_{ц}-{\stackrel{\wedge }{\varphi }}_{а}\right)$$ , вычитанием из значения оценки пеленга цели $${\stackrel{\wedge }{\varphi }}_{ц}$$ значения оценки угла поворота антенны $${\stackrel{\wedge }{\varphi }}_{а}$$ и усиление его постоянным K₁, зависящим от свойств привода антенны, формировании сигнала ошибки сопровождения по угловой скорости $$\Delta \omega =\left(\stackrel{\wedge }{\omega }{}_{ц}-{\stackrel{\wedge }{\omega }}_{а}\right)$$ , вычитанием из значения оценки угловой скорости цели $$\stackrel{\wedge }{\omega }{}_{ц}$$ значения оценки угловой скорости поворота антенны $${\stackrel{\wedge }{\omega }}_{а}$$ и усиление его постоянным K₂, зависящим от свойств привода антенны, формировании сигнала ошибки сопровождения по угловой скорости $$\Delta \omega =\left(\stackrel{\wedge }{\omega }{}_{ц}-{\stackrel{\wedge }{\omega }}_{а}\right)$$ , вычитанием из значения оценки угловой скорости цели $$\stackrel{\wedge }{\omega }{}_{ц}$$ значения оценки угловой скорости поворота антенны $${\stackrel{\wedge }{\omega }}_{а}$$ и усиление его постоянным K₂, зависящим от свойств привода антенны, формировании сигналов оценки угловой скорости цели $${\stackrel{\wedge }{\omega }}_{ц}$$ , его первой $${\stackrel{\wedge }{\dot{\omega }}}_{ц}$$ и второй производной $$\stackrel{\wedge }{\ddot{\omega }}{}_{ц}$$ , усилении их коэффициентами K₃, K₄, K₅ соответственно. Коэффициенты назначают на стадии разработки угломера и по их значениям определяют коэффициенты усиления соответствующих усилителей.

Использование изобретения позволит осуществлять в угломерах высокоточное устойчивое сопровождение сверхманевренных целей по направлению при использовании обычных инерционных приводов антенн, не требуя изменения конструкции привода антенны.

Кроме того, заявленный способ формирования сигнала управления инерционным приводом антенны позволяет получить большое количество реализации, адаптированных под конкретный вид привода антенны и требуемый закон изменения сопровождаемых координат. Причем эти реализации, соответствующие в общем случае соотношению (24), будут отличаться лишь значениями весовых коэффициентов.

ЛИТЕРАТУРА

1. Меркулов В.И., Дрогалин В.В., Канащенков А.И. и др. Авиационные системы радиоуправления. T.1. Принципы построения систем радиоуправления. Основы синтеза и анализа. / Под ред. А.И. Канащенкова и В.И. Меркулова. - М.: Радиотехника, 2003.

2. Меркулов В.И. [и др.]. Авиационные системы радиоуправления. Т.2. Радиоэлектронные системы самонаведения. Под ред. А.И. Канащенкова и В.И. Меркулова. - М. Радиотехника, 2003. - 390 с.

Изобретение относится к радиоэлектронным системам сопровождения, в частности к следящим системам по направлению (измерителям углов и угловых скоростей линии визирования), в которых используется инерционный привод антенны, и может быть использовано для эффективного управления инерционными следящими системами по направлению в режиме сопровождения различных воздушных объектов, включая интенсивно маневрирующие. Технический результат - повышение точности и устойчивости сопровождения по направлению интенсивно маневрирующих объектов (ИМО). Для этого способ учитывает в законе управления угловую скорость линии визирования, ее первую и вторую производные, а также инерционные свойства привода антенны, при этом в способе в сигнале управления дополнительно учитываются скорость линии визирования, ее первая и вторая производные. 6 ил.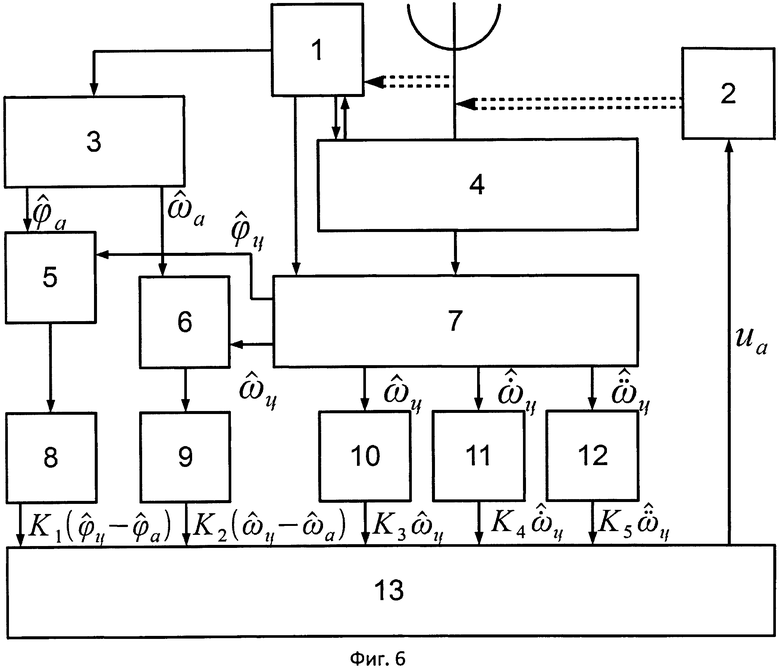

Способ управления инерционным приводом антенны, состоящий в том, что формируют сигналы ошибок сопровождения по пеленгу и угловой скорости цели вычитанием из значения оцененного сигнала пеленга цели значения оцененного сигнала угла поворота антенны и вычитанием из значения оцененного сигнала угловой скорости цели значения оцененного сигнала угловой скорости поворота антенны , усиливая их постоянными коэффициентам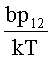и и 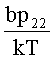, зависящими от свойств привода антенны, отличающийся тем, что дополнительно учитывают в сигнале оценки угловой скорости линии визирования , ее первой 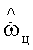и второй 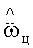производных, усиленные различными коэффициентами , и 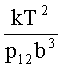, зависящими от параметров привода антенны угломера, и складывают их с усиленными сигналами ошибок сопровождения 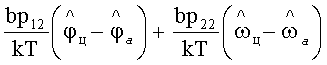, образуя сигнал управления приводом антенны
,
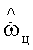где и - оценки угла поворота антенны и ее угловой скорости, и - оценки пеленга цели и угловой скорости линии визирования, и 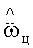- оценки первой и второй производных угловой скорости линии визирования, T - постоянная времени привода угломера, b - коэффициент усиления привода угломера, p₁₂ и p₂₂ - весовые коэффициенты оценки текущего состояния, k - коэффициент штрафа за величину сигнала управления.