Изобретение относится к системам управления, в частности к сложным системам, включающим совместно функционирующие подсистемы с различными динамическими свойствами.
В процессе функционирования сложных систем управления, в которых конечная цель может быть достигнута различными способами [1], возникает задача согласования динамичности различных информационных и управляющих подсистем (устройств), используемых на различных этапах их работы. Под динамичностью систем далее будем понимать их способность реагировать на изменение условий функционирования. От того, в какой степени согласованы динамические свойства подсистем зависит совершенство системы в целом. Вместе с тем в условиях современного стандартизированного производства комплектующие элементы (узлы, устройства), определяемые номенклатурой выпускаемых изделий, как правило, по своим динамическим свойствам не соответствуют всему полю конкретных условий применения сложных систем, поэтому необходимо применить специальные меры по согласованию этих свойств. Кроме того, достаточно часто объекты, на которые направлено целевое воздействие таких систем, имеют сложные, порой непредсказуемые законы функционирования.
Типичными представителями сложных систем являются современные авиационные системы радиоуправления [1]. В этих системах достижение конечного результата (поражение цели) достигается в несколько этапов (дальнее, ближнее наведение, применение средств поражения) с использованием на каждом из них разных методов наведения и различных информационных средств (радиолокационных, оптико-электронных систем и систем радиотехнической разведки, и т.д.). В связи с этим весьма актуальной является задача разработки способов, обеспечивающих согласование динамических свойств подсистем в широком поле условий применения в рамках совместного функционирования в составе сложных технических систем. Следует отметить, что, несмотря на актуальность, данному вопросу не уделяется достаточно внимания в зарубежных и отечественных публикациях [2, 3].
Известен способ компенсации несоответствия динамических свойств, заключающийся использовании пропорционально-дифференциальных управляющих элементов, алгоритмы работы которых основаны на решении уравнения Беллмана [1, стр. 68-72]. При его использовании, сигнал управления формируется на основе полученных измерений, пропорционально разнице управляемых и требуемых координат состояния:

где u - сигнал управления; хт и ху, 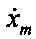 и
и  - требуемые и управляемые координаты состояния и их производные по времени; k1 и k2 - коэффициенты пропорциональности.
- требуемые и управляемые координаты состояния и их производные по времени; k1 и k2 - коэффициенты пропорциональности.
Недостатком описанного способа является отсутствие учета различия динамических свойств входящих в систему подсистем, в связи с чем, при наличии высоких производных во входных сигналах, ошибка управления может нарастать со временем. Этот недостаток особенно сильно проявляется при использовании прототипа при сопровождении интенсивно маневрирующих целей.
Задачей изобретения является преодоление указанного недостатка, разработка способа формирования сигналов управления подсистемами, обеспечивающего согласование динамических свойств функционально связанных подсистем в процессе их совместного функционирования в составе сложных систем.
Поставленная задача достигается тем, что сигнал управления, определяемый взвешенной суммой ошибок функционирования, дополняется слагаемыми, учитывающими более высокие производные координат состояния по сравнению с известными алгоритмами. Данная задача будет решаться на основе экономичной в вычислительном отношении модификации алгоритма оптимизации в рамках линейно-квадратично-гауссовской постановки [4], когда состояние системы определяется линейными уравнениями в процессе минимизации квадратичного функционала качества при наличии гауссовских возмущений.
Технический результат, который может быть получен от использования предлагаемого изобретения, заключается в улучшении показателей эффективности системы в целом, за счет снижения влияния несоответствия динамических свойств отдельных подсистем в системах обеспечения бессрывного сопровождения интенсивно маневрирующей цели.
Сущность предлагаемого изобретения заключается в том, что в системе измеряют фазовые координаты состояния входящих в систему подсистем в процессе их совместного функционирования, формируют сигнал управления подсистемами в виде взвешенной суммы оценок измерений и их производных, обеспечивающий компенсацию несоответствия динамических свойств подсистем на последующих этапах функционирования.
В качестве математического аппарата, решающего эту задачу, использовалась модификация статистической теории оптимального управления (СТОУ), которая позволяет для системы [5]

предназначенной для отработки процесса

сформировать сигнал управления [5]

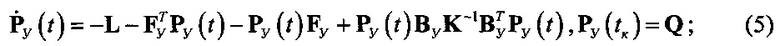
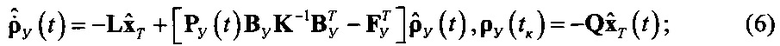
оптимальный по минимуму функционала качества

В (2) - (7):
t - текущее время;
tк - время окончания управления;
хт и ху - n-мерные векторы состояния;
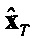 и
и 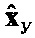 - оптимальные оценки векторов хт и ху;
- оптимальные оценки векторов хт и ху;
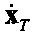 и
и  - производные по времени векторов хт и ху;
- производные по времени векторов хт и ху;
FT и FУ - динамические матрицы внутренних связей соответствующих систем;
u - r-мерный (r≤n) вектор сигналов управления;
BУ - матрица эффективности управления и;
ξУ и ξТ - центрированные гауссовские векторы шумов состояния;
Q - неотрицательно определенная матрица штрафов за ошибки в момент времени tK окончания управления;
L - матрица штрафов за текущие ошибки;
K - положительно определенная матрица штрафов за величину сигнала управления и;
РУ и  - симметричная матрица весовых коэффициентов текущего состояния ху и ее производная по времени;
- симметричная матрица весовых коэффициентов текущего состояния ху и ее производная по времени;
 и
и 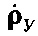 - оценка вектора, учитывающего внешние воздействия хт и его производная по времени;
- оценка вектора, учитывающего внешние воздействия хт и его производная по времени;
М - знак условного математического ожидания.
В дальнейшем для упрощения записей зависимость векторов и матриц от времени будет опущена. Необходимо отметить, что использование (4)-(6) не позволяет в явном виде учесть в законе управления несоответствие динамических свойств подсистем в процессе их совместного функционирования. В связи с этим целесообразно преобразовать исходное выражение к виду, в котором это несоответствие будет учтено в явном виде. В общем случае несоответствие динамических свойств (2) и (3) можно оценить вектором возникающих за счет него ошибок:

изменение которого во времени можно найти посредством решения векторного уравнения:

Учитывая в (9) выражения (2) и (3) получим:
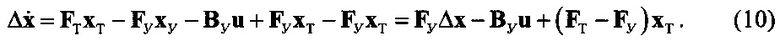
Решение этого неоднородного уравнения состоит из решения однородной части, определяемого первым слагаемым FУΔx, и частного решения неоднородного уравнения, определяемого вторым и третьим слагаемыми -BУu+(FT-FУ)хТ.
Если динамические свойства управляющей системы (2) соответствуют требуемым значениям (FУ=FT), то ошибка будет убывать вплоть до нуля, со скоростью, определяемой ее динамическими свойствами (FУ). В случае несоответствия динамических свойств (FУ≠FT), в решении (10) появляется вынужденная составляющая, зависящая от характера изменения хТ и воздействующего управления и. Отсюда следует, что выбором сигнала управления можно скомпенсировать несоответствие динамических свойств системы (2) при отработке входного воздействия (3).
Найдем управляющий сигнал, который будет минимизировать ошибку управления при FУ≠FТ. При использовании общих соотношений (4)-(6) для (10), полагая, что Δх=у получим:

где ξyu=(FT-FУ)xТ - измеряемое возмущение. Тогда, с учетом (11), сигнал управления, минимизирующий (7), определяемый соотношениями (4)-(6) преобразуется к виду:


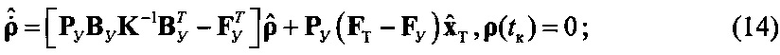
где было учтено, что в рассматриваемом случае требуемое значение уТ=0.
Необходимо отметить, что в законе управления (12)-(14) вектор р, наряду со свойствами управителя (FУ, РУ, BУ) и требованиями экономичности (K), учитывает влияние несоответствия динамических свойств (FT-FУ) при заданном законе изменения хт с весом, определяемым матрицей РУ. В общем виде закон (12)-(14) может быть представлен в виде соотношения:

где Kш 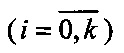 - коэффициенты, зависящие от несоответствия динамических свойств (FT-FУ).
- коэффициенты, зависящие от несоответствия динамических свойств (FT-FУ).
Эффективность предложенного способа устранения несоответствия динамических свойств проверим на примере системы сопровождения цели по направлению, в которой осуществляется согласование динамических свойств.
В качестве модели состояния системы сопровождения воспользуемся типовым уравнением привода антенны [6]:

а в качестве модели движения цели используем кинематические уравнения [6]:

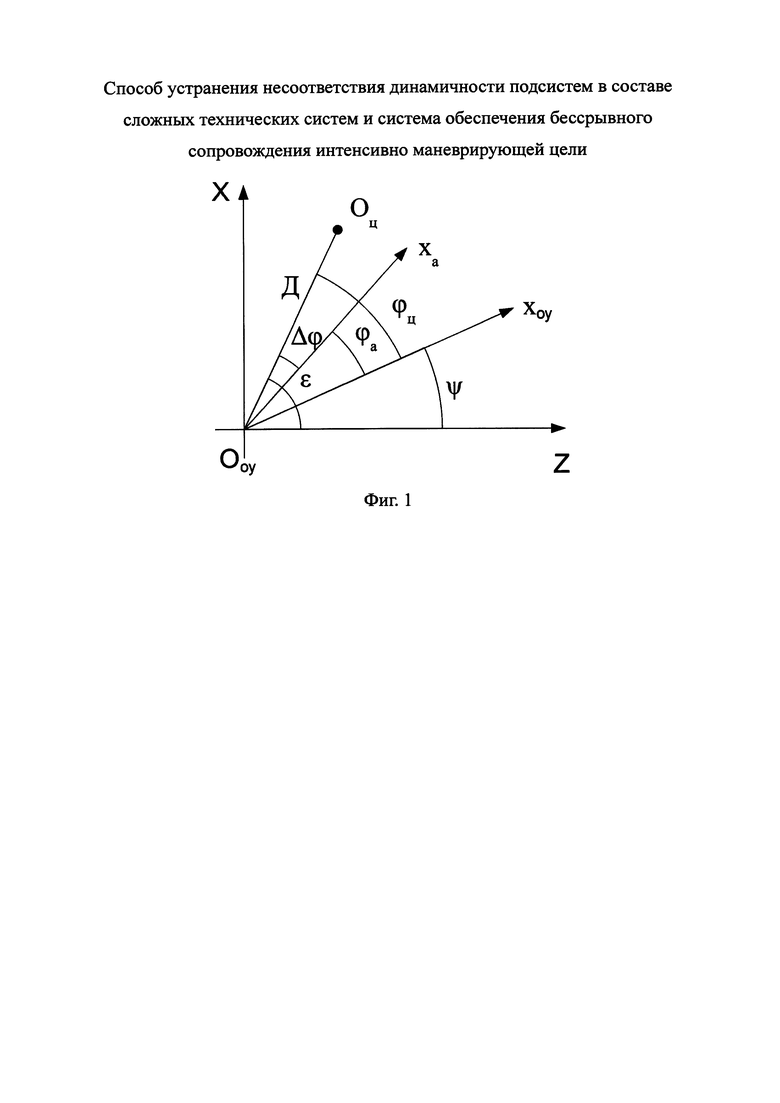
где ϕа и ωа - угол поворота антенны относительно продольной оси носителя и угловая скорость ее перемещения, Т - постоянная времени привода угломера, b - коэффициент его усиления, ϕц и ωц - пеленг цели и угловая скорость линии визирования, Д и 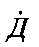 - дальность до цели и ее производная, jц и jн - поперечные ускорения цели и носителя, ξа и ξц - шумы состояния привода и цели. Взаимное геометрическое расположение цели и носителя РЛС в одной плоскости показано на фигуре 1, на котором точками Ооу и Оц показано расположение объекта управления и цели, Ха - соответствует равносигнальному направлению антенны, а Хоу - продольной оси носителя РЛС.
- дальность до цели и ее производная, jц и jн - поперечные ускорения цели и носителя, ξа и ξц - шумы состояния привода и цели. Взаимное геометрическое расположение цели и носителя РЛС в одной плоскости показано на фигуре 1, на котором точками Ооу и Оц показано расположение объекта управления и цели, Ха - соответствует равносигнальному направлению антенны, а Хоу - продольной оси носителя РЛС.
Достоинством модели (17) является ее адекватность реальным условиям перемещения цели в широком поле условий применения. Это обусловливается не только учетом зависимости линейных и угловых перемещений, но и возможностью за счет манипуляции поперечными ускорениями цели и носителя РЛС реализовать самые разнообразные законы изменения угловых координат, в том числе и с переменными временными показателями.
Исходя из (8) и (16), (17) можно определить ошибки сопровождения по углу и угловой скорости:

Необходимо подчеркнуть, что при появлении в (17) третьей и более высоких производных ϕц в угломере с приводом (16) появляются нарастающие ошибки сопровождения (18) приводящие, в конечном счете, к срыву этого процесса [7].
Сопоставляя (16)-(18) и (2), (3), представим в явном виде векторы состояния и динамические матрицы связей системы:
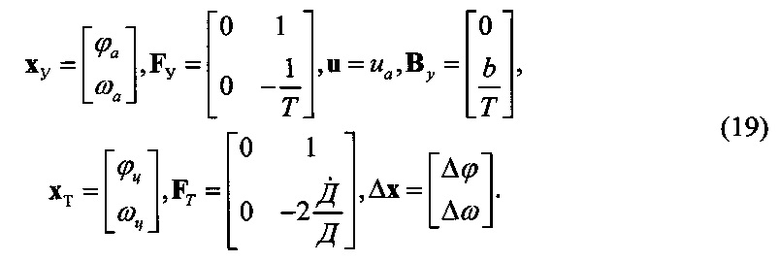
В свою очередь несоответствие динамических свойств РЛС и цели определяется матрицей:

Из (20) следует, что для соответствия динамических свойств следящей системы и цели необходимо выполнение условия 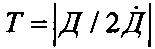 . Однако, при Т=const обеспечить это условие невозможно, поскольку Д и
. Однако, при Т=const обеспечить это условие невозможно, поскольку Д и  меняются в процессе сопровождения. В связи с этим, целесообразно для решения этой задачи использовать способ формирования сигнала управления угломером по правилу (15), при условии, что матрицы РУ, Q, L и вектор р введены в общем виде:
меняются в процессе сопровождения. В связи с этим, целесообразно для решения этой задачи использовать способ формирования сигнала управления угломером по правилу (15), при условии, что матрицы РУ, Q, L и вектор р введены в общем виде:
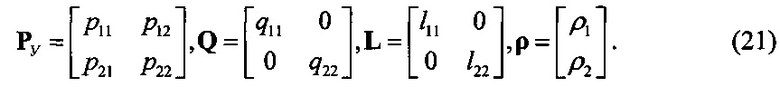
Коэффициенты (21) выбираются согласно принципу равнопрочности [1], заключающемся в том, что ошибка по каждой координате вносит одинаковый вклад в сигнал управления и устанавливающим каждый коэффициент обратно пропорциональным дисперсии значения соответствующей ему координаты. Однако в реальных условиях применения, как правило, вклад ошибок по различным координатам состояния различен. В частности, при наведении ракет ошибки по углам вносят больший вклад, чем ошибки по дальностям; ошибки более высоких производных координат состояния, как правило, вносят меньший вклад, чем ошибки производных меньших порядков. В связи с этим, в дальнейшем коэффициенты могут быть уточнены в процессе имитационного моделирования, исходя из реальных условий применения моделируемой системы.
Тогда используя (19)-(21) в формулах (12)-(14), получим:
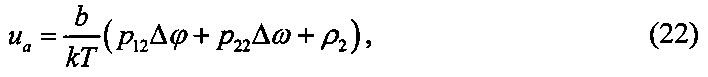

Можно заметить, что система уравнений (23), не решаемая в общем случае в аналитическом виде, должна решаться численно в обратном времени от tк к t. Следовательно, сигнал управления (22) не может быть получен в режиме реального времени.
Поскольку момент окончания управления, как правило, неизвестен, то будет достаточно выбрать конечное время работы системы заведомо больше максимально возможного времени работы следящей системы:

В таком случае можно считать, что требуемое условие будет выполняться на всем участке работы следящей системы.
С целью проверки справедливости утверждения (24), проводилось имитационное моделирование процесса сопровождения цели угломером, с использованием моделей (16) и (17). Графики зависимостей р12 (сверху) и р22 (снизу) от времени, полученные в процессе моделирования, представлены на фигуре 2. Анализ переходных процессов в изменениях p12, р22, имеющих при этом место, при различных соотношениях коэффициентов штрафов свидетельствуют о том, что в реальном диапазоне значений Т и b время регулирования не превышает двух-трех секунд. Установившийся характер этих зависимостей на большей части временного диапазона позволяет найти стационарное решение системы (23) при условии 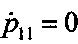 ,
,  ,
,  , которое имеет место при t<tк. Принимая во внимание условие (24) можно утверждать, что в течение всего времени работы tРЛС значения р12, р22 будут постоянными. Это дает возможность при вычислении (23) использовать их установившееся значение. Тогда:
, которое имеет место при t<tк. Принимая во внимание условие (24) можно утверждать, что в течение всего времени работы tРЛС значения р12, р22 будут постоянными. Это дает возможность при вычислении (23) использовать их установившееся значение. Тогда:
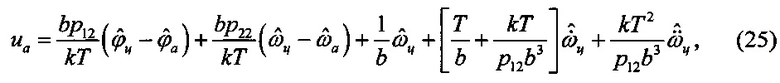
где были учтены выводы теоремы статистической эквивалентности о замене координат состояния их оценками [4].
Анализ закона управления (25) позволяет сделать следующие заключения:
- полученный закон отличается от классического тем, что в нем наряду с ошибками по углу и угловой скорости учтены угловая скорость линии визирования и ее производные;
- варьируя значениями коэффициентов b, р12, р22, k, Т можно получить широкий спектр законов управления, адаптированных под конкретный тип привода антенны, обеспечивающих сопровождение интенсивно маневрирующих целей;
- для реализации полученного закона сопровождения в угломере требуется оценивать пеленг цели, угол поворота антенны и его производную, угловую скорость линии визирования, и две ее производных;
- предложенный алгоритм управления инерционным приводом угломера не накладывает принципиальных ограничений на возможность его реализации.
Исследование полученного алгоритма проводилось по результатам имитационного моделирования сложных пространственных эволюций интенсивно маневрирующей цели, содержащих высокие производные угловых координат, определяемых законами изменения угла и угловой скорости:

которые не соответствуют модели (17), положенной в основу синтеза закона управления. Достоинством (26) является то, что манипулируя 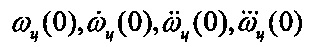 можно получить законы изменения ϕц и ωц практически любой сложности. Наряду с моделированием (26), моделировался привод (16) и алгоритм управления (25).
можно получить законы изменения ϕц и ωц практически любой сложности. Наряду с моделированием (26), моделировался привод (16) и алгоритм управления (25).
В ходе моделирования полученный закон сравнивался с используемыми на практике модификациями, в которых учитываются только ошибки по углу, либо ошибки по углу и угловой скорости:


Кроме того, проводилось сравнение полученного алгоритма (25) с его упрощенными вариантами:

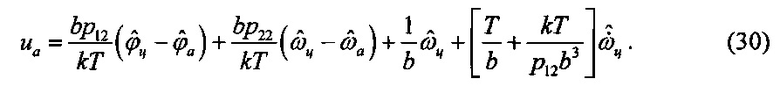
Полученные в ходе моделирования зависимости относительных ошибок сопровождения по углу (слева) и угловой скорости (справа) от времени отображены на фигуре 3, где различным линиям соответствуют различные алгоритмы управления: 1 - (25), 2 - (30), 3 - (29), 4 - (28), 5 - (27). Из рисунков видно, что упрощенные варианты управления (27)-(28), не учитывающие производные угловой скорости не способны устойчиво сопровождать интенсивно маневрирующие цели.
По результатам моделирования можно сделать следующие выводы:
- система устойчиво отрабатывает первоначальные ошибки захвата любых знаков при любом их сочетании, даже при достаточно большом времени регулирования (16), что иллюстрируется графиками зависимостей относительных ошибок сопровождения цели по пеленгу и угловой скорости приведенными на фигуре 4, где различными линиями изображены зависимости для различных знаков ошибок захвата: 1 - Δϕ(0)>0, Δω(0)>0, 2 - Δϕ(0)>0, Δω(0)<0, 3 - Δϕ(0)<0, Δω(0)>0, 4 - Δϕ(0)<0, Δω(0)<0;
- результаты исследования показали, что сигнал управления способен обеспечить сопровождение цели, бортовой пеленг которой изменяется по сложным законам с минимальными ошибками сопровождения, что иллюстрируется графиками зависимостей ошибок сопровождения цели по углу и по угловой скорости на фигуре 3, где различными линиями изображены зависимости ошибок для алгоритмов различной сложности.
На основе результатов проведенного анализа следует отметить, что описанный способ управления инерционным приводом следящего угломера, в котором дополнительно учитываются угловая скорость и ее производные, позволяет создать систему сопровождения по направлению, обеспечивающую в отличие от существующих бессрывное высокоточное сопровождение интенсивно маневрирующих целей.
Таким образом, проведенные исследования позволяют сделать следующие заключения:
1. Предложенный способ позволяет скомпенсировать несоответствие динамичности подсистем в процессе совместного функционирования, не накладывая принципиальных ограничений на возможность его реализации;
2. Для реализации предлагаемого способа необходимо формировать оценки производных координат цели более высокого порядка;
3. Система сопровождения, построенная на основе предложенного способа, позволяет обеспечить высокоточное бессрывное сопровождение интенсивно маневрирующих целей.
На основе результатов проведенного анализа следует отметить, что описанный способ управления приводом следящего угломера, в котором дополнительно учитываются угловая скорость и ее производные, позволяет устранить недостатки и негативные последствия классических методов управления в существующих системах сопровождения по направлению, обеспечивая устойчивое высокоточное сопровождение интенсивно маневрирующих объектов.
Упрощенная структура системы, реализующей предложенный способ, показана на фигуре 5, где:
1 - первичный измеритель;
2 - фильтр, формирующий оценки 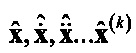 ;
;
3 - блок усилителей, формирующий сигналы 
4 - сумматор, формирующий сигнал управления и согласно (15);
5 - управляющий элемент;
Функциональное назначение представленной на фигуре 5 структурной схемы соединения подсистем системы управления заключается в формировании сигнала управления в виде взвешенной суммы оценок  фазовых координат системы с коэффициентом K0 и оценок их производных
фазовых координат системы с коэффициентом K0 и оценок их производных 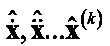 с коэффициентами K1, K2…Kk являющимися функциями несоответствия динамических свойств fi(FT-FУ), где
с коэффициентами K1, K2…Kk являющимися функциями несоответствия динамических свойств fi(FT-FУ), где  .
.
Использование изобретения позволит осуществлять совместное высокоточное устойчивое функционирование подсистем с различными динамическими свойствами в широком диапазоне условий применения, не требуя изменения конструкции первичных измерителей системы отработки и не накладывая ограничений на вид согласуемых подсистем. Также следует отметить, что информационное обеспечение получаемых алгоритмов управления может быть осуществлено в существующих системах с учетом реальных ограничений, что свидетельствует о возможности практической реализации метода.
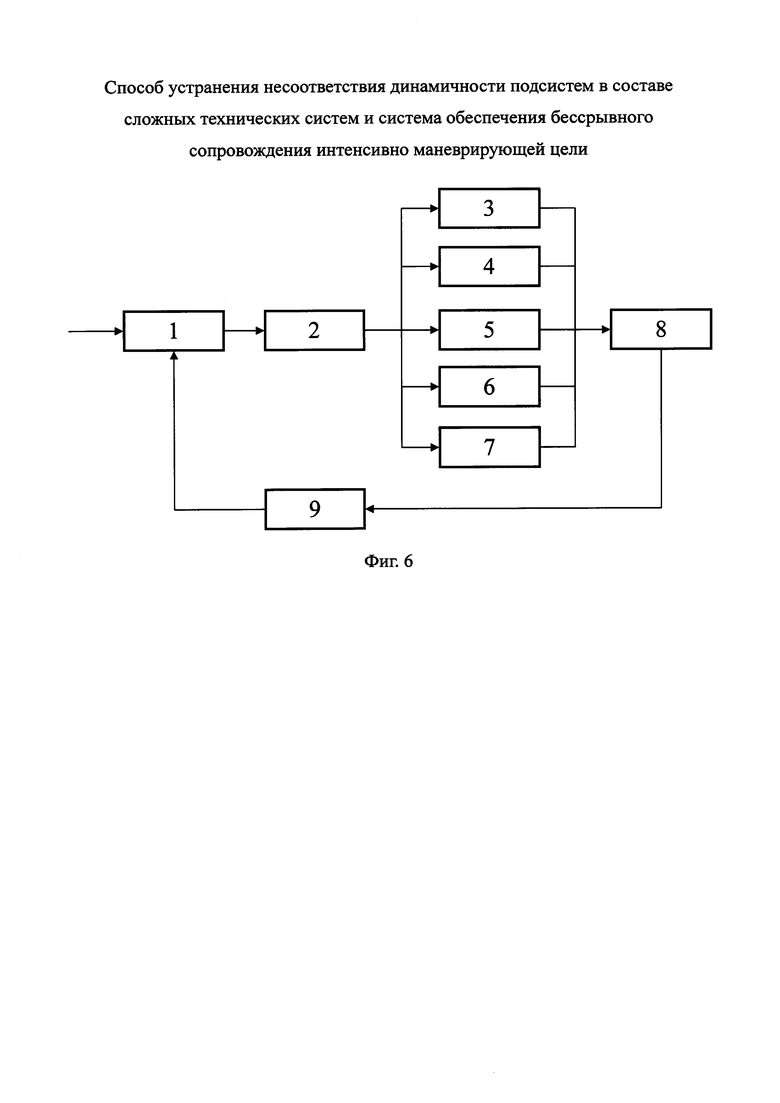
На фигуре 6 представлена схема системы обеспечения бессрывного сопровождения интенсивно маневрирующей цели с использованием предлагаемого способа устранения несоответствия динамических свойств подсистем, где:
1 - антенна,
2 - фильтр, формирующий оценки 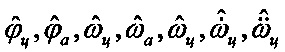 ,
,
3 - усилитель, формирующий сигнал 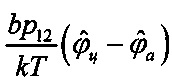 ,
,
4 - усилитель, формирующий сигнал 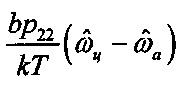 ,
,
5 - усилитель, формирующий сигнал 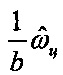 ,
,
6 - усилитель, формирующий сигнал 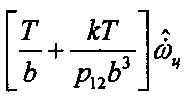 ,
,
7 - усилитель, формирующий сигнал  ,
,
8 - сумматор, формирующий сигнал управления ua,
9 - привод антенны.
Литература
1. Меркулов В.И., Дрогалин В.В., Канащенков А.И. и др. Авиационные системы радиоуправления. Т. 1. Принципы построения систем радиоуправления. Основы синтеза и анализа. / Под ред. А.И. Канащенкова и В.И. Меркулова. - М.: Радиотехника, 2003.
2. Меркулов В.И. Динамичность авиационных комплексов и бортовые радиоэлектронные системы. Радиотехника. - 2010, №1. - С. 88-96.
3. Ильчук А.Р., Меркулов В.И., Самарин О.А., Юрчик И.А. Влияние интенсивного маневрирования целей на показатели эффективности системы первичной обработки сигналов в бортовых РЛС. Радиотехника. - 2003, №6.
4. Черноусько Ф.А., Колмановский В.Б. Оптимальное управление при случайных возмущениях. - М.: Наука, 1978.
5. Максимов М.В., Меркулов В.И. Радиоэлектронные следящие системы. Синтез методами оптимального управления. - М.: Радио и связь, 1990.
6. Меркулов В.И., Дрогалин В.В., Канащенков А.И. и др. Авиационные системы радиоуправления. Т. 2. Радиоэлектронные системы самонаведения / Под ред. А.И. Канащенкова и В.И. Меркулова. - М.: Радиотехника, 2003.
7. Перов А.И., Замолодчиков В.Н., Чиликин В.М. Радиоавтоматика. Учебник для вузов. - М.: Радиотехника, 2014.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ ИНЕРЦИОННЫМ ПРИВОДОМ АНТЕННЫ, ОБЕСПЕЧИВАЮЩИЙ УСТОЙЧИВОЕ СОПРОВОЖДЕНИЕ ИНТЕНСИВНО МАНЕВРИРУЮЩИХ И ВЫСОКОСКОРОСТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ С ПОВЫШЕННОЙ АДАПТАЦИЕЙ К МАНЕВРУ НОСИТЕЛЯ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2598001C2 |
| Способ наведения инерционного летательного аппарата с учетом несоответствия динамических свойств цели и перехватчика | 2019 |
|
RU2727777C1 |
| Способ нелинейного управления инерционным приводом антенны, обеспечивающий высокую устойчивость сопровождения интенсивно маневрирующих объектов | 2017 |
|
RU2661346C1 |
| СПОСОБ УПРАВЛЕНИЯ ИНЕРЦИОННЫМ ПРИВОДОМ АНТЕННЫ, ОБЕСПЕЧИВАЮЩИЙ УСТОЙЧИВОЕ СОПРОВОЖДЕНИЕ ИНТЕНСИВНО МАНЕВРИРУЮЩИХ И ВЫСОКОСКОРОСТНЫХ ВОЗДУШНЫХ ОБЪЕКТОВ | 2014 |
|
RU2571363C2 |
| СПОСОБ МНОГОСТУПЕНЧАТОЙ ФИЛЬТРАЦИИ ДЛЯ СИСТЕМ АВТОСОПРОВОЖДЕНИЯ | 2015 |
|
RU2616188C1 |
| Способ перехвата интенсивно маневрирующих высокоскоростных воздушно-космических объектов | 2017 |
|
RU2666069C1 |
| СПОСОБ УПРАВЛЕНИЯ ПОЛОЖЕНИЕМ ОСИ АНТЕННЫ БОРТОВОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИИ ПРИ СОПРОВОЖДЕНИИ МЕНЕВРИРУЮЩЕЙ ВОЗДУШНОЙ ЦЕЛИ | 2020 |
|
RU2758446C1 |
| СПОСОБ ИНДИВИДУАЛЬНОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА НА ВОЗДУШНУЮ ЦЕЛЬ В СОСТАВЕ ПЛОТНОЙ ГРУППЫ | 2020 |
|
RU2742626C1 |
| СПОСОБ ТРАССОВОГО СОПРОВОЖДЕНИЯ ВОЗДУШНЫХ МАНЕВРИРУЮЩИХ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ ПО ПЕЛЕНГОВОЙ ИНФОРМАЦИИ ОТ ОДНОПОЗИЦИОННОЙ СИСТЕМЫ РАДИОТЕХНИЧЕСКОЙ РАЗВЕДКИ ВОЗДУШНОГО БАЗИРОВАНИЯ | 2017 |
|
RU2660498C1 |
| МОНОИМПУЛЬСНОЕ РАДИОЛОКАЦИОННОЕ УСТРОЙСТВО СОПРОВОЖДЕНИЯ ПО НАПРАВЛЕНИЮ | 2004 |
|
RU2273863C1 |




Изобретение относится к системам управления. Способ формирования сигнала управления для сопровождения цели заключается в том, что сигнал управления формируется по закону на основе динамических матриц внутренних связей систем, обобщенного вектора состояния системы и вектора сигналов управления. Сигнал управления состоит из взвешенной суммы фазовых координат и их производных, входящих в сигнал управления с пропорциональными коэффициентами, зависящими от несоответствия динамических свойств динамических матриц внутренних связей систем. Система формирования сигнала управления для инерционного пеленгатора включает измеритель, фильтр, усилитель, сумматор, управляющий элемент. Дополнительно введены усилители с коэффициентами, зависящими от разности матриц и фильтры высоких производных отслеживаемых координат. Значения несоответствия по производным поступают на вход сумматора. Улучшаются показатели эффективности системы. 2 н.п. ф-лы, 6 ил.
1. Способ формирования сигнала управления для сопровождения цели, заключающийся в том, что сигнал управления формируется по закону:

в результате чего сигнал управления состоит из взвешенной суммы фазовых координат и их производных, входящих в сигнал управления с пропорциональными коэффициентами, зависящими от несоответствия динамических свойств FТ и FУ, где:
x - обобщенный вектор состояния системы;
FТ и FУ - динамические матрицы внутренних связей соответствующих систем;
u - r-мерный (r≤n) вектор сигналов управления.
2. Система формирования сигнала управления, реализующая способ по п. 1 для инерционного пеленгатора и включающая измеритель, фильтр, усилитель, сумматор, управляющий элемент, отличающаяся тем, что в нее дополнительно введены усилители с коэффициентами, зависящим от разности матриц FТ и FУ, фильтры высоких производных отслеживаемых координат, при этом значения несоответствия по производным поступают на вход сумматора, усиленные коэффициентами, зависящими от разности матриц FТ и FУ, получаемыми при решении уравнений из п. 1.
| СПОСОБ АВТОМАТИЧЕСКОГО СОПРОВОЖДЕНИЯ ЦЕЛЕЙ В РЕЖИМЕ ОБЗОРА | 2001 |
|
RU2207589C2 |
| ИНФОРМАЦИОННО-ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА БЕСПИЛОТНОГО САМОЛЕТА-ИСТРЕБИТЕЛЯ | 2010 |
|
RU2418267C1 |
| СПОСОБ РАНЖИРОВАНИЯ ЦЕЛЕЙ | 2000 |
|
RU2190863C2 |
| СПОСОБ ПРОПОРЦИОНАЛЬНОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ НА НАЗЕМНЫЕ ОБЪЕКТЫ | 1999 |
|
RU2148235C1 |
| СПОСОБ КОМАНДНОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА НА НАЗЕМНЫЕ ЦЕЛИ | 2009 |
|
RU2408846C1 |
Авторы
Даты
2017-04-28—Публикация
2015-05-13—Подача