Предлагаемое техническое решение относится к области измерительной техники для измерения угла поворота и угловой скорости и может найти применение в метрологии, измерительных системах и системах управления различными объектами.
Широко известен способ калибровки угловых датчиков с помощью эталонных датчиков, у которых погрешность преобразования угла много раз меньше, чем ожидаемая погрешность калибруемого датчика. В этом случае любые расхождения в получаемых значениях углов, задаваемых с помощью эталонного датчика и зарегистрированные на выходе системы калибровки, однозначно трактуются как погрешность калибруемого датчика. Применение данного способа калибровки угловых датчиков не вызывало каких-либо затруднений в случаях, когда ожидаемая погрешность калибруемого датчика лежала в диапазоне от (15…20) угловых секунд и выше. Для этого достаточно было взять в качестве эталонного датчика датчик с погрешностью измерений порядка (1,5…2,0) угловых секунды, достаточно просто приобретаемом у отечественных или зарубежных изготовителей углоизмерительных приборов.
Заметно сложнее осуществить калибровку угловых датчиков, ожидаемая погрешность которых должна быть в пределах (1,5…2,0) угловых секунд. Согласно предписаниям приведенного выше способа калибровки погрешность датчика, выбранного в качестве эталонного, должна быть порядка (0,15…0,2) угловой секунды. Преобразователи данного класса точности относятся к дорогим, уникальным приборам. Например, угловой датчик модели RON-905 известной фирмы Dr. Heidenhain (Германия) при погрешности преобразования ±0,4 угловой секунды стоит на рынке порядка 12000€ или 780000 рублей (в ценах 2015 года).
Снижение погрешности измерений до ±0,2 угловой секунды за счет использования дополнительного электронного блока приводит к увеличению стоимости измерительного комплекта (в ценах 2015 года) до 1000000 рублей.
Известно техническое решение процедуры калибровки угловых датчиков (см. Portman V., Peschansky В. Phase-statistical method and device for high precise and high efficiency angular measurements. Precision Engineering, v. 25, 2001, p. 309), которое допускает использование в качестве эталонного датчика прибора, класс точности которого сопоставим с ожидаемым классом точности калибруемого прибора. Благодаря использованию фазостатистического метода обеспечивается требуемая точность калибровки угловых датчиков при заметном снижении экономических затрат.
Суть фазостатистического способа калибровки состоит в том, что берут две шкалы, имеющие по n штрихов, из которых одна является калибруемой, а другая - «эталонной», устанавливают их на общую ось вращения так, чтобы, с одной стороны, иметь возможность вращать их синхронно относительно считывающих головок, а с другой стороны, иметь возможность менять их взаимное расположение. При синхронном вращении шкал регистрируют взаимное расположение каждого штриха одной шкалы относительно штрихов другой шкалы. Здесь эталонная шкала обозначена в кавычках потому, что к ней не предъявляется требование обязательной малости собственной погрешности. Оба датчика могут быть одного класса. Но у калибруемой шкалы необходимо иметь некоторый репер, например метку начала оборота.
Результат измерения взаимного смещения штрихов запоминают в виде файла данных F1:

в котором порядок размещения измеренных смещений штрихов по фазе ΔФi привязан к метке начала оборота калибруемой шкалы. В свою очередь, фазовый сдвиг ΔФi между двумя штрихами может быть представлен в виде трех слагаемых (фиг. 1):

Здесь слагаемое Δφ0 - это постоянный сдвиг штрихов одной шкалы относительно штрихов другой, обусловленный случайным положением шкал при их установке на ось вращения. В дальнейшем эта составляющая, как правило, не берется во внимание, т.к. ее вклад одинаков для всех штрихов, и по этой причине она вносит только общее смещение по фазе. Слагаемые δφ1i и δφ2i - случайные разбросы положений i-x штрихов эталонной и калибруемой шкал относительно их идеального положения соответственно. δφ1 и δφ2 характеризуют качество изготовления каждой из используемых шкал.
После того как файл данных F1 зарегистрирован, одну шкалу разъединяют с осью и поворачивают ее относительно другой шкалы на один штрих, т.е. на угол Δφ, равный:

Затем повторяют цикл измерения смещений штрихов одной шкалы относительно другой. Результат измерения запоминают в виде нового файла данных F2.
После этого шкалу смещают еще раз на угол Δφ и повторяют цикл измерений. Результат измерения запоминают в виде нового файла данных F3. И так далее, пока одна шкала не провернется относительно другой на целый оборот. К этому времени в памяти процессора, регистрирующего результаты измерений, образуется матрица данных размерности [n×n].
После формирования матрицы полученные данные складывают построчно и усредняют на число строк матрицы. В результате указанных манипуляций формируется новый файл данных F.
При этом каждый элемент сформированного файла будет характеризовать отклонение каждого штриха шкалы калибруемого датчика относительно его идеального положения. И, что самое важное, вклад погрешности шкалы эталонного датчика в результатах измерений будет минимизирован.
Чтобы показать это, представим каждый элемент нового файла следующим образом:
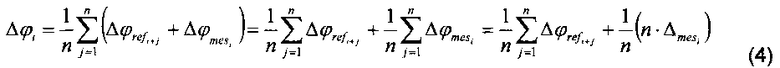
где i=(1…n) - текущий номер штриха шкалы, к началу оборота которой «привязаны» данные, j=(1…m) - текущий номер сдвига по фазе взаимного расположения шкал, Δφref - угловое отклонение положения i-того штриха эталонного растра, Δφmes - угловое отклонение положения i-того штриха калибруемого растра. Первое слагаемое выражения (4) - это усредненное значение вклада в результат определения Δφi, вносимого всеми n штрихами эталонного растра. Второе слагаемое этого выражения - это усредненное значение вклада вносимого i-тым штрихом калибруемого растра за n измерений. Из курса математики известно, что интеграл по замкнутому контуру равен нулю, если в подынтегральной функции отсутствует особая точка. Первое слагаемое в выражении (4) может быть заменено на интеграл по замкнутому контуру, если выполнить предельный переход n→∞. Поэтому чем точнее выполняется условие n→∞, тем точнее первое слагаемое выражения (4) может быть заменено на интеграл по замкнутому контуру и, соответственно, тем точнее первое слагаемое выражения (4) будет равно нулю. Таким образом, фазостатистический метод, в принципе, позволяет точно измерить отклонения в положениях штрихов от их идеального значения.
Однако данное техническое решение имеет существенный недостаток: слишком значительна длительность процедуры калибровки. Например, если калибровке подвергается датчик, у которого число штрихов n=36000, то если даже на набор одного файла данных тратится 1 секунда, то процедура измерений затягивается на 10 часов, что уже само по себе много. На самом же деле на набор одного файла данных уходит существенно больше времени. Поэтому в таком исходном виде фазостатистический метод не нашел широкого применения.
Известно другое техническое решение (см. Клисторин И.Ф., Кирьянов В.П., Кирьянов А.В. Оценка потенциальной точности датчиков угловых перемещений с лимбами, изготовленными по способу кругового сканирования // Датчики и системы, 2006. №1. С. 25-29), взятое в качестве прототипа, по которому фазостатистический способ калибровки используется в варианте, когда число взаимных смещений двух шкал m устанавливается существенно меньшим, чем число штрихов n в используемых шкалах. В этом случае результат калибровки i-того штриха калибруемого растра можно представить следующим образом:
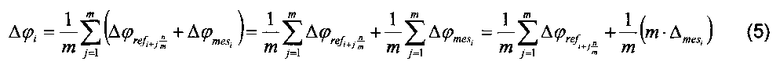
где i=(1…n) - текущий номер штриха шкалы, к началу оборота которой «привязаны» данные, j=(1…m) - текущий номер сдвига по фазе взаимного расположения шкал, 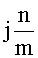
Здесь в правой части выражения (5) второе слагаемое - (Δmes i) представляет собой усредненное значение углового смещения i-ого штриха калибруемой шкалы относительно его истинного положения, а первое слагаемое: 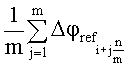
В данном техническом решении для оценки точности процедуры калибровки предложено использовать параметр, называемый классом точности прибора. Имеется в виду прибора, взятого в измерительной схеме в качестве эталонного. Класс точности, как правило, паспортизируется производителем. Кроме того, было предложено количественному показателю класса точности поставить в соответствие доверительный интервал 3σ, в котором с вероятностью 98% лежат все результаты измерений, выполненные с этим прибором. Здесь σ - это среднеквадратичное отклонение результатов измерений. Считая, что итоговый результат (5) формируется путем сложения m случайных значений погрешности положения штрихов шкалы эталонного датчика, было также предложено вклад от сложения m значений погрешности выбранных штрихов шкалы датчика, взятого в качестве эталонного, в результат калибровки оценивать по закону сложения случайных величин в соответствии со следующим выражением:

Например, для широко распространенного углового преобразователя модели ROD-800 в каталогах немецкой фирмы Dr. Heidenhain приводится класс точности, соответствующий ±1,0 угловой секунде. Если эти значения трактовать как границы доверительного интервала, то σ будет лежать в пределах ±0,33 угловой секунды. При m=10 значение δ будет оцениваться на уровне ±0,103 угловой секунды, что хорошо согласуется с требованиями к метрологическим показателям датчика, выбираемого в качестве эталонного в соответствии с классической методикой.
Однако данный набор операций, характеризующий известный способ калибровки, взятый в данной заявке в качестве прототипа, имеет заметный недостаток. Прежде всего утверждение, что используемые m значений погрешности выбранных штрихов шкалы датчика, взятого в качестве эталонного, представляют собой случайные величины, не совсем корректно. Действительно, абсолютные значения каждого из m значений погрешности выбранных штрихов шкалы датчика, взятого в качестве эталонного, можно рассматривать как случайные. Но в ходе процедуры калибровки от одного сличения шкал к другому эти значения остаются неизменными. Поэтому их необходимо рассматривать как систематические составляющие погрешности пространственного положения штрихов шкалы.
В целом систематические составляющие погрешности характеризуются спектральным составом пространственных гармоник. Спектральный состав пространственных гармоник однозначно характеризуют форму кривой погрешности каждой конкретной шкалы, который остается постоянным от эксперимента к эксперименту. При известном спектральном составе инструментальной погрешности шкалы, выбираемой в качестве эталона сравнения, результат калибровки другой шкалы может быть оценен с более высокой точностью.
Недостатком известного технического решения является повышенный уровень неопределенности калибровки углового датчика.
Перед авторами ставилась задача разработать способ калибровки углового датчика, позволяющий на порядок уменьшить неопределенность калибровки углового датчика.
Предложено поставленную задачу решить тем, что в известном способе калибровки углового датчика, включающем использование калибруемого углового датчика и датчика, выбранного в качестве эталона сравнения, установленных на общей оси вращения с возможностью последовательного изменения их взаимного расположения в пределах полного оборота, при этом изменение взаимного расположения шкалы калибруемого углового датчика и шкалы датчика, выбранного в качестве эталона сравнения, осуществляют одинаковыми шагами, равными Δφ=2π/m, где m - целое число, при каждом выбранном расположении шкал измеряют взаимное положение штрихов шкалы калибруемого углового датчика относительно штрихов шкалы датчика, выбранного в качестве эталона сравнения, результаты измерений регистрируют с момента появления метки начала шкалы калибруемого углового датчика, после выполнения m сличений результаты, относящиеся к одному и тому же штриху калибруемого углового датчика, складывают и усредняют на число сличений m, элементы полученного файла данных используют в качестве характеристики пространственного отклонения штрихов калибруемого углового датчика от их идеальных положений, заданных в конструкторской документации, дополнительно в каждом из m выбранных сличений расположений шкал регистрируют пространственное положение метки начала шкалы датчика, выбранного в качестве эталона сравнения, определяют функцию погрешности шкалы датчика, выбранного в качестве эталона сравнения, путем пересчета зарегистрированных данных, при котором зарегистрированные данные смещают на полученное значение позиции метки начала шкалы датчика, выбранного в качестве эталона сравнения, определяют вклад шкалы датчика, выбранного в качестве эталона сравнения, в результат калибровки шкалы калибруемого углового датчика, сформировавшийся за m сличений, и вычитают его из результата калибровки калибруемого углового датчика.
Технический эффект заявляемого способа калибровки углового датчика заключается в уменьшении неопределенности калибровки углового датчика до 1% от калибруемого значения и длительности процедуры калибровки за счет применения малого количества сличений.
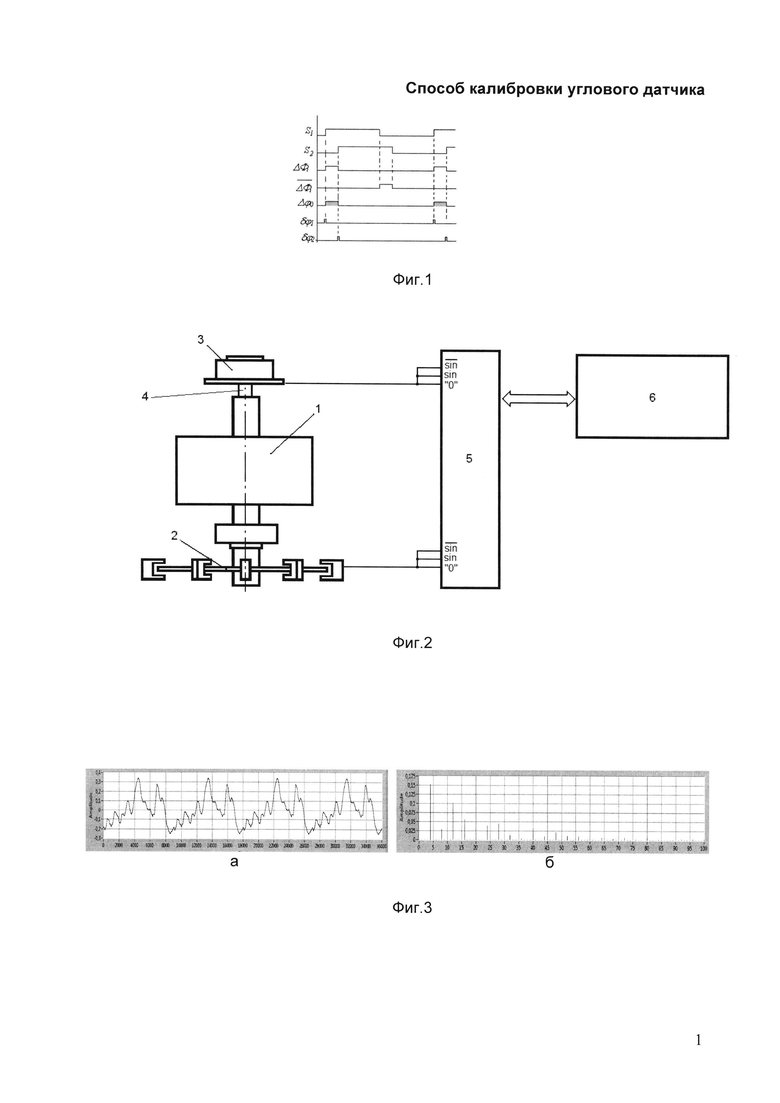
На фиг. 1 представлен фазовый сдвиг ΔФi между двумя штрихами одной шкалы.
На фиг. 2 представлена система калибровки углового датчика, где 1 - прецизионный шпиндель, 2 - калибруемый угловой датчик, 3 - эталонный датчик, 4 - муфта, 5 - электронный блок обработки, 6 - управляющий компьютер.
На фиг. 3 (а) представлена кривая погрешности калибруемого углового датчика с четырьмя считывающими головками; (б) представлен спектральный состав кривой погрешности калибруемого углового датчика.
На фиг. 4 представлена (а) кривая погрешности датчика ROD-800 (вместе с соединительной муфтой), (б) спектр гармоник кривой погрешности датчика ROD-800 вместе с соединительной муфтой.
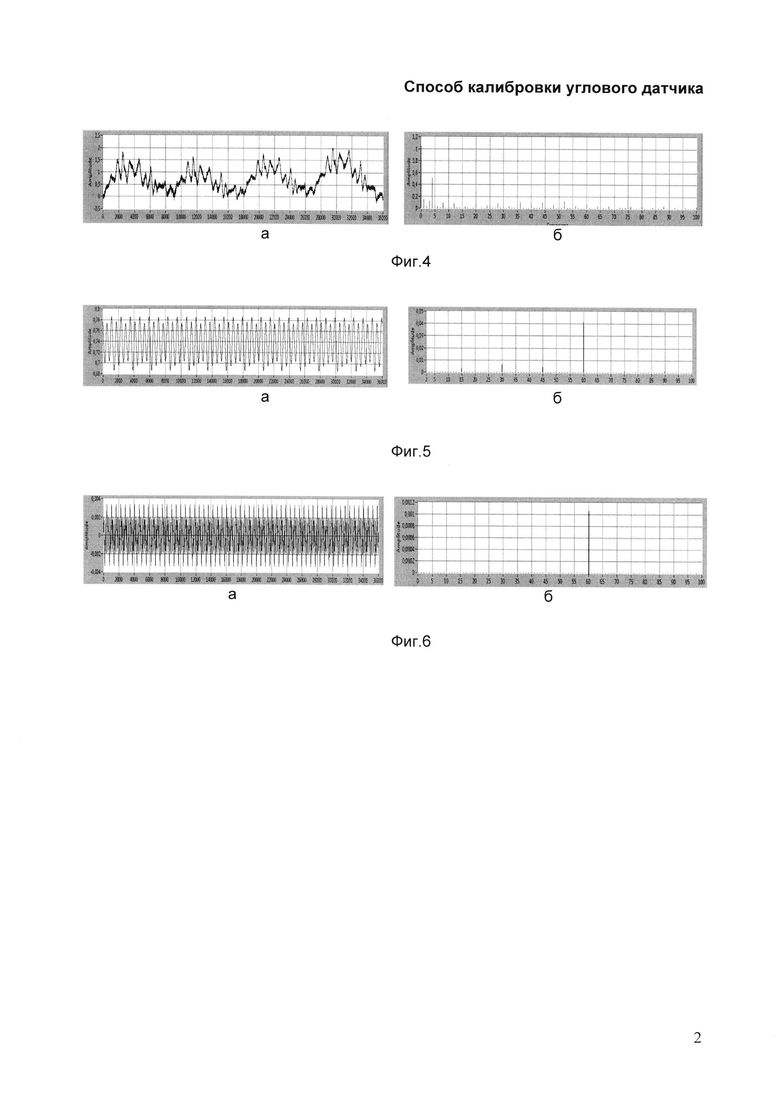
На фиг. 5 представлена (а) кривая поправок в результат калибровки углового датчика, вносимых датчиком ROD-800, (б) спектр гармоник кривой поправок.
На фиг. 6 представлен результат компьютерного моделирования вклада калибруемого углового датчика в результат собственной калибровки: фиг. 6(а) - функция искажений, вносимых со стороны калибруемого углового датчика в кривую поправок, фиг. 6(б) - спектр гармоник функции искажений, вносимых со стороны калибруемого углового датчика в кривую поправок.
Заявляемый способ калибровки углового датчика реализуется следующим образом. Технически предложено одновременно с регистрацией пространственного положения штрихов шкалы датчика, взятого в качестве эталона сравнения, регистрировать также и пространственное положение метки начала шкалы датчика, используемого в качестве эталона сравнения. После обработки матрицы данных по известному ранее алгоритму и получения файла данных, характеризующих отклонение каждого штриха шкалы калибруемого углового датчика относительно их идеального положения, производят переформатирование данных, заключающееся в «перепривязке» измеренных данных к метке начала оборота эталонной шкалы. Если в k-м эксперименте метка начала оборота эталонной шкалы совпала с q-штрихом шкалы калибруемого углового датчика, то, вычтя из каждой координаты зарегистрированных штрихов значение координаты q-ого штриха, получают новую строку данных, значения адресов которых «привязаны» к метке начала оборота эталонной шкалы. Применив данную операцию к каждой строке исходной матрицы, получают новую матрицу данных. В свою очередь, применив к полученной новой матрице известный алгоритм обработки, получают новый файл, каждый элемент которого характеризует отклонение каждого штриха шкалы эталонного датчика относительно их идеального положения, т.е. представляет собой кривую погрешности эталонной шкалы. По аналогии с прототипом каждый элемент нового файла можно представить следующим образом:
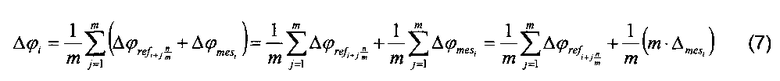
Несложно убедиться в том, что здесь оценка отклонения каждого штриха шкалы датчика, взятого в качестве эталона сравнения, искажена, в свою очередь, вкладом от m штрихов калибруемой шкалы.
Оценку вклада шкалы эталонного датчика в результат калибровки шкалы калибруемого углового датчика выполняют с помощью дополнительной процедуры, имитирующей процедуру фазостатистической калибровки. Для этого массив данных Δφi, полученный после первой дополнительной операции и характеризующий отклонение каждого штриха шкалы эталонного датчика относительно их идеального положения, сдвигают на N/m номеров и складывают с исходным массивом. Затем исходный массив сдвигают на 2N/m номеров и складывают с предыдущим результатом сложения. Затем исходный массив сдвигают на 3N/m номеров и складывают с последним результатом сложения. И так далее. Наконец, исходный массив сдвигают на (m-1)N/m номеров и складывают с предыдущим. Полученный массив усредняют на m и получают новый массив, характеризующий вклад шкалы эталонного датчика в результат калибровки пространственного положения штрихов калибруемого углового датчика.
В целом результат оценки вклада шкалы эталонного датчика представляет собой периодическую функцию, спектральный состав которой содержит только избранные гармоники, номера которых кратны числу сдвигов m. При этом каждое значение вклада эталонной шкалы искажено вкладом со стороны калибруемой шкалы, участвующей в эксперименте. Этот вклад формируется в результате m реальных сдвигов шкал и в соответствии с физикой процесса представляет собой периодическую функцию, спектральный состав которой содержит только избранные гармоники, номера которых также кратны числу сдвигов m. В результате компьютерного моделирования вклада эталонной шкалы вклад калибруемой шкалы в результат собственной калибровки не изменяется в связи с когерентностью фаз периодической функции при ее кратных сдвигах.
Если теперь результат компьютерного моделирования вклада эталонной шкалы вычесть из результатов оценки погрешности пространственного положения штрихов калибруемого углового датчика, то результат калибровки будет свободен от неточности пространственного положения штрихов эталонного датчика. Но точность калибровки шкалы контролируемого калибруемого углового датчика будет все же ограничена вкладом собственных высокочастотных составляющих спектра гармоник, которые «экранируют» процесс их компенсации.
Технический эффект заявляемого способа калибровки углового датчика, состоящий в уменьшении (на порядок) неопределенности калибровки углового датчика, оценим на следующем примере. Пусть поставлена задача калибровки углового датчика встроенного типа, используемого в углоизмерительной машине, создаваемой на основе аэростатического шпинделя. В упрощенном виде система калибровки углового датчика представлена на фиг. 2. В нее входят: прецизионный шпиндель 1 на аэростатическом подвесе, калибруемый угловой датчик 2, имеющий несколько считывающих головок, эталонный датчик 3, муфта 4, электронный блок обработки 5 и управляющий компьютер 6.
Для однозначности оценок примем, что калибруемый угловой датчик 2 выполнен по схеме фотоэлектрического преобразователя встраиваемого типа на базе регулярного растра с 36000 штрихами и имеет четыре считывающие головки, а в качестве эталонного датчика 3 использован коммерчески доступный угловой преобразователь модели ROD-800, соединяемый с ротором шпинделя 1 через соединительную муфту 4 модели ЛИР-805. При этом при размыкании муфты 4 проскальзывание осуществляется со стороны соединения муфты 4 и ротора, т.е. муфта 4 и угловой преобразователь модели ROD-800 выступают как единое целое (т.е. представляют собой практически аналог более дорогого преобразователя RON-905, имеющего встроенную муфту).
Пусть в результате применения фазостатистического метода, выполненного с шагом сдвига, равным двадцати четырем градусам (15 сдвигов), была получена калибровочная кривая для калибруемого углового датчика 2 с четырьмя считывающими головками, представленная на фиг. 3а. Спектральный состав пространственных гармоник калибровочной кривой представлен на фиг. 3б. Накопленная погрешность калибруемого углового датчика 2 составляет значение ±0,3 угловой секунды. Спектр представлен гармониками с номерами, кратными четырем: 4-я, 8-я, 12-я и т.д., что полностью согласуется с теорией путевого усреднения в угловых датчиках (см., например, Ионак В.Ф. Приборы кинематического контроля. - М.: Машиностроение, 1981. 128 с.).
Неопределенность калибровки, вносимая датчиком ROD-800, согласно (6) при 15 сдвигах по абсолютной величине составит: ±0,085 угловой секунды (σ=±0,33 угловой секунды, 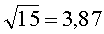
Неопределенность результатов калибровки может быть уменьшена за счет использования предлагаемого способа калибровки углового датчика. Для этого предусмотрим в каждом сдвиге шкал регистрацию координаты нулевой метки шкалы, взятой в качестве эталона сравнения, и применим дополнительные операции, изложенные в данной заявке выше.
После перепривязки данных построчное сложение последних позволяет получить кривую погрешности датчика ROD-800 (вместе с соединительной муфтой) (фиг. 4а).
Как следует из оценки пиковых значений полученной кривой, накопленная погрешность эталонного датчика лежит в пределах ±1,0 угловой секунды (что хорошо согласуется с классом точности данного прибора, гарантируемого производителем). Спектр кривой погрешности содержит, кроме прогнозируемых гармоник, кратных 4-м, также «запрещенные» теорией: 1-ю, 2-ю, 3-ю, 5-ю и т.д. гармоники. Наиболее вероятно, что «запрещенные» гармоники вносятся соединительной муфтой 4. При этом «разрешенные» теорией 4-я, 8-я и т.д. гармоники, относящиеся непосредственно к калибруемому угловому датчику, представлены наиболее значимо (фиг. 4б).
Следующей операцией предлагаемого способа является определение с помощью компьютерного моделирования вклада эталонного датчика в результат калибровки. Для этого, как было описано выше, массив данных, характеризующий отклонение каждого штриха шкалы эталонного датчика относительно их идеального положения, сдвигается на 2400 номеров и складывается с исходным массивом. Затем исходный массив сдвигается на 4800 номеров и складывается с результатом предыдущего сложения. Затем исходный массив сдвигается на 7200 номеров и складывается с предыдущим результатом. И так далее. Наконец, исходный массив сдвигается на 33600 номеров и складывается с предыдущим. Полученный массив усредняют на 15 и получают новый массив, характеризующий вклад шкалы эталонного датчика в результат калибровки пространственного положения штрихов калибруемого углового датчика. Кривая поправок в результат калибровки углового датчика представлена на фиг. 5(а), спектр гармоник кривой поправок представлен на фиг. 5(б).
Как следует из результатов модельного эксперимента, вклад эталонного датчика в погрешность калибровки по абсолютной величине достигает значения ±0,047 угловой секунды, который создается в основном 60-й гармоникой, но заметно также присутствие 15-й, 30-й и 45-й гармоник. В относительных единицах неопределенность калибровки, вносимая эталонным датчиком, вычисленная на основе анализа спектра кривой погрешности эталонного датчика, составляет 15,6%. Полученная оценка показывает, что сам по себе фазостатистический метод при ограниченном числе сдвигов обеспечивает более высокое качество калибровки, чем это считалось ранее.
Более того, знание конкретного вклада эталонного датчика в неопределенность калибровки углового датчика позволяет повысить точность метода.
Для этого выполняют третью дополнительную операцию предлагаемого способа: вычитание вклада эталонного датчика из калибровочной кривой. Это позволяет полностью устранить дестабилизирующий вклад эталонного датчика.
Но в оценках вклада эталонного датчика имеется вклад со стороны высокочастотной части спектра гармоник кривой погрешности калибруемого углового датчика, который ограничивает результативность компенсации погрешности калибровки углового датчика. Остаточная неопределенность калибровки углового датчика создается из-за того, что при вычитании эти высокочастотные составляющие маскируют соответствующие пространственные гармоники собственного измерительного растра.
Для оценки предельно достигаемой неопределенности калибровки углового датчика углоизмерительной машины выполним компьютерное моделирование вклада со стороны измерительного растра калибруемого углового датчика в собственную калибровку. Для этого указанную выше процедуру 15-кратного сдвига кривой погрешности повторим для калибруемого углового датчика. Результат компьютерного моделирования представлен на фиг. 6. Здесь на фиг. 6а представлена функция искажений, вносимых со стороны калибруемого углового датчика в кривую поправок, на фиг. 6б - спектр гармоник кривой функции искажений. Для использованных 15 сдвигов происходит подавление всех гармоник, вплоть до 60-й. Она и определяет вклад со стороны измерительного растра калибруемого углового датчика в погрешность собственной калибровки. Этот вклад от данного измерительного растра не превысит ±0,003". Поэтому относительная величина неопределенности калибровки углового датчика после вычитания вклада эталонного датчика составит 1% от калибруемого значения, что можно рассматривать как метрологически надежный результат калибровки углового датчика.
| название | год | авторы | номер документа |
|---|---|---|---|
| Эталон единицы плоского угла | 2016 |
|
RU2637727C1 |
| Способ угловых измерений | 2021 |
|
RU2782353C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТОЧНОСТИ ИЗГОТОВЛЕНИЯ УГЛОИЗМЕРИТЕЛЬНЫХ СТРУКТУР, НАНОСИМЫХ НА ПРОЗРАЧНЫЙ НОСИТЕЛЬ | 2003 |
|
RU2242715C1 |
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ ИЗМЕРЕНИЯ УГЛА ПОВОРОТА | 2010 |
|
RU2433413C1 |
| СПОСОБ КАЛИБРОВКИ ГРУППЫ СРЕДСТВ ИЗМЕРЕНИЙ ПЛОСКОГО УГЛА С СУММАРНЫМ ДИАПАЗОНОМ ШКАЛ НЕ МЕНЕЕ 360° | 2007 |
|
RU2377499C2 |
| СПОСОБ РЕГИСТРАЦИИ ФАЗЫ КВАДРАТУРНЫХ СИГНАЛОВ | 2018 |
|
RU2692965C1 |
| Способ построения углового преобразователя абсолютного типа | 2016 |
|
RU2634329C1 |
| УСТРОЙСТВО С КОМПЛЕКСИРОВАННЫМИ НОСИТЕЛЯМИ РАВНОМЕРНЫХ УГЛОВЫХ ШКАЛ РАЗНОЙ ДИСКРЕТНОСТИ ДЛЯ КАЛИБРОВКИ УГЛОЗАДАЮЩИХ И УГЛОМЕРНЫХ ПРИБОРОВ | 2012 |
|
RU2489682C1 |
| Способ повышения точности синтеза топологии элементов | 2017 |
|
RU2675077C1 |
| Способ изготовления эталона для проверки преобразователей угла поворота | 1973 |
|
SU578649A1 |
Изобретение относится к области измерительной техники для измерения угла поворота и угловой скорости и может найти применение в метрологии, измерительных системах и системах управления различными объектами. Техническим результатом изобретения является уменьшение неопределенности калибровки углового датчика до 1% и длительности процедуры калибровки. Способ калибровки углового датчика включает использование калибруемого углового датчика и датчика, выбранного в качестве эталона сравнения, установленных на общей оси вращения. При этом изменение взаимного расположения шкалы калибруемого углового датчика и шкалы датчика, выбранного в качестве эталона сравнения, осуществляют одинаковыми шагами, равными Δφ=2 π/m, где m - целое число, при каждом выбранном расположении шкал измеряют взаимное положение штрихов шкалы калибруемого углового датчика относительно штрихов шкалы датчика, выбранного в качестве эталона сравнения. Результаты измерений регистрируют с момента появления метки начала шкалы калибруемого углового датчика, после выполнения m сличений результаты, относящиеся к одному и тому же штриху калибруемого углового датчика, складывают и усредняют на число сличений m. В каждом из m выбранных сличений расположений шкал дополнительно регистрируют пространственное положение метки начала шкалы датчика, выбранного в качестве эталона сравнения, определяют функцию погрешности шкалы датчика, выбранного в качестве эталона сравнения, при котором зарегистрированные данные смещают на полученное значение позиции метки начала шкалы датчика, выбранного в качестве эталона сравнения, определяют вклад шкалы датчика, выбранного в качестве эталона сравнения, в результат калибровки шкалы калибруемого углового датчика, сформировавшийся за m сличений, и вычитают его из результата калибровки калибруемого углового датчика. 6 ил.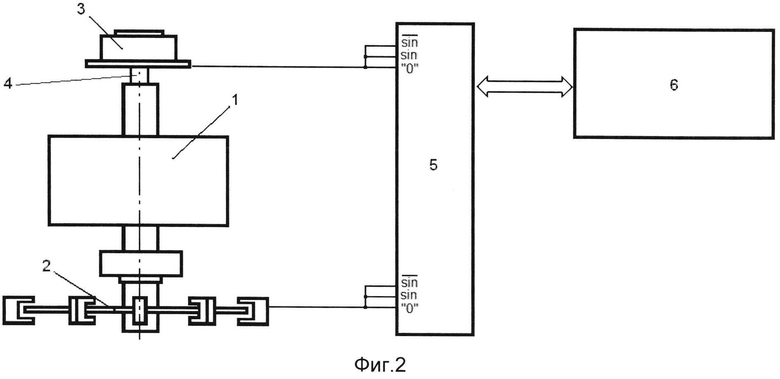
Способ калибровки углового датчика, включающий использование калибруемого углового датчика и датчика, выбранного в качестве эталона сравнения, установленных на общей оси вращения с возможностью последовательного изменения их взаимного расположения в пределах полного оборота, при этом изменение взаимного расположения шкалы калибруемого углового датчика и шкалы датчика, выбранного в качестве эталона сравнения, осуществляют одинаковыми шагами, равными Δφ=2 π/m, где m - целое число, при каждом выбранном расположении шкал измеряют взаимное положение штрихов шкалы калибруемого углового датчика относительно штрихов шкалы датчика, выбранного в качестве эталона сравнения, результаты измерений регистрируют с момента появления метки начала шкалы калибруемого углового датчика, после выполнения m сличений результаты, относящиеся к одному и тому же штриху калибруемого углового датчика, складывают и усредняют на число сличений m, элементы полученного файла данных используют в качестве характеристики пространственного отклонения штрихов калибруемого углового датчика от их идеальных положений, заданных в конструкторской документации, отличающийся тем, что в каждом из m выбранных сличений расположений шкал дополнительно регистрируют пространственное положение метки начала шкалы датчика, выбранного в качестве эталона сравнения, определяют функцию погрешности шкалы датчика, выбранного в качестве эталона сравнения, путем пересчета зарегистрированных данных, при котором зарегистрированные данные смещают на полученное значение позиции метки начала шкалы датчика, выбранного в качестве эталона сравнения, определяют вклад шкалы датчика, выбранного в качестве эталона сравнения, в результат калибровки шкалы калибруемого углового датчика, сформировавшийся за m сличений, и вычитают его из результата калибровки калибруемого углового датчика.
| Клисторин И.Ф., Кирьянов В.П., Кирьянов А.В | |||
| "Оценка потенциальной точности датчиков угловых перемещений с лимбами, изготовленными по способу кругового сканирования" // Датчики и системы, 2006 | |||
| RU 94024867 A1, 10.05.1996 | |||
| АВТОМАТИЗИРОВАННАЯ УСТАНОВКА ДЛЯ КАЛИБРОВКИ ИНКЛИНОМЕТРОВ | 2002 |
|
RU2249689C2 |
| Преобразователь время-код | 1985 |
|
SU1310770A1 |
Авторы
Даты
2016-07-27—Публикация
2015-05-26—Подача