Изобретение относится к вычислительной технике и может использоваться для быстрого выполнения математических вычислений, встречающихся при реализации различных устройств обработки сигналов и, в частности, при аппаратной реализации нейронных сетей типа многослойного персептрона (Multilayer Perceptron, MLP).
На момент подачи заявки применение массива умножителей для аппаратной реализации операции скалярного умножения является сложным и дорогостоящим решением, поскольку для аппаратной реализации каждой процедуры умножения, входящих в состав скалярного умножения, требуется применение сложных архитектур, как правило, состоящих из сдвиговых регистров, сумматоров и т.п. Различным способам осуществления операции умножения посвящается большое количество изобретений [US 4622650, РФ №2485574]. Тем не менее на настоящий момент простых решений, сопоставимых по простоте, например, с сумматорами, не существует. Это становится особенно актуально для векторов больших размерностей, когда для быстрого (параллельного) вычисления скалярного умножения требуется применение множества умножителей. В связи с этим, например, разработчики аппаратного обеспечения концентрируют усилия на реализации нейронных сетей типа RBF (Radial Basis Function Network), в которых вычисление скалярного произведения не требуется, а требуются только вычисления разниц векторов [US 5359700]. Однако такое решение не может использоваться для реализации скалярного умножения.
Настоящее изобретение использует возможность провести эквивалентные вычисления меньшей сложности, для получения результата скалярного умножения входного вектора на постоянный векторный множитель и опционального сложения с константой.
Целью изобретения является достижение следующего технического результата: уменьшение сложности аппаратной реализации процедуры вычисления скалярного произведения векторов и опционального сложения, а также возможность применения устройств, осуществляющих операции вычисления квадрата евклидовых расстояний между векторами для реализации скалярного умножения.
Технический результат способа заключается в следующем:
- упрощение схемы устройств, производящих вычисления скалярного произведения входного вектора на вектор параметров и опционального сложения (уменьшение необходимого числа вентилей для реализации);
- возможности использования существующих устройств для аппаратного параллельного вычисления суммы квадратов разниц компонент векторов для аппаратного параллельного вычисления скалярного произведения.
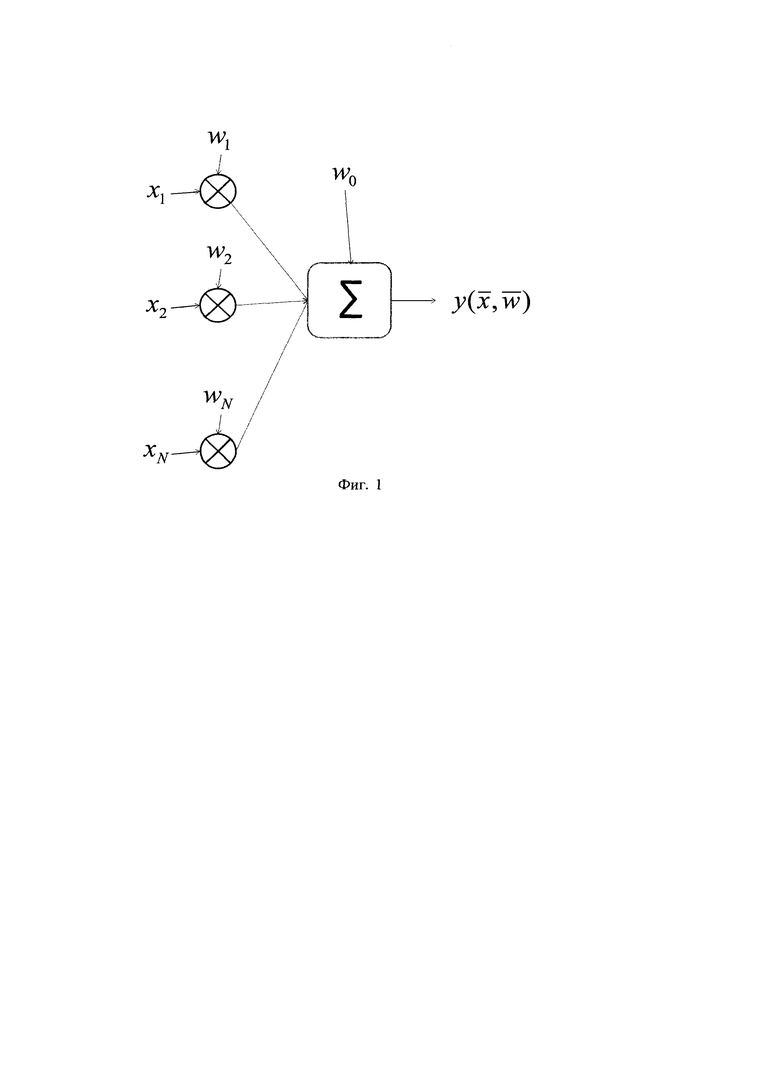
На Фиг. 1 представлен классический способ вычисления скалярного произведения входного вектора 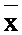
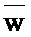
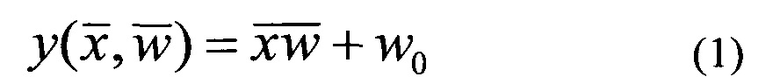
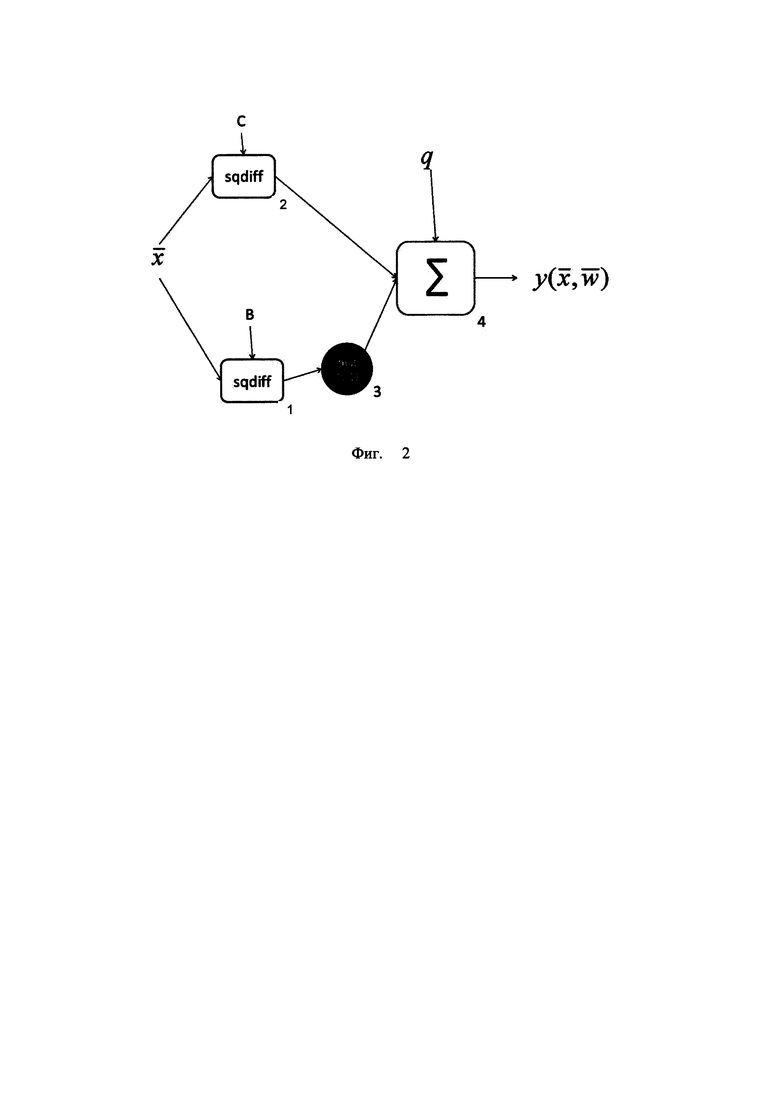
На Фиг. 2 представлен альтернативный способ, являющийся предметом данной заявки. Значения компонент входного вектора одновременно подаются на два одинаковых блока 1 и 2, осуществляющих расчет суммы квадратов разниц компонент входного вектора с компонентами предварительно рассчитанных и загруженных векторов В и С. Затем модуль 3 осуществляет изменение знака результата, полученного в блоке 1. Суммирующий модуль 4 осуществляет сложение цифровых сигналов, полученных из модулей 2 и 3, а также складывает этот результат с предварительно рассчитанным и загруженным в устройство 4 весовым коэффициентом q. Для того чтобы способ, указанный на Фиг. 2, реализовывал вычисления, эквивалентные устройству, указанному на Фиг. 1, то есть выполнял вычисления по формуле 1, но без применения умножителей, необходимо заранее рассчитать значения загружаемых векторных коэффициентов В и С, а также скалярного коэффициента q по следующим формулам:
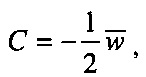

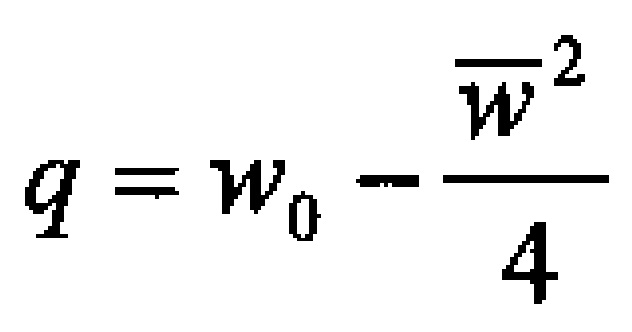
Устройство, предложенное в данной заявке (см. Фиг. 2), фактически реализует вычисления, описываемые следующим выражением:
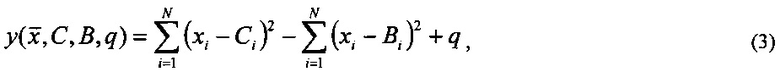
где N - количество компонент входного вектора 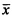 . Для реализации операции возведения в квадрат возможно применение универсальных просмотровых таблиц. Универсальны они в том смысле, что не требуется изменять значения этих таблиц при изменении входного сигнала, весового вектора и смещения. Что касается операции умножения на (-1), то из уровня техники следует, что такая операция фактически сводится только к установке одного знакового бита. Таким образом, предлагаемый способ не требует применения умножителей. Эквивалентность (3) выражению (1) при условии (2) показывается ниже.
. Для реализации операции возведения в квадрат возможно применение универсальных просмотровых таблиц. Универсальны они в том смысле, что не требуется изменять значения этих таблиц при изменении входного сигнала, весового вектора и смещения. Что касается операции умножения на (-1), то из уровня техники следует, что такая операция фактически сводится только к установке одного знакового бита. Таким образом, предлагаемый способ не требует применения умножителей. Эквивалентность (3) выражению (1) при условии (2) показывается ниже.
Если осуществить раскрытие скобок в выражении (3)
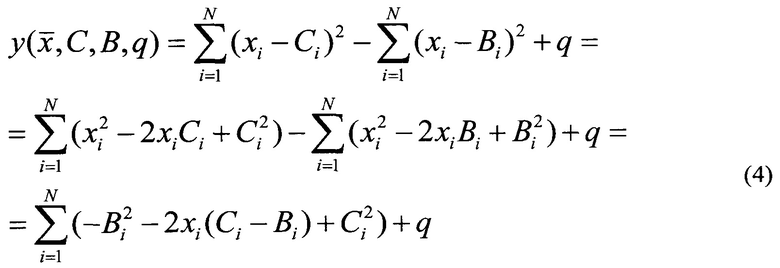
становится видно, что существует множество способов выбора значений векторов В, С и скаляра q, при которых выражение (3) эквивалентно выражению (1). Для этого должны выполняться следующие условия:
C,-5,=-w,/2
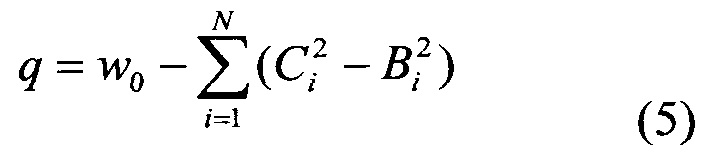
В частности, предложенные в выражении (2) значения предварительно рассчитанных значений векторов В, С и скаляра q удовлетворяют условиям (5).
Можно предложить и другие значения B, C, q, удовлетворяющие (5).
Например: 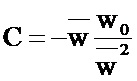
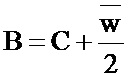
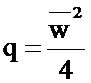
Компьютерное моделирование предложенного способа также показывает эквивалентность вычислений с точностью до ошибок округления. Например, при 10 млн попыток расчетов со случайно (диапазон -1…+1) инициализированными весами и смещениями и случайном входном векторе размерности 10 показывает среднее отклонение в расчетах классического и предлагаемого способа с одинарной точностью (плавающая точка, 32 bit) менее 10-4, а максимальное отклонение менее 10-3. Максимальная ошибка округления возникает в редких случаях при малых значениях модуля вектора весового коэффициента при большом абсолютном значении смещения. Для нейронных сетей, как правило, такие случаи означают, что нейрон работает в насыщении, и его выход слабо зависит от входа, а в этом случае незначительные отклонения не принципиальны, так как в этой точке функции активации имеют практически нулевую производную.
Данное изобретение позволяет применять устройства для параллельного расчета сигнала выхода нейронных сетей типа RBF для аппаратного ускорения расчета нейронных сетей типа MLP, применяющих скалярное умножение. В зависимости от гибкости устройств - либо в текущем состоянии, либо после несложной доработки или пост-процессинга. Например, аппаратно реализованный нейрочип Cognimem CM1K позволяет одновременно рассчитывать до 1024 расстояний между 256-мерными векторами и позволяет таким образом ускорять расчет сетей типа RBF. Предлагаемое изобретение позволяет расширить возможности подобных архитектур для применения их для реализации чрезвычайно популярного класса нейронных сетей типа MLP (использующих скалярное умножение).
| название | год | авторы | номер документа |
|---|---|---|---|
| СКАЛЯРНО-ВЕКТОРНЫЙ ПРОЦЕССОР | 2021 |
|
RU2781355C1 |
| ВЕКТОРНОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2024 |
|
RU2830044C1 |
| МАТРИЧНО-ВЕКТОРНЫЙ УМНОЖИТЕЛЬ С НАБОРОМ РЕГИСТРОВ ДЛЯ ХРАНЕНИЯ ВЕКТОРОВ, СОДЕРЖАЩИМ МНОГОПОРТОВУЮ ПАМЯТЬ | 2019 |
|
RU2795887C2 |
| АНАЛОГОВАЯ АППАРАТНАЯ РЕАЛИЗАЦИЯ НЕЙРОННЫХ СЕТЕЙ | 2020 |
|
RU2796649C2 |
| ОПРЕДЕЛЕНИЕ МЕЖДУ СКАЛЯРНЫМ И ВЕКТОРНЫМ КВАНТОВАНИЕМ В КОЭФФИЦИЕНТАХ АМБИОФОНИИ ВЫСШЕГО ПОРЯДКА | 2015 |
|
RU2656833C1 |
| СПОСОБ РАЗДЕЛЕНИЯ ОПЕРАЦИИ СВЕРТКИ НА УСТРОЙСТВЕ С МАТРИЧНЫМИ УМНОЖИТЕЛЯМИ НА ОСНОВЕ СИСТОЛИЧЕСКИХ МАССИВОВ | 2024 |
|
RU2830039C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОМПИЛЯЦИИ НЕЙРОННЫХ СЕТЕЙ | 2024 |
|
RU2835757C1 |
| Метод построения процессоров для вывода в сверточных нейронных сетях, основанный на потоковых вычислениях | 2020 |
|
RU2732201C1 |
| Устройство для выполнения векторно-скалярных операций над действительными числами | 1990 |
|
SU1718215A1 |
| Устройство для вычисления скалярного произведения двух векторов | 1981 |
|
SU1179369A1 |
Изобретение относится к вычислительной технике и может использоваться для быстрого выполнения математических вычислений в нейронных сетях типа Multilayer Perceptron (MLP). Техническим результатом является уменьшение сложности устройства. Устройство содержит два блока, осуществляющих расчет суммы квадратов разниц компонент входного вектора и предварительно рассчитанных векторов, блок изменения знака результата и блок суммирования. 2 ил.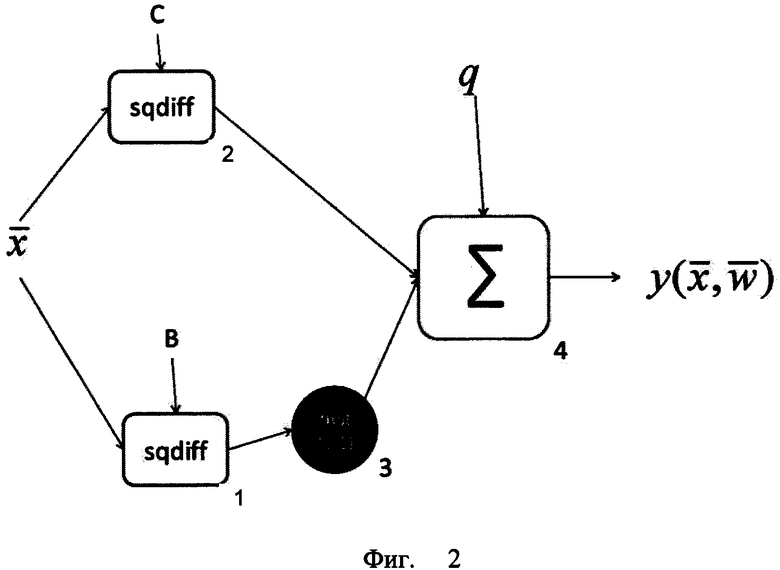
Способ осуществления операции скалярного умножения произвольного вектора 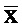
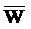
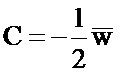
В=0,
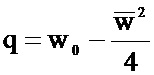
загружают вектор В в блок 1, загружают вектор С в блок 2, загружают весовой коэффициент q в суммирующий модуль 4, значения компонент входного вектора одновременно подают на блоки 1 и 2, в блоке 1 осуществляют расчет суммы квадратов разниц компонент произвольного вектора 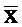
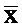
| US 5359700 A, 25.10.1994 | |||
| US 5061866 A, 29.10.1991 | |||
| US 4622650 A, 11.11.1986 | |||
| Скалярный умножитель векторов | 1988 |
|
SU1619254A1 |
| СПОСОБ ОРГАНИЗАЦИИ УМНОЖЕНИЯ ЧИСЕЛ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2012 |
|
RU2485574C1 |
Авторы
Даты
2017-02-02—Публикация
2014-05-28—Подача