Предлагаемый способ управления может быть использован в космической технике при организации облета Луны космическим аппаратом (КА), находящимся, например, в составе околоземной орбитальной станции (ОС). Предполагается, что после проведения облета Луны КА возвращается на исходную околоземную орбиту для последующей стыковки с ОС [1. «Луна. Шаг к технологиям освоения Солнечной системы» под. ред. В.П. Легостаева, М., РКК «Энергия», 2011].
Известен способ управления, выбранный в качестве аналога, в котором выполняется облет Луны с использованием КА «Зонд-7», выводимом на опорную орбиту с помощью ракеты-носителя (РН) «Протон». После выведения на околоземную орбиту КА «Зонд-7» выполняет отлетный импульс для облета Луны по возвратной траектории [2. В.И. Левантовский «Механика космического полета в элементарном изложении», М., Наука, 1980]. Основным недостатком такого способа управления является то, что КА после облета Луны входит в атмосферу Земли с последующим приземлением в заданном районе и, таким образом, использование этого КА многократно невозможно.
Известен способ управления КА для облета Луны, выбранный в качестве прототипа, включающий приложение к КА, находящемуся на исходной околоземной орбите, импульса для перелета к Луне продолжительностью t1, импульса для перехода на селеноцентрическую орбиту, на которой КА выполняет полет продолжительностью t2 и импульса для обратного перелета к Земле продолжительностью t3 [2]. В качестве КА рассматривался космический корабль (КК) «Аполлон-12», выводимый на опорную орбиту с помощью РН «Сатурн-5». После выведения КК выполняет отлетный импульс для перелета к Луне. После перехода на селеноцентрическую орбиту КК и выполнения заданного по программе полета числа витков вокруг Луны КК выполняет отлетный импульс для перелета к Земле с последующим входом в атмосферу и посадкой в заданном районе, что так же, как и в аналоге исключает его многократное использование и является основным недостатком.
Задачей изобретения является выполнение облета Луны с последующим возвращением КА на исходную околоземную орбиту для стыковки с ОС и возможностью многократного использования КА.
Техническим результатом изобретения является возможность отработки КА, предназначенного для многократных перелетов между околоземной ОС и ОС, расположенной на орбите Луны.
Технический результат достигается благодаря тому, что в способе управления КА при облете Луны, включающем приложение к КА, находящемуся на исходной околоземной орбите, импульса для перелета к Луне продолжительностью t1, импульса для перехода на селеноцентрическую орбиту, на которой КА выполняет полет продолжительностью t2 и импульса для обратного перелета к Земле продолжительностью t3, в отличие от известного способа после завершения перелета к Земле КА возвращают в плоскость исходной околоземной орбиты, для чего определяют продолжительность t2 по формуле
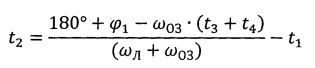 ,
,
где ϕ1 - угол между линией Земля-Луна и плоскостью исходной околоземной орбиты в момент приложения отлетного импульса,
ωОЗ - угловая скорость прецессии плоскости исходной околоземной орбиты,
ωЛ - угловая скорость вращения Луны относительно Земли,
t4 - интервал времени, необходимый для согласования высоты орбиты КА с высотой исходной околоземной орбиты,
и в одном из апексов селеноцентрической орбиты к КА прикладывают импульс для поворота линии узлов на угол Δϕ в направлении, перпендикулярном плоскости орбиты, определенный по формуле
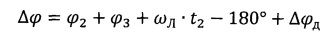 ,
,
где ϕ2 - угол между линией Луна-Земля и плоскостью селеноцентрической орбиты в момент прилета КА к Луне,
ϕ3 - угол между линией Луна-Земля и плоскостью селеноцентрической орбиты в момент приложения импульса для обратного перелета к Земле,
Δϕд - определяемый расчетным путем поправочный угол, парирующий возмущения селеноцентрической орбиты от Земли и Солнца и отличия проекций углов ϕ2 и ϕ3 на плоскость экватора Земли от их истинных значений.
Предлагаемый способ рассмотрим на примере КА, пристыкованного к ОС, находящейся на исходной околоземной орбите. Технический результат в предлагаемом способе управления достигается за счет того, что после отделения от ОС и приложения отлетного импульса КА переводится на траекторию перелета к Луне. По достижении окололунной орбиты выполняется тормозной импульс для перехода КА на селеноцентрическую орбиту. По истечении заданного времени нахождения КА на этой орбите выполняется импульс для обратного перелета к Земле. После перелета к Земле за счет нескольких торможений в атмосфере Земли переходит на так называемые тормозные эллипсы [2], постепенно снижая высоту орбиты вплоть до высоты орбиты ОС. Затем КА вновь пристыковывается к ОС.
Заданное время нахождения на селеноцентрической орбите необходимо для совпадения плоскостей орбит ОС и КА после завершения торможения КА в атмосфере Земли. КА выполняет отлетный импульс с исходной плоскости околоземной орбиты. Вследствие вращения Луны с угловой скоростью ωЛ~13.2°/сутки отлет к Луне в этой системе координат выполняется с некоторым упреждающим углом ϕ1~27° [3. «Основы теории полета космических аппаратов» под ред. Г.С. Нариманова, Машиностроение, Москва, 1972] между линией Земля-Луна и плоскостью исходной орбиты. Вследствие нецентральности гравитационного поля Земли исходная околоземная орбита, на которой находится ОС имеет угловую скорость прецессии плоскости ωОЗ, составляющую около 5° в сутки [3]. Поэтому за время, складывающееся из времени перелета к Луне t1, времени нахождения на селеноцентрической орбите t2, обратного перелета к Земле t3, и времени после обратного перелета до возвращения КА в плоскость орбиты ОС t4, исходная плоскость орбиты ОС за счет прецессии развернется на угол
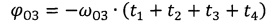
в направлении по часовой стрелке, если смотреть в проекции на плоскость экватора Земли со стороны Северного полюса. Теперь рассмотрим вращательное движение Луны. К началу обратного перелета линия Луна-Земля развернется относительно начального положения плоскости исходной орбиты ОС на угол ϕЛ, рассчитываемый по формуле
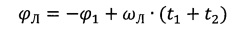
Для совмещения плоскостей орбиты прилета и орбиты ОС необходимо, чтобы линия Луна-Земля на момент отлета, находилась в плоскости исходной околоземной орбиты, т.е. ϕЛ=180°-ϕОЗ.
Решая это уравнение, относительно t2 можно получить допустимое время нахождения КА на селеноцентрической орбите
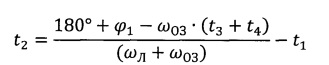
Для оптимального возвращения на Землю с минимальными топливными затратами необходимо, чтобы в момент приложения импульса для отлета угол упреждения между линией Луна-Земля и плоскостью селеноцентрической орбиты составлял ϕ3~60÷70° [3]. Если скорость КА, образованная геометрической добавкой к орбитальной скорости КА на селеноцентрической орбите отлетного импульса и линейной скорости вращения Луны (~1 км/с), не превосходит геоцентрическую параболическую скорость, то КА через некоторое время после выхода из сферы действия Луны поворачивает к Земле и его траектория будет близка к направлению линии Луна-Земля [3].
Предположим, что после перелета к Луне угол между плоскостью селеноцентрической орбиты и линией Луна-Земля составит ϕ2~75° [3], что соответствует переходу на полярную селеноцентрическую орбиту. За время нахождения на селеноцентрической орбите t2, линия Луна-Земля повернется на угол ωЛ⋅t2 и фактический угол между линией Луна-Земля и селеноцентрической орбитой составит: 180°-ϕ2-ωЛ⋅t2, при условии, что плоскости эклиптики и экватора Земли совпадают.
Для оптимального обратного перелета к Земле необходимо повернуть плоскость селеноцентрической орбиты на угол Δϕ, чтобы обеспечить на момент отлета оптимальный угол ϕ3, т.е.
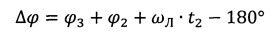
Как известно из курса начертательной геометрии: если стороны угла не параллельны плоскости проекции, то угол проецируется на эту плоскость с искажением. Так как плоскость вращения Луны находится в плоскости, близкой к плоскости эклиптики, составляющей с плоскостью экватора Земли угол ε≈23.5°, то проекция углов будет несколько отличаться от значений плоских углов между линией Луна-Земля и плоскостью селеноцентрической орбиты. Это несоответствие при заданном угле ε составит до нескольких градусов. Также возможно отличие этой формулы вследствие изменения положения плоскости селеноцентрической орбиты (до нескольких градусов) из-за влияния гравитационного поля Земли и Солнца, которое может проявляться на высокоэллиптической селеноцентрической орбите. Все вышесказанное требует введения в формулу для определения угла поворота Δϕ поправочного угла Δϕд, определяемого расчетным путем и достигающим значения до 10°. Таким образом, формула для определения поворота плоскости селеноцентрической орбиты окончательно имеет вид:
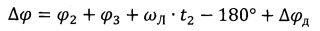
Сущность изобретения поясняется фиг. 1÷6, где
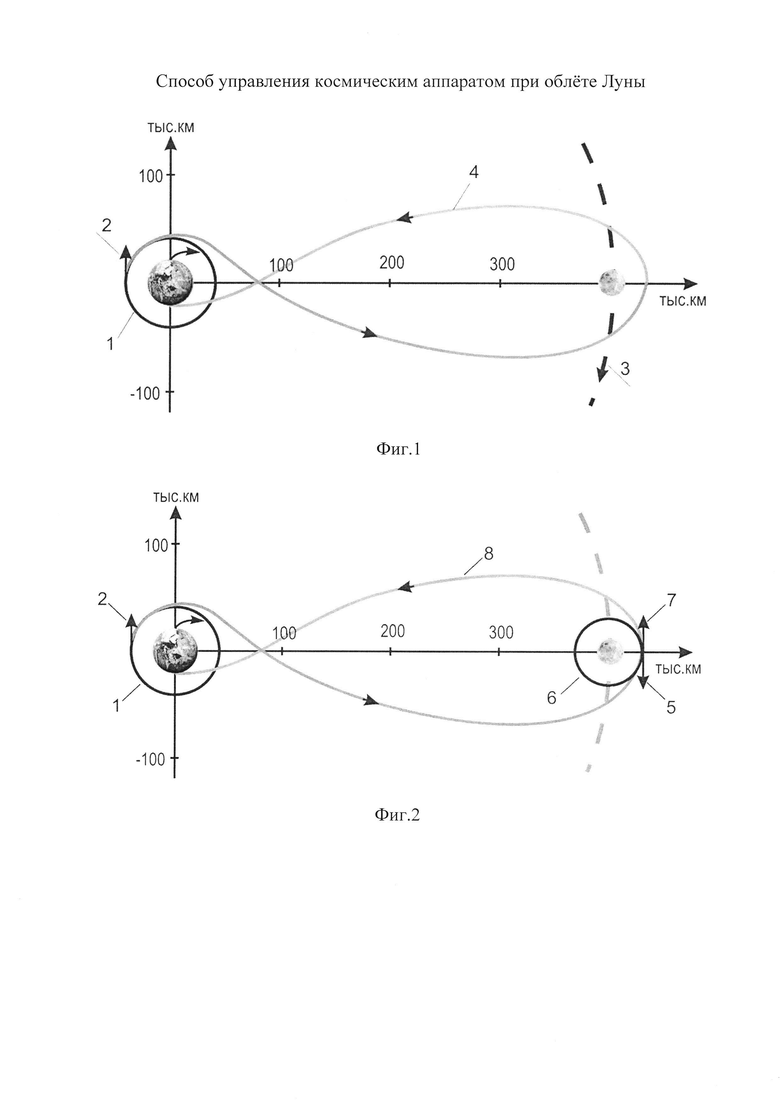
на фиг. 1 показана схема полета аналога - облет Луны с использованием КА «Зонд-7»,
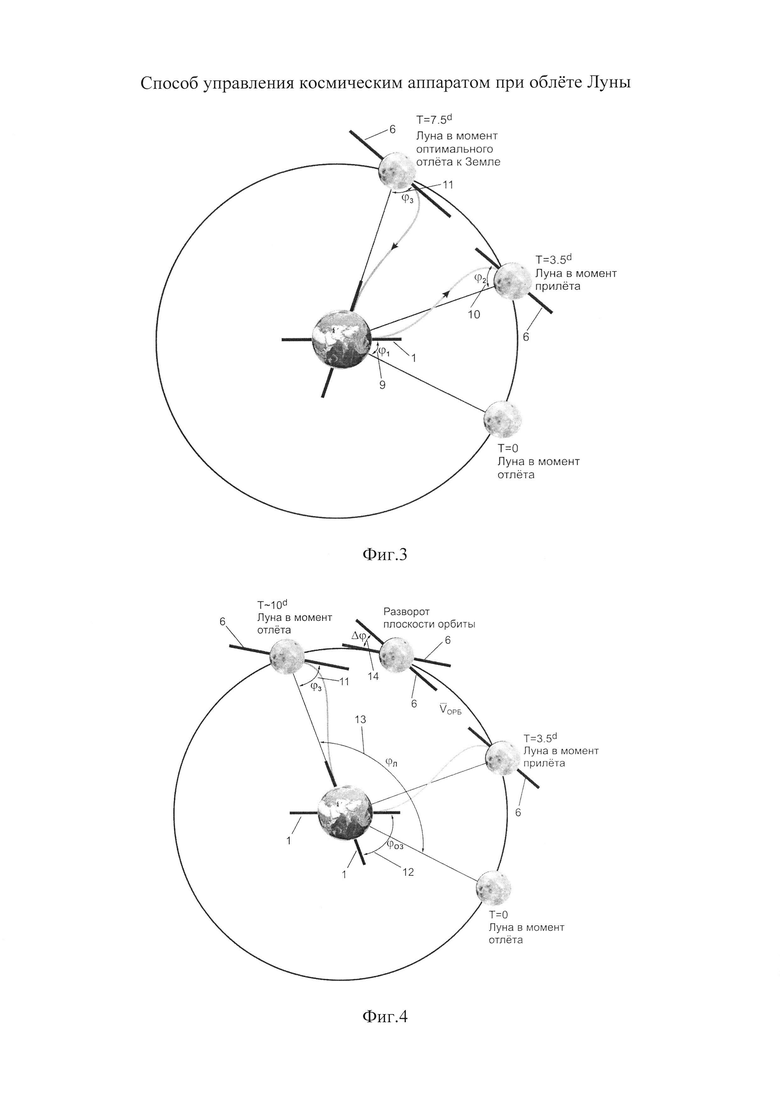
на фиг. 2 приведена схема полета прототипа - перелета на окололунную орбиту по схеме КК «Апполон-12»,
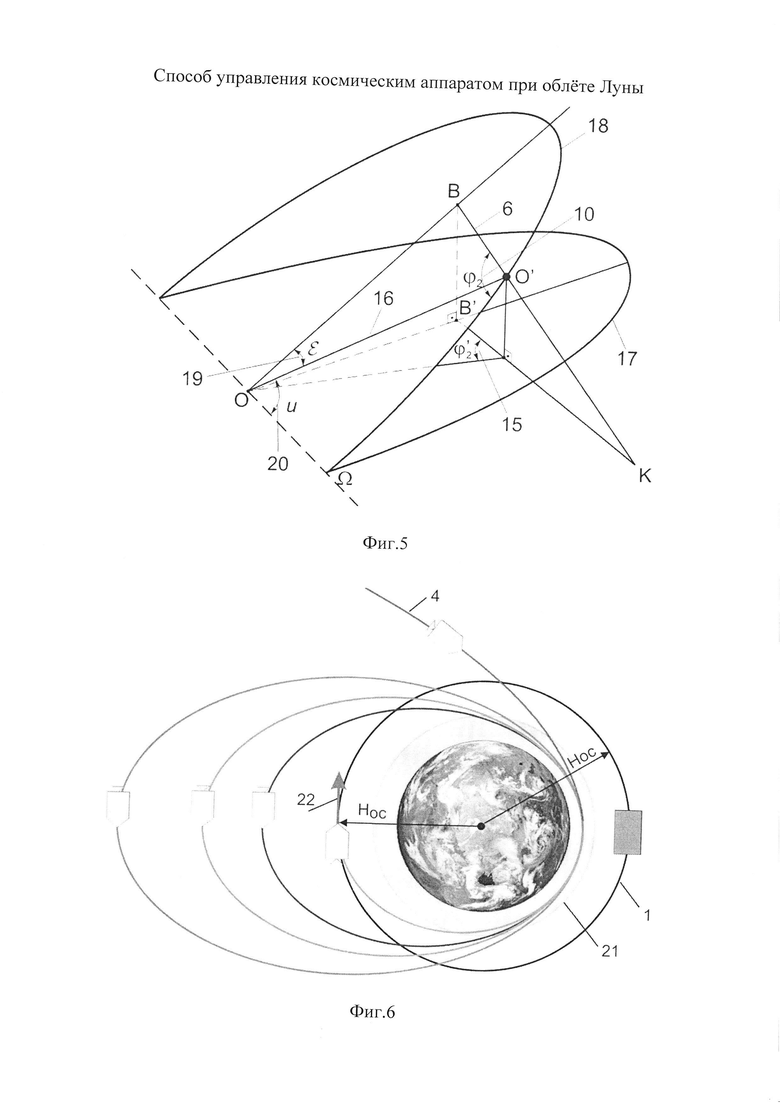
на фиг. 3 представлена схема, поясняющая определение наиболее благоприятных условий для отлета отлет прототипа к Земле,
на фиг. 4 поясняется схема полета КА по предлагаемому способу,
на фиг. 5 приведена проекция угла ϕ2 на плоскость экватора Земли,
на фиг. 6 представлена схема с последовательными прохождениями на заданном расстоянии от Земли и последующим выходом на орбиту ОС.
На фиг. 1-6 отмечены следующие позиции:
1 - исходная околоземная орбита, 2 - отлетный импульс к Луне, 3 - направление движения Луны, 4 - возвратная траектория КА после облета Луны, 5 - тормозной импульс, 6 - селеноцентрическая орбита, 7 - отлетный импульс для перелета к Земле, 8 - траектория перелета к Земле, 9 - упреждающий угол ϕ1, 10 - угол ϕ2, 11 - угол упреждения ϕ3, 12 - угол поворота ϕОЗ, 13 - угол поворота Луны ϕЛ, 14 - угол разворота плоскости Δϕ, 15 - проекция  угла ϕ2, 16 - линия Луна-Земля, 17 - плоскость экватора Земли, 18 - плоскость вращения Луны вокруг Земли, 19 - угол ε наклона эклиптики, 20 - угол u положения Луны, 21 - атмосфера Земли, 22 - импульс перехода КА на орбиту околоземной ОС.
угла ϕ2, 16 - линия Луна-Земля, 17 - плоскость экватора Земли, 18 - плоскость вращения Луны вокруг Земли, 19 - угол ε наклона эклиптики, 20 - угол u положения Луны, 21 - атмосфера Земли, 22 - импульс перехода КА на орбиту околоземной ОС.
На фиг. 1 показана траектория облета Луны с использованием КА «Зонд-7» в системе отсчета, вращающейся вместе с линией Земля-Луна. После выведения КА находится на исходной околоземной орбите (1). В заданной точке орбиты к КА прикладывают отлетный импульс (2), после чего КА облетает Луну со стороны ее движения вокруг Земли (3) и по возвратной траектории прилетает к Земле (4) с последующим приземлением в заданном районе.
На фиг. 2 приведена схема полета прототипа - перелета на окололунную орбиту по схеме КК «Апполон-12» также в системе отсчета вращающейся вместе с линией Земля-Луна. После приложения отлетного импульса (2), КК перелетает в окрестность Луны, где после выдачи тормозного импульса (5) переходит на селеноцентрическую орбиту (6). Через ~ 4 суток, когда появляются условия для оптимального перелета к Земле с минимальными топливными затратами [3], КА выполняет отлетный импульс (7) и возвращается на Землю по траектории прилета (8) с последующей посадкой в заданном районе.
На фиг. 3 в проекции на плоскость экватора Земли представлена схема, поясняющая определение оптимальных условий, позволяющих выполнить отлет прототипа к Земле с минимальным расходом топлива. КА выполняет отлетный импульс с исходной плоскости околоземной орбиты (1), представленной линией пересечения этой плоскости с плоскостью земного экватора. Вследствие вращения Луны с угловой скоростью ωЛ~13.2°/сутки отлет к Луне в этой системе координат выполняется с некоторым упреждающим углом ϕ1 (9). После достижения Луны КА переходит на селеноцентрическую орбиту (6), плоскость которой представлена линией пересечения этой плоскости с лунным экватором и образующей угол ϕ2 (10) с линией Луна-Земля. Для оптимального возвращения на Землю необходимо, чтобы в момент приложения импульса для отлета (7) угол упреждения ϕ3 (11) составлял ~60÷70°.
На фиг. 4 также в проекции на плоскость экватора Земли поясняется схема полета КА по предлагаемому способу. За полное время полета КА, включающее перелет к Луне, нахождение на селеноцентрической орбите (6), обратный перелет КА к Земле и время перехода от тормозных эллипсов на орбиту с высотой орбиты ОС, плоскость исходной орбиты ОС (1) повернется вдоль экватор Земли на угол ϕОЗ (12). Для совпадения плоскостей орбит КА и ОС на момент стыковки КА с ОС необходимо, чтобы к моменту начала обратного отлета угол ϕОЗ (12) соответствовал углу ϕЛ (13), т.е. в момент отлета линия Луна-Земля находилась в плоскости исходной околоземной орбиты (1), которую она займет на момент стыковки КА с ОС. Это условие определяет продолжительность нахождения КА на селеноцентрической орбите. При этом для перелета КА к Земле с минимальными топливными затратами необходимо, чтобы к моменту отлета угол ϕ3 был равен оптимальному ~60÷70°, что требует выполнения разворота плоскости селеноцентрической орбиты (6) на угол Δϕ (14).
На фиг. 5 приведена проекция 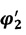 (15) угла ϕ2 (10), образованного линией Луна-Земля (16), обозначаемой ОО', и плоскостью селеноцентрической орбиты (6), обозначаемая линией О'В, на плоскость экватора Земли (17), представленной треугольником КВВ'. Плоскость вращения Луны вокруг Земли (18) близка к плоскости эклиптики и наклонена под углом ε (19) к плоскости экватора Земли. Положение Луны относительно узла Ω определяется углом u (20).
(15) угла ϕ2 (10), образованного линией Луна-Земля (16), обозначаемой ОО', и плоскостью селеноцентрической орбиты (6), обозначаемая линией О'В, на плоскость экватора Земли (17), представленной треугольником КВВ'. Плоскость вращения Луны вокруг Земли (18) близка к плоскости эклиптики и наклонена под углом ε (19) к плоскости экватора Земли. Положение Луны относительно узла Ω определяется углом u (20).
На фиг. 6 представлена схема перехода КА с возвратной траектории (4) за счет последовательных прохождений в атмосфере Земли (21) на исходную орбиту околоземной ОС (1). КА входит в атмосферу Земли со 2-й космической скоростью. После первого торможения КА в атмосфере он переходит на эллиптическую орбиту. Последовательные прохождения атмосферы проводятся до тех пор, пока очередной апогей орбиты не достигнет высоты орбиты орбитальной станции НОС. После чего в апогее орбиты выполняется импульс (22) для окончательного перевода КА на орбиту околоземной ОС с последующей с ней стыковкой.
Рассмотрим пример. Пусть V1 - отлетный импульс для перелета к Луне (~3200 м/с), а длительности перелета к Луне t1 и обратно к Земле t3 составляют по 3.5 суток. Примем также, что продолжительность нахождения КА на переходных тормозных эллипсах для согласования высоты орбиты прилета и высоты орбиты ОС t4 - 1.5 суток. Определим по представленной формуле необходимую длительность нахождения на селеноцентрической орбите t2:
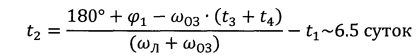
Импульс перехода на селеноцентрическую орбиту V2 зависит от параметров этой орбиты. Для экономии топлива желательно перейти на орбиту с как можно более высоким апоселением. Кроме того, поворот плоскости на высокоэллиптической орбите потребует также меньших затрат. Наиболее оптимальным был бы переход на высокоэллиптическую орбиту с периодом, близким к t2. Эта орбита имеет апоселений около 120 тыс.км, но при этом она очень неустойчива и положение ее плоскости подвержено сильному влиянию со стороны гравитационных полей Земли и Солнца. Рассмотрим переход на орбиту с периодом, близким по значению к половине t2, и с апоселением около 55 тыс.км. В этом случае V2~220 м/с.
Определим по формуле значение необходимого поворота Δϕ селеноцентрической орбиты:
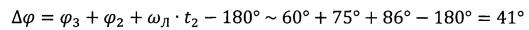
Численный расчет дает значение около 52°, что соответствует необходимости увеличения Δϕ на величину поправочного угла Δϕд~11°. Таким образом, окончательная формула для определения угла поворота плоскости селеноцентрической орбиты имеет вид:
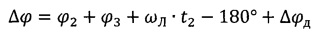
Необходимость введения поправочного угла Δϕд возникает вследствие изменения положения плоскости селеноцентрической орбиты из-за влияния Земли и Солнца. Это возмущение тем сильнее, чем более вытянута орбита [2]. Также в угле Δϕд учитывается отличие в значениях углов ϕ3 и ϕ2 от их проекций на плоскость экватора Земли. На фиг. 5 представлена проекция угла 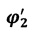 , отличающаяся по величине от угла ϕ2, и в качестве примера представлена формула, по которой она определяется, справедливая на интервале ϕ2>u:
, отличающаяся по величине от угла ϕ2, и в качестве примера представлена формула, по которой она определяется, справедливая на интервале ϕ2>u:
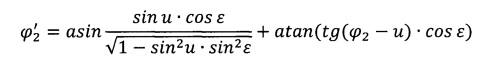
Наиболее оптимальная точка приложения импульса для поворота плоскости в одном из апексов селеноцентрической орбиты относительно экватора Луны. Численный пример показывает, что для орбиты с апоселением около 55 тыс.км поворот плоскости орбиты на угол Δϕ=52° потребует импульса V3~255 м/с.
И, наконец, импульс отлета к Земле с этой высокоэллиптической орбиты составит V4~575 м/с.
Таким образом, за вычетом отлетного импульса V1 необходимый суммарный импульс для выполнения облета составит:
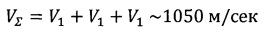
В случае если селеноцентрическая орбита будет круговой с высотой орбиты около 100 км, то потребуется суммарная скорость VΣ~2750 м/с.
Общая продолжительность облета составит:
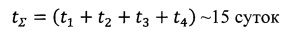
В целом можно сделать вывод, что предлагаемый способ управления позволит выполнить облет Луны и вернуться на исходную околоземную орбиту с затратами топлива чуть больше 1 км/с.
Изобретение относится к межорбитальным перелётам в системе Земля-Луна. Способ включает отстыковку КА от околоземной орбитальной космической станции (ОКС) и перевод на траекторию перелёта к Луне. Затем КА выводят на селеноцентрическую орбиту. По пребывании там заданное время КА переводят на траекторию перелета к Земле в плоскости, совпадающей с плоскостью исходной околоземной орбиты ОКС в заданный момент стыковки. Для этого на селеноцентрической орбите выполняют поворот плоскости орбиты КА на заданный угол. Далее, путём нескольких торможений в атмосфере Земли КА снижается до высоты орбиты ОКС. Затем КА вновь стыкуется с ОКС. Техническим результатом изобретения является возможность многократных перелетов, например, между околоземной и окололунной ОКС при относительно небольших затратах характеристической скорости (немного более 1 км/с) и за время около 15 сут. 6 ил.
Способ управления космическим аппаратом при облете Луны, включающий приложение к космическому аппарату, находящемуся на исходной околоземной орбите, импульса для перелета к Луне продолжительностью t1, импульса для перехода на селеноцентрическую орбиту, на которой космический аппарат выполняет полет продолжительностью t2, и импульса для обратного перелета к Земле продолжительностью t3, отличающийся тем, что после завершения перелета к Земле космический аппарат возвращают в плоскость исходной околоземной орбиты, для чего определяют продолжительность t2 по формуле
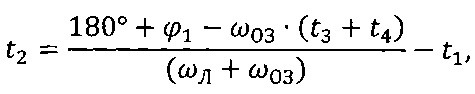
где ϕ1 - угол между линией Земля-Луна и плоскостью исходной околоземной орбиты в момент приложения отлетного импульса,
ωОЗ - угловая скорость прецессии плоскости исходной околоземной орбиты,
ωЛ - угловая скорость вращения Луны относительно Земли,
t4 - интервал времени, необходимый для согласования высоты орбиты космического аппарата с высотой исходной околоземной орбиты,
и в одном из апексов селеноцентрической орбиты к космическому аппарату прикладывают импульс для поворота линии узлов на угол Δϕ в направлении, перпендикулярном плоскости орбиты, определенный по формуле
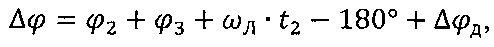
где ϕ2 - угол между линией Луна-Земля и плоскостью селеноцентрической орбиты в момент прилета космического аппарата к Луне,
ϕ3 - угол между линией Луна-Земля и плоскостью селеноцентрической орбиты в момент приложения импульса для обратного перелета к Земле,
Δϕд - определяемый расчетным путем поправочный угол, парирующий возмущения селеноцентрической орбиты от Земли и Солнца и отличия проекций углов ϕ2 и ϕ3 на плоскость экватора Земли от их истинных значений.
| В.И | |||
| Левантовский | |||
| Механика космического полета в элементарном изложении | |||
| М., Наука, 1970, c.219-223 | |||
| СПОСОБ ВЫВЕДЕНИЯ СПУТНИКА НА ГЕОСТАЦИОНАРНУЮ ОРБИТУ | 1999 |
|
RU2164880C1 |
| СПОСОБ ВЫВЕДЕНИЯ НЕСКОЛЬКИХ СПУТНИКОВ НА НЕКОМПЛАНАРНЫЕ ОРБИТЫ С ИСПОЛЬЗОВАНИЕМ СИЛЫ ЛУННОГО ПРИТЯЖЕНИЯ | 1997 |
|
RU2219109C2 |
| Приспособление для перекатки колесных пар по железнодорожному пути | 1918 |
|
SU2665A1 |
| WO 2000013971 A2, 16.03.2000. | |||
Авторы
Даты
2017-03-28—Публикация
2015-09-15—Подача